Abstract
The present study aimed to investigate the presence of asymmetric stochastic volatility and leverage effects within the Nasdaq-100 index. This index is widely regarded as an important indicator for investors. We focused on the nine leading stocks within the index, which are highly popular and hold significant weight in the investment world. These stocks are Netflix, PayPal, Google, Intel, Microsoft, Amazon, Tesla, Apple, and Meta. The study covered the period between 3 January 2017 and 30 January 2023, and we employed the EViews and WinBUGS applications to conduct the analysis. We began by calculating the logarithmic difference to obtain the return series. We then performed a sample test with 100,000 iterations, excluding the first 10,000 samples to eliminate the initial bias of the coefficients. This left us with 90,000 samples for analysis. Using the results of the asymmetric stochastic volatility model, we evaluated both the Nasdaq-100 index as a whole and the volatility persistence, predictability, and correlation levels of individual stocks. This allowed us to evaluate the ability of individual stocks to represent the characteristics of the Nasdaq-100 index. Our findings revealed a dense clustering of volatility, both for the Nasdaq-100 index and the nine individual stocks. We observed that this volatility is continuous but has a predictable impact on variability. Moreover, apart from Intel, all the stocks in the model exhibited both leverage effects and the presence of asymmetric relationships, as did the Nasdaq-100 index. Overall, our results show that the characteristics of stocks in the model are like the volatility characteristic of the Nasdaq-100 index and can represent it.
Keywords:
Nasdaq-100; asymmetrical stochastic volatility; leverage effect; persistence of volatility JEL Classification:
C11; C22; G17
1. Introduction
The integration of markets with each other, while offering positive opportunities for financial depth, has also brought about adverse fluctuations. Crises originating in one nation, financial upheavals, or other market-affecting events have, due to this interconnectedness, reverberated across borders, disrupting the macroeconomic equilibrium of other nations and engendering heightened economic complexity (Beine et al. 2010).
Consequently, nations have increasingly incorporated these considerations into their macroeconomic policy formulations, resulting in the cultivation of more intricate economic structures. This trajectory underscores the imperative to mitigate adverse market effects for participants while maximizing positive returns, particularly since the 1980s, coinciding with the acceleration of global liberalization initiatives.
In contrast to uncertainty, which is defined as a scenario in which the probability distribution is unknown, risk is defined as a situation in which a decision must be made about a known event and this probability distribution is known (Knight et al. 2002). From a financial standpoint, the concept of risk involves the possibility of expected income deviating from the norm. Risks are categorized as systematic and unsystematic. Systematic risks encompass those inherent to the market that cannot be eliminated or substantially mitigated, thus influencing macroeconomic equilibrium, such as market, political, inflation, interest rate, and exchange rate risks. Conversely, unsystematic risks pertain to those within the purview of market participants to minimize in accordance with their risk preferences, exemplified. Financial risk and management risk can be exemplified in this group.
The distribution of risk and return determines investments for financial market participants. There is a link between these two things. Times of higher risk are predicted to bring about an increase in profitability, while times of lower risk are likely to bring about a reduction in profitability. For this reason, it is essential to analyze stock exchanges and estimate profitability based on economic cycles. Although the concept of volatility is perceived as equivalent to risk in meaning, it should not be considered in the same context as risk. Because while the concept of risk presents undesirable, negative results, the concept of volatility presents us with the positive or negative volatility (mobility) of an asset in financial terms (Poon 2005).
Asymmetric volatility, colloquially referred to as volatility asymmetry, delineates situations wherein new information elicits disparate magnitudes of price adjustments, signifying that positive and negative shocks exert unequal impacts on return series volatility (Cappiello et al. 2006). Although often conflated, asymmetric effects and leverage effects hold distinct implications. The leverage effect underscores the varying impact of different shocks on the stock market, positing that asset price declines (increases) elevate (diminish) company leverage levels, thereby amplifying (mitigating) equity shareholders’ risk and consequently enhancing (dampening) stock volatility.
Investment decisions within financial markets are predicated upon the balance of risk and return distributions, which exhibit an interdependent relationship. Heightened risk is often associated with increased profitability during periods of volatility, whereas reduced risk typically corresponds with diminished profitability. Hence, the analysis of stock exchanges and the forecast of profitability economic cycles assume critical importance.
Market integration has resulted in both bad and positive oscillations, whilst offering potential for greater financial depth. Indeed, because of this integration, other countries’ macroeconomic balances have been upset by potential crises in other nations, financial disruptions, or other news that impacts markets, resulting in increasingly complicated economies for those nations. Market globalization brings about harmful oscillations even as it promotes financial depth. The macroeconomic equilibrium of other countries might be upset by crises or financial upheavals in one country, leading to increasingly complex economies. Since the beginning of global liberalization in the 1980s, macroeconomic policies have taken these factors into account more and more to minimize negative effects and maximize returns for market participants. This highlights the growing importance of volatility in both theoretical and practical contexts.
Although the concept of volatility is perceived at an equivalent level to risk in terms of meaning, it should not be considered within the same framework as risk. This is because the concept of risk presents undesirable, negative outcomes, whereas the concept of volatility provides us with the volatility (fluctuation) of an asset in a positive or negative direction from a financial perspective. The concept of volatility is particularly an indicator aimed at measuring the width of deviation from the average value of a specific series in financial literature.
When different countries engage in mutual competition in certain products, a crisis in one country can deeply affect the macroeconomic structure of another. The contagion effect can manifest itself, for example, when a devaluation in one country makes the products produced by rival countries expensive in terms of trade, thereby triggering a crisis in those countries. The 1998 Russian crisis can be cited as an example of this situation.
A growing body of research, particularly in the last several years, has been dedicated to studying how market and country volatility interact. Financial market players now have the chance to diversify their portfolios more efficiently thanks to this trend. Exchange rates, trade strategies, risk hedging, asset pricing, and the creation of successful regulatory policies all depend on the interaction of volatility in financial markets. Volatility asymmetry, another name for asymmetric volatility, describes a scenario in which various degrees of price fluctuations are triggered by new information. Stated differently, the existence of asymmetric effects suggests that the volatility of returns in a series is not equally affected by positive and negative shocks.
An indicator of the varying degrees of impact these various shocks have on the stock market is the leverage effect. The leverage effect states that when asset values fall or rise, a company’s level of debt rises or falls, which in turn raises or lowers the risk taken by shareholders. Consequently, the stock’s volatility rises or falls.
In the fast-paced realm of global finance, one name stands out as a symbol of innovation, technology, and unparalleled success: NASDAQ. For over five decades, the NASDAQ stock market has been at the forefront of transforming the way the world trades stocks, reshaping the financial landscape, and powering the dreams of countless investors and entrepreneurs. The primary objective of this article is to systematically and comprehensively explain ideas related to the non-stationarity in financial markets, observe different approaches, research methods, and the general findings obtained. It aims to examine the mutual behavior of non-stationarity fluctuations within the framework of a selected sample stock group, specifically the Nasdaq-100 stock market index. Additionally, the article seeks to contribute to the literature by presenting literary insights to resolve discrepancies related to stochastic volatility models and volatility measurement incorporated in a limited amount of foreign and domestic research. Furthermore, the article aims to conduct a mutual assessment by comparing the degree of volatility effects of highly capitalized stocks discussed in terms of the stock group with the highest capitalization within the Nasdaq-100. Founded in 1971, NASDAQ, which stands for the National Association of Securities Dealers Automated Quotations, began as an ambitious experiment. It set out to introduce groundbreaking technology to the traditional stock market, revolutionizing how securities are bought and sold. What emerged was not just a trading platform but a dynamic marketplace that redefined the very essence of financial transactions.
Today, NASDAQ is not merely a stock exchange; it is a global economic force. With its headquarters in the heart of New York City’s financial district, NASDAQ has become synonymous with cutting-edge technology, rapid trading, and some of the world’s most iconic companies. Its journey from a fledgling electronic exchange to a global financial powerhouse is a testament to the power of innovation and adaptability in the world of finance. Figure 1 displays how the Nasdaq-100 index changed more quickly between 2013 and 2023.
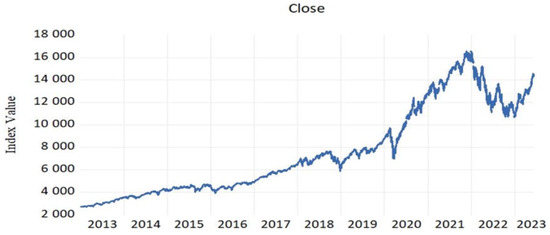
Figure 1.
Index Value of NASDAQ (2013–2023). Source. https://www.nasdaq.com/market-activity/index/comp/historical (accessed on 15 February 2023).
In the ever-shifting landscape of global finance, stock indices stand as the compass guiding investors through the labyrinth of market fluctuations. Among these financial benchmarks, the Nasdaq Composite Index holds a special place, renowned for its technology-focused composition and dynamic performance. As we embark on a journey into the world of investments and market analysis, it is crucial to unravel the significance and implications of the Nasdaq Index Value.
The Nasdaq Composite Index, often abbreviated as the Nasdaq, stands as a symbol of innovation, expansion, and the swift progression of the digital era. As of the latest data available up to September 2021, this index encompasses a diverse spectrum of companies, ranging from established technology behemoths to burgeoning disruptors, all of which exert significant influence on shaping our digital trajectory.
The purpose of this session is to thoroughly examine the fundamentals of the Nasdaq Index Value. We’ll look at its theoretical underpinnings, describe how it is calculated, and discuss why the financial industry holds it in such high respect. Beyond the realm of numbers, we will also talk about the tangible impacts of changes in the Nasdaq Index Value on investors, companies, and the economy as a whole. Regardless of your degree of experience navigating the complexities of the stock market, this article aims to give you invaluable insights into the critical role that the Nasdaq Index Value plays as a barometer of market vitality and a harbinger of future trajectories within innovation-driven economies.
Based on some features, this study distinguishes itself from other research in the literature. One of the most recent accelerated stochastic volatility models among the volatility models, the dynamic structured asymmetric stochastic volatility model of Asai and McAleer (2005), was employed in our investigation. The fundamental properties of asset returns include things like leptokurtic asset return distributions, return clusters, and the leverage effect (Yu and Meyer 2006). We selected the stochastic volatility model as the primary model for the study because it plays a significant role in elucidating certain time series characteristics in finance.
The SV model is preferable in this regard (Pellegrini and Rodrigez 2007). For instance, it performs better than deterministic models when making future projections for a specific time frame and when dealing with extreme kurtosis in financial data. However, it is simpler to ascertain and comprehend the statistical characteristics of stochastic volatility models. Furthermore, it is simpler to generalize stochastic volatility models to multivariate structures. The GARCH model only takes into account one error component, whereas the SV model takes into account two error processes, meaning that the SV model offers a better in-sample fit. The SV model’s predictive power effectiveness suggests that it is a more useful tool for risk management than other models in the GARCH family.
By addressing the pertinent study periods, it is also possible to indirectly examine the likelihood of the Nasdaq-100 index and linked equities to have an asymmetric or symmetrical effect with the interaction of macro influences like the COVID-19 outbreak and the Russia–Ukraine war.
2. Literature Review
Stock market volatility is a key area of interest in financial research due to its influence on pricing, risk management, and investment decisions. In the past decade, significant attention has been given to exploring asymmetric stochastic volatility and the leverage effect in stock returns. These phenomena provide valuable insights into the dynamics and risk characteristics of stock markets. This comprehensive literature review aims to consolidate the current state of knowledge by examining articles published in the last 10 years.
Numerous studies have investigated asymmetric stochastic volatility using advanced econometric techniques. For instance, Sumner et al. (2010) examined the presence of asymmetric volatility in the US stock market and found strong evidence supporting its existence. They employed a GARCH (Generalized Autoregressive Conditional Heteroskedasticity) framework and demonstrated that negative shocks have a more significant impact on volatility than positive shocks. Similarly, Li et al. (2016) explored the Chinese stock market and identified significant asymmetric volatility, indicating that negative shocks lead to larger and more persistent volatility responses compared to positive shocks.
Furthermore, recent research by Brownlees and Engle (2017) focused on investigating asymmetric volatility in international stock markets. They employed a regime switching GARCH model and found evidence of asymmetric volatility across different countries and regions. Their results indicated that negative shocks have a more pronounced impact on volatility, suggesting the presence of asymmetry in stock market dynamics.
The relationship between stock returns and subsequent volatility, known as the leverage effect, has also been the subject of much research in the last 10 years. The asymmetric effects of positive and negative returns on future volatility have been the topic of research. Bollerslev et al. (2013), for example, studied the leverage effect in European stock markets and discovered that positive stock returns are connected to lower volatility in the future, whereas negative returns are linked to increased volatility. They used the GARCH paradigm and offered solid empirical data supporting the leverage effect.
Similarly, Liu et al. (2015) examined the leverage effect in the context of emerging markets. They employed a multivariate GARCH model and confirmed a negative relationship between stock returns and future volatility, indicating the presence of the leverage effect. Their findings suggested that downside risk plays a more significant role in shaping stock market dynamics than upside risk.
Researchers have utilized various econometric methodologies to analyze asymmetric stochastic volatility and the leverage effect in stock returns. Advanced models such as GARCH, EGARCH (Exponential GARCH), and stochastic volatility models have been widely employed.
For instance, Ding et al. (2014) applied a threshold GARCH model to investigate asymmetric volatility in the Chinese stock market. They found strong evidence of asymmetry during different market regimes, suggesting that stock returns have different effects on volatility depending on the market conditions. The threshold GARCH model allowed for a more accurate representation of the nonlinear relationship between returns and volatility.
In another study, Chen et al. (2019) employed a Markov-switching asymmetric power GARCH approach to explore asymmetric volatility in Chinese stock markets. Their findings supported the presence of significant asymmetry in different market conditions. The Markov-switching approach captured the regime-switching dynamics of volatility, allowing for a more comprehensive analysis of asymmetric volatility.
Furthermore, utilizing data from 14 January 2000 to 9 March 2019, Aliyev et al. (2020) analyzed and assessed the volatility of the Nasdaq-100, a non-financial, inventive, and high-tech stock index, employing univariate symmetric and asymmetric GARCH models. According to their findings, the index exhibits an asymmetric leverage effect, meaning that negative shocks have a greater impact on volatility than positive shocks of equivalent size.
Conversely, Alexander et al. (2021) derived analytical formulas for the first four conditional moments of the forward and aggregated returns and variances for a GJR-GARCH (1,1) specification with a generic innovation distribution. Furthermore, for time horizons that become longer, they deduced the bounds of these moments and defined regularity requirements for the moments of aggregated returns to converge to normal moments. They wrote in their research that the Johnson SU and Edgeworth expansion distribution fitting to our closed-form equations for better returns moments is used empirically in empirical studies, employing nearly thirty years of daily equity index, exchange rate, and interest rate data.
Joshi et al. (2022) conducted a similar study to ours, carefully examining the relationship between the Indian stock market index and major world economies between 2005 and 2020. They used a variety of indices that included important economies such as Brazil, the US, Russia, China, Japan, Hong Kong, and South Korea. Their study, which makes use of the T-GARCH model, methodically investigates both symmetric and asymmetric interactions between these indices, emphasizing the significant influence of the Indian stock market on these international indicators. Their results clearly show that there is a volatility transmission from the Indian stock market to the global indexes. This is supported by strong evidence of notable asymmetric effects in conditional volatility, which highlights the widely acknowledged impact of negative news on major financial benchmarks.
Yaya et al. (2022) investigated the asymmetric correlations between oil price shocks and a variety of financial indices, such as the S&P green bond index, which is based on green bonds and alternative energy, and MSCI indices. They evaluated the effects of several oil shocks, including economic activity, petroleum consumption demand, petroleum stock demand, and petroleum supply shocks, on these indices using the GARCH–MIDAS model. Their research revealed an uneven reaction of the volatility of green investments to oil shocks, indicating that the volatility of green investments is affected differently by positive and negative oil shocks.
The empirical evidence from the past 10 years consistently supports the presence of asymmetric stochastic volatility and the leverage effect in stock returns. For instance, studies by Lu and Lai (2012), Guo et al. (2017), and Wu et al. (2019) provide further confirmation of these phenomena across different stock markets and asset classes.
Understanding the presence of asymmetric stochastic volatility and the leverage effect has profound implications for investors, policymakers, and researchers. These phenomena can significantly impact risk management strategies, option pricing, and portfolio allocation decisions. By incorporating these effects into financial models and risk management practices, investors can make more informed decisions and effectively manage their portfolios.
Potential avenues for further research could include analyzing the effects of asymmetric volatility on derivative pricing, analyzing how market sentiment influences asymmetry, and analyzing cross-national differences in the leverage effect. To further our understanding of these processes, more sophisticated econometric models that can capture the nuances of asymmetric volatility and the leverage impact should be developed.
To sum up, this thorough literature analysis offers a thorough understanding of the leverage impact in stock returns as well as the existence of asymmetric stochastic volatility. A review of papers written during the last ten years shows a strong body of empirical data proving these occurrences exist. Through the integration of these impacts into financial models and risk management methodologies, decision-makers and investors can become more knowledgeable. Research projects in the future should carry out further investigation and improvement of our comprehension of these occurrences, advancing investment techniques and financial econometrics.
3. Econometric Method
The development of integration among financial markets has made the volatility structure of assets increasingly important, alongside the optimization of returns. Engle’s (1982) study first introduced the modeling of volatility, marking a fundamental starting point for volatility modeling. Before this study, modeling of the mean of financial asset returns was performed, but with Engle’s work, the variance modeling was also included. Engle’s study noted that the variance changes over time and that the constancy of variance is not always valid due to unexpected shocks. This study became popularly known as Autoregressive Conditional Heteroscedasticity (ARCH) in the literature (Engle 1982).
Subsequently, Bollerslev (1986) proposed the Generalized Autoregressive Conditional Heteroscedasticity (GARCH) model by extending the ARCH model, thus contributing to deterministic volatility models. In the following years, studies were conducted to investigate the impact of positive and negative news on volatility, which led to the inclusion of symmetric and asymmetric deterministic models in the literature, depending on whether the effects of positive and negative news on volatility are the same or different (Hentschel 1995).
With Taylor’s (1986) study, Stochastic Volatility (SV) models have introduced a different perspective on the volatility structure of assets as an alternative approach to deterministic models in modeling volatility. The main characteristic of stochastic volatility models is that volatility is included as an unobservable, i.e., latent, variable in the analyses. While the volatility structure can be modeled deterministically as an observable variable in ARCH-type models, it is treated as an unobservable variable in alternative stochastic volatility models (Broto and Ruiz 2004). Another advantage of stochastic volatility models, compared to GARCH models, is that they provide more effective parametric results, particularly in one-period-ahead forecasts (Das and Ghanem 2009).
The presence of asymmetric relationships was first addressed in the literature by (Harvey and Shephard 1996). In this study, they related the sign of the volatility obtained using the Kalman filter to the return series. Similarity functions in this study were calculated using the Quasi-Maximum Likelihood (QML) method.
According to Harvey and Shephard’s model:
In Equation (1), the parameter σ represents the scaling factor and includes a constant term effect on ht. εt represents a zero-mean random variable. Furthermore, when the absolute value of ϕ is less than 1, ht and therefore yt are stationary. According to Harvey and Shephard, there is a correlation relationship between the error terms of the mean and volatility models that exhibits simultaneous movement, represented as corr(εt, ηt) = ρ.
After Harvey and Shephard’s (1996) research, Jacquier et al. (2004) contributed by developing an asymmetric stochastic volatility model for discrete time, and modeled their work in a structure that takes the MCMC method in this study.
According to this model, the covariance matrix rt ≡ (εt,ηt)′ ∑*. Accordingly, ∑* is expressed:
If the coefficient ρ is negative, εt changes will be higher and will occur simultaneously. On the other hand, a positive development is associated with a decrease in εt volatility. Even for intermediate correlation values, an asymmetric leverage effect can be exhibited. This situation shows that in the Jacquier et al. (2004) study, the expected value of E[ht] will be 60% higher for negative shocks than for positive shocks when the correlation coefficient is −0.6 and εt value is 1.5 (Jacquier et al. 2004).
The contributions to the asymmetric stochastic volatility model continued with the study by (Yu 2005). In this study, Yu criticized the work of (Jacquier et al. 2004) and proposed the following model for asymmetric stochastic volatility:
According to Equation (4), Yu (2005) proposed a representation of the model that incorporates intertemporal correlation instead of contemporaneous correlation, i.e., corr(εt, ηt+1) = ρ. In addition, it was observed that the MCMC method provided more reliable results compared to the QML method by comparing them. Yu also combined Harvey and Shephard’s (1996) model with Jacquier et al.’s (2004) model to create the following model:
In this model, correlations are allowed at both time delays, but with varying degrees of correlation.
Another contribution to asymmetric SV models was made by (Asai and McAleer 2005). They proposed a model that explains asymmetric relationships based on the direct negative correlation between changes in volatility and returns, which they referred to as a dynamic asymmetric volatility model (dynamic ASV). The model is expressed as follows:
: The constant term of the volatility model
: Volatility persistence (continuity)
: Error term of the mean model
: Error term of the volatility model
: and represents the correlation coefficient between them.
In display (7), when the significance of the coefficient r is considered, an asymmetric relationship can be observed, and when the r coefficient is less than 0, dynamic leverage effects on volatility can be observed. Stochastic volatility models work with Bayesian techniques, and methods such as Effective Importance Sampling (EIS) and Monte Carlo Markov Chain (MCMC) are quite popular. In this study, the MCMC method is used to calculate the dynamic leverage effect on volatility. The main purpose of MCMC methods is to produce variables by repeatedly sampling a Markov chain (Kim et al. 1998). The main idea underlying the method is to calculate the joint posterior distribution function of the parameters to be estimated by multiplying the prior distribution function and the likelihood function of the data set. The prior density function is expressed in Equation (8):
With the likelihood function of the prior distribution, the combined form gives the posterior distribution of the model. In the formula, with ω notation, P(ω) represents the a priori probability function of ω and represents the likelihood function. The combination of the prior distribution with the likelihood function gives the posterior distribution of the model. For the case ω′ = (ω1, …, ωN) illustrates the posterior distribution function in cases when there are multiple parameter variables on Equation (9):
If ω1 is known in the model, it will be the a priori distribution of ω2, and if the parameters are independent, it will be as follows.
4. Data Set and Empirical Findings
In our study, we focused on the companies that form the foundation of the Nasdaq-100 index and constitute a significant part of the market value, namely Netflix (NFLX), Paypal (PYPL), Google (GOOGL), Intel (INTC), Microsoft (MSFT), Amazon (AMZN), Tesla (TSLA), and Apple (AAPL). For each of these stocks, we applied the dynamic ASV model using 1529 observations for the period between 3 January 2017 and 31 January 2023. The time chosen for the study tries to focus on new financial instruments and their investment behavior implications for traditional investment instruments by investors, while also containing the effects of a volatile period like COVID-19. According to this Table 1 represents stock units and market values (by billion USD) on Nasdaq-100.

Table 1.
Stock unit and total market values.
The above table shows the market value and weight of each stock in the index. It is observed that the nine major stock units have approximately 45% value weight in the Nasdaq-100 market value. In the selection of stocks for the study, not only market value was taken into consideration, but also the popularity of the constituents among investors in the Nasdaq-100 was considered and used in the modeling. As stated in the selection of these stocks, it is important that their market share has a very high weight in the Nasdaq-100 index but, on the other hand, it is thought that since they are generally high-technology stocks, they have an advantage in terms of investor diversity and therefore, based on these movements, they may have the power to represent/influence the Nasdaq-100 index. Accordingly, stocks such as Microsoft, Apple, Amazon, and Google are at the top of the ranking in terms of market capitalization and weight, while other stocks with low market capitalization and weight were included in the study due to their popularity among market participants. It can be argued that all the stocks we have selected are suitable for testing the Nasdaq-100 characteristic in terms of both market value and popularity. The descriptive statistics of the return series and their corresponding graphs are presented in Table 2 and Figure 2, respectively:

Table 2.
Descriptive statistics for selected stocks and Nasdaq-100.
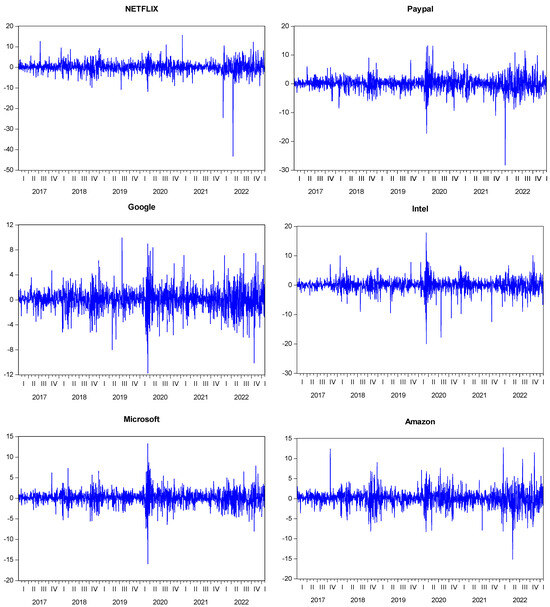
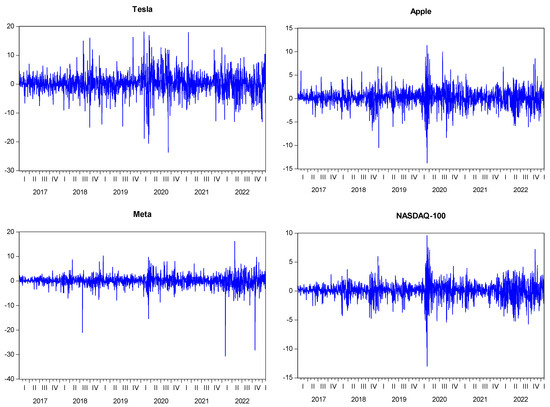
Figure 2.
Graphs of return series for units used in the study. Source: Prepared by the authors with EViews model output.
When examining the values of descriptive statistics in Table 2, particularly the skewness referred to as the third moment and kurtosis known as the fourth moment, it is demonstrated that financial asset returns possess a leptokurtic characteristic that does not support the assumption of normal distribution. This information is further supported by the Jarque–Bera statistics. As can be observed, every row’s standard deviation value is higher than the mean. These lines also have a high variation and volatility. Stated otherwise, the fact that the numbers derived from the division of the standard deviation by the mean exceed the coefficient of 1 indicates a significant level of volatility, particularly in financial data. Maximum and minimum values indicate the lowest and highest return values of the relevant variable. A median value indicates the median value of the series. According to the table, it is seen that the averages for all global variables are centered around zero, and there is a negative average only for Intel stock. It is noted that the series does not follow a normal distribution because the kurtosis values are significantly greater than the value of 3, which is thought to have a normal distribution. Furthermore, the left-negative skewness scenario with a long-left tail is identified by the fact that all variable skewness values have negative coefficients. Another finding that supports that the series is not suitable for normal distribution is that the Jarque–Bera statistics obtained through the formulation, considering the kurtosis and skewness values, take values far from zero and the series moves away from the normal distribution. Furthermore, the left-negative skewness scenario with a long-left tail is identified by the fact that all variable skewness values have negative coefficients. Additionally, the statistical significance of the probability values indicates the reliability of the values presented in Table 2. Figure 2 confirms that the differenced return series exhibits a stationary process over time, validating its suitability for our analysis.
In this study, a model was constructed using return series, where the return series were obtained using the ln(Pt/Pt−1) × 100 equation, and model predictions were made using the WinBugs 1.4 program. In this context, 100,000 iterations were sampled, and the first 10,000 samples were excluded to remove the initial bias of the coefficients, and the remaining 90,000 samples were used for analysis. Therefore, the high number of samples is expected to produce more accurate parametric results, and the exclusion of the first 10% is intended to remove dependence on the initial values (prior distributions). Distribution assumptions for the study were made using the values in Ishihara and Omori’s (2012) study through MCMC estimation. Accordingly, the reference values of μ~Inverse-Normal(−10,1), ρ~Inverse-Uniform(−1,1), ϕ~Inverse-Beta(20,1.5), ~Inverse-Gamma(2.5,0.025) were used as prior distributions. The initial values used for the ASV model parameters were μ = −9, = 100, ρ = −4, ϕ = 0.95. The ASV model parameter results for the selected stocks are presented in detail in Table 3:

Table 3.
ASV model results for selected stocks.
The reason for the interest in the stochastic volatility model with dynamic leverage is the view that negative news increases the volatility of any financial asset more than positive news. Therefore, we expect this value to have a negative sign and be statistically significant in the table indicators. According to the results obtained from the model for Netflix, all five parameters were statistically significant at the 5% level of significance. One of these parameters, , represents the persistence of volatility (volatility clustering) and provides a result close to 1 with a value of 0.89, indicating a high level of volatility clustering and the persistence of volatility continuity. Another important parameter for measuring volatility, the coefficient , expresses the standard deviation of the error term of the volatility model for Netflix. This parameter is used to calculate the variance of the error term of the volatility model and to represent the variability of volatility as variance. Consequently, it takes a value such as ( = 0.197), which indicates that the variability of Netflix stock volatility is close to zero. The parameter being close to 1 and the parameter being close to 0 indicate that the structure of Netflix stock volatility is not highly floating. The coefficient , which is another important parameter, expresses the direct relationship between changes in volatility and returns for Netflix. According to the model results, this parameter has a coefficient of −0.26 at the 5% level of statistical significance, indicating that there is an asymmetric relationship between changes in volatility and returns, and the negative value of the parameter coefficient indicates the presence of a weak leverage effect. Additionally, the low Monte Carlo error values from the model results prove that the model’s error margin is also very low.
The next section of the table presents the statistical significance of all parameter values based on the model results obtained for the PayPal stock. The persistence parameter of potential volatility clustering, , is statistically significant at the 5% level and close to 1 with a value of 0.95, indicating the presence of intense volatility clustering and thus, the continuity of volatility. Another parameter for measuring volatility, the coefficient , obtains an approximate value of 0.29, representing the variability of volatility as variance, with a result of approximately ( = 0.088). This indicates that the variability of PayPal stock volatility is low. These results demonstrate the predictability of PayPal volatility. Another important parameter, the coefficient , expresses the direct correlation between changes in volatility and returns for PayPal. The model results indicate that this parameter is statistically significant for PayPal, indicating the presence of an asymmetric effect between changes in volatility and returns. Furthermore, the negative sign of this parameter signifies the existence of a leverage effect between shock effects on PayPal returns and volatility, with a significant but weak level of −0.33.
According to the model results obtained for Google stock, all stochastic model parameters are statistically significant. The parameter for volatility persistence, , is statistically significant and, due to its value of 0.92, it indicates a high level of clustering of volatility, suggesting the presence of volatility persistence. The parameter has a coefficient value of 0.37, and the resulting variance of this value is approximately ( = 0.138), indicating a low level of volatility variability in the market for Google. These parameter values suggest that the predictability of Google stock volatility can be estimated. Another parameter, the coefficient , represents the direct relationship between changes in Google stock volatility and Google returns. The model results for Google indicate that this parameter is statistically significant at a 5% level of significance, indicating the presence of both asymmetric effects and leverage effects between changes in volatility and returns.
According to the results of the model obtained for Intel stock, except for the parameter, all others are statistically significant. The parameter, with a value close to 0.90 and near 1, indicates that the stock has a high degree of volatility clustering. The coefficient in the model for Intel also obtains a value of approximately 0.47, and because of the variance, this indicator takes a value of approximately ( = 0.22). The fact that the value of 0.22 is relatively far from zero suggests that the volatility of Intel is high, and that the predictability of the stock’s volatility is somewhat lower than that of other stocks examined in the study. The parameter, which helps us to express the direct correlation relationship between changes in volatility and returns, although supporting an asymmetric relationship and a leverage effect as a coefficient, is statistically insignificant at the 5% significance level in the model result. This indicates that there is no asymmetric relationship and leverage effect between changes in volatility and returns. Therefore, one of the findings for the Intel stock is that changes in volatility exhibit symmetric behavior.
According to the model results for Microsoft, all parameters are statistically significant. indicates a high level of volatility persistence with an approximate value of 0.95. The parameter obtains a value of approximately 0.31, and because of the variance, this indicator yields a value of approximately ( = 0.096). Accordingly, the volatility variability for Microsoft stock is at a low level. The parameter demonstrates a statistically significant and strong correlation at a 5% significance level, with a coefficient of −0.48, indicating the presence of both asymmetric and leverage effects between shocks experienced by Microsoft returns and shocks experienced by Microsoft volatility.
According to the model results for Amazon, all parameters demonstrate statistical significance. indicates a dense volatility clustering with an approximate value of 0.95. The parameter obtains a value of approximately 0.307, and because of the variance, this indicator yields a value of approximately ( = 0.094). Therefore, the volatility variability for Amazon stock is at a low level. The proximity of the parameter to 1 and the parameter to 0 indicates that the volatility of Amazon stock is predictable. The parameter demonstrates a statistically significant correlation at a 5% significance level, with a coefficient of −0.31, indicating the presence of both an asymmetric relationship and leverage effect between shocks experienced by Amazon returns and shocks experienced by Amazon volatility.
According to the model results for Tesla, all parameters exhibit statistical significance. indicates a high level of volatility persistence with an approximate value of 0.91. The parameter obtains a value of approximately 0.38, and because of the variance, this value yields an approximate result of ( = 0.15). Therefore, the volatility variability for Tesla stock is at a low level. The trade-off relationship between the and parameters supports the predictability of volatility for Tesla. The parameter demonstrates a statistically significant and weak correlation at a 5% significance level, with a coefficient of −0.171, indicating the presence of both asymmetric effects and leverage effects between shocks experienced by Tesla returns and shocks experienced by Tesla volatility.
According to the model results for Apple, all parameters are statistically significant. indicates a dense volatility clustering with an approximate value of 0.94. The parameter obtains a value of approximately 0.30, and because of the variance, this indicator yields an approximate result of ( = 0.09). Therefore, the volatility variability for Apple stock is at a low level. When examining the relationship between and , it supports the predictability of Apple stock volatility. The parameter demonstrates a statistically significant correlation at a 5% significance level, with a coefficient of −0.4572, indicating the presence of both an asymmetric relationship and a leverage effect between shocks experienced by Apple returns and shocks experienced by Apple volatility.
According to the model results for Meta, all parameters exhibit statistical significance. indicates a high level of volatility persistence with an approximate value of 0.92. The parameter obtains a value of approximately 0.42, and because of the variance, this indicator yields an approximate value of ( = 0.18). Therefore, the volatility variability for Meta stock is at a low level. The parameter demonstrates a statistically significant correlation, with a coefficient of −0.27, between shocks experienced by Meta returns and shocks experienced by Meta volatility. This indicates the presence of both a leverage effect and an asymmetric relationship. Table 4 represents the ASV model results for its plain form of Nasdaq-100 index.

Table 4.
ASV model results for the Nasdaq-100 index.
According to the model results for the Nasdaq-100 index, all parameters are statistically significant. indicates a highly dense volatility clustering with an approximate value of 0.96, signifying persistence in volatility. The parameter obtains a value of approximately 0.28, and because of the variance, this indicator yields an approximate value of ( = 0.08). Therefore, the volatility variability for the Nasdaq index is at a low level. When examining the relationship between and , it supports the predictability of the index’s volatility. The parameter demonstrates a statistically significant and strong correlation at a 5% significance level, with a coefficient of approximately −0.64, indicating the presence of both a leverage effect and an asymmetric relationship between shocks experienced by Nasdaq returns and shocks experienced by Nasdaq volatility. The model results also suggest that other stocks included in the Nasdaq index exhibit high volatility clustering and display similar characteristics in terms of asymmetric structure and the presence of leverage effects, except for Intel stock. These findings highlight the common features and fluctuations in the Nasdaq-100 index based on positive and negative shocks in the market. Apart from all these parameters in both tables, the fact that the MC error values of the obtained models are less than 0.05, which is regarded as the threshold value, indicates that the model predictions reach actual econometric model results, given that the Monte Carlo error values indicated in the table are indicators of the accuracy of the model structure.
5. Conclusions
There has recently been a growing tendency among financial market participants to examine the volatility interaction among markets, enabling them to diversify their portfolios more effectively and allocate their investments with greater efficiency. The interaction of volatility in financial markets is crucial for asset pricing, currency and trading strategies, hedging, and effective regulatory strategies. Numerous studies in the literature have measured the spread of volatility on various indices of different countries, considering their relationships with other financial asset types and indices. However, studies that utilize ASV models for the Nasdaq-100 index and its major stocks are limited. Therefore, this study used dynamic leverage-effective stochastic volatility models to make predictions for major stocks within the Nasdaq-100. Subsequently, an ASV model was estimated for the Nasdaq-100 index itself, and the results were compared with those obtained from individual stock predictions.
The return series in this WinBugs-applied study was first computed by taking the logarithmic difference, with 1529 observations for each variable. This is because, in contrast to price series, return series typically satisfy the requirements for statistical significance in terms of stationarity condition. Our study’s findings for each stock unit closely match those of previous literature reviews. Results comparable to those of earlier literature research were obtained, especially with regard to their volatile structure. As one might imagine, the primary cause of this state of affairs is the peculiar way in which projections are priced, as evidenced by the observable fluctuations in the Nasdaq-100 index’s volatile process in relation to other financial instruments. Regarding the asymmetric relationship, our study’s conclusion indicates a strong leverage effect and asymmetric relationship, even though this scenario is seen in other comparable stocks that are frequently employed in other literature research.
During the research, several tasks were set forth, and results were obtained. The companies with the highest capitalization within the Nasdaq-100 index were selected, and asymmetric effects were investigated. Within the framework of stochastic models, additions introduced to asymmetric volatility models by Harvey and Shephard (1996), Jacquier et al. (2004), Yu (2005), Asai and McAleer (2005) were detailed, and theoretical development concepts were discussed. The non-stationary trends of the presented stocks were measured mathematically; a scrutiny of the characteristic features of these stocks and the Nasdaq-100 index was conducted from a descriptive statistical perspective; in addition to measuring dispersion, the spread effects of profitability were measured through correlation counterparts. In many earlier studies, the analysis of the relationship between deterministic model structures and volatility directions prevails in the respective topics. However, in this research, the discussion of volatility relationships is approached dynamically through conditional stochastic volatility models, yielding more realistic and precise parametric results. Another advantage of this research is its unique contribution to the literature, as there is no other study that collectively and reciprocally evaluates a wide range of asymmetric effects in predicting as extensively as is carried out in the literature on dynamic asymmetric stochastic volatility. This research can be considered as an important empirical study with broad significance written on the topic of dynamic asymmetric stochastic volatility when compared to the existing literature. The correlation relationship between the volatility continuity of stocks, the predictability of volatility, and the impact of shocks on the volatility of currencies in response to shocks that occur in their own returns were evaluated based on the results obtained from the dynamic leverage-effective SV model predictions. Based on these results, the presence of volatility density was determined for all stocks included in the analysis. In general, when considering stocks, it was empirically proven that there is a high volatility clustering for all stocks and that this volatility is continuous and predictable. Another limitation of our study is to determine the presence of asymmetric relations/leverage effects for these stocks. Our findings have shown that there is no asymmetric relationship between changes in volatility and returns for the Intel financial asset and no leverage effect for this stock. In this context, an asymmetric relationship and a leverage effect were found in all eight of the other stocks.
According to the results of the ASV model that fully encompasses the Nasdaq-100 index, there is a high volatility clustering and low volatility variability, thereby proving that volatility is predictable. Additionally, the strong correlation between the shocks experienced by Nasdaq returns and the shocks experienced by its volatility indicates the presence of both a leverage effect and an asymmetric relationship.
Specifically, similar findings were obtained in terms of their volatile structures. This can be attributed to the fact that the volatile process of financial markets is more visible in terms of variable variance compared to other tools, and price forecasting predictions can show unusual trends. The empirical results obtained in our study are particularly important for the selection of indexes/stocks to be added to the portfolio, portfolio management, determination of risk level, and risk hedging. Similarly, the measurement of volatility level is an important indicator for providing investment strategies.
It is noteworthy that recent years have witnessed scholarly works bearing a resemblance to our own investigation. These studies exhibit similarities with our research in both subject matter and methodology. For instance, Aliyev et al. (2020), Alexander et al. (2021), Joshi et al. (2022), and Yaya et al. (2022), among others, exemplify such works. However, our study distinguishes itself from others both in methodological approach and the object of analysis. For instance, Aliyev et al. (2020) represents the closest parallel to our investigation, albeit focusing on preceding periods. Our study centers on the NASDAQ-100, yielding findings that exhibit substantial proximity. Conversely, Alexander et al. (2021) examined Johnson SU and Edgeworth utilizing a similar methodology. Additionally, Joshi et al. (2022) and Yaya et al. (2022) undertook analogous inquiries. Joshi et al. (2022) employed akin methodologies to juxtapose the Indian stock market index against major global counterparts, yielding significant insights. Yaya et al. (2022) scrutinized oil price shocks and pivotal financial indicators employing a comparable model, assessing the ramifications of positive and negative oil price fluctuations on the burgeoning green economy. Consequently, our study diverges from extant literature predominantly due to our separate analysis of both indices and individual stocks.
With the increasing number of studies focusing on examining volatility structures, our research provides valuable information on the careful selection of investment opportunities for various indices and other financial assets with high volatility structures. In this sense, our study is one of the ways to investigate the mentioned volatility structures, and it is believed to shed light on the complex volatility structure by helping researchers with various empirical research techniques in this area. The research can be extended by including other popular tools to understand the volatility dynamics in financial markets better and can offer more comprehensive insights for investors to embrace the nature of financial markets. Simultaneously, while the econometric method and econometric model principles demonstrated in this research are adequate for time and frequency observations, time series analysis can be continuously explored in any other factor or group of country samples. The direction of the counterparts of the parameters obtained in the results of the research can be considered in the planning of investments to increase profitability in stocks. Comparative research with methodologies like the methodology discussed here can also be conducted within the framework of the research.
Author Contributions
Conceptualization, M.G.; methodology, M.G. and E.S.; software, U.Y.; validation, E.S. and U.Y.; resources, E.S.; data curation, U.Y. and M.G.; writing—original draft preparation, M.G. and E.S.; writing—review and editing, M.G. and E.S.; visualization, U.Y.; supervision, E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request from the authors.
Conflicts of Interest
Research and publication ethics were complied with in the study. There is no conflict of interest between the authors of the study that could affect the results.
References
- Alexander, Carol, Emese Lazar, and Silvia Stanescu. 2021. Analytic moments for GJR-GARCH (1, 1) processes. International Journal of Forecasting 37: 105–24. [Google Scholar] [CrossRef]
- Aliyev, Fuzuli, Richard Ajayi, and Nijat Gasim. 2020. Modelling asymmetric market volatility with univariate GARCH models: Evidence from Nasdaq-100. The Journal of Economic Asymmetries 22: e00167. [Google Scholar] [CrossRef]
- Asai, Manabu, and Michael McAleer. 2005. Dynamic asymmetric leverage in stochastic volatility models. Econometric Reviews 24: 317–32. [Google Scholar] [CrossRef]
- Beine, Michel, Antonio Cosma, and Robert Vermeulen. 2010. The dark side of global integration: Increasing tail dependence. Journal of Banking & Finance 34: 184–92. [Google Scholar]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Daniela Osterrieder, Natalia Sizova, and George Tauchen. 2013. Risk and return: Long-run relations, fractional cointegration, and return predictability. Journal of Financial Economics 108: 409–24. [Google Scholar] [CrossRef]
- Broto, Carmen, and Esther Ruiz. 2004. Estimation methods for stochastic volatility models: A survey. Journal of Economic Surveys 18: 613–49. [Google Scholar] [CrossRef]
- Brownlees, Christian, and Robert F. Engle. 2017. SRISK: A conditional capital shortfall measure of systemic risk. The Review of Financial Studies 30: 48–79. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric dynamics in the correlations of global equity and bond returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Chen, Ting, Zhenyu Gao, Jibao He, Wenxi Jiang, and Wei Xiong. 2019. Daily price limits and destructive market behavior. Journal of Econometrics 208: 249–64. [Google Scholar] [CrossRef]
- Das, Sonjoy, and Roger Ghanem. 2009. A bounded random matrix approach for stochastic upscaling. Multiscale Modeling & Simulation 8: 296–325. [Google Scholar]
- Ding, Haoyuan, Terence Tai-Leung Chong, and Sung Y. Park. 2014. Nonlinear dependence between stock and real estate markets in China. Economics Letters 124: 526–29. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the Econometric Society 50: 987–1007. [Google Scholar] [CrossRef]
- Guo, Kun, Yi Sun, and Xin Qian. 2017. Can investor sentiment be used to predict the stock price? Dynamic analysis based on China stock market. Physica A: Statistical Mechanics and Its Applications 469: 390–96. [Google Scholar] [CrossRef]
- Harvey, Andrew C., and Neil Shephard. 1996. Estimation of an asymmetric stochastic volatility model for asset returns. Journal of Business & Economic Statistics 14: 429–34. [Google Scholar]
- Hentschel, Ludger. 1995. All in the family nesting symmetric and asymmetric garch models. Journal of Financial Economics 39: 71–104. [Google Scholar] [CrossRef]
- Ishihara, Tsunehiro, and Yasuhiro Omori. 2012. Efficient Bayesian estimation of a multivariate stochastic volatility model with cross leverage and heavy-tailed errors. Computational Statistics & Data Analysis 56: 3674–89. [Google Scholar]
- Jacquier, Eric, Nicholas G. Polson, and Peter E. Rossi. 2004. Bayesian Analysis of Stochastic Volatility Models with Fat-Tails and Correlated Errors. Journal of Econometrics 122: 185–212. [Google Scholar]
- Joshi, Nisarg A., Vishalkumar Jani, and Dhyani Mehta. 2022. Volatility analysis and volatility spillover across equity markets between India and major global indices. Asian Journal of Management 13: 215–22. [Google Scholar] [CrossRef]
- Kim, Sangjoon, Neil Shephard, and Siddhartha Chib. 1998. Stochastic volatility: Likelihood inference and comparison with ARCH models. Review of Economic Studie 65: 361–93. [Google Scholar] [CrossRef]
- Knight, John L., Stephen E. Satchell, and Jun Yu. 2002. Theory & methods: Estimation of the stochastic volatility model by the empirical characteristic function method. Australian & New Zealand Journal of Statistics 44: 319–35. [Google Scholar]
- Li, Qing, Yuanzhu Chen, Li Ling Jiang, Ping Li, and Hsinchun Chen. 2016. A tensor-based information framework for predicting the stock market. ACM Transactions on Information Systems (TOIS) 34: 1–30. [Google Scholar] [CrossRef]
- Liu, Qiang, Shuxin Guo, and Gaoxiu Qiao. 2015. VIX forecasting and variance risk premium: A new GARCH approach. The North American Journal of Economics and Finance 34: 314–22. [Google Scholar] [CrossRef]
- Lu, Xun-Fa, and Kin-Keung Lai. 2012. Relationship between stock indices and investors’ sentiment index in Chinese financial market. Xitong Gongcheng Lilun Yu Shijian/System Engineering Theory and Practice 32: 621–29. [Google Scholar]
- Pellegrini, Santiago, and Alejandro Rodrigez. 2007. Financial Econometrics and SV Models. Available online: http://halweb.uc3m.es/esp/Personal/personas/spellegr/esp/Curso_Cordoba/Tutorial_Guide.pdf (accessed on 18 April 2024).
- Poon, Ser-Huang. 2005. A Practical Guide to Forecasting Financial Market Volatility. Hoboken: John Wiley & Sons, p. 1. [Google Scholar]
- Sumner, Steven, Robert Johnson, and Luc Soenen. 2010. Spillover effects among gold, stocks, and bonds. Journal of Centrum Cathedra 2: 106–20. [Google Scholar] [CrossRef]
- Taylor, Stephen J. 1986. Modelling Financial Time Series. Singapore: World Scientific. [Google Scholar]
- Wu, Wenbo, Jiaqi Chen, Liang Xu, Qingyun He, and Michael L. Tindall. 2019. A statistical learning approach for stock selection in the Chinese stock market. Financial Innovation 5: 20. [Google Scholar] [CrossRef]
- Yaya, OlaOluwa S., Ahamuefula E. Ogbonna, and Xuan Vinh Vo. 2022. Oil shocks and volatility of green investments: GARCH-MIDAS analyses. Resources Policy 78: 102789. [Google Scholar] [CrossRef]
- Yu, Jun. 2005. On leverage in a stochastic volatility model. Journal of Econometrics 127: 165–78. [Google Scholar] [CrossRef]
- Yu, Jun, and Renate Meyer. 2006. Multivariate stochastic volatility models: Bayesian estimation and model comparison. Econometric Reviews 25: 361–84. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).