1. Introduction
The notion of operational risk management process in organizations is an ongoing effort to identify, analyze, and assess the organization’s risks and to respond to each scenario on strategic and operational management levels (ISO 31000:2018(en), Risk management—Guidelines n.d. (
ISO 2018)). During the risk identification stage, the possible causes of disruptions and the magnitude of events are examined for external and internal factors. Next, the risk analysis process quantifies each event’s risk level based on likelihood, results, and control mechanisms for reducing the risk and their effectiveness. Finally, a comprehensive risk assessment can be considered, and decisions can be made concerning addressing each risk.
The final stages of the risk assessment process in current practice consist of appraising the undesired outcomes of a process based on answering the questions “What is the likelihood of occurrence?” and “If it does go wrong, what are the consequences?”. Both questions are subjective; thus, assessing the likelihood is not an objective truth and largely depends on the experience and personality of the assessor. In other words, the current state-of-the-art risk assessment process in operational management involves uncertainty regarding the events (as systems’ complexity increases) and uncertainty regarding the risk analysis.
In recent years, the complexity of processes in projects and organizations has increased considerably (
Qazi et al. 2016;
Lochan et al. 2021), and such complexity contributes to the uncertainty of events (
Aven and Zio 2011). In addition, the lack of knowledge and proper information regarding the process and the relations between factors significantly influences the ability to reach a high level of precision (
Thomas et al. 2013). A new method that emphasizes the importance of knowledge on risk assessment was described in a paper (
Aven 2013) that conditioned the risk level in the risk matrix as a function of knowledge of the system and the factors.
One of the most prominent challenges in risk management today is the auditor’s subjectivity bias in determining the risk levels. While risk matrices (
Elmontsri 2014) are still one of the most prominent evaluation tools for auditors, it is well known that they have several inherent limitations in defining and categorizing risk (
Ball and Watt 2013). The most prominent restriction, as can be seen in Anthony Cox’s paper (
Anthony Cox 2008), states that the severity ratings in these matrices still depend on subjective risk attitudes. Others also point to significant deficiencies in the risk assessment process due to subjectivity, heuristics, and arbitrariness in ranking the risks (
Thomas et al. 2013). Those deficiencies in everyday practice can be called cognitive biases and the human factor in the process. Significant cognitive biases such as anchoring, conformity, or overconfidence biases can inadvertently affect the accuracy and precision of the likelihood assessment process (
Selvik and Abrahamsen 2017).
Considering the limitation mentioned above, there are many cases where, in practice, there are significant gaps in risk assessments that were conducted at the same organization by different auditors. There is no simple method to determine which auditor is more accurate, but it is clear that a lack of consistency between assessments is undesired. For example, we analyzed a few actual risk surveys conducted in 2015–2023 in industrial companies and service organizations. We compared two risk surveys for each company, that were conducted at the same time period, and studied the gaps between the different auditors. Specifically, we looked at four risk surveys containing 71 items. By analyzing the differences between the auditors, we could see an average difference of 24% between the risk levels evaluated by different auditors, which exemplifies the inconsistency in the risk evaluation results. This gap in the research is our focus in this work. The current literature does not provide an adequate methodology to reduce the variance and bias effect on the assessment process.
In our work, we provide a methodology that will decrease the variance in human auditors and consequently improve the reliability and accuracy of the risk assessment outcome. We decompose risk into its atomic subcomponents and evaluate these subcomponents directly. These subcomponents will then be combined to assess the original risk matrix (
Zampeta and Chondrokoukis 2022). Our central intuition is that the magnitude of human error and their variance in subjective assessment will reduce when assessing smaller risk factors. This intuition stems from two sources. First, compounded risk is more complex to evaluate as different individuals can quantify it differently due to cognitive biases. A comprehensive article (
Kleinmuntz 1990) suggests that combining intuition and a systematic approach can reduce biases due to subjective constraints and support decision-makers to improve precision. Second, from a statistical point of view, replacing a single measurement characterized by a variance σ2 with the average from n measurements, each characterized by a variance σ2, decreases the average result’s variance to σ2/n. This property of variance of sample mean may reduce the volatility of the multifactor mean versus a single factor parameter of the assessment (
Todinov 2017). In our literature review, we did not find papers in the field of our topic of research and no other frameworks to reduce uncertainty were suggested by scholars. There are papers that relate to the mitigation of uncertainty in the operational process (
Durugbo and Erkoyuncu 2016), although their focus is not on risk assessment methods but only in quality control and managerial procedures.
Our framework utilizes techniques from causal inference and Directed Acyclic Graph (DAG) modeling (
Shrier and Platt 2008) to study the mechanism behind the uncertainty and complexity in assessing the likelihood function of risk. By utilizing DAG for modeling, we can reveal the main components that affect the likelihood of risk mechanisms to quantify and define these factors precisely.
The new framework was evaluated both in an experimental setting and a simulation. In the experimental setting, we let human auditors assess a case study using the traditional method (a single score) and the new framework of sub-factors. The findings show that our new approach of segmentation into sub-factors significantly reduced the variance of the assessments compared to the traditional evaluation. Using a Monte Carlo approach, the simulation study included two groups of randomly selected scores. The first group generated a single factor, and the second group was programmed to generate six sub-factors and calculated the total likelihood score based on the formula. This simulation also significantly reduced the variance in the new framework and provided an additional mathematical verification for the new methodology of segmentation and deconstruction of the risk.
In
Section 2, we discuss the current practice in risk assessment process and introduce our method of analyzing the sources of uncertainty in operations and the basic structure of our framework. In
Section 3, we present the application of the new methodology in an experimental study and in a simulation of some stochastic processes. In
Section 4, we discuss the implications of the novel framework and in
Section 5, we conclude and suggest some research directions in this area.
2. Framework of Deconstructing the Risk Function
2.1. The Current Practice
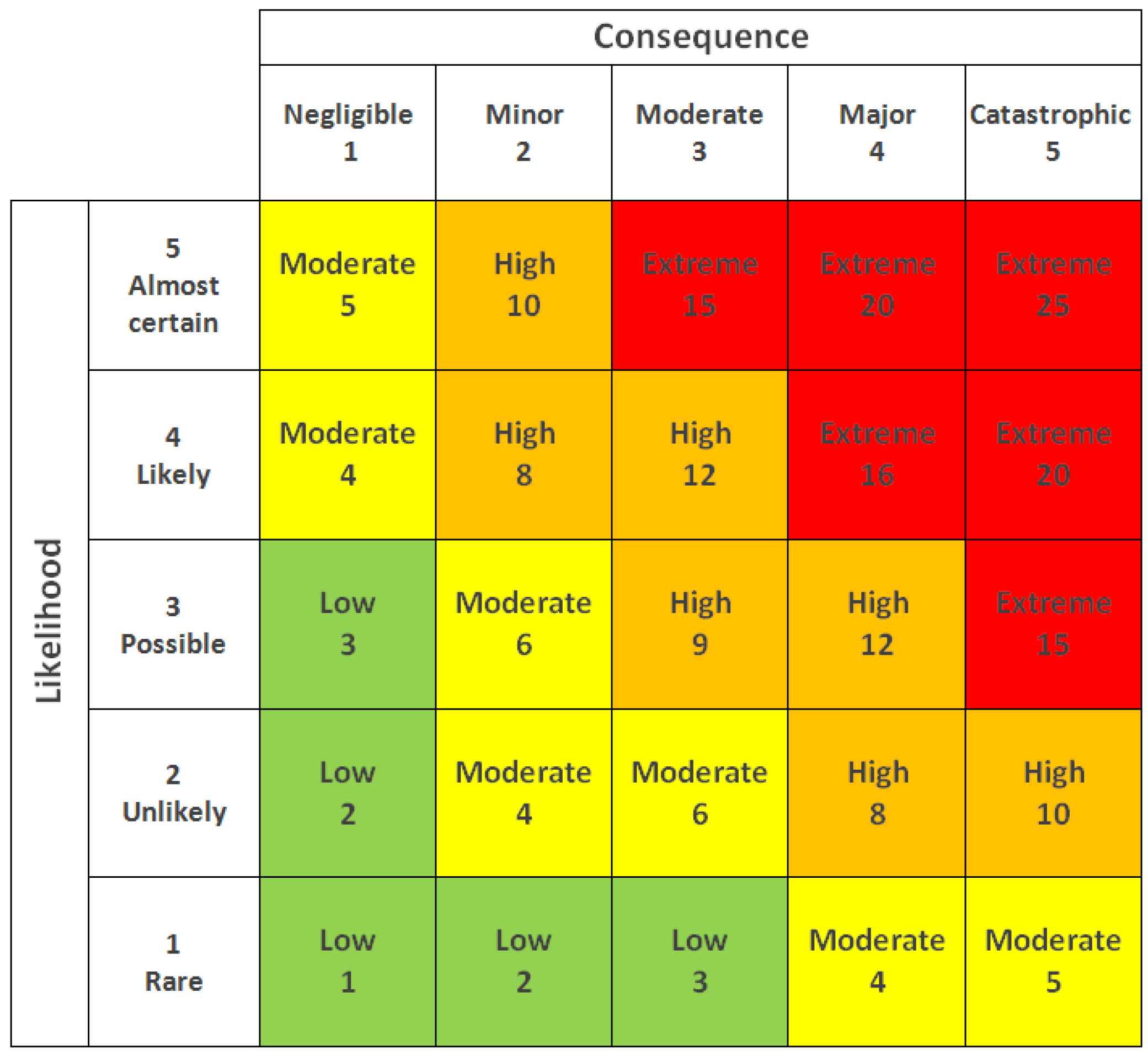
The risk matrix is the primary tool for assessing and prioritizing risks based on their likelihood and impact today (
Burstein and Zuckerman 2023). It visually represents potential risks, allowing organizations to make informed decisions about allocating resources for risk mitigation. The matrix (see
Figure 1) typically consists of a grid with two axes: (1) likelihood: this axis represents the likelihood or frequency of a risk event occurring; it is often categorized as low, medium, or high; (2) consequence: this axis represents the potential consequences or severity of a risk event if it were to occur. Impact is also often categorized as low, medium, or high.
The matrix is divided into different cells or zones, each corresponding to a combination of likelihood and impact. These cells are usually color-coded or labeled to indicate the level of risk associated with that combination. Standard labels for the cells include “low risk”, “medium risk”, and “high risk”. By plotting individual risks on the matrix, organizations can quickly identify and prioritize those that pose the most significant threats. This helps develop a targeted risk management strategy, focusing efforts and resources on mitigating the most critical risks. Additionally, it facilitates communication and decision making among stakeholders by providing a clear visual representation of the overall risk landscape.
Assessments of likelihood and consequence are the basic steps in determining the calculated risk score level in the matrices (risk = likelihood × consequence) (
Burstein and Zuckerman 2023). Due to the biases, any small error in the likelihood directly affects the computed result. The consequence score is quantitative and thus easier to assess relatively accurately. In contrast, the likelihood score is more qualitative and obscure and highly susceptible to the auditors’ judgment and bias.
This source of variance is a systematic problem of the risk matrix method; it reflects the differences between assessors and can lead to wrong information that reaches the decision-makers. Due to many cognitive biases affecting the likelihood score, different auditors have different histories, personalities, and judgments, which is a given fact. Therefore, we suggest improving the variance by breaking down the likelihood structure. Our method will try to minimize the overall influence on the final score.
2.2. The Sources of Uncertainty in the Risk Analysis Process
Our research is based on developing a simple-to-apply framework for deconstructing the likelihood factor into its essential elements of sub-factors. The intuition behind the segmentation into sub-factors arose due to the understanding that some sources of uncertainty are related to an aleatory process and some lack of knowledge regarding the process parameters (
Burstein and Zuckerman 2023). We can also relate free will and human factor interests and judgment as a source of uncertainty and unpredictability. Firstly, we can classify the different sub-factors into two main classes: the first consists of objective factors and the other of subjective factors. Here are some examples of factors belonging to each of these classes:
Objective factors—machine output and tolerance, equipment maintenance according to specifications, mean time between failures, compliance with best practice standards, level of redundancy, and systems back-up and controls.
Subjective factors—level of human resource integrity, level of personal training and awareness, level of process complexity, and level of variance or entropy in the process.
The class of objective factors consists of mechanisms or systems that allow us to obtain a relatively objective and quantifiable measure regarding the likelihood of risk. For instance, the mean time between failures (MTBF) is a well-known measure in which we can review experience (e.g., machine logs) to obtain an objective and reliable measure. The class of subjective factors consists of factors that are harder to quantify and often rely on subjective and qualitative evaluation. For example, the level of human resource integrity is a factor that measures, among others, the level of professionalism and commitment to the organization and to its mission. These values are more abstract and will probably have a high level of variability between different auditors.
One of the primary findings from our experience in real-world practice is that the uncertainty in the risk assessment process may be composed of a mixture of factors contributing to the total likelihood in many different directions. For example, in some cases in operational risk, we can identify situations where two minor risk factors can generate a very high-risk outcome due to positive feedback or cross effect and even the presence of an unobserved cofactor that amplifies the impact (sort of constructive interference). The combination of the threshold conditions of risk occurrence with the factors contribute to system failure. In our deconstruction framework, we can reduce the uncertainty of the assessment by quantitatively improving our understanding of the mechanism and factors behind these elements.
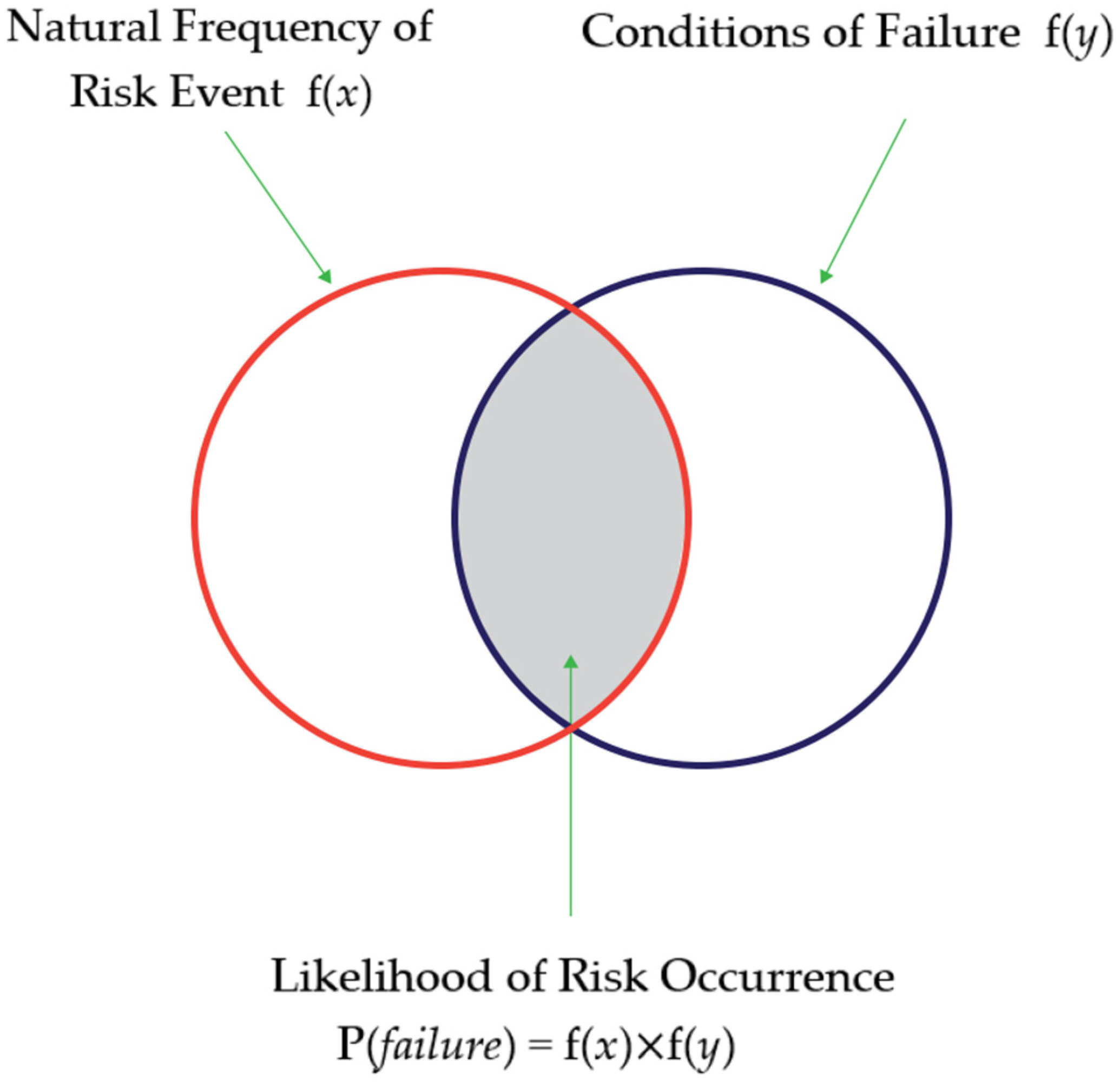
In
Figure 2, we schematically describe the zone where the realization of two components might cause, with some likelihood, the occurrence of the risky event. These components are the natural frequency of the risk event to happen, f(
x), and the conditions for failure in dealing with it, f(
y). We posit that the risk occurrence is contingent on these two conditions; elsewhere, if any of them are not realized, the likelihood of a risk event is zero. The product f(
x)
f(
y) is the likelihood we seek when proposing this new formula.
2.3. The Natural Frequency of Risk Event-f(x)
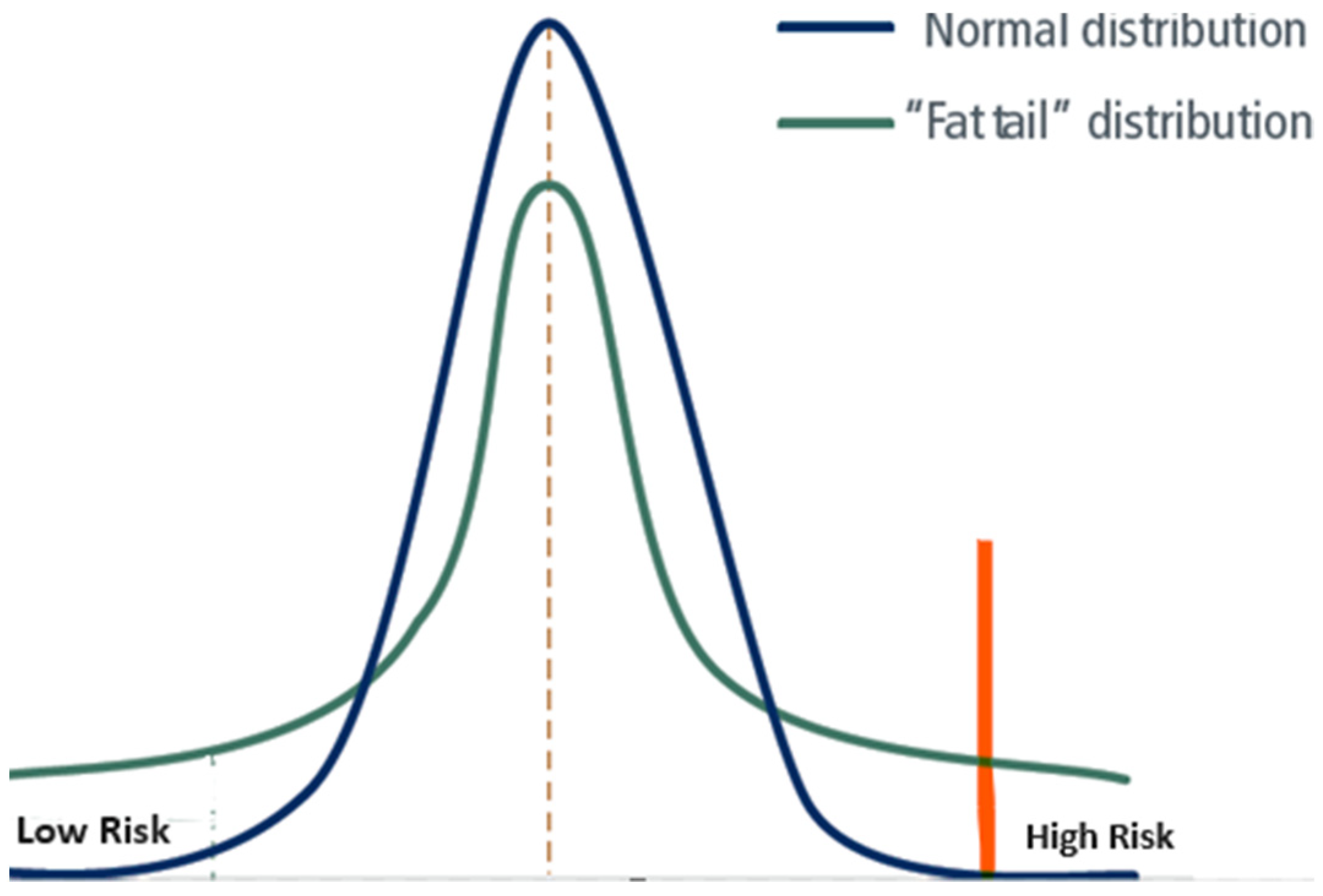
This element consists of the frequency of the risk occurrence (low, medium, high) and the volatility or variance of the risk (low, medium, high). Thus, X = {frequency, variance}. We suggest that high variance can significantly increase the likelihood even if the expected risk frequency is relatively low because it “shifts” the likelihood density function into a fat tail distribution. In practical terms, we suggest that there is an amplifying effect when a high variance of the mean increases the area at the right end of the distribution. For example, when comparing two independent systems with a similar normal distribution of failure probabilities, we expect to find a higher risk of failure in the system with a higher variance on the same mean as shown in
Figure 3.
Table 1 depicts the effect of variance on the likelihood score. From our point of view, very few auditors are paying the required attention to this serious effect. Neglecting the fat tails’ frequency of risk can increase errors and variance in the assessment. In this proposed method, the likelihood is computed as a function of the frequency of the occurrence, its variance. We mean that if the likelihood of event is low but the variance of outcomes is medium (or high) or in the case that the likelihood is medium but the variance is high, then that effect increases the risk likelihood due to the uncertainty span. In contrast, a very low variance will not reduce the likelihood; it is a one-directional effect. This methodology can improve the precision in determining the natural frequency of risk events, a major parameter in the risk assessment process.
For example, let us assume that the likelihood of the occurrence is 4 (medium) and the variance is 5 (high). We compute f(
x) to be 5 from these two parameters and the matrix below. The increase in risk level from 4 to 5 is due to the “fat tail” as given by the high variance level (of 5) and can be clearly seen in
Figure 3 that there is higher density in the right “tail” of the distribution.
2.4. Conditions for Failure Occurrence-f(y)
Our method of refining the sources of uncertainty is based on analyzing the likelihood of failure using a Directed Acyclic Graph (DAG). The DAG helps break down factors and reveal the flow of association and causation. Prior research suggests that DAG modeling can reduce bias in causal inferences about exposure (
Shrier and Platt 2008). We will use a DAG-based model to better understand the causes of the likelihood of failure in a system or an operational process.
Defining the root factors and their relations to the outcome is one of the most crucial steps in understanding and analyzing the causes or likelihood of failures. In
Figure 3, we can see our suggestion for modeling the main sub-factors and variance generators on the likelihood of risk. If a need arises for more accuracy and precision, one can keep drilling further to a higher resolution by breaking each sub-factor into another layer of its sub-factors. In this study, we focused on the manufacturing industry just as a way to prove a concept of the framework. It can be utilized by some minor modifications or by adding a few sub-factors to fit it to other domains by finding the relevant sub-factors that influence the likelihood of a failure or a crisis and applying the novel methodology. We do not claim that the proposed model, as depicted in
Figure 4, is optimal. Moreover, it is most probable that risk analysis in different sectors (e.g., financial vs. industrial sectors) will require a unique adaptation of the framework for better results. However, the level of granularity, as depicted in
Figure 3, and the generic definition of the sub-factors provided were sufficient for presenting our framework and its evaluation.
We analyzed the likelihood of an event failing and devised four main sub-factors that substantially influence this outcome. The following details represent the main sources used in our formula to calculate the likelihood of failure. In our descriptions, we used values ranging from 1 (low-risk grade) to 6 (high-risk grade), but these values are ad-hoc and can be arranged as desired.
Level of complexity—This, for example, can be described as the number of parts or moving parts in a mechanical system. In the context of a man-machine interface, it can be expressed as the number of options, elements, gauges, or operating buttons. In an organization, it can imply the number of functions or employees participating in a process. It can also be the number of outcomes and levels of entropy in the process. A value of 1 will signify low levels of complexity, while 6 will signify a high level of complexity.
Stability and predictability—The stability of a process can be viewed as the tolerance of the output in a process or the ability to predict a failure in a system based on its historical records. This is related to variance in the process and the ability to extrapolate an outcome based on the existing data and knowledge. In cases of randomness or stochastic process, the grade will be low, 1, and in a stable and deterministic process, the grade will be high, 6.
Command, control, and redundancy—This sub-factor relates to the mechanisms and procedures taking place in the process that aim to reduce or prevent the chance of problems. In susceptible system elements, redundancy can be crucial to minimize failure. In cases of a well-controlled and redundant system, we will grade it as low risk, 1; cases with no controls or redundancy will be graded as 6.
Knowledge, understanding, and training—Assessment of the organizational structure, organization culture, and human resource procedures that include training and qualifications to reduce sources of failure or crisis out of control. Another aspect of this sub-factor can be the auditor’s knowledge of the process and system. Proper knowledge, understanding, and training will result in a low-risk value of 1, while poor knowledge and experience will result in a high-risk value of 6.
2.5. A Computational Example of the Framework
As used in practice, the basic notion of calculating risk levels is based on one parameter representing the likelihood and one parameter representing the consequence—their multiplication results in the risk level that goes into the risk matrices. For example, when a procedure is assessed to have a likelihood level of 4 and a consequence of 5, the risk level of this procedure will result in . As pointed out in the body of this article, the consequence assessment is much more structured and easier to quantify, but the likelihood is more challenging to estimate due to its obscureness and fuzziness.
Using our proposed method for calculating the likelihood, we can see the following computation occurring:
First, we begin by computing the natural frequency of the event, f
(x). For instance, let us assume that the frequency of the event is 4 and the variance of frequency is 6. We compute f
(x) as 5 from these two and the likelihood matrix, the increase in frequency from 4 to 5 is due to the “fat tail” as given by the high variance level of 6 and can be clearly seen in
Figure 3. Next, we compute the likelihood of failure, f
(y). We measure and quantify the values of the four sub-factors as follows: complexity (C)
5, stability and predictability
, command, control, and redundancy (R)
4, and knowledge, understanding, and training (K)
4. We take their average and arrive at 4.75 (denoted as P). Finally, we can compute the likelihood of the risk occurring, which is the product of the two functions; therefore, it is
. In our opinion, the reconstruction of the likelihood function in the new framework is more precise, less biased, and volatile. In the next section, we test our hypothesis in questionnaires and the simulation of an operational process.
3. Experimental Design and Results
To evaluate and analyze the performance of our model, we designed and conducted both an experimental study by questionaries and a simulation of a process using the Monte Carlo approach. The experiments were designed to verify the claims that applying this framework will result in fewer variations among auditors of the same situation, comparing our new method to the traditional method.
3.1. Human Evaluation Study
The study was designed to compare two groups of independent auditors that receive the same descriptions of two operational processes in each company. We formed two groups of auditors: one that used the new risk assessment framework (by a few sub-factors), and the second group conducted the traditional framework (a single number). Each group of auditors was asked to assess two textual descriptions of an operational scenario containing (1) a low-risk and (2) a high-risk level; the auditors in the first group were asked to assess the risk level of the process by the new method of a few factors that combined to a calculated total risk score. The auditors in the second group were asked to do the same but with the traditional method of ranking the risk level by only one parameter between 1 (low) and 6 (high). Our goal was to realize whether the new framework significantly reduces the variance between auditors within the group compared to the second group, which uses traditional risk assessment methods.
We conducted this study twice. The first run was on a high-risk operational scenario due to poor controls, and the second was a scenario of a well-controlled operation resulting in a low-risk operation. For the auditors of the new method, we calculated the risk level based on the data of the sub-factors they produced.
The process we applied in this study consisted of 35 randomly selected auditors aged 30–60 who were asked to reply to an internet-based questionnaire. We designed the study so that each person received a text (see
Appendix A) that reflects a risk situation in an operational system. In one questionnaire, we were asked to assess the risk level traditionally (one score of 1–6 represents the risk level). In the other questionnaire, we were asked to assess the risk level using the new methodology by a set of six parameters (as explained in
Section 2.5). We compute the total risk score in the new framework by calculating the average risk level of the sub-factors that construct the event multiplied by the likelihood level.
The low-risk scenario study showed the following: The traditional method resulted in an average likelihood score of 2.189 compared to a low average likelihood score of 0.806 when using the new method. Similarly, the variance of the results was 1.126 for the traditional method and 0.21 for the new method. This amounts to a reduction of 76.14% in the variance between the groups. The difference in variance was significant using an analysis of variance test (p 0.00194).
In the second part of the study, the high-risk scenario, the number of auditors was 35, and the results showed the following: The traditional method resulted in an average likelihood score of 5.058 compared to a low average likelihood score of 3.663 when using the new method. Similarly, the variance of the results was 0.306 for the traditional method and 0.073 for the new method. This amounts to a reduction of 81.35% in the variance between the groups. This study’s results proved significant as we computed a p < 0.001 using an analysis of variance test.
3.2. Simulation Study
A complementary study to assess the mathematical validity of our proposed method was conducted using a Monte Carlo simulation. The simulation included two groups of randomly selected scores; the first group generated a single factor score, and the second group was programmed to generate six parameters that represent the sub-factors of the framework and calculated the total likelihood score based on the formula. We simulated 1998 iterations and then conducted the same Levene test, (
Lim and Loh 1996) using the same procedure we used in the human evaluation study. The simulation was performed in different cases ranging from low-risk to mid-risk and high-risk scenarios that were tuned by the tolerance of the intervals of the random scores’ generator. We then tested the
p-values to check the equality of variance between groups of traditional and new methods of risk assessments. The results of Levene’s test of the simulations reflect significantly lower variance in the new methodology.
The low-risk scenario simulation showed that the traditional method resulted in an average of 0.32985 likelihood compared to 0.10025 when using the new method. Similarly, the variance was 0.06137 for the traditional method and 0.010733 for the new method. This amounts to a reduction of 82.51% in the variance between the groups. The difference in variance was significant using an analysis of variance with Levene’s test (F 1628.75; p 5.4204 × 10−299).
The medium-risk scenario simulation showed that the traditional method resulted in an average of 0.5841 compared to 0.2667 when using the new method. Similarly, the variance of the traditional method was 0.033185 and 0.015682 for the new method. This amounts to a reduction of 53.34% in the variance between the groups. The difference in variance was significant using Levene’s test (F = 506.47; p 1.0708 × 10−105).
Last, the high-risk scenario simulation showed that the traditional method resulted in an average of 0.733183 likelihood compared to 0.61941 when using the new method. Similarly, the variance was 0.04697 for the traditional method and 0.03448 for the new method. The difference in variance was significant using an analysis of variance with Levene’s test (F 4.93; p 0.0264), although the improvement in this case is much lower.
4. Discussion
The results of both the questionnaire study and the simulations point out that the methodology of sub-factor assessments and calculating, as we suggest, can significantly reduce the variance of the likelihood risk score comparing the traditional method of one-factor assessment. In the questionnaire study, we received p-values that ranged between 0.00194 and 0.000679 and a substantial variance reduction of 76.14–81.35%. The simulation study of a similar structure resulted in a very significant improvement of variance reduction and p-values in the range of 0.0264–5.4204 × 10−299 and variance reduction improvement up to 82.5%. In this study, we also found an interesting fact in the simulations: the improvement in variation was greater in lower-risk and medium-risk scenarios compared to the high-risk scenarios. This can lead to future research and analyses to identify the causes that may occur due to the closeness to the limit of 100% likelihood in high-risk situations.
The main reason for breaking down each event to its predecessors is to get to the root cause of the given event and reduce their interdependencies. In many cases, weak or strong interactions between sub-factors may produce positive or negative feedback or cross-action (“noise”). We address this situation by trying to give each sub-factor the risk level as objective as possible and by applying the formula that calculates the average risk level of all the sub-factors, which increases the precision and reduces the “noise” that can be an effect of these unobserved interactions. In future work, we will suggest continuing with deconstructing more layers of the cause factors to increase the accuracy and objectivity.
We believe applying the new methodology can be useful in practice and research. The segmentation of the likelihood factor into its sub-factors and calculation in the proposed formula that considers the frequency and the variance of the expected likelihood of conditions to risk occurrence combined with the average factors of a failure, given the basic conditions, can reduce errors and bias in the assessment.
5. Conclusions
In our research, we addressed the issue of reducing the uncertainty and bias due to the subjectivity of human auditors that conduct risk assessments. Our direction was that segmenting likelihood into its sub-factors could reduce the risk level assessment variance. In this work, we did not focus on the consequence part of the risk equation (i.e., risk = likelihood × consequence) and only tried to improve the precision of the likelihood factor. We designed and conducted a study of two groups of auditors. One used the new framework, and the second assessed the same process in the regular method of a single likelihood parameter. We expanded the research with a simulation in the same approach. Analysis of the questionnaire study results and the simulation of the risk assessment process conclude that there is an improvement in precision in applying the new framework by a significant reduction in the variance of risk assessment.
The new framework that we developed is easy to apply. The formula for calculating the likelihood of risk was tested and compared to the traditional risk assessment process that does not apply segmentation of sub-factors. The research shows that it is feasible to have accurate and precise assessments when applying a simple-to-use model. This framework has many applications and can be easily adopted in industry. Our vision is to continue in this line of action to reduce the biases and uncertainty in risk management by applying a mathematical formula used in a large database and refining the accuracy by fine-tuning the sub-factors and their ranges.
Regarding the limitation of our study, first and foremost, it was conducted on a relatively small sample of human auditors and had only two different risk scenarios. Although we robustly conducted the study by conducting a large-scale simulation (30 runs of 1998 respondents each), it will be worthwhile to increase the sample size and try to add more sub-factors to increase the resolution and sensitivity of the risk assessment.
Future studies can take various paths. One research study can improve both the accuracy and precision of likelihood assessment by combining machine learning techniques that can fit a well-known likelihood level to some sub-factors that we estimate and to be able to predict by the algorithm the precise and accurate risk level that fits best with the sub-factors that we find in the process. Another future research challenge could be adding one more layer to the DAG model that may allow the deconstructing of the sub-factors to another level, increasing the precision and sensitivity of the assessment process even further. Finally, one can also conduct a broader experimental setting by comparing human auditors using the new framework on a more varied set of industries and organizations. Applying this new framework to large-scale data can be useful for training a deep learning model that may reduce uncertainty in risk assessment missions. In this paper, we focused primarily on applying this novel framework as a new concept in the industry. The initial results are good, but in future work, we can try to increase the precision and accuracy of the modal by “fine-tuning” the parameters with the adjustments of weights of the sub-factors to the model.