Pricing of Pseudo-Swaps Based on Pseudo-Statistics †
Abstract
Preface
1. Introduction
2. Pseudo-Statistics
3. Pseudo-Swaps
3.1. Swaps
3.2. Pseudo-Swaps
4. Financial Data Used
- –
- Apple Inc. (AAPL)
- –
- Alphabet Inc. Class C (GOOG).
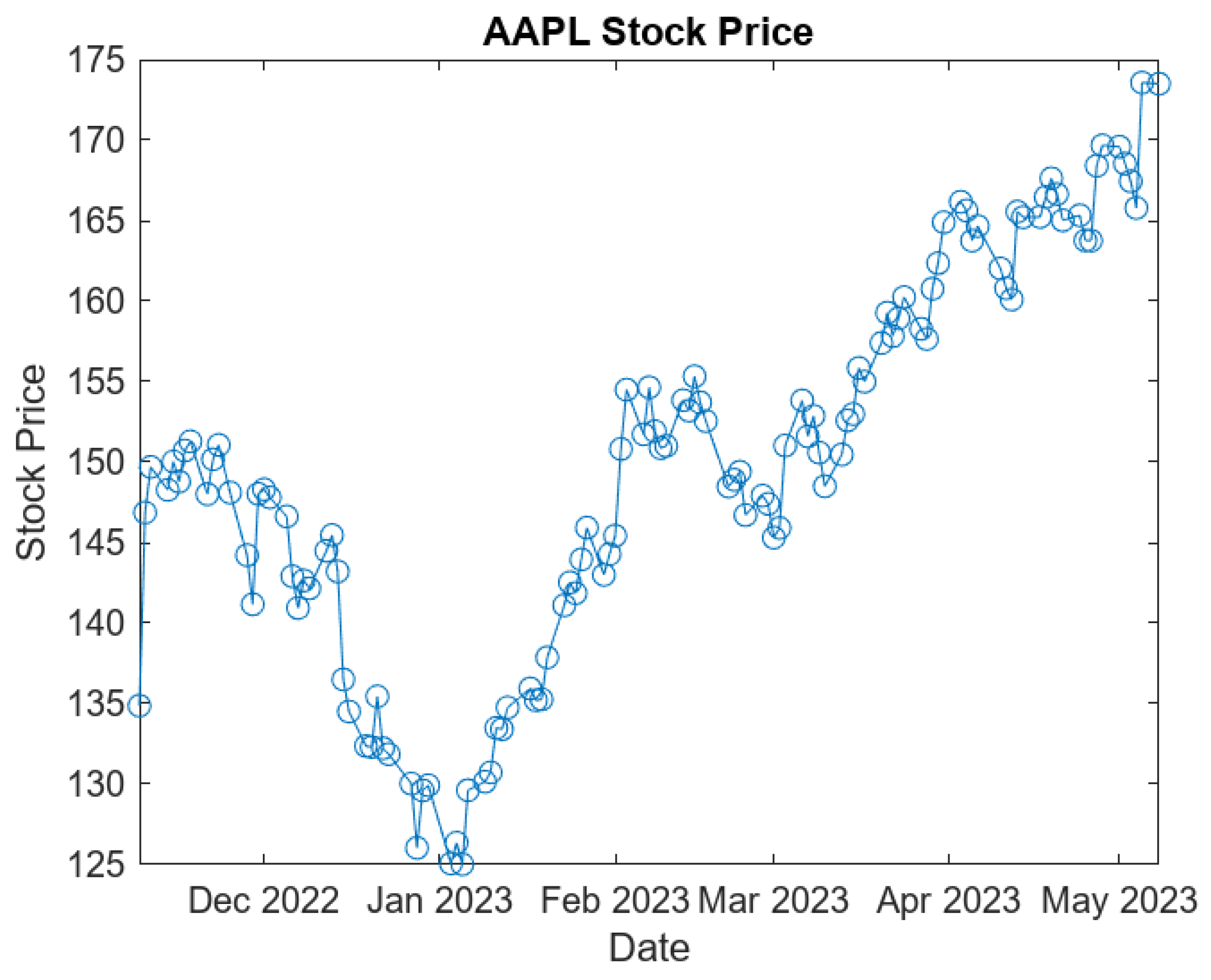
4.1. 6-Month Data Sets
- –
- Time in Years of First Data Entry:
- –
- Time in Years of Last Data Entry:
- –
- Duration of Data Collection in Years: .
- AAPL Daily Closing Data at time :
- GOOG Daily Closing Data at time :
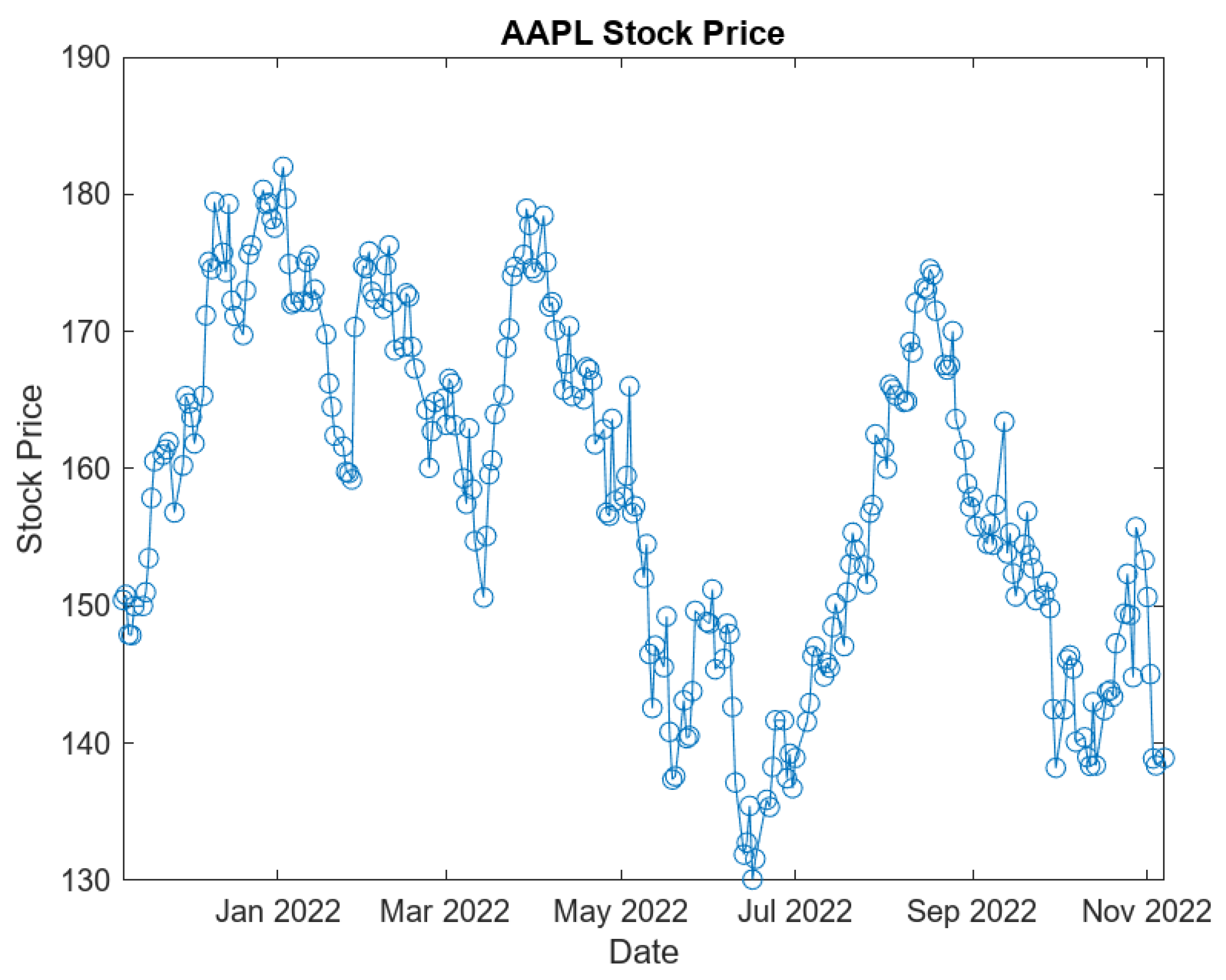
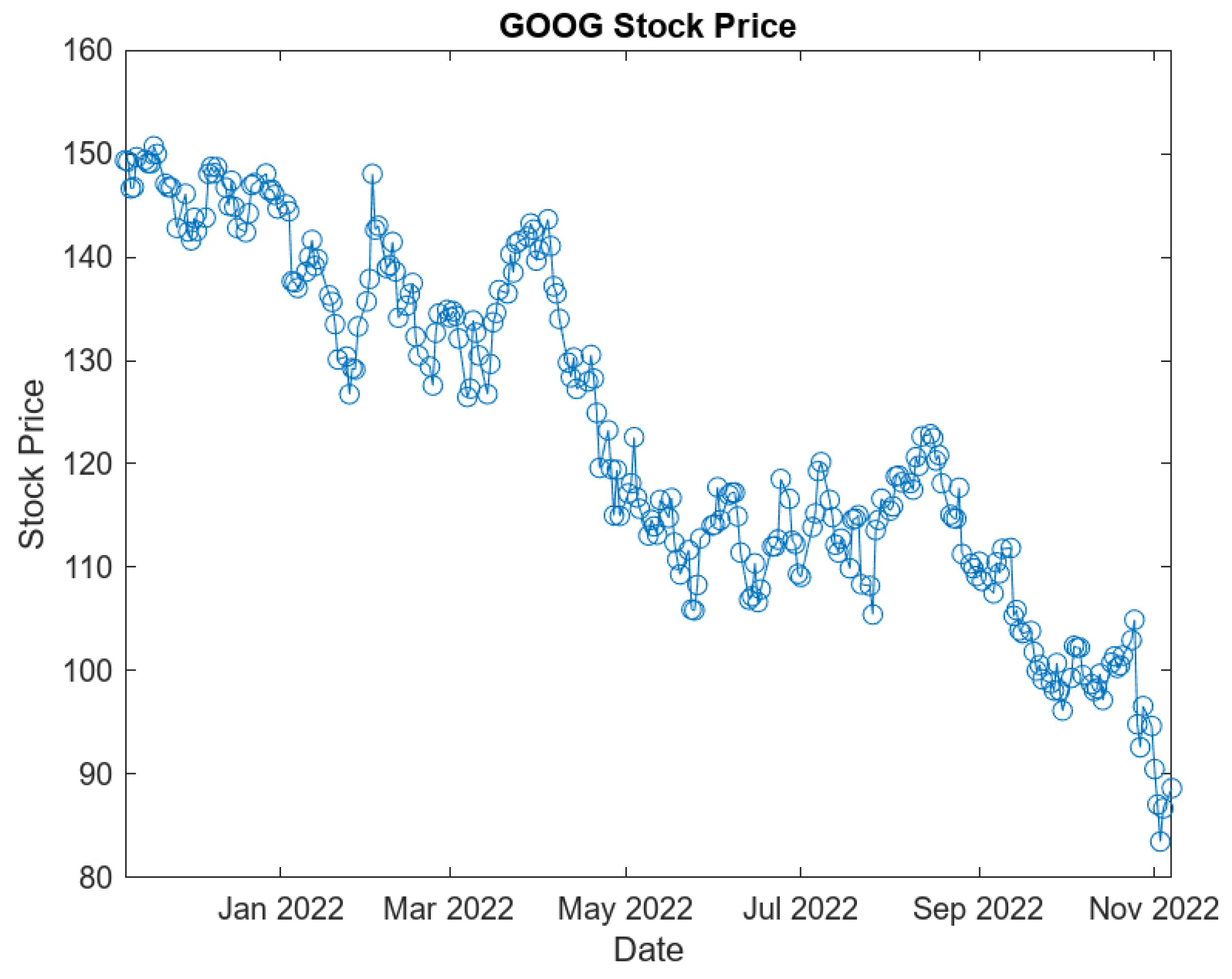
4.2. One-Year Data Sets
- –
- Time in Years of First Data Entry:
- –
- Time in Years of Last Data Entry:
- –
- Duration of Data Collection in Years: .
- AAPL Daily Closing Data at time :
- GOOG Daily Closing Data at time :
5. Logarithmic Return of Stock Price
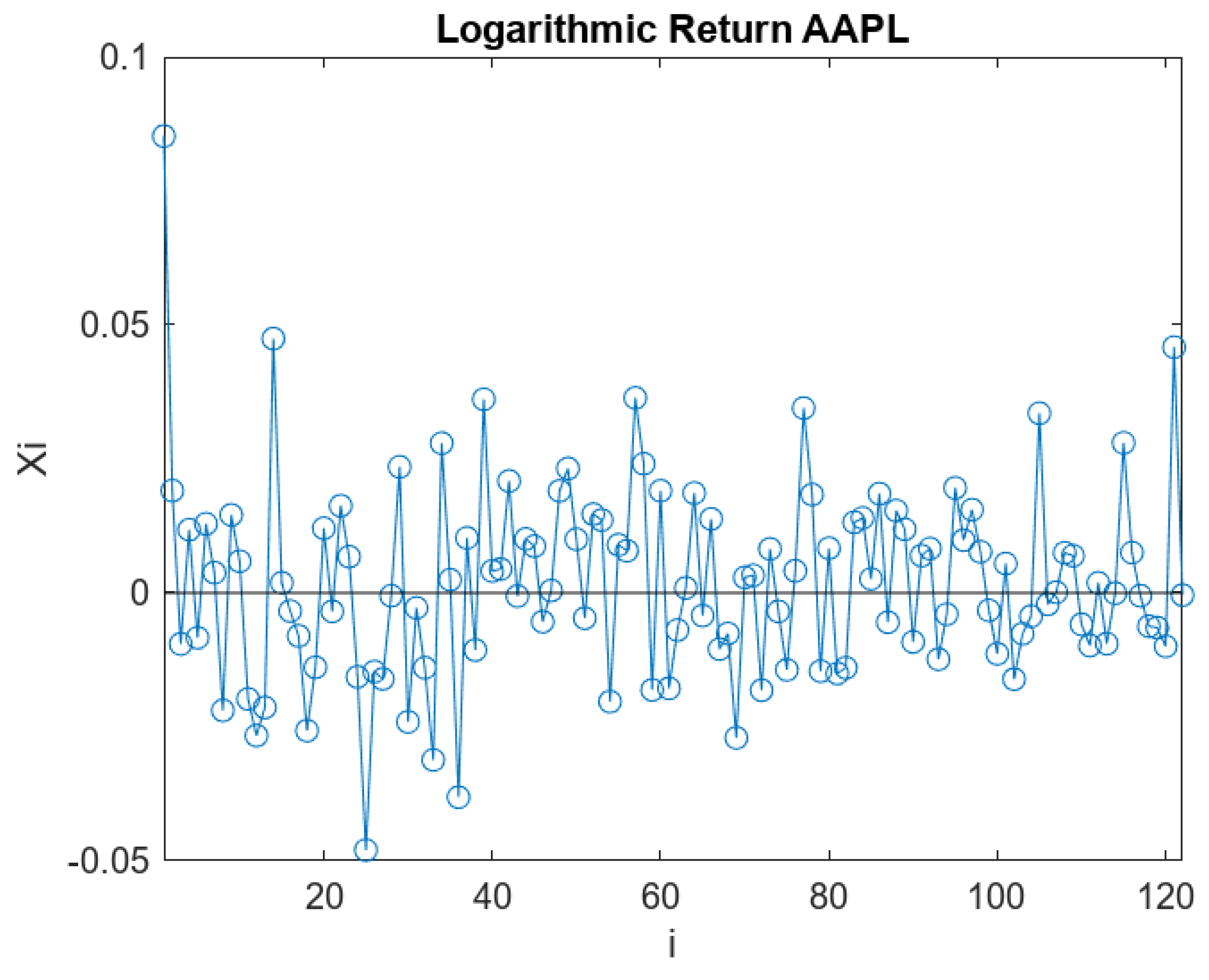
5.1. 6-Month Data Sets: Logarithmic Return and Arithmetic Mean
- Logarithmic Return of AAPL:
- Arithmetic Mean of :
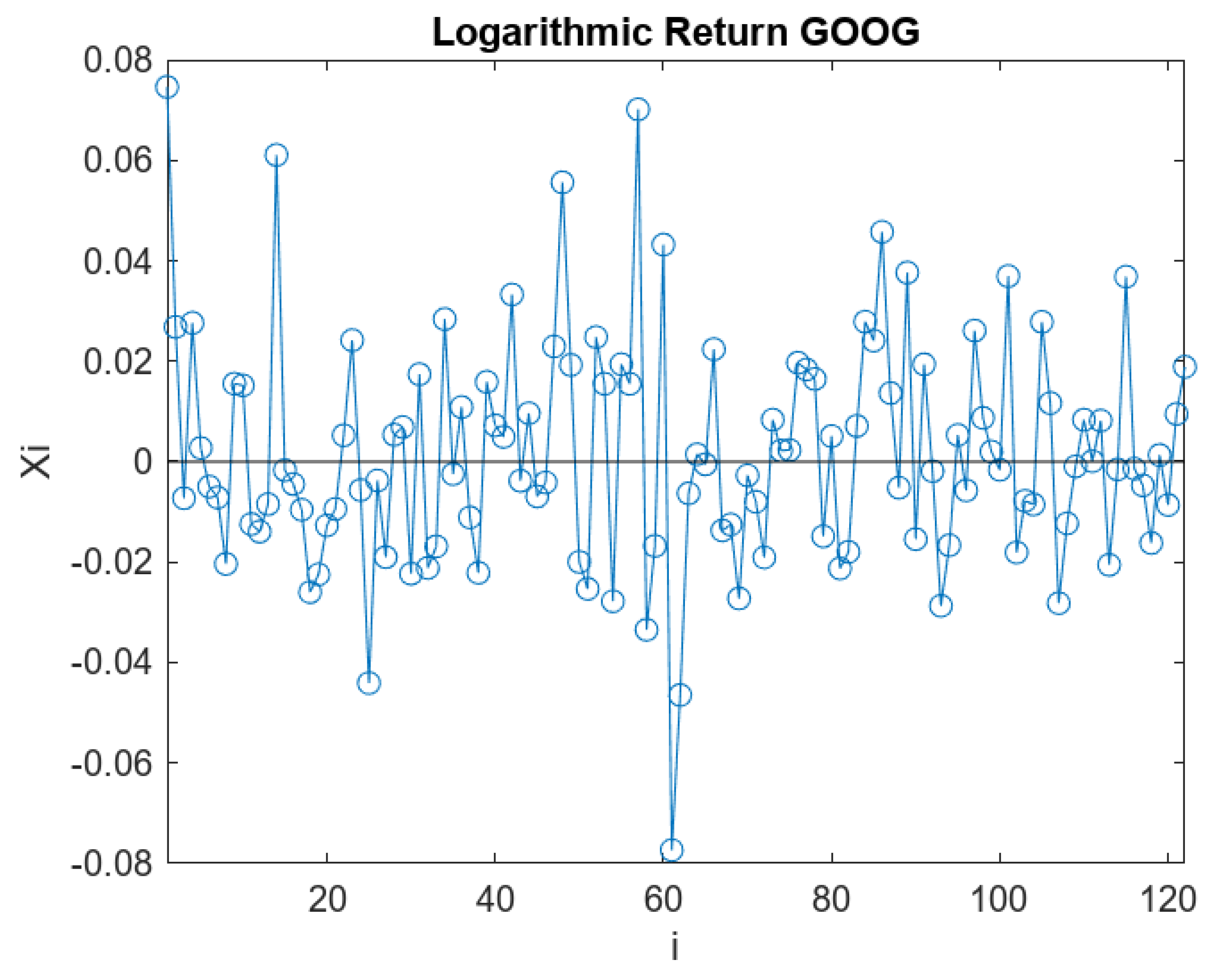
- Logarithmic Return of GOOG:
- Arithmetic Mean of :
5.2. One-Year Data Sets: Logarithmic Return and Arithmetic Mean
- Logarithmic Return of AAPL:
- Arithmetic Mean of :
- Logarithmic Return of GOOG:
- Arithmetic Mean of :
6. Expected Sample Variance and Brockhaus–Long Approximation for Expected Sample Volatility
- –
- Maturity Date in Years: T
- –
- Number of Logarithmic Return Entries: n.
- –
- GARCH(1,1) Constant: C
- –
- Kurtosis of Logarithmic Returns: .
6.1. AAPL: Expected Variance and Volatility
- –
- Maturity Date in Years:
- –
- Number of Logarithmic Return Entries:
- –
- Kurtosis of AAPL Logarithmic Returns:
- –
- Short Volatility: .
- Expected Sample Variance:
- Expected Sample Volatility:
6.2. GOOG: Expected Variance and Volatility
- –
- Maturity Date in Years:
- –
- Number of Logarithmic Return Entries:
- –
- Kurtosis of GOOG Logarithmic Returns:
- –
- Short Volatility: .
- Expected Sample Variance:
- Expected Sample Volatility:
7. Realized Pseudo-Volatility Square and Pseudo-Variance Swap Payoff
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
7.1. AAPL: Realized Pseudo-Volatility Square and Pseudo-Variance Swap Payoff
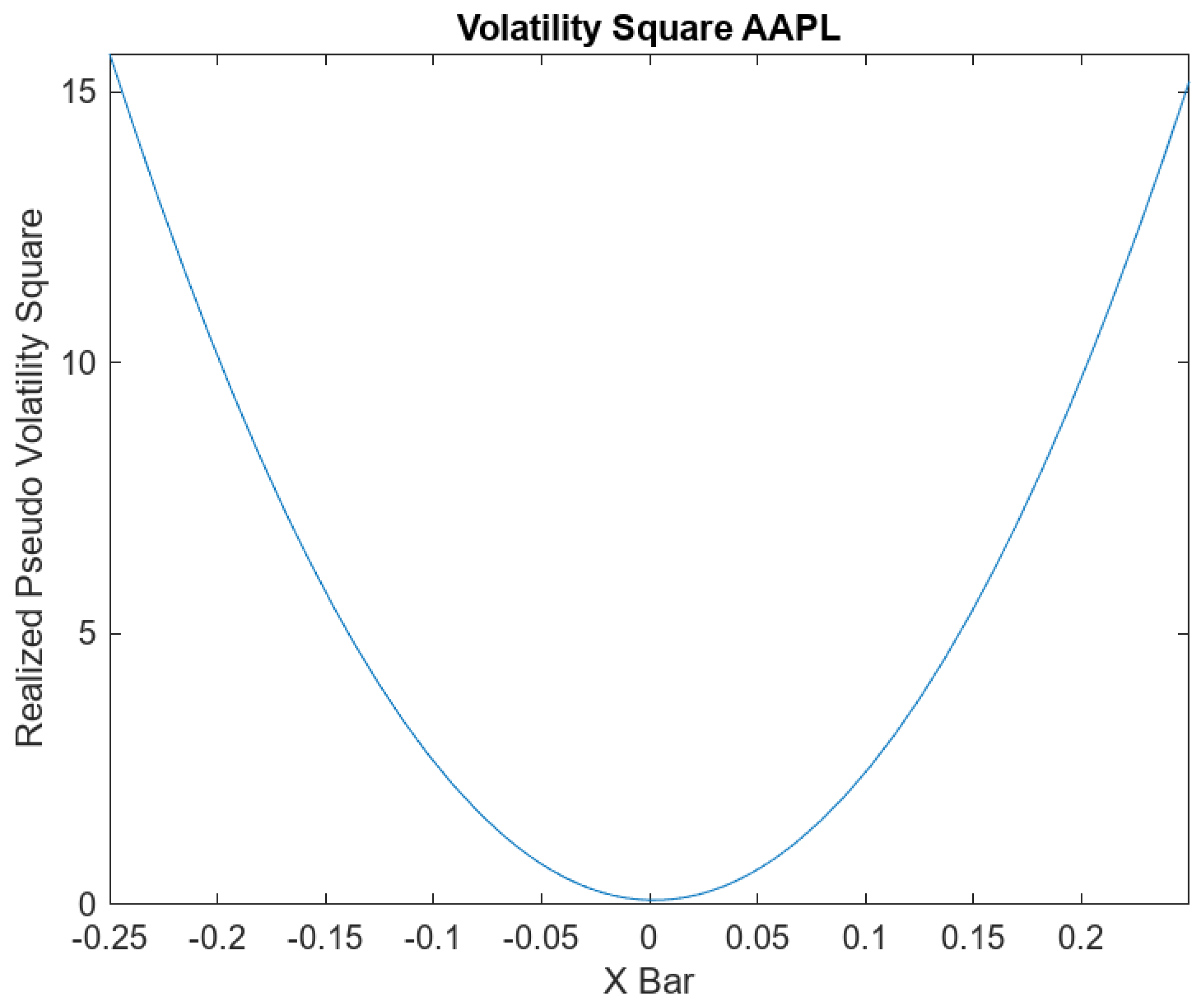
- Realized Pseudo-Volatility Square of AAPL:
- –
- Maturity Date:
- –
- Position Taken: .
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Variance Swap with Underlying of Variance of AAPL:
7.2. GOOG: Realized Pseudo-Volatility Square and Pseudo-Variance Swap Payoff
- Realized Pseudo-Volatility Square of GOOG:
- –
- Maturity Date:
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Variance Swap with Underlying of Variance of GOOG:
8. Realized Pseudo-Volatility and Pseudo-Volatility Swap Payoff
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
8.1. AAPL: Realized Pseudo-Volatility and Pseudo-Volatility Swap Payoff
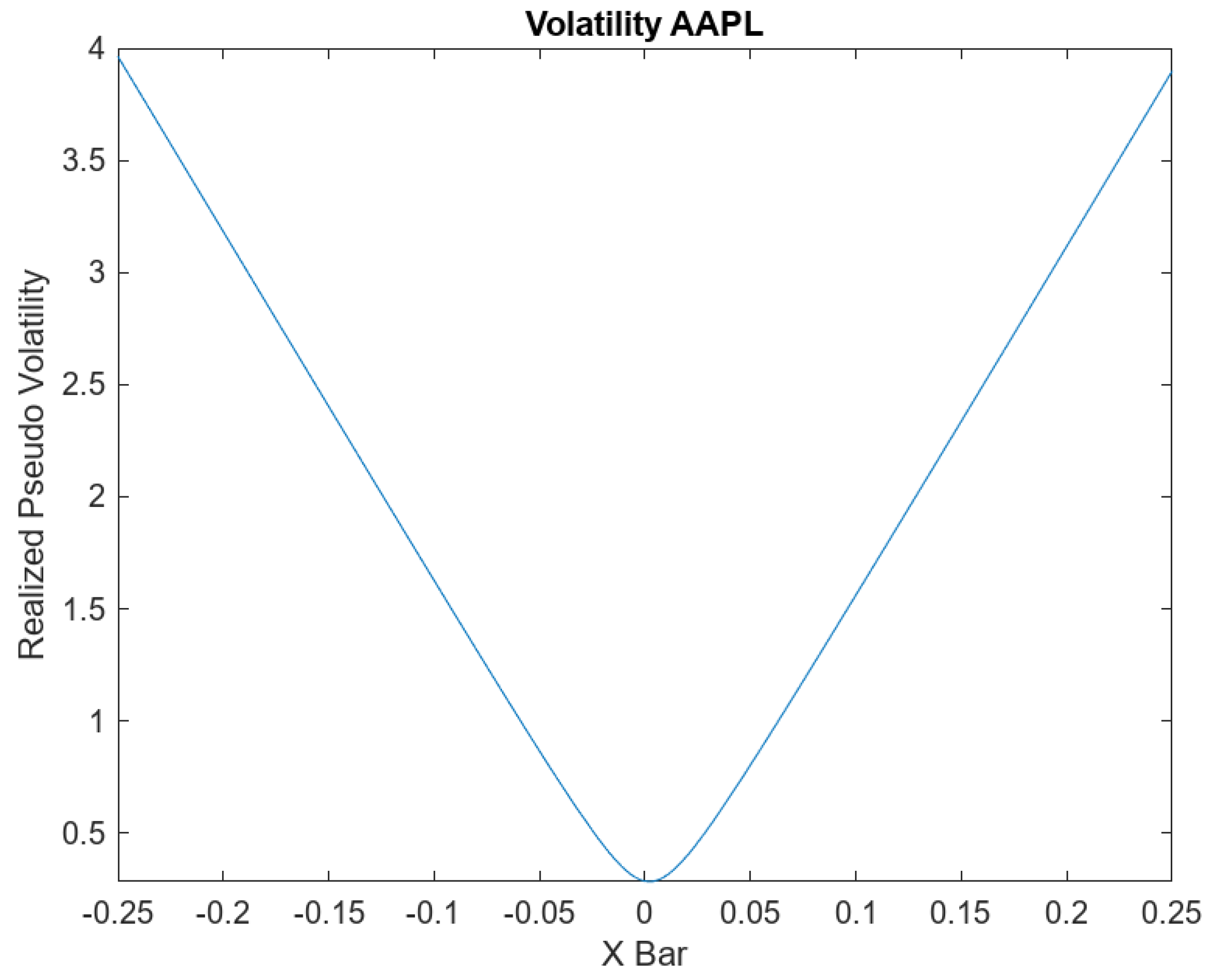
- Realized Pseudo-Volatility of AAPL:
- –
- Maturity Date:
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Volatility Swap with Underling of Volatility of AAPL:
8.2. GOOG: Realized Pseudo-Volatility and Pseudo-Volatility Swap Payoff
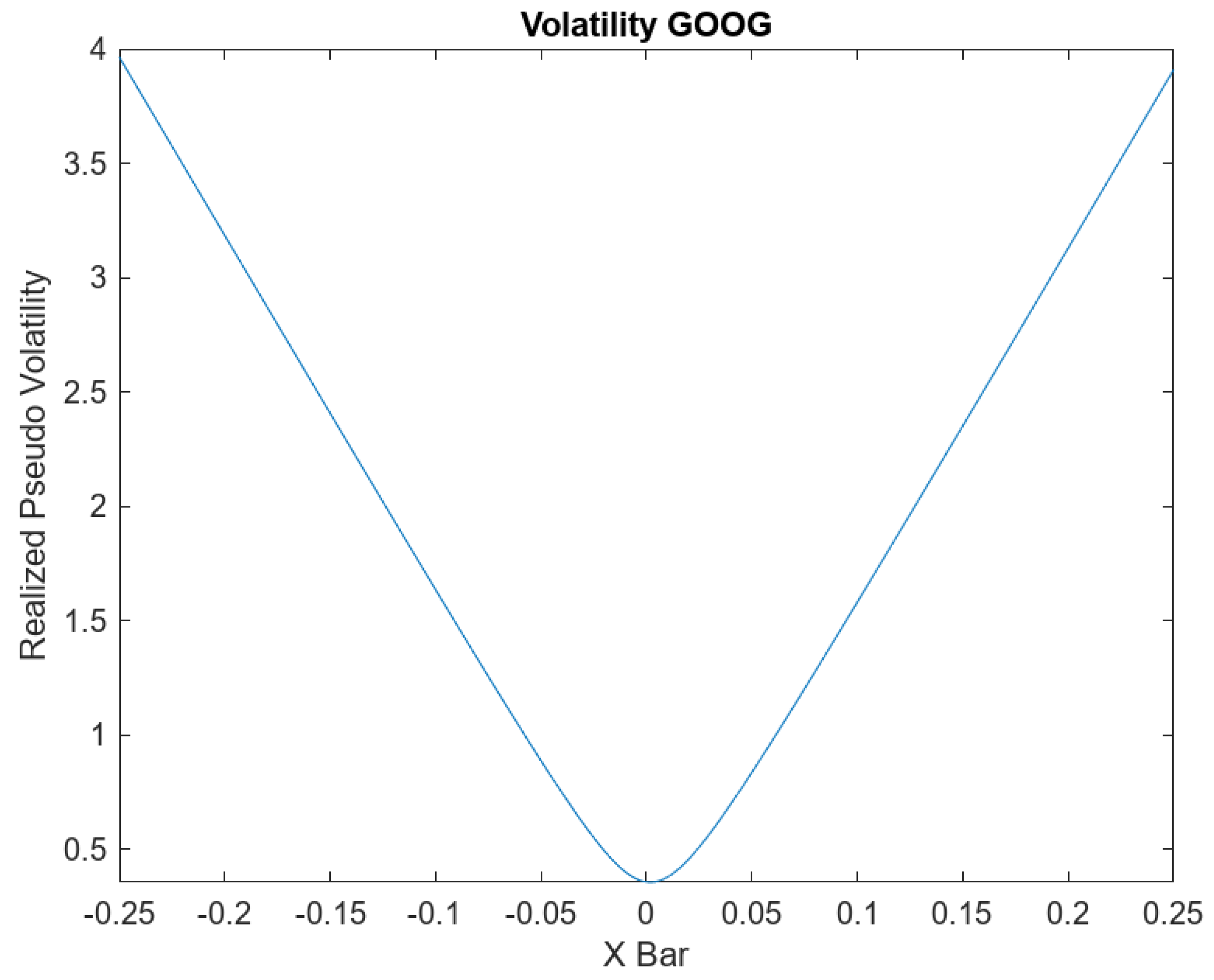
- Realized Pseudo-Volatility of GOOG:
- –
- Maturity Date:
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Volatility Swap with Underling of Volatility of GOOG:
9. Expected Sample Covariance
9.1. : Expected Variance
- –
- Maturity Date in Years:
- –
- Number of Logarithmic Return Entries:
- –
- Kurtosis of GOOG Logarithmic Returns:
- –
- Short Volatility: .
- Expected Sample Variance:
9.2. : Expected Variance
- –
- Maturity Date in Years:
- –
- Number of Logarithmic Return Entries:
- –
- Kurtosis of GOOG Logarithmic Returns:
- –
- Short Volatility: .
- Expected Sample Variance:
9.3. Calculating the Expected Sample Covariance of AAPL and GOOG
- Expected Sample Covariance of AAPL and GOOG:
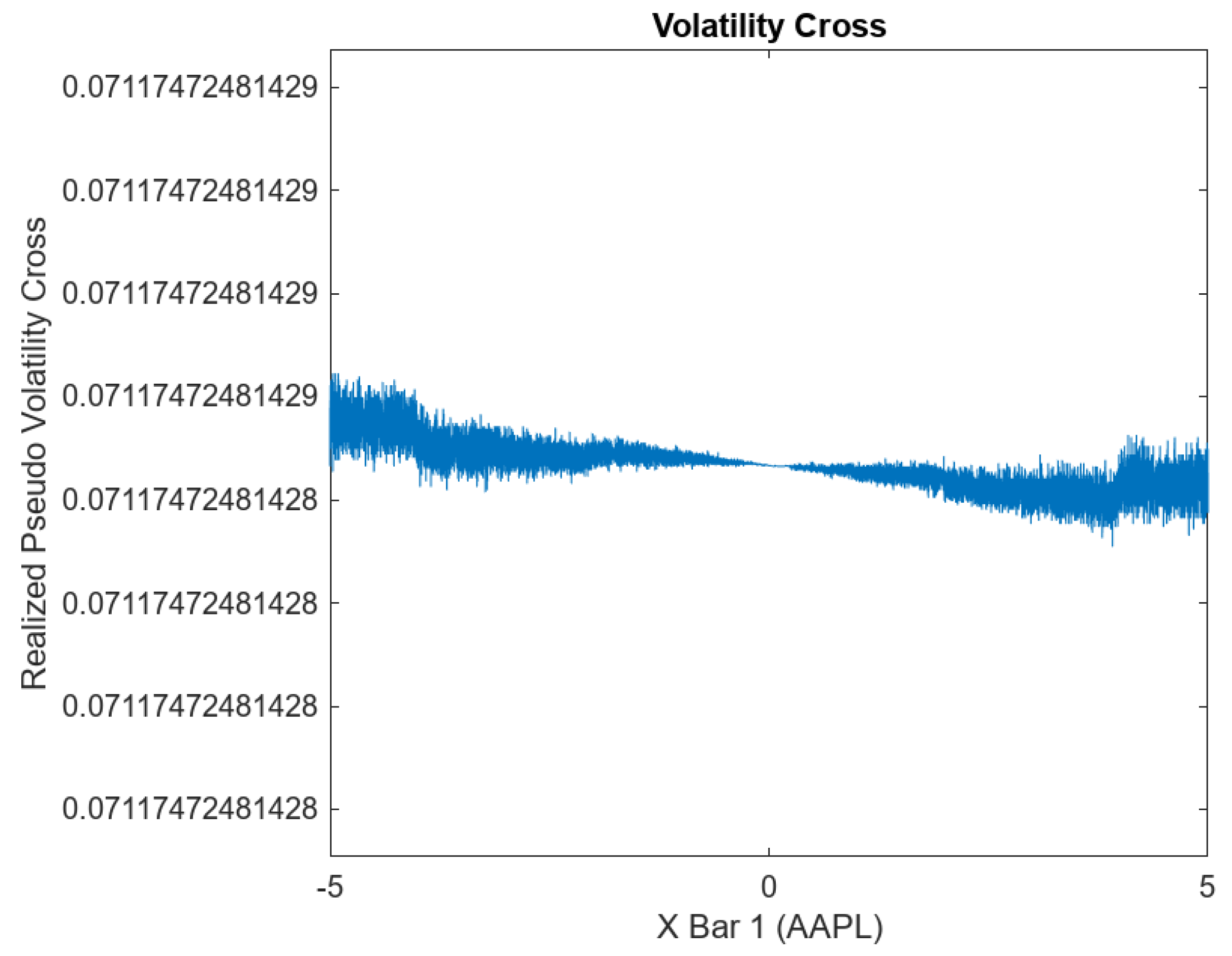
10. Realized Pseudo-Volatility Cross and Pseudo-Covariance Swap Payoff
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Realized Pseudo-Volatility Cross of AAPL and GOOG:
- –
- Maturity Date:
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Covariance Swap with Underlying of Covariance of AAPL and GOOG:
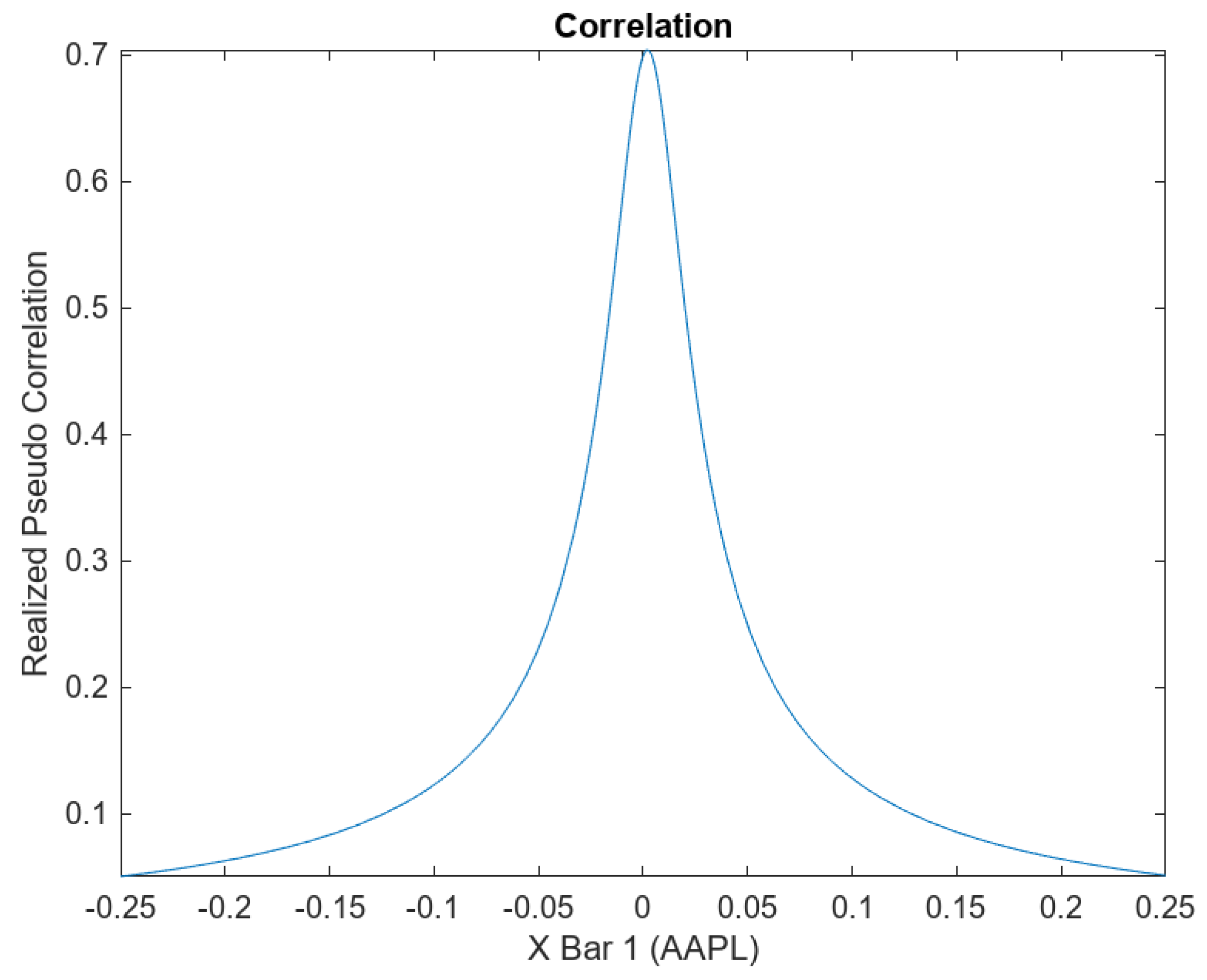
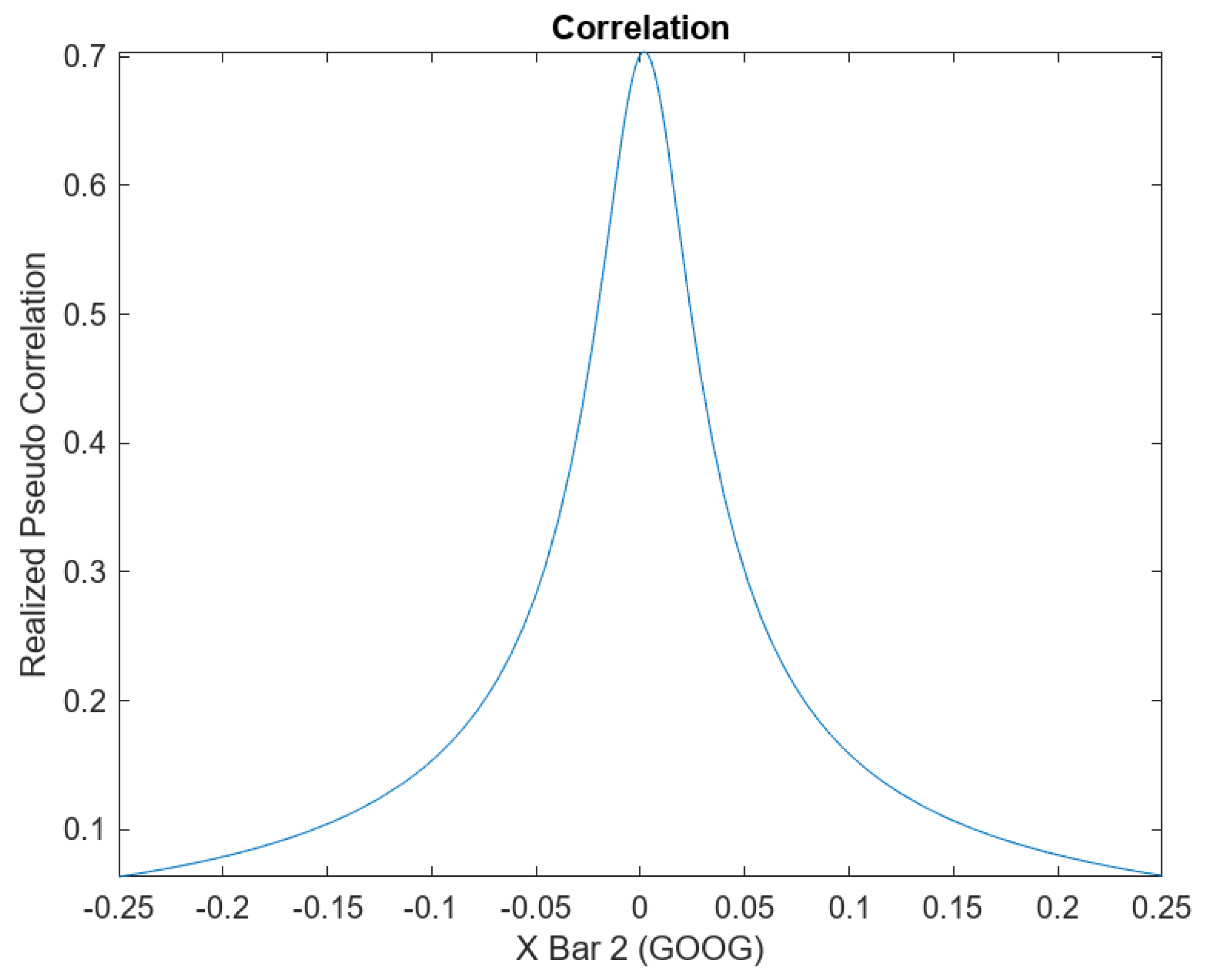
11. Realized Pseudo-Correlation and Pseudo-Correlation Swap Payoff
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Realized Pseudo-Correlation of AAPL and GOOG:
- –
- Maturity Date:
- –
- Position Taken:
- –
- Converting Parameter:
- –
- Strike Price: .
- Payoff of Pseudo-Correlation Swap with Underlying of Covariance of AAPL and GOOG:
12. Comparing the Approach Based on the Cox–Ingresoll–Ross Model to the Realized Pseudo-Statistic Approach
- –
- Apple Inc. (AAPL)
- –
- Alphabet Inc. Class C (GOOG)
13. Realized Variance and Variance Swap Payoff
13.1. Calculating the Realized Discretely Sampled Variance Using the CIR Model
- –
- Maturity Date:
- –
- Number of Logarithmic Return Data Points: .
- AAPL Realized Discretely Sampled Variance:
- –
- Maturity Date:
- –
- Number of Logarithmic Return Data Points: .
- GOOG Realized Discretely Sampled Variance:
13.2. Variance Swap Payoffs
- –
- Strike Price AAPL
- –
- Strike Price GOOG .
- AAPL Variance Swap Payoff:
- GOOG Variance Swap Payoff:
14. Realized Volatility and Volatility Swap Payoff
14.1. Calculating the Realized Discretely Sampled Volatility Using the CIR Model
- AAPL Realized Discretely Sampled Volatility:
- GOOG Realized Discretely Sampled Volatility:
14.2. Volatility Swap Payoffs
- –
- Strike Price AAPL
- –
- Strike Price GOOG .
- AAPL Volatility Swap Payoff:
- GOOG Volatility Swap Payoff:
15. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| CIR | Cox–Ingresoll–Ross |
| AAPL | Apple Inc. |
| GOOG | Alphabet Inc. Class C |
References
- Badescu, Andrei, Anatoliy Swishchuk, Raymond Cheng, Stephan Lawi, Hammouda Mekki, Asrat Gashaw, Yuanyuan Hua, Marat Molyboga, Tereza Neocleous, and Yuri Petratchenko. 2002. Price Pseudo-Variance, Pseudo-Covariance, Pseudo-Volatility, and Pseudo-Correlation Swaps-In Analytical Closed-Forms. In Sixth PIMS Industrial Problems Solving Workshop. Vancouver: University of British Columbia, pp. 45–55. [Google Scholar]
- Benth, Fred Espen, Martin Groth, and Rodwell Kufakunesu. 2007. Valuing Volatility and Variance Swaps for a Non-Gaussian Ornstein–Uhlenbeck Stochastic Volatility Model. Applied Mathematical Finance 14: 347–63. [Google Scholar] [CrossRef]
- Brenner, Menachem, and Dan Galai. 1989. New Financial Instruments for Hedging Changes in Volatility. Financial Analysts Journal 45: 61–65. [Google Scholar] [CrossRef]
- Brenner, Menachem, and Dan Galai. 1993. Hedging Volatility in Foreign Currencies. The Journal of Derivatives 1: 53–59. [Google Scholar] [CrossRef]
- Brenner, Menachem, and Dan Galai. 1996. Options on Volatility. In Option Embedded Bonds: Price Analysis, Credit Risk and Investment Strategies. Edited by Israel Nelken. New York: Irwin Professional Pub, pp. 273–86. [Google Scholar]
- Brockhaus, Oliver, and Douglas Long. 2000. Volatility Swaps Made Simple. Risk-London Magazine Limited 13: 92–96. [Google Scholar]
- Carr, Peter, and Dilip Madan. 2001. Towards a theory of volatility trading. In Option Pricing, Interest Rates and Risk Management, Handbooks in Mathematical Finance. Cambridge: Cambridge University Press, vol. 22, pp. 458–76. [Google Scholar]
- Carr, Peter, and Roger Lee. 2009. Volatility Derivatives. Annual Review of Financial Economics 1: 319–39. [Google Scholar] [CrossRef]
- Demeterfi, Kresimir, Emanuel Derman, Michael Kamal, and Joseph Zou. 1999. A guide to volatility and variance swaps. The Journal of Derivatives 6: 9–32. [Google Scholar] [CrossRef]
- Derman, Emanuel, Iraj Kani, and Michael Kamal. 1997. Trading and hedging local volatility. Journal of Financial Engineering 6: 233–68. [Google Scholar]
- Dupire, Bruno. 1993. Model art. Risk 6: 118–24. [Google Scholar]
- Dupire, Bruno. 1996. A unified theory of volatility. In Derivatives Pricing: The Classic Collection. London: Risk Books London, pp. 185–96. [Google Scholar]
- Fleming, Jeff, Barbara Ostdiek, and Robert E. Whaley. 1995. Predicting stock market volatility: A new measure. The Journal of Futures Markets (1986–1998) 15: 265. [Google Scholar]
- Galai, Dan. 1979. A proposal for indexes for traded call options. The Journal of Finance 34: 1157–72. [Google Scholar] [CrossRef]
- Gastineau, Gary L. 1977. An index of listed option premiums. Financial Analysts Journal 33: 70–75. [Google Scholar] [CrossRef]
- Grünbichler, Andreas, and Francis A. Longstaff. 1996. Valuing futures and options on volatility. Journal of Banking & Finance 20: 985–1001. [Google Scholar]
- Habtemicael, Semere, and Indranil Sengupta. 2016a. Pricing Covariance Swaps for Barndorff-Nielsen and Shephard Process Driven Financial Markets. Annals of Financial Economics 11: 1650012. [Google Scholar] [CrossRef]
- Habtemicael, Semere, and Indranil Sengupta. 2016b. Pricing Variance and Volatility Swaps for Barndorff-Nielsen and Shephard Process Driven Financial Markets. International Journal of Financial Engineering 3: 1650027. [Google Scholar] [CrossRef]
- Issaka, Aziz, and Indranil SenGupta. 2017. Analysis of Variance based Instruments for Ornstein–Uhlenbeck Type Models: Swap and Price Index. Annals of Finance 13: 401–34. [Google Scholar] [CrossRef]
- Javaheri, Alireza, Paul Wilmott, and Espen Haug. 2004. GARCH and Volatility swaps. Quantitative Finance 4: 589–95. [Google Scholar] [CrossRef]
- Neuberger, Anthony. 1994. The Log Contract. The Journal of Portfolio Management 20: 74–80. [Google Scholar] [CrossRef]
- Neuberger, Anthony J. 1990. Volatility Trading. London: Institute of Finance and Accounting, London Business School. [Google Scholar]
- Salvi, Giovanni, and Anatoliy V. Swishchuk. 2014. Covariance and Correlation Swaps for Financial Markets with Markov-Modulated Volatilities. International Journal of Theoretical and Applied Finance 17: 1450006. [Google Scholar] [CrossRef]
- Schoutens, Wim. 2005. Moment swaps. Quantitative Finance 5: 525–30. [Google Scholar] [CrossRef]
- Sengupta, Indranil. 2016. Generalized BN-S Stochastic Volatility Model for Option Pricing. International Journal of Theoretical and Applied Finance 19: 1650014. [Google Scholar] [CrossRef]
- Swishchuk, Anatoliy. 2004. Modeling of Variance and Volatility Swaps for Financial Markets with Stochastic Volatilities. Wilmott Magazine 2: 64–72. [Google Scholar]
- Swishchuk, Anatoliy. 2005. Modelling and Pricing for Stochastic Volatilities with Delay. Wilmott Magazine 19: 63–73. [Google Scholar]
- Swishchuk, Anatoliy. 2006. Modeling and pricing of variance swaps for multi-factor stochastic volatilities with delay. Canadian Applied Mathematics Quarterly 14: 439–67. [Google Scholar]
- Swishchuk, Anatoliy, and Nelson Vadori. 2014. Smiling for the Delayed Volatility Swaps: Smiling for the Delayed Volatility Swaps. Wilmott 2014: 62–73. [Google Scholar] [CrossRef][Green Version]
- RBC Financial Group Team. 2002. Price Pseudo-Variance, Pseudo-Covariance, Pseudo-Volatility, and Pseudo-Correlation Swaps-in Analytical Close Form. In Proceedings of the 6th Annual PIMS Industrial Problem Solving Workshop. Vancouver: University of British Columbia. [Google Scholar]
- Whaley, Robert E. 1993. Derivatives on market volatility: Hedging tools long overdue. The Journal of Derivatives 1: 71–84. [Google Scholar] [CrossRef]





| Value | Standard Error | T Statistic | p Value | |
|---|---|---|---|---|
| Constant | ||||
| GARCH{1} | ||||
| ARCH{1} |
| Value | Standard Error | T Statistic | p Value | |
|---|---|---|---|---|
| Constant | ||||
| GARCH{1} | ||||
| ARCH{1} |
| Value | Standard Error | T Statistic | p Value | |
|---|---|---|---|---|
| Constant | ||||
| GARCH{1} | ||||
| ARCH{1} |
| Value | Standard Error | T Statistic | p Value | |
|---|---|---|---|---|
| Constant | ||||
| GARCH{1} | 1 | |||
| ARCH{1} | 1 |
| Value Obtained November 2022 to May 2023 | Using CIR Model | Using Realized Pseudo-Statistic Approach |
|---|---|---|
| AAPL Realized Variance | 0.0816 | 0.0805 |
| GOOG Realized Variance | 0.1277 | 0.1269 |
| AAPL Variance Swap Payoff | 0.0684 | 0.0673 |
| GOOG Variance Swap Payoff | 0.1094 | 0.1086 |
| AAPL Realized Volatility | 0.2856 | 0.2838 |
| GOOG Realized Volatility | 0.3574 | 0.3563 |
| AAPL Volatility Swap Payoff | 0.1758 | 0.1740 |
| GOOG Volatility Swap Payoff | 0.2307 | 0.2296 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franco, S.; Swishchuk, A. Pricing of Pseudo-Swaps Based on Pseudo-Statistics. Risks 2023, 11, 141. https://doi.org/10.3390/risks11080141
Franco S, Swishchuk A. Pricing of Pseudo-Swaps Based on Pseudo-Statistics. Risks. 2023; 11(8):141. https://doi.org/10.3390/risks11080141
Chicago/Turabian StyleFranco, Sebastian, and Anatoliy Swishchuk. 2023. "Pricing of Pseudo-Swaps Based on Pseudo-Statistics" Risks 11, no. 8: 141. https://doi.org/10.3390/risks11080141
APA StyleFranco, S., & Swishchuk, A. (2023). Pricing of Pseudo-Swaps Based on Pseudo-Statistics. Risks, 11(8), 141. https://doi.org/10.3390/risks11080141






