Formulating MCoVaR to Quantify Joint Transmissions of Systemic Risk across Crypto and Non-Crypto Markets: A Multivariate Copula Approach
Abstract
:1. Introduction
2. Multivariate Risk Models
2.1. Benchmark Models
2.2. Johnson’s Models
- System of Bounded Distributions (SB)This system is derived using , with and . The resulting distribution for is bounded since
- System of Lognormal Distributions (SL)This system is constructed using , with and . The resulting distribution for is bounded from below since
- System of Unbounded Distributions (SU)This system is determined using , with and . The resulting distribution for is unbounded since
2.3. Copulas
- Gaussian or normal copula , which is derived from as follows:
- 1.
- A combination of the normal copula and Student’s t margins , , results in an I-variate model with the following joint distribution function:
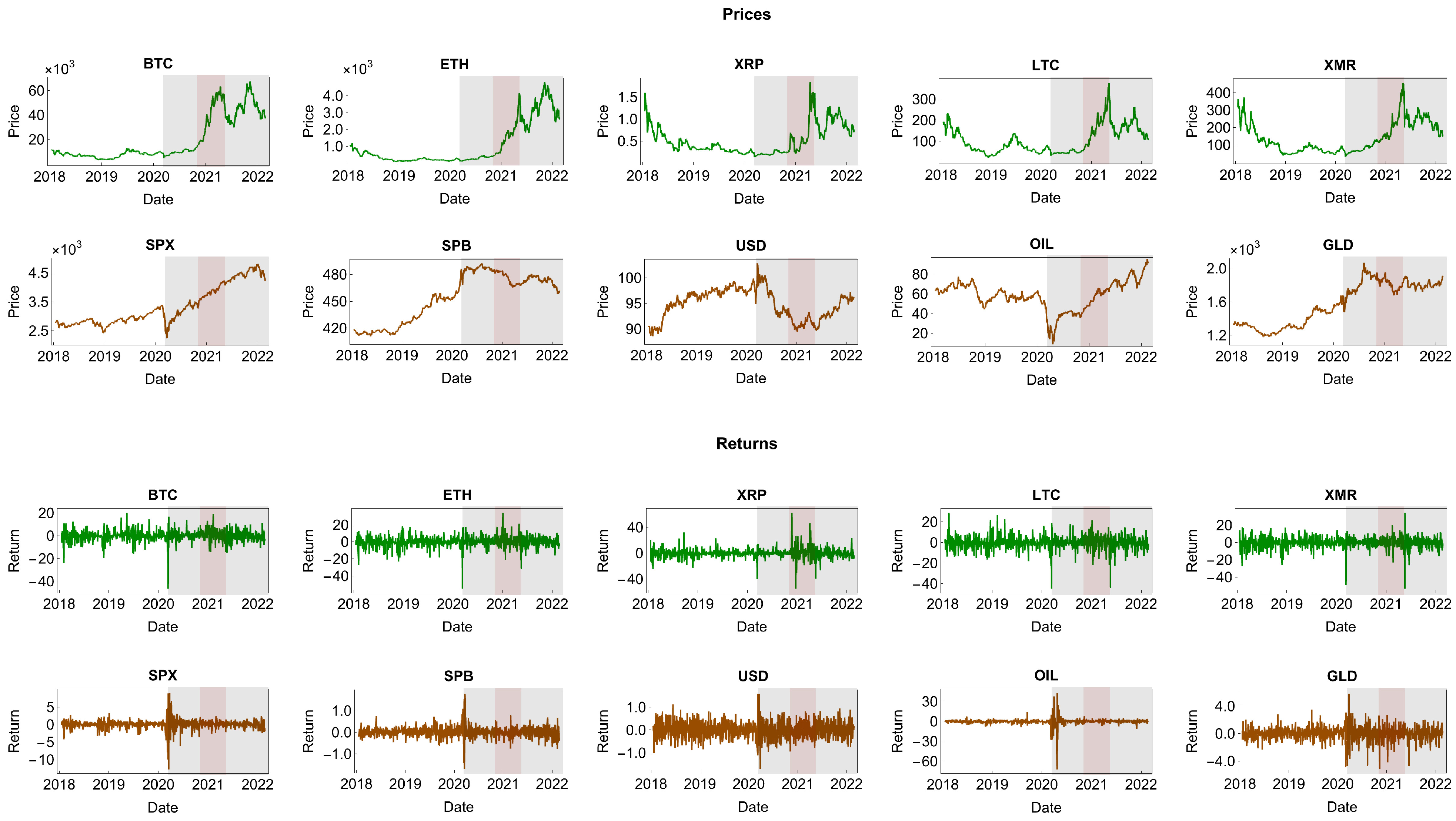
- 2.
- A combination of Student’s t copula and normal margins , , results in an I-variate model with the following joint distribution function:
- 3.
- A combination of Student’s t copula and Student’s t margins , , results in an I-variate model with the following joint distribution function:9
- 4.
- A combination of Student’s t copula and Johnson’s SU margins , , results in an I-variate model with the following joint distribution function:
3. MCoVaR Formulation
- For a given index set , we denote by or simply for all .
- For a given matrix , we denote and by and , respectively, for all , , and .
- For a given function , we denote by for all .
3.1. MCoVaR Based on Benchmark Models
3.2. MCoVaR Based on Johnson’s SU Models
3.3. MCoVaR Based on Copulas
- 1.
- If is a normal copula, then for all and , the conditional distribution function of and its inverse are given byand
- 2.
- If is Student’s t copula, then for all and , the conditional distribution function of and its inverse are formulated as follows:and
- 1.
- If is a normal copula, then for all and , the MCoVaR of at the level, defined in Definition 2, is given by
- 2.
- If is Student’s t copula, then for all and , the MCoVaR of at the level, defined in Definition 2, is given by
- From Equation (54), we obtain the MCoVaR formula for the N–T model by replacing with .
- From Equation (55), we derive the MCoVaR formula for the T–N model by replacing with .
- From Equation (55), we construct the MCoVaR formula for the T–T model by replacing with .
- From Equation (55), we build the MCoVaR formula for the T–SU model by replacing with .
4. MCoVaR Forecasts and Their Conditional Coverage and Backtesting Performances
- For the multivariate normal model, we estimate its mean vector and covariance matrix Σ using the moment matching method as follows: and , with
- For the multivariate Student’s t model, we estimate its mean vector and covariance matrix Σ using the moment matching method. Once their estimators and have been derived, we then estimate its degrees of freedom using the maximum likelihood method as follows:
- For the multivariate Johnson’s SU model, we estimate its mean vector , covariance matrix , and shape parameter vectors and using the moment matching method as follows: , , , and , with
- For the copula-based multivariate models, we first estimate the parameter vector of each margin i using the moment matching or maximum likelihood method and then determine a collection of pseudo observations, with . We estimate the parameter matrix of the normal and Student’s t copulas by matching the dependence measures as follows: , with . We then estimate the degrees of freedom of Student’s t copula using the maximum likelihood method as follows:
4.1. Conditional Coverage Performance of MCoVaR Forecasts
4.2. Backtesting Performance of MCoVaR Forecasts
5. Empirical Results
- Case 1: if the targeted asset j is a crypto asset, the conditioning set consists of all the remaining crypto assets being jointly in distress, and the conditioning set contains all the non-crypto assets being jointly in normal states;
- Case 2: if the targeted asset j is a crypto asset, the conditioning set consists of all the non-crypto assets being jointly in distress, and the conditioning set contains all the remaining crypto assets being jointly in normal states;
- Case 3: if the targeted asset j is a non-crypto asset, the conditioning set consists of all the crypto assets being jointly in distress, and the conditioning set contains all the remaining non-crypto assets being jointly in normal states;
- Case 4: if the targeted asset j is a non-crypto asset, the conditioning set consists of all the remaining non-crypto assets being jointly in distress, and the conditioning set contains all the crypto assets being jointly in normal states.
5.1. Data
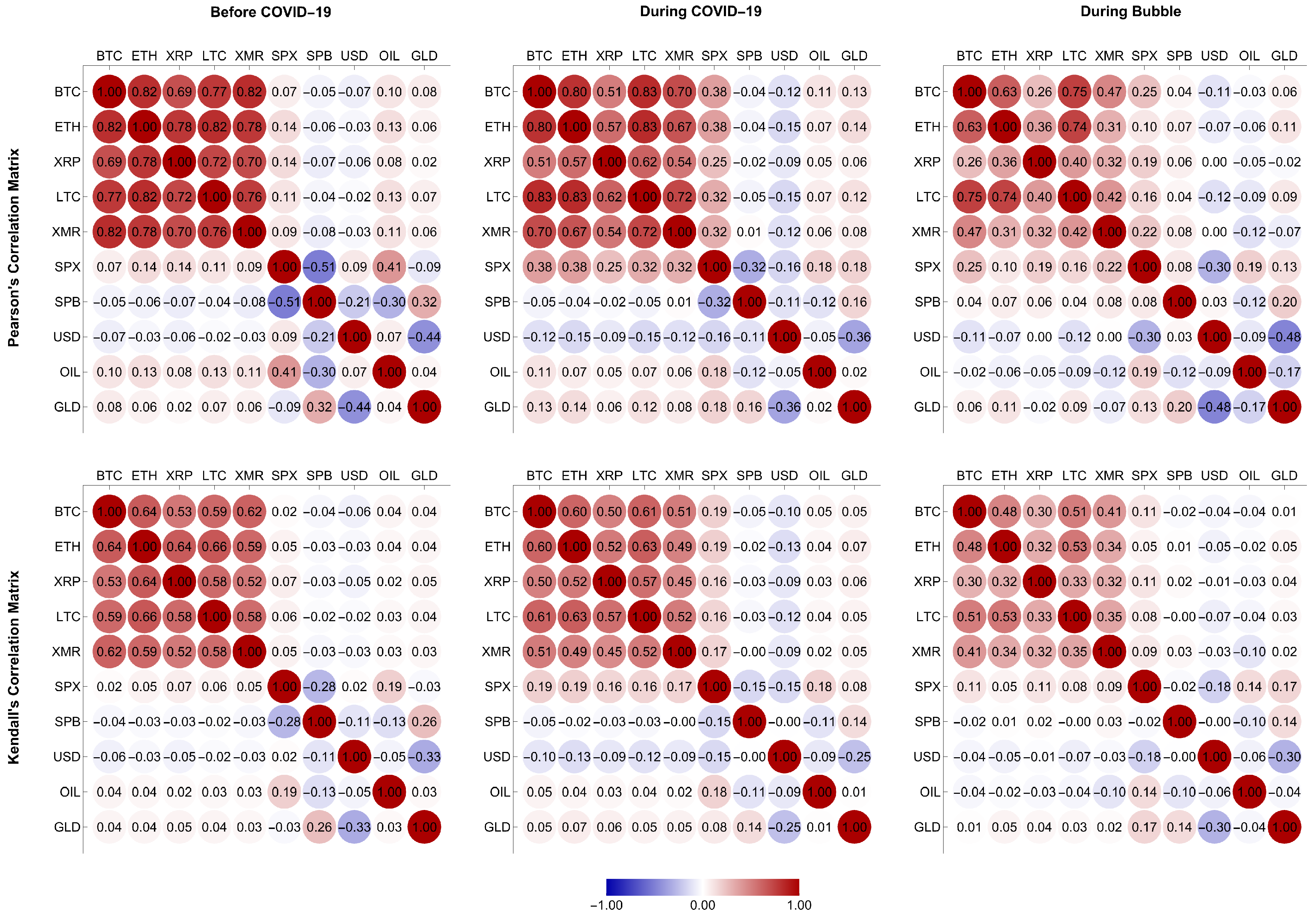
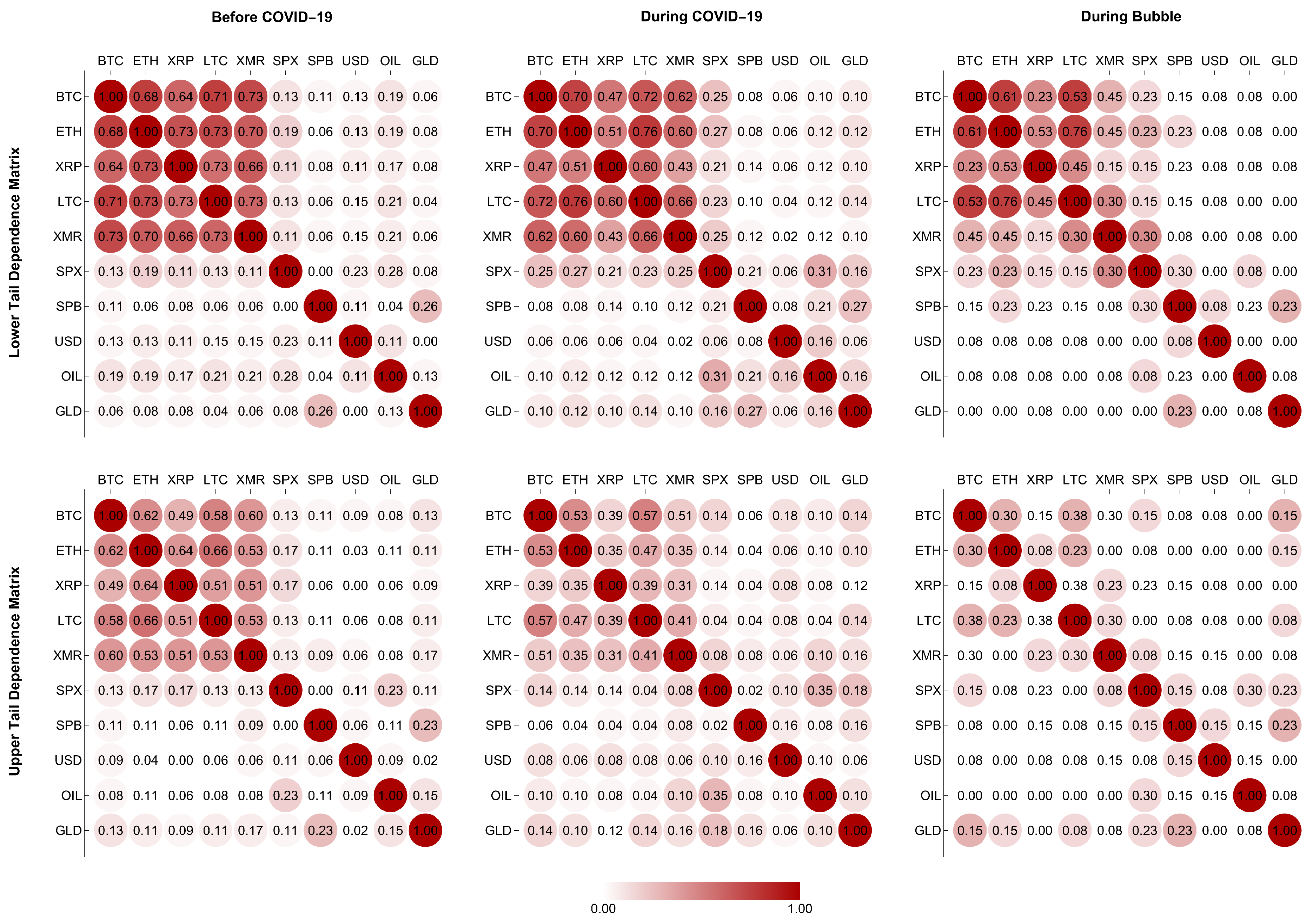
5.2. Conditional Coverage and Backtesting Performances of MCoVaR Forecasts
5.3. Quantifying Joint Transmissions of Systemic Risk Using MCoVaR Forecasts
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | It is well known that VaR is elicitable because there exists a loss or scoring function, particularly an asymmetric piecewise-linear loss function, minimized by VaR; see Gneiting (2011). This fact makes the VaR forecast easy to backtest using some backtesting procedures, such as unconditional coverage and independence tests (Christoffersen 1998; Kupiec 1995), coverage probabilities (Hakim et al. 2022; Kabaila and Syuhada 2008), or expected asymmetric loss functions (Bernardi and Catania 2016; González-Rivera et al. 2004; Jiménez et al. 2022; Le 2020; Syuhada et al. 2021). Since the MCoVaR systemic risk measure is basically the VaR risk measure of a targeted entity’s risk conditional on other entities’ risks, it is also an elicitable risk measure. This motivated us to rely on MCoVaR (instead of other systemic risk measures, such as MCoES, MES, and SRISK) for systemic risk quantification and propose backtesting techniques for the MCoVaR forecast evaluation. |
| 2 | We denote the probability functions that correspond to the distribution functions , , , and as follows: , , , and , respectively. |
| 3 | Embrechts et al. (2003b) stated that if the joint distribution function of and is exchangeable, i.e., , then and . |
| 4 | |
| 5 | According to Remark 1, the resulting coefficient of the lower and upper tail dependence of our proposed Student’s t model is different from the coefficient of the lower and upper tail dependence of Student’s t model discussed in Demarta and McNeil (2005). |
| 6 | The corresponding function is called the copula density. |
| 7 | Student’s t copula constructed in this study using our proposed standardized Student’s t distribution , with Pearson’s correlation matrix , is different from the one discussed in Demarta and McNeil (2005). |
| 8 | According to Remark 1 as well as Notes 5 and 7, the coefficient of the lower and upper tail dependence of our proposed Student’s t copula is different from the coefficient of the lower and upper tail dependence of Student’s t copula discussed in Demarta and McNeil (2005). |
| 9 | If Student’s t margins have common degrees of freedom that equal the degrees of freedom of Student’s t copula, then their joint distribution is , as discussed in Section 2.1. |
| 10 | In their original works, Bernardi and Petrella (2015) and Bernardi et al. (2017) considered the same significance level for the VaR of each distressed asset . In this study, we generalize their ()MCoVaR definition by allowing the conditioning assets in to be distressed at different levels. |
| 11 | The notation denotes the indicator function of any set A, with a value of if and zero otherwise. |
| 12 | Our asymmetric loss function is different from the one proposed by previous studies, e.g., González-Rivera et al. (2004) and Bernardi and Catania (2016), i.e., , with . |
| 13 | A period before 16 January 2018 encompasses the 2017 crypto bubble, as documented by Bazán-Palomino (2022) from the first week of March 2017 to the second week of January 2018. Meanwhile, during a period spanning from 24 February 2022 up to present, the geopolitical conflict between Russia and Ukraine occurred and impacted global financial markets. However, these two periods are out of the scope of this study. |
References
- Abadie, Alberto. 2002. Bootstrap Tests for Distributional Treatment Effects in Instrumental Variable Models. Journal of the American Statistical Association 97: 284–92. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Markus K. Brunnermeier. 2016. CoVaR. American Economic Review 106: 1705–41. [Google Scholar] [CrossRef]
- Agosto, Arianna, and Alessia Cafferata. 2020. Financial Bubbles: A Study of Co-explosivity in the Cryptocurrency Market. Risks 8: 34. [Google Scholar] [CrossRef]
- Akhtaruzzaman, Md, Sabri Boubaker, Duc K. Nguyen, and Molla R. Rahman. 2022. Systemic Risk-Sharing Framework of Cryptocurrencies in the COVID–19 Crisis. Finance Research Letters 47: 102787. [Google Scholar] [CrossRef] [PubMed]
- Almeida, Dora, Andreia Dionísio, Isabel Vieira, and Paulo Ferreira. 2022. Uncertainty and Risk in the Cryptocurrency Market. Journal of Risk and Financial Management 15: 532. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas Dimpfl. 2021. The Volatility of Bitcoin and Its Role as a Medium of Exchange and a Store of Value. Empirical Economics 61: 2663–83. [Google Scholar] [CrossRef]
- Baur, Dirk G., KiHoon Hong, and Adrian D. Lee. 2018. Bitcoin: Medium of Exchange or Speculative Assets? Journal of International Financial Markets, Institutions & Money 54: 177–89. [Google Scholar]
- Bazán-Palomino, Walter. 2022. Interdependence, Contagion and Speculative Bubbles in Cryptocurrency Markets. Finance Research Letters 49: 103132. [Google Scholar] [CrossRef]
- Bernal, Oscar, Jean-Yves Gnabo, and Grégory Guilmin. 2014. Assessing the Contribution of Banks, Insurance and Other Financial Services to Systemic Risk. Journal of Banking & Finance 47: 270–87. [Google Scholar]
- Bernard, Carole, and Claudia Czado. 2015. Conditional Quantiles and Tail Dependence. Journal of Multivariate Analysis 138: 104–26. [Google Scholar] [CrossRef]
- Bernardi, Mauro, and Lea Petrella. 2015. Interconnected Risk Contributions: A Heavy-Tail Approach to Analyze U.S. Financial Sectors. Journal of Risk and Financial Management 8: 198–226. [Google Scholar] [CrossRef]
- Bernardi, Mauro, and Leopoldo Catania. 2016. Comparison of Value-at-Risk Models Using the MCS Approach. Computational Statistics 31: 579–608. [Google Scholar] [CrossRef]
- Bernardi, Mauro, Antonello Maruotti, and Lea Petrella. 2017. Multiple Risk Measures for Multivariate Dynamic Heavy-Tailed Models. Journal of Empirical Finance 43: 1–32. [Google Scholar] [CrossRef]
- Bernardi, Mauro, Fabrizio Durante, and Piotr Jaworski. 2016. CoVaR of Families of Copulas. Statistics & Probability Letters 120: 8–17. [Google Scholar]
- Bianchi, Michele L., Giovanni De Luca, and Giorgia Rivieccio. 2023. Non-Gaussian Models for CoVaR Estimation. International Journal of Forecasting 39: 391–404. [Google Scholar] [CrossRef]
- Bonaccolto, Giovanni, Nicola Borri, and Andrea Consiglio. 2023. Breakup and Default Risks in the Great Lockdown. Journal of Banking & Finance 147: 106308. [Google Scholar]
- Borri, Nicola. 2019. Conditional Tail-Risk in Cryptocurrency Markets. Journal of Empirical Finance 50: 1–19. [Google Scholar] [CrossRef]
- Caferra, Rocco, and David Vidal-Tomás. 2021. Who Raised from the Abyss? A Comparison between Cryptocurrency and Stock Market Dynamics during the COVID-19 Pandemic. Finance Research Letters 43: 101954. [Google Scholar] [CrossRef]
- Cao, Zhili. 2013. Systemic Risk Measures, Banking Supervision and Financial Stability. Ph.D. thesis, Université de Toulouse 1 Capitole, Toulouse, France. [Google Scholar]
- Castillo-Brais, Brenda, Ángel León, and Juan Mora. 2022. Estimating Value-at-Risk and Expected Shortfall: Do Polynomial Expansions Outperform Parametric Densities? Mathematics 10: 4329. [Google Scholar] [CrossRef]
- Catania, Leopoldo, and Stefano Grassi. 2022. Forecasting Cryptocurrency Volatility. International Journal of Forecasting 38: 878–94. [Google Scholar] [CrossRef]
- Chan, Joshua C. C., and Dirk P. Kroese. 2010. Efficient Estimation of Large Portfolio Loss Probabilities in t-Copula Models. European Journal of Operational Research 205: 361–67. [Google Scholar] [CrossRef]
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative Bubbles in Bitcoin Markets? An Empirical Investigation into the Fundamental Value of Bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef]
- Chen, Yan, Dongxu Mo, and Zezhou Xu. 2022. A Study of Interconnections and Contagion among Chinese Financial Institutions Using a ΔCoVaR Network. Finance Research Letters 45: 102395. [Google Scholar] [CrossRef]
- Cherubini, Umberto, and Elisa Luciano. 2001. Value-at-risk Trade-off and Capital Allocation with Copulas. Economic Notes: Review of Banking, Finance and Monetary Economics 30: 235–56. [Google Scholar] [CrossRef]
- Choi, Pilsun, and Kiseok Nam. 2008. Asymmetric and Leptokurtic Distribution for Heteroscedastic Asset Returns: The SU-Normal Distribution. Journal of Empirical Finance 15: 41–63. [Google Scholar] [CrossRef]
- Choi, Pilsun, Insik Min, and Keehwan Park. 2012. SU-ΔCoVaR. Economics Letters 115: 218–20. [Google Scholar] [CrossRef]
- Choudhury, Tonmoy, Harald Kinateder, and Biwesh Neupane. 2022. Gold, Bonds, and Epidemics: A Safe Haven Study. Finance Research Letters 48: 102978. [Google Scholar] [CrossRef] [PubMed]
- Christoffersen, Peter F. 1998. Evaluating Interval Forecasts. International Economic Review 39: 841–62. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Saralees Nadarajah, and Stephen Chan. 2015. Statistical Analysis of the Exchange Rate of Bitcoin. PLoS ONE 10: e0133678. [Google Scholar] [CrossRef]
- Corbet, Shaen, Charles Larkin, and Brian Lucey. 2020. The Contagion Effects of the COVID-19 Pandemic: Evidence from Gold and Cryptocurrencies. Finance Research Letters 35: 101554. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, and Larisa Yarovaya. 2018. Datestamping the Bitcoin and Ethereum Bubbles. Finance Research Letters 26: 81–88. [Google Scholar] [CrossRef]
- Demarta, Stefano, and Alexander J. McNeil. 2005. The t Copula and Related Copulas. International Statistical Review 73: 111–29. [Google Scholar] [CrossRef]
- Ding, Peng. 2016. On the Conditional Distribution of the Multivariate t Distribution. The American Statistician 70: 293–95. [Google Scholar] [CrossRef]
- Embrechts, Paul, and Andrea Höing. 2006. Extreme VaR Scenarios in Higher Dimensions. Extremes 9: 177–92. [Google Scholar] [CrossRef]
- Embrechts, Paul, Andrea Höing, and Alessandro Juri. 2003a. Using Copulae to Bound the Value-at-Risk for Functions of Dependent Risks. Finance and Stochastics 7: 145–67. [Google Scholar] [CrossRef]
- Embrechts, Paul, Filip Lindskog, and Alexander McNeil. 2003b. Modelling dependence with copulas and applications to risk management. In Handbook of Heavy Tailed Distributions in Finance. Edited by Svetlozar T. Rachev. Amsterdam: Elsevier Science B.V., pp. 329–84. [Google Scholar]
- Girardi, Giulio, and A. Tolga Ergün. 2013. Systemic Risk Measurement: Multivariate GARCH Estimation of CoVaR. Journal of Banking & Finance 37: 3169–80. [Google Scholar]
- Gneiting, Tilmann. 2011. Making and Evaluating Point Forecasts. Journal of the American Statistical Association 106: 746–62. [Google Scholar] [CrossRef]
- González-Rivera, Gloria, Tae-Hwy Lee, and Santosh Mishra. 2004. Forecasting Volatility: A Reality Check Based on Option Pricing, Utility Function, Value-at-Risk, and Predictive Likelihood. International Journal of Forecasting 20: 629–45. [Google Scholar] [CrossRef]
- Gurrola, Pedro. 2008. Capturing Fat-Tail Risk in Exchange Rate Returns Using SU Curves: A Comparison with the Normal Mixture and Skewed Student Distributions. The Journal of Risk 10: 73–100. [Google Scholar] [CrossRef]
- Hakim, Arief, A. N. M. Salman, Yeva Ashari, and Khreshna Syuhada. 2022. Modifying (M)CoVaR and Constructing Tail Risk Networks through Analytic Higher-Order Moments: Evidence from the Global Forex Markets. PLoS ONE 17: e0277756. [Google Scholar] [CrossRef]
- Hakwa, Brice, Manfred Jäger-Ambrożewicz, and Barbara Rüdiger. 2015. Analysing Systemic Risk Contribution Using a Closed Formula for Conditional Value at Risk through Copula. Communications on Stochastic Analysis 9: 131–58. [Google Scholar] [CrossRef]
- Haykir, Ozkan, and Ibrahim Yagli. 2022. Speculative Bubbles and Herding in Cryptocurrencies. Financial Innovation 8: 78. [Google Scholar] [CrossRef]
- Jang, Sung M., Eojin Yi, Chang Kim, and Kwangwon Ahn. 2019. Information Flow between Bitcoin and Other Investment Assets. Entropy 21: 1116. [Google Scholar] [CrossRef]
- Jaworski, Piotr. 2017. On Conditional Value at Risk (CoVaR) for Tail-Dependent Copulas. Dependence Modeling 5: 1–19. [Google Scholar] [CrossRef]
- Jiménez, Inés, Andrés Mora-Valencia, and Javier Perote. 2020a. Risk Quantification and Validation for Bitcoin. Operations Research Letters 48: 534–41. [Google Scholar] [CrossRef]
- Jiménez, Inés, Andrés Mora-Valencia, and Javier Perote. 2022. Semi-Nonparametric Risk Assessment with Cryptocurrencies. Research in International Business and Finance 59: 101567. [Google Scholar] [CrossRef]
- Jiménez, Inés, Andrés Mora-Valencia, Trino-Manuel Ñíguez, and Javier Perote. 2020b. Portfolio Risk Assessment under Dynamic (Equi)Correlation and Semi-Nonparametric Estimation: An Application to Cryptocurrencies. Mathematics 8: 2110. [Google Scholar] [CrossRef]
- Johnson, N. L. 1949. Systems of Frequency Curves Generated by Method of Translation. Biometrika 36: 149–76. [Google Scholar] [CrossRef]
- Kabaila, Paul. 1999. An Efficient Simulation Method for the Computation of a Class of Conditional Expectations. Australian & New Zealand Journal of Statistics 41: 331–36. [Google Scholar]
- Kabaila, Paul, and Syuhada Khreshna. 2008. Improved Prediction Limits for AR(p) and ARCH(p) Processes. Journal of Time Series Analysis 29: 213–23. [Google Scholar] [CrossRef]
- Karimalis, Emmanouil N., and Nikos K. Nomikos. 2018. Measuring Systemic Risk in the European Banking Sector: A Copula CoVaR Approach. The European Journal of Finance 24: 944–75. [Google Scholar] [CrossRef]
- Koenker, Roger, and Gilbert Bassett. 1978. Regression Quantiles. Econometrica 46: 33–50. [Google Scholar] [CrossRef]
- Kuan, Chung-Ming, Jin-Huei Yeh, and Yu-Chin Hsu. 2009. Assessing Value at Risk with CARE, the Conditional Autoregressive Expectile Models. Journal of Econometrics 8: 87–107. [Google Scholar] [CrossRef]
- Kupiec, Paul H. 1995. Techniques for Verifying the Accuracy of Risk Measurement Models. The Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Le, Trung H. 2020. Forecasting Value at Risk and Expected Shortfall with Mixed Data Sampling. International Journal of Forecasting 36: 1362–79. [Google Scholar] [CrossRef]
- Li, Jianping, Xiaoqian Zhu, Cheng-Few Lee, Dengsheng Wu, Jichuang Feng, and Yong Shi. 2015. On the Aggregation of Credit, Market and Operational Risks. Review of Quantitative Finance and Accounting 44: 161–89. [Google Scholar] [CrossRef]
- Li, Yanshuang, Xintian Zhuang, Jian Wang, and Zibing Dong. 2021. Analysis of the Impact of COVID-19 Pandemic on G20 Stock Markets. The North American Journal of Economics and Finance 58: 101530. [Google Scholar] [CrossRef]
- Mainik, Georg, and Eric Schaanning. 2014. On Dependence Consistency of CoVaR and Some Other Systemic Risk Measures. Statistics & Risk Modeling 31: 49–77. [Google Scholar]
- McNeil, Alexander J., and Johanna Nešlehová. 2009. Multivariate Archimedean Copulas, d-Monotone Functions and ℓ1-Norm Symmetric Distributions. The Annals of Statistics 37: 3059–97. [Google Scholar] [CrossRef] [PubMed]
- McNeil, Alexander J., Rüdiger Frey, and Paul Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools, rev. ed. Princeton: Princeton University Press. [Google Scholar]
- Moreno, David, Marcos Antoli, and David Quintana. 2022. Benefits of Investing in Cryptocurrencies When Liquidity Is a Factor. Research in International Business and Finance 63: 101751. [Google Scholar] [CrossRef]
- Nadarajah, Saralees, and Samuel Kotz. 2005. Mathematical Properties of the Multivariate t Distribution. Acta Applicandae Mathematicae 89: 53–84. [Google Scholar] [CrossRef]
- Núñez, José A., Mario I. Contreras-Valdez, and Carlos A. Franco-Ruiz. 2019. Statistical Analysis of Bitcoin during Explosive Behavior Periods. PLoS ONE 14: e0213919. [Google Scholar] [CrossRef] [PubMed]
- Patra, Saswat. 2021. Revisiting Value-at-Risk and Expected Shortfall in Oil Markets under Structural Breaks: The Role of Fat-Tailed Distributions. Energy Economics 101: 105452. [Google Scholar] [CrossRef]
- Rehman, Mobeen U., Paraskevi Katsiampa, Rami Zeitun, and Xuan V. Vo. 2022. Conditional Dependence Structure and Risk Spillovers between Bitcoin and Fiat Currencies. Emerging Markets Review. in press. [Google Scholar] [CrossRef]
- Rosenberg, Joshua V., and Til Schuermann. 2006. A General Approach to Integrated Risk Management with Skewed, Fat-Tailed Risks. Journal of Financial Economics 79: 569–614. [Google Scholar] [CrossRef]
- Sharif, Arshian, Chaker Aloui, and Larisa Yarovaya. 2020. COVID-19 Pandemic, Oil Prices, Stock Market, Geopolitical Risk and Policy Uncertainty Nexus in the US Economy: Fresh Evidence from the Wavelet-Based Approach. International Review of Financial Analysis 70: 101496. [Google Scholar] [CrossRef]
- Sklar, Abe. 1959. Fonctions de Répartition à n Dimensions et Leurs Marges. Publications de l’Institut de Statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Som, Ankit, and Parthajit Kayal. 2022. A Multicountry Comparison of Cryptocurrency vs Gold: Portfolio Optimization through Generalized Simulated Annealing. Blockchain: Research and Applications 3: 100075. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, and Arief Hakim. 2020. Modeling Risk Dependence and Portfolio VaR Forecast through Vine Copula for Cryptocurrencies. PLoS ONE 15: e0242102. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, Arief Hakim, and Risti Nur’aini. 2021. The Expected-Based Value-at-Risk and Expected Shortfall Using Quantile and Expectile with Application to Electricity Market Data. Communications in Statistics: Simulation and Computation. in press. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, Arief Hakim, Djoko Suprijanto, Intan Muchtadi-Alamsyah, and Lukman Arbi. 2022a. Is Tether a Safe Haven of Safe Haven amid COVID-19? An Assessment against Bitcoin and Oil Using Improved Measures of Risk. Resources Policy 79: 103111. [Google Scholar] [CrossRef]
- Syuhada, Khreshna, Djoko Suprijanto, and Arief Hakim. 2022b. Comparing Gold’s and Bitcoin’s Safe-Haven Roles against Energy Commodities during the COVID-19 Outbreak: A Vine Copula Approach. Finance Research Letters 46: 102471. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y. L. 1990. The Multivariate Normal Distribution. New York: Springer. [Google Scholar]
- Torri, Gabriele, Rosella Giacometti, and Tomáš Tichý. 2021. Network Tail Risk Estimation in the European Banking System. Journal of Economic Dynamics & Control 127: 104125. [Google Scholar]
- Troster, Victor, Aviral K. Tiwari, Muhammad Shahbaz, and Demian N. Macedo. 2019. Bitcoin Returns and Risk: A General GARCH and GAS Analysis. Finance Research Letters 30: 187–93. [Google Scholar] [CrossRef]
- van Dorp, Johan R., and Michael C. Jones. 2020. The Johnson System of Frequency Curves—Historical, Graphical, and Limiting Perspectives. The American Statistician 74: 37–52. [Google Scholar] [CrossRef]
- Venkataraman, Sree V., and S. V. D. Nageswara Rao. 2016. Estimation of Dynamic VaR Using JSU and PIV Distributions. Risk Management 18: 111–34. [Google Scholar]
- Vidal-Tomás, David. 2022. Which Cryptocurrency Data Sources Should Scholars Use? International Review of Financial Analysis 81: 102061. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, Chi Xie, Danyan Wen, and Longfeng Zhao. 2019. When Bitcoin Meets Economic Policy Uncertainty (EPU): Measuring Risk Spillover Effect from EPU to Bitcoin. Finance Research Letters 31: 489–97. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, Xin-yu Ma, and Hao-yu Wu. 2020. Are Stablecoins Truly Diversifiers, Hedges, or Safe Havens against Traditional Cryptocurrencies as Their Name Suggests? Research in International Business and Finance 54: 101225. [Google Scholar] [CrossRef]
- Xu, Qiuhua, Yixuan Zhang, and Ziyang Zhang. 2021. Tail-Risk Spillovers in Cryptocurrency Markets. Finance Research Letters 38: 101453. [Google Scholar] [CrossRef]
- Yi, Shuyue, Zishuang Xu, and Gang-Jin Wang. 2018. Volatility Connectedness in the Cryptocurrency Market: Is Bitcoin a Dominant Cryptocurrency? International Review of Financial Analysis 60: 98–114. [Google Scholar] [CrossRef]
- Yu, Jiang, Yue Shang, and Xiafei Li. 2021. Dependence and Risk Spillover among Hedging Assets: Evidence from Bitcoin, Gold, and USD. Discrete Dynamics in Nature and Society 2021: 2010705. [Google Scholar] [CrossRef]
| Model | Abbreviation | Asymmetry | Leptokurticity | Tail Dependence | |
|---|---|---|---|---|---|
| 1 | Normal | N | No | No | No |
| 2 | Student’s t | T | No | Yes | Yes |
| 3 | Johnson’s SU | SU | Yes | Yes | No |
| 4 | Normal copula with Student’s t margins | N–T | No | Yes | No |
| 5 | Student’s t copula with normal margins | T–N | No | No | Yes |
| 6 | Student’s t copula with Student’s t margins | T–T | No | Yes | Yes |
| 7 | Student’s t copula with Johnson’s SU margins | T–SU | Yes | Yes | Yes |
| Case | j | Transmission Direction | ||
|---|---|---|---|---|
| 1 | C | Cs | NCs | C ← Cs |
| 2 | C | NCs | Cs | C ← NCs |
| 3 | NC | Cs | NCs | NC ← Cs |
| 4 | NC | NCs | Cs | NC ← NCs |
| BTC | ETH | XRP | LTC | XMR | SPX | SPB | USD | OIL | GLD | |
|---|---|---|---|---|---|---|---|---|---|---|
| Before COVID-19 | ||||||||||
| Mean | −0.07 | −0.31 | −0.32 | −0.25 | −0.33 | 0.01 | 0.03 | 0.01 | −0.12 | 0.04 |
| Variance | 19.71 | 32.55 | 34.94 | 33.66 | 37.90 | 1.17 | 0.05 | 0.12 | 6.36 | 0.62 |
| Skewness | −0.35 a | −0.48 a | 0.38 a | 0.40 a | −0.34 a | −1.13 a | −0.03 | 0.08 | −2.50 a | −0.18 |
| Excess Kurtosis | 4.07 b | 2.64 b | 3.94 b | 3.24 b | 2.01 b | 8.03 b | 4.45 b | 0.89 b | 30.85 b | 4.15 b |
| Jarque–Bera | 391.04 c | 181.39 c | 369.32 c | 255.06 c | 103.44 c | 1590.81 c | 454.52 c | 19.09 c | 22,280.80 c | 398.57 c |
| During COVID-19 | ||||||||||
| Mean | 0.32 | 0.53 | 0.24 | 0.15 | 0.20 | 0.08 | −0.01 | −0.00 | 0.20 | 0.03 |
| Variance | 23.96 | 43.66 | 70.72 | 43.44 | 43.22 | 2.53 | 0.07 | 0.15 | 35.52 | 1.36 |
| Skewness | −1.77 a | −1.23 a | 0.36 a | −1.46 a | −2.01 a | −1.04 a | 0.46 a | 0.31 a | −2.68 a | −0.37 a |
| Excess Kurtosis | 17.53 b | 12.57 b | 14.14 b | 8.96 b | 16.86 b | 16.71 b | 9.03 b | 1.66 b | 54.97 b | 4.30 b |
| Jarque–Bera | 6695.15 c | 3435.93 c | 4199.63 c | 1858.86 c | 6290.78 c | 5937.76 c | 1730.33 c | 66.21 c | 63,846.39 c | 399.99 c |
| During Bubble | ||||||||||
| Mean | 0.99 | 1.79 | 1.34 | 1.36 | 0.92 | 0.18 | −0.02 | −0.03 | 0.46 | −0.02 |
| Variance | 25.61 | 48.37 | 160.36 | 50.00 | 34.48 | 0.83 | 0.05 | 0.11 | 4.81 | 1.26 |
| Skewness | −0.13 | 0.71 a | 0.64 a | −0.62 a | −0.50 a | −0.30 | 0.14 | 0.13 | −0.21 | −1.00 a |
| Excess Kurtosis | 1.60 b | 3.77 b | 7.10 b | 1.27 b | 2.62 b | 0.50 | 2.07 b | −0.10 | 1.83 b | 3.70 b |
| Jarque–Bera | 17.11 c | 101.20 c | 324.21 c | 19.33 c | 49.52 c | 3.90 | 28.02 c | 0.43 | 22.64 c | 109.28 c |
| i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BTC | ETH | XRP | LTC | XMR | SPX | SPB | USD | OIL | GLD | |
| Before COVID-19 | ||||||||||
| N | 1.13% | 1.10% | 1.00% | 0.82% | 0.96% | 1.42% | 0.92% | 0.72% | 2.53% | 1.22% |
| T | 0.82% | 0.81% | 0.73% | 0.60% | 0.70% | 1.03% | 0.69% | 0.52% | 1.87% | 0.91% |
| SU | 1.06% | 1.00% | 1.03% | 0.88% | 0.93% | 1.12% | 0.99% | 0.71% | 1.61% | 1.15% |
| During COVID-19 | ||||||||||
| N | 1.86% | 1.73% | 1.56% | 1.65% | 2.22% | 1.77% | 1.32% | 0.77% | 3.11% | 1.11% |
| T | 1.26% | 1.15% | 1.04% | 1.09% | 1.49% | 1.20% | 0.91% | 0.50% | 2.13% | 0.75% |
| SU | 1.28% | 1.30% | 1.47% | 1.23% | 1.46% | 1.49% | 1.31% | 0.86% | 2.62% | 1.02% |
| During Bubble | ||||||||||
| N | 1.99% | 2.10% | 2.75% | 2.02% | 2.15% | 1.73% | 1.86% | 1.48% | 1.83% | 2.66% |
| T | 1.67% | 1.74% | 2.32% | 1.69% | 1.80% | 1.46% | 1.57% | 1.25% | 1.54% | 2.25% |
| SU | 1.89% | 1.99% | 3.28% | 1.82% | 1.94% | 1.65% | 1.91% | 1.56% | 1.90% | 2.17% |
| Before COVID-19 | ||||||||||
| N | 0.41% | 0.39% | 0.37% | 0.30% | 0.33% | 0.54% | 0.34% | 0.24% | 1.04% | 0.44% |
| T | 0.25% | 0.24% | 0.22% | 0.19% | 0.20% | 0.32% | 0.20% | 0.15% | 0.61% | 0.26% |
| SU | 0.44% | 0.38% | 0.43% | 0.36% | 0.40% | 0.50% | 0.74% | 0.26% | 1.03% | 0.74% |
| During COVID-19 | ||||||||||
| N | 0.71% | 0.67% | 0.64% | 0.62% | 0.90% | 0.72% | 0.50% | 0.28% | 1.49% | 0.42% |
| T | 0.36% | 0.34% | 0.32% | 0.32% | 0.45% | 0.36% | 0.26% | 0.15% | 0.72% | 0.21% |
| SU | 0.96% | 0.76% | 0.71% | 0.60% | 0.72% | 0.72% | 0.75% | 0.54% | 2.12% | 0.36% |
| During Bubble | ||||||||||
| N | 0.79% | 0.95% | 1.35% | 0.81% | 0.86% | 0.65% | 0.76% | 0.53% | 0.67% | 1.17% |
| T | 0.60% | 0.72% | 1.00% | 0.61% | 0.65% | 0.48% | 0.57% | 0.39% | 0.50% | 0.87% |
| SU | 0.98% | 1.12% | 2.97% | 0.85% | 1.00% | 0.78% | 1.01% | 0.60% | 1.11% | 1.16% |
| i | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BTC | ETH | XRP | LTC | XMR | SPX | SPB | USD | OIL | GLD | |
| Before COVID-19 | ||||||||||
| N | 37.58% | 48.55% | 49.50% | 48.87% | 52.00% | 9.55% | 1.87% | 2.89% | 21.66% | 6.61% |
| T | 35.68% | 45.99% | 46.95% | 46.34% | 49.27% | 9.04% | 1.78% | 2.74% | 20.58% | 6.27% |
| SU | 37.92% | 49.19% | 45.50% | 44.24% | 51.72% | 10.48% | 1.81% | 2.70% | 25.71% | 6.51% |
| During COVID-19 | ||||||||||
| N | 41.18% | 55.89% | 69.54% | 56.62% | 56.36% | 13.51% | 2.28% | 3.19% | 49.51% | 10.09% |
| T | 37.47% | 50.97% | 63.75% | 51.59% | 51.52% | 12.39% | 2.08% | 2.93% | 45.50% | 9.26% |
| SU | 43.83% | 58.24% | 65.02% | 61.08% | 63.66% | 14.01% | 2.02% | 2.83% | 57.97% | 9.83% |
| During Bubble | ||||||||||
| N | 42.21% | 57.39% | 101.53% | 61.90% | 49.12% | 7.63% | 1.79% | 2.79% | 18.50% | 9.67% |
| T | 41.21% | 56.45% | 99.82% | 60.54% | 48.28% | 7.45% | 1.75% | 2.74% | 18.14% | 9.46% |
| SU | 42.33% | 52.02% | 99.03% | 68.33% | 52.73% | 7.85% | 1.72% | 2.67% | 18.94% | 11.07% |
| Before COVID-19 | ||||||||||
| N | 10.44% | 13.50% | 13.74% | 13.54% | 14.40% | 2.62% | 0.52% | 0.80% | 6.01% | 1.83% |
| T | 11.68% | 15.04% | 15.39% | 15.13% | 16.13% | 2.92% | 0.58% | 0.89% | 6.71% | 2.05% |
| SU | 12.83% | 16.12% | 14.65% | 13.91% | 16.59% | 3.74% | 0.61% | 0.79% | 10.38% | 2.19% |
| During COVID-19 | ||||||||||
| N | 11.49% | 15.53% | 19.50% | 15.66% | 15.65% | 3.77% | 0.63% | 0.89% | 13.92% | 2.77% |
| T | 13.00% | 17.62% | 22.30% | 17.70% | 17.72% | 4.28% | 0.72% | 1.02% | 15.92% | 3.15% |
| SU | 17.05% | 21.93% | 24.01% | 22.21% | 24.43% | 5.39% | 0.71% | 0.85% | 25.01% | 3.31% |
| During Bubble | ||||||||||
| N | 11.85% | 16.02% | 28.93% | 17.04% | 13.87% | 2.13% | 0.50% | 0.78% | 5.13% | 2.66% |
| T | 12.72% | 17.33% | 31.22% | 18.21% | 14.89% | 2.28% | 0.53% | 0.84% | 5.54% | 2.87% |
| SU | 13.35% | 15.96% | 33.91% | 21.02% | 17.36% | 2.34% | 0.54% | 0.74% | 6.00% | 3.73% |
| C | Case 1 (C ← Cs) | Case 2 (C ← NCs) | NC | Case 3 (NC ← Cs) | Case 4 (NC ← NCs) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | During | During | Before | During | During | Before | During | During | Before | During | During | ||||
| COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | ||||
| and , | |||||||||||||||
| BTC | N | 3.26% | 4.82% | 5.25% | 2.26% | 4.28% | 7.13% | SPX | N | 1.74% | 3.31% | 3.89% | 3.74% | 3.52% | 6.44% |
| T | 3.40% | 5.10% | 5.23% | 1.64% | 2.70% | 5.14% | T | 4.93% | 4.54% | 4.33% | 2.64% | 3.09% | 4.55% | ||
| SU | 3.78% | 6.96% | 6.47% | 2.30% | 3.23% | 7.78% | SU | 1.69% | 3.00% | 4.08% | 3.29% | 3.86% | 6.74% | ||
| N–T | 1.34% | 2.94% | 5.87% | 2.80% | 3.22% | 8.39% | N–T | 1.35% | 1.24% | 4.02% | 2.42% | 3.08% | 6.56% | ||
| T–N | 4.11% | 7.28% | 7.75% | 2.23% | 3.44% | 6.93% | T–N | 1.98% | 2.89% | 4.36% | 2.37% | 2.94% | 5.53% | ||
| T–T | 1.82% | 3.32% | 6.74% | 2.05% | 2.34% | 6.34% | T–T | 1.53% | 1.47% | 4.15% | 2.00% | 2.32% | 5.32% | ||
| T–SU | 4.73% | 9.93% | 9.14% | 2.24% | 2.39% | 6.79% | T–SU | 1.58% | 2.51% | 4.15% | 2.10% | 2.75% | 5.49% | ||
| ETH | N | 3.35% | 4.60% | 6.72% | 3.73% | 2.53% | 6.53% | SPB | N | 1.29% | 1.95% | 3.65% | 3.37% | 3.87% | 7.23% |
| T | 3.62% | 4.77% | 6.82% | 2.45% | 1.70% | 4.48% | T | 4.51% | 2.45% | 3.98% | 3.50% | 3.24% | 4.84% | ||
| SU | 3.43% | 5.48% | 10.51% | 4.08% | 2.38% | 6.85% | SU | 1.13% | 2.28% | 3.72% | 3.73% | 4.99% | 8.44% | ||
| N–T | 1.65% | 2.67% | 5.60% | 4.06% | 3.06% | 8.28% | N–T | 1.17% | 1.32% | 4.69% | 2.58% | 2.73% | 5.48% | ||
| T–N | 4.87% | 6.80% | 9.12% | 3.32% | 2.93% | 6.62% | T–N | 1.36% | 1.85% | 5.10% | 2.21% | 2.38% | 4.84% | ||
| T–T | 2.06% | 3.16% | 6.19% | 3.08% | 2.19% | 6.12% | T–T | 1.31% | 1.47% | 4.88% | 2.11% | 2.18% | 4.29% | ||
| T–SU | 5.31% | 7.90% | 10.61% | 3.60% | 2.24% | 6.51% | T–SU | 1.12% | 1.71% | 4.77% | 2.21% | 2.53% | 5.07% | ||
| XRP | N | 2.52% | 3.04% | 5.42% | 2.57% | 2.97% | 6.20% | USD | N | 1.21% | 1.82% | 3.73% | 3.26% | 3.09% | 4.00% |
| T | 2.66% | 3.08% | 5.63% | 1.85% | 2.22% | 4.60% | T | 4.20% | 2.37% | 4.13% | 2.87% | 3.70% | 6.30% | ||
| SU | 3.13% | 3.98% | 9.52% | 2.79% | 4.01% | 7.08% | SU | 1.28% | 1.81% | 3.96% | 3.43% | 3.78% | 4.45% | ||
| N–T | 1.29% | 1.16% | 3.25% | 2.92% | 3.39% | 7.02% | N–T | 1.31% | 1.24% | 3.79% | 2.27% | 2.34% | 4.56% | ||
| T–N | 3.51% | 5.28% | 7.96% | 2.28% | 2.98% | 6.54% | T–N | 1.41% | 1.42% | 3.88% | 2.08% | 2.12% | 4.18% | ||
| T–T | 1.69% | 1.59% | 3.44% | 2.15% | 2.51% | 5.10% | T–T | 1.44% | 1.34% | 3.92% | 1.96% | 2.01% | 4.00% | ||
| T–SU | 4.27% | 6.11% | 13.73% | 2.25% | 3.02% | 7.63% | T–SU | 1.51% | 1.32% | 3.87% | 2.04% | 2.14% | 4.12% | ||
| LTC | N | 2.25% | 5.82% | 6.41% | 2.75% | 2.46% | 5.51% | OIL | N | 3.30% | 3.20% | 3.24% | 8.07% | 5.80% | 5.08% |
| T | 2.25% | 5.84% | 6.31% | 1.82% | 1.75% | 3.81% | T | 6.17% | 3.24% | 3.60% | 4.37% | 3.62% | 4.17% | ||
| SU | 2.93% | 5.92% | 7.75% | 2.85% | 5.86% | 6.50% | SU | 1.80% | 2.89% | 3.21% | 7.08% | 6.41% | 5.51% | ||
| N–T | 1.20% | 2.70% | 5.14% | 3.07% | 3.00% | 7.36% | N–T | 1.34% | 1.44% | 3.10% | 2.86% | 2.52% | 6.33% | ||
| T–N | 2.85% | 7.56% | 6.97% | 2.31% | 2.57% | 5.56% | T–N | 3.07% | 3.30% | 3.39% | 3.84% | 3.76% | 5.35% | ||
| T–T | 1.48% | 3.32% | 5.83% | 2.37% | 2.12% | 5.24% | T–T | 1.39% | 1.73% | 3.24% | 2.33% | 1.98% | 5.04% | ||
| T–SU | 3.91% | 7.69% | 7.89% | 2.49% | 2.70% | 5.18% | T–SU | 1.65% | 2.14% | 3.16% | 3.26% | 3.81% | 5.22% | ||
| XMR | N | 2.42% | 5.68% | 4.35% | 3.22% | 3.03% | 8.81% | GLD | N | 2.18% | 1.64% | 3.36% | 2.70% | 4.88% | 4.34% |
| T | 2.58% | 6.17% | 4.59% | 2.07% | 2.06% | 6.31% | T | 4.91% | 2.14% | 3.50% | 1.84% | 3.01% | 4.66% | ||
| SU | 3.18% | 4.68% | 4.88% | 3.30% | 4.04% | 10.34% | SU | 1.93% | 1.77% | 2.90% | 2.70% | 5.67% | 5.43% | ||
| N–T | 1.36% | 2.84% | 3.98% | 3.75% | 3.06% | 10.65% | N–T | 1.52% | 1.34% | 2.88% | 2.34% | 2.85% | 5.51% | ||
| T–N | 3.00% | 7.05% | 6.15% | 2.84% | 3.38% | 8.70% | T–N | 2.03% | 1.73% | 3.75% | 2.43% | 2.57% | 4.80% | ||
| T–T | 1.65% | 3.37% | 4.47% | 2.67% | 2.40% | 7.97% | T–T | 1.66% | 1.52% | 2.94% | 2.03% | 2.28% | 4.46% | ||
| T–SU | 3.89% | 5.79% | 6.72% | 2.88% | 2.72% | 8.84% | T–SU | 1.58% | 1.61% | 2.93% | 2.50% | 2.62% | 4.63% | ||
| and , | |||||||||||||||
| BTC | N | 1.58% | 2.54% | 3.11% | 0.89% | 2.23% | 5.16% | SPX | N | 0.70% | 1.69% | 2.10% | 1.92% | 1.78% | 4.93% |
| T | 1.55% | 2.21% | 2.81% | 0.52% | 0.93% | 2.49% | T | 3.18% | 2.36% | 2.39% | 0.82% | 1.11% | 1.97% | ||
| SU | 2.62% | 10.65% | 7.41% | 0.90% | 1.51% | 5.56% | SU | 0.70% | 1.70% | 2.75% | 1.77% | 1.96% | 5.45% | ||
| N–T | 0.58% | 2.91% | 6.82% | 1.06% | 1.44% | 6.59% | N–T | 0.46% | 0.50% | 2.46% | 1.05% | 1.43% | 4.44% | ||
| T–N | 2.22% | 4.72% | 5.29% | 0.73% | 1.28% | 3.51% | T–N | 0.74% | 1.38% | 2.34% | 0.82% | 1.13% | 2.62% | ||
| T–T | 0.59% | 3.83% | 8.23% | 0.60% | 0.83% | 3.10% | T–T | 0.44% | 0.50% | 2.25% | 0.64% | 0.67% | 2.59% | ||
| T–SU | 4.41% | 19.07% | 11.05% | 1.10% | 1.77% | 3.58% | T–SU | 0.67% | 1.52% | 2.58% | 0.94% | 1.43% | 3.09% | ||
| ETH | N | 1.65% | 2.36% | 4.48% | 2.03% | 1.14% | 5.00% | SPB | N | 0.52% | 0.83% | 1.93% | 1.68% | 2.08% | 5.10% |
| T | 1.56% | 2.02% | 3.99% | 0.84% | 0.62% | 2.17% | T | 2.93% | 1.11% | 2.15% | 1.20% | 1.00% | 2.28% | ||
| SU | 2.11% | 5.80% | 12.76% | 2.28% | 0.85% | 5.20% | SU | 0.56% | 1.49% | 2.28% | 1.90% | 3.07% | 7.19% | ||
| N–T | 0.79% | 2.36% | 6.12% | 2.03% | 1.33% | 6.23% | N–T | 0.44% | 0.54% | 3.05% | 1.19% | 1.30% | 3.68% | ||
| T–N | 2.84% | 4.33% | 7.27% | 1.22% | 1.06% | 3.23% | T–N | 0.48% | 0.71% | 3.09% | 0.75% | 0.90% | 2.18% | ||
| T–T | 0.78% | 3.07% | 7.22% | 1.09% | 0.74% | 2.72% | T–T | 0.41% | 0.51% | 2.78% | 0.67% | 0.78% | 2.35% | ||
| T–SU | 4.30% | 11.27% | 14.49% | 2.16% | 1.45% | 3.37% | T–SU | 0.54% | 1.03% | 3.12% | 1.48% | 1.67% | 3.43% | ||
| XRP | N | 1.15% | 1.50% | 3.44% | 1.21% | 1.41% | 4.28% | USD | N | 0.46% | 0.78% | 1.96% | 1.74% | 1.48% | 2.31% |
| T | 1.15% | 1.48% | 3.60% | 0.63% | 0.90% | 2.37% | T | 2.78% | 1.04% | 1.90% | 1.08% | 1.49% | 3.75% | ||
| SU | 1.90% | 2.37% | 12.32% | 1.33% | 2.40% | 6.38% | SU | 0.50% | 0.90% | 2.14% | 1.83% | 1.94% | 2.66% | ||
| N–T | 0.64% | 0.56% | 2.42% | 1.33% | 1.56% | 5.07% | N–T | 0.48% | 0.51% | 2.03% | 1.05% | 1.08% | 2.58% | ||
| T–N | 1.77% | 3.31% | 5.84% | 0.80% | 1.16% | 3.68% | T–N | 0.48% | 0.51% | 1.77% | 0.74% | 0.74% | 1.77% | ||
| T–T | 0.77% | 0.68% | 2.60% | 0.67% | 0.81% | 2.46% | T–T | 0.45% | 0.46% | 1.69% | 0.68% | 0.64% | 1.61% | ||
| T–SU | 3.35% | 4.98% | 21.19% | 1.19% | 1.93% | 8.69% | T–SU | 0.48% | 0.55% | 1.79% | 0.92% | 1.08% | 1.86% | ||
| LTC | N | 1.04% | 3.35% | 3.93% | 1.31% | 1.09% | 3.43% | OIL | N | 1.55% | 1.62% | 1.57% | 5.41% | 3.69% | 3.11% |
| T | 0.97% | 2.71% | 3.55% | 0.69% | 0.58% | 1.50% | T | 4.16% | 1.82% | 1.57% | 1.35% | 1.36% | 1.90% | ||
| SU | 1.80% | 6.48% | 8.98% | 1.40% | 3.09% | 4.42% | SU | 1.27% | 2.16% | 1.63% | 6.23% | 4.88% | 3.61% | ||
| N–T | 0.76% | 2.29% | 5.96% | 1.37% | 1.41% | 5.13% | N–T | 0.61% | 0.49% | 1.56% | 1.59% | 1.17% | 4.26% | ||
| T–N | 1.42% | 4.96% | 4.37% | 0.78% | 0.90% | 2.57% | T–N | 1.31% | 1.51% | 1.51% | 1.67% | 1.80% | 2.36% | ||
| T–T | 0.78% | 3.07% | 6.86% | 0.78% | 0.67% | 2.28% | T–T | 0.58% | 0.45% | 1.30% | 1.30% | 0.59% | 2.22% | ||
| T–SU | 2.81% | 10.26% | 8.88% | 1.29% | 1.32% | 2.30% | T–SU | 1.15% | 1.95% | 1.50% | 2.67% | 3.87% | 2.98% | ||
| XMR | N | 1.05% | 3.21% | 2.51% | 1.65% | 1.52% | 7.57% | GLD | N | 0.88% | 0.66% | 1.58% | 1.22% | 2.95% | 2.76% |
| T | 1.05% | 2.73% | 2.53% | 0.64% | 0.81% | 3.19% | T | 3.19% | 0.94% | 1.74% | 0.54% | 0.88% | 2.38% | ||
| SU | 2.37% | 4.20% | 4.43% | 1.75% | 2.49% | 9.65% | SU | 1.12% | 0.78% | 1.49% | 1.57% | 3.66% | 3.68% | ||
| N–T | 0.80% | 2.48% | 3.47% | 1.95% | 1.63% | 9.67% | N–T | 0.58% | 0.48% | 1.30% | 1.03% | 1.45% | 3.38% | ||
| T–N | 1.42% | 4.47% | 3.77% | 0.96% | 1.48% | 5.00% | T–N | 0.76% | 0.65% | 1.65% | 0.92% | 1.00% | 2.01% | ||
| T–T | 0.88% | 3.38% | 3.93% | 0.81% | 1.06% | 4.02% | T–T | 0.55% | 0.45% | 1.18% | 0.85% | 0.73% | 1.75% | ||
| T–SU | 3.42% | 6.13% | 7.60% | 1.44% | 1.66% | 5.26% | T–SU | 0.87% | 0.62% | 1.55% | 1.91% | 1.39% | 2.21% | ||
| C | Case 1 (C ← Cs) | Case 2 (C ← NCs) | NC | Case 3 (NC ← Cs) | Case 4 (NC ← NCs) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | During | During | Before | During | During | Before | During | During | Before | During | During | ||||
| COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | ||||
| and , | |||||||||||||||
| BTC | N | 27.31% | 35.38% | 62.62% | 18.56% | 23.87% | 28.95% | SPX | N | 9.55% | 17.70% | 11.20% | 8.24% | 11.18% | 8.89% |
| T | 18.06% | 22.21% | 39.16% | 28.68% | 33.11% | 45.36% | T | 6.70% | 10.11% | 7.99% | 11.89% | 14.59% | 12.29% | ||
| SU | 42.14% | 41.23% | 57.19% | 15.59% | 20.47% | 28.04% | SU | 10.17% | 22.22% | 10.90% | 8.17% | 10.22% | 9.23% | ||
| N–T | 43.65% | 42.49% | 42.04% | 12.54% | 18.90% | 27.24% | N–T | 11.65% | 22.61% | 10.32% | 9.60% | 13.43% | 10.50% | ||
| T–N | 22.31% | 27.89% | 51.47% | 20.46% | 26.69% | 33.12% | T–N | 9.09% | 14.22% | 8.65% | 11.27% | 14.95% | 12.06% | ||
| T–T | 27.56% | 32.47% | 54.39% | 19.08% | 27.87% | 36.85% | T–T | 7.91% | 12.00% | 8.07% | 13.92% | 18.15% | 12.33% | ||
| T–SU | 26.45% | 37.89% | 55.23% | 20.95% | 29.84% | 36.43% | T–SU | 9.05% | 13.46% | 8.50% | 13.61% | 18.58% | 11.93% | ||
| ETH | N | 36.00% | 41.02% | 64.98% | 25.65% | 31.96% | 45.56% | SPB | N | 1.69% | 2.51% | 2.33% | 1.66% | 2.19% | 3.15% |
| T | 24.38% | 30.03% | 38.41% | 36.66% | 44.93% | 60.42% | T | 1.34% | 1.83% | 1.89% | 2.07% | 2.73% | 3.09% | ||
| SU | 50.34% | 67.05% | 64.11% | 22.66% | 27.26% | 40.50% | SU | 1.67% | 2.62% | 2.35% | 1.65% | 2.15% | 2.76% | ||
| N–T | 50.91% | 61.73% | 66.48% | 14.96% | 25.67% | 39.39% | N–T | 1.72% | 2.63% | 2.27% | 1.71% | 2.48% | 2.48% | ||
| T–N | 25.81% | 29.61% | 41.23% | 24.83% | 35.21% | 48.50% | T–N | 1.56% | 2.25% | 1.96% | 1.90% | 2.72% | 2.89% | ||
| T–T | 32.96% | 35.84% | 53.89% | 22.24% | 36.34% | 53.14% | T–T | 1.45% | 1.98% | 1.88% | 2.10% | 3.09% | 2.79% | ||
| T–SU | 30.29% | 44.65% | 37.71% | 25.55% | 38.33% | 50.02% | T–SU | 1.49% | 1.98% | 1.89% | 2.08% | 3.06% | 2.83% | ||
| XRP | N | 43.32% | 98.81% | 197.73% | 30.58% | 60.02% | 108.40% | USD | N | 3.15% | 3.43% | 2.67% | 3.06% | 3.93% | 2.93% |
| T | 29.76% | 46.38% | 101.04% | 48.81% | 82.47% | 186.28% | T | 2.50% | 2.94% | 2.50% | 3.89% | 4.23% | 3.12% | ||
| SU | 52.54% | 157.57% | 202.63% | 26.86% | 53.52% | 109.91% | SU | 3.18% | 3.44% | 2.63% | 3.02% | 3.64% | 2.88% | ||
| N–T | 50.74% | 134.95% | 217.40% | 21.42% | 36.55% | 104.65% | N–T | 3.09% | 3.39% | 2.83% | 2.91% | 3.61% | 3.14% | ||
| T–N | 31.14% | 45.13% | 116.49% | 32.35% | 55.69% | 122.50% | T–N | 2.78% | 3.09% | 2.66% | 3.14% | 3.70% | 3.23% | ||
| T–T | 37.19% | 49.08% | 134.84% | 33.53% | 57.86% | 147.66% | T–T | 2.61% | 2.91% | 2.56% | 3.32% | 3.82% | 3.29% | ||
| T–SU | 33.91% | 50.79% | 132.49% | 33.54% | 59.18% | 147.06% | T–SU | 2.64% | 2.89% | 2.58% | 3.26% | 3.77% | 3.26% | ||
| LTC | N | 33.87% | 37.91% | 69.47% | 29.80% | 26.65% | 37.87% | OIL | N | 23.03% | 61.19% | 19.74% | 29.59% | 61.22% | 19.48% |
| T | 30.74% | 25.40% | 46.05% | 44.53% | 39.34% | 54.59% | T | 16.69% | 38.73% | 17.61% | 32.64% | 73.56% | 27.12% | ||
| SU | 36.29% | 58.43% | 51.70% | 26.02% | 22.11% | 35.78% | SU | 24.39% | 68.83% | 20.35% | 41.17% | 71.34% | 19.71% | ||
| N–T | 39.46% | 62.73% | 78.73% | 22.50% | 21.68% | 38.96% | N–T | 26.66% | 49.34% | 21.06% | 30.96% | 54.53% | 21.91% | ||
| T–N | 32.05% | 29.10% | 56.09% | 31.62% | 30.88% | 47.68% | T–N | 21.27% | 43.99% | 18.51% | 31.93% | 65.34% | 25.12% | ||
| T–T | 35.29% | 37.35% | 60.40% | 33.70% | 30.61% | 52.29% | T–T | 19.27% | 27.17% | 17.84% | 41.06% | 78.61% | 27.31% | ||
| T–SU | 35.17% | 43.63% | 64.91% | 32.60% | 33.16% | 53.50% | T–SU | 20.73% | 36.58% | 18.34% | 43.49% | 88.83% | 26.97% | ||
| XMR | N | 38.00% | 56.22% | 109.22% | 29.07% | 41.64% | 44.70% | GLD | N | 6.89% | 11.37% | 8.94% | 7.01% | 11.91% | 8.04% |
| T | 28.25% | 38.02% | 58.34% | 44.98% | 59.48% | 79.00% | T | 5.03% | 8.66% | 8.10% | 8.96% | 15.01% | 9.79% | ||
| SU | 60.06% | 118.40% | 86.95% | 26.91% | 38.47% | 45.59% | SU | 7.08% | 12.16% | 9.31% | 7.41% | 13.40% | 8.08% | ||
| N–T | 64.91% | 110.63% | 86.82% | 25.76% | 36.71% | 38.96% | N–T | 6.56% | 12.73% | 10.19% | 6.85% | 11.85% | 9.29% | ||
| T–N | 29.37% | 46.00% | 74.55% | 35.75% | 47.55% | 47.78% | T–N | 5.75% | 10.05% | 8.86% | 7.49% | 12.66% | 10.07% | ||
| T–T | 36.73% | 48.59% | 76.23% | 39.00% | 53.47% | 56.23% | T–T | 5.21% | 9.19% | 8.49% | 8.50% | 15.10% | 11.46% | ||
| T–SU | 36.59% | 60.78% | 71.84% | 39.82% | 57.14% | 56.46% | T–SU | 5.42% | 9.59% | 9.09% | 8.34% | 14.76% | 11.59% | ||
| and , | |||||||||||||||
| BTC | N | 9.91% | 3.98% | 4.44% | 4.99% | 6.42% | 8.02% | SPX | N | 2.74% | 7.54% | 2.82% | 2.24% | 3.01% | 2.76% |
| T | 5.23% | 5.80% | 6.26% | 14.81% | 13.34% | 14.14% | T | 2.96% | 4.52% | 2.05% | 5.35% | 8.37% | 3.32% | ||
| SU | 12.30% | 52.24% | 11.87% | 4.29% | 6.31% | 8.71% | SU | 3.27% | 12.47% | 2.32% | 2.51% | 3.00% | 2.71% | ||
| N–T | 20.22% | 74.31% | 17.70% | 3.37% | 5.35% | 7.57% | N–T | 4.04% | 11.65% | 2.65% | 3.16% | 4.67% | 2.51% | ||
| T–N | 7.26% | 3.30% | 3.48% | 7.07% | 9.44% | 13.29% | T–N | 2.88% | 5.57% | 3.07% | 6.02% | 8.88% | 2.18% | ||
| T–T | 13.00% | 12.87% | 10.48% | 9.96% | 14.47% | 17.71% | T–T | 3.58% | 7.03% | 2.74% | 6.85% | 15.28% | 2.93% | ||
| T–SU | 10.58% | 21.00% | 9.12% | 9.38% | 14.59% | 16.98% | T–SU | 3.49% | 7.00% | 2.47% | 6.81% | 14.99% | 3.11% | ||
| ETH | N | 9.41% | 10.24% | 8.79% | 6.86% | 8.48% | 11.78% | SPB | N | 0.47% | 0.73% | 0.68% | 0.44% | 0.62% | 0.75% |
| T | 6.55% | 9.94% | 12.13% | 19.38% | 21.85% | 21.51% | T | 0.51% | 0.74% | 0.73% | 0.86% | 1.38% | 0.94% | ||
| SU | 13.56% | 69.27% | 16.70% | 6.62% | 7.74% | 11.16% | SU | 0.49% | 0.91% | 0.69% | 0.43% | 0.58% | 0.74% | ||
| N–T | 21.74% | 73.10% | 42.33% | 4.21% | 7.05% | 11.31% | N–T | 0.50% | 0.85% | 0.65% | 0.48% | 0.75% | 0.67% | ||
| T–N | 8.16% | 12.91% | 7.23% | 8.31% | 12.07% | 15.10% | T–N | 0.46% | 0.67% | 0.63% | 0.65% | 1.96% | 1.08% | ||
| T–T | 11.20% | 20.13% | 24.71% | 11.90% | 18.13% | 21.37% | T–T | 0.49% | 0.77% | 0.65% | 1.07% | 1.86% | 1.06% | ||
| T–SU | 10.10% | 22.10% | 12.19% | 11.46% | 19.12% | 19.06% | T–SU | 0.49% | 0.75% | 0.64% | 1.03% | 1.89% | 0.86% | ||
| XRP | N | 26.67% | 162.34% | 253.69% | 8.13% | 16.18% | 36.97% | USD | N | 0.82% | 0.90% | 0.71% | 0.82% | 1.15% | 0.73% |
| T | 11.06% | 28.36% | 72.89% | 22.58% | 62.31% | 51.68% | T | 0.86% | 1.06% | 0.83% | 1.34% | 1.67% | 1.02% | ||
| SU | 15.26% | 40.88% | 43.06% | 7.26% | 16.32% | 46.27% | SU | 0.83% | 0.92% | 0.70% | 0.80% | 0.97% | 0.72% | ||
| N–T | 27.86% | 57.63% | 103.03% | 6.03% | 11.67% | 48.23% | N–T | 0.81% | 0.90% | 0.76% | 0.77% | 0.97% | 0.80% | ||
| T–N | 8.02% | 26.93% | 123.92% | 11.46% | 18.42% | 187.87% | T–N | 0.77% | 0.87% | 0.77% | 1.05% | 1.31% | 0.91% | ||
| T–T | 14.91% | 41.83% | 58.79% | 16.88% | 44.22% | 77.43% | T–T | 0.79% | 0.91% | 0.78% | 1.16% | 1.40% | 0.99% | ||
| T–SU | 12.40% | 35.10% | 35.44% | 15.26% | 41.37% | 49.88% | T–SU | 0.79% | 0.90% | 0.77% | 1.13% | 1.35% | 0.96% | ||
| LTC | N | 12.49% | 4.76% | 5.16% | 7.95% | 7.03% | 9.82% | OIL | N | 6.70% | 23.31% | 5.49% | 12.81% | 23.34% | 5.29% |
| T | 8.57% | 7.67% | 8.34% | 17.29% | 20.39% | 25.83% | T | 6.55% | 21.44% | 7.16% | 19.88% | 39.20% | 10.52% | ||
| SU | 13.04% | 23.98% | 19.27% | 7.20% | 5.90% | 9.48% | SU | 9.02% | 33.45% | 5.87% | 29.67% | 35.16% | 5.44% | ||
| N–T | 24.80% | 28.33% | 20.72% | 6.55% | 5.60% | 10.54% | N–T | 9.85% | 21.97% | 6.26% | 13.82% | 26.50% | 6.81% | ||
| T–N | 4.71% | 14.10% | 5.07% | 11.45% | 10.27% | 16.48% | T–N | 6.53% | 14.18% | 5.99% | 23.81% | 101.26% | 12.65% | ||
| T–T | 13.45% | 23.64% | 12.43% | 14.80% | 15.29% | 23.59% | T–T | 7.57% | 16.71% | 6.69% | 56.09% | 116.15% | 8.52% | ||
| T–SU | 9.44% | 37.71% | 13.56% | 14.66% | 16.12% | 22.32% | T–SU | 8.49% | 21.69% | 6.60% | 41.07% | 112.13% | 8.52% | ||
| XMR | N | 17.42% | 42.76% | 82.97% | 7.76% | 11.39% | 12.44% | GLD | N | 1.87% | 3.27% | 2.37% | 1.90% | 3.65% | 2.17% |
| T | 9.53% | 13.36% | 27.95% | 22.77% | 30.31% | 35.27% | T | 1.91% | 3.89% | 3.13% | 5.07% | 4.94% | 4.55% | ||
| SU | 14.74% | 38.56% | 21.96% | 7.48% | 12.27% | 14.03% | SU | 2.03% | 3.77% | 2.72% | 2.21% | 4.60% | 2.17% | ||
| N–T | 23.65% | 48.67% | 25.60% | 7.39% | 11.14% | 11.50% | N–T | 1.93% | 4.07% | 3.23% | 2.02% | 3.66% | 2.66% | ||
| T–N | 9.90% | 19.41% | 40.51% | 12.86% | 17.12% | 24.75% | T–N | 1.70% | 3.09% | 2.68% | 2.78% | 9.40% | 4.49% | ||
| T–T | 12.70% | 37.64% | 15.68% | 19.42% | 43.62% | 27.02% | T–T | 1.83% | 3.82% | 3.45% | 5.04% | 5.19% | 6.22% | ||
| T–SU | 12.01% | 59.91% | 15.78% | 17.89% | 45.05% | 25.80% | T–SU | 1.83% | 3.77% | 3.44% | 5.03% | 5.17% | 5.69% | ||
| Model | Lowest RMSE of Estimated MCoCP | Lowest Expected MCoAL | ||||
|---|---|---|---|---|---|---|
| Before | During | During | Before | During | During | |
| COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | |
| and , | ||||||
| N | 1 | 0 | 5 | 2 | 0 | 3 |
| T | 6 | 4 | 8 | 10 | 6 | 8 |
| SU | 0 | 0 | 0 | 2 | 2 | 2 |
| N–T | 8 | 10 | 6 | 6 | 8 | 5 |
| T–N | 0 | 0 | 0 | 0 | 2 | 0 |
| T–T | 4 | 6 | 1 | 0 | 1 | 1 |
| T–SU | 1 | 0 | 0 | 0 | 1 | 1 |
| and , | ||||||
| N | 0 | 0 | 3 | 4 | 3 | 5 |
| T | 6 | 5 | 10 | 3 | 4 | 1 |
| SU | 0 | 0 | 0 | 1 | 2 | 3 |
| N–T | 4 | 3 | 1 | 6 | 5 | 4 |
| T–N | 0 | 0 | 1 | 6 | 6 | 5 |
| T–T | 10 | 12 | 5 | 0 | 0 | 1 |
| T–SU | 0 | 0 | 0 | 0 | 0 | 1 |
| C | Case 1 (C ← Cs) | Case 2 (C ← NCs) | NC | Case 3 (NC ← Cs) | Case 4 (NC ← NCs) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | During | During | Before | During | During | Before | During | During | Before | During | During | ||||
| COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | COVID-19 | COVID-19 | Bubble | ||||
| and , | |||||||||||||||
| BTC | N | 6.85 * | 7.12 * | 6.90 * | −0.72 | 1.26 * | 1.13 * | SPX | N | 0.11 * | 1.02 * | 0.52 * | −0.24 | −0.45 | 0.10 * |
| T | 7.24 * | 7.66 * | 7.90 * | 2.26 * | 4.63 * | 4.63 * | T | 0.41 * | 1.51 * | 0.79 * | 0.75 * | 1.12 * | 0.92 * | ||
| SU | 9.72 * | 12.34 * | 8.85 * | −0.71 | 1.46 * | 1.23 * | SU | 0.15 * | 1.80 * | 0.65 * | −0.27 | −0.54 | 0.14 * | ||
| N–T | 9.09 * | 10.52 * | 10.17 * | −0.83 | 0.32 * | 0.00 | N–T | 0.10 * | 0.98 * | 0.37 * | −0.15 | −0.11 | 0.40 * | ||
| T–N | 6.76 * | 7.44 * | 7.45 * | −0.15 | 1.58 * | 1.40 * | T–N | 0.18 * | 0.85 * | 0.41 * | 0.24 * | 0.44 * | 0.66 * | ||
| T–T | 7.53 * | 8.56 * | 9.02 * | 0.48 * | 2.37 * | 2.30 * | T–T | 0.24 * | 0.98 * | 0.50 * | 0.54 * | 0.95 * | 0.93 * | ||
| T–SU | 8.52 * | 11.48 * | 9.19 * | 0.45 * | 2.84 * | 2.17 * | T–SU | 0.30 * | 1.31 * | 0.53 * | 0.63 * | 1.23 * | 0.96 * | ||
| ETH | N | 9.25 * | 9.86 * | 9.66 * | 1.03 * | 0.89 * | 1.02 * | SPB | N | −0.01 | 0.05 * | 0.03 * | −0.13 | −0.16 | 0.17 * |
| T | 9.66 * | 10.61 * | 11.16 * | 4.47 * | 5.60 * | 6.18 * | T | 0.06 * | 0.17 * | 0.11 * | 0.06 * | 0.12 * | 0.39 * | ||
| SU | 12.92 * | 16.50 * | 10.71 * | 1.08 * | 0.91 * | 1.00 * | SU | −0.01 | 0.08 * | 0.04 * | −0.13 | −0.17 | 0.24 * | ||
| N–T | 12.07 * | 13.57 * | 16.00 * | 0.30 * | 0.33 * | 0.41 * | N–T | −0.02 | 0.01 * | 0.01 * | −0.03 | −0.04 | 0.08 * | ||
| T–N | 9.31 * | 9.96 * | 10.32 * | 1.55 * | 1.97 * | 2.36 * | T–N | 0.00 | 0.04 * | 0.03 * | 0.04 * | 0.07 * | 0.14 * | ||
| T–T | 10.29 * | 11.32 * | 13.39 * | 1.87 * | 3.02 * | 3.46 * | T–T | 0.02 * | 0.07 * | 0.05 * | 0.10 * | 0.18 * | 0.23 * | ||
| T–SU | 11.68 * | 14.31 * | 10.50 * | 2.22 * | 3.44 * | 2.83 * | T–SU | 0.01 * | 0.07 * | 0.05 * | 0.09 * | 0.17 * | 0.21 * | ||
| XRP | N | 8.29 * | 9.22 * | 10.10 * | −0.99 | 0.72 * | 3.35 * | USD | N | −0.02 | −0.04 | −0.01 | −0.23 | −0.36 | −0.39 |
| T | 9.03 * | 11.29 * | 13.50 * | 3.87 * | 9.92 * | 15.88 * | T | 0.08 * | 0.13 * | 0.10 * | 0.09 * | 0.03 * | −0.21 | ||
| SU | 10.27 * | 15.48 * | 13.92 * | −0.87 | 0.80 * | 3.87 * | SU | −0.02 | −0.04 | −0.01 | −0.23 | −0.35 | −0.39 | ||
| N–T | 11.77 * | 17.32 * | 24.22 * | −0.28 | 0.71 * | 5.32 * | N–T | −0.02 | −0.07 | −0.02 | −0.28 | −0.35 | −0.32 | ||
| T–N | 8.55 * | 11.67 * | 14.04 * | 1.19 * | 3.38 * | 8.88 * | T–N | 0.01 | −0.03 | 0.02 * | −0.19 | −0.25 | −0.25 | ||
| T–T | 9.73 * | 12.86 * | 18.74 * | 1.91 * | 4.48 * | 13.18 * | T–T | 0.04 * | 0.02 * | 0.05 * | −0.10 | −0.13 | −0.20 | ||
| T–SU | 9.18 * | 14.29 * | 17.18 * | 1.86 * | 5.18 * | 11.97 * | T–SU | 0.03 * | 0.02 | 0.04 * | −0.12 | −0.13 | −0.21 | ||
| LTC | N | 8.82 * | 11.17 * | 11.73 * | 1.00 * | −1.31 | −1.71 | OIL | N | 0.28 * | 0.25 | −0.72 | 1.54 * | 0.26 | −1.00 |
| T | 9.41 * | 11.66 * | 12.97 * | 5.11 * | 3.06 * | 2.74 * | T | 1.05 * | 3.09 * | 0.06 | 4.43 * | 7.86 * | 0.92 * | ||
| SU | 10.21 * | 19.85 * | 17.18 * | 0.89 * | −1.42 | −1.91 | SU | 0.49 * | 0.41 | −0.84 | 3.74 * | 0.72 * | −1.21 | ||
| N–T | 12.10 * | 14.94 * | 13.96 * | 0.90 * | −0.84 | −1.11 | N–T | 0.07 * | −0.31 | −0.67 | 0.68 * | 0.04 | −0.35 | ||
| T–N | 8.91 * | 10.69 * | 10.66 * | 2.46 * | 0.32 * | 0.72 * | T–N | 0.28 * | 0.25 | −0.35 | 1.53 * | 2.30 * | 0.45 * | ||
| T–T | 10.24 * | 12.19 * | 12.57 * | 3.07 * | 1.41 * | 1.95 * | T–T | 0.48 * | 0.61 * | −0.15 | 2.89 * | 3.47 * | 1.06 * | ||
| T–SU | 9.29 * | 16.12 * | 14.59 * | 2.91 * | 1.69 * | 1.93 * | T–SU | 0.62 * | 1.21 * | −0.22 | 3.95 * | 6.91 * | 0.98 * | ||
| XMR | N | 9.43 * | 8.85 * | 5.53 * | −0.16 | 0.94 * | −0.86 | GLD | N | 0.06 * | 0.01 | −0.15 | 0.12 * | 0.12 * | −0.88 |
| T | 10.03 * | 10.10 * | 7.08 * | 4.22 * | 6.99 * | 4.72 * | T | 0.29 * | 0.52 * | 0.20 * | 0.94 * | 1.48 * | −0.16 | ||
| SU | 12.88 * | 18.81 * | 8.89 * | −0.17 | 1.30 * | −1.24 | SU | 0.07 * | −0.02 | −0.21 | 0.21 * | 0.29 * | −1.04 | ||
| N–T | 12.62 * | 13.51 * | 10.74 * | 0.41 * | 0.94 * | −0.67 | N–T | 0.08 * | 0.07 * | −0.05 | 0.17 * | −0.09 | −0.26 | ||
| T–N | 9.16 * | 8.84 * | 7.22 * | 2.11 * | 3.00 * | 1.30 * | T–N | 0.13 * | 0.17 * | 0.07 * | 0.42 * | 0.33 * | 0.07 * | ||
| T–T | 10.69 * | 10.64 * | 9.31 * | 3.02 * | 4.68 * | 2.66 * | T–T | 0.18 * | 0.30 * | 0.16 * | 0.69 * | 0.78 * | 0.29 * | ||
| T–SU | 11.43 * | 14.91 * | 10.42 * | 3.22 * | 6.20 * | 2.67 * | T–SU | 0.19 * | 0.34 * | 0.18 * | 0.69 * | 0.86 * | 0.31 * | ||
| and , | |||||||||||||||
| BTC | N | 9.69 * | 10.06 * | 9.75 * | −1.02 | 1.78 * | 1.60 * | SPX | N | 0.16 * | 1.44 * | 0.73 * | −0.34 | −0.64 | 0.14 * |
| T | 13.40 * | 15.51 * | 14.02 * | 7.42 * | 12.63 * | 11.36 * | T | 1.21 * | 3.67 * | 1.67 * | 2.53 * | 4.05 * | 2.42 * | ||
| SU | 20.87 * | 30.80 * | 16.89 * | −1.12 | 2.72 * | 2.01 * | SU | 0.30 * | 4.61 * | 1.07 * | −0.53 | −1.12 | 0.22 * | ||
| N–T | 28.51 * | 31.63 * | 23.59 * | −1.31 | 0.54 * | 0.00 | N–T | 0.25 * | 3.10 * | 0.62 * | −0.34 | −0.27 | 0.68 * | ||
| T–N | 9.45 * | 10.40 * | 10.44 * | 1.06 * | 3.66 * | 3.62 * | T–N | 0.36 * | 1.34 * | 0.67 * | 0.77 * | 1.22 * | 1.22 * | ||
| T–T | 19.38 * | 20.76 * | 18.45 * | 2.91 * | 8.11 * | 7.36 * | T–T | 0.87 * | 3.27 * | 1.03 * | 3.00 * | 5.46 * | 2.15 * | ||
| T–SU | 16.73 * | 26.64 * | 16.83 * | 2.96 * | 10.58 * | 6.68 * | T–SU | 1.00 * | 3.83 * | 1.06 * | 2.94 * | 5.77 * | 2.13 * | ||
| ETH | N | 13.09 * | 13.94 * | 13.66 * | 1.46 * | 1.26 * | 1.45 * | SPB | N | −0.01 | 0.07 * | 0.04 * | −0.18 | −0.23 | 0.24 * |
| T | 17.70 * | 21.47 * | 19.92 * | 11.80 * | 16.02 * | 15.73 * | T | 0.20 * | 0.50 * | 0.28 * | 0.34 * | 0.60 * | 0.88 * | ||
| SU | 25.74 * | 40.64 * | 22.12 * | 1.73 * | 1.62 * | 1.65 * | SU | −0.01 | 0.17 * | 0.07 * | −0.22 | −0.32 | 0.51 * | ||
| N–T | 34.61 * | 38.36 * | 48.01 * | 0.47 * | 0.55 * | 0.73 | N–T | −0.03 | 0.03 * | 0.02 * | −0.06 | −0.08 | 0.18 * | ||
| T–N | 12.99 * | 13.96 * | 14.45 * | 3.58 * | 4.65 * | 5.57 * | T–N | 0.03 * | 0.09 * | 0.07 * | 0.14 * | 0.21 * | 0.27 * | ||
| T–T | 24.61 * | 26.48 * | 33.43 * | 5.77 * | 10.09 * | 12.28 * | T–T | 0.09 * | 0.27 * | 0.19 * | 0.42 * | 0.82 * | 0.80 * | ||
| T–SU | 21.33 * | 32.09 * | 20.17 * | 6.24 * | 12.39 * | 8.31 * | T–SU | 0.08 * | 0.26 * | 0.15 * | 0.40 * | 0.75 * | 0.59 * | ||
| XRP | N | 11.72 * | 13.04 * | 14.28 * | −1.41 | 1.02 * | 4.74 * | USD | N | −0.03 | −0.06 | −0.01 | −0.33 | −0.51 | −0.55 |
| T | 17.15 * | 24.92 * | 26.59 * | 12.41 * | 29.38 * | 39.61 * | T | 0.32 * | 0.53 * | 0.31 * | 0.57 * | 0.57 * | −0.10 | ||
| SU | 21.85 * | 42.04 * | 33.46 * | −1.39 | 1.61 * | 8.25 * | SU | −0.04 | −0.07 | −0.01 | −0.36 | −0.55 | −0.55 | ||
| N–T | 35.84 * | 69.49 * | 102.16 * | −0.48 | 1.43 * | 14.67 * | N–T | −0.03 | −0.12 | −0.02 | −0.43 | −0.55 | −0.46 | ||
| T–N | 11.96 * | 16.38 * | 20.06 * | 3.54 * | 7.55 * | 16.84 * | T–N | 0.05 * | 0.01 * | 0.07 * | −0.14 | −0.21 | −0.26 | ||
| T–T | 24.54 * | 38.98 * | 64.95 * | 7.51 * | 19.82 * | 70.83 * | T–T | 0.14 * | 0.18 * | 0.15 * | 0.07 * | 0.09 * | −0.12 | ||
| T–SU | 17.53 * | 33.49 * | 40.01 * | 6.23 * | 19.19 * | 39.81 * | T–SU | 0.12 * | 0.15 * | 0.12 * | 0.02 | 0.06 | −0.15 | ||
| LTC | N | 12.48 * | 15.79 * | 16.58 * | 1.41 * | −1.85 | −2.41 | OIL | N | 0.39 * | 0.36 | −1.02 | 2.18 * | 0.36 | −1.41 |
| T | 17.55 * | 23.04 * | 22.41 * | 13.68 * | 10.86 * | 9.48 * | T | 3.10 * | 10.31 * | 1.24 * | 11.10 * | 23.87 * | 3.78 * | ||
| SU | 20.62 * | 46.49 * | 31.20 * | 1.41 * | −2.28 | −2.94 | SU | 1.20 * | 1.13 | −1.49 | 10.47 * | 2.02 * | −2.10 | ||
| N–T | 33.36 * | 44.56 * | 30.14 * | 1.51 * | −1.32 | −1.74 | N–T | 0.19 * | −0.98 | −1.31 | 1.89 * | 0.13 * | −0.70 | ||
| T–N | 12.43 * | 14.91 * | 14.91 * | 5.12 * | 2.21 * | 3.31 * | T–N | 0.69 * | 1.20 * | −0.14 | 3.17 * | 5.64 * | 1.48 * | ||
| T–T | 23.64 * | 29.00 * | 24.20 * | 9.41 * | 5.96 * | 7.41 * | T–T | 2.05 * | 3.88 * | 0.54 * | 15.46 * | 26.78 * | 4.71 * | ||
| T–SU | 17.01 * | 33.68 * | 25.25 * | 7.60 * | 7.62 * | 7.60 * | T–SU | 2.75 * | 7.16 * | 0.35 * | 18.43 * | 36.61 * | 3.81 * | ||
| XMR | N | 13.34 * | 12.51 * | 7.82 * | −0.23 | 1.33 * | −1.22 | GLD | N | 0.08 * | 0.01 | −0.21 | 0.16 * | 0.17 * | −1.25 |
| T | 18.68 * | 21.28 * | 13.56 * | 12.44 * | 20.21 * | 13.93 * | T | 0.89 * | 1.80 * | 0.84 * | 2.61 * | 4.41 * | 0.65 * | ||
| SU | 25.11 * | 49.38 * | 18.80 * | −0.28 | 2.59 * | −2.22 | SU | 0.13 * | −0.05 | −0.38 | 0.41 * | 0.61 * | −1.76 | ||
| N–T | 33.42 * | 43.30 * | 28.71 * | 0.69 * | 1.81 * | −1.21 | N–T | 0.16 * | 0.16 * | −0.10 | 0.36 * | −0.21 | −0.53 | ||
| T–N | 12.78 * | 12.42 * | 10.24 * | 4.89 * | 6.46 * | 4.09 * | T–N | 0.26 * | 0.39 * | 0.25 * | 0.87 * | 0.91 * | 0.48 * | ||
| T–T | 23.82 * | 27.11 * | 21.78 * | 9.80 * | 17.64 * | 10.84 * | T–T | 0.56 * | 1.16 * | 0.71 * | 2.56 * | 3.77 * | 1.69 * | ||
| T–SU | 20.69 * | 35.20 * | 21.14 * | 9.28 * | 23.37 * | 10.33 * | T–SU | 0.55 * | 1.17 * | 0.74 * | 2.27 * | 3.24 * | 1.64 * | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hakim, A.; Syuhada, K. Formulating MCoVaR to Quantify Joint Transmissions of Systemic Risk across Crypto and Non-Crypto Markets: A Multivariate Copula Approach. Risks 2023, 11, 35. https://doi.org/10.3390/risks11020035
Hakim A, Syuhada K. Formulating MCoVaR to Quantify Joint Transmissions of Systemic Risk across Crypto and Non-Crypto Markets: A Multivariate Copula Approach. Risks. 2023; 11(2):35. https://doi.org/10.3390/risks11020035
Chicago/Turabian StyleHakim, Arief, and Khreshna Syuhada. 2023. "Formulating MCoVaR to Quantify Joint Transmissions of Systemic Risk across Crypto and Non-Crypto Markets: A Multivariate Copula Approach" Risks 11, no. 2: 35. https://doi.org/10.3390/risks11020035
APA StyleHakim, A., & Syuhada, K. (2023). Formulating MCoVaR to Quantify Joint Transmissions of Systemic Risk across Crypto and Non-Crypto Markets: A Multivariate Copula Approach. Risks, 11(2), 35. https://doi.org/10.3390/risks11020035






