Abstract
This paper features an analysis of the relative effectiveness, in terms of the Adjusted R-Square, of a variety of methods of modelling realized volatility (RV), namely the use of Gegenbauer processes in Auto-Regressive Moving Average format, GARMA, as opposed to Heterogenous Auto-Regressive HAR models and simple rules of thumb. The analysis is applied to two data sets that feature the RV of the S&P500 index, as sampled at 5 min intervals, provided by the OxfordMan RV database. The GARMA model does perform slightly better than the HAR model, but both models are matched by a simple rule of thumb regression model based on the application of lags of squared, cubed and quartic, demeaned daily returns.
1. Introduction
This paper features the application of time series modelling techniques to the modelling of RV. In this particular case, RV sampled at 5 min, as supplied by the OxfordMan Institute (see: https://realized.oxford-man.ox.ac.uk/data, accessed on 22 March 2022), was used. We compare the effectiveness of Gegenbauer processes in Auto-Regressive Moving Average format, GARMA models, as opposed to Heterogenous Auto-Regressive HAR models and other rules of thumb, based on demeaned squared, cubed and quartic daily returns, as methods for modelling and forecasting daily 5 min RV. The aim of the paper is to explore whether sophisticated models out-perform simple rules of thumb.
Over the past 100 years, considerable advances have been made in time series modelling. Yule (1926) and Slutsky (1927) developed the stochastic analysis of time series and developed the concepts of autoregressive (AR) and moving average (MA) models. Box and Jenkins (1970) suggested methods for applying autoregressive moving average (ARMA) or autoregressive integrated moving average (ARIMA) models to find the best fit of a time-series model to past values of a time series.
A contrary view of the approriateness of this approach has been promoted by Commandeur and Koopman (2007), who suggested that the Box–Jenkins approach is fundamentally problematic. They have championed the adoption of alternative state-space methods to counter the contention that many real economic series are not truly stationary, despite differencing.
In the 1980s, attention switched to the consideration of the issues related to stationarity and non-stationary time series, fractional integration and cointegration. Granger and Joyeux (1980) and Hosking (1981) focussed attention on fractionally integrated autoregressive moving average (ARFIMA or FARIMA) processes. Unit root testing to assess the stationarity of a time series became established via the application of the Dickey–Fuller test, following the work of Dickey and Fuller (1979).
Engle and Granger (1987) developed the concept of cointegration, whereby two time series might be individually integrated and non-stationary I(1), but some linear combination of them might possess a lower order of integration and be stationary, in which case the series are said to be cointegrated. Many of these conceptual developments have important applications to economic and financial time series, and to economic theory in these discipline areas.
One of the common features of many time series of financial data sets is that the variance of the series is not homoscedastic, and that these features concerned are autocorrelated. The Autoregressive Conditional Heteroskedasticity (ARCH) model that incorporates all past error terms was developed by Engle (1982). Bollerslev (1986) further generalised it to GARCH by including lagged term conditional volatility. Therefore, GARCH predicts that the best indicator of future variance is a weighted average of long-run variance, the predicted variance for the current period, and any new information in this period, as captured by the squared residuals. GARCH models provide an estimate of the conditional variance of a financial price time series.
The concept of RV and associated metrics were developed by Andersen et al. (2001), Andersen et al. (2003), and Barndorff-Nielsen and Shephard (2002). This alternative approach measures the variance directly from the observed values of the price series. These RV measures are theoretically sound, high-frequency, nonparametric-based estimators of the variation of the price path of an asset during the times at which the asset trades frequently on an exchange.
The modelling of the variance of financial time series and the use of RV is the focus of this paper. In the empirical analysis, we use RV 5 min estimates from Oxford-Man for the S&P500 Index as the RV benchmark. Their database contains daily (close to close) financial returns and a corresponding sequence of daily realized measures .
Corsi (2009, p. 174) suggests “an additive cascade model of volatility components defined over different time periods. The volatility cascade leads to a simple AR-type model in the realized volatility with the feature of considering different volatility components realized over different time horizons, and which he termed as being a “Heterogeneous Autoregressive model of Realized Volatility”. We make use of the Corsi (2009) HAR model to model RV in some of the empirical tests included in this paper.
However, the main focus of this paper is the application of Gegenbauer processes to the modelling of RV. Gegenbauer processes were introduced by Hosking (1981) and further developed by Anděl (1986) and Gray et al. (1989). The latter proposed the class of time series models known as Gegenbauer ARMA, or, as abbreviated, GARMA processes, which are the central focus of this paper.
In the current paper, we compare the effectiveness of GARMA models, as opposed to HAR models and other rules of thumb, based on demeaned squared daily returns, as methods for modelling and forecasting daily 5 min RV.
The paper is a further companion piece to two previous studies in the topic’s general area, namely, Allen and McAleer (2020) and Allen (2020), that compared the effectiveness of stochastic volatility (SV), vanilla GARCH and HAR models, as opposed to simple rules of thumb, in their effectiveness as tools for capturing the RV of major stock market indices.
The current paper concentrates on the S&P500 index and examines whether GARMA, HAR or simple rules of thumb better capture the RV sampled at 5 min intervals, as provided by Oxford-Man, of the S&P500 Index. Thus, the central concern is what is the best method of capturing the long memory properties of a historical time series of RV5 for the S&P500 index. This is in contrast with the two previously mentioned studies, which contrasted the effectiveness of the volatility models per se.
The benchmark is provided by the estimates of RV5, in a sample of daily estimates of RV5, running from 8 May 1997 to 30 August 2013 with 4096 observations, plus a longer-period sample of RV5, also based on the S&P500 Index, running from 4 January 2000 to 30 April 2020, comprising 5099 observations. This is the same data set as used in Allen (2020).
The motivation for this paper is provided by Poon and Granger (2005, p. 507), who observed that: “as a rule of thumb, historical volatility methods work equally well compared with more sophisticated ARCH class and SV models.” This paper similarly seeks to explore whether simple rules of thumb, in this case based on the use of a regression model featuring squared demeaned daily returns, with the subsequent addition of cubed and quartic powers of them, perform as well as more sophisticated time series models.
2. Previous Work and Econometric Models
Recent reviews of the literature on the nature and applications of Gegenbauer processes are provided by Hunt et al. (2021) and Dissanayake et al. (2018). Peiris et al. (2005) and Peiris and Thavaneswaran (2007) considered long memory models driven by heteroskedastic GARCH errors. Peiris and Asai (2016) returned to this topic, and Guegan (2000) combined Gegenbauer processes with integrated GARCH (GIGARCH) to include the attributes of long memory, seasonality and heteroskedasticity at the same time, in the modelling of volatility.
2.1. The Basic GEGENBAUER Model
Let be a stationary random process with the autocovariance and the autocorrelation function where . The spectral density function (sdf) is denoted by:
where is the Fourier frequency.
There are various ways in which the long memory component of the Gegenbauer model can be specified, as discussed in Dissanayake et al. (2018). In the analysis that follows, we utilise the R package GARMA, as developed by Hunt (2022a).
A Gegenbauer process is a long memory process generated by the dynamic equation:
where and is a short memory process characterised by a positive and bounded spectral density, . If (1) is a Gegenbauer process of order or a GARMA process. Dissanayake et al. (2018) mention that (1) complies with the definition of a long memory process at the frequency . According to (1), arises from filtering the process by the infinite impulse response
It can be shown that a stationary Gegenbauer process contains an unbounded spectrum at and is long memory when . This special frequency is called the Gegenbauer or G-frequency, as outlined by Dissanayake et al. (2018, p. 416).
The k-factor GARMA model as fit by the GARMA package, as in Hunt (2022a), is specified as:
- where represents the short-memory autoregressive component of order
- represents the short memory moving average component of order
- represents the long-memory Gegenbauer component (there may in general be k of these),
- represents integer differencing (currently only = 0 or 1 is supported),
- represents the observed process,
- represents the random component of the model—these are assumed to be uncorrelated but identically distributed variates,
- represents the Backshift operator, defined by
When then this is just a short memory model, as would be represented by an ARIMA model.
Dissanayake (2015) considered a class of Gegenbauer processes generated by Gaussian white noise and GARCH errors and suggested that many other models could be nested within this framework. He explored a number of related issues and used state space modelling to explore seasonal Gegenbauer processes.
Phillip (2018) applied a Gegenbauer long memory stochastic volatility model with leverage and a bivariate Student’s t-error distribution to describe the innovations of the observation and latent volatility jointly and demonstrated its effectiveness in applications to Cryptocurrency time series. He demonstrated by means of MCMC runs for various values of [u; d], that when d is low, and as u → 0. the convergence of u to its true value gets slower. This is an expected result, since as d → 0, the process has less information and becomes “less long-memory”.
2.2. Heterogenous Autoregressive Model (HAR)
Corsi (2009, p. 174) suggests “an additive cascade model of volatility components defined over different time periods. The volatility cascade leads to a simple AR-type model in the realized volatility with the feature of considering different volatility components realized over different time horizons and which he termed as a Heterogeneous Autoregressive model of Realized Volatility”. Corsi (2009) suggests that his model can reproduce the main empirical features of financial returns (long memory, fat tails, and self-similarity) in a parsimonious way. He writes his model as:
where is the daily integrated volatility, and and are, respectively, the daily, weekly, and monthly (ex post) observed realized volatilities.
2.3. Historical Volatility Model (HISVOL)
Poon and Granger (2005) discuss various practical issues involved in forecasting volatility. They suggest that the HISVOL model has the following form:
where is the expected standard deviation at time , is the weight parameter, and is the historical standard deviation for periods indicated by the subscripts. Poon and Granger (2005) suggest that this group of models include the random walk, historical averages, autoregressive (fractionally integrated) moving average, and various forms of exponential smoothing that depend on the weight parameter .
We use a simple form of this model in which the estimate of is the previous day’s demeaned squared return. Poon and Granger (2005) review 66 previous studies and suggest that implied standard deviations appear to perform best, followed by historical volatility and GARCH, which have roughly equal performance.
Barndorff-Nielsen and Shephard (2003) point out that taking the sums of squares of increments of log prices has a long tradition in the financial economics literature. See, for example, Poterba and Summers (1986), Schwert (1989), Taylor and Xu (1997), Christensen and Prabhala (1998), Dacorogna et al. (1998), and Andersen et al. (2001). Shephard and Sheppard (2010) p. 200, footnote 4) note that: “Of course, the most basic realized measure is the squared daily return”. We utilise this approach as the basis of our historical volatility model. Furthermore, Perron and Shi (2020) show how the squared low-frequency returns can be expressed in terms of the temporal aggregation of a high-frequency series in relation to volatility measures.
3. Results
3.1. The Data Sets
To expedite a direct comparison with previous work on the HAR model, we use the R library package ’HARModel’ by Sjoerup (2019). This contains data featuring RV measures from the SP500 index from April 1997 to August 2013, and we use the RV5 measures on the S&P500 Index sampled at 5 min intervals.
Table 1 provides a statistical description of this RV5 data set, together with that of another slightly longer data set, taken from 2000 to 2020, also featuring S&P500 index RV5 data taken from Allen and McAleer (2020). Both data sets feature RV5 estimates taken from the Oxford-Man Realized library.

Table 1.
Descriptive statistics RV5 data sets.
One of the features of estimates of RV is that the data time series displays long-memory characteristics. Long memory refers to the association between observations in a time series that are ever larger sample intervalling and is also referred to as long-range dependence. It basically refers to the level of statistical dependence between two points in the time series sampled at increasing intervals.
Figure 1 displays the long memory characteristics of the two RV5 time series that we analyse. The first panel in the two plots displays the basic series of RV5, and the two large spikes in RV5 correspond to the effects on volatility of the Global Financial Crisis (GFC) that occurred in 2008. The two panels marked ACF and PACF refer to the autocorrelation and partial autocorrelation statistics.
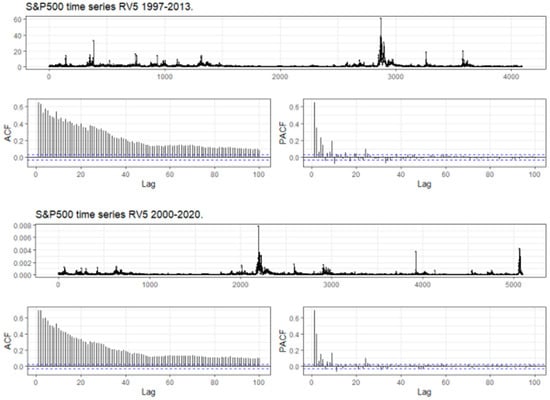
Figure 1.
Plots of the RV5 samples for the S&P500 index and their long-range dependence. (Dashed blue line represents error bands).
The R GARMA package, Hunt (2022a), was used to generate the two graphs. The program was instructed to use 100 lags of daily observations. The blue lines in the bottom two sets of panels display the standard error bands. The long memory properties of RV5 are apparent in both sets of diagrams in that the ACF statistics remain well outside the error bands for 100 lags, and the PACF is outside the error bands for up to 30 lags.
These long memory characteristics are used in Corsi’s (2009) HAR model and will be a feature of the Gegenbauer models that we fit to the data sets.
3.2. The Basic HAR Model
Table 2 provides summary descriptions of the HAR models fitted to the two RV5 data sets, and Figure 2 provides plots of the fits. The results presented in Table 2 show that the basic HAR model does an excellent job of capturing the time series properties of RV5. All the estimates are significant at a one percent level, as are the F statistics, and the Adjusted R-squares are 52 percent for the period 1997–2013 and 56 percent for the period 2000–2020, respectively.

Table 2.
Summary of the HAR models fitted to the RV5 data sets.
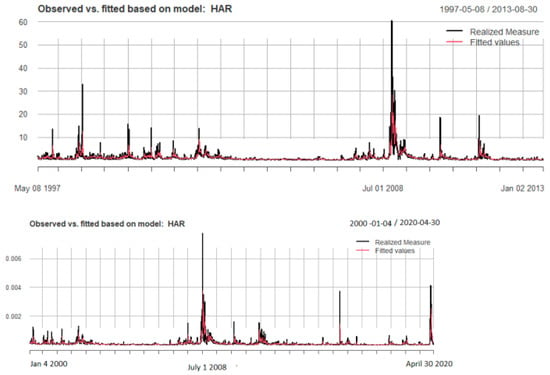
Figure 2.
Plots of fitted HAR models.
The plots in Figure 2 confirm this but do suggest that the large periodic peaks in RV5 are not captured so effectively by the HAR model. The question remains as to whether the Gegenbauer model will perform more effectively.
3.3. Gegenbauer Results
The R library package (GARMA), Hunt (2022a), was used to fit GARMA models to the RV5 series for the S&P500 index as sourced from the Oxford-Man library. This shorter RV series, for the S&P500 from 1997 to 2013, was taken from the HARmodel R library package, Sjoerup (2019).
A detailed summary of the methods used in the GARMA package is available in Hunt (2022b). The GARMA package provides the ability to fit stationary, univariate GARMA models to a time series and to forecast from those models. The garma() function in the GARMA package is the main function for estimating the parameters of a GARMA model. It provides three methods of parameter estimation: the Whittle method, (Whittle 1953), the conditional sum-of-squares (CSS) method, (for a discussion, See Hunt (2022b) chp. 2, eq. 2.3.2) and the WLLS method. The latter, the Whittle Log Least-Squares method, was proposed by Hunt (2022b, chp. 3). The Whittle method was used in the estimations reported in the paper.
A summary of the Gegenbauer model estimated for this data is shown in Table 3. A potential advantage of the Gegenbauer model is that it is non-linear and more flexible than the HAR model.

Table 3.
Gegenbauer estimation for RV5 with GARMA for the S&P500 from 1997–2013, constant included with no trend.
The results of a regression of the fit from the Gegenbauer model for this data on the actual RV5 estimates for the S&P500 index for this period are shown in Table 4. The HAR model regression for this period, shown in the first half of Table 2, had an Adjusted R-squared of 0.52. The result for the Gegenbauer model estimation is an Adjusted R-squared of 0.567, and so the non-linear model does show an increased explanatory power.

Table 4.
Regression of RV5 on Gegenbauer model estimates, 1997–2013.
We also fitted the Gegenbauer model to the longer time-period of RV estimates running from 2000 to 2020 and present the results in Table 5.

Table 5.
Gegenbauer estimation for RV5 with GARMA for the S&P500 from 2000 to2020, constant included with no trend.
We regressed the actual daily RV5 series for the longer period from 2000 to 2020, and the results are shown in Table 6. The slope coefficient is significant at the 1 per cent level and is very close to 1, whilst the Adjusted R-square is 0.59, and the F statistics for the regression, with a value of 7326, is also significant at the 1 percent level. The Adjusted R-square for the HAR model for the same period was 0.56, so the Gegenbauer model provides a marginally better fit than the HAR model.

Table 6.
Regression of RV5 on Gegenbauer model estimates, 2000–2020.
3.4. How Do Rule of Thumb Approaches Perform?
The next issue is how squared demeaned end-of-day returns perform as a simple rule-of-thumb method to explain RV5. Table 7 presents the results of the regression of RV5 for the longer period of 2000 to 2020 on 20 lags of squared demeaned daily returns.

Table 7.
Regression of RV5 on squared demeaned daily returns for 2000 to 2020; OLS, using observations 21–5099 ( = 5079); Dependent variable: rv5.
It can be seen in Table 7 that 20 lags of squared demeaned returns do not perform quite as well as the Gegenbauer or HAR models but still have an Adjusted R-Square of 54 percent, which is a marginal 2 percent less than the HAR model and 5 percent less than the Gegenbauer model. Only 4 of the 20 lags used in this rule-of-thumb approach are insignificant. The Durbin–Watson statistic of 1.43 suggests that a considerable amount of autocorrelation remains in the residuals.
The application of Ramsey Reset tests (Ramsey 1969), suggests that squares and cubes of the explanatory variable could add to the power of the regression. Table 8 reports the results of adding 10 lags of cubed demeaned SPRET and 10 lags of demeaned SPRET to the power 4.

Table 8.
Regression of RV5 on squared, cubed and quartic daily demeaned returns for 2000 to 2020; OLS, using observations 21–5099 ( = 5079); variable: rv5.
This is essentially another non-linear model, but admittedly, we now have 40 explanatory variables in the model in the form of lags of three explanatory variables. The Adjusted R-Square now increases to over 59 percent, which matches the power of the Gegenbauer model. Admittedly, the Durbin–Watson statistic is still a relatively low 1.54. This suggests that there is still autocorrelation in the residuals, which could be exploited further in enhanced modifications of the model.
The above regression is quite clumsy and contains some redundant terms. An anonymous reviewer suggested that we apply a lasso technique to reduce the size of the regression. This is not entirely consistent with using a ‘rule of thumb’ approach, and it would be a simple matter to drop the redundant terms in the regression above.
The adaptive lasso regression uses different penalties (weights) for different regressors when running a lasso regression. Under certain conditions, as applied to those weights, the results will have the so-called oracle property, see Zou (2006) as opposed to the standard lasso approach.
Zou (2006) derives a necessary condition for the lasso variable selection to be consistent. His version of the lasso, the adaptive lasso, employs adaptive weights that are used for penalizing different coefficients in the penalty. He demonstrates that the adaptive lasso enjoys oracle properties, namely, that it performs as well as if the true underlying model were given in advance. Zou (2006) suggests that y = (y1, …, yn)T is the response vector and xj= (x1j, …, xnj)T, j = 1, …, p, are the linearly independent predictors. He lets X = [x1,…,xp] be the predictor matrix. He assumes that E[y|x] = β*1x1 + ··· + β*pxp. The data are assumed to be centred so the intercept is not included in the regression equation. He lets A = {j: βj∗ ≠ 0} and then assumes that |A| = p0 < p. This implies that the true model depends only on a subset of the predictors.
If we denote by (δ), the coefficient estimator is produced by a fitting procedure δ. Then, the arguments of Fan and Li (2001) can be adopted and δ can be termed as being an oracle procedure if (δ) (asymptotically) has the following oracle properties:
- Identifies the right subset model, {j: j≠ 0} = A
- Has the optimal estimation rate, √n ((δ)A − β*A) → d N(0,Σ*), where Σ* is the covariance matrix knowing the true subset model.
The lasso is a regularization technique for simultaneous estimation and variable selection Tibshirani (1996). The lasso estimates are defined as:
where λ is a nonnegative regularization parameter. The second term in the expression above is the so-called “ℓ1 penalty,” which is crucial for the success of the lasso. The lasso continuously shrinks the coefficients toward 0 as λ increases, and some coefficients are shrunk to exactly 0 if λ is sufficiently large.
Zou proposes the adaptive lasso, in which adaptive weights are used for penalizing different coefficients in the ℓ1 penalty and he demonstrates that the adaptive lasso enjoys the oracle properties. He employs (ols) to construct the adaptive weights in the adaptive lasso; and suggests that the computation procedure involves the employment of the LARS algorithm (Efron et al. 2004).
We implemented this version of the adaptive lasso technique using a GRETL function package containing code submitted by Schreiber (2023). Table 9 shows the regression screening results chosen by the technique as applied to the variables in Table 8.

Table 9.
Regressors chosen by the adaptive lasso technique applied to the variables in Table 8.
These variables chosen were then applied in a new variant of the rule of thumb OLS regression of RV5 on the various lags of squared, cubed and quartic demeaned returns chosen by the adaptive lasso technique. The results are shown in Table 10.

Table 10.
Regression of RV5 on squared, cubed and quartic daily demeaned returns for 2000 to 2020 as chosen by the adaptive lasso technique.
The results of the application of the adaptive lasso technique shown in Table 10 confirm the previous findings reported in Table 8, namely, that a rule-of-thumb method using squared, cubed, and quartic end-of-day returns in the explanation of RV5 matches those obtained by application of the Gegenbauer technique.
4. Conclusions
In this paper, we have explored the use of the Gegenbauer process or GARMA model to capture the behaviour of RV5 volatility of the S&P500 index, as reported by the OxfordMan database. The results suggest that the non-linear Gegenbauer model performs slightly better than the HAR model in capturing RV5. However, a simplified rule of thumb model based on the use of lagged, squared, cubed, and quartic, demeaned daily returns performed equally well. These results, for the S&P500 index, suggest that non-linear models perform better than linear ones in the capture of long memory properties of RV5 and that sophisticated models do not necessarily dominate rules of thumb.
Author Contributions
Conceptualization, D.E.A. and S.P.; methodology, D.E.A. and S.P.; software, D.E.A. and S.P.; validation, D.E.A. and S.P.; formal analysis, D.E.A.; investigation, D.E.A.; resources, S.P.; data curation, D.E.A.; writing—original draft preparation, D.E.A.; writing—review and editing, D.E.A. and S.P.; visualization, D.E.A.; project administration, S.P.; funding acquisition, S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Index data were obtained from Yahoofinance on 20/3/2022. The realized volatility data were originally obtained from Oxford-Man at http://realized.oxford-man.ox.ac.uk (accessed on 1 January 2020), but this data base has recently been removed from public availability.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Allen, David E., and Michael McAleer. 2020. Do we need stochastic volatility and Generalised Autoregressive Conditional Heteroscedasticity? Comparing squared end-of-day returns on FTSE. Risks 8: 12. [Google Scholar] [CrossRef]
- Allen, David Edmund. 2020. Stochastic volatility and GARCH: Do squared end-of-day returns provide similar information? Journal of Risk and Financial Management 13: 202. [Google Scholar] [CrossRef]
- Anděl, Jiří. 1986. Long memory time series models. Kybernetika 22: 105–23. [Google Scholar]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Heiko Ebens. 2001. The distribution of realized stock return volatility. Journal of Financial Economics 61: 43–76. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 529–626. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002. Econometric analysis of realised volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society, Series B 63: 253–80. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2003. Realized power variation and stochastic volatility models. Bernoulli 9: 243–65. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroscedasticity. Journal of Econometrics 31: 307–327. [Google Scholar] [CrossRef]
- Box, George E. P., and Gwilym M. Jenkins. 1970. Times Series Analysis. Forecasting and Control. San Francisco: Holden-Day. [Google Scholar]
- Christensen, Bent J., and Nagpurnanand R. Prabhala. 1998. The relation between implied and realized volatility. Journal of Financial Economics 37: 125–50. [Google Scholar] [CrossRef]
- Commandeur, Jacques J. F., and Siem Jan Koopman. 2007. Introduction to State Space Time Series Analysis. Oxford: Oxford University Press. [Google Scholar]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- Dacorogna, Michel M., Ulrich A. Muller, Richard B. Olsen, and Olivier V. Pictet. 1998. Modelling short term volatility with GARCH and HARCH. In Nonlinear Modelling of High Frequency Financial Time Series. Edited by C. Dunis and B. Zhou. Chichester: Wiley. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Dissanayake, G. S., M. Shelton Peiris, and Tommaso Proietti. 2018. Fractionally Differenced Gegenbauer Processes with Long Memory: A Review. Statistical Science 33: 413–26. [Google Scholar] [CrossRef]
- Dissanayake, Gnanadarsha Sanjaya. 2015. Advancement of Fractionally Differenced Gegenbauer Processes with Long Memory. Ph.D. thesis, School of Mathematics and Statistics, University of Sydney, Sydney, NSW, Australia. [Google Scholar]
- Efron, Bradley, Trevor Hastie, Iain Johnstone, and Robert Tibshirani. 2004. Least Angle Regression. The Annals of Statistics 32: 407–99. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Clive W. J. Granger. 1987. Co-integration and error correction: Representation, estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Fan, Jianqing, and Runze Li. 2001. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. Journal of the American Statistical Association 96: 1348–60. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Roselyne Joyeux. 1980. An introduction to long-memory time series models and fractional differencing. Journal of Time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Gray, Henry L., Nien-Fan Zhang, and Wayne A. Woodward. 1989. On generalized fractional processes. Journal of Time Series Analysis 10: 233–57, Erratum in Journal of Time Series Analysis 15: 561–62. [Google Scholar] [CrossRef]
- Guegan, Dominique. 2000. A new model: The k-factor GIGARCH process. Journal of Signal Processing 4: 265–71. [Google Scholar]
- Hosking, J. R. M. 1981. Fractional differencing. Biometrika 68: 165–76. [Google Scholar] [CrossRef]
- Hunt, Richard. 2022a. Garma: Fitting and Forecasting Gegenbauer ARMA Time Series Models, R Package Version 0.9.11. Available online: https://CRAN.R-project.org/package=garma (accessed on 3 October 2023).
- Hunt, Richard. 2022b. Investigations into Seasonal ARMA Processes. Ph.D. thesis, School of Mathematics and Statistics, University of Sydney, Sydney, NSW, Australia. [Google Scholar]
- Hunt, Richard, Shelton Peiris, and Neville Weber. 2021. Estimation methods for stationary Gegenbauer processes. Statistical Papers 63: 1707–41. [Google Scholar] [CrossRef]
- Peiris, M. Shelton, and Manabu Asai. 2016. Generalized fractional processes with long memory and time dependent volatility revisited. Econometrics 4: 37. [Google Scholar] [CrossRef]
- Peiris, Shelton, David Allen, and Udara Peiris. 2005. Generalised autoregressive models with conditional heteroscedasticity: An application to financial time series modelling. In The 2004 Workshop on Research Methods: Statistics and Finance, Proceedings of the 2004 Workshop on Research Methods: Statistics and Finance. Edited by Eric J. Beh, Robert G. Clark and J. C. W Rayner, Wollongong: University of Wollongong, pp. 75–83. ISBN 1 74128 107 5. [Google Scholar]
- Peiris, M. Shelton, and Aera Thavaneswaran. 2007. An introduction to volatility models with indices. Applied Mathematics Letters 20: 177–82. [Google Scholar] [CrossRef][Green Version]
- Perron, Pierre, and Wendong Shi. 2020. Temporal aggregation and Long Memory for asset price volatility. Journal of Risk and Financial Management 13: 181. [Google Scholar] [CrossRef]
- Phillip, Andrew. 2018. On Gegenbauer long memory stochastic volatility models: A Bayesian Markov chain Monte Carlo approach with applications. Ph.D. thesis, School of Mathematics and Statistics, University of Sydney, Sydney, NSW, Australia. [Google Scholar]
- Poon, Ser-Huang, and Clive Granger. 2005. Practical issues in forecasting volatility. Financial Analysts Journal 61: 45–56. [Google Scholar] [CrossRef]
- Poterba, James M., and Lawrence H. Summers. 1986. The persistence of volatility and stock market fluctuations. American Economic Review 76: 1124–41. [Google Scholar]
- Ramsey, James Bernard. 1969. Tests for Specification Errors in Classical Linear Least Squares Regression Analysis. Journal of the Royal Statistical Society, Series B 31: 350–71. [Google Scholar] [CrossRef]
- Schreiber, Sven. 2023. adalasso.gfn GRETL Code Function. Available online: https://gretl.sourceforge.net/cgi-bin/gretldata.cgi?opt=SHOW_FUNCS (accessed on 3 October 2023).
- Schwert, G. William. 1989. Why does stock market volatility change over time? Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
- Shephard, Neil, and Kevin Sheppard. 2010. Realising the future: Forecasting with high-frequency-based volatility (HEAVY) models. Journal of Applied Econometrics 25: 197–231. [Google Scholar] [CrossRef]
- Sjoerup, Emil. 2019. HARModel: Heterogeneous Autoregressive Models. R Package Version 1.0. Available online: https://CRAN.R-project.org/package=HARModel (accessed on 3 October 2023).
- Slutsky, Eugen. 1927. The summation of random causes as the source of cyclic processes. Econometrica 5: 105–46. [Google Scholar] [CrossRef]
- Taylor, Stephen J., and Xinzhong Xu. 1997. The incremental volatility information in one million foreign exchange quotations. Journal of Empirical Finance 4: 317–40. [Google Scholar] [CrossRef]
- Tibshirani, Robert. 1996. Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society, Ser. B 58: 267–88. [Google Scholar] [CrossRef]
- Whittle, Peter. 1953. The analysis of multiple stationary time series. Journal of the Royal Statistical Society. Series B (Methodological) 15: 125. [Google Scholar] [CrossRef]
- Yule, G. Udny. 1926. Why do we sometimes get nonsense correlations between timeseries? A study in sampling and the nature of time-series. Journal of the Royal Statistical Society 89: 1–63. [Google Scholar] [CrossRef]
- Zou, Hui. 2006. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association 101: 1418–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).