Taguchi Risk and Process Capability

Abstract

Process control methods, in general, and quality, in particular, most often refer to the measures taken especially to the finished product, as well as to the technological process, in order to maintain its performance within certain statistical parameters. Genichi Taguchi is the first who developed a quality control approach, used first in Japan and later in industrialized economies, a procedure widespread in quality under the name Taguchi method. Within the Taguchi method, he imposed a key term average loss attached to a process /characteristic in case it deviates, compared to a target value/objective, considered optimal. The Taguchi methodology is especially oriented towards the design phase, different from the classic approach oriented towards the final control phase upon delivery, or towards the supervision of the processes. This new approach aims to design processes and products so that they are as insensitive as possible (robust) to the influence of external, disruptive factors of the processes. In our paper, the capability indicators of the processes and their connection with the Taguchi risk are also presented. A link is also made between the statistical measurement of uncertainty and the Taguchi risk with an example in a process from the mechanical industry.

1. Introduction

The development of management science in the last decade has focused concerns in the direction of optimizing activities in the field of risk analysis and assessment. Risks are inherent in every economic, social or political activity.

A risk is an uncertain event, which may not occur, but unlike uncertainty or insecurity, risk has the specific possibility of being described by probability laws, even if it is related to “fluid” elements such as uncertainty and loss (Bârsan-Pipu and Popescu 2003).

Both uncertainty and risk are in their structure “impregnated” with the element of randomness, a state that allows the use of probabilistic–statistical tools. The goal pursued is minimization—of both risks and possible losses—for which purpose different operational research tools are used. From the multitude of risks—technical, financial, bankruptcy, environmental, debt, country, military conflict, as well as other specific risks—in this work, we will focus on the Taguchi risk. Professor Genichi Taguchi is famous in the field of qualitology for his contribution to the theory and practice of the statistical design of industrial experiments. A new concept introduced by Taguchi represented Quality Loss Function (Taguchi 1992), which is a way to determine how each imperfect product generates a loss for individuals, companies and finally for society.

Activities to improve quality and reduce the risk of loss must not be carried out prior to the transition to the real-time quality control stage, but must be carried out offline with the meaning, in this context, that the respective stage must precede the online phase of the actual development phase of the processes. A component in the Taguchi approach is the concern for reducing variability from technical specifications where each quality characteristic must have a certain nominal value or a target value, and the effects that may occur as a result of the deviation from the target value are measured by quadratic loss.

Through this approach, now generically called the Taguchi method, the aim is to obtain a robust process under the action of internal or external disturbing factors. It is a new approach of the management of industrial processes, compared to the classic, Shewhartian, process control and monitoring concept. The novelty that completes this methodology seeks to counter the effects of noise factors, which disrupt the process from the design phase of the processes and of the product.

2. Literature Review

An extensive presentation of the Taguchi method is made in the Alexis (1998) monograph, where its essence is emphasized, which essentially consists in combining quality engineering with statistical methods to increase quality and reduce costs by improving process design. The work Introduction to Quality Engineering (Taguchi 1986) is the first book that presents specific methods that establish quality responsibility as belonging to all decision-makers in the company, and turn everyone into specialists involved in the process control. The respective methods were later developed (Taguchi 1992; Taguchi et al. 2004) on topics such as: online quality engineering, quality loss function calculation, signal-to-noise ratio, robust engineering, Mahalanobis–Taguchi systems and many others.

Literature on the subject of the Taguchi method can be grouped into several broad themes. The theoretical foundation of the method is the concern of a large number of authors, including Ben-Gal and Dror (2016), Ritholtz (2023) who explain the fundamentals of the method. Petrescu et al. (2004) develop and analyze the issue of uncertainty and Surbhi (2017) tries to clarify the difference between risk and uncertainty, a concern also present in De Groot and Thurik (2018) and Kang et al. (2016). The modeling of uncertainty is also developed by Oberkampf et al. (2012), and uncertainty in the development of strategies is treated by Bratianu (2015). Holton (2019) deals with the specificity of risk in finance. Dizikes (2010) analytically presents Frank Knight’s work on risk (Knight 1921), which analyzes competition in a free market using the concept of risk. Yasuhiro (2019) compares, in the mirror, the problem of approaching uncertainty and risk to two great thinkers in the economic field, Keynes and Knight.

Project management is addressed by Usmani (2022), who emphasizes the importance of risk management, and Gollier and Kimball (2018) evaluate some innovative contributions in risk economics. Sharpe (2018) uses algebra and subjective probabilities to measure risk. Security risk management is proposed by Yalcinkaya et al. (2019).

Quality engineering is the field in which Jayaswal and Patton (2006) develop an integrated technology to address software quality. The ability of processes for non-normal distributions was developed by Chan et al. (1988) on the case of the Weibull distribution. Partheeban et al. (2019) apply the Taguchi method to the technological process of turning and the robust design and its illustration through a case study is carried out by Nataraj et al. (2006).

Theoretical and applied medicine is another field with many applications; for example, the early detection of breast cancer is the concern of Sudharsan and Ng (2000) and self-medication, a major health problem in rural India, is the subject of Singh (2021). The calibration of glucose measuring instruments using the Taguchi loss function is carried out by Krouwer (2016).

Research and innovative practice is another area of major interest, where Aksoy et al. (2022) review the TOPSIS fuzzy technique through the Taguchi method, and the optimization of the parameters of some processes using the Minitab16^® software is present in Salari et al. (2019). The assumption of the normality of the distribution of parameters is applied by Li et al. (2007) and the development of a strategy based on Taguchi risk assessment, in the production of innovative medicines, is developed by Cogdill and Drennen (2008). Yang et al. (2007) illustrate the Taguchi method in biomechanical analysis and Wright (2014) presents a range of models for identifying uncertainty under climate change conditions.

In economic practice, a Taguchi inspiration diagram is proposed by Martins and Oke (2020) and Emovon and Norman (2020) apply the method in the maintenance of marine navigation systems. The radiation risk study is carried out by Kanzaki (2019), and at the macroeconomic level, Gallagher et al. (2013) study the problem of food safety. Holton (2019) study financing risks and costs, as well as Rachev et al. (2011). Buch et al. (2023) addresses the problem of value at risk (VaR) in the financial field, a field also studied by Artzner et al. (1999).

3. Statistical Uncertainty

As is known, there is a diversity of measurements, such as measuring customer satisfaction, economic results, poverty, inflation, unemployment, national production, etc. In this work, we are particularly concerned with technical measurement, the so-called engineering measurement Eisenhart (1962) shows that measurement represents the allocation of numbers to certain material objects and Petrescu et al. (2004) emphasizes that the measurement process provides correct results when the processes are in a state of statistical control, so we can identify a law for the distribution statistics of these values, which is frequently the normal law, using the parameters’ mean and the variance of the measured quantity, respectively (Isaic and Dragan 2018). In the most common situations, the values follow the Gauss–Laplace law, and the mean proves to be a good substitute for the so-called “true value” of the measurement.

A measurement operation is in a state of statistical control if there are quantitative measures of repeatability and reproducibility. Repeatability is a measure of the variability between the sequence of recorded values and reproducibility is a measure of the variability between two or more different measurements. The indicators are the associated standard deviations and the so-called repeatability/reproducibility limits, respectively,

$$Pr.\left\{\left|\delta \right|\le r\left(orR\right)\right\}=95\mathrm{\%}$$

(1)

where $\left|\delta \right|$ is the absolute value of the difference between two results of a measurement.

Uncertainty is defined as a doubt about the validity of the result of a measurement. It also has a standardized operational definition (Guide-ISO 2010): “Uncertainty (of measurement) is a parameter associated with the result of a measurement that characterizes the dispersion of values that can reasonably be attributed to the measurement”.

Statistically, the standard uncertainty is expressed by the quadratic deviation and represents an estimate of the internal variability of the string of observations $\left\{x_i,x_2,..,x_n\right\}$ on the measurement.

The standard deviation (s) is calculated as follows: $s=\sqrt{s^2}$ and the variance (Var(x))

$$s^2=\frac{1}{n-1}\sum (x_i-\bar{x}{)}^2, \mathrm{where}: \bar{x}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.\left(\sum x_i\right)$$

(2)

It should be noted that s does not represent an unbiased estimator of the theoretical standard deviation ($\sigma$), but s² is such an estimator for the variance.

The size s²/n is the experimental variance of the mean and represents a measure of the uncertainty of the mean. In statistical quality control (SQC), the expressions $\mu -3\sigma /\sqrt{n}$, and $\mu +3\sigma /\sqrt{n}$ are the control limits for the process mean. If X is a normally distributed variable, about 0.27% of the variable’s values will fall outside the control limits, so, on average, only 1 out of 370 subgroup means (i.e., $1:0.027\approx 370.37037\approx 370$) will be outside the limits, in the case of a stable statistical process:

$$Pr\left\{\left|X-M\left(X\right)\right|\le 3·\sqrt{Var\left(X\right)}\right\}\approx 0.973$$

(3)

The global or extended uncertainty is—according to the Guide-ISO (2010)—a quantity that defines an “interval around the result of a measurement”, in which a high fraction of the distribution of values is expected to be included.

The U indicator is determined as follows: U =$K·u_c\left(y\right)$, where K is an extrapolation factor that usually has values between 2 and 3, and u_c(y) is the compound standard uncertainty. The measurement Y is evaluated indirectly, first measuring the elements x_i, $i=\overline{1,N}$ and the composite standard uncertainty denoted by $u_c\left(y\right)$ is

$$u_c^2\left(y\right)={{\sum }_{i=1}^N\left[\frac{\upsilon f}{\upsilon x_i}\right]}^2·u^2\left(x_i\right)$$

(4)

where u($x_i$) = $s \left(x_i\right)$—the estimated standard deviation in x_i—and the sizes x_i are considered uncorrelated and the shape of the function f does not strongly deviate from the linear model.

Finally, the result of a measurement can be expressed as follows

$$Y=y\pm U,$$

(5)

where y is an estimate of the measure Y, and the interval [y − U, y + U] is the domain that covers a significant proportion of the values of the measure Y.

If Y is a normally distributed variable, obviously, the interval $\left[\bar{y}-2s,\bar{y}+2s\right]$ contains approximately 95.45% of the values of Y, and if K = 3, then $\left[\bar{y}-3s,\bar{y}+3s\right]$ contains approximately 99.73% of the values.

The values of K are not placed only in the interval [2, 3], being possible to assign other values for the extrapolation factor. In the situation where the measure Y is not normally distributed, we recommend the use of the Wilks procedure (Porter 2019) by which the number of necessary measurements y₁, y₂, … y_n is determined so that the extreme values (y_min şi y_max) are considered natural tolerances.

4. Taguchi Risk and Process Monitoring

The concrete manifestation of risks is expressed by the possibility of unwanted events and the statistical modeling of risk has, as its working hypothesis, the fact that the risk can be equated with the possibility of suffering a damage. This possibility can be measured by a probability and the risk appears as a function of the probability of the occurrence of this unwanted phenomenon. Mathematically, both uncertainty and risk are modeled by means of random variables. Thus, the risk is a continuous random variable $X:\xi \to R$ where $\xi ,K,P$ is a probability field. If $S\left(\xi \right)$ is the set of all variables defined on $\xi$, and $M\subset S\left(\xi \right),$ a subset of $S\left(\xi \right)$, then a function $r:M\to R$ is a so-called risk measure $r(X)$.

Nowadays, risk management is increasingly becoming a distinct field of scientific management. The risk variant proposed by Taguchi, which bears his name, aims to improve the performance of a process, in parallel with reducing the design and execution costs of the offline products. This situation means that the quality improvement activities are carried out before the transition to the quality control phase, respectively the online phase.

The effects that may occur as a result of the deviation from the target value can be measured by the quadratic loss function. In this case, the loss refers to the cost that may occur when using a product whose quality characteristics significantly deviate from the target/objective value.

In Introduction to Quality Engineering, Taguchi promotes a new quality management (Taguchi 1986). The approach to the quality of the manufacturing processes must be carried out not through direct actions on the centering and variability of the process, as in the classic system, but through actions aimed at reducing the variability compared to the fixed target (A). Most often, the quality characteristics (X) of the processes follow the normal distribution law as a characteristic assumed to be equal to the mean value of the process (μ = A) and the deviation from the target/objective value being δ, $\delta =\left|\mu -A\right|$. Inspired by the quadratic Gauss function, it was revitalized by Taguchi in the context of process control, with the form $f\left(x\right)=k{\left(x-x_0\right)}^2$, k and x₀ being given constants.

Loss quality function $L(x,A)$ proposed by Taguchi as an expression of performance loss has the form

$$L_A\left(x\right)=k{\left(x-A\right)}^2$$

(6)

where A is the target value of the measurable characteristic $X$, and $L(x,A)$ is the loss quality function. Then the Taguchi type risk is the average value of the variable $L_A\left(x\right)$

$${ R}_A\left(x\right)=E\left[L\left(x,A\right)\right]={\int }_{D}L(x,A)f\left(x\right)dx$$

(7)

where $f(x)=F_X^{\prime }(x)$, and $D$ is the domain definition of $X$ (usually $\left[0,+\infty \right)$).

Denoting by K_δ the loss for deviation $\delta =\left|x-A\right|$ from the target (A) of the feature,

$$L_A\left(x\right)= k·{\delta }^2=K_{\delta }$$

(8)

from where

$$k =\frac{K_{\delta }}{{\delta }^2}$$

(9)

Obviously, if $x=A$ we have L(A) = 0 and calculating the mean value of the quality loss function results as follows:

$$E\left[L_A\left(x\right)\right]=E\left[k{\left(x-A\right)}^2\right]=k·E{\left(x-A\right)}^2$$

(10)

We can expand this as

$$E\left[L_A\left(x,A\right)\right]=k\left[E\left(X^2\right)-2AE\left(X\right)+A^2\right]=k\left[Var\left(X\right)+{\left(E\left(X\right)-A\right)}^2\right]$$

(11)

In the case of the normality of the characteristic, $X~N(\mu ,{\sigma }^2)$, the Taguchi-type risk becomes $E\left[L_A(x,A)\right]=k\left[{\sigma }^2+(\mu -A{)}^2\right]$, and its estimate, based on observational data, has the form

$${\widehat{R}}_A\left(x\right)=k\left[s^2+(\bar{X}-A{)}^2\right]$$

(12)

where $\bar{X}$ and $s^2$ have the previously mentioned meanings.

The profile literature abounds in indicators for measuring risk and Artzner et al. (1999) introduce the concept of coherent measure of risk (r), which can differentiate these indicators. This function (r) has the following properties:

• monotony if $X\le Y than r\left(X\right)\le r\left(Y\right)$
• subadditivity: $\left(r\right(X+Y)\le r(X)+r(Y\left)\right)$
• positive homogeneity$\left(r\right(kX)=kr(X),\forall k\ge 0); \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{y},$
• invariance to translations$\left(r\right(X+C)=r(X)+C,\forall C\ge 0),$

Most of the indices proposed in the profile literature do not meet these conditions and therefore do not provide a correct measure of risk. In the situation where the average $\bar{X}$ is significantly close to the objective value A, then the standard deviation changes as follows:

$$s_1=s \left(\frac{A}{\bar{X}}\right)$$

(13)

If $A\approx \bar{X}$, then $s_1\approx s$, and the loss function becomes

$$E\left[L(x,A)\right]\approx k{s}_1^2=k{\left[s\frac{A}{\bar{X}}\right]}^2=k{A}^2{\left(\frac{s}{\bar{X}}\right)}^2$$

(14)

and the relation of the Tagughi risk estimator (8) becomes (15) by replacing $A^2 \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \bar{X}$

$${\widehat{R}}_T\left(x\right)=k^2{s}^2=k{\overrightarrow{X}}^2{\left(\frac{s}{\overrightarrow{X}}\right)}^2$$

(15)

We find that both in relation (14) and in (15) the coefficient of variation appears ($s/\overline{X}$), and the reverse of this indicator is used by Taguchi as a performance indicator.

$\overline{X}/s$—signal to noise ratio (SNR)—represents the signal/noise ratio or the disturbance coefficient. Relation (13) shows that, if $A=0$, then $s_{1 }=0$, a limiting case in which all recorded values are identical. Thus, hypothesis (13) becomes valid only if $A\ne 0$. If $A=0$ we must start from relation (12), which can be written highlighting the SNR indicator—signal to noise ratio, so depending on the spread of values

$${\widehat{R}}_A\left(x\right)=k^2{s}^2\left[1+{\left(\frac{\bar{X}}{s}\right)}^2\right]=k{s}^2\left[1+{\left(SNR\left(X\right)\right)}^2\right]$$

(16)

If X is a measurable quality characteristic, for which there is a target value $A\ne 0$, the average Taguchi type-risk

$${\widehat{R}}_A\left(x\right)=k^2{A}^2{\left(\frac{s}{\stackrel{̿}{X}}\right)}^2,k>0 \mathrm{g}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n} \mathrm{t}\mathrm{h}\mathrm{a}\mathrm{t}$$

(17)

cannot be lower than the ratio $E(s^2)/E({\overline{X}}^2)$ adjusted by a constant, that is

$$E\left[{\widehat{R}}_A\left(x\right)\right]>k{A}^2\frac{E\left(s^2\right)}{E\left({\bar{X}}^2\right)}$$

(18)

As X is a variable, not a constant, in base (18) the strict inequality occurs:

$$E\left(\frac{1}{X}\right)>\frac{1}{E\left(X\right)}$$

(19)

useful property in practical applications.

5. Taguchi Risk and Process Performance Indicators

The more the distribution of the characteristic is stronger symmetrical and the sampling mean $\left(\bar{X}\right)$ is located closer to the target value (A), the lower the associated risk, and the indicator $s_1^2{=s}^2+(\bar{X}-A{)}^2$ used to calculate the modified potential index of the process $\left({\widehat{I}}_{pm}\right)$ approaches $s^2$—and, finally, ${\widehat{I}}_{pm}\approx {\widehat{I}}_p$, where ${\widehat{I}}_p$—the potential index is determined as a ratio between the scattering field and six sigma

$${\widehat{I}}_p=ITS/6s$$

(20)

where: $ITS=TS-TI$it is the length of the interval specified by the tolerances, which delimits the area of normal development of the process. The variability of the process characteristics is therefore measured by the capability index $I_{pk}$, as a measure of the centering of the process, so of the distance from the center of the field of tolerance TC ($TC=\frac{TS-TI}{2}$), which is established as:

$$I_{pk}=\min \{ \frac{\left|\mu -TI\right|}{3\sigma } ; \frac{\left|TS-\mu \right|}{3\sigma } \}$$

(21)

The relevance in the characterization of processes is also the potential index corrected with the target value or the precision index, proposed by Taguchi himself, determined in the form:

$${\widehat{I}}_{pm}=\frac{TS-TI}{6\sqrt{s^2+{\left(\bar{X}-A\right)}^2}}$$

(22)

Based on the relationship (19) between the precision index and the Taguchi risk, the following can be determined:

$$E\left[L_A(x,A)]\cong \right.{\widehat{R}}_A(x,A)=k·{\left( \frac{TS-TI}{6}·\frac{1}{{\widehat{I}}_{pm}} \right)}^2=k{·\left( \frac{ITS}{6} ·\frac{1}{{\widehat{I}}_{pm}} \right)}^2$$

(23)

If the process takes place at a SPL—specific performance level—of 3 sigma, the potential index $I_p=1.00$, and if the objective is to develop the process at the level of SPL = 6 sigma, then the previous relationship becomes

$$E\left[L_A(x,A)]=\right.k·{\left(\frac{\sigma }{{\widehat{I}}_{pm}} \right)}^2$$

(24)

or by its estimate

$${\widehat{R}}_A(x,A)=k{·\left(\frac{s}{{\widehat{I}}_{pm}}\right)}^2$$

(25)

and in this case the risk decreases the lower the variability of the process (given by s) and the closer the average $\bar{X}$ of the process is to the target value (A). This assumes the normality of the characteristic, the centering as close as possible to A and a variability between $-3s$ and $+3s$.

Generalizing, for performance levels specified as 3, 4, 5 and, respectively, 6 sigma, to which correspond values of SPL $\in \left\{1.00;1.33;1.67;2.00\right\}$, respectively, then the Taguchi risk can be expressed as a function of the performance specified for the process and the precision index:

$$\left[L_A(x,A)] \right.=k·{\left( \frac{SPL}{6}· \frac{1}{I_{pm}}\right)}^2$$

(26)

The target parameters for the 6 sigma level are a potential index ${\widehat{I}}_p\ge 2$ and a capability index ${\widehat{I}}_{pm}\ge 1.5$ which means an admitted defective fraction of 3.4 ppm (defective units per million). Another indicator that characterizes the processes is the Risk Value (VaR) which is the p-quantile of the distribution of X, i.e., $x_p$ defined as:

$$\mathit{VaR}\left(X\right)=\mathit{Pr}ob\left\{X\le x_p\right\}=p \mathrm{or} \mathit{Pr}ob\left\{X>x_p\right\}=1-p$$

(27)

The practical use of the indicator is limited because $VaR$ is not a coherent measure of risk, because it does not meet all the conditions stated by Artzner, as demonstrated by Chan et al. (1988).

6. Case Study

At the SAE flywheel, the rocker pin SEP 251-2-55 from the construction of a compressed air compressor for electric locomotives. The following tolerances were recorded for the R3 feature that raised the most rejections during quality control: TI = 263.479 mm, respectively TS = 263.679 mm. The target value A = 263.579 mm indicates the center of the interval [TS – TI], so $A=\frac{TS+TI }{2}=263.579$. After taking a sample of 39 pieces, under the conditions of a statistically stable process, the result was a mean = 263,582, respectively, a variance $s^2=0.0002789$, so s = 0.0167. We determine the Taguchi potential index (20): ${\widehat{I}}_p=ITS/6s=\frac{0.200}{6 · 0.0168}=1.996 \cong 2$, which indicates a corresponding process from the point of view of variability. To assess the centering of the process, we determine the specific index (21)

$${\widehat{I}}_{pk}=\min \{ \frac{\left|263.479-263.582\right|}{3 · 0.1296} ; \frac{\left|263.679-263.582\right|}{3 · 0.1296} \}=\left(1.936;\right.\left.2.056\right)$$

value range that covers the size ${\widehat{I}}_p\cong 2$, so we can appreciate that the process is well centered.

Next, we establish the size, $O=\left|\mu -A\right|/\sigma$, where $A=(TS-TI)/2$, and if we work, obviously, with the estimates:

$$o=\frac{\bar{X}-A}{s}=\frac{263.582-263.579}{0.0167}=0.1796$$

The capability index (22) can also be written:

$${\widehat{I}}_{pm}=\frac{\frac{TS-TI}{6·\sigma }}{ \sqrt{1+{\frac{\overline{(X}-A)}{s^2}}^2}}=\frac{{\widehat{I}}_p}{ \sqrt{1+O^2}}=\frac{1.996}{\sqrt{1+{0.1796}^2}}=1.9646$$

value that indicates a proper centering

If the performance level is fixed at 2 and the average of the process, then, following a process research, the result is $\bar{x}=263.582$ mm and s = 0.0167, then the precision index (26) has the estimated value 1.9646, a situation that indicates a localization of the distribution in relation to objective A at an acceptable level. Wright’s capability index (Wright 1995), which applies a correction for data asymmetry, is determined as follows:

$${\widehat{I}}_w=\frac{\delta -\left[\bar{x}-\right.\left.A\right]}{3·\sqrt{s^2+{(\bar{x}-A)}^2+\left|{\beta }_1\right|·s^2}}=2.246$$

where ${\beta }_1$ is the asymmetry coefficient of the observation data (0.31), and d is the half distance of the tolerance field $d=(TS-TI)/2=100$, and the target/objective A = $(TS+TI)/2=263.579$, respectively. The value of the Wright index (2.246), in the absence of asymmetry, would have coincided with the size of the potential index −2. If the process takes place at the three sigma level, then $I_p=1$, and the Taguchi risk for TS − TI = 12 s, with formula (26) results:

$$\left[L_A\left(x\right)\right]=k·{\left(\frac{0.2}{6}·\frac{1}{1.9646}\right)}^2=k· 0.0002879$$

The constant k in compliance is expressed in monetary units. If the deviation δ is even 1, then k = A_d representing the cost of a non-compliant product unit (so with characteristic values higher than TS or lower than TI). In the studied case, the cost of a defective unit is 83.5 EUR/unit, so k =$\raisebox{1ex}{$83.5$}\!\left/ \!\raisebox{-1ex}{$0.04$}\right.=2087.5$ so that the estimated average loss results: ${\widehat{R}}_A\left(x\right)=2087.5\left[{0.0167}^2+(\overline{263.582}-263.574{)}^2\right]=0.716$EUR.

In order to calculate the Taguchi risk for a process carried out under Six Sigma conditions, so for which the specific performance level (SPL) is equal to 2, it results in:

$$E\left[L_{6\sigma }\right]=k· {\left(\frac{SPL·\sigma }{{\widehat{I}}_{pm}}\right)}^2=k· {\left(\frac{2·0.0167}{1.9646}\right)}^2=k·0.000289 \mathrm{e}\mathrm{u}\mathrm{r}\mathrm{o}\mathrm{s}/\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}\mathrm{u}\mathrm{c}\mathrm{t} \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}.$$

7. Comments

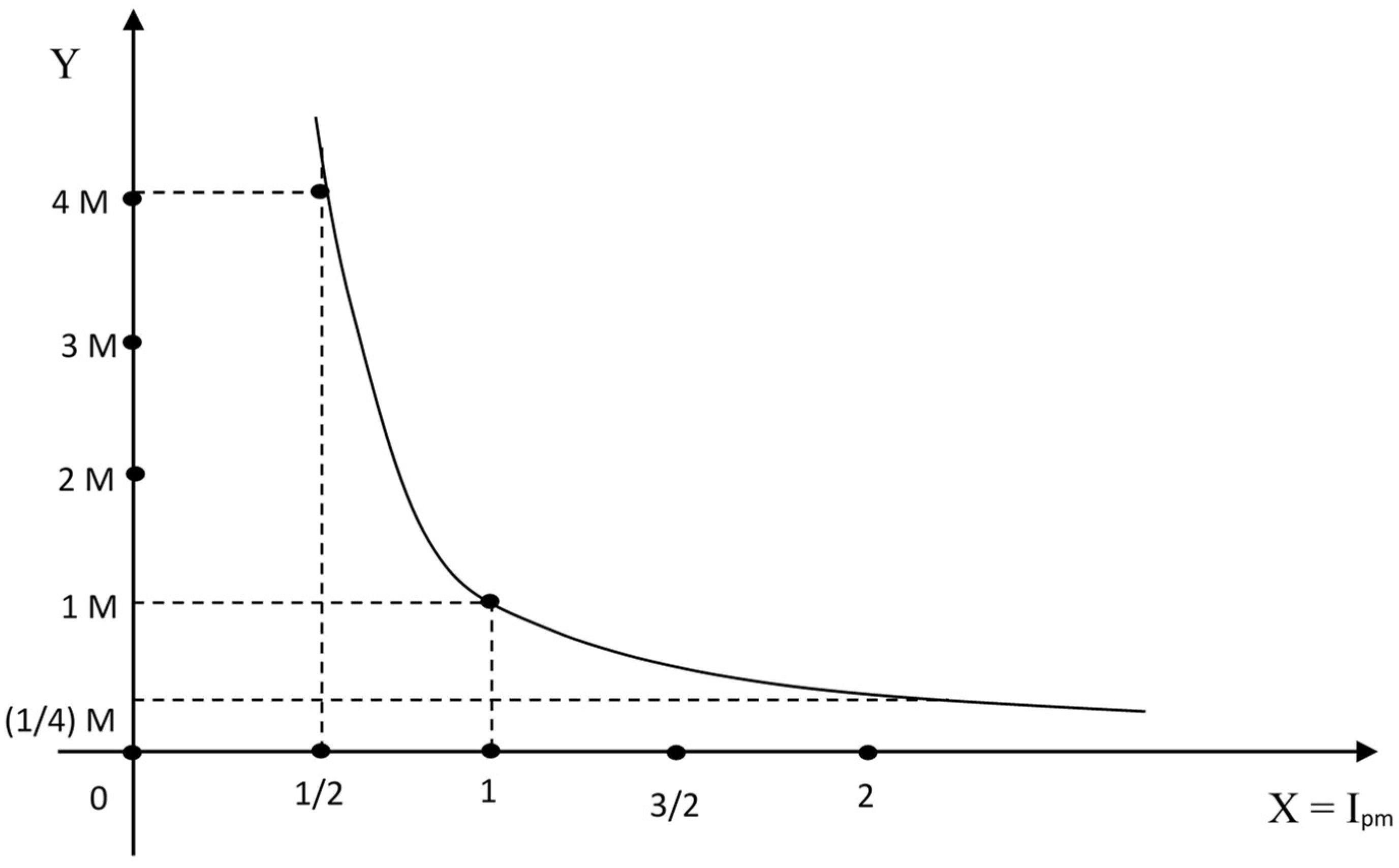
The Taguchi-type risk can be considered as a function of the length of the TS-TI interval expressed in units of standard deviations. The relationship between the capability index ${\widehat{I}}_{pm}$ and the Taguchi risk is a hyperbolic-type function, (Figure 1), where ${\widehat{I}}_{pm}=X$, and $R=M/X^2$.

Another comment is required. In the case of robust processes and under statistical control, the occurrence of defects is a less frequent event and it is not wrong to assume that it is a rare event, in which case the Poisson model becomes applicable:

$$X:p_k=\mathrm{P}\mathrm{r}\left\{X=k\right\}=\frac{e^{-\lambda }{\lambda }^k}{k!}, k=\mathrm{0,1},2,\dots ;\lambda >0;e\approx 2.71828; \sum p_k=1,$$

In this particular case, the target value A is desired to be zero (A = 0), so the objective is zero defects per product unit, in which case the average loss in this case becomes:

$$L(x,A)=E(X-A{)}^2=Var(X)+{\left[E\left(X\right)-A\right]}^2=Var(X)+E^2(X)=\lambda +{\lambda }^2$$

Since A = 0 and for the Poisson case we have the specific property $E(X)=Var(X)=\lambda$, and if the average loss is fixed at the $P$ level, from the equation $\lambda +{\lambda }^2=P$, it is deduced:

$$\lambda =\frac{1}{2}\left[-1+\sqrt{1+4P}\right]$$

If $X_i$ is the number of non-conformities per product unit $(i)$, then ${\displaystyle \sum X_i/n}$ is the estimate of the average ($\lambda$) and the decision on the progress of the process can be made as follows: if ${\displaystyle \sum X_i\le A_c}$, then the control ends by accepting the process, and if ${\displaystyle \sum X_i>A_c}$, then the process is rejected. Here, $A_c$— the acceptance number,—as well as the number of the control sample will have to be determined according to the statistical risks ($\alpha$ and $\beta$) as well as the specific losses associated with the supplier and the beneficiary. Risks, in general, but also the Taguchi risk, being a tool of the offline management of process quality management (SQC), lend themselves to mathematical simulations.

Risk simulation is a method by which the calculation model is represented in order to analyze the behavior or performances depending on the change of the input variables. The action involves decomposing the process into phases, sequences and components whose behavior can be described in terms of a probability distribution, for each of the possible states of the system. After the construction of the model, we move on to the manipulation of the random variables using the probability distributions validated by appropriate tests. Manipulation involves changing the values of decision probabilities, multiplication factors, statistical risks ($\alpha$ and $\beta$), etc., running the program through a software and, finally, choosing the convenient version of the risk and organizing the process according to this option.

8. Conclusions

Following the approach taken, we reach the conclusion that, for complex products and processes, capability control in the context of the Six Sigma approach and the reduction of the Taguchi risk value results in the following:

→

Reaching the Six Sigma capability level is not achieved quickly and spectacularly, but requires a constant and long-term effort to correct and re-correct the process;

→

Initially, an ad hoc analysis must be carried out, in the short term, to establish the initial state of the process and determine the intervention and correction strategy on the process;

→

Bringing the process to a state of statistical stability by reducing the variability of the basic characteristic followed and then reaching the optimality state;

→

Identifying possible errors and limiting their occurrence;

→

Data collection on the essential characteristics observed during the process;

→

Eliminating outliers and validating the normality of the characteristic distribution;

→

Correction of the ability indices in case the distribution of the observed characteristic is of non-Gaussian type;

→

Establishing the capability of the process for the case of the distribution with a strong skewness, respectively with abnormal kurtosis.

If in the presented material, both the theoretical aspects and the application concerned technological processes in the field of quality control (SPC), the capability of the processes and the monitoring of the Taguchi risk has an area of applicability to processes in the most general sense, processes also found in other fields, such as for example in the administration, the bureaucratic process from the registration of a petition to the resolution and communication of an answer, in medical care, from the arrival of a patient to the hospital and the completion of the stages of investigation, diagnosis and treatment, or in the banking system, from the receipt of a requests for a loan, analysis of the client’s creditworthiness, establishment of guarantees, evaluation of the pledged goods, until the release of the requested amount to the client, etc. All these activities imply a sequence of evaluations, expertise carried out in a process in which different experts are involved and the taking of stage decisions, until the formulation of the final decision are processes affected by risks and possible errors. These processes involve measurements as well as, inevitably, the chance of producing errors with not only financial implications, so establishing the Taguchi risk and optimizing the development of these processes is not only opportune but also possible.