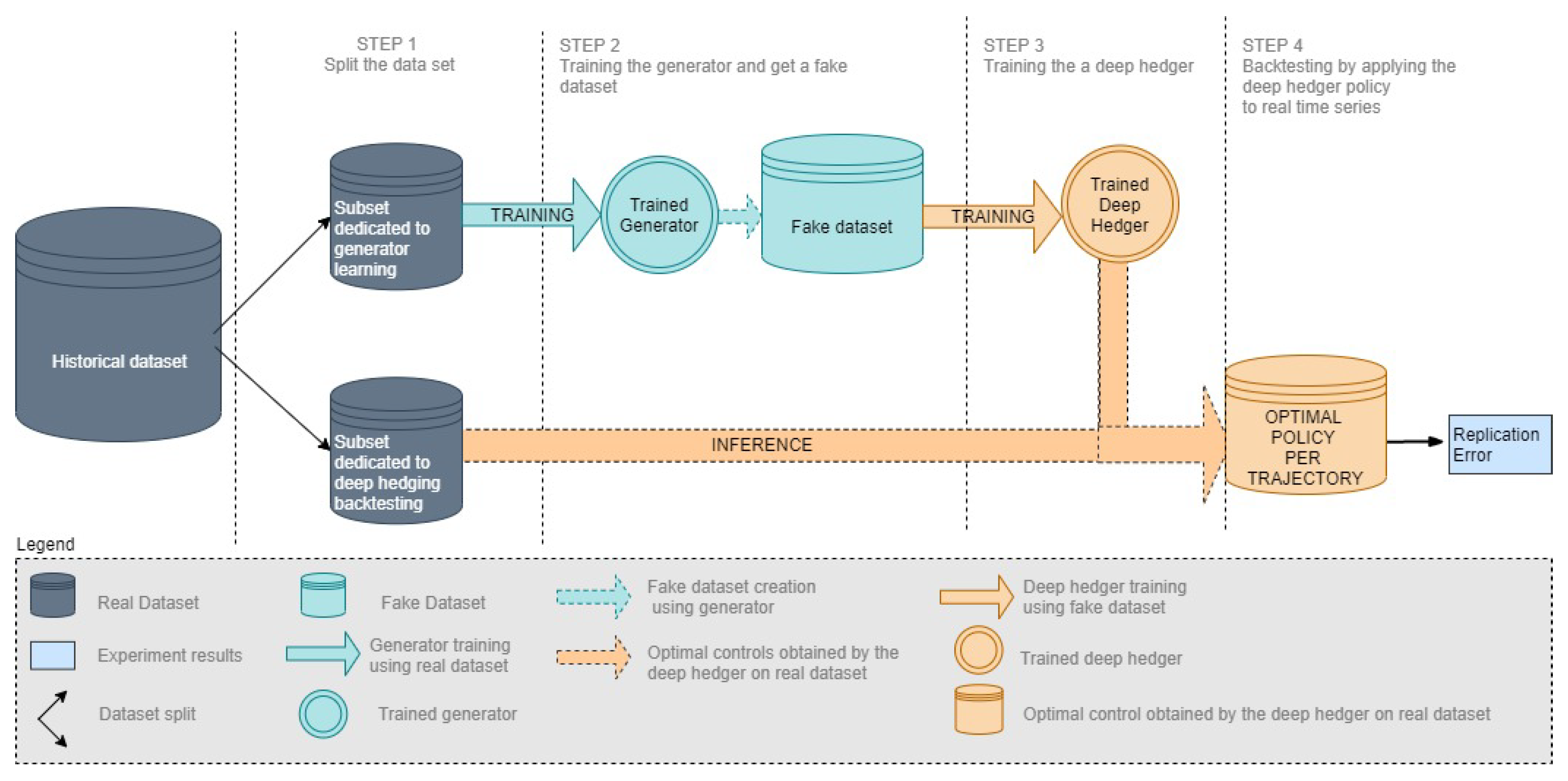
The samples from the previously tested generators are used to (deep) hedge options on commodity derivatives. By comparing the replication errors on the basis of historical data, these numerical tests allow to go beyond the classical market statistics by comparing the different generators on an operational problem.
3.3.1. Deep Hedging
A self-financing strategy is a
d-dimensional
-adapted process
on some probability space
, where
is the terminal date. Some market prices
valued on
of an underlying asset are given and observed on a discrete time grid
, where
is the spot. For the sake of simplicity, the time grid is assumed regular with mesh size
. The terminal value of the portfolio at time
is
and defined as:
where
will be referred to as the premium. The portfolio is re-balanced every day. There are no controls at the last date. A global approach is considered to learn the optimal policies as done in
Fecamp et al. (
2020), minimising a global criteria, in opposition of local schemes (reviewed in
Germain et al. (
2021)). A contingent claim pays
at time
T. The risk hedging problem leads to the following optimization problem
where the function
ℓ indicates the quadratic loss and
the payoff.
The optimal policy
is approximated by a feed-forward neural network, called deep hedger. The model learns the optimal controls which minimise a hedging risk at the terminal value
T. The network consists in 3 hidden layers of 10 units each with Relu activation. Adam optimizer is used, with learning rate at 1 × 10
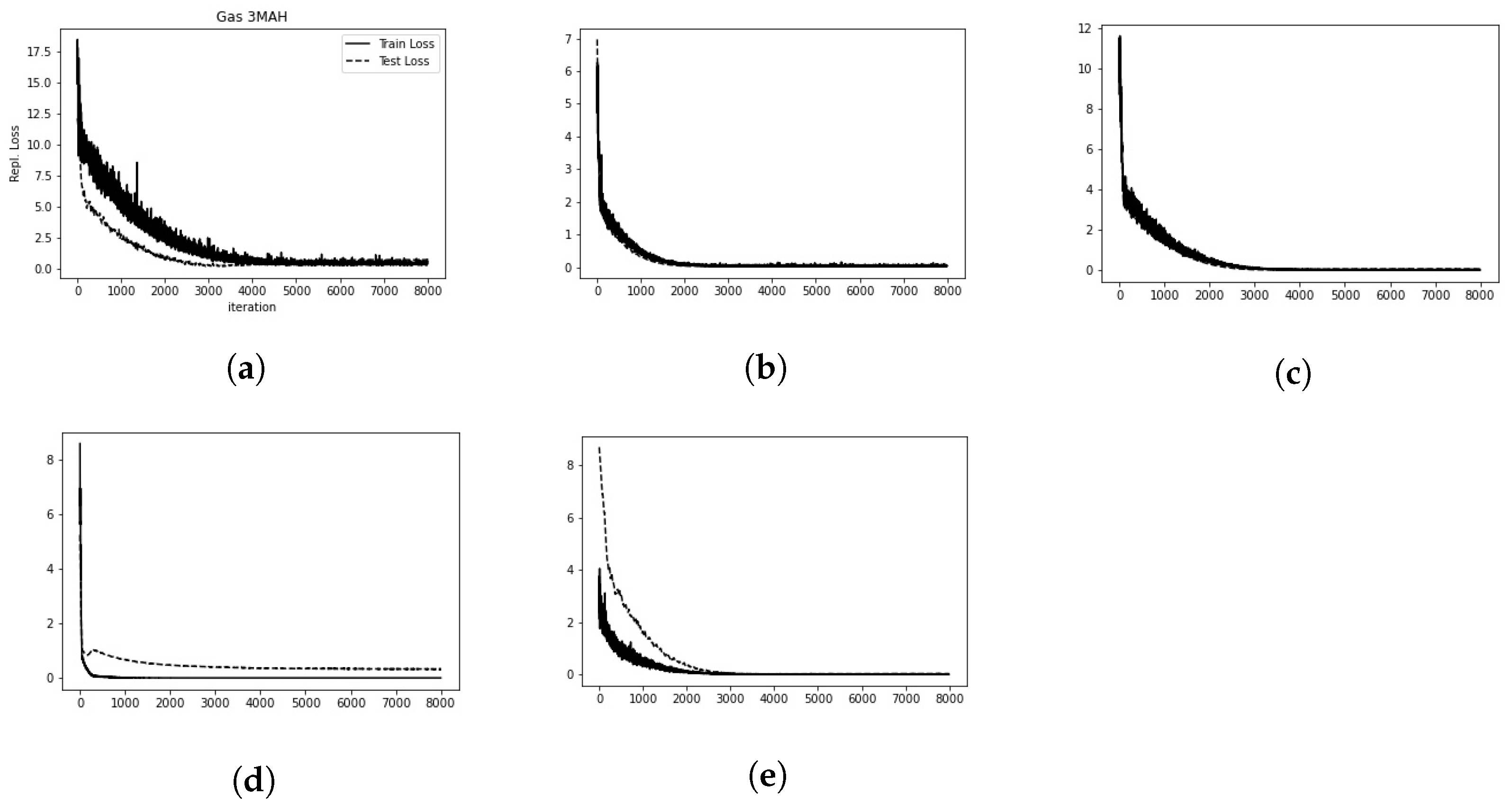
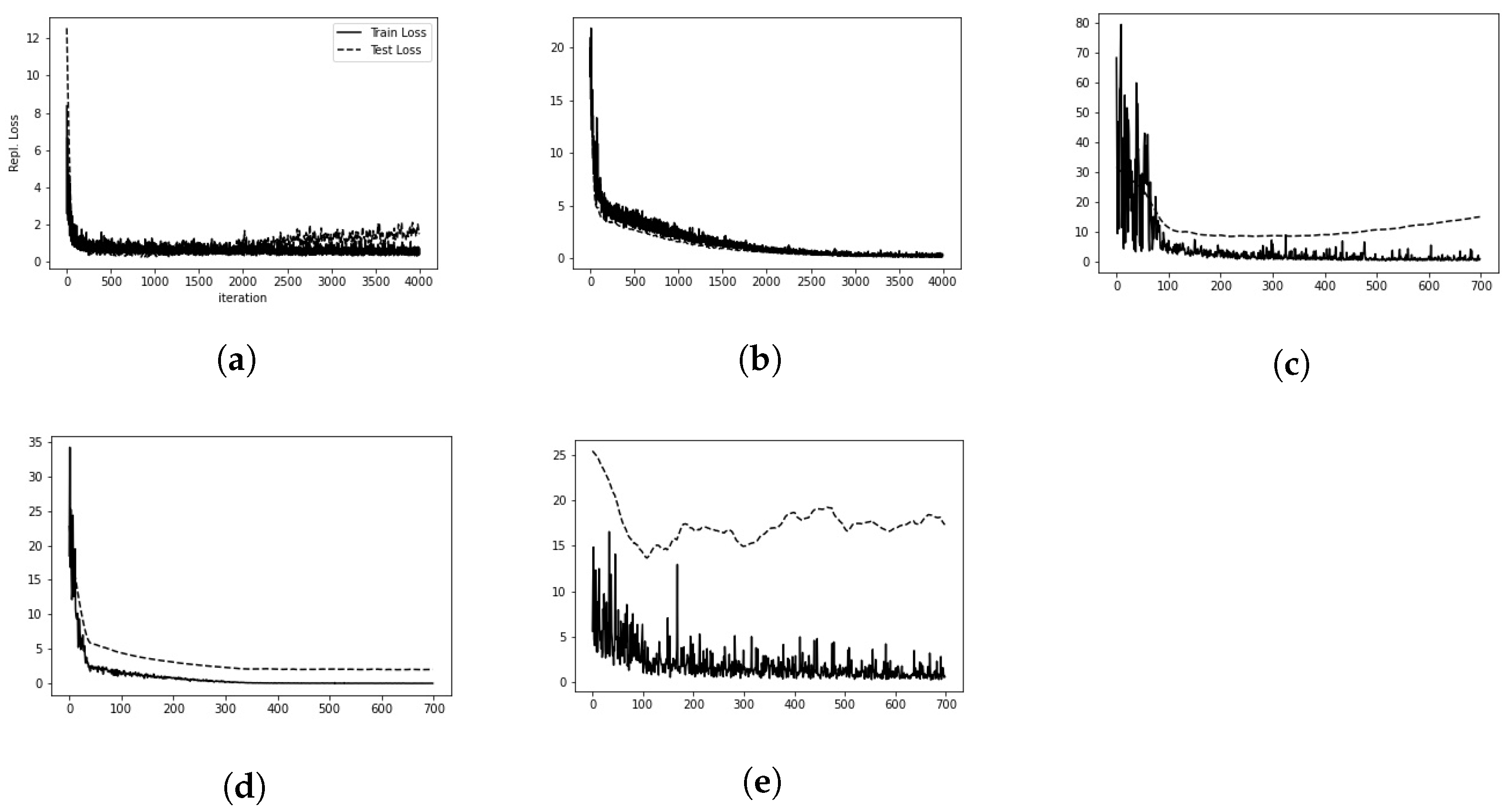
. The number of iterations is 10.000 and batch size is 300. There are four deep hedgers as there are four generators, each hedgers being trained on the samples of a generator. During the training, at each iteration of the deep hedger the generators simulate new data. The training set includes 211 historical price sequences of 30 dates on where the different evaluation scores are computed. The four different hedging policies are then tested on unobserved price time series from the historical data set.
Figure 3 illustrates the full data-driven methods for risk hedging.
The deep hedger is an approximation of the optimal policy that contributes to the replication error of the hedged portfolios. In order to dissociate the nature of the replication error, that may come either from the underlying model or from the hedging policy estimation, an additional deep hedger is trained on a calibrated GBM. These replication errors of the hedged portfolios are used to evaluate the accuracy of the generators. If the synthetic prices are sufficiently realistic, no significant gap in the replication should be observed between a hedging strategy applied on the simulations and on the historical time series.
3.3.2. Hedging Evaluation Metrics
Hedging strategies put emphasis to reduce losses at the expense of gains. In order to focus on the losses associated with the different strategies, some risk metrics such as VaR or ES are considered. The standard deviation is also considered, but can be misleading because high gains will increase its value. To evaluate how a hedging strategy reduces the error, a score called the hedging effectiveness is defined:
where RiskMetric quantifies the risk (i.e., the variations) of profit and loss (PnL). The score belongs to
, the greater, the better, and measures the improvement of the risk by hedging a position. A score of 1 means that no losses are observed. The hedging effectiveness score is computed in two steps. First, historical scenarios allow to evaluate the PnL of the hedging strategy for each scenario path. This back-testing builds a distribution of the strategy PnL from the scenarios. Thereafter, the pre-defined risk measure is evaluated with respect to this PnL distribution and derives the hedging effectiveness score. Three risk measures are studied:
Standard deviation (Stdev): Standard deviation measures the amount of variation of the values in samples.
Value-at-Risk (VaR): VaR measures tail loss, and is defined as the loss level that shall not be exceeded with a certain confidence level during a certain period of time.
Expected shortfall (ES): ES is an alternative to VaR, which gives the expected loss in the worst few cases for a certain confidence level.
However, the standard deviation treats the variations in profit and loss indifferently, while the primary interest of hedging is to reduce losses and VaR may underestimate tail risk when the extreme loss is huge despite low probability. Therefore, a set of metrics is considered and a mean is also included as a RiskMetric. For both VaR and ES a confidence level of 95% is chosen in the numerical results below.
3.3.3. Call Option Hedging
Deep hedgers are trained on synthetic data produced by the generative methods listed out in
Section 2. The hedging occurs on a daily basis on an at-the-money call option of payoff
. The Black-Scholes (BS) model (
Black and Scholes 1973) derives a closed formula which is used as baseline for the replication loss and premium comparison, and should not be confused with GBM which is a deep hedger trained on GBM samples. The four options are separately hedged on each of the markets previously described with maturities
days and strikes
. Spots are respectively
for electricity,
for gas,
for coal and
for fuel. The training and testing losses of the deep hedgers are provided in
Appendix A.
Table 2 reports the replication errors of deep hedgers back-tested on unobserved historical prices. Initial risk indicates
the risk of the payoff without hedging. The deep hedging policies bring improvements on every options compared to the initial risk and the BS model. The policy learned with CEGEN samples provides a significant lower replication loss than every other methods. On the oil case however, the very specific case where CEGEN did not manage to get correct QVar (
Table 1), the replication loss is significantly higher (and close to BS). COTGAN, SIGGAN and TSGAN have close results, improving against BS. In particular, COTGAN does not stand out despite the good performances from
Table 1. The results with hedging options are consistent with the first analysis. CEGEN outperforms the other generators in most of the cases, even if every methods provide relevant hedging policies in terms of replication loss.
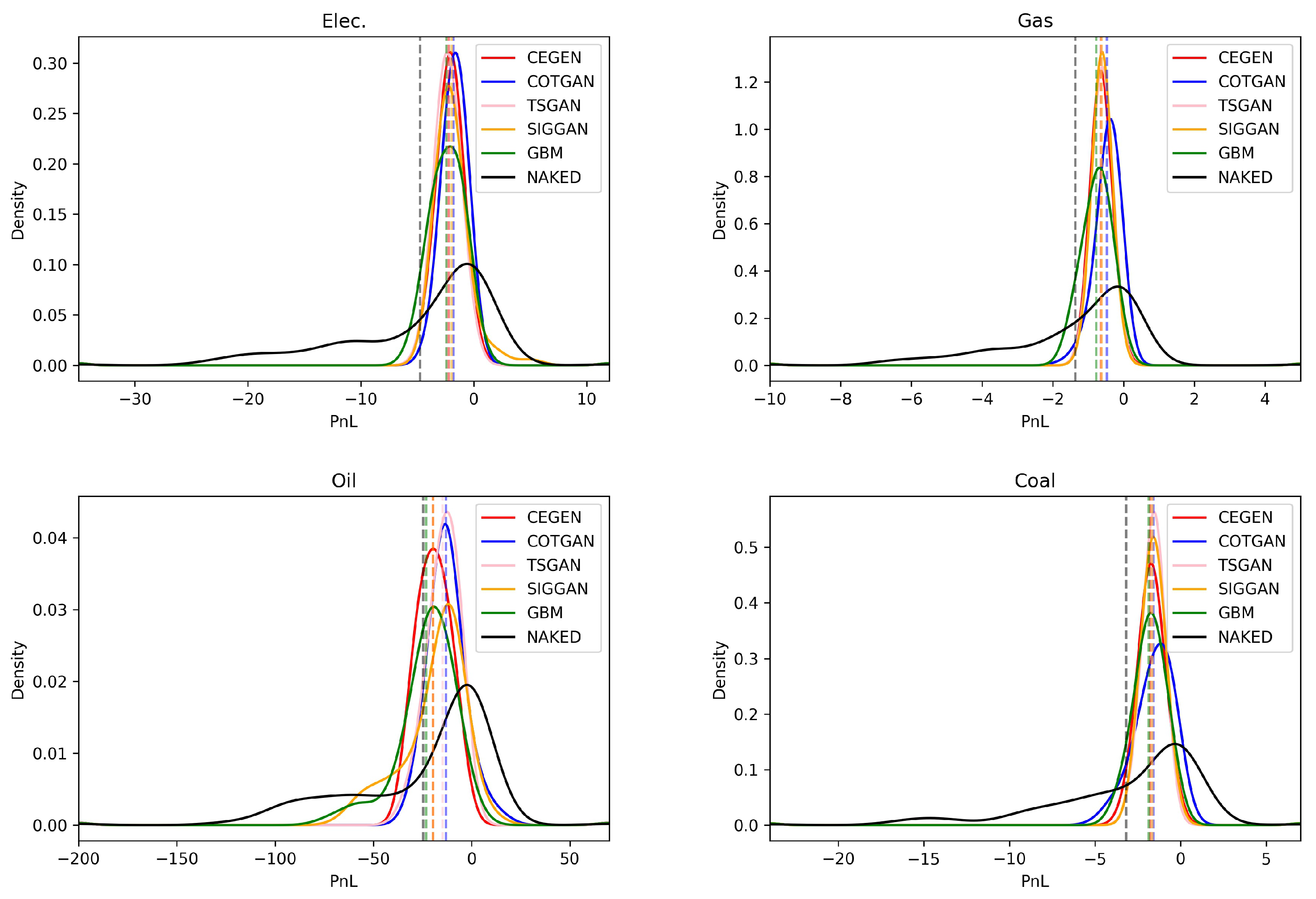
Figure 4 illustrates the PnL distributions for each deep hedger trained on each generator, alongside with the distribution of the initial risk. TSGAN outperforms the other generators, by always being consistently in the top 2 of the least risky PnL distributions. CEGEN also presents high performances on every commodities, unlike the SIGGAN and the GBM which weaken on fuel, with notably a high tail risk.
An options trader determines a selling price according to the hedging strategy of the PnL distribution. In order to be attractive in the market, the trader has to offer a low price, slightly higher than the average of the PnL distribution, to make a profit. However, if this distribution is too dispersed, the trader has to cover the risk of big losses by offering a higher price. In the case of fuel, using the GBM or SIGGAN strategies, the trader must not make a mistake by proposing a low price in spite of a significant recentering of the distribution around the average because the tail risk is very high. Another observation is that in all cases below, the vertical lines representing the averages of the different distributions are higher for the hedging strategies than for the naked strategy. However, under the assumption of no arbitrage, the average PnL should be the same when hedging or not. If this looks profitable, especially for the COTGAN whose averages are the highest, it is not necessarily a sign of good performance. On the contrary, it may be because of bad hedging evaluation, but in the context of a bullish market, it may turn to its advantage.
Table 3 reports the hedging ratios for the Stdev, VaR and ES risk metrics. At first sight, it seems difficult to distinguish the best generator. COTGAN outperforms sporadically the other methods, but TSGAN provides a better ratio with the Stdev metric. CEGEN has close results and stand out on the gas case. On these hedging scores, determining the best model is not sufficient, but analysing the controls obtained by the associated policies could allow a more in-depth comparison.
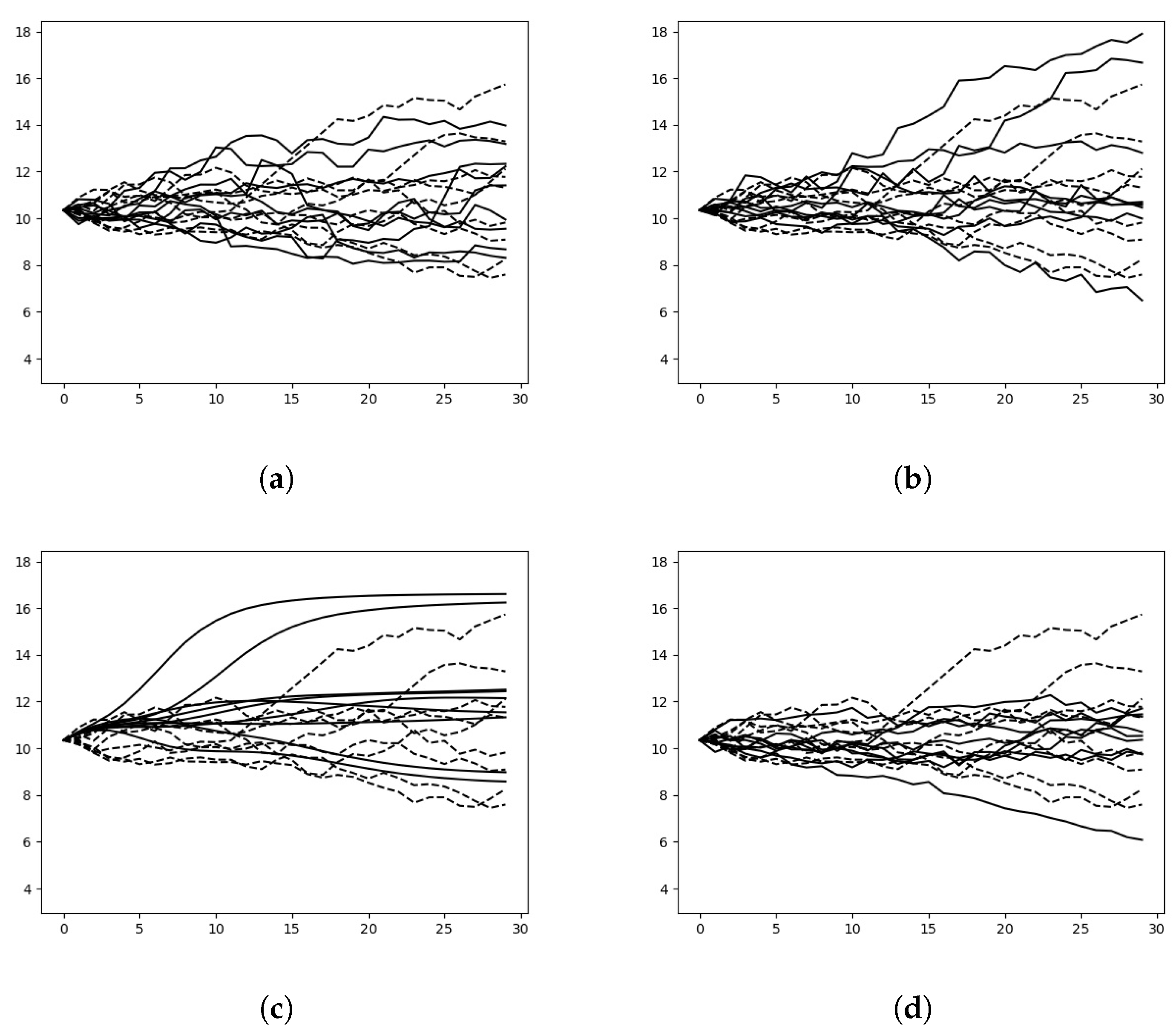
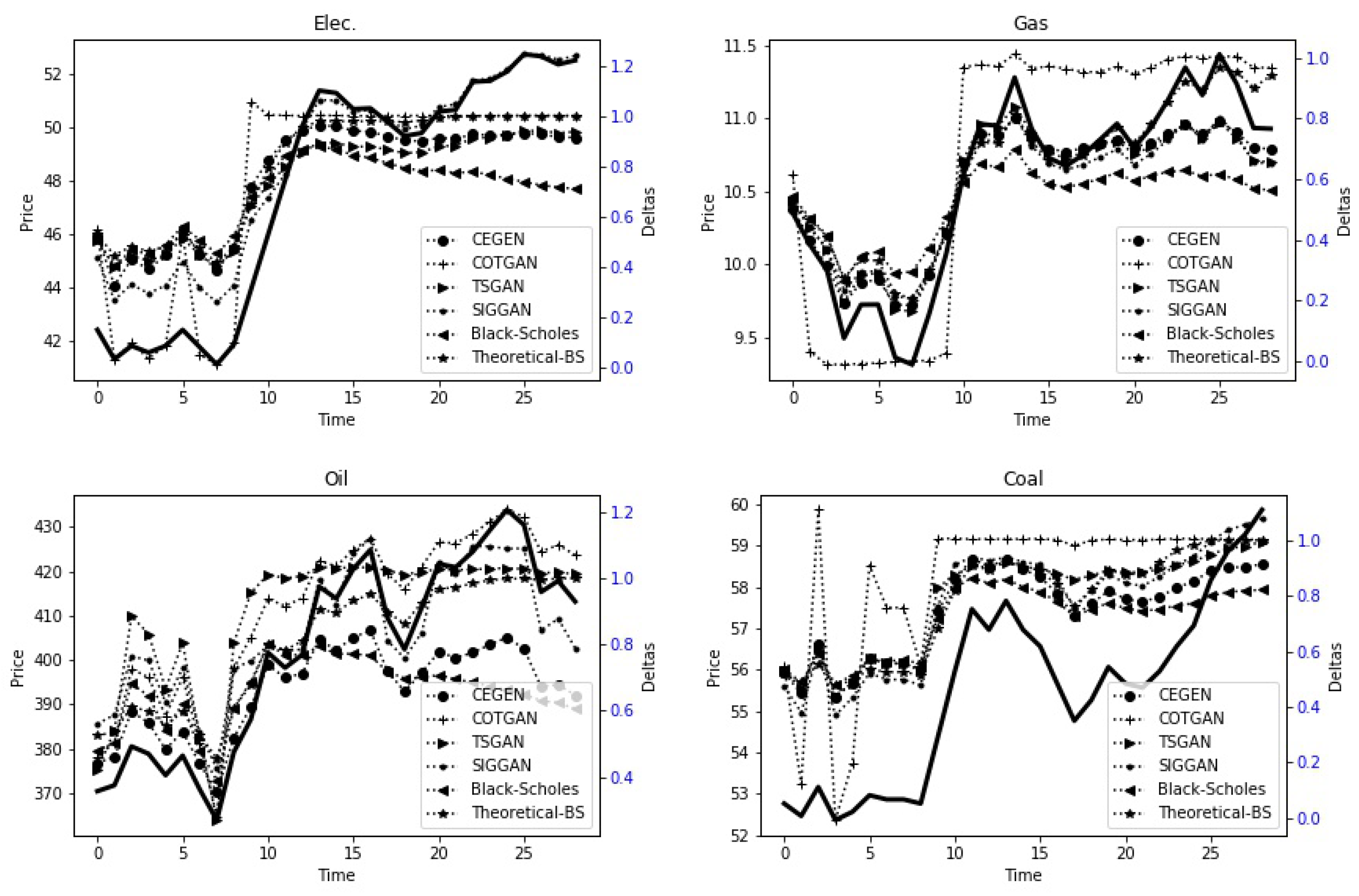
The controls from each model on a single historical price trajectory are illustrated in
Figure 5. The policies of CEGEN and SIGGAN are very reactive to the price, and propose similar policy on each option. COTGAN as for it provides low volatility controls on electricity and gas data, in the opposite on oil and fuel the deep hedger seem to follow the price of the commodity. Such instability may question the validity of the policy, and would need further analysis. This is consistent with the
Table 1 and the unrealistic smooth curves that did not have significant price fluctuations shown in the
Figure 2. In all cases, TSGAN and BS controls are relatively consistent and appear to be unaffected by the price, buying the same amount of asset over time during the period.
The hedging results are closely related with the time series accuracy of
Section 3.1, the strategies that stand out are the ones obtained from CEGEN and TSGAN. However, considering the hedging ratio as evaluation metric, COTGAN samples are the most realistic of the set of tested generators. When training the deep hedger, it seems that smooth price time series can be enough to learn an average strategy. A deep look on the obtained controls seems necessary.
3.3.4. Spread Option Hedging
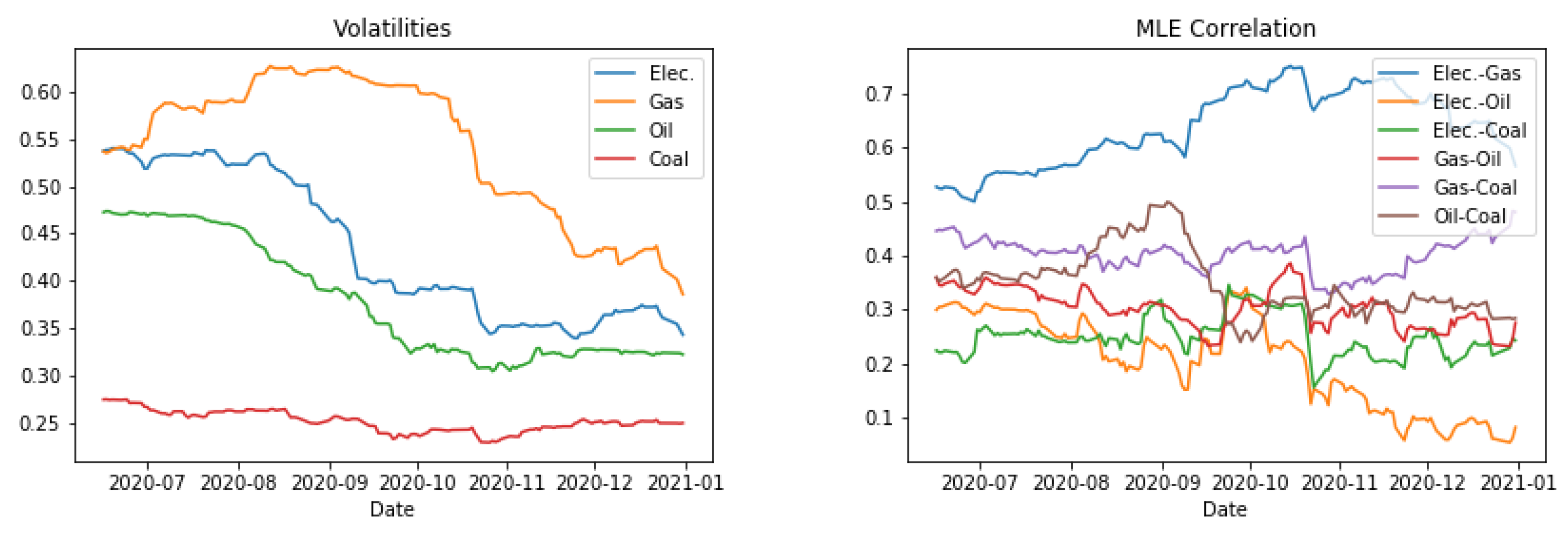
A call option on the spread between gas and coal has a payoff . The spread is the price difference between these two commodities, where the strike is the initial spread . As in the previous section, the maturity remains 30 days and the hedge portfolio is rebalanced everyday. Although the success of the hedge still depends heavily on a correct representation of the gas and coal time series individually, this is no longer the only condition for learning a good strategy. Generators must also represent the joint distribution of these prices to correctly train a deep hedger on the spread. In particular, the generators’ appreciation of the historical correlation is crucial to the correct modelling of prices.
Table 4 reports the hedging effectiveness scores for the risk metrics alongside the PnL. Here, COTGAN and CEGEN outperform the other methods. However, in the case of COTGAN, the smooth price trajectories (illustrated in
Figure 2) do not seem to affect the scores. In practice, such trajectories could not be used.
Figure 6 highlights a significant difference between the CEGEN-based strategy and the others. A surprising result is TSGAN, which is ranked among the best generators, is now in third place. This is nevertheless consistent with
Table 1 indicating a poor replication of the correlation.
CEGEN seems to be the generator of choice for a case where the correlation between different time series has to be taken into account. However, despite the very good performance in the univariate hedging case, TSGAN fails to perform well in this situation.