Abstract
When the uni-variate risk measure analysis is generalized into the multi-variate setting, many complex theoretical and applied problems arise, and therefore the mathematical models used for risk quantification usually present model risk. As a result, regulators have started to require that the internal models used by financial institutions are more precise. For this task, we propose a novel multi-variate risk measure, based on the notion of the Wasserstein barycenter. The proposed approach robustly characterizes the company’s exposure, filtering the partial information available from individual sources into an aggregate risk measure, providing an easily computable estimation of the total risk incurred. The new approach allows effective computation of Wasserstein barycenter risk measures in any location–scatter family, including the Gaussian case. In such cases, the Wasserstein barycenter Value-at-Risk belongs to the same family, thus it is characterized just by its mean and deviation. It is important to highlight that the proposed risk measure is expressed in closed analytic forms which facilitate its use in day-to-day risk management. The performance of the new multi-variate risk measures is illustrated in United States market indices of high volatility during the global financial crisis (2008) and during the COVID-19 pandemic situation, showing that the proposed approach provides the best forecasts of risk measures not only for “normal periods”, but also for periods of high volatility.
1. Introduction
There is a variety of risk measures based on profit and loss distribution to quantify the different types of risk; examples include the variance, the Value-at-Risk, and the Conditional Value-at-Risk; see McNeil et al. (2015), Wagalath and Zubelli (2018), Arias-Serna et al. (2021), Faroni et al. (2022), Nageri (2022), and references there, for a detailed review of the investment-portfolio-risk nexus. Perhaps the most commonly used risk measure in finance is the Value-at-Risk (VaR), which has received the honor of being utilized in industry regulations.
However, when the well-known uni-variate VaR analysis is generalized into the multi-variate setting, many complex theoretical and applied problems arise. For example, under the restriction of a perfect dependence, the simple summation approach computes the total risk through summation of the stand-alone risks (see Embrechts et al. (2013) and Li et al. (2015)). For a large number of assets, the variance-covariance approach fails, as estimation of the corresponding matrix is extremely cumbersome due to the high amount of correlations (see McNeil et al. (2015)). The number of unknown parameters of the GARCH model rises exponentially with the number of assets, and its estimation will not be possible even for a modest number of assets (Pesaran and Pesaran (2010), Engle and Kroner (1995)). The copula approach attains a robust structure for dependence in a financial time series by producing joint distributions with known non-Gaussian marginal distributions. Modeling the marginal distributions by copulas allows for VaR computations with better performance than classical approaches, but involves some intractable assumptions in the context of risk measures, which are difficult to elucidate; a similar quotation for the multi-variate extreme value theory has also been addressed by Jin and Lehnert (2018) and Barone-Adesi et al. (2018).
Inspired by the above discussions, as well as some interesting insights collected by Li et al. (2012) and Kiesel et al. (2016) for risk models in the banking industry, and in order to cope with risk management in situations where multiple competing models are formulated for the various scenarios, new risk measure should be utilized, Papayiannis and Yannacopoulos (2018), which is capable of combining efficiently the information provided by all partial models into an aggregate model; this work proposes a new multi-variate risk measure model based on the notion of the Wasserstein barycenter of probability distributions under a location–scatter family. The new approach allows effective computation of Wasserstein barycenter risk measures in any location–scatter family, including the Gaussian case. In particular, we demonstrate that the Wasserstein barycenter VaR of a location–scatter family belongs to the same location–scatter family, which allows us to obtain closed-form expressions for the Wasserstein barycenter risk measures, turning our proposal into a methodology that is easy to apply in practice. Incorporating the concept of Wasserstein distance in the quantification of risk measures allows for preserving such important properties as the comparison of distributions with different supports, which makes the proposed methodology very suitable for risk quantification in financial and insurance risk management.
The concept in probability theory has been brought into financial models by proposing Fréchet risk measures, which are calibrated through a certain metrization of the probability measure space. In this case, the well-studied Wasserstein metric supports the method and provides fundamental connections for the rising concept of barycenter, in the sense of Agueh and Carlier (2011); this is considered seminal for a number of generalizations and applications (see, e.g., Bigot et al. (2018), Álvarez Esteban et al. (2018), Le Gouic and Loubes (2017), and the references therein). The Wasserstein metric has notably enriched the risk management literature (see, e.g., Feng and Erik (2018), Wang et al. (2020), Pesenti (2022), and Liu and Liu (2022)).
The proposed model is compared with GARCH models under a portfolio characterized by S&P500 and NASDAQ stock indices. The results show that the Wasserstein Barycenter VaR presented an excellent performance being close to the expected number of exceptions. Unlike the GARCH models, our model only requires knowledge of the mean and deviation for VaR quantification, regardless of the number of assets considered in the portfolio, which represents an advantage over the GARCH models, in which the number of unknown parameters rises exponentially with the number of assets. The new model was also implemented for United States market indices, characterized by high volatility during the COVID-19 pandemic situation and during the global financial crisis (2008). The new approach can fit the volatile movements of the returns and predicts future losses notably, in comparison with classical multi-variate VaR approaches. The results indicated that the proposed approach provides the best forecasts of risk measures not only for “normal periods”, but also for periods of high volatility.
The remainder of this paper is structured as follows: Preliminaries about risk measures and the Wasserstein barycenter are given in Section 2. Then, in Section 3, the Wasserstein barycenter in risk measures is defined, and results for Wasserstein barycenter VaR and CVaR estimations are given under the considered family of location–scatter distributions; we demonstrate that the Wasserstein barycenter VaR of a location–scatter family belongs to the same location–scatter family. Section 4 details the application of the proposed method in a portfolio consisting of major U.S. stock market indices. Section 5 draws some conclusions. Appendix A provides the proofs of the theorems presented in Section 3.
2. Preliminaries
This section provides the necessary background regarding risk measures and the barycenter in a Wasserstein space.
2.1. Risk Measures
Given a random variable X on a probability space , we denote its distribution function (d.f.) by ; unless otherwise stated, is the ordinary inverse of . We consider X as a loss variable and, hence, is called the expected loss.
The most commonly used risk measure in the financial area is the Value-at-Risk, which has been defined Rockafellar and Uryasev (2002) as follows:
The Value-at-Risk for a portfolio with loss variable X at the confidence level is a real number, such that
If the loss X has a distribution with mean and standard deviation , and , then for the -percentile of the assumed distribution can be calculated in a straightforward manner, using the equation
Usually, the approaches described assume constant volatility over time. However, it is possible to incorporate models describing non-constant volatilities. In practice, there are numerous ARCH and GARCH models that can be chosen from (see, e.g., Stavroyiannis et al. (2012), Han et al. (2014), Gabrielsen et al. (2015), and the references therein).
Although the Value-at-Risk thus defined may reflect risk aversion and satisfies important properties such as monotonicity, positive homogeneity, and translation invariance, it lacks some desirable properties, such as sub-additivity, which is the mathematical statement of the response of risk concentration—a basic reality in risk management. Among other objections raised regarding , we can also mention that it is unable to account for the consequences of the established threshold being surpassed and that, in general, it is not continuous with respect to the parameter Arias-Serna et al. (2016).
A measure of risk closely related to Value-at-Risk is the Conditional Value-at-Risk, defined as the conditional expected value of the . It is defined, in Rockafellar and Uryasev (2000), as follows.
The Conditional Value-at-Risk of the loss associated with the confidence level is the mean of the -tail loss distribution
2.2. Barycenters in the Wasserstein Space
Let be the set of all probability measures defined on with a finite second-order moment. Denote as the subset of absolutely continuous measures, and consider as a generic probability space. If in are two measures, then denotes the set of all probability measures in the product set . Here, and are the corresponding first and second marginals.
For two measures in , the quadratic transportation cost between and (also referred as the transportation cost with a quadratic cost function) is defined as follows:
The transportation cost with quadratic cost function endows the set with a metric, called the 2-Wasserstein distance or Monge–Kantorovich distance metric, which is given by
When , the 2-Wasserstein distance in the real line is simply given by the quantile-like expression:
where and are the quantile functions of and , respectively.
The Wasserstein metric has notably enriched the risk management literature; see, for example, Kiesel et al. (2016) and Feng and Erik (2018).
Now, in Euclidean space, the barycenter of points with weights , , is defined as
In fact, b is the unique minimizer of
Motivated by the Euclidean version, the Wasserstein barycenter can be defined as follows.
Definition 1.
Let be random probability measures over , endowed with positive weights satisfying . The measure is a Wasserstein barycenter if μ is a minimizer of the functional
This fact will be denoted by
The empirical consistency of the Wasserstein barycenter has been studied in Agueh and Carlier (2011), Boissard et al. (2015), and Le Gouic and Loubes (2017).
In order to introduce a fundamental result, we recall the definition of a location–scatter family
Definition 2.
If denotes the set of positive definite matrices, and is a random vector with measure , then the set of probability laws defined by
is a location–scatter family induced by positive definite affine transformations from .
The Wasserstein barycenters of measures on a location–scatter family satisfy the following remarkable property (see Agueh and Carlier (2011), Álvarez Esteban et al. (2011), and Álvarez Esteban et al. (2018)).
Proposition 1
(Theorem 3.10. Álvarez Esteban et al. (2018)). Let and . Assume that, for every , the measure . Then, the unique barycenter, of μ also belongs to . The mean of is and the covariance matrix, , is the only positive definite root of the equation
This result means that the Wasserstein barycenters are closed with respect to the location–scatter family. An interesting case follows for N Gaussian measures on
Proposition 2
(Theorem 2.4. Álvarez Esteban et al. (2011)). Consider N Gaussian measures on with corresponding means and positive definite covariances . Let be positive weights with . Then, the unique barycenter of the normal measures is the Gaussian distribution with mean and covariance matrix , which is the only positive definite root of the equation
According to Álvarez Esteban et al. (2016), Wasserstein barycenters inherit the strong computational problems of the classical optimal transportation. However, in the real line, some explicit distributions can be obtained.
Proposition 3.
Let be the quantile functions corresponding to in the real line. Thus, the barycenter of is the probability with quantile function where are positive weights such that .
Finally, using Proposition 3, with N Gaussian distributions, , , on , then the barycenter is a Gaussian .
This notable aspect will be used below, in the context of risk measures.
3. Wasserstein Barycenter Risk Measures
This section proposes Wasserstein Barycenter Risk Measures based on the portfolio loss distributions in finance, which are typically statistical quantities describing the conditional or unconditional loss distribution of the portfolio over some pre-determined time horizon.
We consider risk measures such as VaR and CVaR for a loss random variable defined by Here, are real random variables attributed to risk types endowed with positive weights (where ) and over a fixed time period T. For computation of these risk measures, a joint law for the random vector is required. The Wasserstein barycenter can be regarded as the aggregate model for a certain set of probability measures. It is also suitable for reaching an “average” distribution. The procedure also considers an optimal selection for the positive weights. They are connected with the source credibility for every prior. Moreover, the weights must be chosen as equal when all priors remain acceptable. Equality also holds under unknowing performance reliability of the competing laws.
We are in a position to define the Wasserstein Barycenter Value-at-Risk.
Definition 3.
Given the aggregate position , a set of measures , a set of quantiles , and , the Wasserstein Barycenter Value-at-Risk is defined as:
where is the quantile function of the Wasserstein barycenter of with weights , where , , .
Next, we use the notable property that the barycenter of distributions of location–scatter families belongs to the same family. This allows use to derive closed-form formulas for the Wasserstein Barycenter risk measures for location–scatter distributions.
Theorem 1.
Let be an aggregated random variable and be location–scatter measures in the real line, with respective means and standard deviations . Then, the Wasserstein Barycenter Value-at-Risk is given by
where , is the cumulative distribution functions of the standard random variable, , and , ,
Proof.
See Appendix A. □
The Wasserstein Barycenter Conditional Value-at-Risk is established next:
Theorem 2.
Let be an aggregated random variable and be location–scatter measures in the real line, with respective means and standard deviations . Then, the Wasserstein Barycenter Conditional Value-at-Risk () is given by
where , and are the density and cumulative distribution functions of the standard random variable, respectively, , and , ,
Proof.
See Appendix A. □
We now illustrate Theorems 1 and 2 under the Gaussian distribution.
Corollary 1.
Let be Gaussian measures with corresponding means and standard deviations . Then, the and the are given by
Here, ϕ is the standard Gaussian distribution, is the inverse of the standard Gaussian distribution, , and , ,
4. Empirical Analysis: Portfolio Risk under Gaussian Model
This section focuses on estimation of the multi-variate VaR for a risk portfolio ruled by the NASDAQ and S&P500 stock indices. The NASDAQ log-returns and the S&P500 log-returns are denoted by and , respectively. In this case, the portfolio log-return, , has the form , where and and are the portfolio weights of and , such that . Without loss of generality, a portfolio under equal weights in both indices is considered. However, this is not a strict restriction, and they can change freely. Finally, for the marginal returns, a Gaussian distribution is proposed, and a one-day period VaR is considered.
4.1. Results of Wasserstein Barycenter Approach
We followed the 2972 daily closing prices given by Palaro and Hotta (2006). The database ranged from 2 January 1992 to 1 October 2003, and each stock is ruled by a Gaussian distribution. The VaR estimation accuracy was measured using the Kupiec test for back-testing the method in small quantiles Table 1 provides the descriptive statistics of both series.

Table 1.
Descriptive statistics for log-returns series of daily NASDAQ and S&P500 stock indices.
According to Table 1, the return series distributions of NASDAQ and S&P500 showed small asymmetry but strong kurtosis, particularly for the former. Note also that both series presented positive means (annualized).
The Wasserstein Barycenter VaR is computed by using the equation
where denotes the inverse of the standard Gaussian distribution, and the mean and the standard deviation are computed as , and respectively.
The approach includes both “unfiltered” and “filtered” models. The filtered model considers the volatility changes of the instrument, and is referred to as Wasserstein Barycenter-G*. In the unfiltered model, Wasserstein Barycenter-G and all the , receive the same value of the sample standard deviation. However, in the filtered model, the are estimated using an Exponentially Weighted Moving Average model, where .
The Kupiec test evaluates the performance by computing the number of exceptions in the corresponding test period. In this case, represents the null hypothesis. If m is the number of observations for the test period and x denotes the expected frequency of exceptions, then is the difference between the observed frequency of losses and VaR. The corresponding test statistic is given by
The null hypothesis is rejected, with a 95% confidence level, when . In that case, the VaR estimates generated by the particular VaR model are not statistically meaningful; see McNeil (1999).
The data set under consideration was then divided into sample and test periods, with a selected window of 750 observations. Since we have 2971 observations, we had a total of 2220 tests for VaR at each level.
The corresponding results are presented in Table 2.

Table 2.
Wasserstein Barycenter VaR, for t = 751 to 2971; number of exceptions where the estimated VaR was exceeded by the portfolio loss with p-values of tests are included.
For all levels of , the Wasserstein Barycenter-G* model showed the best performance, in terms of VaR estimation. Moreover, for , the Wasserstein Barycenter-G model also provided satisfactory performance. In terms of the Kupiec test, applied to the number of exceptions for the Wasserstein Barycenter-G* model, the null hypothesis was not rejected for any of the levels under consideration. In particular, high p-values of 0.2837, 0.9223, 0.8653, and 0.1668 were obtained for Wasserstein Barycenter-G * model, which implies that the null hypothesis was not rejected, and p-values of 0.8323 and 0.07130 were obtained for the Wasserstein Barycenter-G model at the levels and , respectively.
4.2. Comparisons
In the context of Li et al. (2012), research by the IFRI and CRO Forum has shown that 60% or more of the studied banks consider simple approaches, such as simple summation and Variance–Covariance methods, for the aggregation of risk, while at least slightly more advanced approaches (e.g., those supported by simulation) were used by only 20% or less of the financial institutions in the survey. Next, we provide a summary of such approaches. Then, performance comparison with the proposed model is described. In the end, the new method is also compared with the hybrid GARCH approach proposed by Palaro and Hotta (2006).
4.2.1. Classic Multivariate VaR Approaches
In this section, we describe computation of the multi-variate VaR under simple summation and variance–covariance approaches at different confidence levels. These approaches are briefly described in the following.
Simple Summation: The integration of N risks is intuitively conducted by aggregating the risks through summation of the particular of each risk , . Thus, the total aggregated VaR, , is expressed as:
see Embrechts et al. (2013) and Li et al. (2015).
Now, the Gaussian model supports several approaches in probability and statistics studies. In particular, calculating the VaR of multi-variate Gaussian models is a common parametric method for multi-variate VaR models. This technique supposes a multi-variate Gaussian distribution (with mean and covariance matrix ) for the returns of the components in the portfolio. The method is characterized as follows:
Variance–Covariance: If and are the deviation and expected portfolio return, respectively, then the estimate of the VaR for the corresponding multi-variate Gaussian distribution returns is given by
where represents the inverse of the standard Gaussian distribution.
The covariance matrix and the mean vector in the Variance–Covariance (Var–Covar) approach are frequently unknown, meaning that the model requires extra estimates taken from the observations; see Li et al. (2012) and Li et al. (2015).
A summary of the results follows:
- According to Table 3, the classic approaches did not predict future losses properly. On one hand, the number of exceptions is small under Simple Summation, which explains an over-estimation of future losses. On the other hand, the number of exceptions was large under variance–covariance, providing an under-estimation of future losses.
 Table 3. VaR for t = 751 to 2971, number of exceptions (in brackets), where the estimated VaR was exceeded by the portfolio loss, with .
Table 3. VaR for t = 751 to 2971, number of exceptions (in brackets), where the estimated VaR was exceeded by the portfolio loss, with . - The Wasserstein Barycenter-G* and Wasserstein Barycenter-G approaches exhibited remarkable performance for future loss predictions. Moreover, the Wasserstein Barycenter approaches are stronger, with respect to the other VaR models because, in the same reference time, they provide a small exception probability, such that a high-level capital reserve is not required. In the set of the analyzed approaches, the VaR Forecasting at all confidence levels was achieved with high performance by the proposed Wasserstein Barycenter-G* model. In fact, the Wasserstein Barycenter-G exhibited better VaR forecasting than Var–Covar and Simple Summation approaches at all confidence levels. The empirical results also demonstrated the known fact that the Simple Approach provides an upper bound for the true VaR. In particular, for a confidence level of 0.1%, a VaR of 0.0387 derived by Wasserstein Barycenter-G* was a third of the value (0.0978) based on the Simple Summation approach. In such a context, our approach provides several possibilities for a wide class of banks. Thus, under a conservative Wasserstein Barycenter VaR, compared with the general average, the proposed method, being indexed by different types of weights, allows for the inclusion of several criteria to improve the results. In contrast, the Var–Covar method was preferably optimistic. Finally, the notable closure property for the barycenter in the location–scatter distribution family requires a profuse knowledge of the prior barycenter under the selected distribution. Then, in the Gaussian case, an exact formula for the Wasserstein Barycenter Value-at-Risk can be derived and applied in the complete reference class of distributions. This opens up an interesting perspective for risk management risk considering series based on non-Gaussian models, as a complete mathematical description of the Wasserstein Barycenter VaR can be found under the selected prior distribution.
4.2.2. Other Multi-Variate VaR Models
Robust multi-variate approaches, including Copula and ARCH models, also involve VaR estimation. However, under a large number of assets, such models tend to produce biased parameter estimations and demand a high computational cost. For completeness, we contrast our approaches with those derived by Palaro and Hotta (2006).
Note that the Wasserstein Barycenter-G* VaR provided the best performance for , , and . When , the estimation matched the result of the hybrid SJC Copula + GARCH-E method, while, for , it was near that of the hybrid SJC Copula + GARCH-E model, which was noted by Palaro and Hotta (2006) as being the best approach. In fact, note that the SJC Copula + GARCH-E method succeeded in VaR forecasting at a 99.5% confidence level, but failed at 90% and 95%. The Table 4 highlighted that our approaches had high performance at all confidence levels.

Table 4.
VaR for t = 751 to 2971, number of exceptions (in brackets), where the estimated VaR was exceeded by the portfolio loss, with
The results show that the Wasserstein Barycenter-G* VaR presented an excellent performance being close to the expected number of exceptions. Unlike the GARCH models, our model only requires knowledge of the mean and deviation for VaR quantification, regardless of the number of assets considered in the portfolio, which represents an advantage over the GARCH models, in which the number of unknown parameters rises exponentially with the number of assets.
4.3. COVID-19: 2020 Stock Market Crash and the Global Financial Crisis (2008)
We end this section by demonstrating the performance of our method in the context of the COVID-19 pandemic situation and during the global financial crisis (2008).
Explicitly, we researched the impact of the COVID-19 pandemic on the 2020 Stock Market Crash, measured in terms of the Wall Street indices of NASDAQ Composite, S&P500, and Dow Jones Industrial Average. These indices reported historical loss levels, only otherwise registered during the financial crisis of 2008; see González and Gallizo (2021), Song et al. (2022), Nageri (2022), Athari et al. (2022), and Athari and Thai Hung (2022). As usual, the complete data set was split into sample and test periods. Sample data ranged from 4 January 2010 to 31 December 2018. The 2264 daily return data for every stock index also refer to the required historical data for a plausible VaR estimation. The test data, used for detecting the VaR performance, ranged from 2 January 2019 to 31 December 2020. The VaR was estimated for each day in the test period (505 days). Finally, the performance of the VaR model was measured through a comparison of the current loss against the estimated VaR. The division for the sample and test periods is summarized in Table 5.

Table 5.
Sample and test periods.
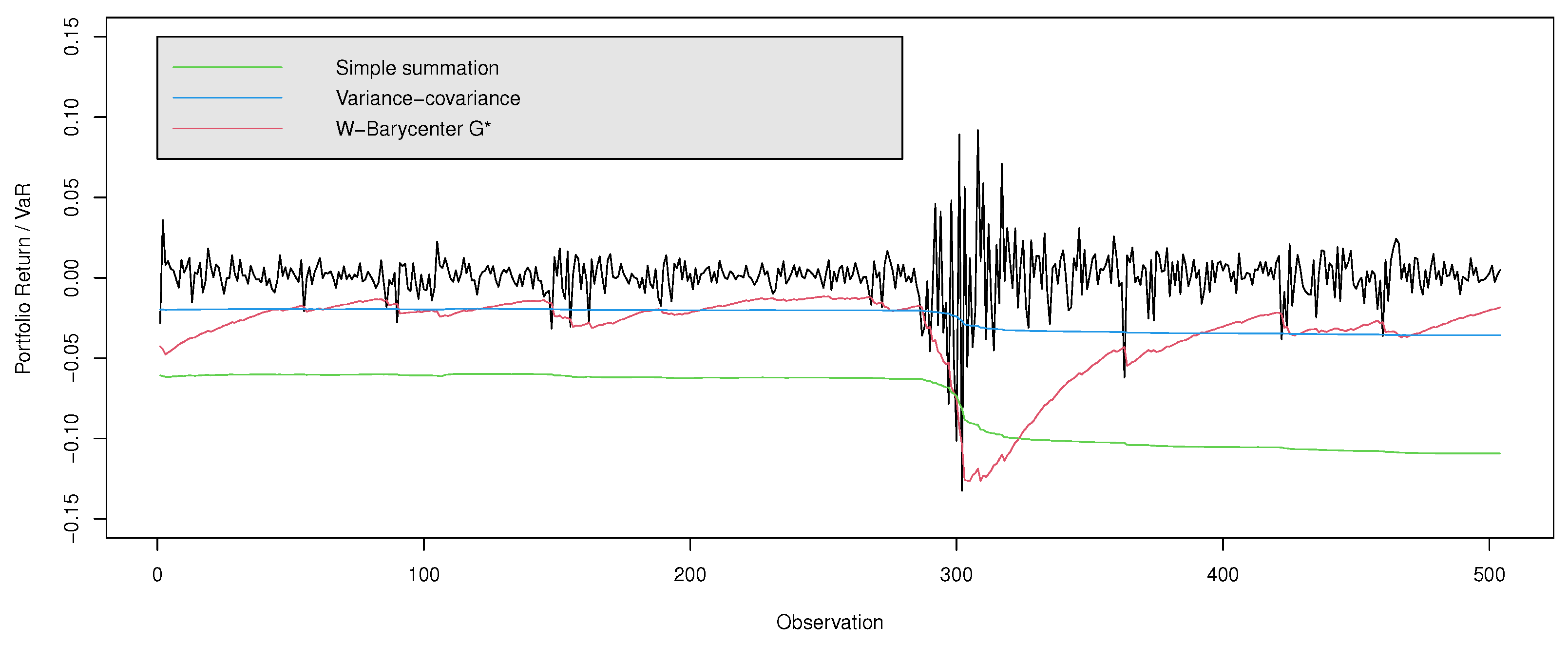
We compared the forecasting performance of the Wasserstein Barycenter-G* method with the classic multi-variate VaR models. The best challenge for both approaches lies in the financial market behavior in the year 2020 and its high volatility. First, Figure 1 shows the forecasts for the next trading day VaR for 2019 and 2020 using both approaches. Under a one-day holding period, the models were computed at a 99% confidence level.
Figure 1.
Daily Return series and VaR during the COVID-19 pandemic.
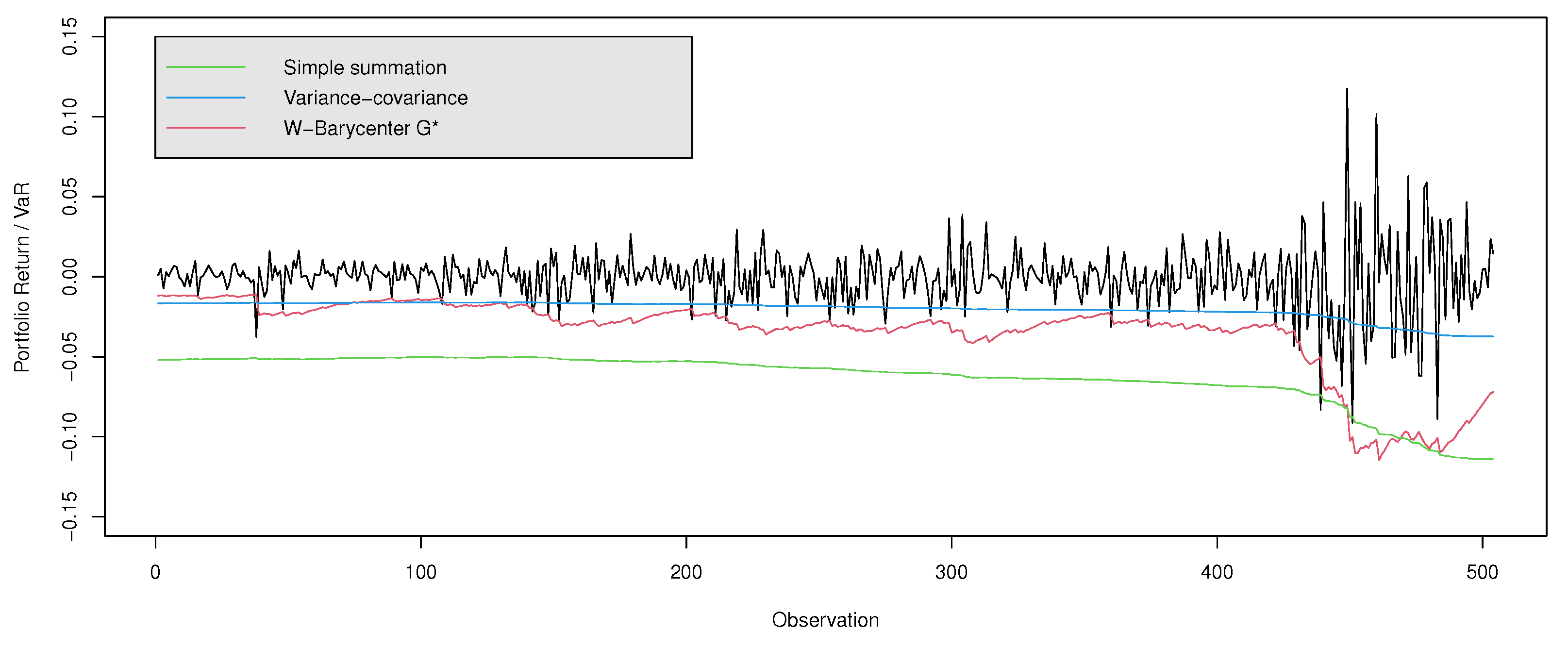
Finally, we also validate the performance of our method in the context of the global financial crisis (2008). We investigated the performance of the same Wall Street indices (NASDAQ Composite, S&P500, and Dow Jones Industrial Average) investigated during the COVID-19 pandemic. As in this last event, these indices reported levels of losses during 2007, 2008, and part of 2009 that have been reported in history, see Degiannakis et al. (2012), Pesaran and Pesaran (2010).
Sample data ranged from 5 January 1998 to 31 December 2006. The 2262 daily return data for every stock index also refer to the required historical data for a plausible VaR estimation. The test data, used for detecting the VaR performance, ranged from 3 January 2007 to 31 December 2008. The VaR was estimated for each day in the test period (504 days). Finally, the performance of the VaR model was measured through a comparison of the current loss against the estimated VaR. The division for the sample and test periods is summarized in Table 6.

Table 6.
Sample and test periods.
As can be seen from Figure 1 and Figure 2, the VaR estimate given by the Wasserstein Barycenter-G* VaR model was highly accurate. The new approach fit the volatile movements of the returns well and predicted future losses much better, in comparison with the classical multi-variate VaR approaches.
Figure 2.
Daily Return series and VaR during the global financial crisis (2008).
As can be seen in both figures, the variance–covariance approach did not follow the strong volatility, and always tended to under-estimate. In terms of the Simple Summation model, the test period showed lower exceptions, but a strong conservative characteristic was noted.
These results indicate that the proposed approach can provide the best forecasts of VaR not only for “normal periods”, but also for the periods of high volatility, such as those presented during the COVID-19 pandemic and the global financial crisis (2008).
5. Conclusions
In this work, we proposed a new multi-variate risk measure model based on the Wasserstein barycenter of probability distributions under a location–scatter family. Considering that the Wasserstein distance in the quantification of risk measures preserves desirable properties such as the comparison of distributions with different supports, so it is suitable for models used in financial and insurance risk management.
We proposed exact formulae for the Wasserstein Barycenter VaR and CVaR for location–scatter families, which makes it a precise model that is easy to implement by risk managers.
The model was compared with GARCH models under a portfolio characterized by S&P500 and NASDAQ stock indices. The results show that the proposed model presented an excellent performance being close to the expected number of exceptions. Unlike the GARCH models, our model only requires knowledge of the mean and deviation for VaR quantification, regardless of the number of assets considered in the portfolio, which represents an advantage over the GAECH models, in which the number of unknown parameters rises exponentially with the number of assets.
The new model was also compared with respect to United States market indices characterized by high volatility during the COVID-19 pandemic situation and during the global financial crisis (2008). The results indicated that the proposed approach provides the best forecasts of risk measures not only for “normal periods”, but also for periods of high volatility.
As future work, it is expected to generalize the proposed methodology to Distortion Risk Measure and Coherent Distortion Risk Measure, such as those investigated in Wang et al. (2020) and Pesenti (2022). Among other possible extensions of our paper, one could introduce new risk indicators as the high-order TCE risk measure studied in Faroni et al. (2022).
Author Contributions
Conceptualization, M.A.A.-S. and J.M.L.; methodology, M.A.A.-S., J.M.L. and F.J.C.-L.; software, M.A.A.-S.; validation, M.A.A.-S., J.M.L. and F.J.C.-L.; formal analysis, M.A.A.-S., J.M.L. and F.J.C.-L.; investigation, M.A.A.-S., J.M.L. and F.J.C.-L.; resources, M.A.A.-S., J.M.L. and CF.J.C.-L.; data curation, M.A.A.-S.; writing—original draft preparation, M.A.A.-S.; writing—review and editing, J.M.L. and F.J.C.-L.; visualization, M.A.A.-S.; supervision, J.M.L. and F.J.C.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://es.investing.com (accessed on 1 June 2022).
Acknowledgments
The authors wish to express their gratitude to the Doctoral School of Mathematics, IT and Telecommunications, University of Toulouse, and to the Doctorate in Modeling and Scientific Computing, University of Medellin.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proofs
Proof of Theorem 1.
By definition, is a real number such that
Therefore,
or, equivalently,
Thus,
Finally,
□
Proof of Theorem 2.
Note that
By letting , we have
□
References
- Agueh, Martial, and Guillaume Carlier. 2011. Barycenters in the Wasserstein space. SIAM Journal on Mathematical Analysis 43: 904–24. [Google Scholar] [CrossRef]
- Arias-Serna, M. Andrea, Francisco J. Caro-Lopera, J. Alberto Echeverri-Arias, Luis C. Franco-Arbelaez, and J. Guillermo Murillo-Gómez. 2016. Information system for the quantification of operational risk in financial institutions. IEEE Xplore Digital Library 1: 3–9. [Google Scholar]
- Arias-Serna, M. Andrea, Francisco J. Caro-Lopera, and Jean-Michel Loubes. 2021. Risk measures: A generalization from the univariate to matrix-variate. Journal of Risk 23: 1–20. [Google Scholar] [CrossRef]
- Athari, Seyed Alireza, Dervis Kirikkaleli, and Tomiwa Adebayo. 2022. World pandemic uncertainty and german stock market: Evidence from markov regime-switching and fourier based approaches. Quality & Quantity 11: 1–14. [Google Scholar] [CrossRef]
- Athari, Seyed Alireza, and Ngo Thai Hung. 2022. Time–frequency return co-movement among asset classes around the covid-19 outbreak: Portfolio implications. Journal of Economics and Finance, 1–21. [Google Scholar] [CrossRef]
- Álvarez Esteban, Pedro C., Eustasio del Barrio, Juan A. Cuesta-Albertos, and Carlos Matrán. 2011. Uniqueness and approximate computation of optimal incomplete transportation plans. Annales de l’Institut Henri Poincaré, Probabilités et Statistiques 47: 358–75. [Google Scholar] [CrossRef]
- Álvarez Esteban, P. C., E. del Barrio, J. A. Cuesta-Albertos, and C. Matrán. 2016. A fixed-point approach to barycenters in Wasserste in space. Journal of Mathematical Analysis and Applications 441: 744–62. [Google Scholar] [CrossRef]
- Álvarez Esteban, Pedro C., Eustasio del Barrio, Juan A. Cuesta-Albertos, and Carlos Matrán. 2018. Wide consensus aggregation in the Wasserstein space. application to location–scatter families. Bernoulli 24: 3147–79. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Kostas Giannopoulos, and Les Vosper. 2018. Estimating the joint tail risk under the filtered historical simulation: An application to the ccp’s default and waterfall fund. The European Journal of Finance 24: 413–25. [Google Scholar] [CrossRef]
- Bigot, Jérémie, Raúl Gouet, Thierry Klein, and Alfredo López. 2018. Upper and lower risk bounds for estimating the Wasserstein barycenter of random measures on the real line. Electronic Journal of Statistics 12: 2253–89. [Google Scholar] [CrossRef]
- Boissard, Emmanuel, Thibaut Le Gouic, and Jean-Michel Loubes. 2015. Distribution’s template estimate with Wasserstein metrics. Bernoulli 21: 740–59. [Google Scholar] [CrossRef]
- Degiannakis, Stavros, Christos Floros, and Alexandra Livada. 2012. Evaluating value-at-risk models before and after the financial crisis of 2008: International evidence. Managerial Finance 38: 436–52. [Google Scholar] [CrossRef]
- Embrechts, Paul, Giovanni Puccetti, and Ludger Rüschendorf. 2013. Model uncertainty and var aggregation. Journal of Banking & Finance 37: 2750–64. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate simultaneous generalized arch. Econometric Theory 11: 122–50. [Google Scholar] [CrossRef]
- Faroni, Silvia, Olivier Le Courtois, and Krzysztof Ostaszewski. 2022. Equivalent risk indicators: Var, tce, and beyond. Risks 10: 142. [Google Scholar] [CrossRef]
- Feng, Y., and S. Erik. 2018. Model Risk Measurement under Wasserstein Distance. Research Paper Series; Sydney: Quantitative Finance Research Centre, University of Technology. [Google Scholar] [CrossRef]
- Gabrielsen, A., A. Kirchiner, Z. Liu, and P. Zagagli. 2015. Forecasting value-at-risk with time-varying variance, skewness and kurtosis in an exponential weighted moving average framework. Annals of Financial Economics 10: 1–29. [Google Scholar] [CrossRef]
- González, Pedro Antonio, and José Luis Gallizo. 2021. Impact of covid-19 on the stock market by industrial sector in chile: An adverse overreaction. Journal of Risk and Financial Management 14: 548. [Google Scholar] [CrossRef]
- Han, C., W. Liu, and T. Chen. 2014. Var/cvar estimation under stochastic volatility models. International Journal of Theoretical and Applied Finance 17: 1450009. [Google Scholar] [CrossRef]
- Jin, Xisong, and Thorsten Lehnert. 2018. Large portfolio risk management and optimal portfolio allocation with dynamic elliptical copulas. Dependence Modeling 6: 19–46. [Google Scholar] [CrossRef]
- Kiesel, Rüdiger, Robin Rühlicke, Gerhard Stahl, and Jinsong Zheng. 2016. The wasserstein metric and robustness in risk management. Risks 4: 32. [Google Scholar] [CrossRef] [Green Version]
- Le Gouic, T., and J. M. Loubes. 2017. Existence and consistency of Wasserstein barycenters. Probability Theory and Related Fields 168: 901–17. [Google Scholar] [CrossRef]
- Li, Jianping, Jichuang Feng, Xiaolei Sun, and Minglu Li. 2012. Risk integration mechanisms and approaches in banking industry. International Journal of Information Technology & Decision Making 11: 1183–213. [Google Scholar] [CrossRef]
- Li, Jianping, Xiaoqian Zhu, Cheng-Few Lee, Dengsheng Wu, Jichuang Feng, and Yong Shi. 2015. On the aggregation of credit, market and operational risks. Review of Quantitative Finance and Accounting 44: 161–89. [Google Scholar] [CrossRef]
- Liu, Wei, and Yang Liu. 2022. Worst-case higher moment coherent risk based on optimal transport with application to distributionally robust portfolio optimization. Symmetry 14: 138. [Google Scholar] [CrossRef]
- McNeil, A. J. 1999. Extreme Value Theory for Risk Managers. New York: Mimeo, ETH Zurich. [Google Scholar]
- McNeil, A. J., R. Frey, and P. Embrechts. 2015. Quantitative Risk Management: Concepts, Techniques and Tools. Princeton: Princeton University Press. [Google Scholar]
- Nageri, Kamaldeen. 2022. Risk-return relationship in the nigerian stock market during pandemic covid-19: Sectoral panel garch approach. Copernican Journal of Finance & Accounting 10: 97–116. [Google Scholar] [CrossRef]
- Palaro, Helder P., and Luiz Koodi Hotta. 2006. Using conditional copula to estimate value at risk. Journal of Data Science 4: 93–115. [Google Scholar] [CrossRef]
- Papayiannis, G. I., and A. N. Yannacopoulos. 2018. Convex risk measures for the aggregation of multiple information sources and applications in insurance. Scandinavian Actuarial Journal 2018: 792–822. [Google Scholar] [CrossRef]
- Pesaran, Bahram, and M. Hashem Pesaran. 2010. Conditional volatility and correlations of weekly returns and the var analysis of 2008 stock market crash. Economic Modelling 27: 1398–416. [Google Scholar] [CrossRef]
- Pesenti, Silvana M. 2022. Reverse sensitivity analysis for risk modelling. Risks 10: 141. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2002. Conditional value-at-risk for general loss distributions. Journal of Banking & Finance 26: 1443–71. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 26: 21–41. [Google Scholar] [CrossRef]
- Song, Ruiqiang, Min Shu, and Wei Zhu. 2022. The 2020 global stock market crash: Endogenous or exogenous? Physica A: Statistical Mechanics and its Applications 585: 126–425. [Google Scholar] [CrossRef]
- Stavroyiannis, S., I. Makris, V. Nikolaidis, and L. Zarangas. 2012. Econometric modeling and value-at-risk using the pearson type-iv distribution. International Review of Financial Analysis 22: 10–17. [Google Scholar] [CrossRef]
- Wagalath, L., and J.P. Zubelli. 2018. A liquidation risk adjustment for value at risk and expected shortfall. International Journal of Theoretical and Applied Finance 21: 1850010. [Google Scholar] [CrossRef]
- Wang, R., Y. Wei, and G. Willmot. 2020. Characterization, robustness and aggregation of signed choquet integrals. Mathematic of Operations Research 45: 993–1015. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).