Machine Learning Models and Data-Balancing Techniques for Credit Scoring: What Is the Best Combination?
Abstract
:1. Introduction
- Which feature selection method is capable of extracting the most informative predictors?
- Which combination of feature selection and machine learning models is best suited in developing a credit-scoring prediction model?
- Do sample-modifying techniques significantly improve classification performance? If yes, which combination of classifiers and oversampling techniques is preferable? Do the results depend on the size of the imbalance?
2. Machine Learning Models
2.1. Machine Learning and Credit Risk: Some Background
2.2. Classification Techniques
2.2.1. Decision Trees
2.2.2. Random Forests
| Algorithm 1 Random Forest |
Given training observations , , the number of features selected for the ensembles, and the number of trees B in the ensemble, we use B trees to construct the random forest. The following steps are performed:
|
2.2.3. Naïve Bayes
2.2.4. Artificial Neural Networks
2.2.5. K-Nearest Neighbor
2.3. Feature Selection Methods
2.3.1. Random Forest Recursive Feature Elimination
| Algorithm 2 RF–RFE |
|
2.3.2. Chi-Squared Feature Selection
2.3.3. Support Vector Machines and L1-Based Feature Selection
2.4. Over- and Undersampling Techniques
2.5. Evaluation Criteria
3. Empirical Analysis
3.1. Dataset Description
3.2. Numerical Details
3.3. Results
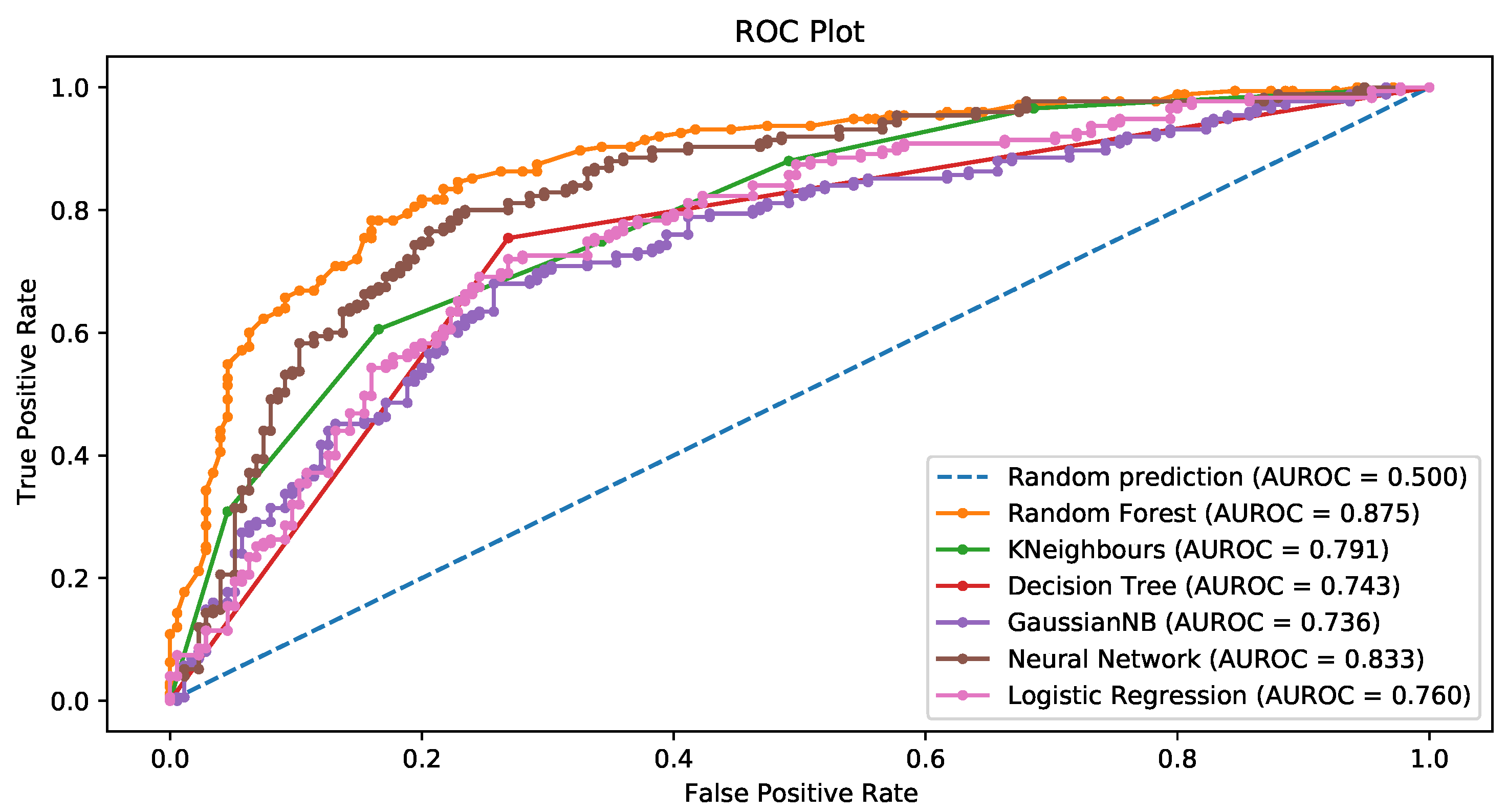
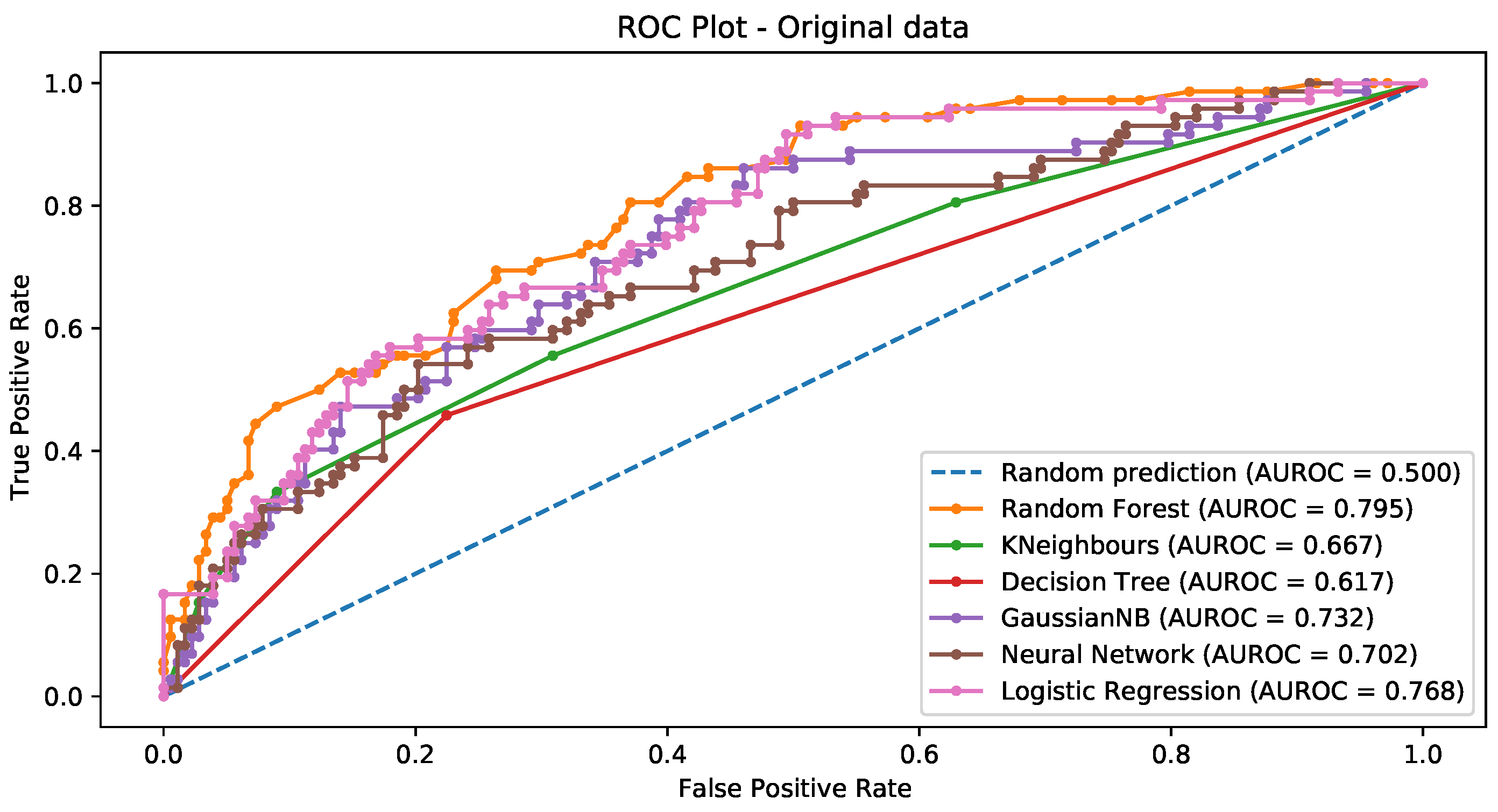
3.3.1. Chi-Squared Feature Selection
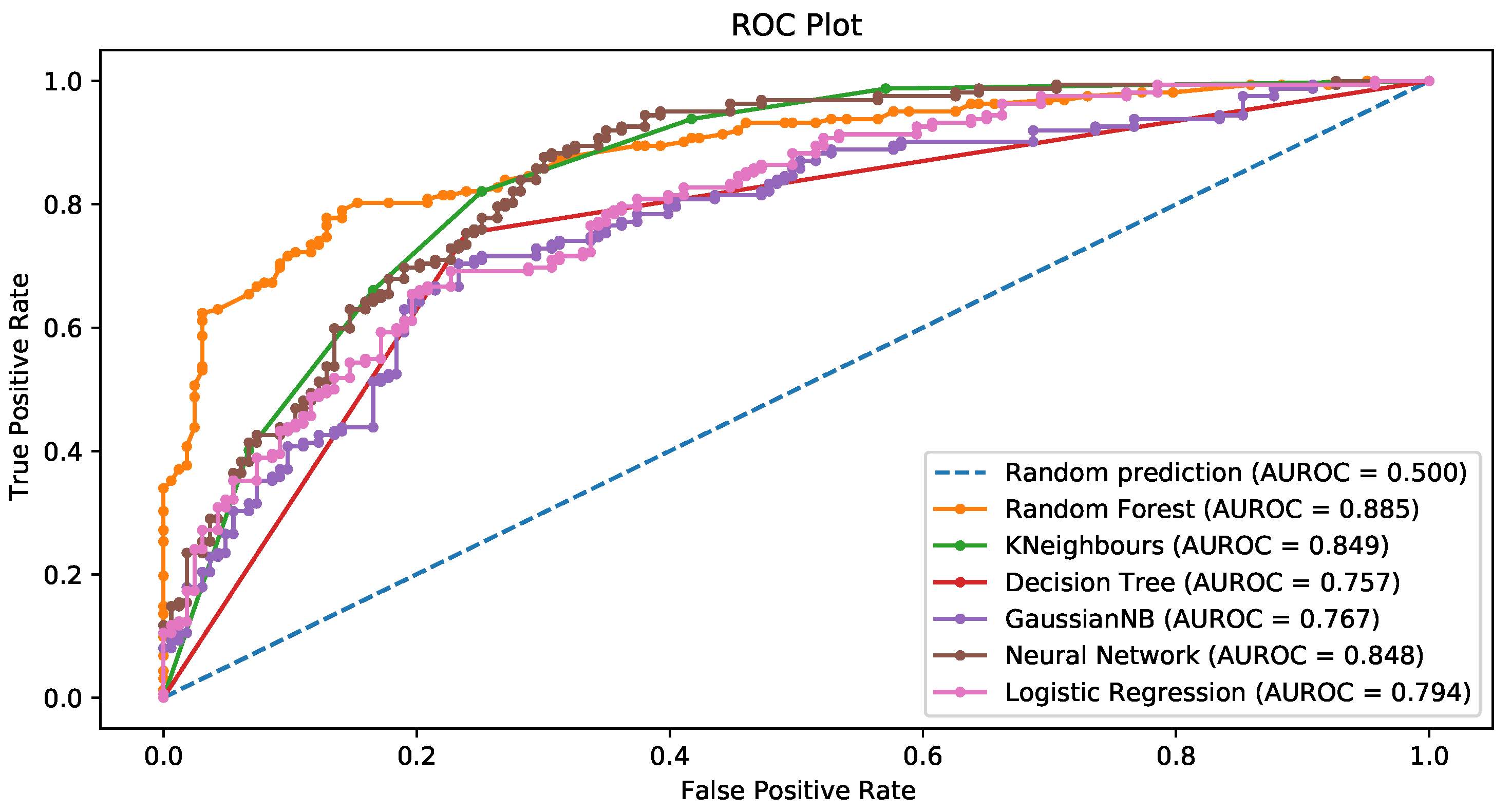
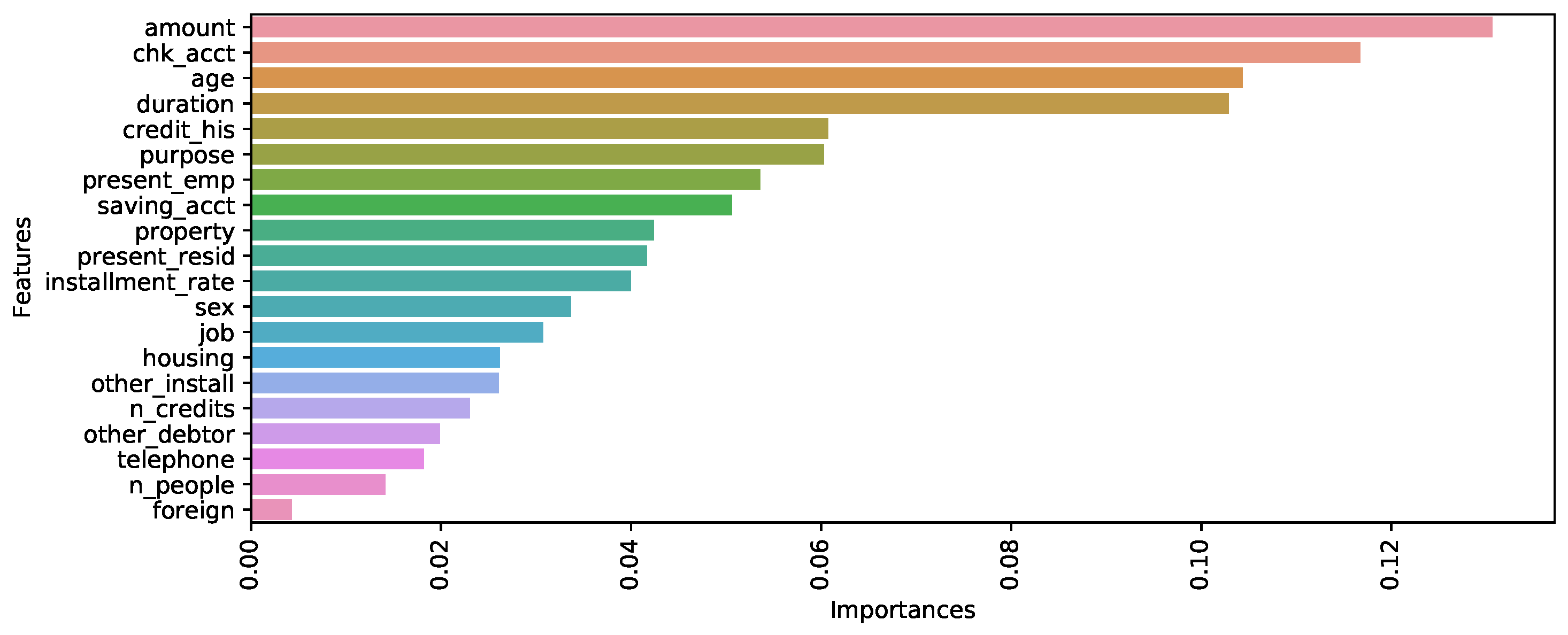
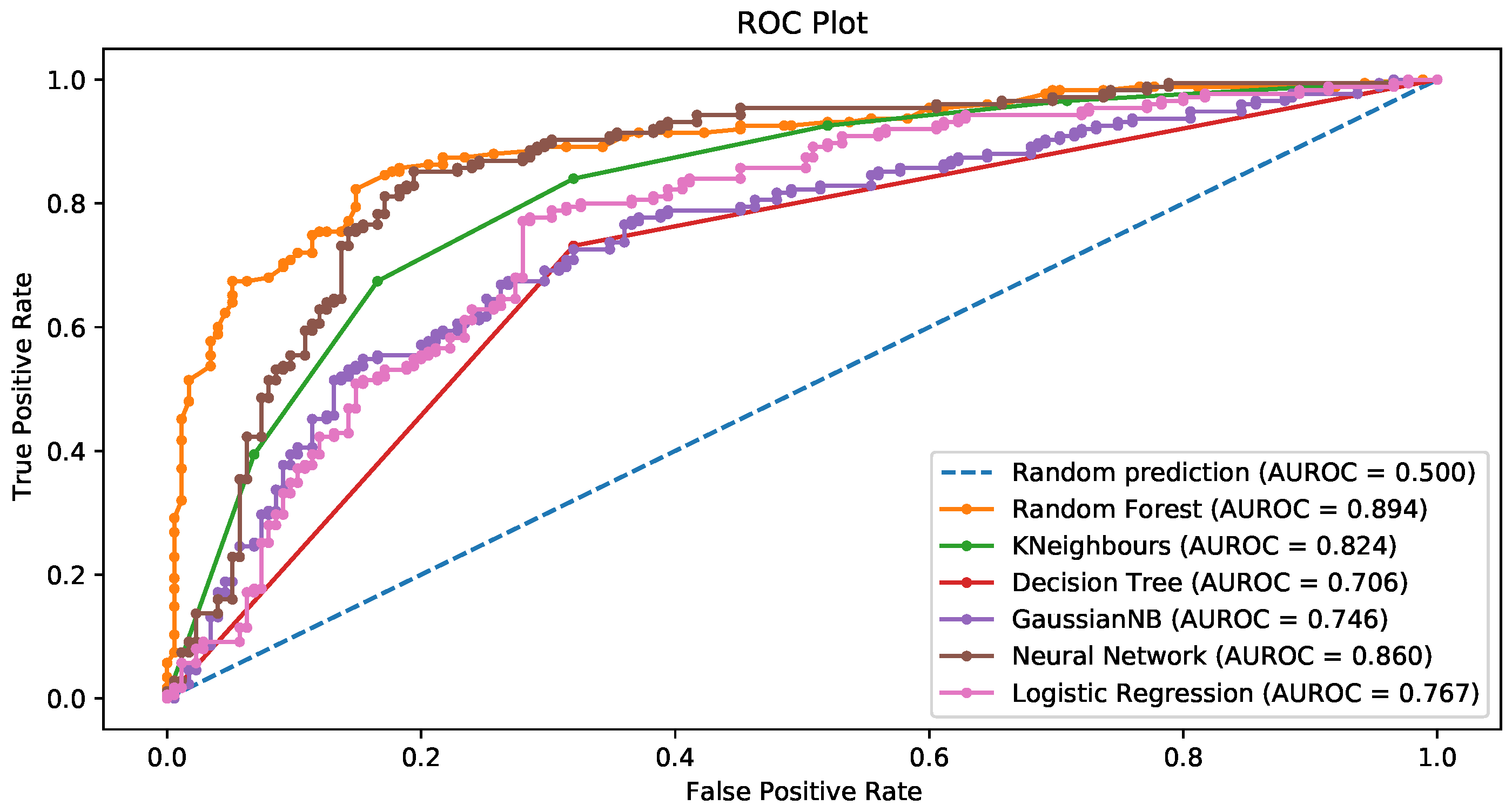
3.3.2. Random Forest Recursive Feature Elimination
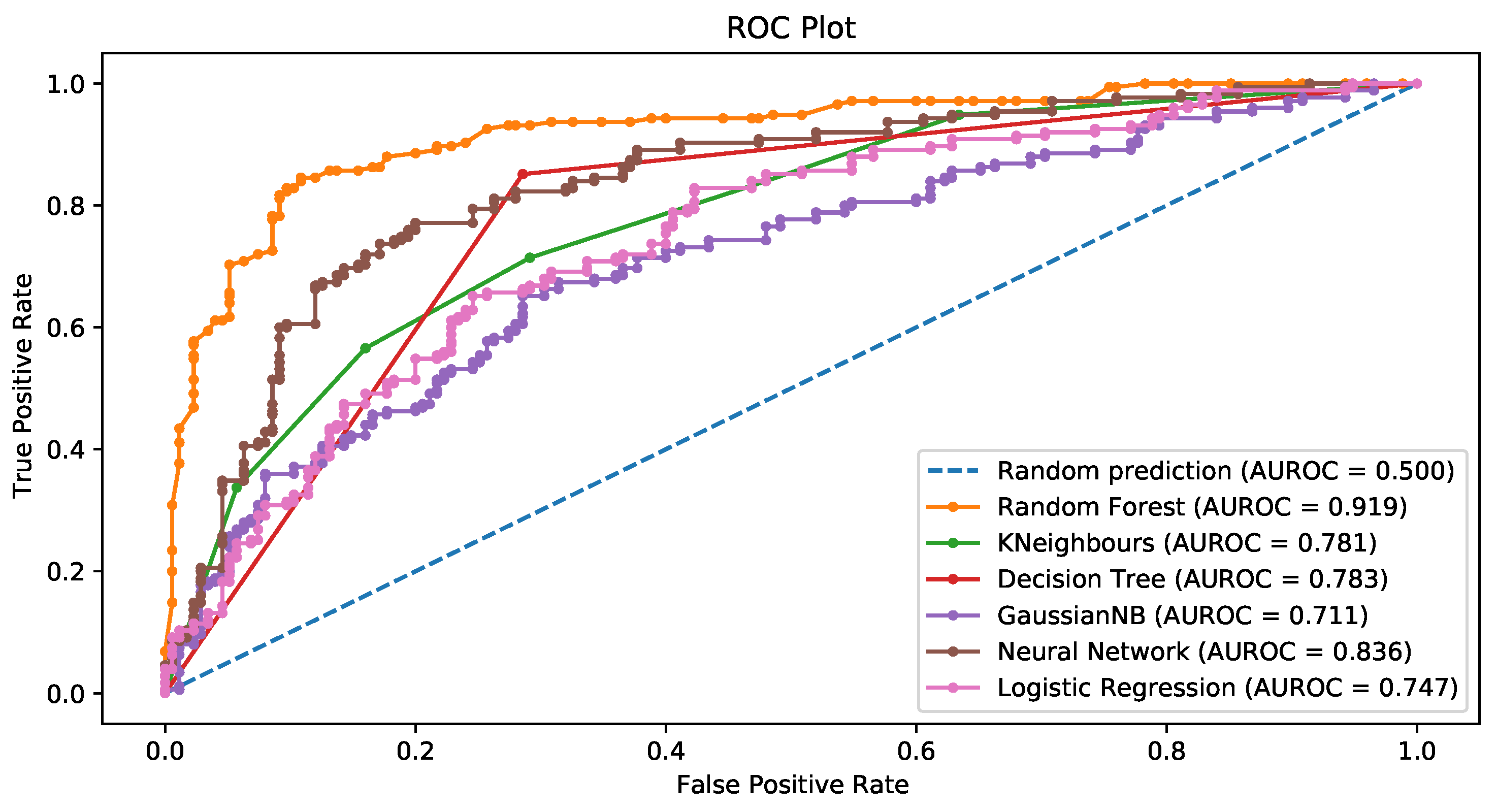
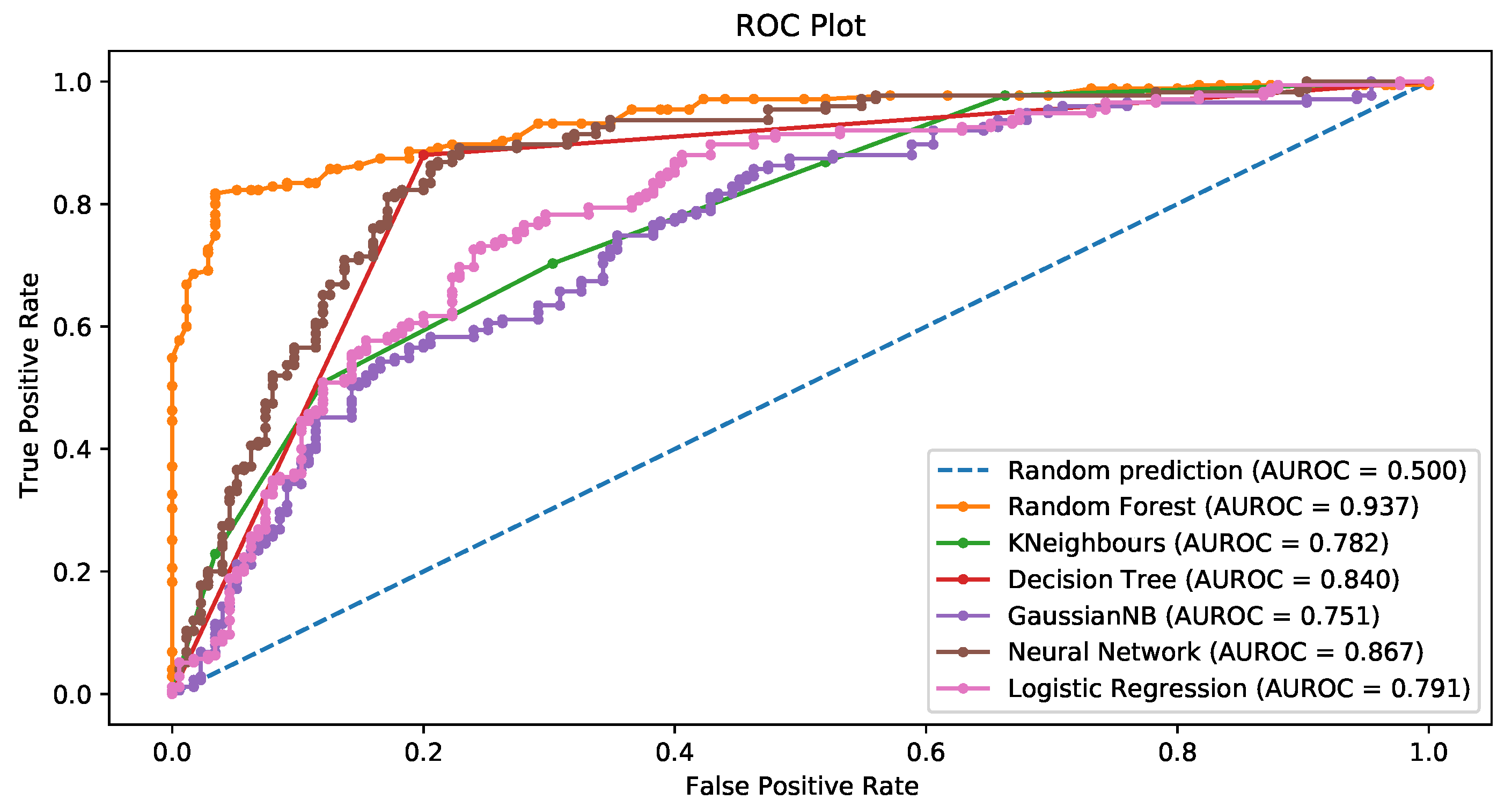
3.3.3. L1-Based Feature Selection
3.3.4. Computational Efficiency
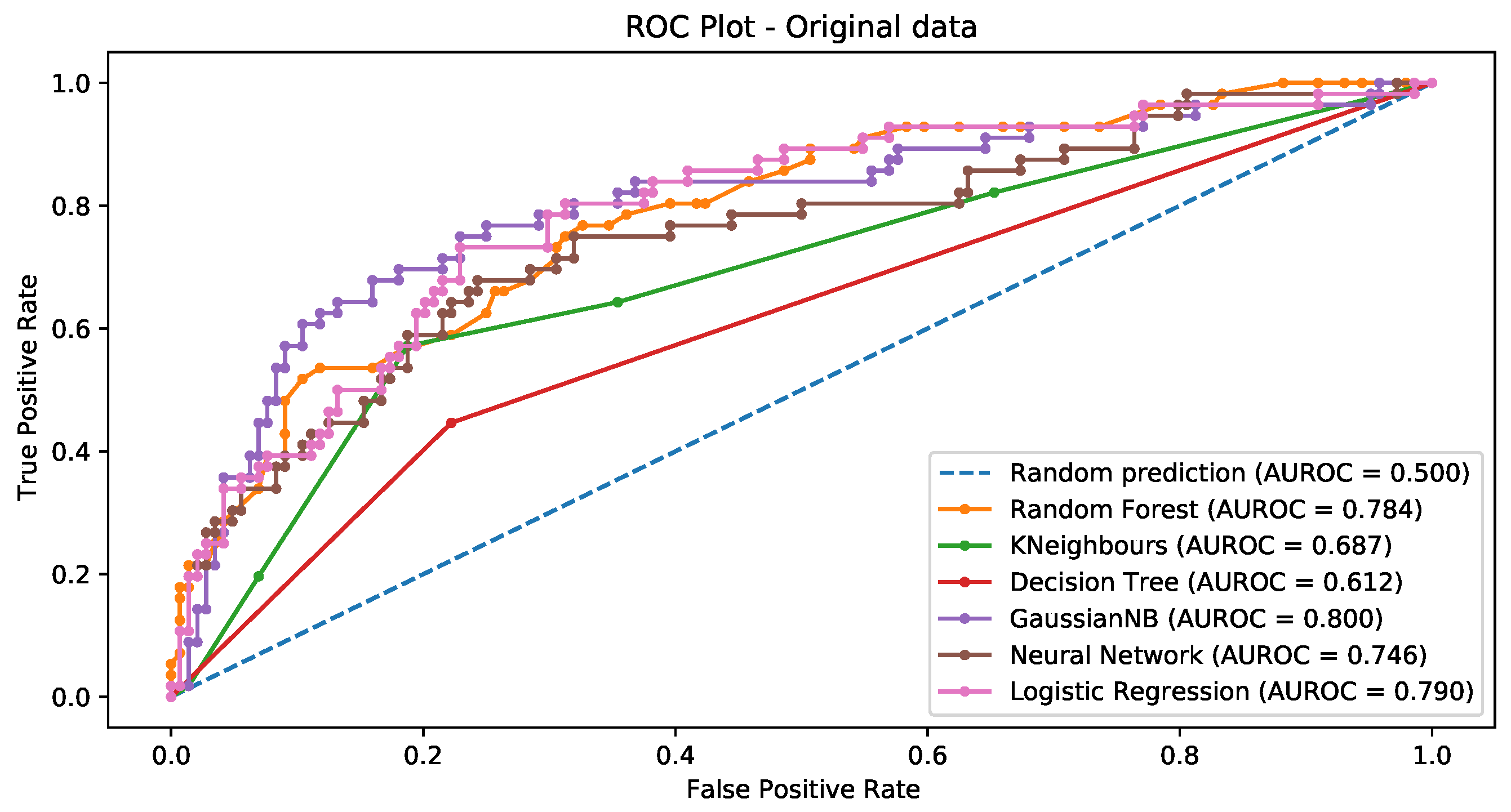
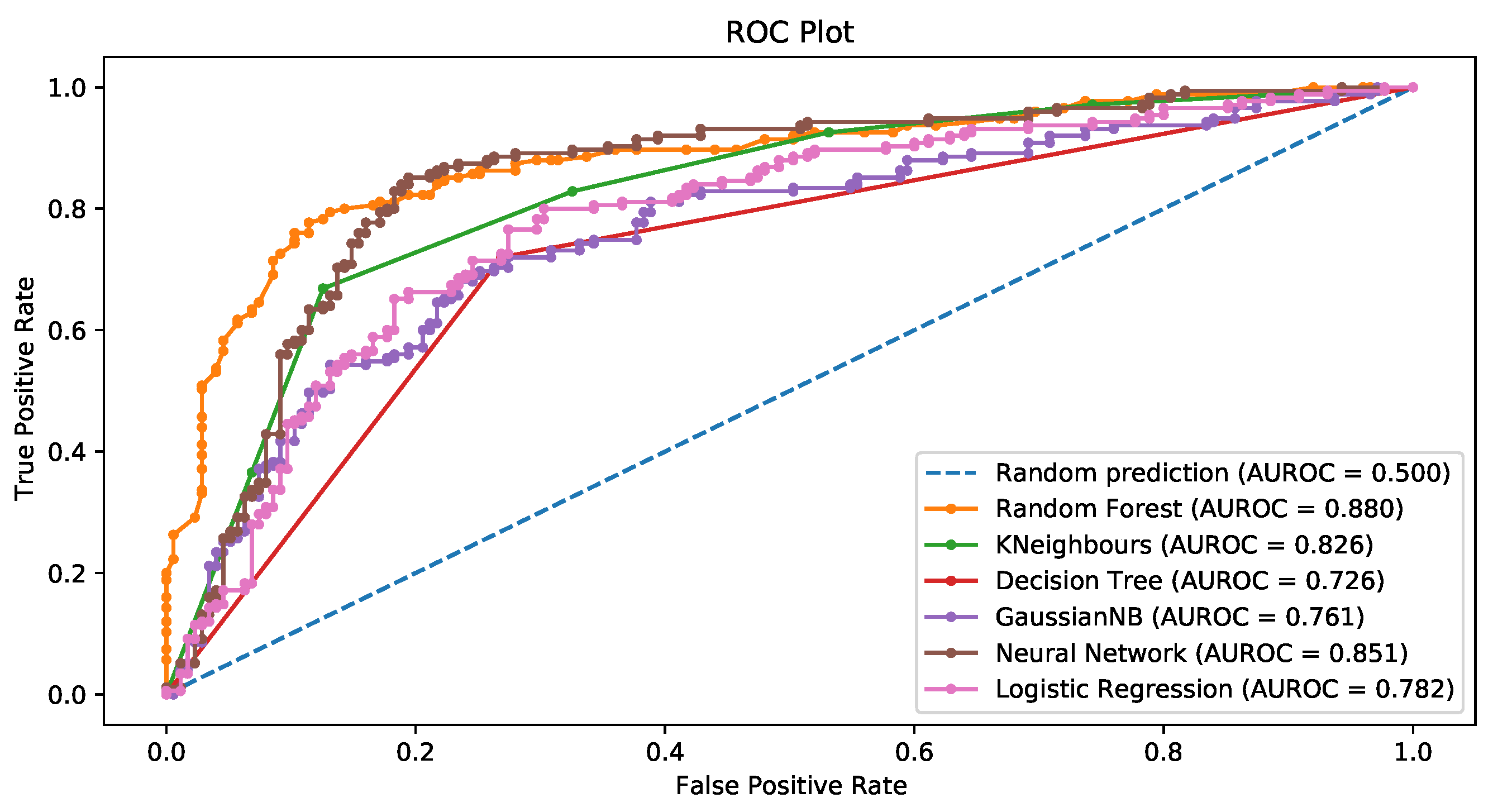
3.3.5. General Comments about the Results
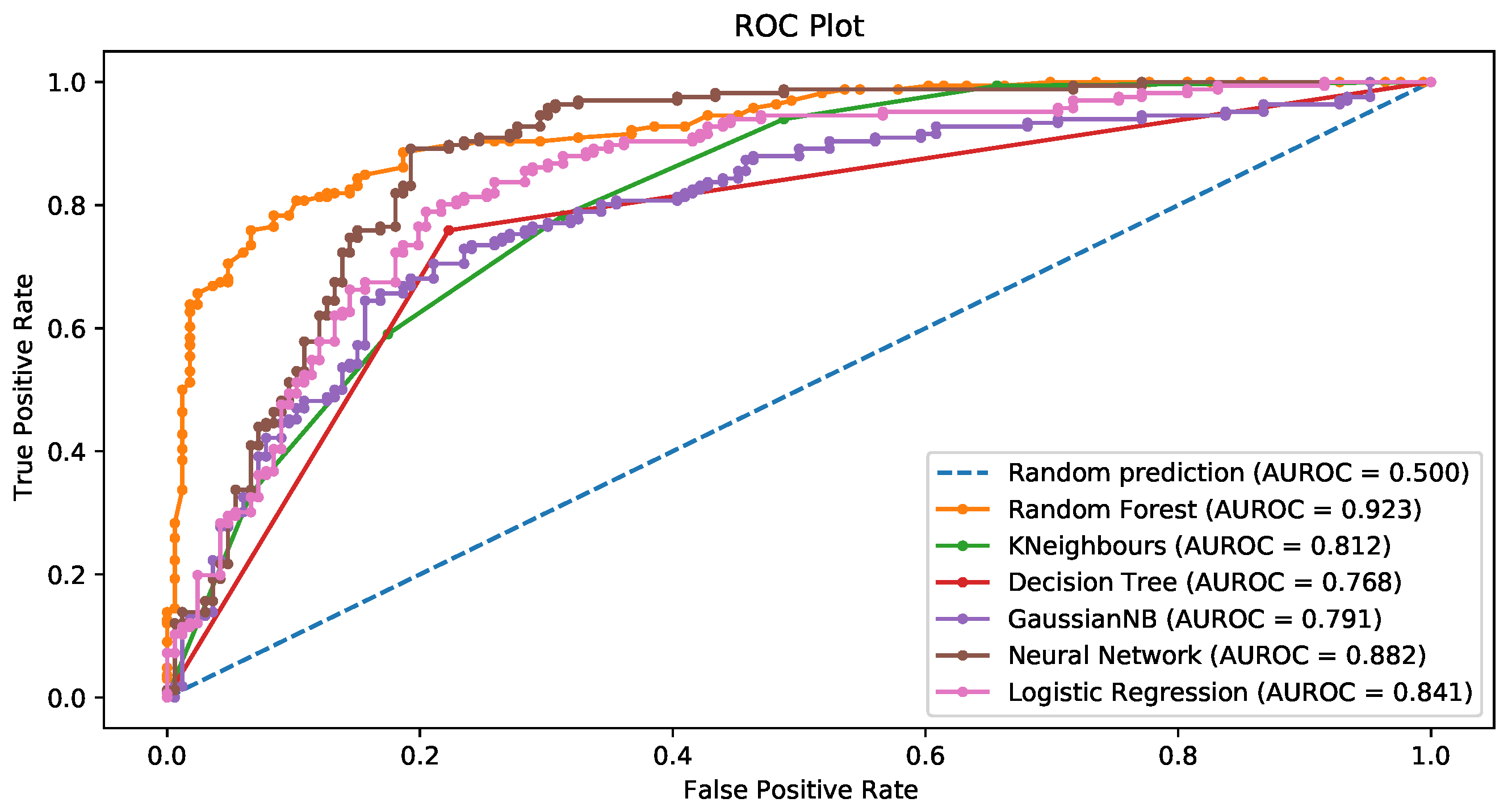
3.3.6. Dealing with a More-Imbalanced Set-Up
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://archive.ics.uci.edu/ml/datasets/statlog+(german+credit+data), accessed on 20 May 2022. |
| 2 | Since K-fold cross-validation gives very similar results, in the following, to save space, we only show the accuracy measures obtained by means of the valuation set approach. |
| 3 | The choice was double-checked by running the algorithm with different values of K, where values of K close to 5 gave the smallest test set MSE. Alternatively, it was possible to select K via cross-validation (James et al. 2021, sct. 5.1.5). |
| 4 | The outcomes are very similar when using the penalty. |
| 5 | See, for example, the default rates for Italy reported in Figure 2 of Moscatelli et al. (2020). |
References
- Alshaer, Hadeel N., Mohammed A. Otair, Laith Abualigah, Mohammad Alshinwan, and Ahmad M. Khasawneh. 2021. Feature selection method using improved Chi Square on Arabic text classifiers: Analysis and application. Multimedia Tools and Applications 80: 10373–90. [Google Scholar] [CrossRef]
- Anderson, Raymond. 2007. The Credit Scoring Toolkit—Theory and Practice for Retail Credit Risk Management and Decision Automation. Oxford: Oxford University Press. [Google Scholar]
- Baesens, Bart, T. Van Gestel, S. Viaene, M. Stepanova, J. Suykens, and J. Vanthienen. 2003. Benchmarking state-of-the-art classification algorithms for credit scoring. Journal of the Operational Research Society 54: 627–35. [Google Scholar] [CrossRef]
- Batista, Gustavo E. A. P. A., Ronaldo C. Prati, and Maria Carolina Monard. 2004. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explorations Newsletter 6: 20–29. [Google Scholar] [CrossRef]
- Bolder, David Jamieson. 2018. Credit-Risk Modelling: Theoretical Foundations, Diagnostic Tools, Practical Examples, and Numerical Recipes in Python. New York: Springer. [Google Scholar]
- Brankl, Janez, M. Grobelnikl, N. Milić-Frayling, and D. Mladenić. 2002. Feature selection using support vector machines. In Data Mining III. Edited by A. Zanasi, C. Brebbia, N. Ebecken and P. Melli. Southampton: WIT Press. [Google Scholar]
- Breiman, Leo. 2001. Random forests. Machine Learning 45: 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, Leo, Jerome H. Friedman, Charles J. Stone, and Richard A. Olshen. 1984. Classification and Regression Trees. London: Chapman and Hall. [Google Scholar]
- Buta, Paul. 1994. Mining for financial knowledge with CBR. AI Expert 9: 34–41. [Google Scholar]
- Chandrashekar, Girish, and Ferat Sahin. 2014. A survey on feature selection methods. Computers & Electrical Engineering 40: 16–28. [Google Scholar]
- Chawla, Nitesh V., Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. 2002. Smote: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research 16: 321–57. [Google Scholar] [CrossRef]
- Chen, Mu-Chen, and Shih-Hsien Huang. 2003. Credit scoring and rejected instances reassigning through evolutionary computation techniques. Expert Systems with Applications 24: 433–41. [Google Scholar] [CrossRef]
- De Castro Vieira, José Rômulo, Flavio Barboza, Vinicius Amorim Sobreiro, and Herbert Kimura. 2019. Machine learning models for credit analysis improvements: Predicting low-income families’ default. Applied Soft Computing 83: 105640. [Google Scholar] [CrossRef]
- Dea, Paul O., Josephine Griffith, and Colm O. Riordan. 2001. Combining feature selection and neural networks for solving classification problems. Paper presented at the 12th Irish Conference on Artificial Intelligence and Cognitive Science, Dublin, Ireland, December 9–10. [Google Scholar]
- Denison, David G. T., Christopher C. Holmes, Bani K. Mallick, and Adrian F. M. Smith. 2002. Bayesian Methods for Nonlinear Classification and Regression. Hoboken: John Wiley & Sons, vol. 386. [Google Scholar]
- Desai, Vijay S., Jonathan N. Crook, and George A. Overstreet Jr. 1996. A comparison of neural networks and linear scoring models in the credit union environment. European Journal of Operational Research 95: 24–37. [Google Scholar] [CrossRef]
- Dopuch, Nicholas, Robert W. Holthausen, and Richard W. Leftwich. 1987. Predicting audit qualifications with financial and market variables. Accounting Review 62: 431–454. [Google Scholar]
- Duffie, Darrell, and Kenneth J. Singleton. 2003. Credit Risk: Pricing, Measurement, and Management. Princeton: Princeton University Press. [Google Scholar]
- Ekin, Oya, Peter L. Hammer, Alexander Kogan, and Pawel Winter. 1999. Distance-based classification methods. INFOR: Information Systems and Operational Research 37: 337–52. [Google Scholar] [CrossRef]
- Friedman, Jerome H. 1991. Multivariate adaptive regression splines. The Annals of Statistics 19: 1–67. [Google Scholar] [CrossRef]
- Ganganwar, Vaishali. 2012. An overview of classification algorithms for imbalanced datasets. International Journal of Emerging Technology and Advanced Engineering 2: 42–47. [Google Scholar]
- Gonzalez, Jesus A., Lawrence B. Holder, and Diane J. Cook. 2001. Graph-based concept learning. In Proceedings of the Florida Artificial Intelligence Research Symposium. Palo Alto: AAAI/IAAI. [Google Scholar]
- Groemping, Ulrike. 2019. South German credit data: Correcting a widely used data set. Reports in Mathematics, Physics and Chemistry, Berichte aus der Mathematik, Physik und Chemie 4: 2019. [Google Scholar]
- Hand, David J., and William E. Henley. 1997. Statistical classification methods in consumer credit scoring: A review. Journal of the Royal Statistical Society: Series A 160: 523–41. [Google Scholar] [CrossRef]
- Haykin, Simon S. Neural Networks: A Comprehensive Foundation, 2nd ed. Upper Saddle River: Prentice Hall PTR.
- He, Haibo, and Edwardo A. Garcia. 2009. Learning from imbalanced data. IEEE Transactions on Knowledge and Data Engineering 21: 1263–84. [Google Scholar]
- Huang, Cheng-Lung, Mu-Chen Chen, and Chieh-Jen Wang. 2007. Credit scoring with a data mining approach based on support vector machines. Expert Systems with Applications 33: 847–56. [Google Scholar] [CrossRef]
- Huang, Zan, Hsinchun Chen, Chia-Jung Hsu, Wun-Hwa Chen, and Soushan Wu. 2004. Credit rating analysis with support vector machines and neural networks: A market comparative study. Decision Support Systems 37: 543–58. [Google Scholar] [CrossRef]
- Hung, Chihli, and Jing-Hong Chen. 2009. A selective ensemble based on expected probabilities for bankruptcy prediction. Expert Systems with Applications 36: 5297–303. [Google Scholar] [CrossRef]
- James, Gareth, Daniela Witten, Trevor Hastie, and Rob Tibshirani. 2021. An Introduction to Statistical Learning, 2nd ed. New York: Springer. [Google Scholar]
- Karels, Gordon V., and Arun J. Prakash. 1987. Multivariate normality and forecasting of business bankruptcy. Journal of Business Finance & Accounting 14: 573–93. [Google Scholar]
- Koh, Hian Chye. 1992. The sensitivity of optimal cutoff points to misclassification costs of type I and type II errors in the going-concern prediction context. Journal of Business Finance & Accounting 19: 187–97. [Google Scholar]
- Leo, Martin, Suneel Sharma, and Koilakuntla Maddulety. 2019. Machine learning in banking risk management: A literature review. Risks 7: 29. [Google Scholar] [CrossRef] [Green Version]
- Makowski, Paul. 1985. Credit scoring branches out. Credit World 75: 30–37. [Google Scholar]
- Moscatelli, Mirko, Simone Narizzano, Fabio Parlapiano, and Gianluca Viggiano. 2020. Corporate default forecasting with machine learning. Expert Systems with Applications 161: 113567. [Google Scholar] [CrossRef]
- Nanda, Sudhir, and Parag Pendharkar. 2001. Linear models for minimizing misclassification costs in bankruptcy prediction. Intelligent Systems in Accounting, Finance & Management 10: 155–68. [Google Scholar]
- Reichert, Alan K., Chien-Ching Cho, and George M. Wagner. 1983. An examination of the conceptual issues involved in developing credit-scoring models. Journal of Business & Economic Statistics 1: 101–14. [Google Scholar]
- Schebesch, Klaus Bruno, and Ralf Stecking. 2005. Support vector machines for classifying and describing credit applicants: Detecting typical and critical regions. Journal of the Operational Research Society 56: 1082–88. [Google Scholar] [CrossRef]
- Shin, Kyung-shik, and Ingoo Han. 2001. A case-based approach using inductive indexing for corporate bond rating. Decision Support Systems 32: 41–52. [Google Scholar] [CrossRef]
- Sindhwani, Vikas, Pushpak Bhattacharya, and Subrata Rakshit. 2001. Information theoretic feature crediting in multiclass support vector machines. In Proceedings of the 2001 SIAM International Conference on Data Mining. Philadelphia: SIAM, pp. 1–18. [Google Scholar]
- Thomas, Lyn C. 2000. A survey of credit and behavioural scoring: Forecasting financial risk of lending to consumers. International Journal of Forecasting 16: 149–72. [Google Scholar] [CrossRef]
- Tomek, Ivan. 1976. Two modifications of cnn. IEEE Transactions on Systems, Man, and Cybernetics 11: 769–72. [Google Scholar]
- Trivedi, Shrawan Kumar. 2020. A study on credit scoring modeling with different feature selection and machine learning approaches. Technology in Society 63: 101413. [Google Scholar] [CrossRef]
- Tsai, Chih-Fong, and Ming-Lun Chen. 2010. Credit rating by hybrid machine learning techniques. Applied Soft Computing 10: 374–80. [Google Scholar] [CrossRef]
- Ustebay, Serpil, Zeynep Turgut, and Muhammed Ali Aydin. 2018. Intrusion detection system with recursive feature elimination by using random forest and deep learning classifier. Paper presented at the 2018 International Congress on Big Data, Deep Learning and Fighting Cyber Terrorism (IBIGDELFT), Ankara, Turkey, December 3–4; pp. 71–76. [Google Scholar]
- Van Gestel, Tony, and Bart Baesens. 2009. Credit Risk Management. Basic Concepts: Financial Risk Components, Rating Analysis, Models, Economic and Regulatory Capital. Oxford: Oxford University Press. [Google Scholar]
- Wang, Gang, Jinxing Hao, Jian Ma, and Hongbing Jiang. 2011. A comparative assessment of ensemble learning for credit scoring. Expert Systems with Applications 38: 223–30. [Google Scholar] [CrossRef]
- Wang, Ke, Senqiang Zhou, Ada Wai-Chee Fu, and Jeffrey Xu Yu. 2003. Mining changes of classification by correspondence tracing. Paper presented at the 2003 SIAM International Conference on Data Mining (SDM), San Francisco, CA, USA, May 1–3. [Google Scholar]
- West, David. 2000. Neural network credit scoring models. Computers & Operations Research 27: 1131–52. [Google Scholar]
- Yu, Lean, Shouyang Wang, and Kin Keung Lai. 2008. Credit risk assessment with a multistage neural network ensemble learning approach. Expert Systems with Applications 34: 1434–44. [Google Scholar] [CrossRef]
- Zhou, Qifeng, Hao Zhou, Qingqing Zhou, Fan Yang, and Linkai Luo. 2014. Structure damage detection based on random forest recursive feature elimination. Mechanical Systems and Signal Processing 46: 82–90. [Google Scholar] [CrossRef]
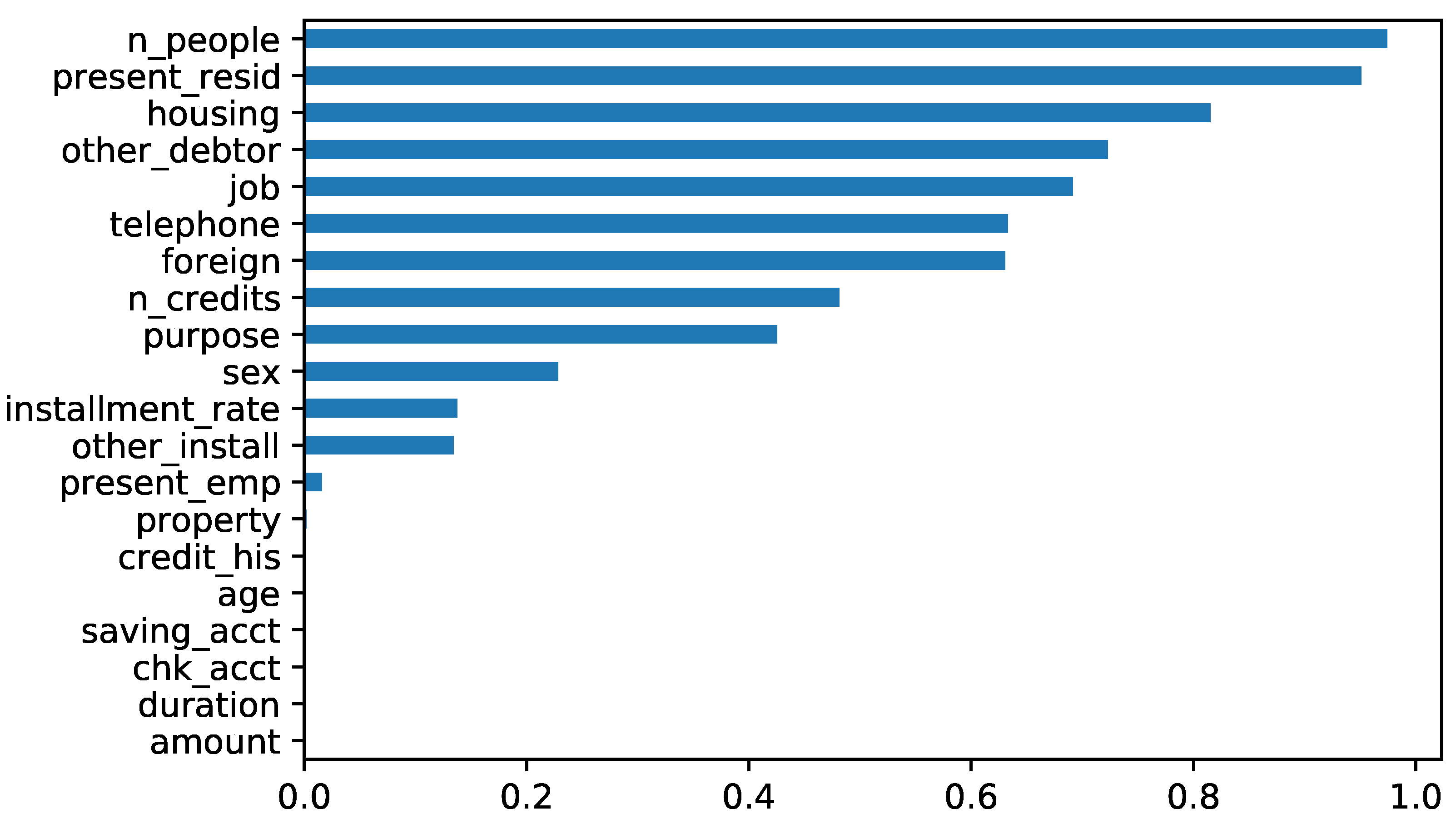



| Predicted | |||
|---|---|---|---|
| Positive | Negative | ||
| Actual | Positive | True positive (TP) | False negative (FN) |
| Negative | False positive (FP) | True negative (TN) | |
| Column Name | Variable Name | Description |
|---|---|---|
| chk acct | Status | Status of the debtor’s checking account with the bank (categorical) |
| duration | Duration | Credit duration in months (quantitative) |
| credit his | Credit history | History of compliance with previous or concurrent credit contracts (categorical) |
| purpose | Purpose | Purpose for which the credit is needed (categorical) |
| amount | Credit amount | The total amount of credit |
| saving acct | Saving accounts | Debtor’s savings (categorical) |
| present emp | Employment duration | Duration of debtor’s employment with current employer (ordinal) |
| installment rate | Personal status sex | The information about both sex and marital status |
| sex | Other debtors | If there is another debtor or a guarantor for the credit (categorical) |
| present resid | Present residence | Length of time (in years) the debtor has lived in the present residence (ordinal) |
| property | Property | The ranking of debetor’s property in ascending order (ordinal) |
| age | Age | Age in years (quantitative) |
| other nstall | Other installment plans | Any credit or installment burden other than the credit given back (categorical) |
| housing | Housing | Status of current residence (categorical) |
| n credit | Number credits | The complete history of credit taken (ordinal) |
| job | Job | The level of debtor’s job (ordinal) |
| n people | People liable | The total number of peers depending on debtor financially (quantitative) |
| telephone | Telephone | The status of registered landline on the debtor’s name (binary) |
| foreign | Foreign worker | If the debtor is a foreign worker (binary) |
| response | Credit risk | Good or bad (binary) |
| Number | Variable | Description |
|---|---|---|
| 1 | Checking accounts | Categorical variable with 4 labels |
| 2 | Duration | Numerical variable |
| 3 | Credit history | Categorical variable with 5 labels |
| 4 | Credit amount | Numerical variable |
| 5 | Saving accounts | Categorical variable with 5 labels |
| 6 | Present age | Numerical variable |
| 7 | Property | Categorical variable with 4 labels |
| Model | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|
| RF—Imbalanced data | 0.746 | 0.470 | 0.870 | 0.755 |
| RF—SMOTE | 0.806 | 0.811 | 0.800 | 0.875 |
| RF—SMOTETomek | 0.838 | 0.799 | 0.878 | 0.910 |
| RF—RandOverSampling | 0.854 | 0.909 | 0.800 | 0.925 |
| DT—imbalanced data | 0.680 | 0.424 | 0.772 | 0.598 |
| DT—SMOTE | 0.743 | 0.754 | 0.731 | 0.743 |
| DT—SMOTETomek | 0.777 | 0.750 | 0.805 | 0.777 |
| DT—RandOverSampling | 0.811 | 0.914 | 0.709 | 0.811 |
| GNB—imbalanced data | 0.752 | 0.742 | 0.755 | 0.795 |
| GNB—SMOTE | 0.691 | 0.714 | 0.669 | 0.736 |
| GNB—SMOTETomek | 0.738 | 0.726 | 0.750 | 0.786 |
| GNB—RandOverSampling | 0.691 | 0.663 | 0.720 | 0.710 |
| KNN—imbalanced data | 0.732 | 0.439 | 0.837 | 0.714 |
| KNN—SMOTE | 0.703 | 0.749 | 0.657 | 0.791 |
| KNN—SMOTETomek | 0.744 | 0.756 | 0.732 | 0.839 |
| KNN—RandOverSampling | 0.680 | 0.731 | 0.629 | 0.771 |
| NN—imbalanced data | 0.74 | 0.5303 | 0.8152 | 0.735 |
| NN—SMOTE | 0.78 | 0.789 | 0.771 | 0.833 |
| NN—SMOTETomek | 0.790 | 0.811 | 0.768 | 0.869 |
| NN—RandOverSampling | 0.763 | 0.771 | 0.754 | 0.839 |
| LR—imbalanced data | 0.768 | 0.4848 | 0.8696 | 0.782 |
| LR—SMOTE | 0.7171 | 0.7257 | 0.7086 | 0.760 |
| LR—SMOTETomek | 0.6954 | 0.6975 | 0.6933 | 0.794 |
| LR—RandOverSampling | 0.6886 | 0.6629 | 0.7143 | 0.747 |
| Number | Variable | Description |
|---|---|---|
| 1 | Credit amount | Numerical variable |
| 2 | Checking accounts | Categorical variable with 4 labels |
| 3 | Age | Numerical variable |
| 4 | Duration | Numerical variable |
| 5 | Credit history | Categorical variable with 5 labels |
| 6 | Purpose | Categorical variable with 4 labels |
| 7 | Present employment since | Categorical variable with 5 labels |
| 8 | Savings account | Categorical variable with 5 labels |
| 9 | Property | Categorical variable with 4 labels |
| 10 | Present residence | Numerical variable |
| Model | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|
| RF—imbalanced data | 0.788 | 0.444 | 0.927 | 0.795 |
| RF—SMOTE | 0.823 | 0.794 | 0.851 | 0.894 |
| RF—SMOTETomek | 0.823 | 0.846 | 0.800 | 0.895 |
| RF—RandOverSampling | 0.843 | 0.869 | 0.817 | 0.932 |
| DT—imbalanced data | 0.684 | 0.458 | 0.775 | 0.617 |
| DT—SMOTE | 0.706 | 0.731 | 0.680 | 0.706 |
| DT—SMOTETomek | 0.7200 | 0.751 | 0.688 | 0.720 |
| DT—RandOverSampling | 0.831 | 0.903 | 0.760 | 0.831 |
| GNB—imbalanced data | 0.708 | 0.486 | 0.798 | 0.732 |
| GNB—SMOTE | 0.694 | 0.703 | 0.686 | 0.746 |
| GNB—SMOTETomek | 0.696 | 0.722 | 0.671 | 0.749 |
| GNB—RandOverSampling | 0.654 | 0.577 | 0.731 | 0.717 |
| KNN—imbalanced data | 0.744 | 0.333 | 0.910 | 0.667 |
| KNN—SMOTE | 0.760 | 0.840 | 0.680 | 0.824 |
| KNN—SMOTETomek | 0.699 | 0.846 | 0.553 | 0.789 |
| KNN—RandOverSampling | 0.706 | 0.714 | 0.697 | 0.771 |
| NN—imbalanced data | 0.712 | 0.431 | 0.826 | 0.702 |
| NN—SMOTE | 0.823 | 0.840 | 0.806 | 0.860 |
| NN—SMOTETomek | 0.796 | 0.882 | 0.712 | 0.865 |
| NN—RandOverSampling | 0.803 | 0.806 | 0.800 | 0.863 |
| LR—imbalanced data | 0.752 | 0.4306 | 0.882 | 0.768 |
| LR—SMOTE | 0.7086 | 0.6971 | 0.72 | 0.767 |
| LR—SMOTETomek | 0.7351 | 0.7337 | 0.6964 | 0.809 |
| LR—RandOverSampling | 0.74 | 0.7543 | 0.7257 | 0.791 |
| Number | Variable | Description |
|---|---|---|
| 1 | Checking accounts | Categorical variable with 4 labels |
| 2 | Duration | Numerical variable |
| 3 | Credit history | Categorical variable with 5 labels |
| 4 | Age | Numerical variable |
| 5 | Credit amount | Numerical variable |
| 6 | Saving account | Categorical variable with 5 labels |
| 7 | Present employment since | Categorical variable with 5 labels |
| 8 | Present Instalment rate | Numerical variable |
| 9 | Property | Categorical variable with 4 labels |
| Model | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|
| RF—imbalanced data | 0.765 | 0.393 | 0.910 | 0.784 |
| RF—SMOTE | 0.820 | 0.811 | 0.829 | 0.880 |
| RF—SMOTETomek | 0.812 | 0.844 | 0.780 | 0.922 |
| RF—RandOverSampling | 0.857 | 0.903 | 0.811 | 0.920 |
| DT—imbalanced data | 0.685 | 0.446 | 0.778 | 0.612 |
| DT—SMOTE | 0.726 | 0.720 | 0.731 | 0.726 |
| DT—SMOTETomek | 0.749 | 0.790 | 0.708 | 0.749 |
| DT—RandOverSampling | 0.840 | 0.886 | 0.794 | 0.840 |
| GNB—imbalanced data | 0.765 | 0.750 | 0.771 | 0.800 |
| GNB—SMOTE | 0.700 | 0.731 | 0.669 | 0.761 |
| GNB—SMOTETomek | 0.758 | 0.844 | 0.673 | 0.803 |
| GNB—RandOverSampling | 0.657 | 0.623 | 0.691 | 0.743 |
| KNN—imbalanced data | 0.745 | 0.571 | 0.812 | 0.687 |
| KNN—SMOTE | 0.751 | 0.829 | 0.674 | 0.826 |
| KNN—SMOTETomek | 0.773 | 0.922 | 0.625 | 0.856 |
| KNN—RandOverSampling | 0.706 | 0.709 | 0.703 | 0.772 |
| NN—imbalanced data | 0.735 | 0.446 | 0.847 | 0.746 |
| NN—SMOTE | 0.829 | 0.851 | 0.806 | 0.851 |
| NN—SMOTETomek | 0.797 | 0.838 | 0.756 | 0.861 |
| NN—RandOverSampling | 0.791 | 0.771 | 0.811 | 0.848 |
| LR—imbalanced data | 0.755 | 0.4286 | 0.8819 | 0.790 |
| LR—SMOTE | 0.7314 | 0.7086 | 0.7543 | 0.782 |
| LR—SMOTETomek | 0.7861 | 0.8072 | 0.7651 | 0.841 |
| LR—RandOverSampling | 0.6857 | 0.6343 | 0.7371 | 0.741 |
| Model | ChiSquare | RF-RFE | L1 |
|---|---|---|---|
| RF—RandOverSampling | 0.6088 | 0.4214 | 0.2902 |
| DT—RandOverSampling | 0.0089 | 0.0109 | 0.0089 |
| GNB—RandOverSampling | 0.0079 | 0.0059 | 0.0079 |
| KNN—RandOverSampling | 0.0448 | 0.0468 | 0.0408 |
| NN—RandOverSampling | 1.8018 | 1.5998 | 1.8516 |
| LR—RandOverSampling | 0.0279 | 0.0259 | 0.0229 |
| Model | Accuracy | Sensitivity | Specificity | AUC |
|---|---|---|---|---|
| RF—Imbalanced | 0.9690 | 0.3889 | 0.9909 | 0.8526 |
| RF—SMOTE | 0.9200 | 0.8858 | 0.9371 | 0.9664 |
| RF—SMOTETomek | 0.9498 | 0.9384 | 0.9552 | 0.9812 |
| RF—RandOverSampling | 0.9846 | 1.000 | 0.9768 | 0.9998 |
| NN—Imbalanced | 0.9724 | 0.3333 | 0.9963 | 0.9445 |
| NN—SMOTE | 0.8756 | 0.8113 | 0.9077 | 0.9511 |
| NN—SMOTETomek | 0.9070 | 0.8524 | 0.9335 | 0.9654 |
| NN—RandOverSampling | 0.8745 | 0.8311 | 0.8962 | 0.9493 |
| LR—Imbalanced | 0.9724 | 0.3222 | 0.9967 | 0.9465 |
| LR—SMOTE | 0.8748 | 0.8022 | 0.9110 | 0.9493 |
| LR—SMOTETomek | 0.9027 | 0.8339 | 0.9361 | 0.9650 |
| LR—RandOverSampling | 0.8737 | 0.8055 | 0.9077 | 0.9479 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussin Adam Khatir, A.A.; Bee, M. Machine Learning Models and Data-Balancing Techniques for Credit Scoring: What Is the Best Combination? Risks 2022, 10, 169. https://doi.org/10.3390/risks10090169
Hussin Adam Khatir AA, Bee M. Machine Learning Models and Data-Balancing Techniques for Credit Scoring: What Is the Best Combination? Risks. 2022; 10(9):169. https://doi.org/10.3390/risks10090169
Chicago/Turabian StyleHussin Adam Khatir, Ahmed Almustfa, and Marco Bee. 2022. "Machine Learning Models and Data-Balancing Techniques for Credit Scoring: What Is the Best Combination?" Risks 10, no. 9: 169. https://doi.org/10.3390/risks10090169
APA StyleHussin Adam Khatir, A. A., & Bee, M. (2022). Machine Learning Models and Data-Balancing Techniques for Credit Scoring: What Is the Best Combination? Risks, 10(9), 169. https://doi.org/10.3390/risks10090169






