Bivariate Copula Trees for Gross Loss Aggregation with Positively Dependent Risks
Abstract
:1. Introduction
- Ground-up loss (total loss without any policy conditions applied)
- Retained loss (loss retained by insured party)
- Gross loss (loss to an insurer after application of policy financial terms)
2. Preliminaries
2.1. Basic Concepts
2.2. Financial Terms
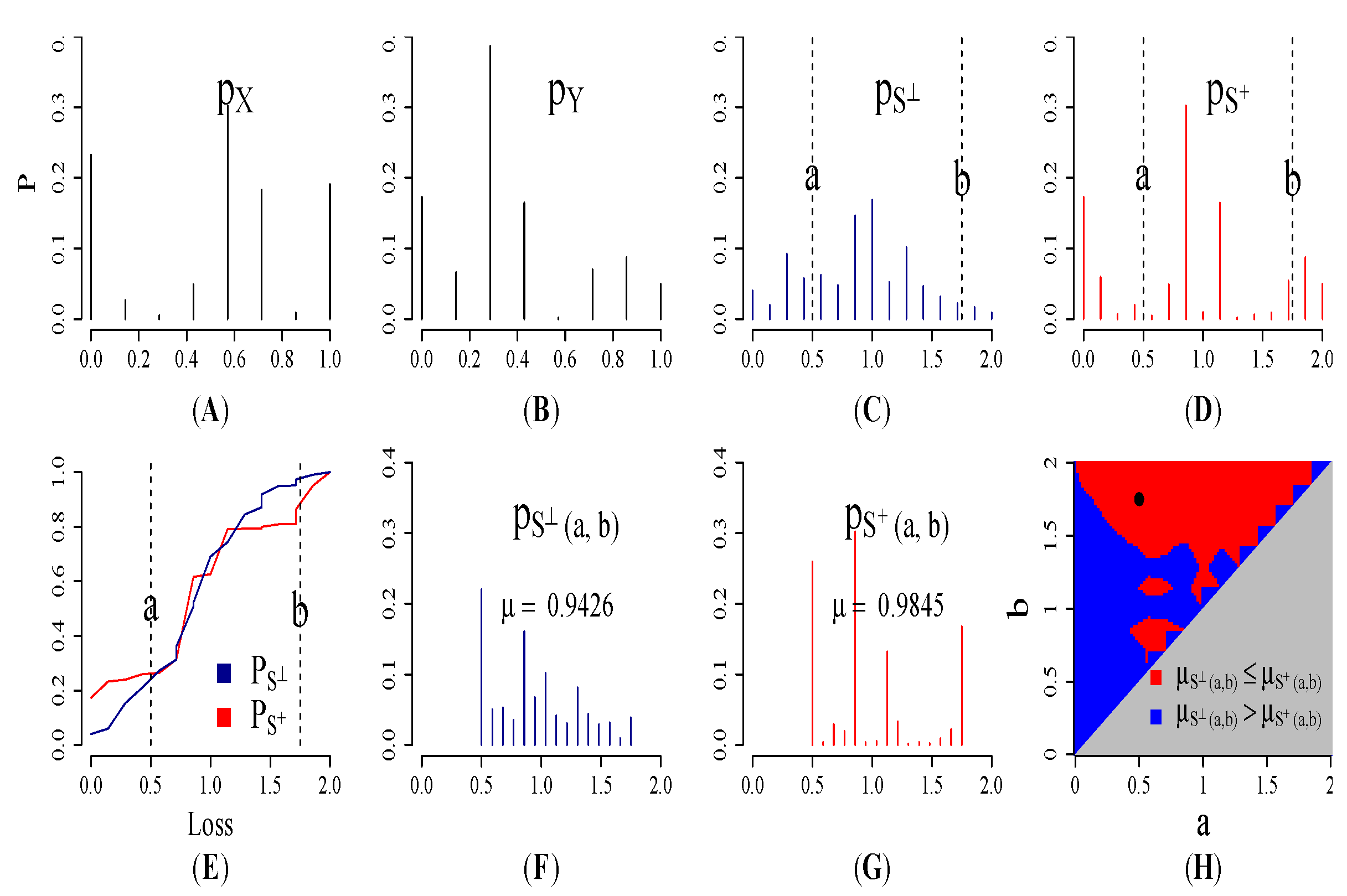
2.3. Ordering the Gross Loss Sums
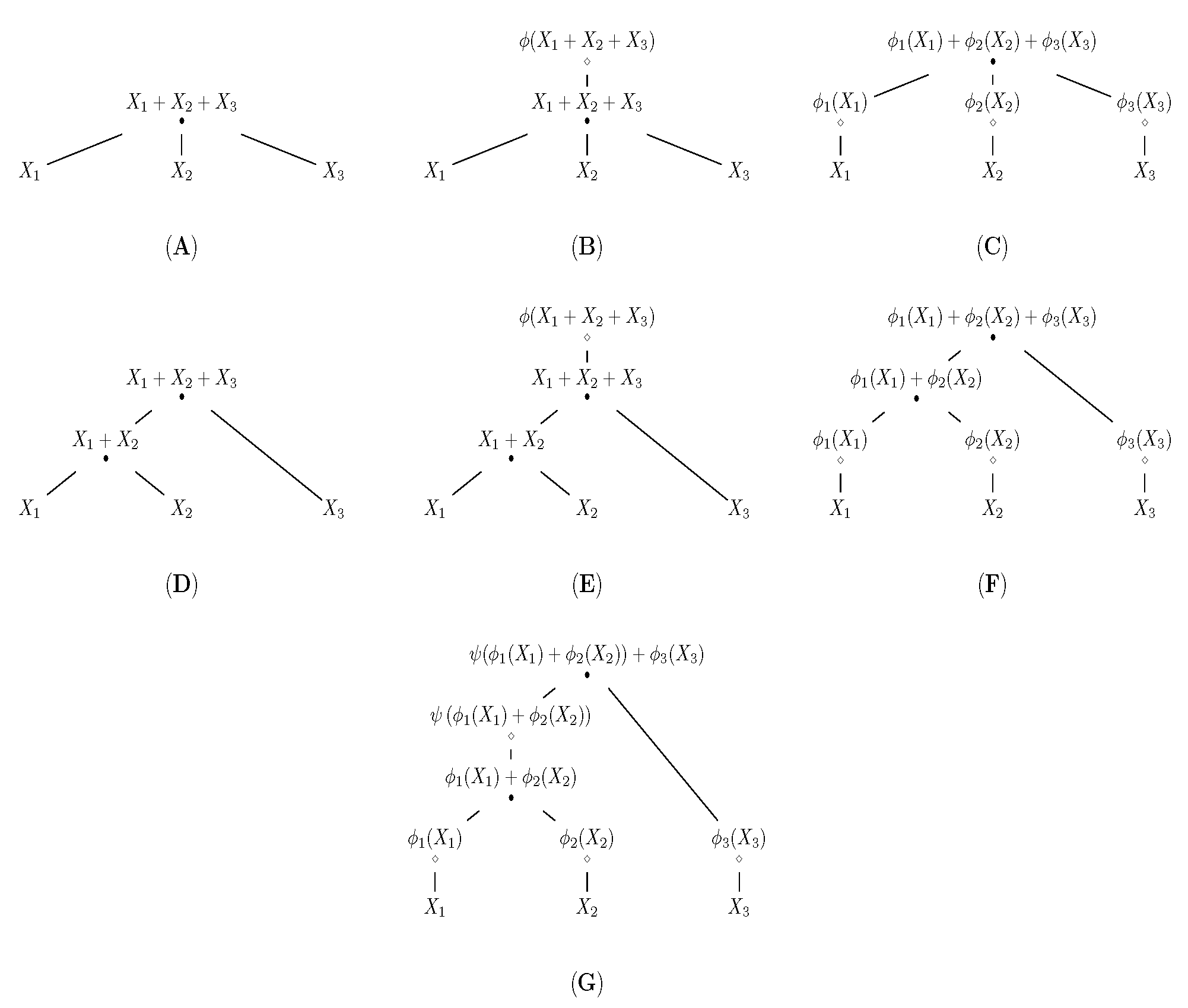
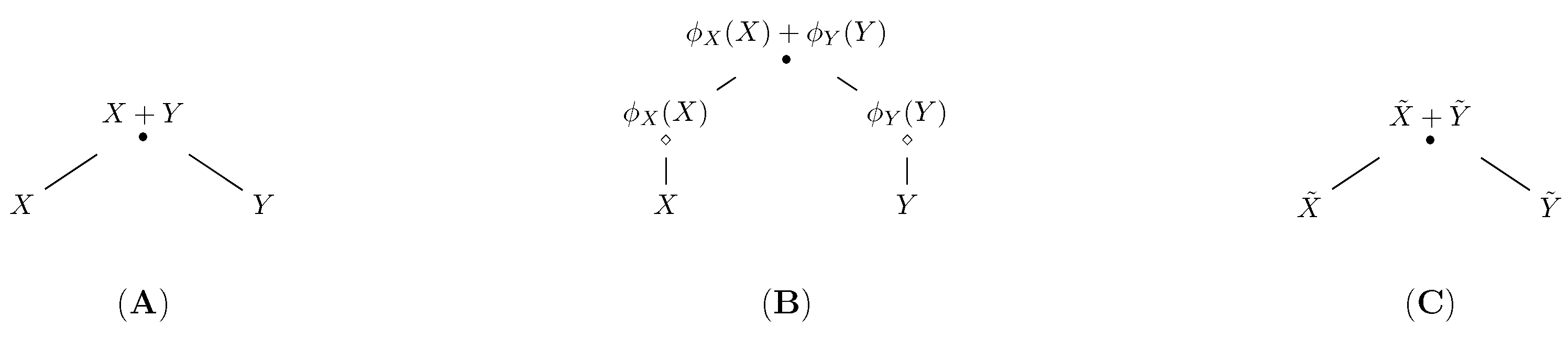
3. Partial Sums and Aggregation Trees
3.1. Copulas at Summation Nodes
| Algorithm 1 Estimate copula parameter and add two risks in ground-up pass |
| INPUT: Pmfs , with support sizes , , copula , (if available) partial derivative , initial and bounds , , correlation , maximum iteration , numeric tolerance . OUTPUT: , .
|
3.2. Covariance Scaling
3.3. A Comment on Back Allocation
4. Computational Aspects
| Algorithm 2 Add two risks in gross loss pass |
| INPUT: Pmfs , with support sizes , , parameterized copula model , decomposition flag. OUTPUT: Pmf of the gross loss sum .
|
| Algorithm 3 Add two risks in gross loss pass using Fréchet copula with covariance scaling |
| INPUT: Pmfs and , financial terms and , covariance . OUTPUT: Pmf of the sum .
|
5. Results
6. Conclusions
7. Future Research
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
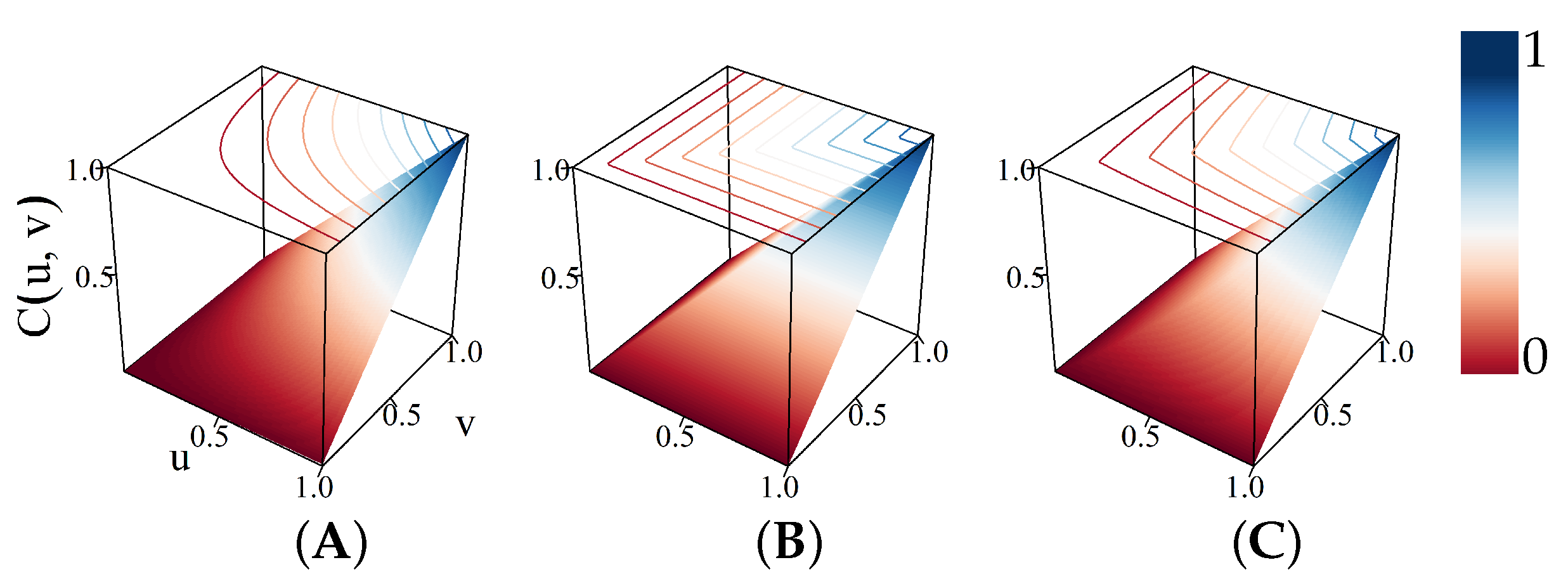
Appendix A. Bivariate Copulas and Their Partial Derivatives
Appendix A.1. Joe Copula
Appendix A.2. Gumbel Copula
Appendix A.3. Morgenstern Copula
Appendix A.4. Student’s t Copula, ν=1 (Cauchy)
Appendix B. Copula pmf on Finite Precision Machine
References
- AIR-Worldwide. 2015. AIR Hurricane Model for the United States. Available online: https://www.air-worldwide.com/publications/brochures/documents/air-hurricane-model-for-the-united-states-brochure (accessed on 18 July 2022).
- AIR-Worldwide. 2017. Earthquake Risk in the United States: A Major Model Update. Available online: https://www.air-worldwide.com/publications/air-currents/2017/Earthquake-Risk-in-the-United-States–A-Major-Model-Update/ (accessed on 18 July 2022).
- Arbenz, Philipp, Christoph Hummel, and Georg Mainik. 2012. Copula based hierarchical risk aggregation through sample reordering. Insurance: Mathematics and Economics 51: 122–33. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bouyé, Eric, Valdo Durrleman, Ashkan Nikeghbali, Gaël Riboulet, and Thierry Roncalli. 2000. Copulas for Finance—A Reading Guide and Some Applications. Available online: http://www.thierry-roncalli.com/download/copula-survey.pdf (accessed on 18 July 2022).
- Bruneton, Jean-Philippe. 2011. Copula-based Hierarchical Aggregation of Correlated Risks. The behaviour of the diversification benefit in Gaussian and Lognormal Trees. arXiv arXiv:1111.1113. Available online: https://arxiv.org/abs/1111.1113 (accessed on 18 July 2022).
- Christofides, Tasos C., and Eutichia Vaggelatou. 2004. A connection between supermodular ordering and positive/negative association. Journal of Multivariate Analysis 88: 138–51. [Google Scholar] [CrossRef] [Green Version]
- Clark, Karen. 2015. Catastrophe Risk. Ottawa: International Actuarial Association, Available online: http://www.actuaries.org/LIBRARY/Papers/RiskBookChapters/IAA_Risk_Book_Iceberg_Cover_and_ToC_5May2016.pdf (accessed on 18 July 2022).
- Colangelo, Antonio, Marco Scarsini, and Moshe Shaked. 2005. Some notions of multivariate positive dependence. Insurance: Mathematics and Economics 37: 13–26. [Google Scholar] [CrossRef]
- Cossette, Hélène, Marie-Pier Côté, Etienne Marceau, and Khouzeima Moutanabbir. 2013. Multivariate distribution defined with Farlie–Gumbel–Morgenstern copula and mixed Erlang marginals: Aggregation and capital allocation. Insurance: Mathematics and Economics 52: 560–72. [Google Scholar] [CrossRef]
- Cossette, Hélène, Thierry Duchesne, and Étienne Marceau. 2003. Modeling catastrophes and their impact on insurance portfolios. North American Actuarial Journal 7: 1–22. [Google Scholar] [CrossRef] [Green Version]
- Côté, Marie-Pier, and Christian Genest. 2015. A copula-based risk aggregation model. The Canadian Journal of Statistics 43: 60–81. [Google Scholar] [CrossRef]
- Deelstra, Griselda, Jan Dhaene, and Michele Vanmaele. 2011. An overview of comonotonicity and its applications in finance and insurance. In Advanced Mathematical Methods for Finance. Edited by Giulia Di Nunno and Bernt Øksendal. Berlin and Heidelberg: Springer. [Google Scholar]
- Denuit, Michel, Jan Dhaene, Marc Goovaerts, and Rob Kaas. 2005. Actuarial Theory for Dependent Risks: Measures, Orders and Models. Hoboken: John Wiley & Sons. [Google Scholar] [CrossRef]
- Denuit, Michel, Christian Genest, and Étienne Marceau. 2002. Criteria for the stochastic ordering of random sums, with actuarial applications. Scandinavian Actuarial Journal 2002: 3–16. [Google Scholar] [CrossRef]
- Derendinger, Fabio. 2015. Copula based hierarchical risk aggregation—Tree dependent sampling and the space of mild tree dependence. arXiv arXiv:1506.03564. Available online: https://arxiv.org/abs/1506.03564 (accessed on 18 July 2022). [CrossRef] [Green Version]
- Dhaene, Jan, Daniël Lindersa, Wim Schoutensa, and David Vyncke. 2014. A multivariate dependence measure for aggregating risks. Journal of Computational and Applied Mathematics 263: 78–87. [Google Scholar] [CrossRef] [Green Version]
- Donnelly, Thomas G. 1973. Algorithm 462: Bivariate normal distribution. Communications of the ACM 16: 638. [Google Scholar] [CrossRef]
- Dunnett, Charles W., and Milton Sobel. 1954. A bivariate generalization of Student’s t-distribution, with tables for certain special cases. Biometrika 41: 153–69. [Google Scholar] [CrossRef]
- Ehiwario, J. C., and S. O. Aghamie. 2014. Comparative study of bisection, Newton-Raphson and secant methods of root-finding problems. IOSR Journal of Engineering 4: 1–7. [Google Scholar]
- Einarsson, Baldvin, Rafał Wójcik, and Jayanta Guin. 2016. Using intraclass correlation coefficients to quantify spatial variability of catastrophe model errors. Paper presented at 22nd International Conference on Computational Statistics (COMPSTAT 2016), Oviedo, Spain, August 23–26; Available online: http://www.compstat2016.org/docs/COMPSTAT2016_proceedings.pdf (accessed on 18 July 2022).
- Geenens, Gery. 2020. Copula modeling for discrete random vectors. Dependence Modeling 8: 417–40. [Google Scholar] [CrossRef]
- Genz, Alan, Frank Bretz, Tetsuhisa Miwa, Xuefei Mi, Friedrich Leisch, Fabian Scheipl, and Torsten Hothorn. 2021. mvtnorm: Multivariate Normal and t Distributions. R package version 1.1-3. Heidelberg: Springer. [Google Scholar]
- Gneiting, Tilmann, and Adrian E. Raftery. 2007. Strictly Proper Scoring Rules, Prediction, and Estimation. Journal of the American Statistical Association 102: 359–78. [Google Scholar] [CrossRef]
- Grossi, Patricia. 2004. Sources, nature and impact of uncertainties in catastrophe modeling. Paper presented at 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, August 1–6; Available online: https://www.iitk.ac.in/nicee/wcee/article/13_1635.pdf (accessed on 18 July 2022).
- Grossi, Patricia, Howard Kunreuther, and Don Windeler. 2005. An Introduction to Catastrophe Models and Insurance. In Catastrophe Modeling: A New Approach to Managing Risk. Edited by Patricia Grossi and Howard Kunreuther. Huebner International Series on Risk, Insurance and Economic Security. Boston: Springer Science+Business Media. [Google Scholar]
- Hürlimann, Werner. 1998. Truncation transforms, stochastic orders and layer pricing. Transactions of the 26th International Congress of Actuaries 4: 135–51. [Google Scholar]
- Joe, Harry. 1997. Multivariate Models and Dependence Concepts. Monographs on Statistics and Applied Probability (Series) 73. London: Chapman and Hall. [Google Scholar]
- Joe, Harry, and Peijun Sang. 2016. Multivariate models for dependent clusters of variables with conditional independence given aggregation variables. Computational Statistics & Data Analysis 97: 114–32. [Google Scholar]
- Kaas, Rob, Jan Dhaene, and Marc J. Goovaerts. 2000. Upper and lower bounds for sums of random variables. Insurance: Mathematics and Economics 27: 151–68. [Google Scholar] [CrossRef] [Green Version]
- Karlin, Samuel, and Albert Novikoff. 1963. Generalized convex inequalities. Pacific Journal of Mathematics 13: 1251–79. [Google Scholar] [CrossRef] [Green Version]
- Kelley, Carl T. 2003. Solving Nonlinear Equations with Newton’s Method. Philadelphia: Society for Industrial and Applied Mathematics. [Google Scholar]
- Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models: From Data to Decisions, 4th. ed. Hoboken: John Wiley & Sons. [Google Scholar]
- Koch, Inge, and Ann De Schepper. 2006. The Comonotonicity Coefficient: A New Measure of Positive Dependence in a Multivariate Setting. Available online: https://ideas.repec.org/p/ant/wpaper/2006030.html (accessed on 18 July 2022).
- Koch, Inge, and Ann De Schepper. 2011. Measuring comonotonicity in m-dimensional vectors. ASTIN Bulletin 41: 191–213. [Google Scholar]
- Linders, Daniël, and Ben Stassen. 2016. The multivariate variance Gamma model: Basket option pricing and calibration. Quantitative Finance 16: 555–72. [Google Scholar] [CrossRef]
- Marri, F., and K. Moutanabbir. 2022. Risk aggregation and capital allocation using a new generalized Archimedean copula. Insurance: Mathematics and Economics 102: 75–90. [Google Scholar] [CrossRef]
- Marshall, Albert W., Ingram Olkin, and Barry C. Arnold. 1979. Inequalities: Theory of Majorization and Its Applications. New York: Academic Press. [Google Scholar]
- Mead, D. G. 1992. Newton’s identities. The American Mathematical Monthly 99: 749–51. [Google Scholar] [CrossRef]
- Mitchell-Wallace, Kirsten, Matthew Jones, John Hillier, and Matthew Foote. 2017. Natural Catastrophe Risk Management and Modelling. Hoboken: Wiley. [Google Scholar]
- Ospina, Raydonal, and Silvia L. P. Ferrari. 2010. Inflated beta distributions. Statistical Papers 51: 111–26. [Google Scholar] [CrossRef] [Green Version]
- Patton, Andrew. 2013. Chapter 16—Copula methods for forecasting multivariate time series. In Handbook of Economic Forecasting. Edited by Graham Elliott and Allan Timmerman. Amsterdam: Elsevier, vol. 2, pp. 899–960. [Google Scholar]
- Sikorski, K. 1982. Bisection is optimal. Numerische Mathematik 40: 111–17. [Google Scholar] [CrossRef]
- Sklar, Abe. 1959. Fonctions de repartition an dimensions et leurs marges. Publications de l’Institut de Statistique de l’Université de Paris 8: 229–31. [Google Scholar]
- Stoyan, Dietrich, and Daryl J. Daley. 1983. Comparison Methods for queues and Other Stochastic Models. New York: Wiley. [Google Scholar]
- Taylor, J. M. 1983. Comparisons of certain distribution functions. Statistics: A Journal of Theoretical and Applied Statistics 14: 397–408. [Google Scholar] [CrossRef]
- Venter, Gary G. 2002. Tails of copulas. Proceedings of the Casualty Actuarial Society 89: 68–113. Available online: https://www.casact.org/sites/default/files/database/proceed_proceed02_2002.pdf (accessed on 18 July 2022).
- Vernic, Raluca. 2016. On the distribution of a sum of Sarmanov distributed random variables. Journal of Theoretical Probability 29: 118–42. [Google Scholar] [CrossRef]
- Wang, Shaun. 1998. Aggregation of correlated risk portfolios: Models and algorithms. Proceedings of the Casualty Actuarial Society 83: 848–937. [Google Scholar]
- Wójcik, Rafał, Charlie Wusuo Liu, and Jayanta Guin. 2019. Direct and hierarchical models for aggregating spatially dependent catastrophe risks. Risks 7: 54. [Google Scholar] [CrossRef] [Green Version]
- Wójcik, Rafał, and Ivelin Zvezdov. 2021. Next Generation Financial Modeling for Commercial Lines. Available online: https://www.air-worldwide.com/publications/air-currents/2021/next-generation-financial-modeling-for-commercial-lines/ (accessed on 18 July 2022).
- Xiao, Qing, and Shaowu Zhou. 2019. Matching a correlation coefficient by a Gaussian copula. Communications in Statistics–Theory and Methods 48: 1728–47. [Google Scholar] [CrossRef]

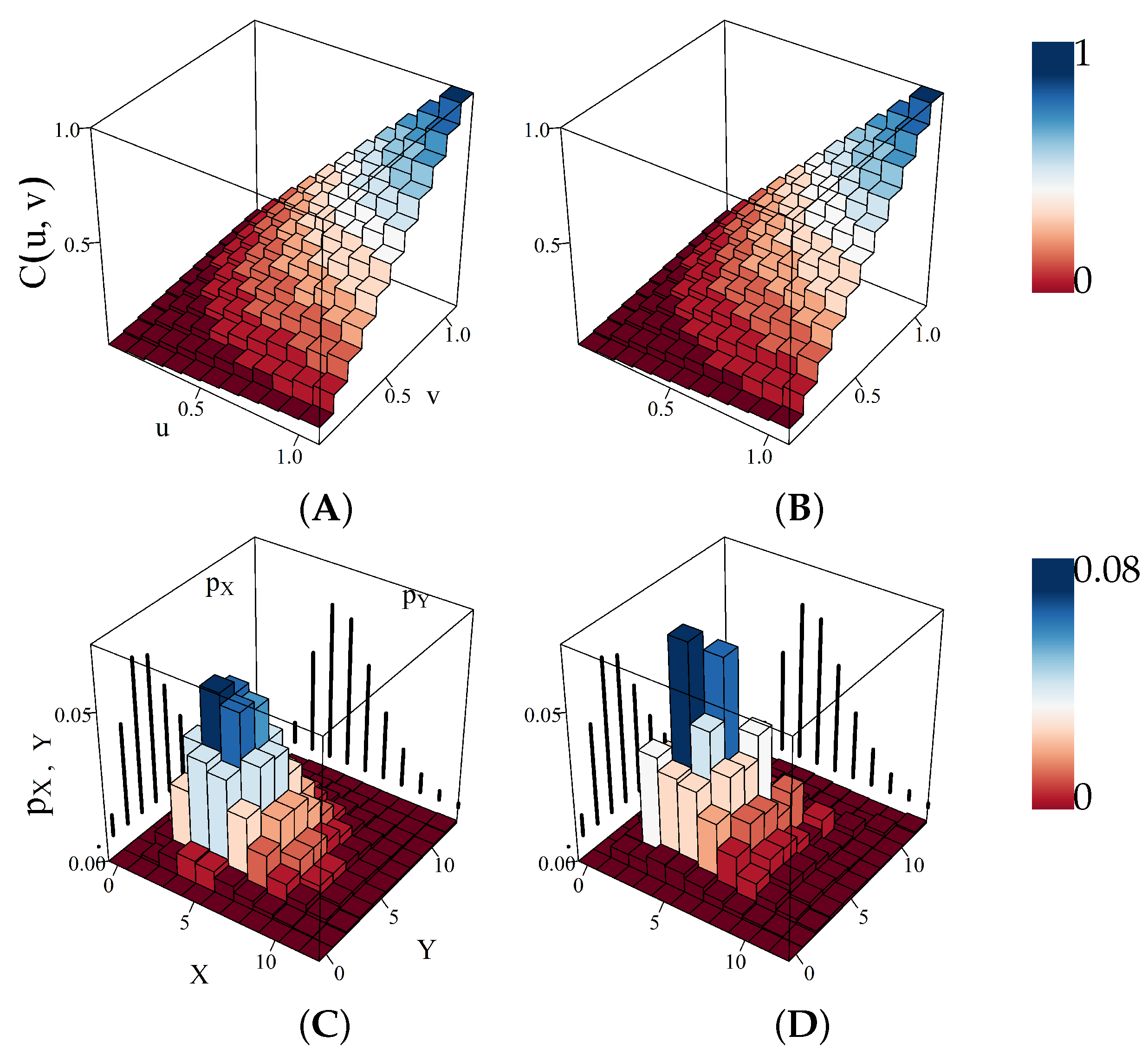



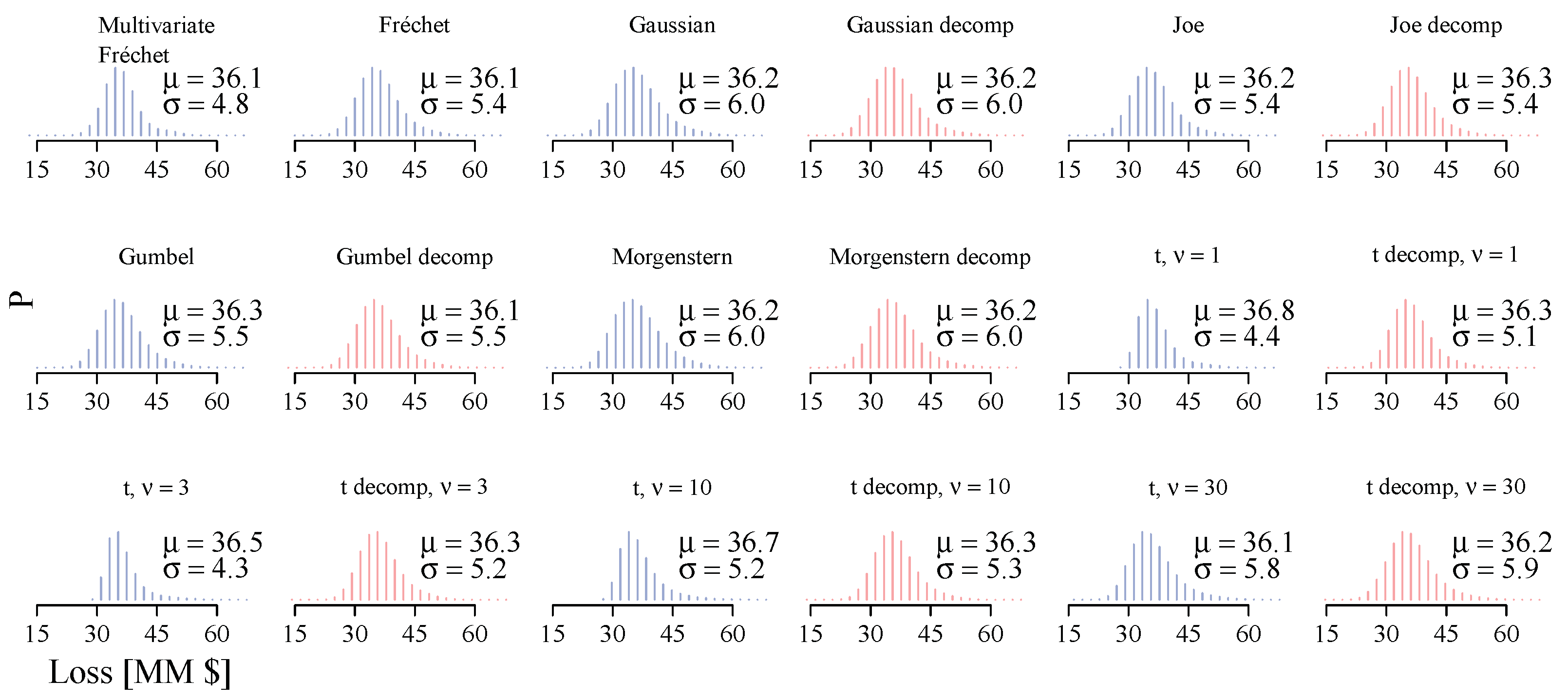
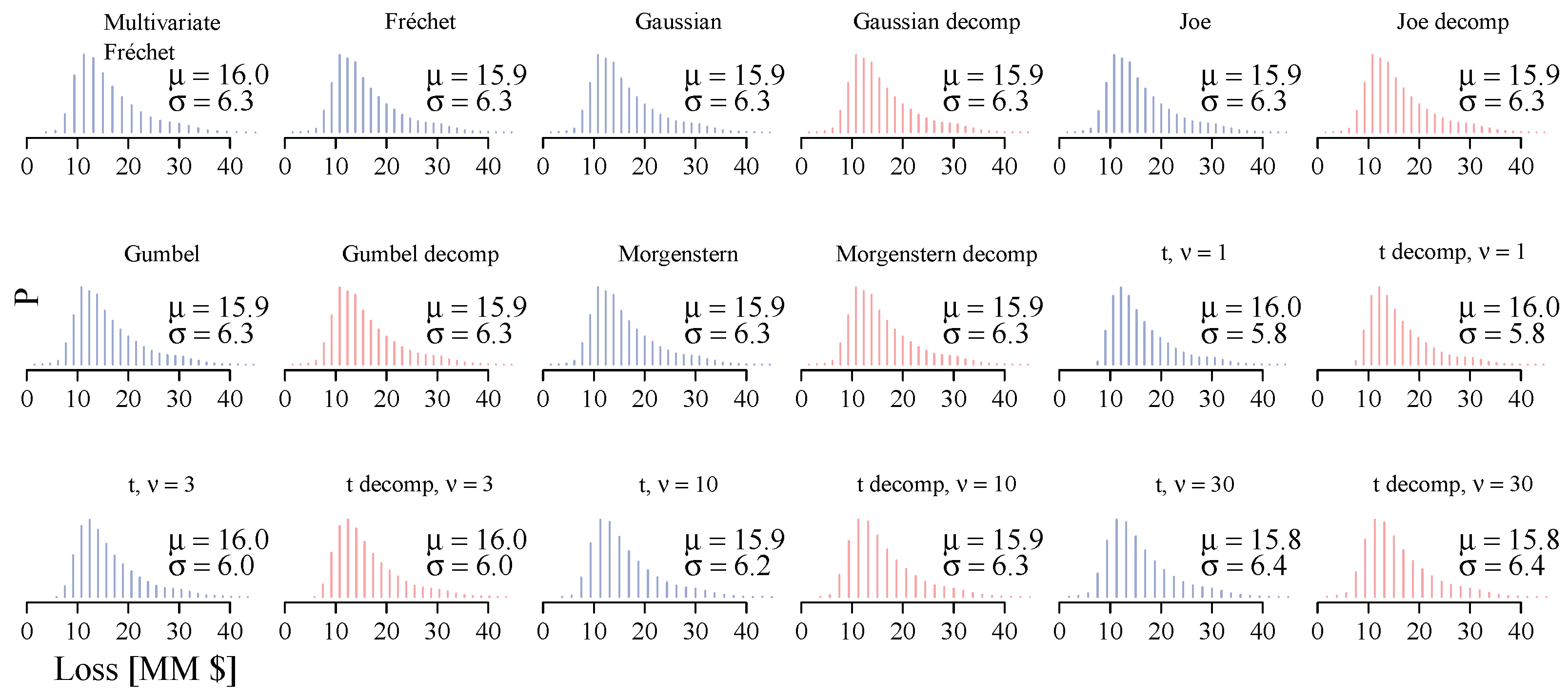
| Name | Parameter | |
|---|---|---|
| Fréchet | ||
| Gaussian * | ||
| Student’s t ** | , , | |
| Gumbel | ||
| Joe | ||
| Morgenstern |
| 5593 (1) | 6130 (1.1) | 315,567 (56.4) | 209,969 (37.5) | 670,001 (119.8) | 130,785 (23.4) |
| Statistic | Portfolio 1 (Large) | Portfolio 2 (Medium) | Portfolio 3 (Small) |
|---|---|---|---|
| Event peril | Hurricane | Hurricane | Earthquake |
| # of risks | 31,896 | 9056 | 1209 |
| # of sub-limits | 3364 | 412 | 19 |
| # of layers | 1778 | 398 | 14 |
| # of policies | 1676 | 398 | 14 |
| Total replacement value ()MM USD) | 671,191 | 25,811 | 14,350 |
| Total ground-up loss | 410 | 1198 | 427 |
| Total ground-up damage ratio | 0.06% | 4.64% | 0.41% |
| Portfolio 1 (Large) | Portfolio 2 (Medium) | Portfolio 3 (Small) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [MM $] | TVaR | TVaR | TVaR | TVaR | TVaR | TVaR | TVaR | TVaR | TVaR | ||||||
| Multivariate Fréchet | 293.2 (1.00) | 276.5 (1.00) | 1167.6 (1.00) | 730.4 (1.00) | 647.5 (1.00) | 36.1 (1.00) | 4.8 (1.00) | 53.6 (1.00) | 48.5 (1.00) | 45.8 (1.00) | 16.0 (1.00) | 6.3 (1.00) | 37.5 (1.00) | 32.7 (1.00) | 29.9 (1.00) |
| Fréchet | 291.0 (0.99) | 271.3 (0.98) | 2000.7 (1.71) | 1035.3 (1.42) | 795.4 (1.23) | 36.1 (1.00) | 5.4 (1.12) | 53.7 (1.00) | 49.2 (1.01) | 46.7 (1.02) | 15.9 (1.00) | 6.3 (1.00) | 37.5 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Gaussian | 290.1 (0.99) | 285.6 (1.03) | 1626.9 (1.39) | 1129.6 (1.55) | 931.2 (1.44) | 36.2 (1.00) | 6.0 (1.25) | 56.3 (1.05) | 51.0 (1.05) | 48.2 (1.05) | 15.9 (1.00) | 6.3 (1.00) | 37.4 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Gaussian decomp | 290.6 (0.99) | 279.9 (1.01) | 2091.4 (1.79) | 1085.4 (1.49) | 823.6 (1.27) | 36.2 (1.00) | 6.0 (1.25) | 57.4 (1.07) | 51.2 (1.06) | 48.2 (1.05) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Joe | 291.2 (0.99) | 183.6 (0.66) | 1141.2 (0.98) | 765.9 (1.05) | 651.5 (1.01) | 36.2 (1.00) | 5.4 (1.13) | 54.3 (1.01) | 49.5 (1.02) | 46.9 (1.02) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Joe decomp | 291.4 (0.99) | 183.5 (0.66) | 1155.2 (0.99) | 769.5 (1.05) | 652.7 (1.01) | 36.3 (1.00) | 5.4 (1.13) | 54.1 (1.01) | 49.4 (1.02) | 47.0 (1.03) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Gumbel | 291.3 (0.99) | 184.5 (0.67) | 1138.9 (0.98) | 767.9 (1.05) | 654.1 (1.01) | 36.3 (1.01) | 5.5 (1.15) | 55.1 (1.03) | 50.0 (1.03) | 47.4 (1.03) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Gumbel decomp | 291.4 (0.99) | 185.0 (0.67) | 1175.8 (1.01) | 773.9 (1.06) | 654.8 (1.01) | 36.1 (1.00) | 5.5 (1.15) | 54.1 (1.01) | 49.5 (1.02) | 47.0 (1.03) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Morgenstern | 293.2 (1.00) | 255.9 (0.93) | 1101.3 (0.94) | 908.7 (1.24) | 812.4 (1.25) | 36.2 (1.00) | 6.0 (1.25) | 55.4 (1.03) | 50.7 (1.04) | 48.1 (1.05) | 15.9 (1.00) | 6.3 (1.00) | 37.4 (1.00) | 32.6 (1.00) | 29.8 (1.00) |
| Morgenstern decomp | 293.2 (1.00) | 238.9 (0.86) | 1718.7 (1.47) | 971.8 (1.33) | 765.7 (1.18) | 36.2 (1.00) | 6.0 (1.25) | 57.1 (1.06) | 51.1 (1.05) | 48.3 (1.05) | 15.9 (1.00) | 6.3 (1.00) | 37.6 (1.00) | 32.7 (1.00) | 29.8 (1.00) |
| Student’s t, | 290.7 (0.99) | 150.3 (0.54) | 794.7 (0.68) | 656.9 (0.90) | 582.3 (0.90) | 36.8 (1.02) | 4.4 (0.93) | 54.2 (1.01) | 49.2 (1.01) | 46.4 (1.01) | 16.0 (1.00) | 5.8 (0.92) | 36.7 (0.98) | 32.0 (0.98) | 29.0 (0.97) |
| Student’s t decomp, | 290.7 (0.99) | 154.1 (0.56) | 788.2 (0.68) | 656.9 (0.90) | 585.1 (0.90) | 36.3 (1.01) | 5.1 (1.06) | 53.4 (1.00) | 48.9 (1.01) | 46.6 (1.02) | 16.0 (1.00) | 5.8 (0.92) | 36.7 (0.98) | 32.0 (0.98) | 29.0 (0.97) |
| Student’s t, | 290.9 (0.99) | 151.1 (0.55) | 916.9 (0.79) | 677.7 (0.93) | 592.9 (0.92) | 36.5 (1.01) | 4.3 (0.90) | 55.6 (1.04) | 49.4 (1.02) | 46.1 (1.01) | 16.0 (1.00) | 6.0 (0.95) | 37.1 (0.99) | 32.3 (0.99) | 29.4 (0.98) |
| Student’s t decomp, | 291.0 (0.99) | 154.4 (0.56) | 791.3 (0.68) | 658.1 (0.90) | 586.2 (0.91) | 36.3 (1.00) | 5.2 (1.08) | 53.4 (1.00) | 49.0 (1.01) | 46.7 (1.02) | 16.0 (1.00) | 6.0 (0.96) | 37.2 (0.99) | 32.3 (0.99) | 29.4 (0.98) |
| Student’s t, | 290.9 (0.99) | 177.8 (0.64) | 1194.1 (1.02) | 794.4 (1.09) | 663.0 (1.02) | 36.7 (1.02) | 5.2 (1.09) | 60.0 (1.12) | 51.8 (1.07) | 48.2 (1.05) | 15.9 (1.00) | 6.2 (0.99) | 37.5 (1.00) | 32.6 (1.00) | 29.7 (0.99) |
| Student’s t decomp, | 291.1 (0.99) | 181.6 (0.66) | 1124.2 (0.96) | 761.4 (1.04) | 649.1 (1.00) | 36.3 (1.00) | 5.3 (1.11) | 53.8 (1.00) | 49.2 (1.01) | 46.9 (1.02) | 15.9 (1.00) | 6.3 (1.00) | 37.5 (1.00) | 32.6 (1.00) | 29.7 (0.99) |
| Student’s t, | 290.9 (0.99) | 256.2 (0.93) | 1596.6 (1.37) | 1056.0 (1.45) | 854.9 (1.32) | 36.1 (1.00) | 5.8 (1.21) | 57.7 (1.08) | 51.3 (1.06) | 48.2 (1.05) | 15.8 (0.99) | 6.4 (1.01) | 37.9 (1.01) | 32.7 (1.00) | 29.7 (1.00) |
| Student’s t decomp, | 291.2 (0.99) | 257.1 (0.93) | 1884.1 (1.61) | 1007.5 (1.38) | 782.8 (1.21) | 36.2 (1.00) | 5.9 (1.22) | 56.6 (1.06) | 50.8 (1.05) | 48.0 (1.05) | 15.8 (0.99) | 6.4 (1.01) | 37.6 (1.00) | 32.7 (1.00) | 29.7 (1.00) |
| Name | Portfolio 1 (Large) | Portfolio 2 (Medium) | Portfolio 3 (Small) |
|---|---|---|---|
| Multivariate Fréchet | 0.43 (1.0) | 0.11 (1.0) | 0.01 (1.0) |
| Fréchet | 0.54 (1.3) | 0.15 (1.3) | 0.01 (1.1) |
| Gaussian | 22.57 (52.5) | 16.81 (152.8) | 0.28 (28.0) |
| Gaussian decomp | 22.72 (52.8) | 18.44 (167.6) | 0.29 (29.4) |
| Joe | 34.89 (81.1) | 15.12 (137.5) | 0.45 (44.5) |
| Joe decomp | 35.02 (81.4) | 15.91 (144.6) | 0.45 (44.8) |
| Gumbel | 52.66 (122.5) | 23.40 (212.7) | 0.63 (63.3) |
| Gumbel decomp | 52.91 (123.0) | 24.04 (218.6) | 0.65 (65.4) |
| Morgenstern | 1.03 (2.4) | 0.49 (4.4) | 0.02 (2.0) |
| Morgenstern decomp | 1.10 (2.6) | 0.50 (4.5) | 0.02 (2.2) |
| Student’s t, | 15.52 (36.1) | 5.28 (48.0) | 0.32 (32.1) |
| Student’s t decomp, | 15.80 (36.7) | 5.85 (53.2) | 0.35 (34.7) |
| Student’s t, | 40.25 (93.6) | 16.30 (148.2) | 1.11 (110.6) |
| Student’s t decomp, | 40.95 (95.2) | 17.26 (156.9) | 1.15 (114.6) |
| Student’s t, | 81.55 (189.7) | 34.18 (310.7) | 2.20 (220.3) |
| Student’s t decomp, | 83.40 (194.0) | 34.55 (314.1) | 2.37 (236.8) |
| Student’s t, | 104.66 (243.4) | 35.76 (325.1) | 3.04 (303.7) |
| Student’s t decomp, | 105.52 (245.4) | 35.83 (325.7) | 3.07 (307.2) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wójcik, R.; Liu, C.W. Bivariate Copula Trees for Gross Loss Aggregation with Positively Dependent Risks. Risks 2022, 10, 144. https://doi.org/10.3390/risks10080144
Wójcik R, Liu CW. Bivariate Copula Trees for Gross Loss Aggregation with Positively Dependent Risks. Risks. 2022; 10(8):144. https://doi.org/10.3390/risks10080144
Chicago/Turabian StyleWójcik, Rafał, and Charlie Wusuo Liu. 2022. "Bivariate Copula Trees for Gross Loss Aggregation with Positively Dependent Risks" Risks 10, no. 8: 144. https://doi.org/10.3390/risks10080144
APA StyleWójcik, R., & Liu, C. W. (2022). Bivariate Copula Trees for Gross Loss Aggregation with Positively Dependent Risks. Risks, 10(8), 144. https://doi.org/10.3390/risks10080144





