Extensions on the Hatzopoulos–Sagianou Multiple-Components Stochastic Mortality Model
Abstract
:1. Introduction
- We extend the stochastic mortality model HS formulated in terms of , using generalised linear models and by adopting various link functions. We illustrate through experimental results that the HS model remains robust and consistent under all modelling variations.
- We introduce a new set of link functions, with a particular focus on heavy-tailed distributions, and we evaluate their applicability in the context of mortality through the HS extensions. This approach leads to the definition of a new estimation methodology for the HS model. To the best of our knowledge, it is the first time that those link functions are evaluated in the mortality modelling domain.
- We compare the efficiency of the new model extensions versus the established mortality models in fitting and forecasting modes. For the latter case, we use an out-of-sample approach to assess the prediction ability of each model by using the Random Walk with Drift (RWD) model and optimum Arima models based on the Bayesian Information Criterion (BIC) test.
- We highlight the lessons learnt to inform the community about the adoption of the various link functions in the models’ estimation methods having witnessed the beneficial impact of this approach to our model’s efficacy.
2. Preliminaries
2.1. Data and Notation
2.2. GLM Framework
- The random component—refers to the probability distribution of the response variable (Y). The components of Y have generated from an exponential family of probability distributions.
- The systematic component—specifies the explanatory variables (X) in the model producing the so-called linear predictor .
- The link function, g—specifies the connection between the random and systematic components. Specifically, it denotes how the expected value of the response relates to the linear predictor of explanatory variables, e.g., .
- The random component: the numbers of deaths follow the Poisson distribution with mean , or the Binomial distribution with mean , so thator
- The systematic component: the effects of age x, calendar year t and cohort are captured through a predictor given by:
- The link function g associating the random component and the systematic component, so thatThere are several link functions that can be used as suggested by (Currie 2016; Haberman and Renshaw 1996) for the context of mortality models, and (McCullagh and Nelder 1989) in the wider context of GLMs. As will be explained in detail in Section 3, in this paper, we extend the HS model and we formulate it in terms of , using a wide set of canonical and non-canonical link functions.
- The set of parameter constraints: most of the stochastic mortality models have identifiability problems in the parameter estimation. In an effort to avoid this issue, a set of parameter constraints is required to ensure unique parameter estimates. Notably, in our case, the HS model does not need any parameter constraints as the model does not face identifiability problems during parameter estimation and always provides a unique solution due to its estimation methodology (Hatzopoulos and Sagianou 2020).
2.3. Hatzopoulos–Sagianou (HS) Model
3. Methodology
3.1. HS Model Using Off-the-Shelf Link Functions
- i
- logit:
- ii
- probit: where is the Normal cumulative distribution function.
- iii
- complementary log–log:)
3.2. Introducing a New Form of Link Functions in the Mortality Modelling
- The cumulative distribution as link function, maps q, , to , so that:orFor instance, some distributions that can be used are: Normal, Logistic, Extreme value, Gumbel, etc.
- The cumulative distribution as link function, maps q, , to , so the logarithmic form of the cumulative distribution is needed to map q, to , the natural scale for regression, so that:orFor instance, some distributions that can be used are: Generalised Pareto, Weibull, Fréchet, etc.
- The cumulative distribution as link function, maps q, , to , so we need the logit of the cumulative distribution so that maps q, to , the natural scale for regression, so that:orFor instance, Beta distribution can be used in this case.
3.2.1. HS Revised Estimation Methodology
4. Application
4.1. Evaluation Metrics
4.2. Evaluation Results
4.2.1. Mortality Data and the Optimum Parameters
- Greece (GR), males, calendar years 1961–2013, individual ages 0–84.
- England and Wales (E&W), males, calendar years 1841–2016, individual ages 0–89.
4.2.2. E&W Data Performance Analysis
E&W Quantitative Analysis
E&W Qualitative Analysis
4.2.3. Greek Data Performance Analysis
GR Quantitative Analysis
GR Qualitative Analysis
4.2.4. Out-of-Sample Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| APC | Age–Period–Cohort |
| BIC | Bayesian Information Criterion |
| CBD | Cairns–Blake–Dowd |
| CDF | Cumulative Distribution Function |
| cll | Complementary Log–Log |
| E&W | England and Wales |
| GLM(s) | Generalised Linear Model(s) |
| HS | Hatzopoulos–Sagianou |
| LC | Lee–Carter |
| lgt | logit |
| MAPE | Mean Absolute Percentage Error |
| MSPE | Mean Squared Percentage Error |
| npar | Number of parameters |
| PE | Percentage Error |
| PL | Plat |
| prbt | Probit |
| prt | Generalised Pareto |
| RH | Renshaw–Haberman |
| RWD | Random Walk with Drift |
| SPCA | Sparse Principal Component Analysis |
| SPCs | Sparse Principal Components |
| UVR | Unexplained Variance Ratio |
Appendix A. Definition of User-Defined Link Functions in MATLAB
- The cumulative distribution as link function g, maps q, , to , so that:
- The cumulative distribution as link function, g, maps q, , to , so the logarithmic form of the cumulative distribution is needed to map q, to , the natural scale for regression, so that:
- The cumulative distribution as link function, g, maps q, , to , so we need the logit of the cumulative distribution so that maps q, to , the natural scale for regression, so that:
link = @(mu) log(gpinv(mu, xi, theta));
derlink = @(mu) 1./(gpinv(mu,xi,theta).*gppdf(gpinv(mu,xi,theta),xi,theta));
invlink = @(eta) gpcdf(exp(eta),xi,theta);
new_F = {link, derlink, invlink};
B = glmfit(Lx,qtx,’binomial’,’link’,new_F,’weights’,etx0,’constant’,’off’)
where B contains the GLM-estimated parameters, etx0 contains the initial exposures, Lx is the matrix of the orthonormal polynomials and qtx is the probability of deaths.Appendix B. Age–Period, Age–Cohort Components and Unexplained Variance Ratio Graphical Representations for E&W Dataset

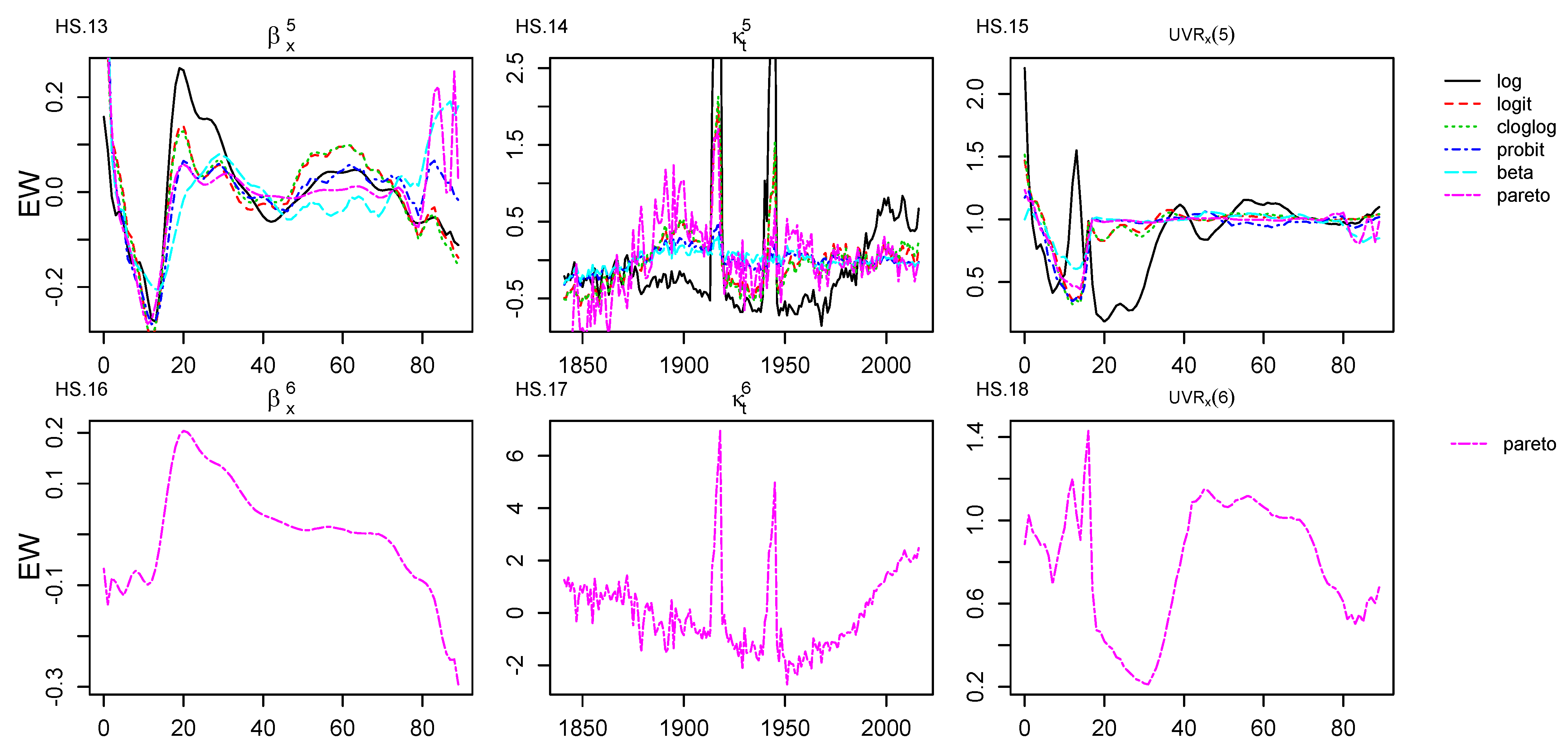
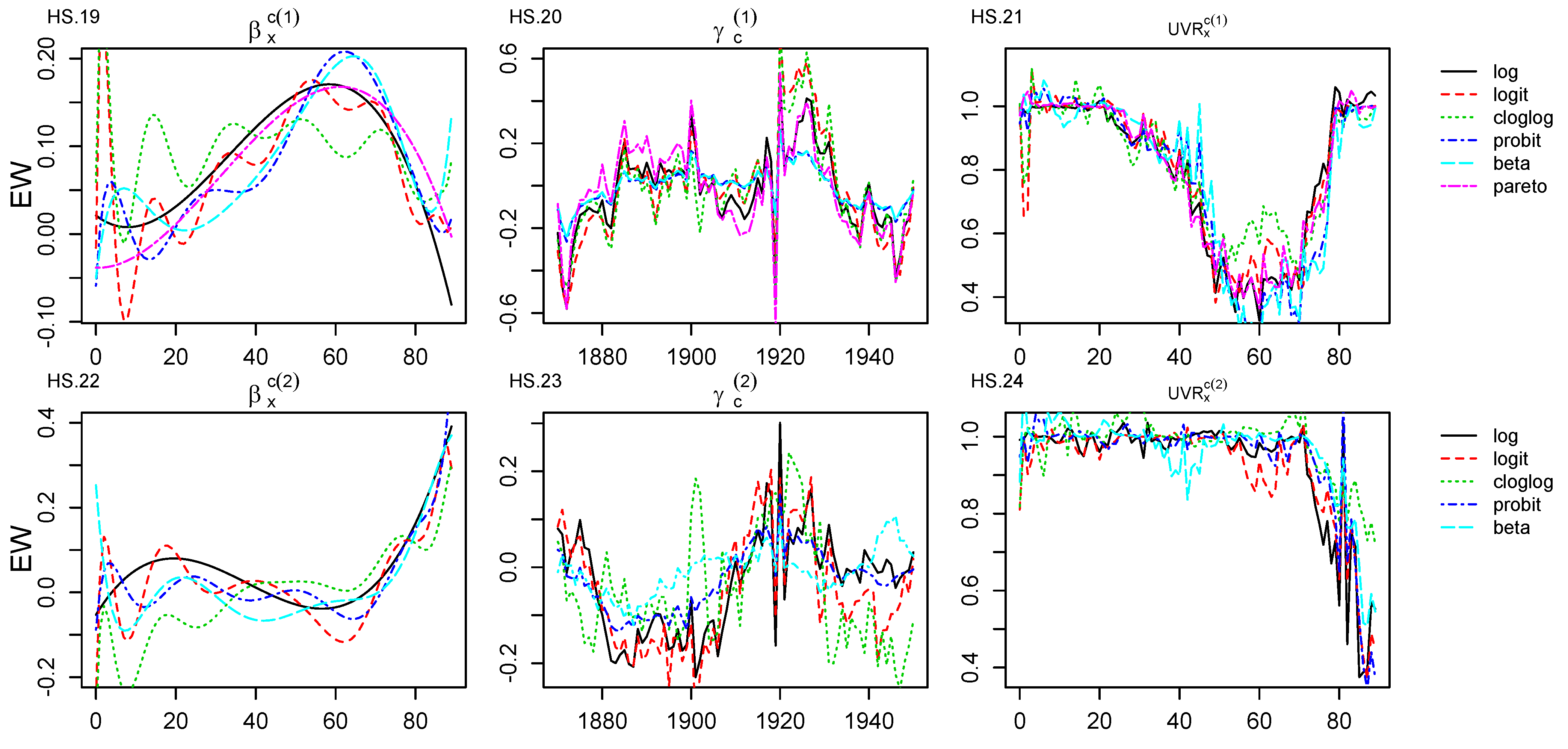
Appendix C. Age–Period, Age–Cohort Components and Unexplained Variance Ratio Graphical Representations for GR Dataset

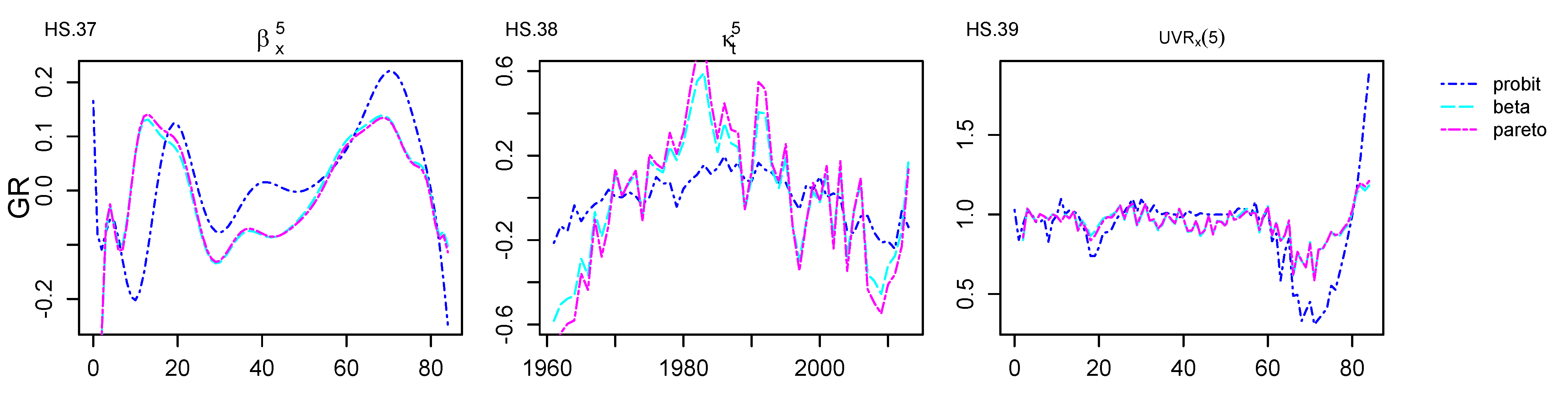
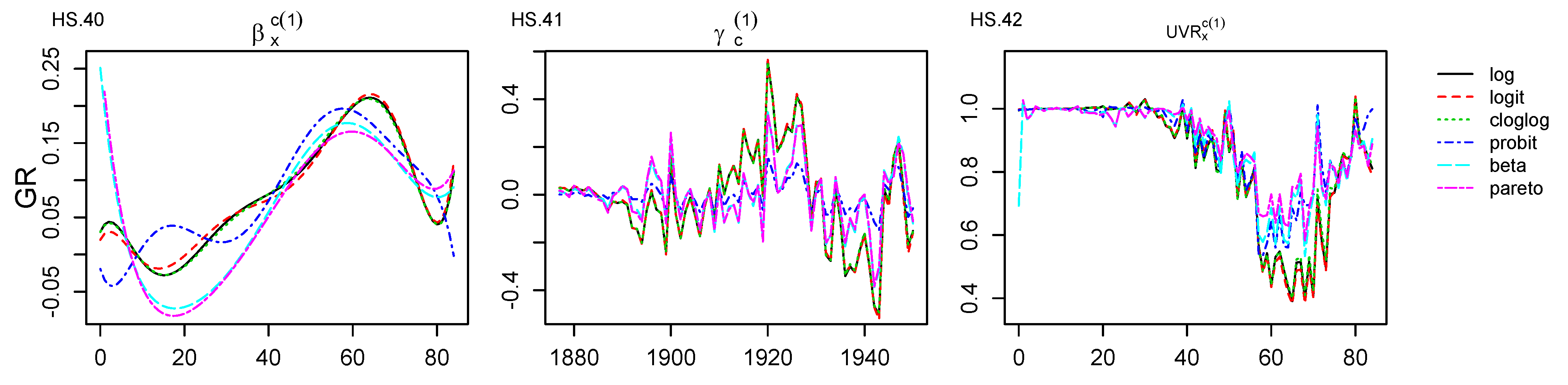
References
- Booth, Heather, and Leonie Tickle. 2008. Mortality modelling and forecasting: A review of methods. Annals of Actuarial Science 3: 3–43. [Google Scholar] [CrossRef]
- Booth, Heather, John Maindonald, and Len Smith. 2002. Applying lee-carter under conditions of variable mortality decline. Population Studies 56: 325–36. [Google Scholar] [CrossRef] [PubMed]
- Butt, Zoltan, Steven Haberman, and Han Lin Shang. 2014. ilc: Lee-Carter Mortality Models Using Iterative Fitting Algorithms. Available online: https://cran.r-project.org/src/contrib/Archive/ilc/ (accessed on 27 February 2022).
- Buxbaum, Jason D., Michael E. Chernew, A. Mark Fendrick, and David M. Cutler. 2020. Contributions of public health, pharmaceuticals, and other medical care to us life expectancy changes, 1990–2015: Study examines the conditions most responsible for changing us life expectancy and how public health, pharmaceuticals, other medical care, and other factors may have contributed to the changes. Health Affairs 39: 1546–56. [Google Scholar] [PubMed]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from england and wales and the united states. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Coughlan, Guy, David Epstein, Alen Ong, Amit Sinha, Javier Hevia-Portocarrero, Emily Gingrich, Marwa Khalaf-Allah, and Praveen Joseph. 2007. Lifemetrics: A Toolkit for Measuring and Managing Longevity and Mortality Risks. Technical Document. New York: JPMorgan Pension Advisory Group. [Google Scholar]
- Currie, Iain D. 2006. Smoothing and Forecasting Mortality Rates with P-Splines. London: Talk Given at the Institute of Actuaries. [Google Scholar]
- Currie, Iain D. 2016. On fitting generalized linear and non-linear models of mortality. Scandinavian Actuarial Journal 2016: 356–83. [Google Scholar] [CrossRef]
- Deprez, Philippe, Pavel V. Shevchenko, and Mario V. Wüthrich. 2017. Machine learning techniques for mortality modeling. European Actuarial Journal 7: 337–52. [Google Scholar] [CrossRef]
- Eurostat. n.d. Database-Your Key to European Statistics. Available online: http://ec.europa.eu/eurostat/data/database (accessed on 27 February 2020).
- Haberman, Steven, and Arthur E. Renshaw. 1996. Generalized linear models and actuarial science. Journal of the Royal Statistical Society Series D the Statistician 45: 407–36. [Google Scholar] [CrossRef]
- Hatzopoulos, Peter, and Aliki Sagianou. 2020. Introducing and evaluating a new multiple-component stochastic mortality model. North American Actuarial Journal 24: 393–445. [Google Scholar] [CrossRef]
- Hatzopoulos, Petros, and Steven Haberman. 2011. A dynamic parameterization modeling for the age-period-cohort mortality. Insurance: Mathematics and Economics 49: 155–74. [Google Scholar] [CrossRef]
- HMD-Greek-Data. n.d. Human Mortality Database-Greek Data. Available online: https://www.mortality.org/Country/Country?cntr=GRC (accessed on 27 February 2022).
- Human-Mortality-Database. n.d. University of California, Berkeley (USA) and Max Planck Institute for Demographic Research (Germany). Available online: http://www.mortality.org (accessed on 27 February 2022).
- Hunt, Andrew, and Andrés M. Villegas. 2015. Robustness and convergence in the lee–carter model with cohort effects. Insurance: Mathematics and Economics 64: 186–202. [Google Scholar] [CrossRef]
- Hunt, Andrew, and David Blake. 2021. On the Structure and Classification of Mortality Models. North American Actuarial Journal 25: S215–S234. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Md Shahid Ullah. 2007. Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis 51: 4942–56. [Google Scholar]
- Hyndman, Rob J., Heather Booth, Leonie Tickle, and John Maindonald. 2015. demography: Forecasting Mortality, Fertility, Migration and Population Data. Available online: https://cran.r-project.org/package=demography (accessed on 27 February 2022).
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the performance of the lee-carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Levantesi, Susanna, and Virginia Pizzorusso. 2019. Application of machine learning to mortality modeling and forecasting. Risks 7: 26. [Google Scholar] [CrossRef] [Green Version]
- Luss, Ronny, and Alexandre d’Aspremont. 2006. DSPCA: A toolbox for sparse principal component analysis. Mathematical Subject Classification: 90C90, 62H25, 65K05. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.140.7948&rep=rep1&type=pdf (accessed on 27 February 2022).
- MATLAB. n.d.a Beta Distribution. Available online: https://www.mathworks.com/help/stats/beta-distribution.html (accessed on 27 February 2022).
- MATLAB. n.d.b Generalized Pareto Distribution. Available online: https://www.mathworks.com/help/stats/generalized-pareto-distribution.html (accessed on 27 February 2022).
- McCullagh, Peter, and John A. Nelder. 1989. Generalized Linear Models, 2nd ed. London: Chapman and Hall. [Google Scholar]
- Millossovich, Pietro, Andrés M. Villegas, and Vladimir Kaishev Kaishev. 2018. StMoMo: An R Package for Stochastic Mortality Modelling. Journal of Statistical Software 84. [Google Scholar] [CrossRef] [Green Version]
- Osmond, Clive. 1985. Using age, period and cohort models to estimate future mortality rates. International Journal of Epidemiology 14: 124–29. [Google Scholar] [CrossRef] [PubMed]
- Plat, Richard. 2009. On stochastic mortality modeling. Insurance: Mathematics and Economics 45: 393–404. [Google Scholar]
- Renshaw, Arthur E., and Steven Haberman. 2006. A cohort-based extension to the Lee-Carter model for mortality reduction factors. Insurance: Mathematics and Economics 38: 556–70. [Google Scholar] [CrossRef]
| Dist | Link Name | Link Function | Mean Function |
|---|---|---|---|
| Binomial | Logit | ||
| Cloglog | |||
| Probit | |||
| Inverse CDF | , if | ||
| , if | |||
| , if |
| Country: E&W | Years: 1841–2016 | Ages: 0–89 (Years) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | |||||||||
| HS_log | 54.50 | 29 | 5 | 4 | 2 | - | - | - | - |
| HS_lgt | 55.19 | 30 | 5 | 14 | 2 | - | - | - | - |
| HS_cll | 6.40 | 30 | 5 | 14 | 2 | - | - | - | - |
| HS_prbt | 9.26 | 30 | 5 | 10 | 2 | - | - | - | - |
| HS_beta | 4.13 | 30 | 5 | 8 | 2 | 6.00 | 1.25 | 4.00 | 1.25 |
| HS_prt | 71.45 | 23 | 6 | 4 | 1 | 16.50 | 1.00 | 11.50 | 1.00 |
| Country: Greece | Years: 1961–2013 | Ages: 0–84 (Years) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | |||||||||
| HS_log | 2.55 | 16 | 4 | 8 | 1 | - | - | - | - |
| HS_lgt | 2.52 | 16 | 4 | 8 | 1 | - | - | - | - |
| HS_cll | 2.58 | 16 | 4 | 8 | 1 | - | - | - | - |
| HS_prbt | 0.21 | 16 | 5 | 8 | 1 | - | - | - | - |
| HS_beta | 2.18 | 20 | 5 | 8 | 1 | 1.25 | 0.50 | 1.00 | 0.25 |
| HS_prt | 3.37 | 20 | 5 | 8 | 1 | 4.00 | 1.00 | 7.00 | 1.00 |
| Model | npar | Log-Likelihood | AIC | BIC | MSPE (%) | MAPE (%) | |
|---|---|---|---|---|---|---|---|
| HS_log | 29 | 1598 | −135,970.84 | 275,137.68 | 287,394.81 | 0.329 | 3.696 |
| HS_lgt | 30 | 1634 | −125,713.76 | 254,695.52 | 267,228.78 | 0.336 | 3.694 |
| HS_cll | 30 | 1634 | −168,056.21 | 339,566.43 | 352,813.03 | 0.449 | 4.707 |
| HS_prbt | 30 | 1622 | −115,111.76 | 233,467.52 | 245,908.73 | 0.346 | 3.693 |
| HS_beta | 30 | 1343 | −129,916.62 | 262,519.24 | 272,820.45 | 0.381 | 3.945 |
| HS_prt | 23 | 1492 | −113,143.64 | 229,271.28 | 240,715.35 | 0.346 | 3.596 |
| Model | npar | Log-Likelihood | AIC | BIC | MSPE (%) | MAPE (%) |
|---|---|---|---|---|---|---|
| LC | 354 | −1,075,745.35 | 2,152,198.70 | 2,154,913.98 | 7.131 | 18.473 |
| RH | 707 | −553,002.06 | 1,107,418.13 | 1,112,841.02 | 5.369 | 14.896 |
| APC | 528 | −1,157,738.25 | 2,316,532.50 | 2,320,582.42 | 20.541 | 23.522 |
| PL | 880 | −762,205.25 | 1,526,170.51 | 1,532,920.37 | 9.136 | 15.737 |
| HS_log | 1598 | −135,970.84 | 275,137.68 | 287,394.81 | 0.329 | 3.696 |
| HS_prt | 1492 | −113,143.64 | 229,271.28 | 240,715.35 | 0.346 | 3.596 |
| Model | npar | Log-Likelihood | AIC | BIC | MSPE (%) | MAPE (%) | |
|---|---|---|---|---|---|---|---|
| HS_log | 16 | 447 | −20,176.13 | 41,246.26 | 44,112.84 | 4.109 | 10.115 |
| HS_lgt | 16 | 447 | −20,069.65 | 41,033.29 | 43,899.88 | 4.080 | 10.065 |
| HS_cll | 16 | 447 | −20,133.42 | 41,160.85 | 44,027.43 | 4.104 | 10.079 |
| HS_prbt | 16 | 516 | −19,569.21 | 40,170.43 | 43,479.50 | 4.078 | 10.074 |
| HS_beta | 20 | 540 | −19,358.74 | 39,797.48 | 43,260.47 | 3.444 | 9.515 |
| HS_prt | 20 | 540 | −19,353.29 | 39,786.59 | 43,249.58 | 3.449 | 9.498 |
| Model | npar | Log-Likelihood | AIC | BIC | MSPE (%) | MAPE (%) |
|---|---|---|---|---|---|---|
| LC | 221 | −21,213.44 | 42,868.89 | 44,286.15 | 4.287 | 11.379 |
| RH | 441 | −18,633.10 | 38,148.19 | 40,976.30 | 3.790 | 9.460 |
| APC | 272 | −21,317.67 | 43,179.33 | 44,923.65 | 5.405 | 12.715 |
| PL | 378 | −19,113.68 | 38,983.36 | 41,407.45 | 5.395 | 10.371 |
| HS_log | 447 | −20,176.13 | 41,246.26 | 44,112.84 | 4.109 | 10.115 |
| HS_prt | 540 | −19,353.29 | 39,786.59 | 43,249.58 | 3.449 | 9.498 |
| Model: HS_prt | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | Years | Ages | |||||||||
| E&W | 1841–2006 | 0–89 | 56.58 | 29 | 6 | 4 | 1 | 15 | 1.00 | 11.50 | 1.00 |
| GR | 1961–2003 | 0–84 | 1.55 | 20 | 3 | 8 | 1 | 5.50 | 1.00 | 11.50 | 1.00 |
| MSPE (%) | MAPE (%) | |||
|---|---|---|---|---|
| RWD | ARIMA | RWD | ARIMA | |
| HS_prt | 3.206 | 5.550 | 13.219 | 18.852 |
| HS_log | 3.221 | 7.135 | 13.271 | 20.800 |
| RH | 271.861 | 271.861 | 58.085 | 58.085 |
| LC | 29.508 | 29.509 | 49.838 | 49.837 |
| PL | 586.784 | 371.845 | 62.748 | 55.635 |
| APC | 86.494 | 84.316 | 46.192 | 46.131 |
| MSPE (%) | MAPE (%) | |||
|---|---|---|---|---|
| RWD | ARIMA | RWD | ARIMA | |
| HS_prt | 8.446 | 8.549 | 14.961 | 15.067 |
| HS_log | 8.691 | 10.390 | 15.332 | 15.857 |
| RH | 8.361 | 8.581 | 15.440 | 15.275 |
| LC | 10.398 | 10.333 | 20.320 | 20.964 |
| PL | 8.860 | 11.163 | 18.402 | 15.148 |
| APC | 10.054 | 10.077 | 21.364 | 21.599 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagianou, A.; Hatzopoulos, P. Extensions on the Hatzopoulos–Sagianou Multiple-Components Stochastic Mortality Model. Risks 2022, 10, 131. https://doi.org/10.3390/risks10070131
Sagianou A, Hatzopoulos P. Extensions on the Hatzopoulos–Sagianou Multiple-Components Stochastic Mortality Model. Risks. 2022; 10(7):131. https://doi.org/10.3390/risks10070131
Chicago/Turabian StyleSagianou, Aliki, and Peter Hatzopoulos. 2022. "Extensions on the Hatzopoulos–Sagianou Multiple-Components Stochastic Mortality Model" Risks 10, no. 7: 131. https://doi.org/10.3390/risks10070131
APA StyleSagianou, A., & Hatzopoulos, P. (2022). Extensions on the Hatzopoulos–Sagianou Multiple-Components Stochastic Mortality Model. Risks, 10(7), 131. https://doi.org/10.3390/risks10070131





