Unit-Linked Tontine: Utility-Based Design, Pricing and Performance †
Abstract
1. Introduction
2. Model Setting
2.1. Unit-Linked Tontine Product
2.2. Financial Market and Mortality Risk
3. Pricing
3.1. General Payment Structure
3.2. Specified Payment Structures
- (A)
- Let us first consider the case where the tontine payout process is equal to the portfolio value V explicitly given in (8), i.e.This means that the tontine payout process at time t simply complies with a money stock amounting to . To generate this amount, the insurance company can invest in the risky and the risk-free asset according to the trading strategy applied in the corresponding portfolio. By the choice given in (14), the full potential of the financial market will be passed on to the customers within a tontine framework. By (2), the total tontine payment to the policyholder at time t in this case is given by .
- (B)
- Second, inspired by participating life insurance policies with guaranteed payments (see, e.g., Briys and de Varenne 1994), we stipulatewhere denotes the guaranteed payment at time t and is the constant participation rate, and where . Thus, the tontine payout process coincides here with a predetermined payment function represented by as long as the financial market performs poorly, i.e., is low, so that holds. On the contrary, if the financial market performs well, i.e., is high, so that , an additional participation in the positive difference at the rate is included. Employing the choice given in (15) can satisfy customers, who appreciate additional guarantee components smoothing uncertain payout structures. By (2), the total tontine payment to the policyholder at time t in this case is given by .
4. Utility Optimization
4.1. General Payment Structure
4.2. Specified Payment Structures
5. Numerical Analysis
5.1. Setup
- For the choice of the value for r, we take account of the current low interest rate environments in many European countries. For example, the average risk-free rate on investments in the United Kingdom in the year 2020 equals only 1.1% (see Statista 2020a);
- For the choice of the value for , we refer to Thomas (2016); Thomas et al. (2010), who mention an estimate of the average risk aversion of British citizens that amounts to 0.85 when considering the power utility function. In Thomas et al. (2010); Waddington et al. (2013), an average risk aversion is obtained;6
- For simplicity, we equate the value for with the one of the risk-free interest rate. This is a common assumption. However, note that the cases and are also considered when letting vary in the sensitivity analyses;
- For the choice of the value for v, we are guided by Royal London (2018). In this report, it is estimated that an average British employee needs to invest £260,000 in her private pension provision to maintain the same standard of living as in her working period during the retirement phase;
- For the choices of the values for and , we follow Milevsky (2020), who presents 9.38 and 88.85 for the two Gompertz parameters for British females. For the choice of the value for , we roughly convert the corresponding applied numbers from Chen and Rach (2019) into our framework, where we take into account that the (implicit) safety loadings included in the premiums, that stem from the usage of the risk neutral probability measure during pricing can depend on the pool size n. As described in Section 3, a higher n implies that less unsystematic mortality risk is incorporated in the tontines and, consequently, lower (implicit) safety loadings can be chosen. We handle this by considering as a function of n. By linearly interpolating, we find . Using this relation guarantees that , and thereby also the (implicit) safety loadings, decreases in n. Note that the condition is fulfilled in all considered instances, such that .
- For the choice of the value for , we first notice that participation rates between 80% and 100% are commonly practiced in reality (see, e.g., Bacinello et al. 2018). Applying the mean value appears appropriate;
- We choose the value for to be equal to . Note that the cases where or are also considered when letting vary in the sensitivity analyses;
5.2. Comparison
- From the individual’s viewpoint, which of the two introduced unit-linked tontine variants is preferred? How does this preference depend on the parameter values?
- From the individual’s viewpoint, how does the introduced unit-linked tontine product perform in comparison to the traditional tontine product with no financial market component? How does this performance ordering depend on the parameter values?
5.2.1. Traditional Tontine and Comparison Approach
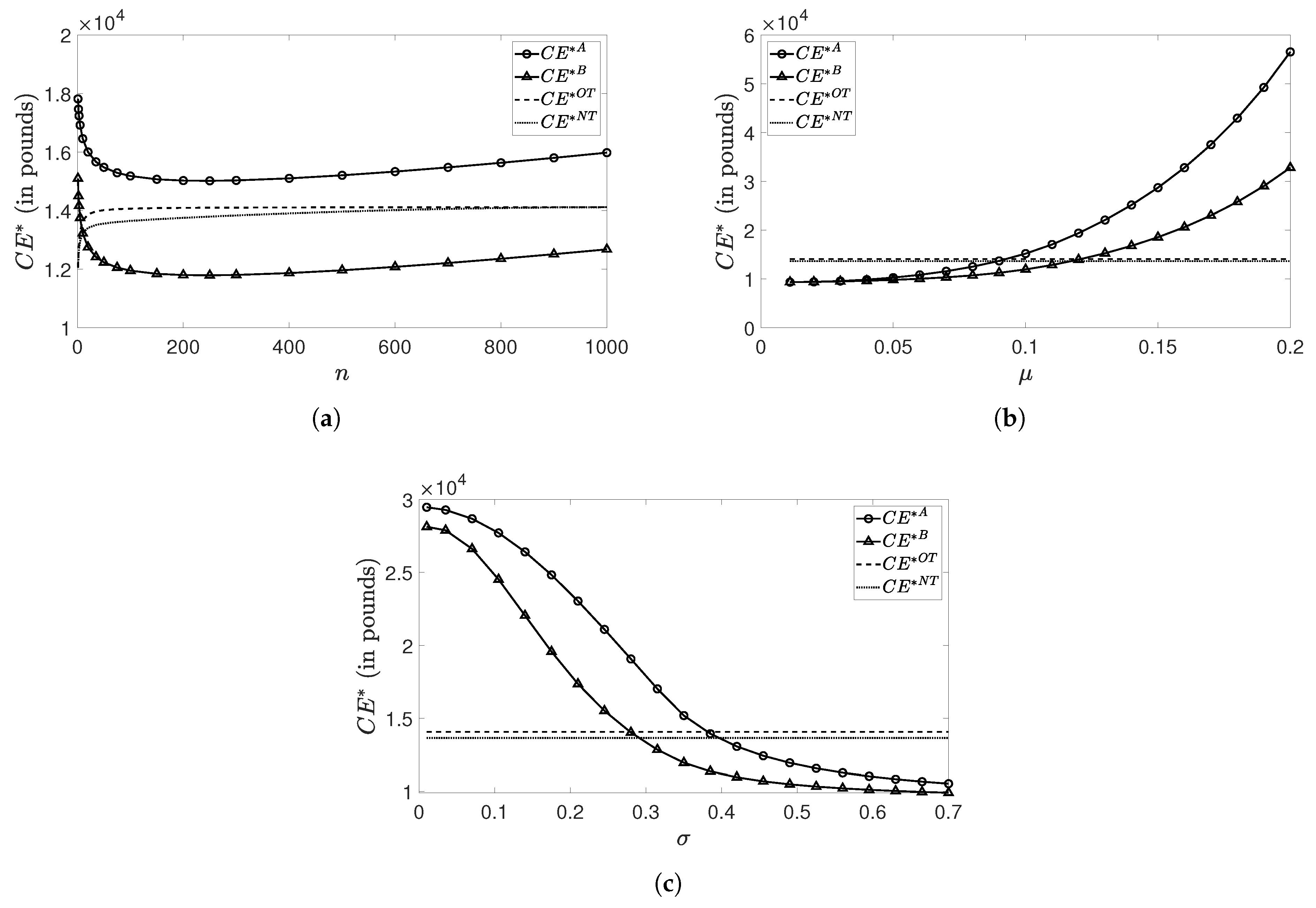
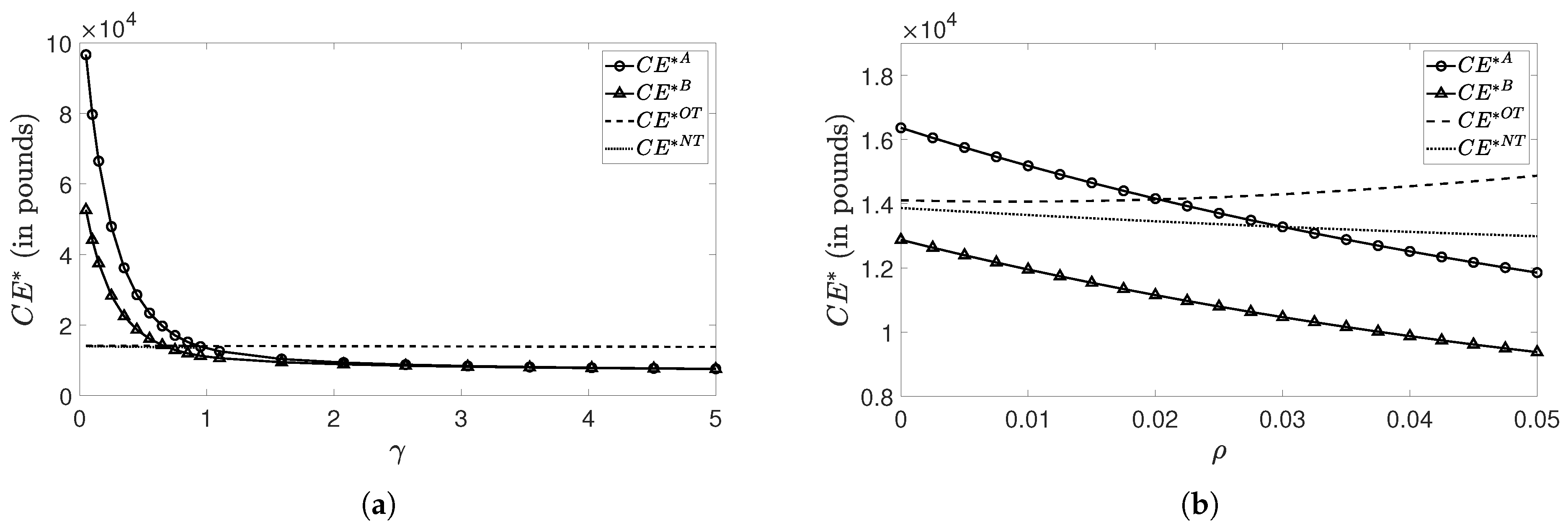
5.2.2. Numerical Results and Sensitivity Analyses
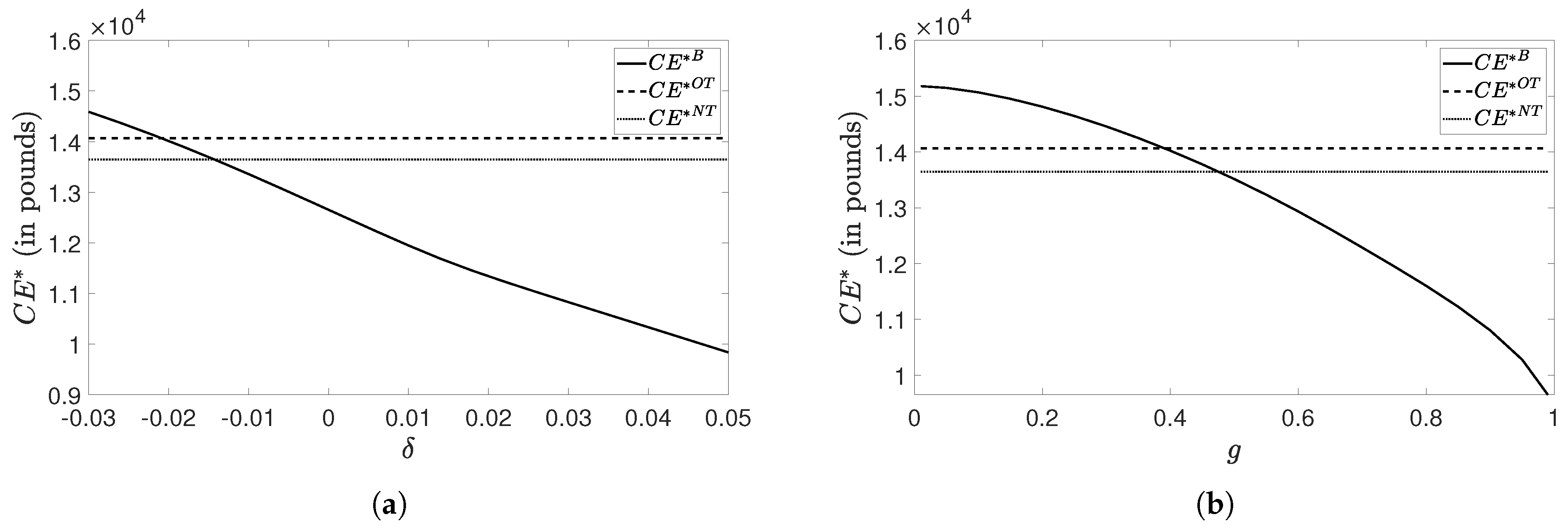
- Overall, we detect in each graph that, like in Table 3, the unit-linked product from Case A provides the policyholder with a higher certainty equivalent than the one from Case B. As such, varying parameter values does not seem to affect the performance order between the two unit-linked tontine alternatives (at least not for the parameters and their ranges under consideration). Nevertheless, the performance of the tontine from Case B more and more approaches that of the one from Case A if decreases or if or increases;
- There exist regions in which the unit-linked tontine variants make the individual better off than the traditional tontine variants. This is not very surprising for Case A, as is known. However, it reveals that our Case B can also outperform the traditional tontine in some parameter constellations. This emphasizes the potential attractiveness of this participating tontine, especially to customers who consider additional guarantee components important. We remark that participants preferring guarantees are typically loss averse, see e.g., Berkelaar et al. (2004); Kahneman and Tversky (1979). In particular, the unit-linked tontine performs well if n is either very low or high, if is high or if , or is low. On the whole, we conclude that if the traditional tontine product is consulted as a basis for comparison, it is possible that the unit-linked counterpart is more successful among the customers and, thus, it seems reasonable to promote it.
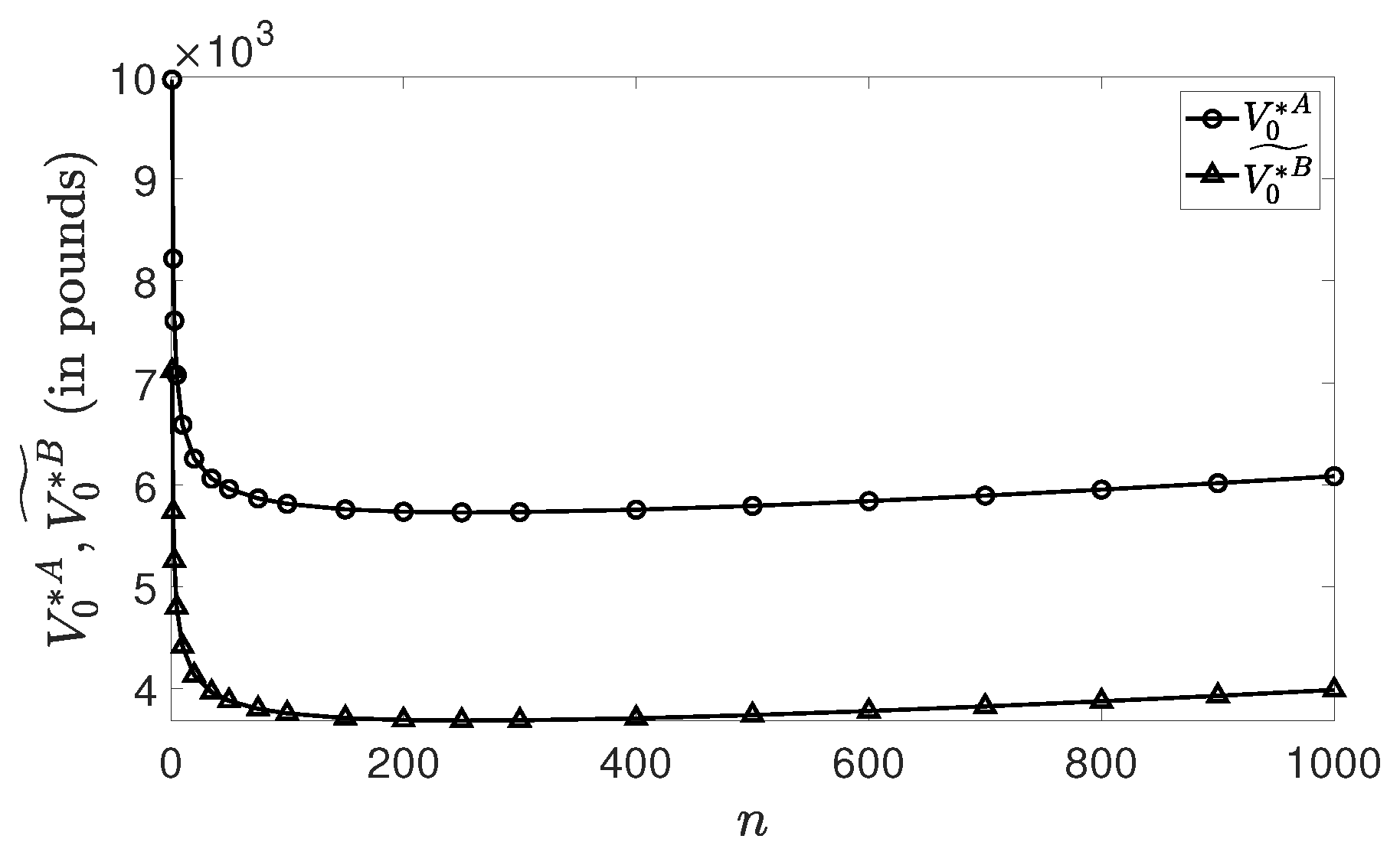
Sensitivity Analyses Regarding n
- Unit-linked products can outperform the traditional tontines (both the natural tontine and the optimal tontine), but can also be beaten by the traditional ones. With the chosen parameters, the unit-linked tontine type A outperforms, while the unit-linked tontine type B is beaten by, the traditional ones;
- For the given parameters, we observe that the unit-linked products with leads to the highest utility level. It is implied that the unit-linked annuity is most favored. However, let us point out that the result depends substantially on the choice of the parameters;
- The main message is that, depending on the design of the unit-linked tontine products including the pool size, the unit-linked tontine product can be attractive for some individuals. Among all these products, there is no dominance in terms of expected utility. The unit-linked products enriches the variety of the products.
Sensitivity Analyses Regarding and
Sensitivity Analyses Regarding and
Sensitivity Analyses Regarding and g
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Derivations
Appendix B. Proofs
Appendix B.1. Proposition 2
Appendix B.2. Proposition 3
Appendix C. Review of Optimization Problem for Traditional Tontine
Appendix D. Overview of Formulas for (Maximized) Discounted Expected Utilities
| 1 | For simplicity, we have assumed log-normal risky asset dynamics, which, as well documented, may not be very realistic. It would be interesting to look at the unit-linked tontine design problem in more general settings where the asset volatility is random when fat-tailed returns and volatility clustering are taken into account (see, e.g., Cont and Tankov 2004; Fouque et al. 2000). The continuity assumption of the stock price is relaxed in order to capture sudden and unpredictable market changes (see, e.g., Cont and Tankov 2004). Also, for such long-term investment problems, it would be more realistic to incorporate interest rate fluctuations (see, e.g., Hull and White 1990; Vasicek 1977). |
| 2 | This assumption is actually fulfilled for our specific choices of and in our numerical analysis, where they are given in (31) in Section 5.1. |
| 3 | |
| 4 | In general, it is true that an optimal value for can theoretically become arbitrarily large, which would not be feasible in reality. However, due to the budget constraint, this can be prevented and, thus, choosing as a decision variable is reasonable. For example, the optimal value for in Case A given in (22) is high only when it is justified, namely if the initial wealth spent by the individual is large or if her survival probability is low, for instance. |
| 5 | It should be pointed out that and can theoretically also serve as decision variables. A practicable option for is presented and discussed in Section 5.1. |
| 6 | We remark that a baseline or another type of utility function may lead to different conclusions. |
| 7 | The discounted expected utility for the natural traditional tontine diverges for too high values of , i.e., goes to minus infinity if . Consequently, we do not consult the natural traditional tontine if attains rather large values. |
| 8 | If the two required values and for Case B introduced in Section 4.2 cannot be uniquely determined for the numerical outcomes in this section, this is adequately reported in the related paragraphs hereinafter. |
| 9 | Due to the divergence of the discounted expected utility for the natural traditional tontine as soon as gets too large, we show, in the case, where varies, only as long as ranges within . Further note that as long as we assess the sensitivity towards a parameter in any analysis in this section, all the remaining parameters attain their baseline values, if not stated otherwise. |
| 10 | In detail, the applied total payments in Figure 3 are determined, for Case A, by , where , for Case B, by , where , and, for the optimal traditional tontine, by . Note that the computation of all depicted quantities is done numerically, where we divide the relevant time line running from to by a constant discretization step size of 0.025, which means that we overall analyze 1401 points, and simulate each occurring random variable 450,000 times. |
References
- Aase, Knut K., and Svein-Arne Persson. 1994. Pricing of Unit-Linked Life Insurance Policies. Scandinavian Actuarial Journal 1994: 26–52. [Google Scholar] [CrossRef]
- Bacinello, Anna Rita, Pietro Millossovich, and An Chen. 2018. The Impact of Longevity and Investment Risk on a Portfolio of Life Insurance Liabilities. European Actuarial Journal 8: 257–90. [Google Scholar] [CrossRef]
- Berkelaar, Arjan B., Roy Kouwenberg, and Thierry Post. 2004. Optimal Portfolio Choice under Loss Aversion. Review of Economics and Statistics 86: 973–87. [Google Scholar] [CrossRef]
- Bernhardt, Thomas, and Catherine Donnelly. 2019. Modern Tontine with Bequest: Innovation in Pooled Annuity Products. Insurance: Mathematics and Economics 86: 168–88. [Google Scholar] [CrossRef]
- Bertsekas, Dimitri P. 2014. Constrained Optimization and Lagrange Multiplier Methods. Cambridge: Academic Press. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The Pricing of Options and Corporate Liabilities. The Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Briys, Eric, and François de Varenne. 1994. Life Insurance in a Contingent Claim Framework: Pricing and Regulatory Implications. The Geneva Papers on Risk and Insurance Theory 19: 53–72. [Google Scholar] [CrossRef]
- Chen, An, and Manuel Rach. 2019. Options on Tontines: An Innovative Way of Combining Tontines and Annuities. Insurance: Mathematics and Economics 89: 182–92. [Google Scholar]
- Chen, An, Peter Hieber, and Jakob Klein. 2019. Tonuity: A Novel Individual-Oriented Retirement Plan. ASTIN Bulletin 49: 5–30. [Google Scholar] [CrossRef]
- Chen, An, Peter Hieber, and Manuel Rach. 2021. Optimal Retirement Products under Subjective Mortality Beliefs. Insurance: Mathematics and Economics 101: 55–69. [Google Scholar] [CrossRef]
- Chen, An, Linyi Qian, and Zhixin Yang. 2020. Tontines with Mixed Cohorts. Scandinavian Actuarial Journal 2021: 437–55. [Google Scholar] [CrossRef]
- Chen, An, Manuel Rach, and Thorsten Sehner. 2020. On the Optimal Combination of Annuities and Tontines. ASTIN Bulletin 50: 95–129. [Google Scholar] [CrossRef]
- Cont, Rama, and Peter Tankov. 2004. Financial Modelling with Jump Processes. CRC Mathematics Series; Chapel Hill: Chapman & Hall. [Google Scholar]
- Dahl, Mikkel, Martin Melchior, and Thomas Møller. 2008. On Systematic Mortality Risk and Risk-Minimization with Survivor Swaps. Scandinavian Actuarial Journal 2008: 114–46. [Google Scholar] [CrossRef]
- Denuit, Michel. 2019. Size-Biased Transform and Conditional Mean Risk Sharing, with Application to P2P Insurance and Tontines. ASTIN Bulletin 49: 591–617. [Google Scholar] [CrossRef]
- Dhaene, Jan, Alexander Kukush, Elisa Luciano, Wim Schoutens, and Ben Stassen. 2013. On the (In-)Dependence between Financial and Actuarial Risks. Insurance: Mathematics and Economics 52: 522–31. [Google Scholar] [CrossRef]
- Donnelly, Catherine, Montserrat Guillén, and Jens Perch Nielsen. 2014. Bringing Cost Transparency to the Life Annuity Market. Insurance: Mathematics and Economics 56: 14–27. [Google Scholar] [CrossRef]
- Ekern, Steinar, and Svein-Arne Persson. 1996. Exotic Unit-Linked Life Insurance Contracts. The Geneva Papers on Risk and Insurance Theory 21: 35–63. [Google Scholar] [CrossRef]
- Forman, Jonathan Barry, and Michael J. Sabin. 2015. Tontine Pensions. University of Pennsylvania Law Review 163: 755–831. [Google Scholar]
- Fouque, Jean-Pierre, George Papanicolaou, and K. Ronnie Sircar. 2000. Derivatives in Financial Markets with Stochastic Volatility. Cambridge: Cambridge School Press. [Google Scholar]
- Gatzert, Nadine, Carin Huber, and Hato Schmeiser. 2011. On the Valuation of Investment Guarantees in Unit-Linked Life Insurance: A Customer Perspective. The Geneva Papers on Risk and Insurance—Issues and Practice 36: 3–29. [Google Scholar] [CrossRef]
- Gemmo, Irina, Ralph Rogalla, and Jan-Hendrik Weinert. 2020. Optimal Portfolio Choice with Tontines under Systematic Longevity Risk. Annals of Actuarial Science 14: 302–15. [Google Scholar] [CrossRef]
- Giulietti, Corrado, Mirco Tonin, and Michael Vlassopoulos. 2020. When the Market Drives You Crazy: Stock Market Returns and Fatal Car Accidents. Journal of Health Economics 70: 102245. [Google Scholar] [CrossRef]
- Gothaer. 2021. Fondsgebundene Rentenversicherung mit Garantien. Gothaer Lebensversicherung AG. Available online: https://www.gothaer.de/privatkunden/rentenversicherung/fondsgebundene-rentenversicherung/ (accessed on 15 February 2021).
- Hu, Wei-Yin, and Jason S. Scott. 2007. Behavioral Obstacles in the Annuity Market. Financial Analysts Journal 63: 71–82. [Google Scholar] [CrossRef]
- Hull, John, and Alan White. 1990. Pricing Interest-Rate-Derivative Securities. The Review of Financial Studies 3: 573–92. [Google Scholar] [CrossRef]
- Kahneman, Daniel, and Amos Tversky. 1979. Prospect Theory: An Analysis of Decision Under Risk. Econometrica: Journal of the Econometric Society 47: 263–92. [Google Scholar] [CrossRef]
- Ledlie, M. Collin, Dermot P. Corry, Gary S. Finkelstein, A. J. Ritchie, K. Su, and D. C. E. Wilson. 2008. Variable Annuities. British Actuarial Journal 14: 327–89. [Google Scholar] [CrossRef]
- Leland, Hayne E. 1985. Option Pricing and Replication with Transactions Costs. The Journal of Finance 40: 1283–301. [Google Scholar] [CrossRef]
- Levy, Haim. 1994. Absolute and Relative Risk Aversion: An Experimental Study. Journal of Risk and Uncertainty 8: 289–307. [Google Scholar] [CrossRef]
- Lin, Yijia, and Samuel H. Cox. 2005. Securitization of Mortality Risks in Life Annuities. Journal of Risk and Insurance 72: 227–52. [Google Scholar] [CrossRef]
- Margaras, Vasilis. 2019. Demographic Trends in EU Regions. Available online: https://ec.europa.eu/futurium/en/system/files/ged/eprs-briefing-633160-demographic-trends-eu-regions-final.pdf (accessed on 15 December 2021).
- Merton, Robert C. 1969. Lifetime Portfolio Selection under Uncertainty: The Continuous-Time Case. The Review of Economics and Statistics 51: 247–57. [Google Scholar] [CrossRef]
- Milevsky, Moshe A. 2015. King William’s Tontine: Why the Retirement Annuity of the Future Should Resemble its Past. Cambridge: Cambridge University Press. [Google Scholar]
- Milevsky, Moshe A. 2020. Calibrating Gompertz in Reverse: What is Your Longevity-Risk-Adjusted Global Age? Insurance: Mathematics and Economics 92: 147–61. [Google Scholar] [CrossRef]
- Milevsky, Moshe A., and Thomas S. Salisbury. 2015. Optimal Retirement Income Tontines. Insurance: Mathematics and Economics 64: 91–105. [Google Scholar] [CrossRef]
- Milevsky, Moshe A., and Thomas S. Salisbury. 2016. Equitable Retirement Income Tontines: Mixing Cohorts without Discriminating. ASTIN Bulletin 46: 571–604. [Google Scholar] [CrossRef]
- Milevsky, Moshe A., Thomas S. Salisbury, Gabriela Gonzalez, and Hanna Jankowski. 2018. Annuities Versus Tontines in the 21st Century: A Canadian Case Study. Available online: https://www.soa.org/globalassets/assets/files/resources/research-report/2018/annuities-vs-tontines.pdf (accessed on 15 December 2021).
- Mitchell, Olivia S. 2002. Developments in Decumulation: The Role of Annuity Products in Financing Retirement. In Ageing, Financial Markets and Monetary Policy. Edited by Alan J. Auerbach and Heinz Herrmann. Berlin: Springer, chp. 3. pp. 97–125. [Google Scholar]
- Møller, Thomas. 1998. Risk-Minimizing Hedging Strategies for Unit-Linked Life Insurance Contracts. ASTIN Bulletin 28: 17–47. [Google Scholar] [CrossRef]
- Peijnenburg, Kim, Theo Nijman, and Bas J. M. Werker. 2016. The Annuity Puzzle Remains a Puzzle. Journal of Economic Dynamics and Control 70: 18–35. [Google Scholar] [CrossRef][Green Version]
- Ramsay, Colin M., and Victor I. Oguledo. 2018. The Annuity Puzzle and an Outline of Its Solution. North American Actuarial Journal 22: 623–45. [Google Scholar] [CrossRef]
- Royal London. 2018. Will we Ever Summit the Pension Mountain? Royal London Policy Paper No. 21. London: Royal London Mutual Insurance Society Limited. [Google Scholar]
- Sabin, Michael J. 2010. Fair Tontine Annuity. Social Science Research Network. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1579932 (accessed on 26 February 2021).
- Schiereck, Dirk, Jochen Ruß, Rolf Tilmes, and Torsten Haupt, eds. 2020. Ruhestandsplanung—Beratungsansatz für die Zielgruppe 50plus. Wiesbaden: Springer. [Google Scholar]
- Schrager, David F., and Antoon A. J. Pelsser. 2004. Pricing Rate of Return Guarantees in Regular Premium Unit Linked Insurance. Insurance: Mathematics and Economics 35: 369–98. [Google Scholar] [CrossRef]
- Schwandt, Hannes. 2018. Wealth Shocks and Health Outcomes: Evidence from Stock Market fluctuations. American Economic Journal: Applied Economics 10: 349–77. [Google Scholar] [CrossRef]
- Sehner, Thorsten. 2021. Life and Long-Term Care Insurance: Valuation and Product Design. Ph.D. dissertation, October 2021. Ulm University of Applied Sciences, Ulm, Germany. [Google Scholar] [CrossRef]
- Sharpe, William Forsyth. 2017. Retirement Income Analysis with Scenario Matrices. Leland Stanford Junior University. Available online: https://web.stanford.edu/~wfsharpe/RISMAT/RIAbook.pdf (accessed on 3 March 2021).
- Smith, Elliot. 2020. Short-Selling Bans Sweep Europe in the Hope of Stemming Stock Market Bleeding. CNBC. Available online: https://www.cnbc.com/2020/03/17/short-selling-bans-sweep-europe-in-hope-of-stemming-stock-market-bleeding.html (accessed on 13 October 2021).
- Statista. 2020a. Average Risk Free Investment Rate in the United Kingdom (UK) 2015–2020. Statista GmbH. Available online: https://www.statista.com/statistics/885750/average-risk-free-rate-united-kingdom/ (accessed on 16 December 2020).
- Statista. 2020b. Distribution of Direct Life Insurance and Reinsurance Gross Written Premiums in the United Kingdom (UK) in 2019, by Lines of Business. Statista GmbH. Available online: https://www.statista.com/statistics/1126649/direct-and-reinsurance-life-premiums-distribution-united-kingdom-uk/ (accessed on 25 February 2021).
- Thomas, Philip J. 2016. Measuring Risk-Aversion: The Challenge. Measurement 79: 285–301. [Google Scholar] [CrossRef]
- Thomas, Philip J., Roger D. Jones, and William J. O. Boyle. 2010. The Limits to Risk Aversion: Part 1. The Point of Indiscriminate Decision. Process Safety and Environmental Protection 88: 381–95. [Google Scholar] [CrossRef]
- Vasicek, Oldrich. 1977. An Equilibrium Characterization of the Term Structure. Journal of Financial Economics 5: 177–88. [Google Scholar] [CrossRef]
- Waddington, Ian, William J. O. Boyle, and James Kearns. 2013. Computing the Limits of Risk Aversion. Process Safety and Environmental Protection 91: 92–100. [Google Scholar] [CrossRef]
- Wakker, Peter P. 2008. Explaining the Characteristics of the Power (CRRA) Utility Family. Health Economics 17: 1329–44. [Google Scholar] [CrossRef] [PubMed]
- Weinert, Jan-Hendrik, and Helmut Gründl. 2020. The Modern Tontine. European Actuarial Journal 11: 49–86. [Google Scholar] [CrossRef]
- Winter, Pascal, and Frédéric Planchet. 2021. Modern Tontines as a Pension Solution: A Practical Overview. Available online: https://www.researchgate.net/publication/355260987_Modern_tontines_as_a_pension_solution_a_practical_overview (accessed on 15 December 2021).
- Yaari, Menahem E. 1965. Uncertain Lifetime, Life Insurance, and the Theory of the Consumer. The Review of Economic Studies 32: 137–50. [Google Scholar] [CrossRef]

| Symbol | Description | Value | Range |
|---|---|---|---|
| n | Initial number of participants | 100 | |
| x | Initial age of the participants | 65 | − |
| Drift rate of the risky asset | 0.1 | ||
| Volatility of the risky asset | 0.35 | ||
| r | Risk-free interest rate | 0.01 | − |
| Measure of the policyholder’s risk aversion | 0.85 | ||
| Subjective discount rate | 0.01 | ||
| v | Available initial wealth | £260,000 | − |
| First Gompertz parameter | 9.38 | − | |
| Second Gompertz parameter under | 88.85 | − | |
| Second Gompertz parameter under | 94.46 | − | |
| Mean parameter of the truncated normal distribution | − | ||
| Variance parameter of the truncated normal distribution | − |
| Symbol | Description | Value | Range |
|---|---|---|---|
| Participation rate | 0.9 | − | |
| Guarantee growth rate | 0.01 | ||
| g | Guaranteed premium fraction | 0.75 |
| £15,180.83 | |
| £11,948.69 | |
| £14,066.46 | |
| £13,647.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, A.; Nguyen, T.; Sehner, T. Unit-Linked Tontine: Utility-Based Design, Pricing and Performance. Risks 2022, 10, 78. https://doi.org/10.3390/risks10040078
Chen A, Nguyen T, Sehner T. Unit-Linked Tontine: Utility-Based Design, Pricing and Performance. Risks. 2022; 10(4):78. https://doi.org/10.3390/risks10040078
Chicago/Turabian StyleChen, An, Thai Nguyen, and Thorsten Sehner. 2022. "Unit-Linked Tontine: Utility-Based Design, Pricing and Performance" Risks 10, no. 4: 78. https://doi.org/10.3390/risks10040078
APA StyleChen, A., Nguyen, T., & Sehner, T. (2022). Unit-Linked Tontine: Utility-Based Design, Pricing and Performance. Risks, 10(4), 78. https://doi.org/10.3390/risks10040078








