An Overview on the Landscape of R Packages for Open Source Scorecard Modelling
Abstract
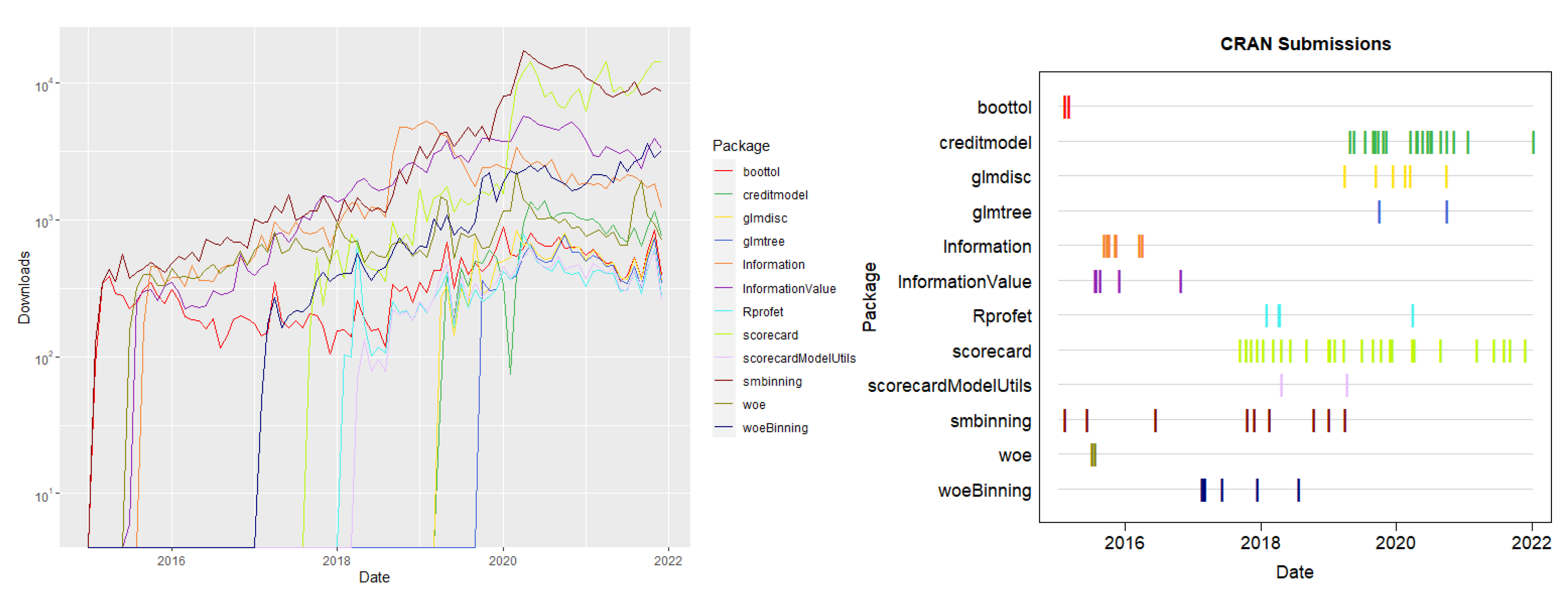
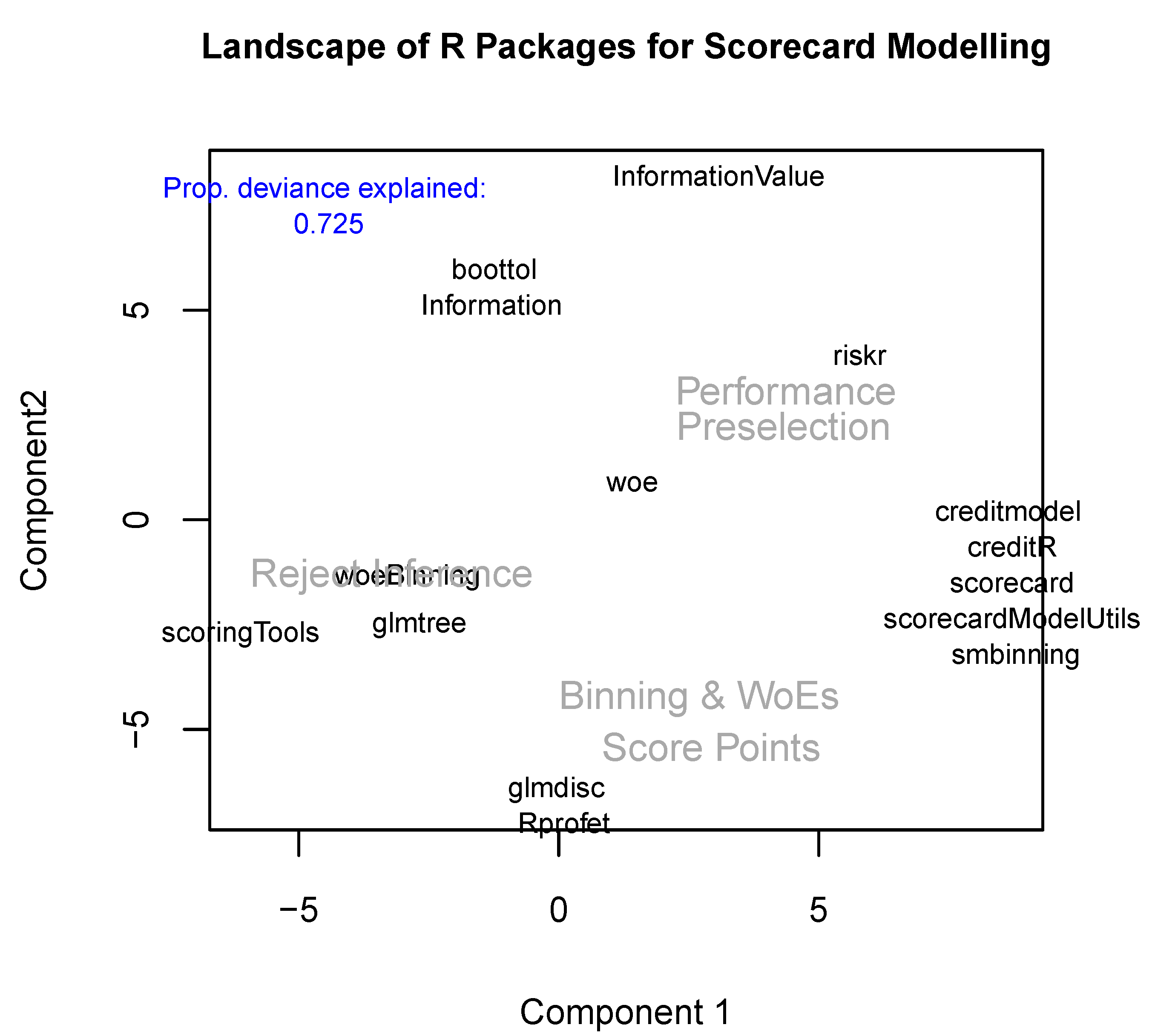
1. Introduction
2. Data

3. Binning and Weights of Evidence
3.1. Overview
3.2. Requirements
3.3. Available Methodology for Automatic Binning
3.4. Manipulation of the Bins


3.5. Applying Bins to New Data

3.6. Binning of Categorical Variables
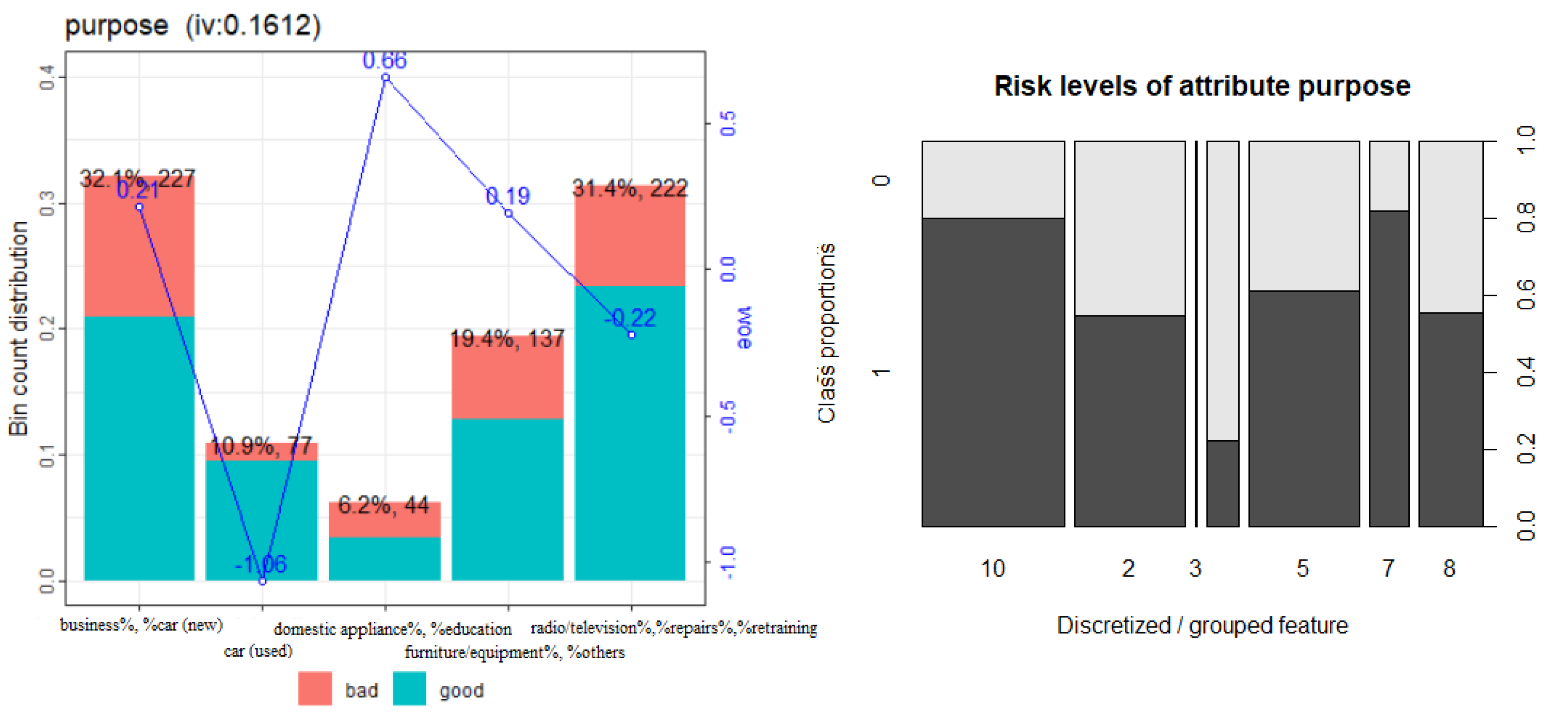
3.7. Weights of Evidence

3.8. Short Benchmark Experiment
3.9. Summary of Available Packages for Binning
4. Preselection of Variables
4.1. Overview
- Information values of single variables;
- Population stability analyses of single variables on recent out-of-time data
- Correlation analyses between variables.
4.2. Information Value

4.3. Population Stability Analysis



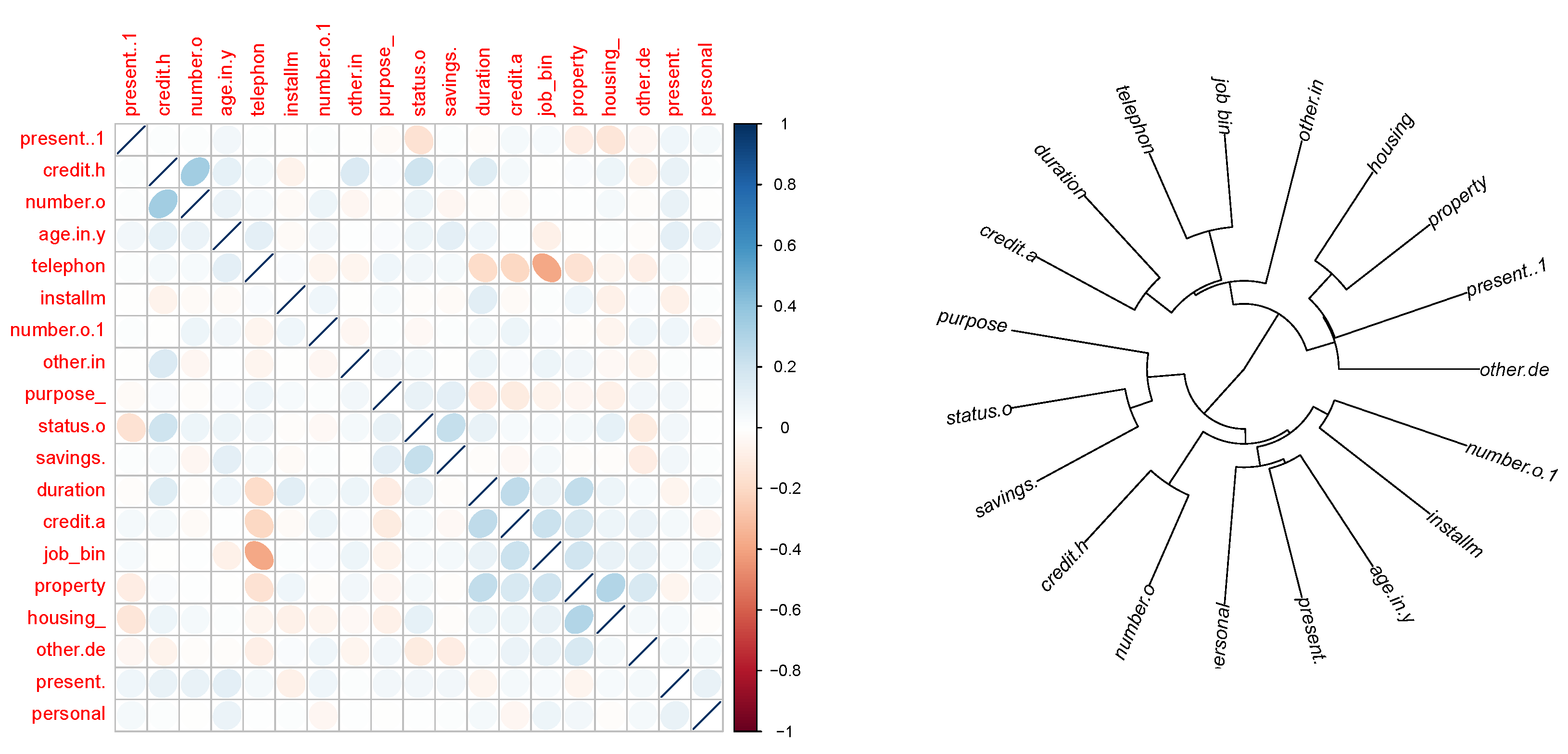
4.4. Correlation Analysis





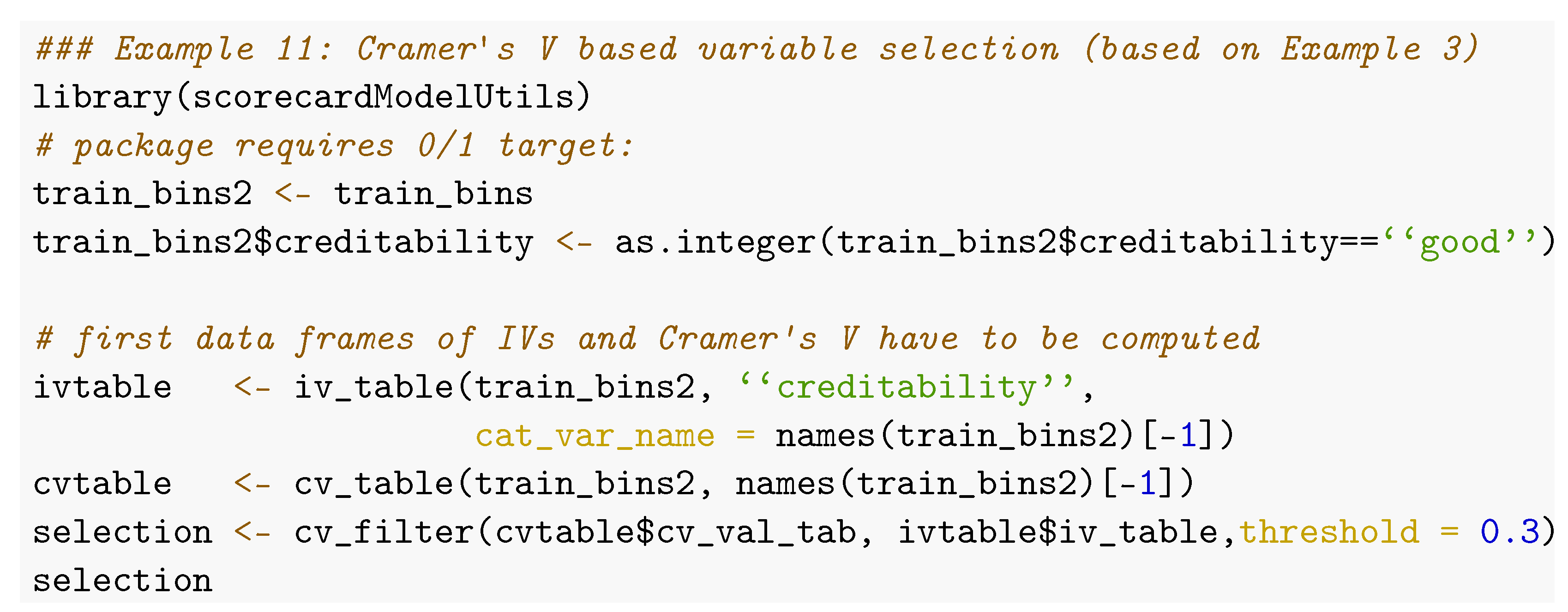
4.5. Further Useful Functions to Support Variable Preselection
5. Multivariate Modelling
5.1. Variable Selection


5.2. Turning Logistic Regression Models into Scorecard Points




5.3. Class Imbalance
6. Performance Evaluation
6.1. Overview
6.2. Discrimination
- Different from standard binary classification problems, credit scores are typically supposed to be increasing if the event (= default-) probability decreases. The function roc() of the package pROC has an argument direction that allows for specifying this.
- In credit scoring applications, it may be given that not all observations of a data set are of equal importance, e.g., it may not be as important to distinguish which of two customers with small default probabilities has the higher score if his or her application will be accepted anyway. The package’s function auc() has an additional argument partial.auc to compute partial area under the curve (Robin et al. 2011).
- Finally, its function ci() can be used to compute confidence intervals for the AUC using either bootstrap or the method of DeLong (DeLong et al. 1988; Sun and Xu 2014), e.g., to support the comparison of two models.




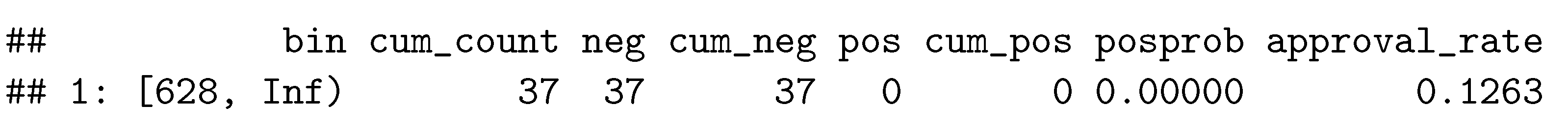

6.3. Performance Summary

6.4. Rating Calibration and Concentration

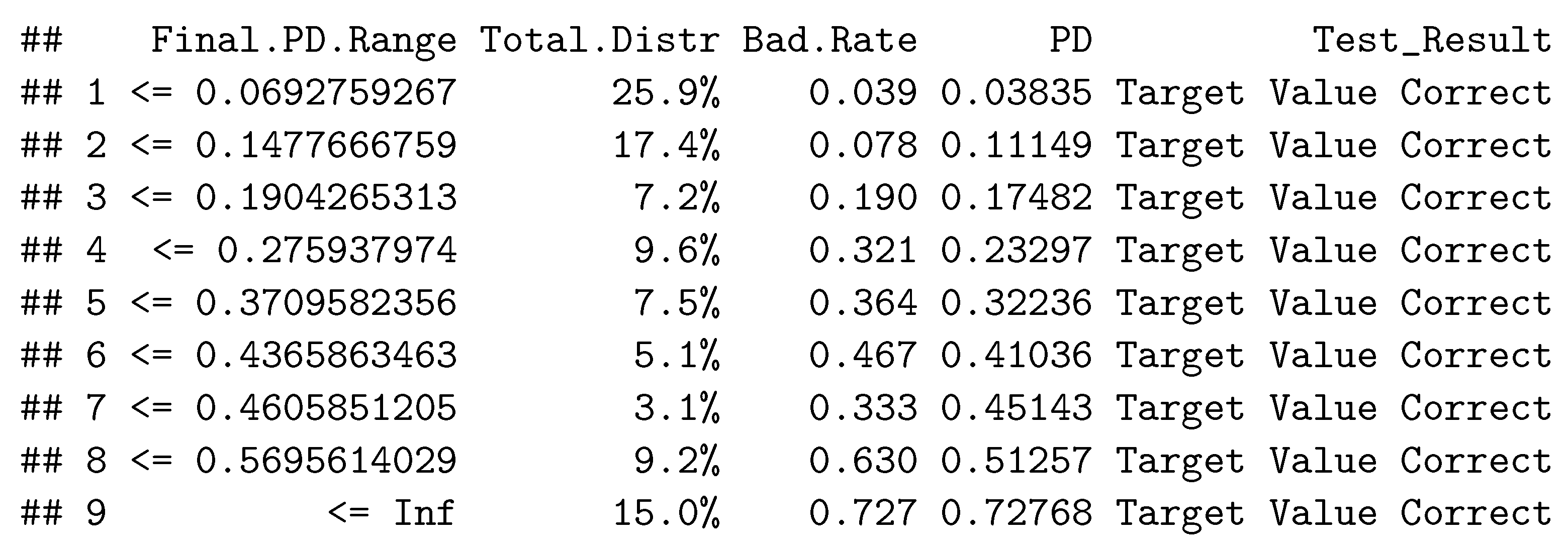
6.5. Cross Validation
7. Reject Inference
7.1. Overview
7.2. Augmentation
7.3. Parcelling

8. Summary and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://www.sas.com/en_us/software/credit-scoring.html (accessed on 15 February 2022). |
| 2 | https://cran.r-project.org/web/views/Finance.html (accessed on 15 February 2022). |
| 3 | https://www.openriskmanual.org/wiki/Credit_Scoring_with_Python (accessed on 15 February 2022). |
| 4 | https://towardsdatascience.com/how-to-develop-a-credit-risk-model-and-scorecard-91335fc01f03 (accessed on 15 February 2022). |
| 5 | https://github.com/ShichenXie/scorecardpy (accessed on 15 February 2022). |
| 6 | https://archive.ics.uci.edu/ml/datasets/South+German+Credit+%28UPDATE%29 (accessed on 15 February 2022). |
| 7 | https://www.lendingclub.com/ (accessed on 15 February 2022). |
| 8 | Note that the package creditmodel supports a pos_flag to define the level of the positive class which currently does not work for Binning and Weights of Evidence. |
| 9 | Argument equal_bins = FALSE or initial bins of equal sample size otherwise. |
| 10 | An example code for the package riskr is given in Snippet 2 of the supplementary code. |
| 11 | An example using a lookup table for the variable purpose is given in Snippet 3 of the supplementary code. |
| 12 | A code example of looping through all (numeric) variables for the package smbinning is given in Snippet 4 of the supplementary code. |
| 13 | An example code for application of this mapping to new data is given in Snippet 5 of the supplementary code. The names of the resulting new levels are the concatenated old levels, separated by commas. Note that the function cannot deal with commas in the original level names: a new level <NA> will be assigned |
| 14 | Using method = “chimerge”. |
| 15 | Using best = TRUE. |
| 16 | This can be easily checked using the variable purpose, cf. e.g., Snippet 6 of the supplementary code. |
| 17 | A code snippet for creating a breaks_list (cf. above) from a binning result using the package woeBinning that can be imported for further use within the package scorecard, e.g., for manual manipulation of the bins is given by the function woeBins2breakslist() in Snippet 7 of the supplementary code |
| 18 | See footnote 10. |
| 19 | Note that the call of glmdisc() ran in an internal error (incorrect number of subscripts on matrix) for more than 10 iterations. For this reason the number of iterations has been reduced to 10 which is much smaller than the default of 1000 iterations and the reported Gini coefficient does still strongly vary among subsequent iterations. For larger numbers of iterations better results might have been possible. |
| 20 | Its argument data denotes the training data, output is a data frame with two variables specifying the variable names of the training data (character) and the corresponding cluster index, as given, e.g., by the result from variable.clustering(). Finally, its arguments variables and clusters denote the names of these two variables in the data frame from the output argument where the clustering results are stored. |
| 21 | A remedy how it can be used in combination with WoE assignment using the package klaR as shown in Example 4 is given in Snippet 9 of the supplementary code. |
| 22 | Snippet 10 of the supplementary code illustrates how the vector x of the names of the input variables in the original data frame can be extracted from the bicglm model after variable selection from Example 12. |
| 23 | For the function augmentation(), this is obtained by rounding the posterior probabilities to the first digit. |
| 24 | Here, the augmented weights within each score-band are computed by . |
| 25 | Within the function parcelling() this is done by sampling the labels from a binomial distribution. |
| 26 | As an exception, the package creditR has been developed as an extension of the package woeBinning. |
| 27 | Cf. corresponding footnotes in the paper. Supplementary code is available under https://github.com/g-rho/CSwR (accessed on 15 February 2022). |
References
- Anagnostopoulos, Christoforos, and David J. Hand. 2019. Hmeasure: The H-Measure and Other Scalar Classification Performance Metrics, R Package Version 1.0-2; Available online: https://CRAN.R-project.org/package=hmeasure (accessed on 15 February 2022).
- Anderson, Raymond. 2007. The Credit Scoring Toolkit: Theory and Practice for Retail Credit Risk Management and Decision Automation. Oxford: Oxford University Press. [Google Scholar]
- Anderson, Raymond. 2019. Credit Intelligence & Modelling: Many Paths through the Forest. Oxford: Oxford University Press. [Google Scholar]
- Azevedo, Ana, and Manuel F. Santos. 2008. KDD, SEMMA and CRISP-DM: A parallel overview. Paper presented at IADIS European Conference on Data Mining 2008, Amsterdam, The Netherlands, July 24–26; pp. 182–85. [Google Scholar]
- Baesens, Bart, Tony Van Gestel, Stijn Viaene, Maria Stepanova, Johan Suykens, and Jan Vanthienen. 2002. Benchmarking state-of-the-art classification algorithms for credit scoring. JORS 54: 627–35. [Google Scholar] [CrossRef]
- Banasik, John, and Jonathan Crook. 2007. Reject inference, augmentation and sample selection. European Journal of Operational Research 183: 1582–94. [Google Scholar] [CrossRef]
- Biecek, Przemyslaw. 2018. DALEX: Explainers for complex predictive models. Journal of Machine Learning Research 19: 1–5. [Google Scholar]
- Binder, Martin, Florian Pfisterer, Michel Lang, Lennart Schneider, Lars Kotthoff, and Bernd Bischl. 2021. mlr3pipelines—Flexible machine learning pipelines in r. Journal of Machine Learning Research 22: 1–7. [Google Scholar]
- Bischl, Bernd, Martin Binder, Michel Lang, Tobias Pielok, Jakob Richter, Stefan Coors, Janek Thomas, Theresa Ullmann, Marc Becker, Anne-Laure Boulesteix, and et al. 2021. Hyperparameter optimization: Foundations, algorithms, best practices and open challenges. arXiv arXiv:2107.05847. [Google Scholar]
- Bischl, Bernd, Tobias Kühn, and Gero Szepannek. 2016. On class imbalance correction for classification algorithms in credit scoring. In Proceedings Operations Research 2014. Edited by Marco Lübbecke, Arie Koster, Peter Lethmathe, Reinhard Madlener, Britta Peis and Grit Walther. Heidelberg: Springer, pp. 37–43. [Google Scholar]
- Bischl, Bernd, Michel Lang, Lars Kotthoff, Julia Schiffner, Jakob Richter, Erich Studerus, Giuseppe Casalicchio, and Zachary Jones. 2016. mlr: Machine learning in R. Journal of Machine Learning Research 17: 1–5. [Google Scholar]
- Bischl, Bernd, Michel Lang, Lars Kotthoff, Patrick Schratz, Julia Schiffner, Jakob Richter, Zachary Jones, Giuseppe Casalicchio, Mason Gallo, Jakob Bossek, and et al. 2020. mlr: Machine Learning in R, R Package Version 2.17.1; Available online: https://CRAN.R-project.org/package=mlr (accessed on 15 February 2022).
- Bischl, Bernd, Olaf Mersmann, Heike Trautmann, and Claus Weihs. 2012. Resampling methods for meta-model validation with recommendations for evolutionary computation. Evolutionary Computation 20: 249–75. [Google Scholar] [CrossRef]
- Bravo, Cristian, Seppe van den Broucke, and Thomas Verbraken. 2019. EMP: Expected Maximum Profit Classification Performance Measure, R Package Version 2.0.5; Available online: https://CRAN.R-project.org/package=EMP (accessed on 15 February 2022).
- Breiman, Leo, Jerome H. Friedman, Richard A. Olshen, and Charles J. Stone. 1984. Classification and Regression Trees. New York: Wadsworth and Brooks. [Google Scholar]
- Brown, Iain, and Christophe Mues. 2012. An experimental comparison of classification algorithms for imbalanced credit scoring data sets. Expert Systems with Applications 39: 3446–53. [Google Scholar] [CrossRef]
- Bücker, Michael, Maarten van Kampen, and Walter Krämer. 2013. Reject inference in consumer credit scoring with nonignorable missing data. Journal of Banking & Finance 37: 1040–45. [Google Scholar]
- Bücker, Michael, Gero Szepannek, Alicja Gosiewska, and Przemyslaw Biecek. 2021. Transparency, Auditability and explainability of machine learning models in credit scoring. Journal of the Operational Research Society 73: 1–21. [Google Scholar] [CrossRef]
- Chavent, Marie, Vanessa Kuentz, Benoit Liquet, and Jerome Saracco. 2017. ClustOfVar: Clustering of Variables, R Package Version 1.1; Available online: https://CRAN.R-project.org/package=ClustOfVar (accessed on 15 February 2022).
- Chavent, Marie, Vanessa Kuentz-Simonet, Benoît Liquet, and Jerome Saracco. 2012. Clustofvar: An r package for the clustering of variables. Journal of Statistical Software 50: 1–6. [Google Scholar] [CrossRef]
- Chawla, Nitesh V., Kevin W. Bowyer, Lawrence O. Hall, and W. Philip Kegelmeyer. 2002. Smote: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research 16: 321–57. [Google Scholar] [CrossRef]
- Chen, Chaofan, Kangcheng Lin, Cynthia Rudin, Yaron Shaposhnik, Sijia Wang, and Tong Wang. 2018. An interpretable model with globally consistent explanations for credit risk. arXiv arXiv:1811.12615. [Google Scholar]
- Chen, Tianqi, and Carlos Guestrin. 2016. Xgboost: A scalable tree boosting system. Paper presented at the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17; pp. 785–94. [Google Scholar] [CrossRef]
- Chen, Tianqi, Tong He, Michael Benesty, Vadim Khotilovich, Yuan Tang, Hyunsu Cho, Kailong Chen, Rory Mitchell, Ignacio Cano, Tianyi Zhou, and et al. 2021. xgboost: Extreme Gradient Boosting, R Package Version 1.5.0.2; Available online: https://CRAN.R-project.org/package=xgboost (accessed on 15 February 2022).
- Cordón, Ignacio, Salvador García, Alberto Fernández, and Francisco Herrera. 2018. Imbalance: Oversampling algorithms for imbalanced classification in r. Knowledge-Based Systems 161: 329–41. [Google Scholar] [CrossRef]
- Cordón, Ignacio, Salvador García, Alberto Fernández, and Francisco Herrera. 2020. imbalance: Preprocessing Algorithms for Imbalanced Datasets, R Package Version 1.0.2.1; Available online: https://CRAN.R-project.org/package=imbalance (accessed on 15 February 2022).
- Crone, Sven F., and Steven Finlay. 2012. Instance sampling in credit scoring: An empirical study of sample size and balancing. International Journal of Forecasting 28: 224–38. [Google Scholar] [CrossRef]
- Crook, Jonathan, and John Banasik. 2004. Does reject inference really improve the performance of application scoring models? Journal of Banking & Finance 28: 857–74. [Google Scholar] [CrossRef]
- Csárdi, Gábor. 2019. cranlogs: Download Logs from the ’RStudio’ ’CRAN’ Mirror, R Package Version 2.1.1; Available online: https://CRAN.R-project.org/package=cranlogs (accessed on 15 February 2022).
- DeLong, Elizabeth R., David M. DeLong, and Daniel L. Clarke-Pearson. 1988. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 44: 837–45. [Google Scholar] [CrossRef]
- Dis, Ayhan. 2020. creditR: A Credit Risk Scoring and Validation Package, R Package Version 0.1.0; Available online: https://github.com/ayhandis/creditR (accessed on 15 February 2022).
- Dua, Dheeru, and Casey Graff. 2019. UCI Machine Learning Repository. Irvine: University of California. [Google Scholar]
- Ehrhardt, Adrien. 2018. scoringTools: Credit Scoring Tools, R Package Version 0.1; Available online: https://CRAN.R-project.org/package=scoringTools (accessed on 15 February 2022).
- Ehrhardt, Adrien. 2020. glmtree: Logistic Regression Trees, R Package Version 0.2; Available online: https://CRAN.R-project.org/package=glmtree (accessed on 15 February 2022).
- Ehrhardt, Adrien, Christophe Biernacki, Vincent Vandewalle, and Philippe Heinrich. 2019. Feature quantization for parsimonious and interpretable predictive models. arXiv arXiv:1903.08920. [Google Scholar]
- Ehrhardt, Adrien, Christophe Biernacki, Vincent Vandewalle, Philippe Heinrich, and Sébastien Beben. 2019. Réintégration des refusés en credit scoring. arXiv arXiv:1903.10855. [Google Scholar]
- Ehrhardt, Adrien, and Vincent Vandewalle. 2020. glmdisc: Discretization and Grouping for Logistic Regression, R Package Version 0.6; Available online: https://CRAN.R-project.org/package=glmdisc (accessed on 15 February 2022).
- Eichenberg, Thilo. 2018. woeBinning: Supervised Weight of Evidence Binning of Numeric Variables and Factors, R Package Version 0.1.6; Available online: https://CRAN.R-project.org/package=woeBinning (accessed on 15 February 2022).
- Fan, Dongping. 2022. creditmodel Toolkit for Credit Modeling, Analysis and Visualization, R Package Version 1.3.1; Available online: https://CRAN.R-project.org/package=creditmodel (accessed on 15 February 2022).
- Financial Stability Board. 2017. Artificial Intelligence and Machine Learning in Financial Services—Market Developments and Financial Stability Implications. Available online: https://www.fsb.org/2017/11/artificial-intelligence-and-machine-learning-in-financial-service/ (accessed on 15 February 2022).
- Finlay, Steven. 2012. Credit Scoring, Response Modelling and Insurance Rating. London: Palgarve MacMillan. [Google Scholar]
- Fox, John, and Sanford Weisberg. 2019. An R Companion to Applied Regression, 3rd ed. Thousand Oaks: Sage. [Google Scholar]
- Fox, John, Sanford Weisberg, Brad Price, Daniel Adler, Douglas Bates, Gabriel Baud-Bovy, Ben Bolker, Steve Ellison, David Firth, Michael Friendly, and et al. 2021. car: Companion to Applied Regression, R Package Version 3.0-12; Available online: https://CRAN.R-project.org/package=car (accessed on 15 February 2022).
- Goodman, Bryce, and Seth Flaxman. 2017. European union regulations on algorithmic decision-making and a “right to explanation”. AI Magazine 38: 50–57. [Google Scholar] [CrossRef]
- Greenwell, Brandon, Bradley Boehmke, Jay Cunningham, and GBM Developers. 2020. gbm: Generalized Boosted Regression Models, R Package Version 2.1.8; Available online: https://CRAN.R-project.org/package=gbm (accessed on 15 February 2022).
- Groemping, Ulrike. 2019. South German Credit Data: Correcting a Widely Used Data Set. Technical Report 4/2019. Berlin: Department II, Beuth University of Applied Sciences Berlin. [Google Scholar]
- Hand, David. 2009. Measuring classifier performance: A coherent alternative to the area under the roc curve. Machine Learning 77: 103–23. [Google Scholar] [CrossRef]
- Hand, David, and William Henley. 1993. Can reject inference ever work? IMA Journal of Management Matehmatics 5: 45–55. [Google Scholar] [CrossRef]
- Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning, 2nd ed. New York: Springer. [Google Scholar]
- Hoffmann, Hans. 1994. German Credit Data Set (statlog). Available online: https://archive.ics.uci.edu/ml/datasets/statlog+(german+credit+data) (accessed on 15 February 2022).
- Hosmer, David W., and Stanley Lemeshow. 2000. Applied Logistic Regression. Hoboken: Wiley. [Google Scholar]
- Hothorn, Thorsten, Kurt Hornik, and Achim Zeileis. 2006. Unbiased recursive partitioning: A conditional inference framework. Journal of Computational and Graphical Statistics 15: 651–74. [Google Scholar] [CrossRef]
- Hothorn, Torsten, and Achim Zeileis. 2015. partykit: A modular toolkit for recursive partytioning in R. Journal of Machine Learning Research 16: 3905–9. [Google Scholar]
- Izrailev, Sergei. 2015. Binr: Cut Numeric Values into Evenly Distributed Groups, R Package Version 1.1; Available online: https://CRAN.R-project.org/package=binr (accessed on 15 February 2022).
- Jopia, Herman. 2019. smbinning: Optimal Binning for Scoring Modeling, R Package Version 0.9; Available online: https://CRAN.Rproject.org/package=smbinning (accessed on 15 February 2022).
- Kaszynski, Daniel. 2020. Background of credit scoring. In Credit Scoring in Context of Interpretable Machine Learning. Edited by Daniel Kaszynski, Bogumil Kaminski and Tomasz Szapiro. Warsaw: SGH, pp. 17–26. [Google Scholar]
- Kaszynski, Daniel, Bogumil Kaminski, and Tomasz Szapiro. 2020. Credit Scoring in Context of Interpretable Machine Learning. Warsaw: SGH. [Google Scholar]
- Kim, HyunJi. 2012. Discretization: Data Preprocessing, Discretization for Classification, R Package Version 1.0-1; Available online: https://CRAN.R-project.org/package=discretization (accessed on 15 February 2022).
- Kuhn, Max. 2008. Building predictive models in r using the caret package. Journal of Statistical Software 28: 1–26. [Google Scholar] [CrossRef]
- Kuhn, Max. 2021. Caret: Classification and Regression Training, R Package Version 6.0-90; Available online: https://CRAN.R-project.org/package=caret (accessed on 15 February 2022).
- Kunst, Joshua. 2020. Riskr: Functions to Facilitate the Evaluation, Monitoring and Modeling process, R Package Version 1.0; Available online: https://github.com/jbkunst/riskr (accessed on 15 February 2022).
- Landgraf, Andrew J. 2016. logisticPCA: Binary Dimensionality Reduction, R Package Version 0.2; Available online: https://CRAN.Rproject.org/package=logisticPCA (accessed on 15 February 2022).
- Landgraf, Andrew J., and Yoonkyung Lee. 2015. Dimensionality reduction for binary data through the projection of natural parameters. arXiv arXiv:1510.06112. [Google Scholar] [CrossRef]
- Lang, Michel, Martin Binder, Jakob Richter, Patrick Schratz, Florian Pfisterer, Stefan Coors, Quay Au, Giuseppe Casalicchio, Lars Kotthoff, and Bernd Bischl. 2019. mlr3: A modern object-oriented machine learning framework in R. Journal of Open Source Software 4: 1903. [Google Scholar] [CrossRef]
- Lang, Michel, Bernd Bischl, Jakob Richter, Patrick Schratz, Giuseppe Casalicchio, Stefan Coors, Quay Au, and Martin Binder. 2021. mlr3: Machine Learning in R—Next Generation, R Package Version 0.13.0; Available online: https://CRAN.R-project.org/package=mlr3 (accessed on 15 February 2022).
- Larsen, Kim. 2016. Information: Data Exploration with Information Theory, R Package Version 0.0.9; Available online: https://CRAN.R-project.org/package=Information (accessed on 15 February 2022).
- Lele, Subhash R., Jonah L. Keim, and Peter Solymos. 2019. ResourceSelection: Resource Selection (Probability) Functions for Use-Availability Data, R Package Version 0.3-5; Available online: https://CRAN.R-project.org/package=ResourceSelection (accessed on 15 February 2022).
- Lessmann, Stefan, Bart Baesens, Hsin-Vonn Seow, and Lyn Thomas. 2015. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. European Journal of Operational Research 247: 124–36. [Google Scholar] [CrossRef]
- Liaw, Andy, and Matthew Wiener. 2002. Classification and regression by randomforest. R News 2: 18–22. [Google Scholar]
- Ligges, Uwe. 2009. Programmieren Mit R, 3rd ed. Heidelberg: Springer. [Google Scholar]
- Little, Roderick, and Donald Rubin. 2002. Statistical Analysis with Missing Data. Hoboken: Wiley. [Google Scholar]
- Louzada, Francisco, Anderson Ara, and Guilherme Fernandes. 2016. Classification methods applied to credit scoring: A systematic review and overall comparison. Surveys in OR and Management Science 21: 117–34. [Google Scholar] [CrossRef]
- Maechler, Martin, Peter Rousseeuw, Anja Struyf, Mia Hubert, and Kurt Hornik. 2021. Cluster: Cluster Analysis Basics and Extensions, R Package Version 2.1.2; Available online: https://CRAN.R-project.org/package=cluster (accessed on 15 February 2022).
- Molnar, Christoph, Bernd Bischl, and Giuseppe Casalicchio. 2018. iml: An R package for Interpretable Machine Learning. JOSS 3: 786. [Google Scholar] [CrossRef]
- Paradis, Emmanuel, Simon Blomberg, Ben Bolker, Joseph Brown, Julien Claude, Hoa Sien Cuong, Richard Desper, Gilles Didier, Benoit Durand, Julien Dutheil, and et al. 2021. ape: Analyses of Phylogenetics and Evolution, R Package Version 5.6.1; Available online: https://CRAN.R-project.org/package=ape (accessed on 15 February 2022).
- Paradis, Emmanuel, and Klaus Schliep. 2018. ape 5.0: An environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35: 526–28. [Google Scholar] [CrossRef]
- Poddar, Arya. 2019. scorecardModelUtils: Credit Scorecard Modelling Utils, R Package Version 0.0.1.0; Available online: https://CRAN.R-project.org/package=scorecardModelUtils (accessed on 15 February 2022).
- Pozzolo, Andrea Dal, Olivier Caelen, and Gianluca Bontempi. 2015. unbalanced: Racing for Unbalanced Methods Selection, R Package Version 2.0; Available online: https://CRAN.R-project.org/package=unbalanced (accessed on 15 February 2022).
- Prabhakaran, Selva. 2016. InformationValue: Performance Analysis and Companion Functions for Binary Classification Models, R Package Version 1.2.3; Available online: https://CRAN.R-project.org/package=InformationValue (accessed on 15 February 2022).
- Robin, Xavier, Natacha Turck, Alexandre Hainard, Natalie Tiberti, Frederique Lisacek, Jean Sanchez, and Markus Müller. 2011. Proc: An open-source package for r and s+ to analyze and compare roc curves. BMC Bioinformatics 12: 1–8. [Google Scholar] [CrossRef]
- Robin, Xavier, Natacha Turck, Alexandre Hainard, Natalia Tiberti, Frederique Lisacek, Jean-Charles Sanchez, Markus Müller, Stefan Siegert, and Matthias Doering. 2021. pROC: Display and Analyze ROC Curves, R Package Version 1.18.0; Available online: https://CRAN.R-project.org/package=pROC (accessed on 15 February 2022).
- Roever, Christian, Nils Raabe, Karsten Luebke, Uwe Ligges, Gero Szepannek, and Marc Zentgraf. 2020. klaR: Classification and visualization, R Package Version 0.6-15; Available online: https://CRAN.R-project.org/package=klaR (accessed on 15 February 2022).
- Rudin, Cynthia. 2019. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nature Machine Intelligence 1: 206–15. [Google Scholar] [CrossRef]
- Ryu, Choonghyun. 2021. dlookr: Tools for Data Diagnosis, Exploration, Transformation, R Package Version 0.5.4; Available online: https://CRAN.R-project.org/package=dlookr (accessed on 15 February 2022).
- Scallan, Gerard. 2011. Class(ic) scorecards—Selecting attributes in logistic regression. Credit Scoring and Credit Control XIII. Available online: https://www.scoreplus.com/papers/paper (accessed on 15 February 2022).
- Schiltgen, Garrett. 2015. Boottol: Bootstrap Tolerance Levels for Credit Scoring Validation Statistics, R Package Version 2.0; Available online: https://CRAN.R-project.org/package=boottol (accessed on 15 February 2022).
- Sharma, Dhuv. 2009. Guide to credit scoring in R. CRAN Documentation Contribution. Available online: https://cran.r-project.org/ (accessed on 15 February 2022).
- Siddiqi, Naeem. 2006. Credit Risk Scorecards: Developing and Implementing Intelligent Credit Scoring, 2nd ed. Hoboken: Wiley. [Google Scholar]
- Sing, Tobias, Oliver Sander, Niko Beerenwinkel, and Thomas Lengauer. 2005. ROCR: Visualizing classifier performance in R. Bioinformatics 21: 7881. [Google Scholar] [CrossRef]
- Sing, Tobias, Oliver Sander, Niko Beerenwinkel, and Thomas Lengauer. 2020. ROCR: Visualizing the Performance of Scoring Classifiers, R Package Version 1.0-11; Available online: https://CRAN.R-project.org/package=ROCR (accessed on 15 February 2022).
- Siriseriwan, Wacharasak. 2019. smotefamily: A Collection of Oversampling Techniques for Class Imbalance Problem Based on SMOTE, R Package Version 1.3.1; Available online: https://CRAN.R-project.org/package=smotefamily (accessed on 15 February 2022).
- Staniak, Mateusz, and Przemysław Biecek. 2019. The Landscape of R Packages for Automated Exploratory Data Analysis. The R Journal 11: 347–69. [Google Scholar] [CrossRef]
- Stratman, Eric, Riaz Khan, and Allison Lempola. 2020. Rprofet: WOE Transformation and Scorecard Builder, R Package Version 2.2.1; Available online: https://CRAN.R-project.org/package=Rprofet (accessed on 15 February 2022).
- Sun, Xu, and Weichao Xu. 2014. Fast implementation of delong’s algorithm for comparing the areas under correlated receiver operating characteristic curves. IEEE Signal Processing Letters 21: 1389–93. [Google Scholar] [CrossRef]
- Szepannek, Gero. 2017. On the practical relevance of modern machine learning algorithms for credit scoring applications. WIAS Report Series 29: 88–96. [Google Scholar]
- Szepannek, Gero. 2019. How much can we see? A note on quantifying explainability of machine learning models. arXiv arXiv:1910.13376. [Google Scholar]
- Szepannek, Gero, and Karsten Lübke. 2021. Facing the challenges of developing fair risk scoring models. Frontiers in Artificial Intelligence 4: 117. [Google Scholar] [CrossRef] [PubMed]
- Therneau, Terry, and Beth Atkinson. 2019. rpart: Recursive Partitioning and Regression Trees, R Package Version 4.1-15; Available online: https://CRAN.R-project.org/package=rpart (accessed on 15 February 2022).
- Thomas, Lynn C., Jonathan N. Crook, and David B. Edelman. 2019. Credit Scoring and its Applications, 2nd ed. Philadelphia: SIAM. [Google Scholar]
- Thoppay, Sudarson. 2015. woe: Computes Weight of Evidence and Information Values, R Package Version 0.2; Available online: https://CRAN.R-project.org/package=woe (accessed on 15 February 2022).
- Verbraken, Thomas, Christian Bravo, Weber Richard, and Baesens Baesens. 2014. Development and application of consumer credit scoring models using profit-based classification measures. European Journal of Operational Research 238: 505–13. [Google Scholar] [CrossRef]
- Verstraeten, Geert, and Dirk Van den Poel. 2005. The impact of sample bias on consumer credit scoring performance and profitability. JORS 56: 981–92. [Google Scholar] [CrossRef]
- Vigneau, Evelyne, Mingkun Chen, and Veronique Cariou. 2020. ClustVarLV: Clustering of Variables Around Latent Variables, R Package Version 2.0.1; Available online: https://CRAN.R-project.org/package=ClustVarLV (accessed on 15 February 2022).
- Vigneau, Evelyne, Mingkun Chen, and El Mostafa Qannari. 2015. ClustVarLV: An R Package for the Clustering of Variables Around Latent Variables. The R Journal 7: 134–48. [Google Scholar] [CrossRef][Green Version]
- Vincotti, Veronica, and David Hand. 2002. Scorecard construction with unbalanced class sizes. Journal of The Iranian Statistical Society 2: 189–205. [Google Scholar]
- Wrzosek, Malgorzata, Daniel Kaszynski, Karol Przanowski, and Sebastian Zajac. 2020. Selected machine learning methods used for credit scoring. In Credit Scoring in Context of Interpretable Machine Learning. Edited by Daniel Kaszynski, Bogumil Kaminski and Tomasz Szapiro. Warsaw: SGH, pp. 83–146. [Google Scholar]
- Xie, Shichen. 2021. scorecard: Credit Risk Scorecard, R Package Version 0.3.6; Available online: https://CRAN.R-project.org/package=scorecard (accessed on 15 February 2022).
- Zumel, Nina, and John Mount. 2014. Practical Data Science with R. New York: Manning. [Google Scholar]

| Unique | sc | woeB | woeB.T | Glmdisc | sMU | Rprof | smb | Cremo | Riskr | |
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. # bins | 6.33 | 4.33 | 6 | 2.67 | 3.67 | 11 | 2.67 | 2 | 2.67 | |
| duration | 32 | 5 | 5 | 5 | 3 | 5 | 13 | 3 | 2 | 3 |
| amount | 663 | 7 | 4 | 6 | 1 | 3 | 11 | 3 | 2 | 3 |
| instRate | 4 | 4 | 4 | 4 | 1 | 4 | 4 | 4 | 2 | 1 |
| residence | 4 | 4 | 4 | 4 | 3 | 2 | 4 | 4 | 3 | 1 |
| age | 52 | 7 | 4 | 7 | 4 | 3 | 9 | 2 | 2 | 2 |
| numCredits | 4 | 2 | 3 | 3 | 2 | 2 | 3 | 4 | 2 | 1 |
| numLiable | 2 | 2 | 3 | 3 | 2 | 1 | 2 | 2 | 2 | 1 |
| LCL | sc | woeB | woeB.T | Glmdisc | sMU | smb | Cremo | Riskr | |
|---|---|---|---|---|---|---|---|---|---|
| duration | 0.170 | 0.297 | 0.259 | 0.264 | 0.265 | 0.299 | 0.248 | 0.162 | 0.248 |
| amount | 0.116 | 0.251 | 0.179 | 0.227 | 0.000 | 0.196 | 0.219 | 0.069 | 0.219 |
| age | 0.078 | 0.179 | 0.169 | 0.222 | 0.189 | 0.200 | 0.187 | −0.003 | 0.187 |
| numLiable | 0.000 | 0.006 | 0.006 | 0.006 | 0.006 | 0.000 | 0.006 | 0.006 | 0.000 |
| numCredits | 0.000 | 0.068 | 0.068 | 0.068 | 0.068 | 0.068 | 0.061 | 0.068 | 0.000 |
| residence | 0.000 | 0.006 | 0.017 | 0.017 | 0.017 | 0.029 | 0.006 | 0.017 | 0.000 |
| instRate | 0.000 | 0.108 | 0.103 | 0.103 | 0.000 | 0.108 | 0.108 | 0.104 | 0.000 |
| sc | smb | woeB | Cremo | Riskr | Glmdisc | sMU | Rprof | klaR | |
|---|---|---|---|---|---|---|---|---|---|
| automatic binning of numerics | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ |
| automatic binning of factors | ✓ | ✗ | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ |
| store and predict numerics | ✓ | ✓ | ✓ | ✓ | (1) | ✓ | ✓ | ✗ | ✗ |
| store and predict factors | ✓ | ✓ | ✓ | ✗ | (1) | ✓ | ✗ | ✗ | ✗ |
| supports bin prediction | ✓ | ✓ | ✓ | ✗ | (1) | ✓ | ✓ | ✗ | ✗ |
| supports WoE prediction | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ |
| summary table | ✓ | ✓ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ |
| plot | ✓ | ✓ | ✓ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ |
| manual modification | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ |
| multiple variables | ✓ | ✗ | ✓ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| supported target levels | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ |
| adjust WoEs | ✓ | ✗ | ✓ | ✗ | ✗ | ✓ | ✓ | ||
| NAs | ✓ | ✓ | ✓ | (2) | ✗ | (3) | (4) | ✓ | |
| new levels | ✗ | ✗ | ✓ | ✗ | (3) | ||||
| level order irrelevant | ✗ | ✓ | ✓ | ✓ | |||||
| min. level size | ✗ | ✓ | ✗ | ✗ | ✗ | (5) | ✗ |
| Package | Function | Target Type | Multiple Variables | WoE Adjustment |
|---|---|---|---|---|
| creditR | IV.calc.data() | both, levels 0/1 | yes | no |
| creditmodel | get_iv_all() | both, levels 0/1 | yes | yes |
| Information | create_infotables() | numeric 0/1 | yes | yes |
| InformationValue | IV() | numeric 0/1 | no | yes |
| klaR | woe() | factor | yes | argument |
| riskr | pred_ranking() | numeric 0/1 | yes | no |
| scorecard | iv() | both | yes | 0.99 |
| scorecardModelUtils | iv_table() | numeric 0/1 | yes | 0.5 |
| smbinning | smbinning.sumiv() | numeric 0/1 | yes | yes |
| Package Function | RiskrPerf() | ScorecardPerf_Eva() | ScorecardModelUtilsGini_Table() | SmbinningSmbinning.Metrics() |
|---|---|---|---|---|
| KS | ✓ | ✓ | ✓ | ✓ |
| AUC | ✓ | ✓ | ✓ | |
| Gini | ✓ | ✓ | ✓ | |
| Divergence | ✓ | |||
| Bin table | ✓ | |||
| Confusion matrix | ✓ | ✓ | ||
| Accuracy | ✓ | ✓ | ||
| Good rate | ✓ | |||
| Bad rate | ✓ | |||
| TPR | ✓ | |||
| FNR | ✓ | ✓ | ||
| TNR | ✓ | |||
| FPR | ✓ | ✓ | ||
| PPV | ✓ | |||
| FDR | ✓ | |||
| FOR | ✓ | |||
| NPV | ✓ | |||
| ROC curve | ✓ | ✓ | ✓ | ✓ |
| Score densities | y | ✓ | |||
| ECDF | ✓ | ✓ | ✓ | |
| Gain chart | ✓ |
| Package | Binning & WoEs | Preselection | Scorecard | Performance | Reject Inference |
|---|---|---|---|---|---|
| boottol | ✓ | ||||
| creditmodel | ✓ | ✓ | ✓ | ✓ | |
| creditR | ✓ | ✓ | ✓ | ✓ | |
| glmdisc | ✓ | ✓ | |||
| glmtree | ✓ | ||||
| Information | ✓ | ||||
| InformationValue | ✓ | ||||
| riskr | ✓ | ✓ | ✓ | ||
| Rprofet | ✓ | ✓ | |||
| scorecard | ✓ | ✓ | ✓ | ✓ | |
| scoringTools | ✓ | ✓ | |||
| scorecardModelUtils | ✓ | ✓ | ✓ | ✓ | |
| smbinning | ✓ | ✓ | ✓ | ✓ | |
| woe | ✓ | ✓ | |||
| woeBinning | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szepannek, G. An Overview on the Landscape of R Packages for Open Source Scorecard Modelling. Risks 2022, 10, 67. https://doi.org/10.3390/risks10030067
Szepannek G. An Overview on the Landscape of R Packages for Open Source Scorecard Modelling. Risks. 2022; 10(3):67. https://doi.org/10.3390/risks10030067
Chicago/Turabian StyleSzepannek, Gero. 2022. "An Overview on the Landscape of R Packages for Open Source Scorecard Modelling" Risks 10, no. 3: 67. https://doi.org/10.3390/risks10030067
APA StyleSzepannek, G. (2022). An Overview on the Landscape of R Packages for Open Source Scorecard Modelling. Risks, 10(3), 67. https://doi.org/10.3390/risks10030067






