Financial Liquidity and Debt Recovery Efficiency Forecasting in a Small Industrial Enterprise

Abstract

Rational small business management necessitates the development of a system for recording important internal information. Companies are obliged to collect statistical data that mainly serves fiscal needs. Exemplary use of such significant data entails financial liquidity (LIQt) and debt recovery efficiency (EVINDt) measures. This work presents constructions of such measures and the manner of their application when they accrue in the form of time series. Both these measures should remain in feedback. Feedback complicates the forecasting of each of the variables that make up this relationship. In the existing forecasting practice, forecasts of such variables have been estimated using empirical equations of a reduced-form model. Such forecasts—in the case of an econometric micromodel—exhibit synchronization properties. This paper presents an empirical system of interdependent equations describing the relationship between financial liquidity and debt collection efficiency. An econometric model was used to build forecasts for both of these characteristics in a small business. An iterative method of forecasting from structural-form equations was used, which guarantees synchronization of forecasts under feedback conditions. The current use of the reduced form of the model to build such forecasts results in divergent forecasts that are not useful in small business management. They can also lead to wrong decisions. In the case under consideration, the forecast value synchronization (convergence) was obtained after five to nine iterations. The more distant the forecasted period is, the greater the number of iterations required to synchronize the forecasts.

1. Introduction

Small business owners do not attach sufficient importance to internal statistical information. They are not interested in the statistical data on their past activity. Almost exclusively, they collect the numerical data that is required by law. In actuality, possession of past information in the form of time series, especially monthly data, facilitates business management. Financial characteristics as well as the numbers describing the intensity of sales and of the manufacturing process are particularly important.

Acquisition of the funds required for the timely payment of liabilities is one of the most important tasks in a small enterprise. Small entity activity is mainly financed by one’s own funds. Very rarely, small companies use bank loans. In Poland, throughout the entire period after 1990, small enterprises faced banks’ reluctance to grant loans.

The financial liquidity of a small enterprise therefore depends on its ability to sell as well as collect receivables for the goods and services sold. The efficiency of debt recovery1 plays a fundamental role in the shaping of a small business entity’s financial liquidity. It is rare that a lack of cash in such a company is supplemented by external funds. Most often, the owner’s own funds, including the amounts accumulated earlier owing to a temporary state of so-called over-liquidity, constitute the resource supplement. The matter taken up in this work entails monthly, i.e., short term, analysis and forecasting2 of financial liquidity and debt recovery efficiency in a small enterprise. The work aims to implement the econometric procedure of building financial liquidity and debt recovery efficiency forecasts under the condition of feedback. The study incorporates time series from an existing small enterprise covering 96 months. The course of action presented in the work can be used by small entrepreneurs in their own financial management, increasing their financial security.

In the financial literature, much attention has been devoted to the issue of liquidity, yet there is a lack of academic works addressing debt collection. At the same time, no research emerges on the measurement of debt collection efficiency. The area of interdependence between financial liquidity, especially in small companies, and debt collection effectiveness constitutes a significant research gap. As a consequence, there is a lack of studies on liquidity and debt collection effectiveness forecasts, including an indication of the benefits for business resulting from such research.

The work is divided into four parts. The introduction is followed by a chapter devoted to research material and methodology, consisting of four subchapters reviewing and discussing the literature on small business liquidity, traditional liquidity measures, small business liquidity against debt collection efficiency, and the econometric empirical micromodel describing the interdependence between liquidity and debt collection efficiency. The third part includes the results and discussion thereof, in which synchronized forecasts of a small company’s financial liquidity and debt collection efficiency are presented using an iterative forecasting method. The article ends with a summary of the results from the research conducted.

2. Materials and Methods

2.1. Overview of the Literature on Financial Liquidity in a Small and Medium Enterprise

In its annual reports on “Small Business Finance” (Bank of England 1997, 1998); In its annual reports on “Small Business Finance” (Bank of England 1997, 1998, 1999a, 1999b), the Bank of England acknowledged the fact that finance management is particularly important for the development and survival of small and micro enterprises. In the literature on the subject, liquidity plays a special role in enterprise management. Small and medium-sized enterprises (SMEs) are perceived as the driving force of any economy (Khan and Ghani 2004). They contribute remarkably to the economic development of each country (Abor and Quartey 2010). There are over 20 million small- and medium-sized enterprises operating in the European Union, constituting 99% of all enterprises functioning in Europe. As such, they constitute the main engine of economic growth, innovation, employment, and social integration.

Maintenance of liquidity in small businesses plays a unique role. Chan and Chen (1991) argue that smaller firms are more sensitive to changes in the economy. Higher leverage, problems with cash flow, and less effective management are characteristics that cause small- and mid-capitalization companies to be riskier than their larger counterparts (Chan and Chen 1991). Liquidity stress testing is important for both internal and external analysts due to its close relation to the company’s day-to-day operations (Bhunia 2010; Jepkorir et al. 2019). Achievement of the expected compromise between liquidity and profitability poses a dilemma in liquidity management (Raheman and Nasr 2007; Mazumder 2020).

An entity’s lack of liquidity may lead to its elimination from economic trade. Practice confirms that bankrupting enterprises usually lacked financial liquidity, despite other positive results of their operations. Maintenance of liquidity in daily operations, which ensures efficient functioning and realization of one’s obligations, is of key significance in working capital management (Eljelly 2004). Proper management of the working capital, i.e., inventories, current receivables, and liabilities, which make up the cash conversion cycle, is extremely important in the day-to-day operations of a company.

Maintenance of financial liquidity in an enterprise is largely determined by the level and structure of working capital. In the course of a company’s day-to-day operations, both the structure and demand for this capital are subject to large fluctuations. This results from the decisions made regarding the purchase of raw materials and other materials or goods, the sale of finished products, the dates of receivables collection, and the settlement of current liabilities.

A low level of working capital may lead to a loss of financial liquidity. Excessive working capital, in turn, means a waste of resources. It may result in unjustified additional costs of raising the capital that finances part of the current assets. When these assets are financed by equity, it can also generate opportunity costs. In small- and medium-sized enterprises, it is very important, therefore, to reduce the risk of losing financial liquidity as a result of immobilizing part of the current assets in hard-to-sell inventories or difficult-to-recover receivables. Effective recovery of debt constitutes the foundation of financial management in an enterprise.

2.2. Traditional Assessment of an Enterprise’s Financial Liquidity

In the literature on the subject, the two most common approaches to financial liquidity used are:

(a)

Static approach—in relation to a specific moment, using basic parts of financial statements, such as: the balance sheet and the profit and loss account;

(b)

Dynamic approach—in relation to a specific reporting period, based on the cash flow statement.

Customary measurement of liquidity is based on data obtained directly from the balance sheet. The ratios used are based on the assessment of the relation of short-term assets to short-term liabilities. Assessment of a company’s financial liquidity is based on a number of classic indicators that are characterized by a greater or a lesser scope of practical application. The most frequently used ratios include: the current ratio of financial liquidity, the quick ratio, and the immediate cash ratio. They are meant to assess the extent to which an enterprise was able to pay off its current liabilities using short-term assets. Each of the above-mentioned ratios covers a different range of payment means in the numerator: from total current assets to the most liquid cash assets. At the same time, calculations are based on measurement of a company’s past financial resources. The ratios determined for a given company are compared with the data from previous periods, the ratios for other companies, and the so-called standards—normative values. It should be taken into account, however, that enterprises operating in various industries have different levels of working capital and exhibit uneven demand for these resources. It is therefore difficult to determine universal reference levels for these ratios.

The current ratio of liquidity has the following form:

$$\mathrm{Current}\mathrm{ratio}=\frac{\mathrm{Current}\mathrm{assets}}{\mathrm{Current}\mathrm{liabilities}}$$

(1)

Current assets include inventories, receivables, short-term securities, and cash. This ratio allows assessment of the extent to which an enterprise is able to cover its short-term liabilities with current assets. It is assumed that the normative value of this ratio should fall within the range (1.2–2). Inventories are considered the least liquid current assets. As such, in order to determine a company’s short-term solvency, the quick ratio of liquidity ratio often is also calculated as follows:

$$\mathrm{Quick}\mathrm{ratio}=\frac{\mathrm{Current}\mathrm{assets}-\mathrm{inventories}-\mathrm{prepayments}}{\mathrm{Current}\mathrm{liabilities}}$$

(2)

The value of the quick ratio should fall in the range from 1 to 1.2. As before, a lower value of this ratio can be a warning signal that a given company may face liquidity difficulties, whereas exceedance of the upper limit may suggest ineffective working capital management on the part of the entity. The immediate (cash) liquidity ratio is a ratio belonging to the same liquidity group, calculated using the following formula:

$$\mathrm{Cash}\mathrm{ratio}=\frac{\mathrm{Liquid}\mathrm{assets}}{\mathrm{Current}\mathrm{liabilities}}$$

(3)

This ratio shows the extent to which an enterprise is able to settle its current liabilities with the most liquid assets, which include cash. It is assumed that pecuniary obligations should constitute at least 16% to 20% of current liabilities in order for an enterprise to be able to settle those liabilities efficiently. There are no standards for this indicator. A view dominates, however, that its value should fall within the range 0.16–0.2. The rule of financial management stipulates that cash resources should be kept to a minimum. Only the assets involved in trading generate appropriate financial results.

Financial liquidity assessment and management is therefore dominated by the above-described static approach, which is based on the analysis of the balance sheet shaping. This happens despite the fact that the essence of financial liquidity entails synchronization of the cash flow streams, i.e., synchronization of cash inflows with cash expenditures, which result from contractual or legal deadlines for settlement of financial obligations. Proper dynamics of these streams is thus important.

In recent economic practice, the view that measures that are based on resources from the previous reporting period are not rational indicators for assessment of a company’s financial standing has been gaining an increasingly stronger position. These measures are solely based on the accounting categories resulting from the rules established and commonly accepted classifications. Their accrual nature as well as the prospect of data manipulation can possibly result in questionable cognitive values.

Assessment of a company’s financial liquidity that is based on the cash flow statement seems to be a much better option. This constitutes a counterbalance to the accrual manner of viewing and assessing a given company’s financial situation. Information on the amount of the cash inflows and outflows is paramount. A cash flow statement combines the balance sheet and the profit and loss account, using cash as an objective and a factual measure of a given company’s operational effectiveness. Such a report presents the revenues and the expenses that occurred in a given reporting period broken down into three types of activity: operational, investment, and financial activity. Financial liquidity can be considered on the basis of the financial flows for a given period. Only a statement of revenues and expenses allows determination of the cash balance in an enterprise.

A statement of cash flows, which is often treated as complementary to the image conveyed by the balance sheet and the profit and loss account, offers a qualitatively new perspective. This allows the comparison of companies, regardless of the accounting conventions used. It also allows a more complete assessment of a given company’s operation, compared with an analysis carried out in a traditional manner.

In addition to the use of simple analytical methods used in enterprises, which are burdened with disadvantages, it is worth incorporating tools that are commonly available but rarely used in finance management, i.e., quantitative methods. Econometric modeling provides effective tools of innovative nature. At the same time, it does not offer too many efficient tools for small enterprises that rarely keep full accounting and do not make comprehensive financial statements. It is worth pointing out that the effectiveness of econometric modeling is conditioned by the amount of the statistical information on a given company’s financial results as well as its revenues and expenses.

2.3. Financial Liquidity and Debt Recovery Efficiency Measurement in a Small Enterprise

An econometric system of interdependent equations describing the relationship between financial liquidity and debt recovery efficiency in a small enterprise is presented below. As such, the measures of liquidity and debt recovery efficiency in a small company need to be presented as well.

The first manner in which liquidity can be measured entails comparison of the value of concurrent cash inflows with the value of finished production (see Sokołowska and Wiśniewski 2008). When CASH_t ≥ PROD_t (t = 1, …, n), the enterprise possesses the cash needed to cover its liabilities in period t. A situation when CASH_t < PROD_t may mean a shortage of cash. It is worth noting, however, that an entrepreneur who mainly has to count on his own precaution can accumulate cash from periods of surplus over liabilities and use it during a period of current shortage. As such, consideration of the cumulative value of cash in subsequent periods of a given year and its comparison with the cumulative value of finished production may be a better solution.

Consequently, in this work, the difference between the cumulative monthly cash inflows and the cumulative value of finished production3 is used as the measure of financial liquidity in a small enterprise, i.e.,

LIQ_t = cum.CASH_t − cum.PROD_t,

(4)

where:

cum.CASH_t = cum.CASH_t-1 + CASH_t, in year t*,

cum.PROD_t = cum.PROD_t-1 + PROD_t, in year t*,

(t* = 1, …, n^*; t = 2, …, 12) and

cum.CASH₁ = CASH₁, and cum.PROD₁ = PROD₁.

Construction of the debt recovery efficiency measure necessitates calculation of the differences between the inflow amounts for the goods sold (CASH_t) and the value of concurrent (SBRUT_t) as well as the 1-month delayed (SBRUT_t−1) and two-month (SBRUT_t−2) gross sales revenues. It is therefore necessary to consider the following differences (Wiśniewski 2009):

VIND0_t = CASH_t − SBRUT_t,

(5)

VIND1_t = CASH_t − SBRUT_t−1,

(6)

VIND2_t = CASH_t − SBRUT_t−2.

(7)

A fully efficient debt recovery should be manifested by the values of the wind0_t measure that are close to zero in each of the periods t (t = 1, …, n). The sum of the values of the measure ${{\displaystyle \sum }}_{\mathrm{t}=1}^{12}\mathrm{VIND}{0}_{\mathrm{t}}$ in year t * (t* = 1, …, n *)4 should be close to 0. This means that the receivables for the goods and services sold were converted into cash. ${{\displaystyle \sum }}_{\mathrm{t}=1}^{12}\mathrm{VIND}{0}_{\mathrm{t}}$ cannot be expected to be positive. If, on the other hand, ${{\displaystyle \sum }}_{\mathrm{t}=1}^{12}\mathrm{VIND}{0}_{\mathrm{t}}$ is significantly lower than zero, it means inefficient debt recovery in the enterprise, which can even threaten its existence.

The measure of debt recovery efficiency (EVIND_t) is the arithmetic (moving) average of the detailed measures of debt recovery efficiency:

EVIND_t = (VIND0_t + VIND1_t + VIND2_t)/3.

(8)

The variable EVIND_t, having the nature of a moving average, is characterized by a much lower dispersion—compared with the detailed measures of debt recovery efficiency.

2.4. The Econometric Model Describing the Interdependence between Financial Liquidity and Debt Recovery Efficiency in an Enterprise

The practice of short-term financial management in a small enterprise requires simultaneous control of its financial liquidity and debt recovery efficiency. A low level of financial liquidity may result from low debt recovery activity. Improvement of debt recovery efficiency results in a company’s better financial liquidity. Decisions in this matter are made on an ongoing basis. We thus assume that the variables LIQ_t and EVIND_t form direct feedback, i.e.,

$${\mathrm{LIQ}}_{\mathrm{t}}\begin{array}{c}\to \\ \leftarrow \end{array}{\mathrm{EVIND}}_{\mathrm{t}}$$

(9)

The hypothetical system of two interdependent equations with endogenous variables LIQ_t and EVIND_t is identifiable ambiguously.

The equation describing financial liquidity contains, among its explanatory variables, an autoregression up to the twelfth order inclusive and an interdependent variable EVIND_t. In addition, the following predetermined variables occur in the equation:

EVIND_t-1, EVIND_t-2, …, EVIND_t-12 − debt recovery efficiency measures delayed by 1, 2, …, 12 months;

dummy variables, used to isolate monthly periodic fluctuations, take the value of 1 for the month distinguished and 0 in other periods (dm1, dm2, …, dm12). Additionally, the time variable t is taken into consideration to account for a possible linear and quadratic trend.

In the equation describing debt recovery efficiency, an explanatory variable LIQ_t and delayed endogenous variables LIQ_t−1, LIQ_t−2, …, LIQ_t−12 appear naturally. Additionally, the following is taken into account: autoregression up to the twelfth order inclusive, dummy variables describing monthly fluctuations, and the time variable t. In both equations, a variable SBRUT_t representing activity in the sales network—gross sales revenues (in PLN thousand) along with its delays from 1 to 12 months (SBRUT_t−1, SBRUT_t−2, …, SBRUT_t−12)—occurs as well. The variable SBRUT_t (along with delays) provides information on the intensity of the sales network service, which is always connected with concurrent debt recovery.

Monthly statistical data collected in a real small enterprise over 8 years was used in the study, i.e., the number of observations in the time series was n = 96. The measure’s construction (8) causes a loss of the two initial observations, which results in a reduction in the number n down to n = 94.

The parameters of both structural-form equations were estimated using the ordinary least squares method (OLS).5 The empirical results were used to estimate the forecasts of the variables LIQ_t and EVIND_t from the structural-form equations, using an iterative method,6 also called the “snail” method. The calculations were carried out using the GRETL package.

3. Results and Discussion

Table 1. Dependent variable: LIQ_t; observations used 1997:03–2003:12 (N = 82).

Variable	Coefficient	Std. Error	t-Statistic	Prob. p
const	35.7892	17.3869	2.0584	0.0433	**
SBRUT_1	0.264044	0.0980122	2.6940	0.0088	***
SBRUT_2	0.335448	0.0777751	4.3131	<0.0001	***
EVIND	1.11045	0.138434	8.0216	<0.0001	***
EVIND_11	−0.559677	0.16928	−3.3062	0.0015	***
dm1	−121.502	12.7075	−9.5614	<0.0001	***
dm9	−71.2396	15.4927	−4.5983	<0.0001	***
dm10	−79.0165	17.8276	−4.4323	<0.0001	***
LIQ_1	0.784919	0.0565033	13.8916	<0.0001	***
LIQ_4	−0.178276	0.054603	−3.2649	0.0017	***
LIQ_8	−0.142219	0.0560837	−2.5358	0.0135	**
LIQ_12	−0.19808	0.0589236	−3.3616	0.0013	***
Mean dependent var.	115.6671		S.D. dependent var.	61.88753
Sum squared resid.	46,539.15		S.E. of regression	25.78459
R-squared	0.849988		Adjusted R-squared	0.826414
F(11,70)	36.05710		Prob(F-statistic)	1.71 × 10−24
Log likelihood	−376.3475		Akaike info criterion	776.6950
Schwarz criterion	805.5756		Hannan-Quinn criterion	788.2901
Autocorrel. coeff. (rho1)	−0.093267		Durbin h-statistic	−0.982984

Source: own calculations using the GRETL package. Significance level: *** p-value ≤ 0.01 and ** 0.01 < p-value ≤ 0.05.

and

Table 2. Dependent variable: EVIND_t; observations used 1997:03–2003:12 (N = 82).

Variable	Coefficient	Std. Error	t-Statistic	Prob. p
Const	1.4823	12.6127	0.1175	0.9068
SBRUT	0.104745	0.0498141	2.1027	0.0395	**
SBRUT_1	−0.165433	0.0577255	−2.8659	0.0056	***
SBRUT_2	−0.343855	0.0654157	−5.2565	<0.0001	***
SBRUT_9	0.144591	0.0503366	2.8725	0.0055	***
LIQ	0.231299	0.0342227	6.7586	<0.0001	***
LIQ_2	−0.227186	0.0391187	−5.8076	<0.0001	***
LIQ_4	0.0773338	0.0342058	2.2608	0.0272	**
LIQ_8	0.0680115	0.0283642	2.3978	0.0195	**
LIQ_12	0.0823227	0.0301587	2.7297	0.0082	***
dm1	42.8764	8.72728	4.9129	<0.0001	***
dm2	28.7364	9.08009	3.1648	0.0024	***
dm3	23.8075	7.36668	3.2318	0.0020	***
dm6	−27.0287	8.3487	−3.2375	0.0019	***
dm7	−30.5163	7.37474	−4.1379	0.0001	***
dm8	−18.4091	7.1938	−2.5590	0.0129	**
dm11	−22.8948	7.9052	−2.8962	0.0052	***
EVIND_1	−0.262529	0.0822912	−3.1902	0.0022	***
EVIND_11	0.24579	0.0916589	2.6816	0.0093	***
Mean dependent var.	−4.453659		S.D. dependent var.	28.56555
Sum squared resid.	10,462.94		S.E. of regression	12.88714
R-squared	0.841699		Adjusted R-squared	0.796470
F(18,63)	18.60978		Prob(F-statistic)	1.10 × 10−18
Log likelihood	−315.1569		Akaike info criterion	668.3137
Schwarz criterion	714.0414		Hannan–Quinn criterion	686.6727
Autocorrel. coeff. (rho1)	0.096296		Durbin h-statistic	1.307605

Source: own calculations using the GRETL package. Significance level: *** p-value ≤ 0.01 and ** 0.01 < p-value ≤ 0.05.

present the empirical equations describing the variables LIQ_t and EVIND_t. They result from parameter estimation carried out via OLS using the GRETL package.

In both equations with endogenous variables that are forming the feedback (LIQ_t, EVIND_t), an external variable (SBRUT_t) appears, both current and with delays. Construction of financial liquidity and debt recovery efficiency forecasts requires prior determination of the variable SBRUT_t. The requisite of a systemic approach to the mechanisms in the enterprise forces consideration of a cycle containing the value of gross sales revenues. The following mechanism possible to occur in a small manufacturing enterprise should therefore be considered:

(10)

where:

CASH—the amount of cash inflows during a t period in thousands of PLN,

SBRUT—gross sales income during a t period in thousands of PLN,

PROD—the value of finished production (in sale prices) during a t period in thousands of PLN,

EMP—the number of employees calculated in full-time employment during a t period (number of people),

SAL—net salary paid to the company’s employees for their work during a t period in thousands of PLN.

Considering the mechanism (9), it is necessary to build an econometric model that would have the nature of a system of interdependent equations. The aim is to obtain an empirical equation describing the variable SBRUT_t, which is presented in

Table 3. Dependent variable: SBRUT_t; observations used 1997:03–2003:12 (N = 82).

Variable	Coefficient	Std. Error	t-Statistic	Prob. p
Const	49.3006	17.0179	2.8970	0.0051	***
PROD	0.314418	0.0822437	3.8230	0.0003	***
PROD_2	0.192879	0.0664748	2.9015	0.0050	***
PROD_4	0.266735	0.0627707	4.2494	<0.0001	***
PROD_6	0.260442	0.082139	3.1707	0.0023	***
PROD_10	−0.208976	0.0646183	−3.2340	0.0019	***
PROD_12	0.386798	0.0777756	4.9733	<0.0001	***
dm2	−56.4333	10.0217	−5.6311	<0.0001	***
dm3	−85.5183	13.8924	−6.1558	<0.0001	***
dm4	−119.789	13.0028	−9.2126	<0.0001	***
dm5	−85.7246	10.6554	−8.0452	<0.0001	***
dm6	−48.7422	9.82865	−4.9592	<0.0001	***
dm8	73.7642	10.896	6.7699	<0.0001	***
dm9	52.2021	9.87142	5.2882	<0.0001	***
SBRUT_11	−0.272401	0.0812169	−3.3540	0.0013	***
Mean dependent var.	119.9622		S.D. dependent var.	57.15374
Sum squared resid.	24,216.31		S.E. of regression	19.01151
R-squared	0.908476		Adjusted R-squared	0.889352
F(14,67)	47.50362		Prob(F-statistic)	3.30 × 10−29
Log likelihood	−349.5635		Akaike info criterion	729.1270
Schwarz criterion	765.2278		Hannan–Quinn criterion	743.6210
Autocorrel. coeff. (rho1)	−0.003106		Durbin–Watson stat.	1.955127

Source: own calculations using the GRETL package. Significance level: *** p-value ≤ 0.01.

. The statistically significant impact of the concurrent variable PROD_t on the gross sales revenues can be noticed. It therefore becomes necessary to describe finished production with an adequate empirical equation, which is presented in

Table 4. Dependent variable: PROD_t; observations used 1997:02–2003:12 (N = 83).

Variable	Coefficient	Std. Error	t-Statistic	Prob. p
Const	−3.90858	18.1577	−0.2153	0.8302
EMP_8	2.73307	0.920238	2.9700	0.0040	***
dm6	−25.1642	9.04259	−2.7828	0.0068	***
dm9	69.4314	9.99448	6.9470	<0.0001	***
dm10	61.4042	8.88592	6.9103	<0.0001	***
dm11	23.6176	8.78676	2.6879	0.0089	***
PROD_3	0.206534	0.0649295	3.1809	0.0021	***
PROD_11	0.235135	0.0640667	3.6702	0.0005	***
Mean dependent var.	104.7747		S.D. dependent var.	38.66778
Sum squared resid.	35,906.28		S.E. of regression	21.88037
R-squared	0.707141		Adjusted R-squared	0.679808
F(7,75)	25.87089		Prob(F-statistic)	1.25 × 10−17
Log likelihood	−369.6697		Akaike info criterion	755.3394
Schwarz criterion	774.6902		Hannan–Quinn criterion	763.1135
Autocorrel. coeff. (rho1)	0.042344		Durbin-Watson stat.	1.910283

Source: own calculations using the GRETL package. Significance level: *** p-value ≤ 0.01.

. In the equation describing PROD_t, the concurrent variable EMP_t turned out to be statistically insignificant, which reduces the system to a recursive mechanism. In Table 4, the volume of employment, delayed by 8 months, is statistically significant. It thus becomes possible to employ a recursive (chain) procedure to estimate PROD_Tp and SBRUT_Tp forecasts for the next 12 months.7 These forecasts are presented in

Table 5. Monthly forecasts of production (PROD_Tp) gross sales revenues (SBRUT_Tp) for the year 2004.

Forecasting Period (T)	PRODTp	Standard Error	SBRUTTp	Standard Error
2004:01	88.684	21.880	168.648	19.011
2004:02	85.928	21.880	95.923	19.011
2004:03	90.416	21.880	93.099	19.011
2004:04	77.993	22.342	47.225	19.011
2004:05	77.377	22.342	43.865	19.011
2004:06	55.791	22.342	54.994	19.011
2004:07	86.220	22.362	102.083	19.011
2004:08	92.371	22.362	164.770	19.011
2004:09	156.544	22.362	203.091	19.011
2004:10	149.041	22.363	146.991	19.011
2004:11	111.608	22.363	156.410	19.011
2004:12	95.7382	22.947	126.777	19.704

Source: own calculations using the GRETL package.

. Having the PROD_Tp and SBRUT_Tp forecasts, it is possible to use an iterative procedure to estimate the LIQ_Tp and EVIND_Tp forecasts.

In the first iteration, the feedback is “broken” (9). The research shows that the first LIQ_Tp forecasts can be estimated assuming realistic hypothetical values of the EVIND_Tp forecasts. In the first iteration, perfect efficiency of debt recovery was presumed, assuming that the forecasts values of EVIND_Tp = 0 (T = 1, 2, …, 12). The forecasts obtained under this assumption are presented in column It.1,

Table 6. Monthly forecasts of the company’s financial liquidity (LIQ_Tp) for the year 2004 in subsequent iterations.

Forecasting Period (T)	It.1	It.2	It.3	It.4	It.5	It.6	It.7	It.8	It.9
2004:01	89.921	94.333	95.464	95.746	95.823	95.849	95.849	95.849	95.849
2004:02	127.35	132.973	135.027	135.688	135.909	135.974	135.999	135.999	135.999
2004:03	137.833	162.894	169.537	171.359	171.902	172.045	172.084	172.109	172.109
2004:04	123.109	145.515	153.723	156.413	157.259	157.528	157.580	157.619	157.619
2004:05	121.819	146.299	152.093	153.742	154.240	154.415	154.477	154.503	154.503
2004:06	102.503	127.248	132.730	133.530	133.506	133.430	133.402	133.398	133.398
2004:07	67.6134	81.926	84.351	84.499	84.268	84.100	83.997	83.954	83.954
2004:08	76.199	86.111	84.967	83.679	83.073	82.839	82.732	82.685	82.685
2004:09	43.403	40.402	36.784	34.708	33.800	33.465	33.365	33.333	33.308
2004:10	57.774	13.359	−1.699	−6.352	−7.761	−8.183	−8.286	−8.314	−8.328
2004:11	115.165	43.355	18.479	10.492	8.152	7.531	7.355	7.337	7.325
2004:12	150.758	98.993	81.718	76.176	74.487	74.008	73.871	73.859	73.849

Source: own calculations using the GRETL package.

.

The financial liquidity forecasts in the first iteration can be used to construct EVIND_Tp forecasts, which are presented in the It.1 column,

Table 7. Monthly forecasts of the company’s debt recovery efficiency (EVIND_Tp) for the year 2004, in nine subsequent iterations.

Forecasting Period (T)	It.1	It.2	It.3	It.4	It.5	It.6	It.7	It.8	It.9
2004:01	3.973	4.991	5.245	5.3147	5.338	5.338	5.338	5.338	5.338
2004:02	1.949	3.000	3.396	3.5396	3.580	3.603	3.603	3.603	3.603
2004:03	18.591	23.121	24.294	24.627	24.710	24.727	24.750	24.750	24.750
2004:04	2.463	5.159	6.294	6.672	6.813	6.832	6.849	6.849	6.849
2004:05	6.916	6.513	6.142	6.005	5.977	5.996	5.992	5.992	5.992
2004:06	5.883	7.054	6.715	6.377	6.195	6.130	6.108	6.108	6.108
2004:07	−0.578	−1.203	−1.343	−1.447	−1.521	−1.588	−1.620	−1.620	−1.620
2004:08	2.406	0.980	0.147	−0.099	−0.149	−0.163	−0.169	−0.169	−0.169
2004:09	−5.213	−6.588	−7.246	−7.546	−7.650	−7.655	−7.646	−7.669	−7.669
2004:10	−33.183	−43.043	−45.552	−46.155	−46.302	−46.326	−46.329	−46.323	−46.323
2004:11	−27.765	−38.289	−41.930	−43.008	−43.278	−43.375	−43.375	−43.377	−43.377
2004:12	10.606	14.014	14.934	15.113	15.129	15.120	15.119	15.119	15.096

Source: own calculations using the GRETL package.

. These EVIND_Tp forecasts allow construction of LIQ_Tp forecasts in the second iteration (It.2 column, Table 6) and their comparison with the forecasts from the first iteration. In the case of a difference, the LIQ_Tp forecasts from the second iteration are used to build EVIND_Tp forecasts in the second iteration. The results are presented in the It.2 column, Table 7. A succeeding comparison ends the procedure, if the forecast values are repeated or a third iteration for the LIQ_Tp forecasts is performed. The calculations are continued until convergence is achieved, i.e., the forecast values are repeated in a subsequent iteration.

It can be noticed that the convergence8 of the EVIND_Tp forecasts for January was obtained after five iterations and for February after six iterations. Successively, after seven iterations, the forecasts for March, April, May, June, July, and August converged. Eight iterations were needed to obtain convergence of the EVIND_Tp forecasts for September, October, and November. Finally, after nine iterations, the EVIND_Tp forecast for December 2004 converged.

The LIQ_Tp forecasts converged slightly differently. The convergent forecast for January appeared after six iterations, whereas for February after seven iterations. After eight iterations, convergent forecasts were obtained for the period from March to August. In turn, after nine iterations, convergent LIQ_Tp forecasts were obtained for the last four months of the year. The iterative procedure applied led to an automatic synchronization of the EVIND_Tp and LIQ_Tp forecast values, as part of the feedback (9).

Table 8. Convergent monthly forecasts of the company’s financial liquidity (LIQ_Tp) and debt recovery efficiency (EVIND_Tp) for the year 2004.

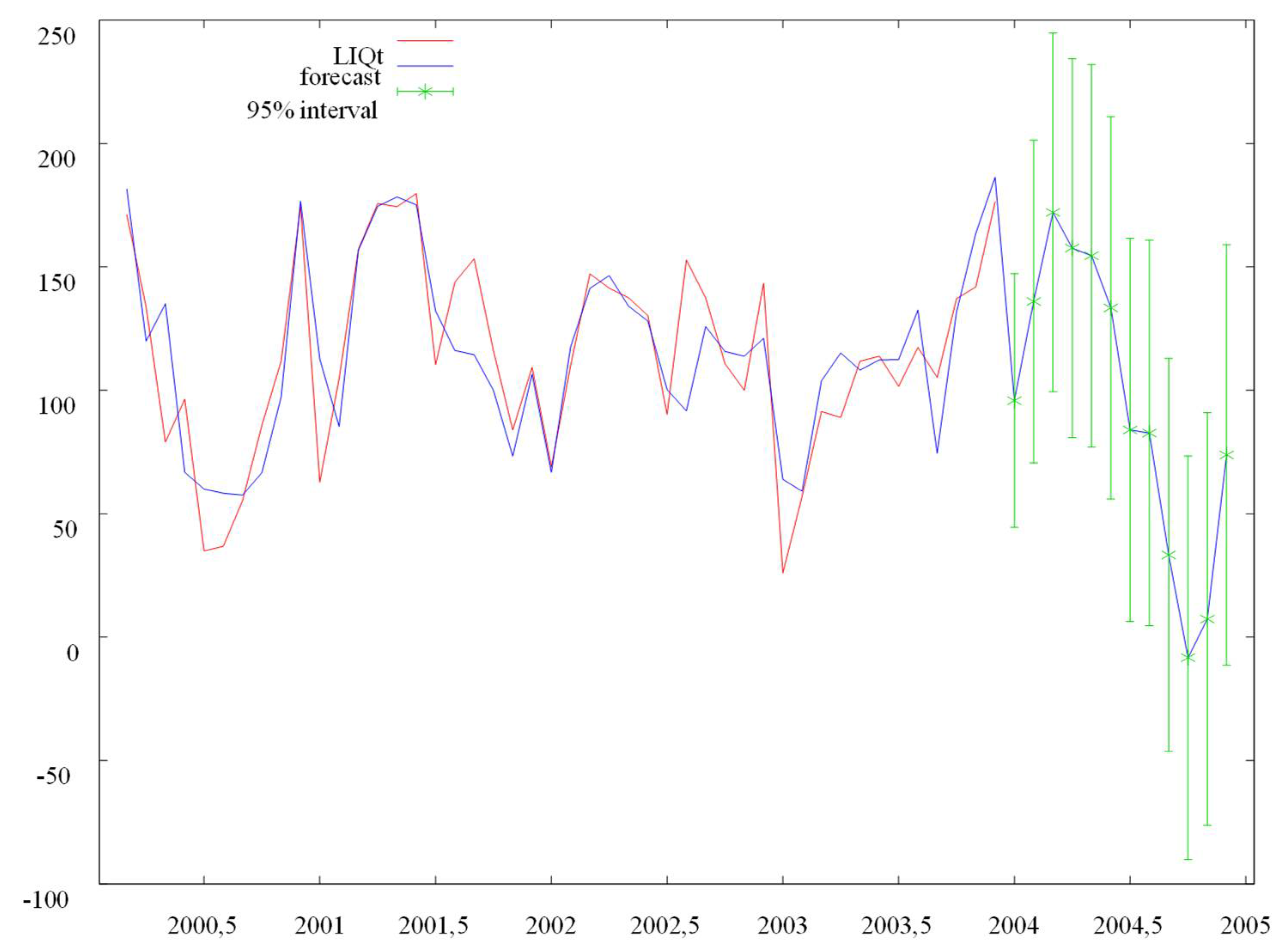
Forecasting Period (T)	Forecasts LIQTp	Forecasts EVINDTp
2004:01	95.849	5.338
2004:02	135.999	3.603
2004:03	172.109	24.750
2004:04	157.619	6.849
2004:05	154.503	5.992
2004:06	133.398	6.108
2004:07	83.954	−1.620
2004:08	82.685	−0.169
2004:09	33.308	−7.669
2004:10	−8.328	−46.323
2004:11	7.325	−43.377
2004:12	73.849	15.096

Source: Table 6 and Table 7.

and Figure 1 and Figure 2 present synchronized convergent forecasts of the financial variables under consideration. Possession of such forecasts facilitates the process of decision rationalization in the area of the company’s financial management.

The forecasts estimated show that in 2004 no risk of losing or low financial liquidity occured in the company. A slight shortage of liquidity in October 2004 is compensated for by a significant excess liquidity in the first half of the year. The well-known principle of prudence exercised by small entrepreneurs who accumulate cash in the periods of excess liquidity makes secure their financial situation. The condition is to maintain or even improve the debt recovery efficiency, which is slightly lower specifically in the periods of increased gross sales revenues. The forecasts presented in Table 8 cannot be a cause of concern for the entrepreneur. On the other hand, they cannot be the reason for the feeling of blissful peace that would lull the entrepreneur into a false sense of security, either.

4. Conclusions

Rational small enterprise management requires the development of a system, within an organization, for collection of important statistical information about its internal functioning. Companies are obliged to register statistical data only, which mainly serve the needs of the state, to secure its tax interests. The type of the statistical data needed for the effective running of a small business must be indicated within the system of educational management specialists. Such information includes all closed-cycle-type elements (10), allowing a large variety of ways for the processing thereof. One example of such use is the dynamic measures of financial liquidity and debt collection efficiency proposed in this paper. The importance of small business liquidity is widely acknowledged while there is little understanding of the issue of debt collection efficiency, especially in terms of its measurement.

Creation of time series for small company variables such as CASH, SBRUT, PROD, EMP, SAL, and further on for LIQ and EVIND should constitute the foundation for business decision rationalization. Demonstration of the possible ways to describe these variables using a system of econometric equations enables familiarization with the volatility mechanisms of important company characteristics. The results of such modeling should be used for forecasting. Forecasts—even if they are not sufficiently accurate—provide entrepreneurs with a view of the direction of changes in the company’s future characteristics. They allow the company to prepare for possible threats to financial liquidity, which should result in intensification of debt collection activities, which in turn prevents the loss of liquidity.

The feedback between the measure of financial liquidity and debt collection efficiency results in the necessity to use the iterative procedure of forecast construction from the econometric micromodel presented in this paper. Only this procedure allows the development of forecasting solutions in which synchronization of the forecast values within this feedback appears. Possible use of the traditional forecasting approach, consisting in the application of reduced form micromodel equations, results in a lack of synchronized forecasts, i.e., in the construction of divergent forecasts. The iterative procedure of forecasting the future values of the variables describing various aspects of an enterprise can increase the effectiveness of small business management, reducing the risk of inaccurate decisions. In the near future, the need to urge small business managers to collect the statistical data indicated here and to use low-complexity econometric methods for diagnosing and forecasting the business’ financial situation will emerge.

Subsequent scientific research on the empirical links between small business liquidity and debt collection efficiency and the variety of directions in which the results can be used may contribute to the development of financial management theory and practice in this group of companies.