Assessing the Impact of the COVID-19 Shock on a Stochastic Multi-Population Mortality Model
Abstract
:1. Introduction
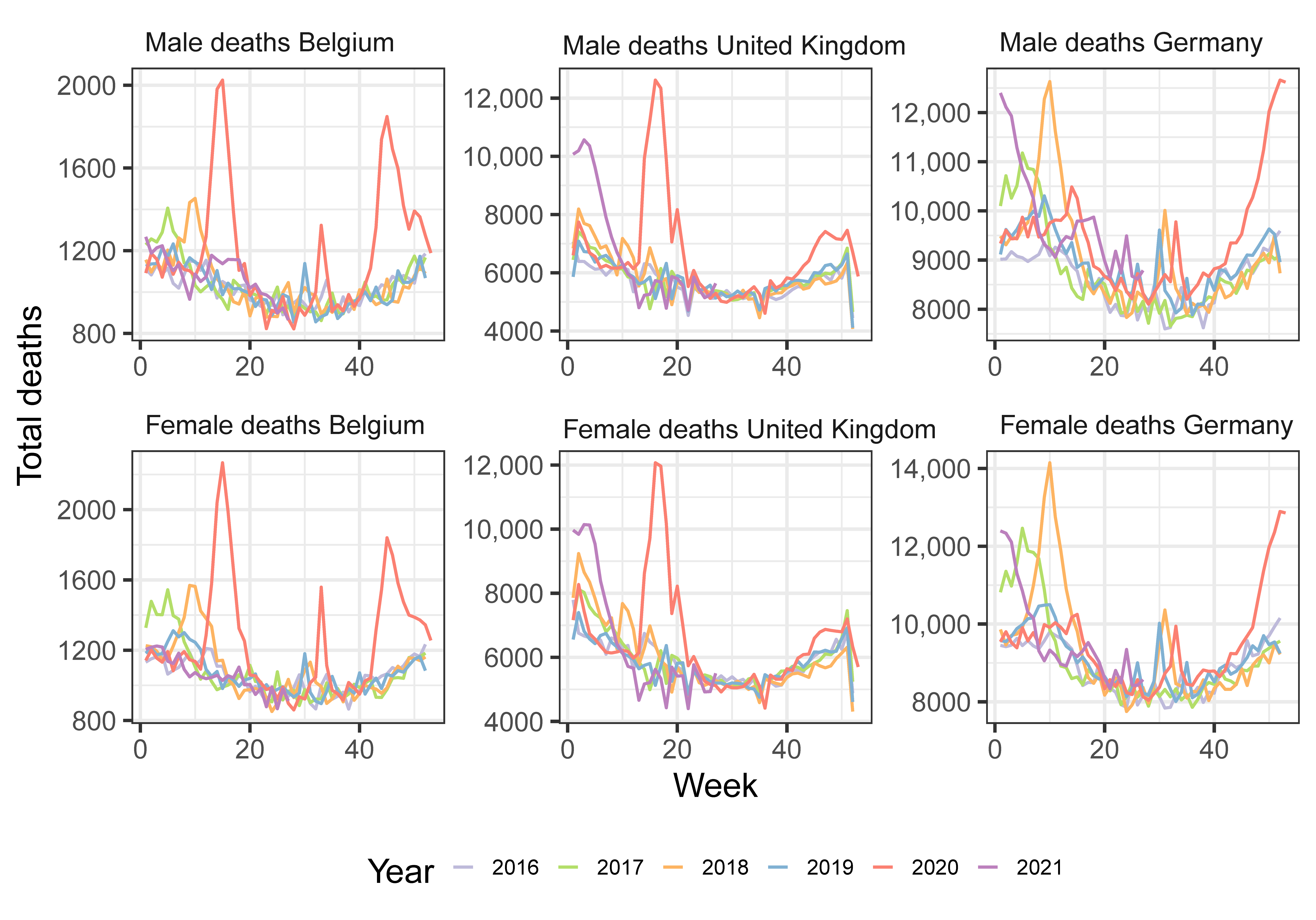
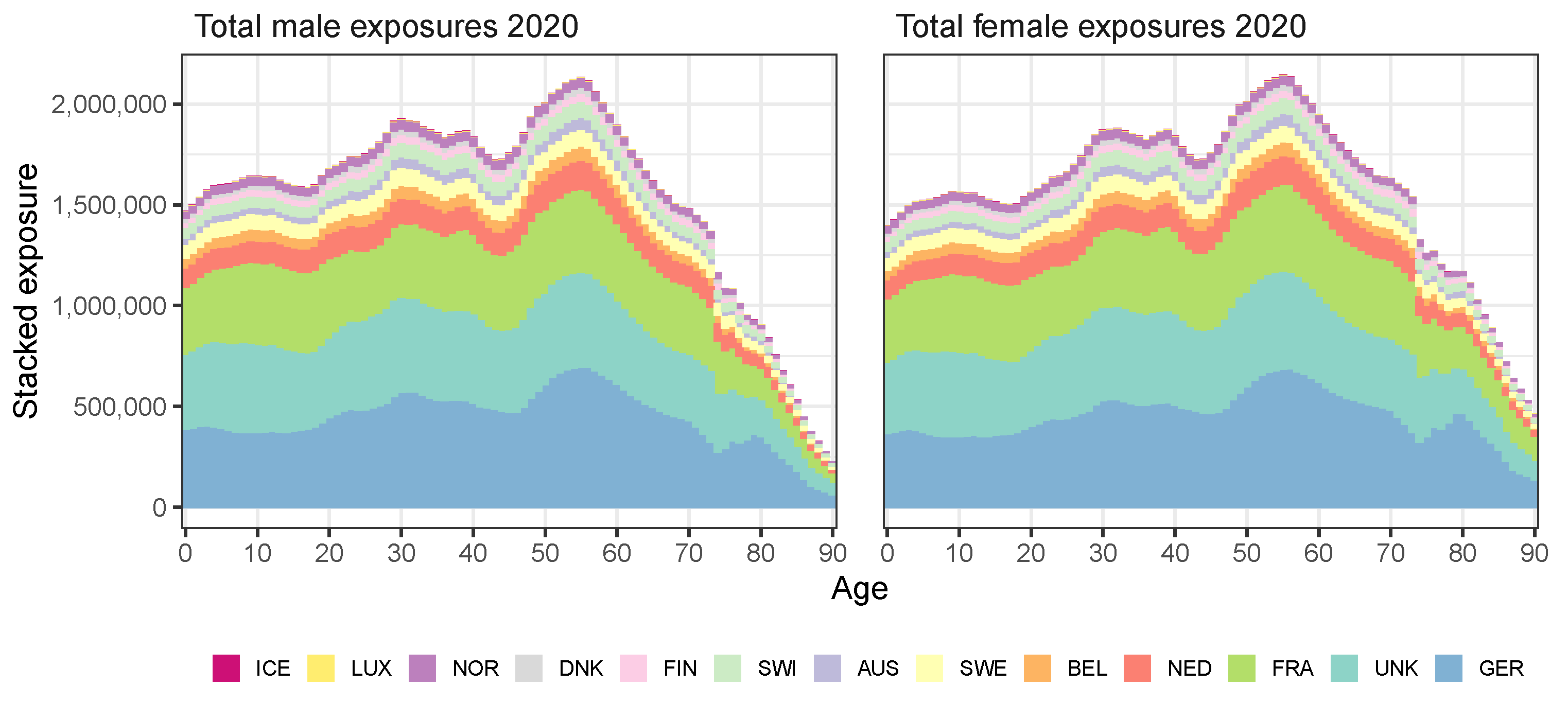
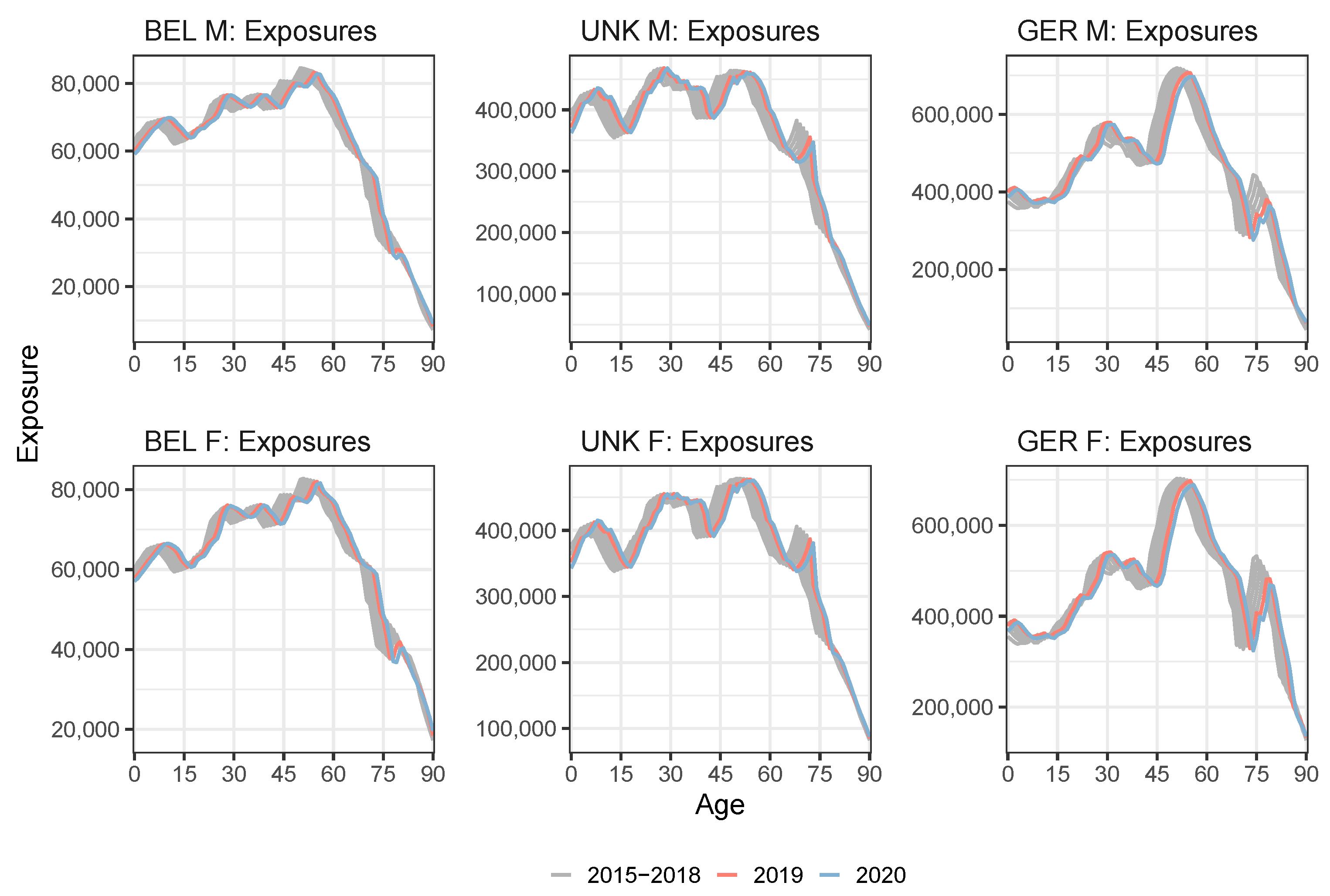
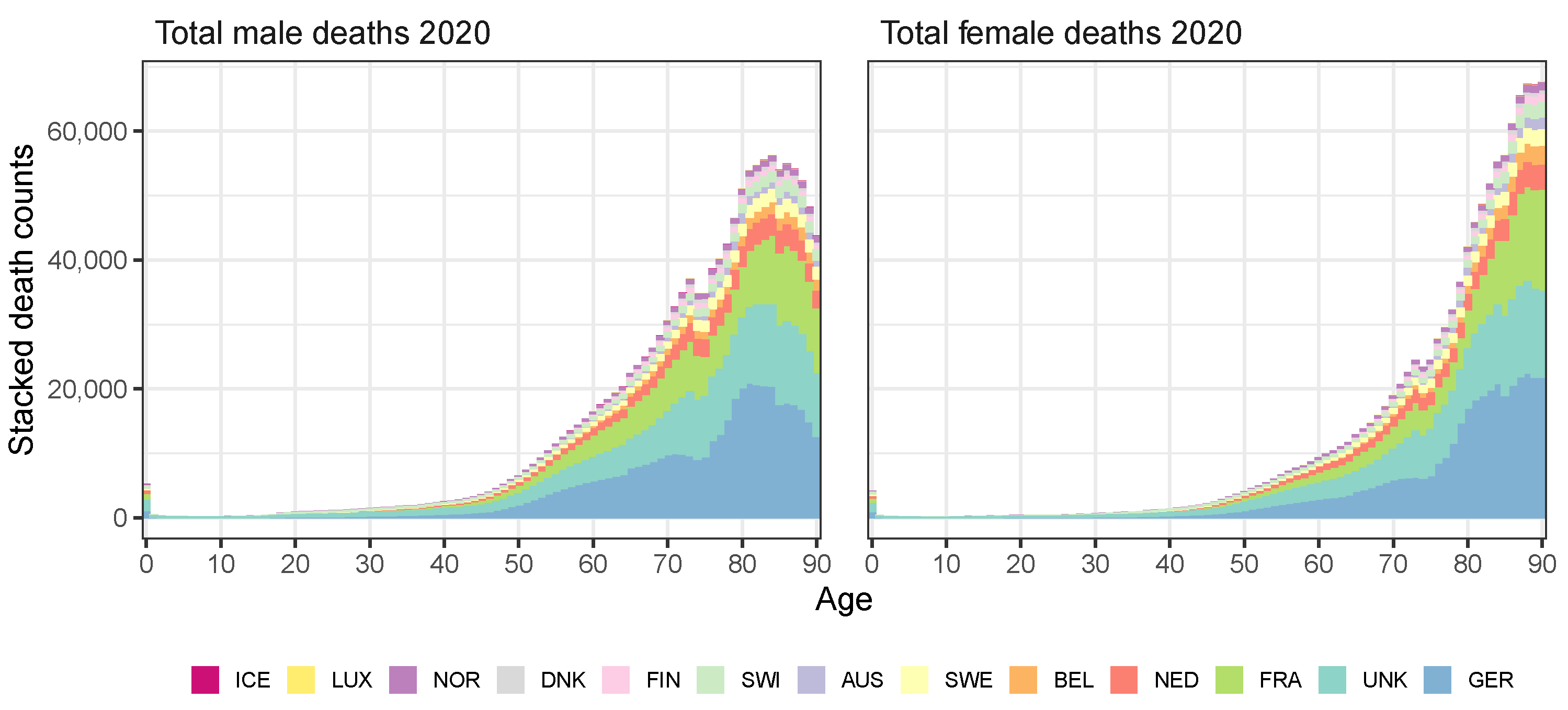
2. Data and Notation
3. A Stochastic Multi-Population Mortality Standard of Type Li and Lee
3.1. The Li and Lee Mortality Model
- 1.
- In a first step, we calibrate the parameters , and in the common mortality trend by assuming that the total number of deaths random variable follows a Poisson distribution with mean . Hereto, we maximize the following Poisson log-likelihood:where and are the observed number of deaths and exposures, respectively, aggregated over the collection of countries. Furthermore, . In this first calibration step, we impose the constraints in Equation (3) on and .
- 2.
- In a second step, we calibrate the country-specific parameters and by assuming that the number of deaths random variable , in the country of interest c, follows a Poisson distribution with mean . Hereto, we maximize the Poisson log-likelihood, conditional on the estimates obtained in step 1:where and are the observed number of deaths and exposures in country c, respectively. Furthermore, we have . In this second calibration step, we impose the Lee and Carter constraints in Equation (3) on and .
3.2. The Time Dynamics
3.3. Generating Future Paths of Mortality Rates and Life Expectancies
3.4. The Li and Lee Mortality Model for the Belgian Population
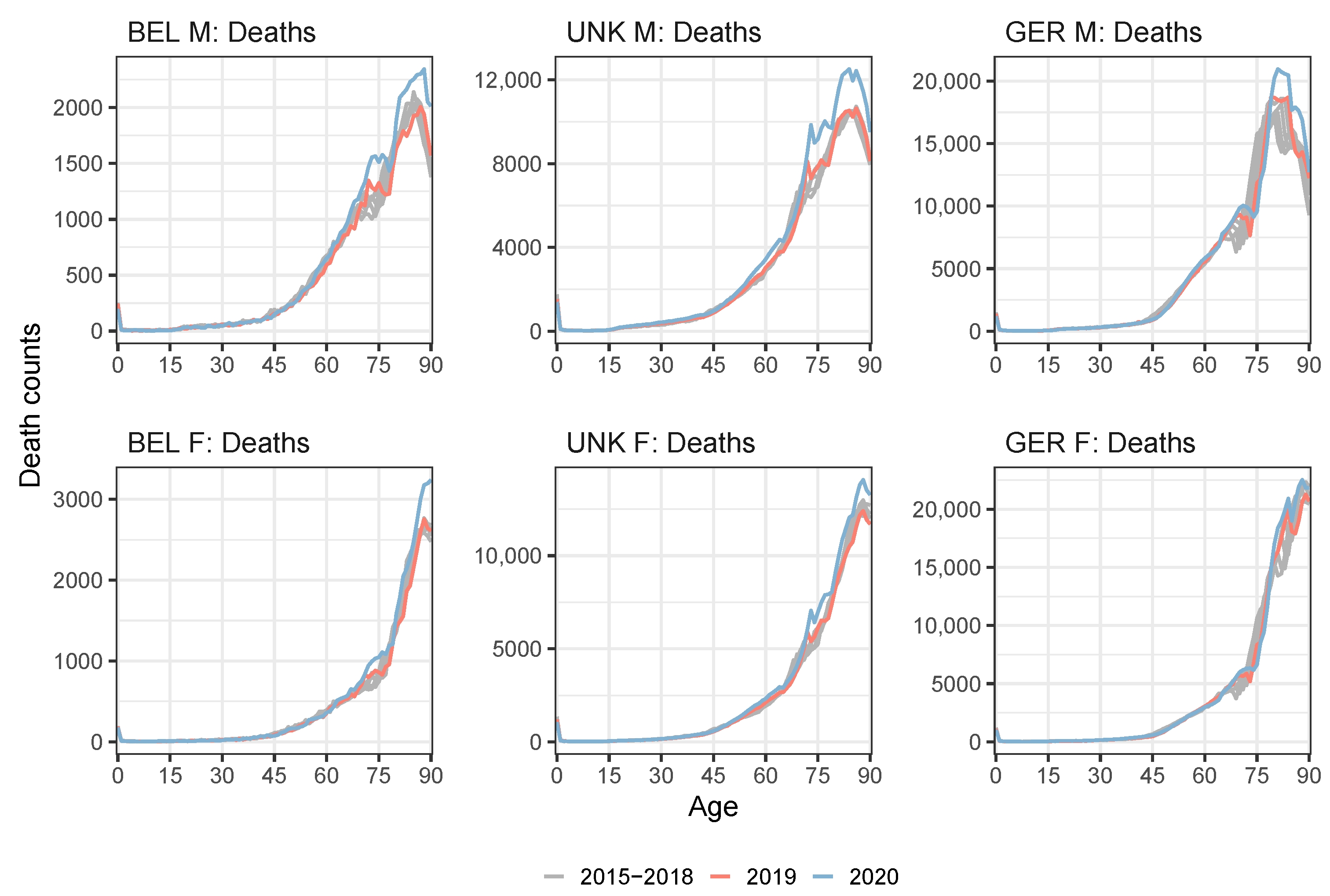
4. Transforming Weekly Mortality Data in Age Buckets to Annual Mortality Data at Individual Ages
4.1. From Weekly to Annual Mortality Data Registered in Age Buckets
4.2. Ungrouping Data from Age Buckets to Individual Ages
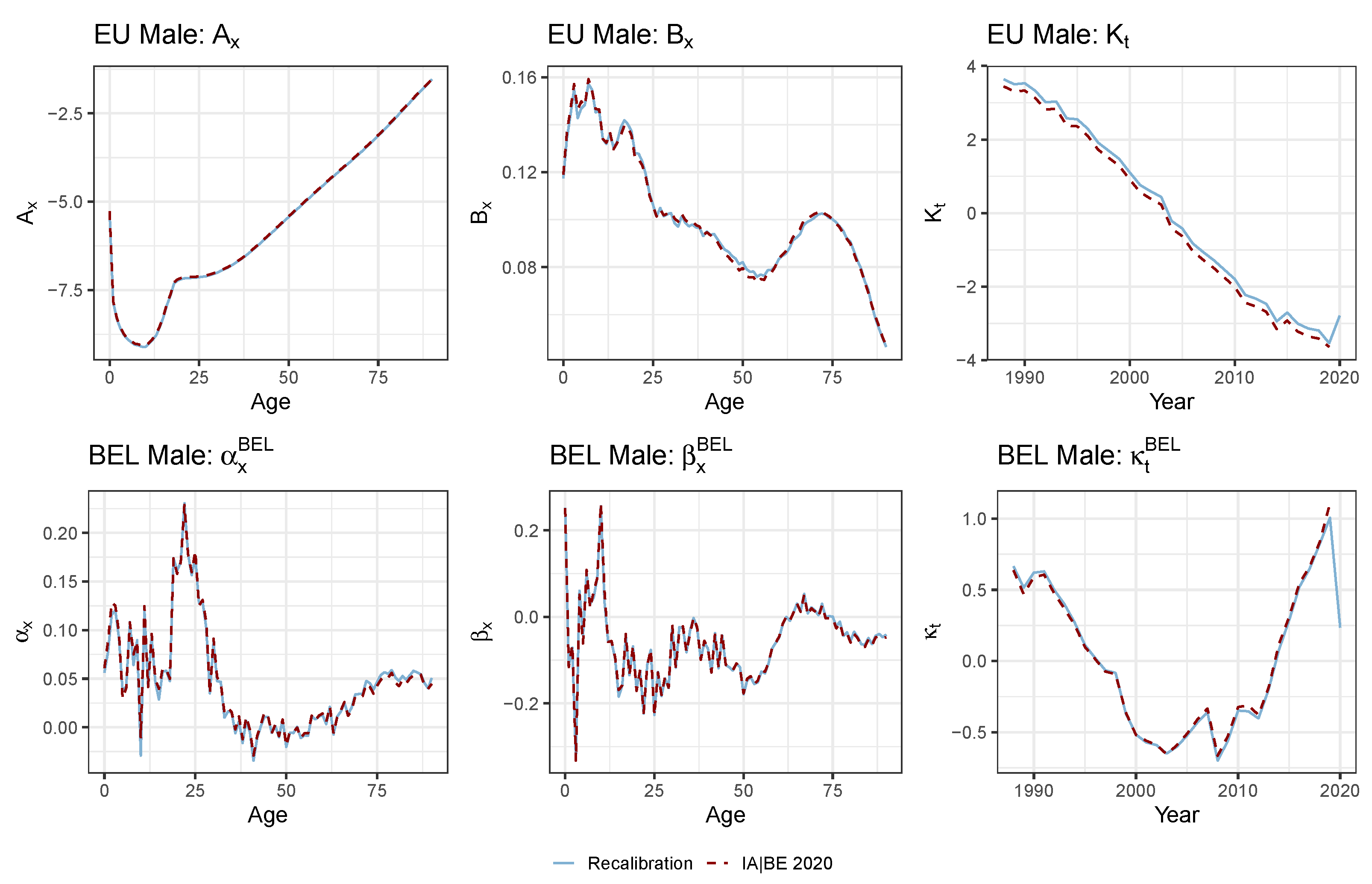
4.3. Applying the Protocol to the Multi-Population Data Set to Recalibrate the Li and Lee Mortality Model for the Belgian Population
5. Assessing the Impact of a Pandemic Shock on the Multi-Population Mortality Model
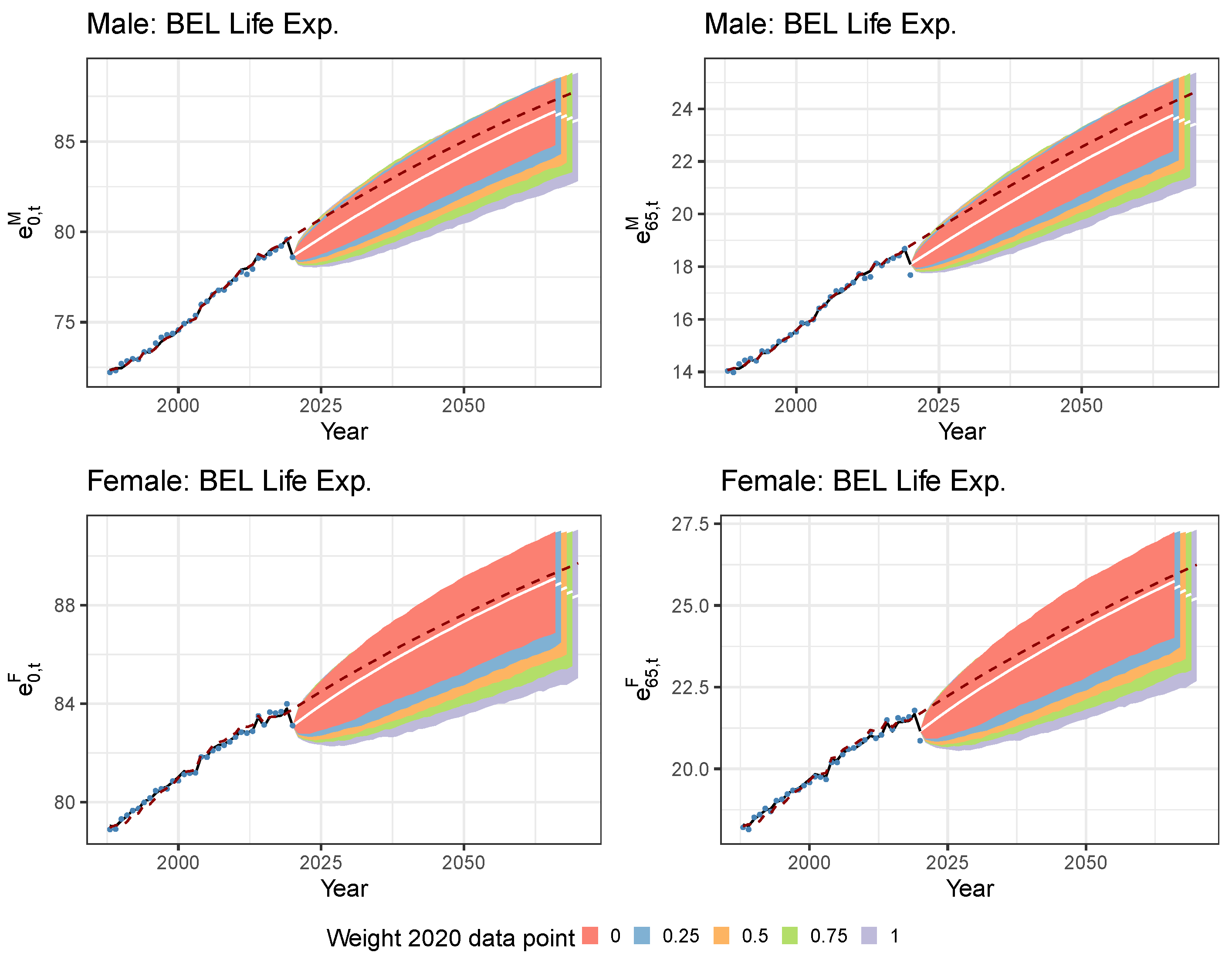
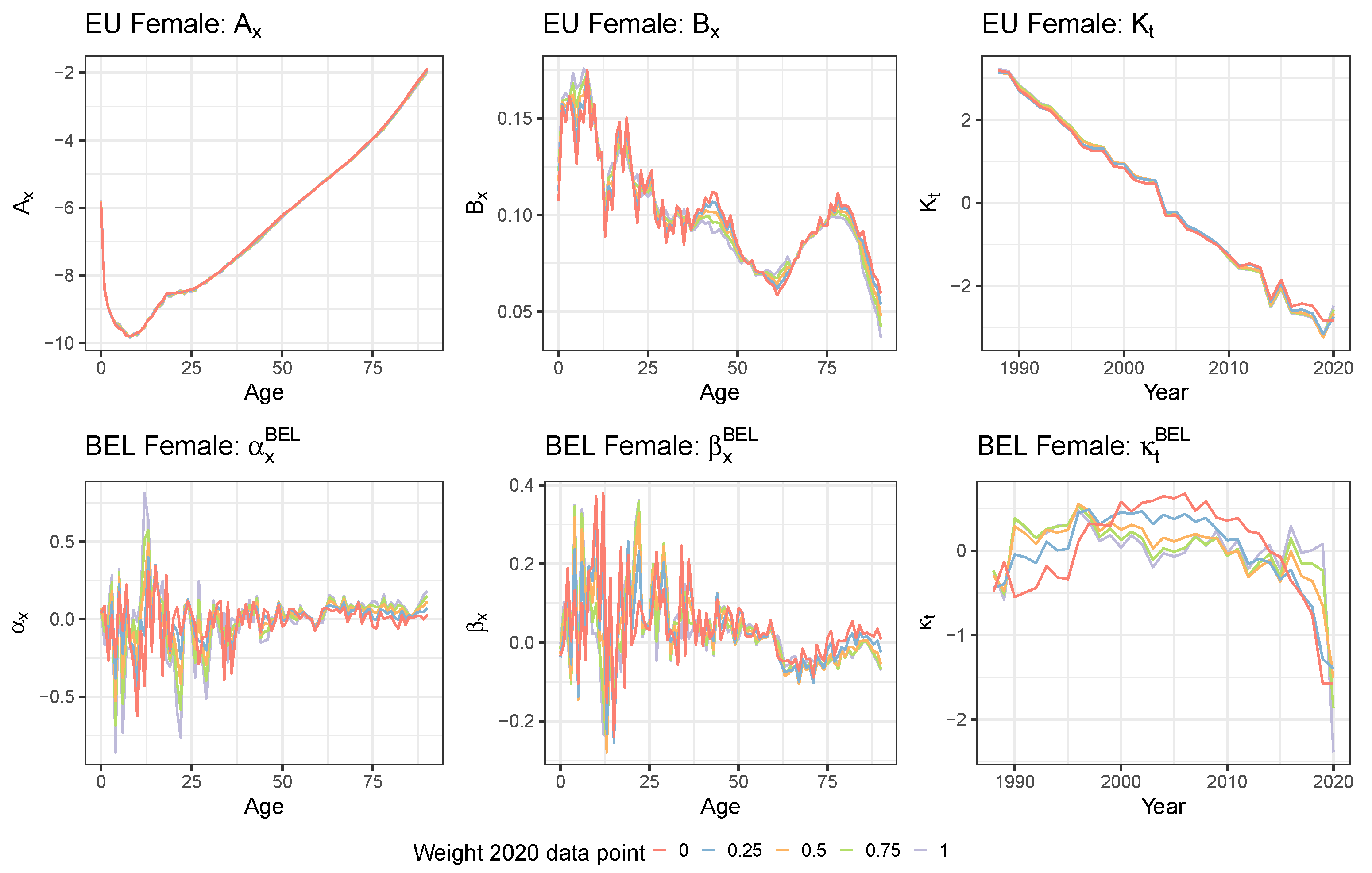
5.1. Limiting the Time Series Likelihood Contribution of the Pandemic Data Point
5.2. Mitigating the Impact of the Pandemic Data Point with a Lee and Miller Inspired Mortality Model
6. Addressing a Mortality Shock in a Mortality Prediction Model: A Literature Review
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Data Sources
| Country | Exposures | Deaths | ||||||
|---|---|---|---|---|---|---|---|---|
| 2017 | 2018 | 2019 | 2020 | 2017 | 2018 | 2019 | 2020 | |
| AUS | HMD | HMD | HMD | STMF | HMD | HMD | HMD | EURO.W |
| BEL | HMD | HMD | EURO | STMF | HMD | HMD | EURO | STATBEL |
| DNK | HMD | HMD | HMD | HMD | HMD | HMD | HMD | HMD |
| FIN | HMD | HMD | HMD | STMF | HMD | HMD | HMD | EURO.W |
| FRA | HMD | HMD | EURO | STMF | HMD | HMD | EURO | STMF |
| GER | HMD | EURO | EURO | STMF | HMD | EURO | EURO | STMF |
| ICE | HMD | HMD | EURO | STMF | HMD | HMD | EURO | EURO.W |
| LUX | HMD | HMD | HMD | STMF | HMD | HMD | HMD | EURO.W |
| NED | HMD | HMD | HMD | STMF | HMD | HMD | HMD | EURO.W |
| NOR | HMD | HMD | EURO | STMF | HMD | HMD | EURO | EURO.W |
| SWE | HMD | HMD | HMD | STMF | HMD | HMD | HMD | EURO.W |
| SWI | HMD | HMD | EURO | STMF | HMD | HMD | EURO | EURO.W |
| UNK | HMD | HMD | STMF | STMF | HMD | HMD | STMF | STMF |
Appendix B. Constructing Virtual Exposure Points
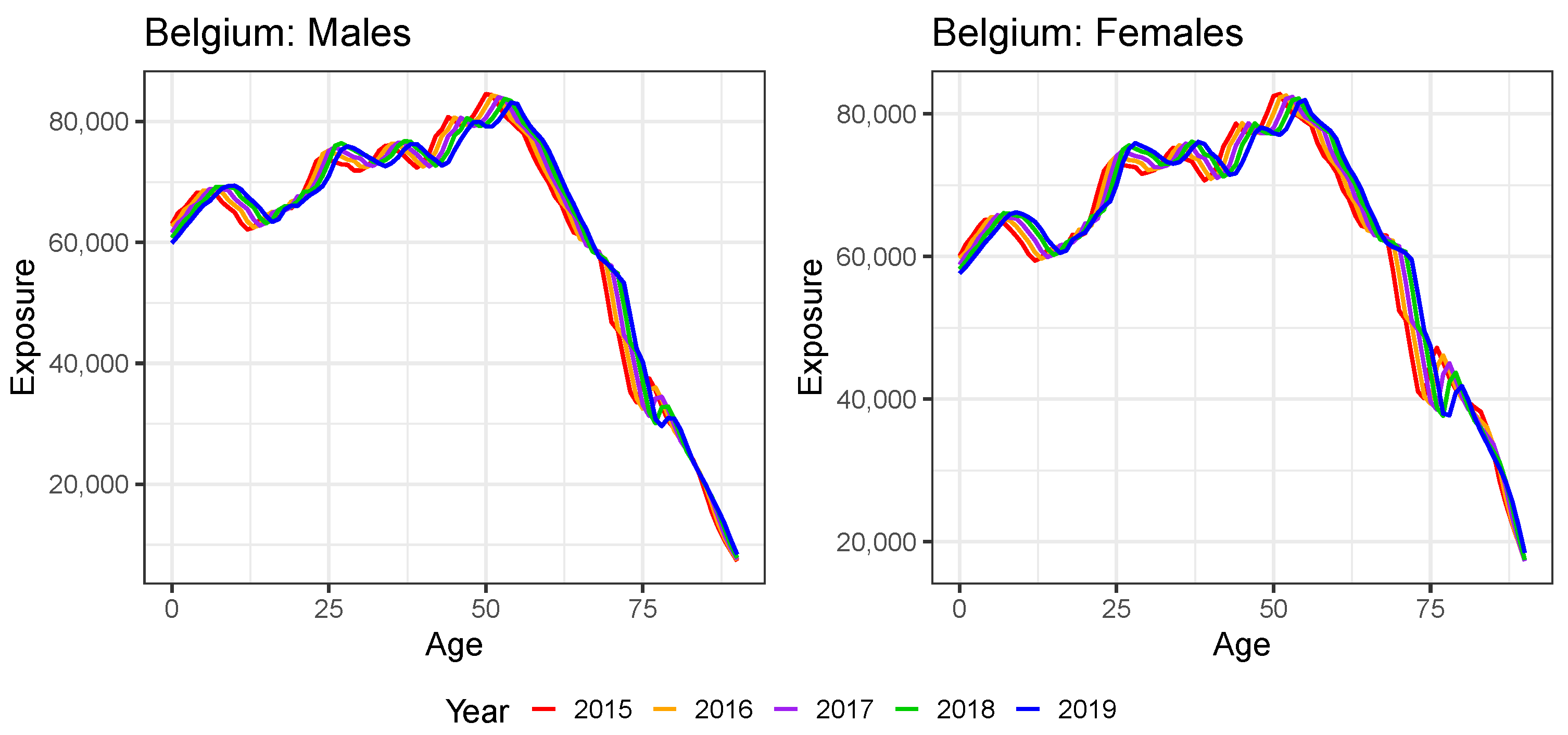
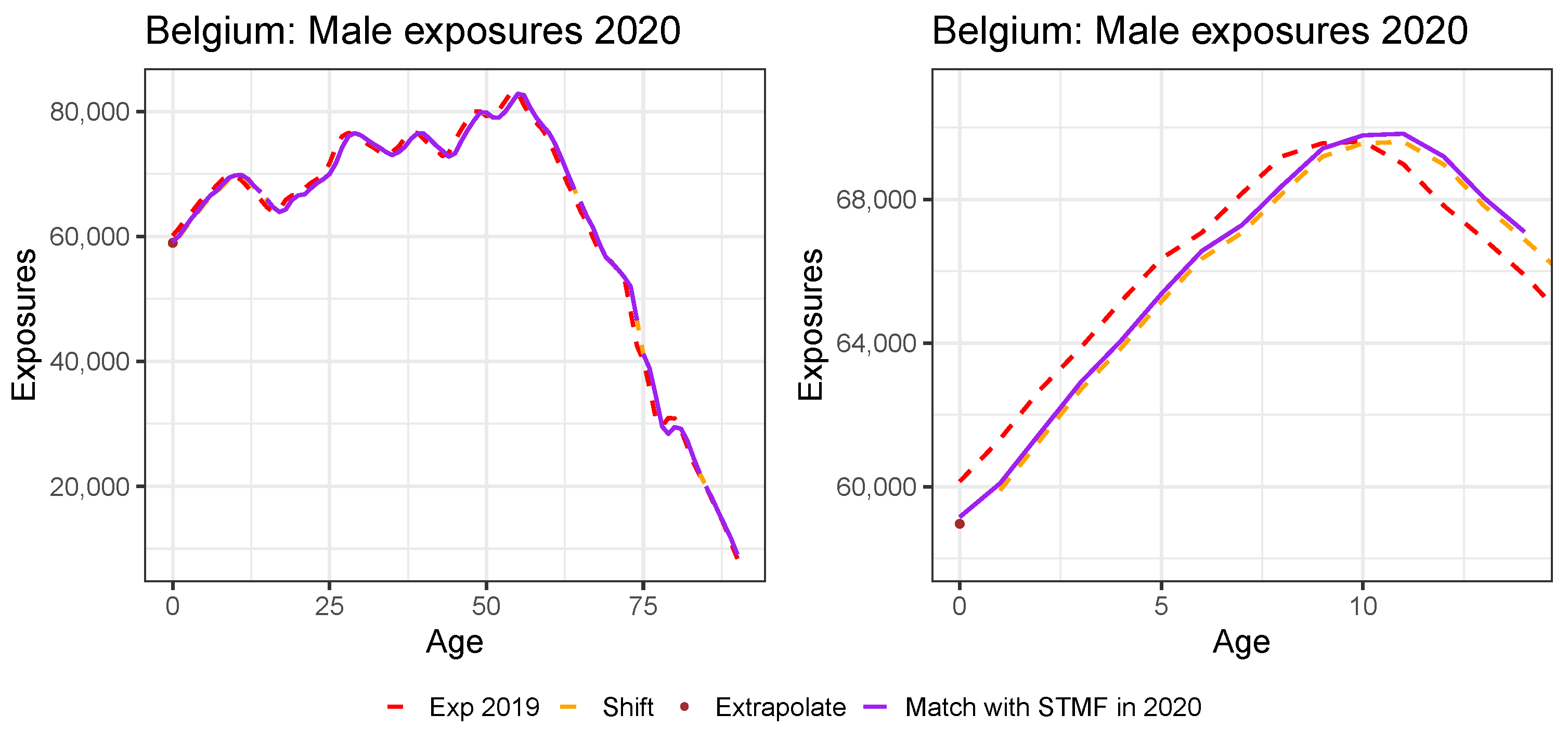
| Age Bucket | Male Exp. | Female Exp. |
|---|---|---|
| 988,713.02 | 944,379.40 | |
| 3,699,434.72 | 3,638,808.41 | |
| 568,101.96 | 618,244.99 | |
| 305,175.72 | 399,015.96 | |
| 112,577.56 | 223,565.55 |
Appendix C. Constructing Virtual Death Counts

| Age Bucket | Male Deaths | Female Deaths |
|---|---|---|
| 410 | 325 | |
| 27 | 27 | |
| 41 | 38 | |
| 115 | 68 | |
| ⋯ | ⋯ | ⋯ |
| 12,730 | 9202 | |
| 15,125 | 12,899 | |
| 14,737 | 17,246 | |
| 12,231 | 24,974 |

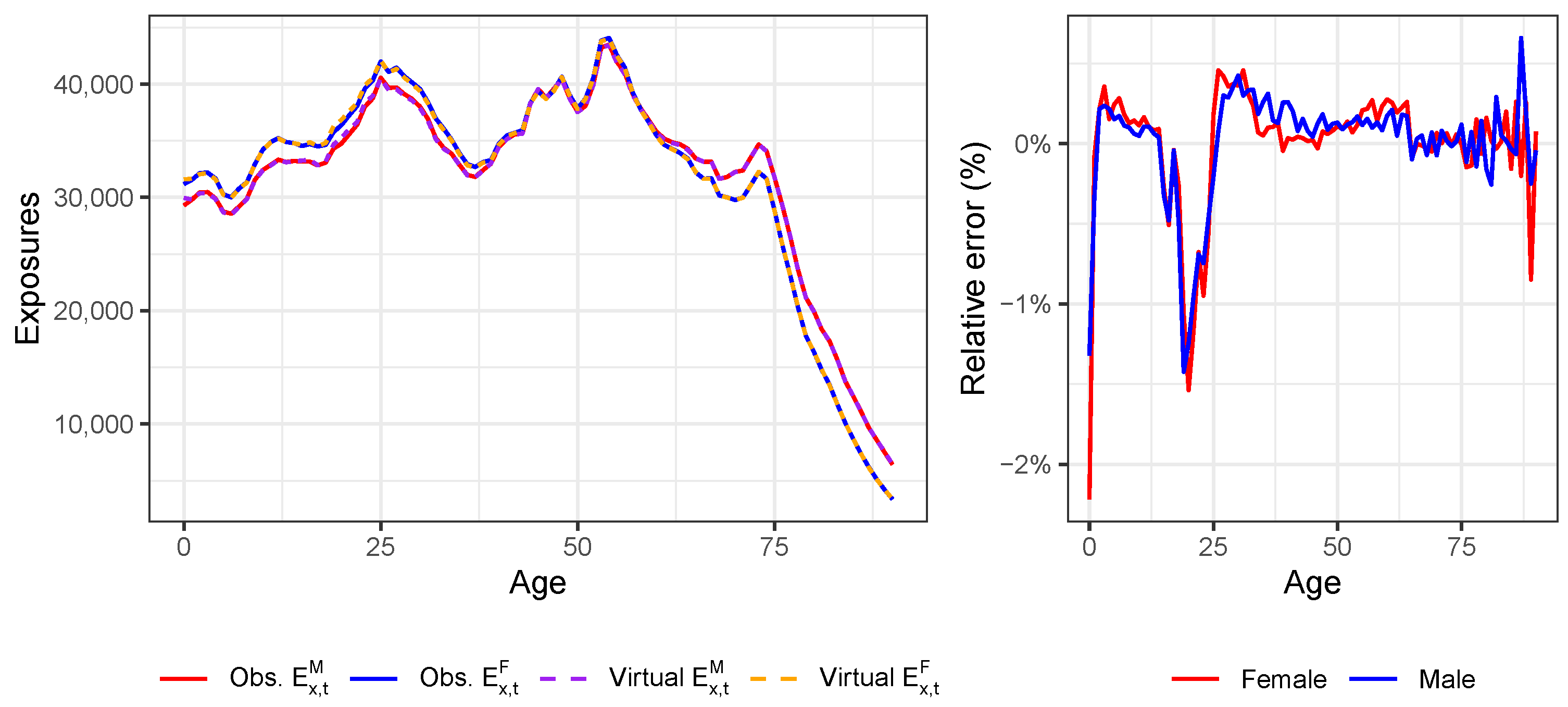
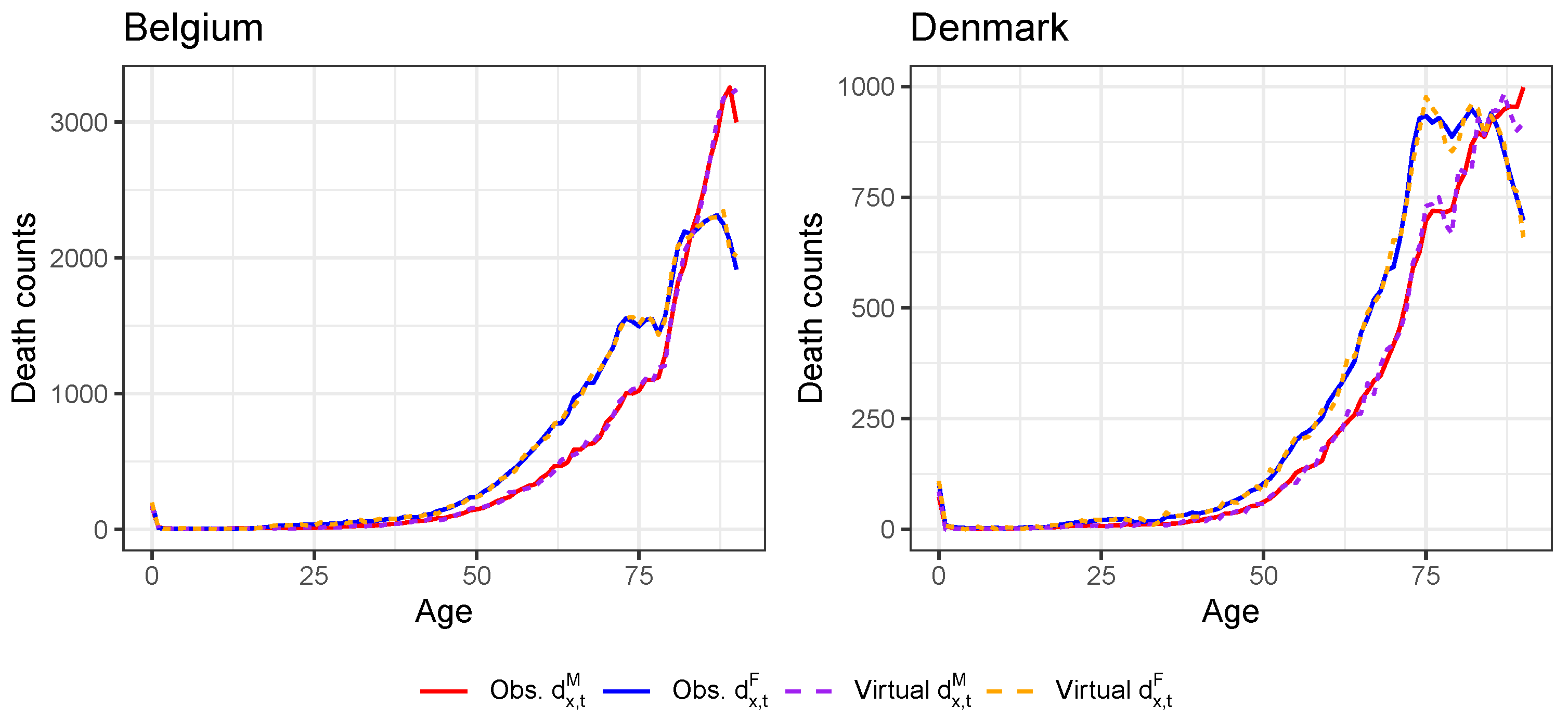
Appendix D. Validation of the Constructed Virtual Death Counts and Exposure Points
| 1 | Numbers are retrieved from https://www.statista.com/statistics/1102209/coronavirus-cases-development-europe/ (accessed on 13 December 2021) and https://www.statista.com/statistics/1102288/coronavirus-deaths-development-europe/ (accessed on 13 December 2021) and represent the situation at 5 December 2021. |
| 2 | These numbers of COVID-19 deaths come from the COVID-19 Dashboard by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU), see https://www.arcgis.com/apps/opsdashboard/index.html#/bda7594740fd40299423467b48e9ecf6 (accessed on 13 December 2021). |
| 3 | See https://ec.europa.eu/info/live-work-travel-eu/coronavirus-response/safe-covid-19-vaccines-europeans_en (accessed on 21 October 2021) for an overview of the approved, European COVID-19 vaccines and those currently under development, as well as corresponding references. |
| 4 | See https://www.actuaries.org.uk/learn-and-develop/continuous-mortality-investigation/cmi-working-papers/mortality-projections (accessed on 9 November 2021). |
| 5 | This database is our primary database and can be consulted at https://www.mortality.org/ (accessed on 13 April 2021). |
| 6 | Eurostat is the statistical office of the European Union, see https://ec.europa.eu/eurostat (accessed on 13 April 2021). |
| 7 | Statbel is the Belgian statistical office, see https://statbel.fgov.be/en (accessed on 13 April 2021). |
| 8 | This information can be explored using the visualization toolkit on https://mpidr.shinyapps.io/stmortality/ (accessed on 30 July 2021). |
| 9 | Eurostat provides weekly death statistics at https://ec.europa.eu/eurostat/web/COVID-19/data (accessed on 30 July 2021). |
| 10 | The years 1992, 1998, 2004, 2009, 2015 and 2020 contain 53 weeks instead of the usual 52 weeks (ISO 8601 standard). |
| 11 | The HMD team uses a Lee and Carter model to extrapolate recent exposures. The documentation can be consulted via https://www.mortality.org/Public/STMF_DOC/STMFNote.pdf (accessed on 30 July 2021). |
| 12 | See https://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=demo_r_mwk_05&lang=en (accessed on 30 July 2021). |
| 13 | Eurostat only provides weekly death counts for Germany for age buckets of length 10. |
| 14 | We use the nlminb-function in the stats-package of R. |
| 15 | See https://data.worldbank.org/indicator/NY.GDP.PCAP.CD (accessed on 16 June 2021). |
| 16 | See https://www.iso.org/iso-8601-date-and-time-format.html (accessed on 3 November 2021). |
| 17 | The years 1992, 1998, 2004, 2009, 2015 and 2020 contain 53 weeks. |
| 18 | |
| 19 | The case corresponds to the Lee and Miller mortality model as discussed in Lee and Miller (2001). |
| 20 | For all countries except the United Kingdom, we do have the annual exposures at an individual age level in 2019 from either HMD or Eurostat (see Table A1). For Denmark, we already have the annual exposures at an individual age level in the year 2020 available from the HMD. |
| 21 | We use the exposure points and to linearly extrapolate to age 0:
|
| 22 | For all countries except the United Kingdom, we do have the annual death counts at individual ages in 2019 from either HMD or Eurostat (see Table A1). For Belgium and Denmark, we even have the annual death counts at an individual age level in 2020 available from HMD and Statbel, respectively. For these two countries, there is no need to create virtual death counts. |
| 23 | For Belgium and Denmark, we already have the death counts at individual ages in 2020 from Statbel and HMD, respectively. We take the average of both ratios. |
| 24 | We only use the weekly death counts collected in age buckets from Eurostat when they match the reported death counts in the larger age buckets from the STMF data series. We do this for safety reasons because some deviations between the weekly death counts on Eurostat and the STMF data series may occur due to for example territorial differences, e.g., France with or without overseas regions. |
References
- Antonio, Katrien, Anastasios Bardoutsos, and Wilbert Ouburg. 2015. Bayesian poisson log-bilinear models for mortality projections with multiple populations. European Actuarial Journal 5: 245–81. [Google Scholar] [CrossRef]
- Antonio, Katrien, Sander Devriendt, and Jens Robben. 2020. The IA∣BE 2020 Mortality Projection for the Belgian Population. Available online: https://katrienantonio.github.io/papers/report_iabe_2020.pdf (accessed on 24 February 2021).
- Antonio, Katrien, Sander Devriendt, Wouter de Boer, Robert de Vries, Anja De Waegenaere, Hok-Kwan Kan, Egbert Kromme, Wilbert Ouburg, Tim Schulteis, Erica Slagter, and et al. 2017. Producing the Dutch and Belgian mortality projections: A stochastic multi-population standard. European Actuarial Journal 7: 297–336. [Google Scholar] [CrossRef]
- Börger, Matthias, Daniel Fleischer, and Nikita Kuksin. 2014. Modeling the mortality trend under modern solvency regimes. ASTIN Bulletin: The Journal of the IAA 44: 1–38. [Google Scholar] [CrossRef] [Green Version]
- Brouhns, Natacha, Michel Denuit, and Jeroen K. Vermunt. 2002. A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics 31: 373–93. [Google Scholar] [CrossRef] [Green Version]
- Cairns, Andrew J. G., David Blake, Kevin Dowd, Guy D. Coughlan, David Epstein, Alen Ong, and Igor Balevich. 2009. A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal 13: 1–35. [Google Scholar] [CrossRef]
- Chen, Hua, and J. David Cummins. 2010. Longevity bond premiums: The extreme value approach and risk cubic pricing. Insurance: Mathematics and Economics 46: 150–61. [Google Scholar] [CrossRef]
- Chen, Hua, and Samuel H. Cox. 2009. Modeling mortality with jumps: Applications to mortality securitization. The Journal of Risk and Insurance 76: 727–51. [Google Scholar] [CrossRef]
- Cox, Samuel H., Yijia Lin, and Shaun Wang. 2006. Multivariate exponential tilting and pricing implications for mortality securitization. Journal of Risk and Insurance 73: 719–36. [Google Scholar] [CrossRef]
- Gungah, Gavakshi, and Jason Narsoo. 2021. A novel EVT-modified Lee-Carter model for mortality forecasting: An application to extreme mortality events. Journal of Statistics and Management Systems, 1–33. [Google Scholar] [CrossRef]
- Haberman, Steven, and Arthur E. Renshaw. 2011. A comparative study of parametric mortality models. Insurance: Mathematics and Economics 48: 35–55. [Google Scholar] [CrossRef] [Green Version]
- Haberman, Steven, Vladimir Kaishev, Pietro Millossovich, Andrés Villegas, Steven Baxter, Andrew Gaches, Sveinn Gunnlaugsson, and Mario Sison. 2014. Longevity Basis Risk: A Methodology for Assessing Basis Risk. Technical Report. London: Institute and Faculty of Actuaries. [Google Scholar]
- Kannisto, Väinö. 1994. Development of Oldest-Old Mortality, 1950–1990: Evidence from 28 Developed Countries. Odense: Odense University Press. [Google Scholar]
- Koninklijk Actuarieel Genootschap. 2018. Prognosetafel AG2018. Available online: https://www.ag-ai.nl/view/41123-PrognosetafelAG2018.pdf (accessed on 1 November 2020).
- Koninklijk Actuarieel Genootschap. 2020. Prognosetafel AG2020. Available online: https://www.ag-ai.nl/view/45902-PrognosetafelAG2020+%28print%29.pdf (accessed on 1 November 2020).
- Lee, Ronald, and Timothy Miller. 2001. Evaluating the performance of the Lee-Carter method for forecasting mortality. Demography 38: 537–49. [Google Scholar] [CrossRef] [PubMed]
- Lee, Ronald D., and Lawrence R. Carter. 1992. Modeling and forecasting U.S. mortality. Journal of the American Statistical Association 87: 659–71. [Google Scholar] [CrossRef]
- Li, Jackie. 2013. A Poisson common factor model for projecting mortality and life expectancy jointly for females and males. Population Studies: A Journal of Demography 67: 111–26. [Google Scholar] [CrossRef] [PubMed]
- Li, Nan, and Ronald Lee. 2005. Coherent mortality forecasts for a group of populations: An extension of the Lee–Carter method. Demography 42: 575–94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Siu-Hang, and Wai-Sum Chan. 2005. Outlier analysis and mortality forecasting: The united kingdom and scandinavian countries. Scandinavian Actuarial Journal 2005: 187–211. [Google Scholar] [CrossRef]
- Liu, Yanxin, and Johnny Siu-Hang Li. 2015. The age pattern of transitory mortality jumps and its impact on the pricing of catastrophic mortality bonds. Insurance: Mathematics and Economics 64: 135–50. [Google Scholar] [CrossRef]
- Pitacco, Ermanno, Michel Denuit, Steven Haberman, and Annamaria Olivieri. 2009. Modeling Longevity Dynamics for Pensions and Annuity Business. London: Oxford University Press. [Google Scholar]
- Rizzi, Silvia, Jutta Gampe, and Paul H. C. Eilers. 2015. Efficient estimation of smooth distributions from coarsely grouped data. American Journal of Epidemiology 182: 138–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schnürch, Simon, Torsten Kleinow, Ralf Korn, and Andreas Wagner. 2021. The impact of mortality shocks on modeling and insurance valuation as exemplified by COVID-19. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3835907 (accessed on 18 June 2021).
- Van Berkum, Frank, Katrien Antonio, and Michel Vellekoop. 2016. The impact of multiple structural changes on mortality predictions. Scandinavian Actuarial Journal 2016: 581–603. [Google Scholar] [CrossRef]
- van Delft, Lotte, and Sarah Huijzer. 2020. Impact of COVID-19 on Dutch Mortality Tables. Available online: https://be.milliman.com/-/media/milliman/pdfs/articles/impact-of-covid-19-on-dutch-mortality-tables.ashx (accessed on 1 November 2020).
- Vanella, Patrizio, Ugofilippo Basellini, and Berit Lange. 2021. Assessing excess mortality in times of pandemics based on principal component analysis of weekly mortality data—The case of COVID-19. Genus 77: 1–36. [Google Scholar] [CrossRef]
- Zhang, Xun, Pu Liao, and Xiaohua Chen. 2021. The negative impact of COVID-19 on life insurers. Frontiers in Public Health 9: 1388. [Google Scholar] [CrossRef] [PubMed]




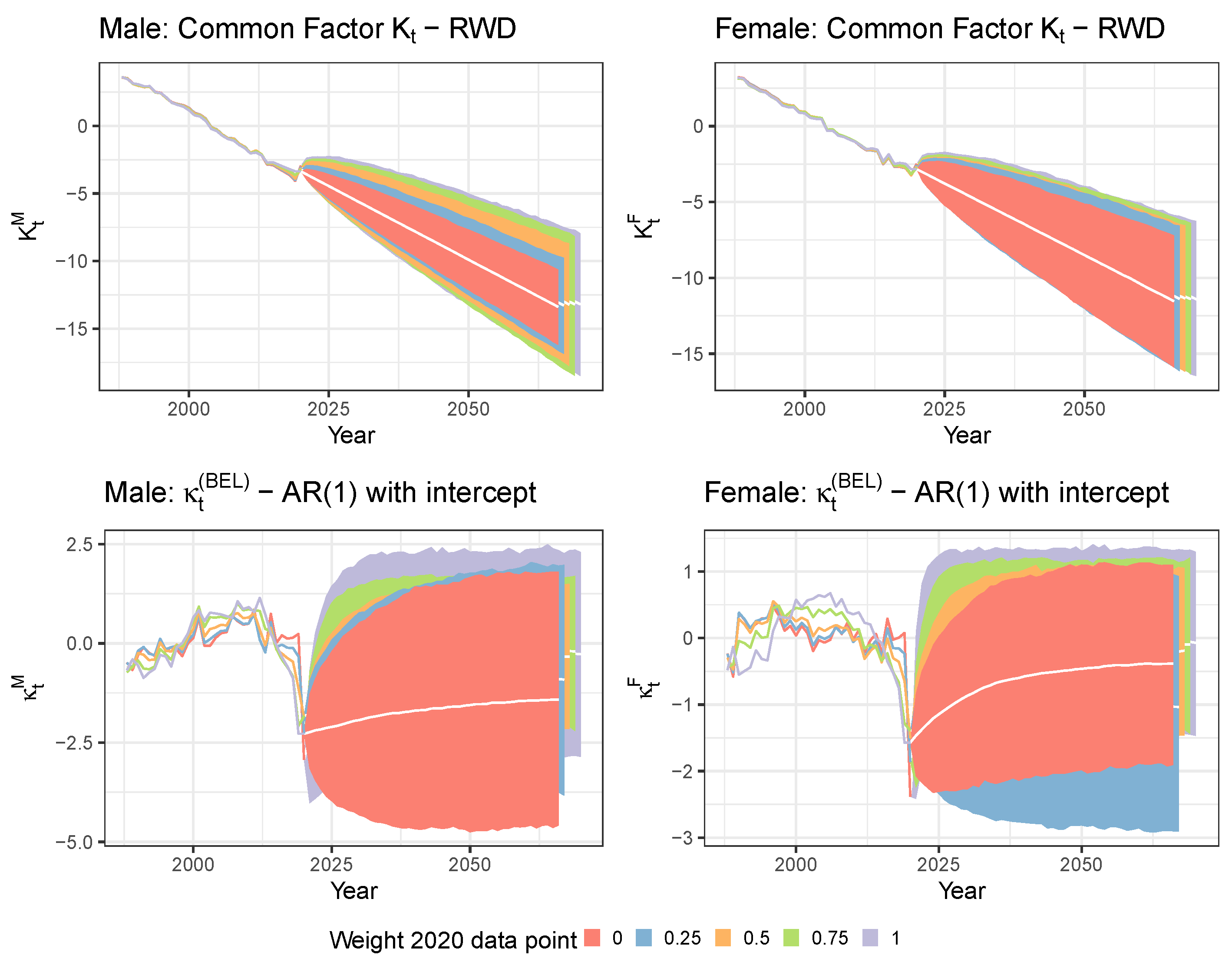
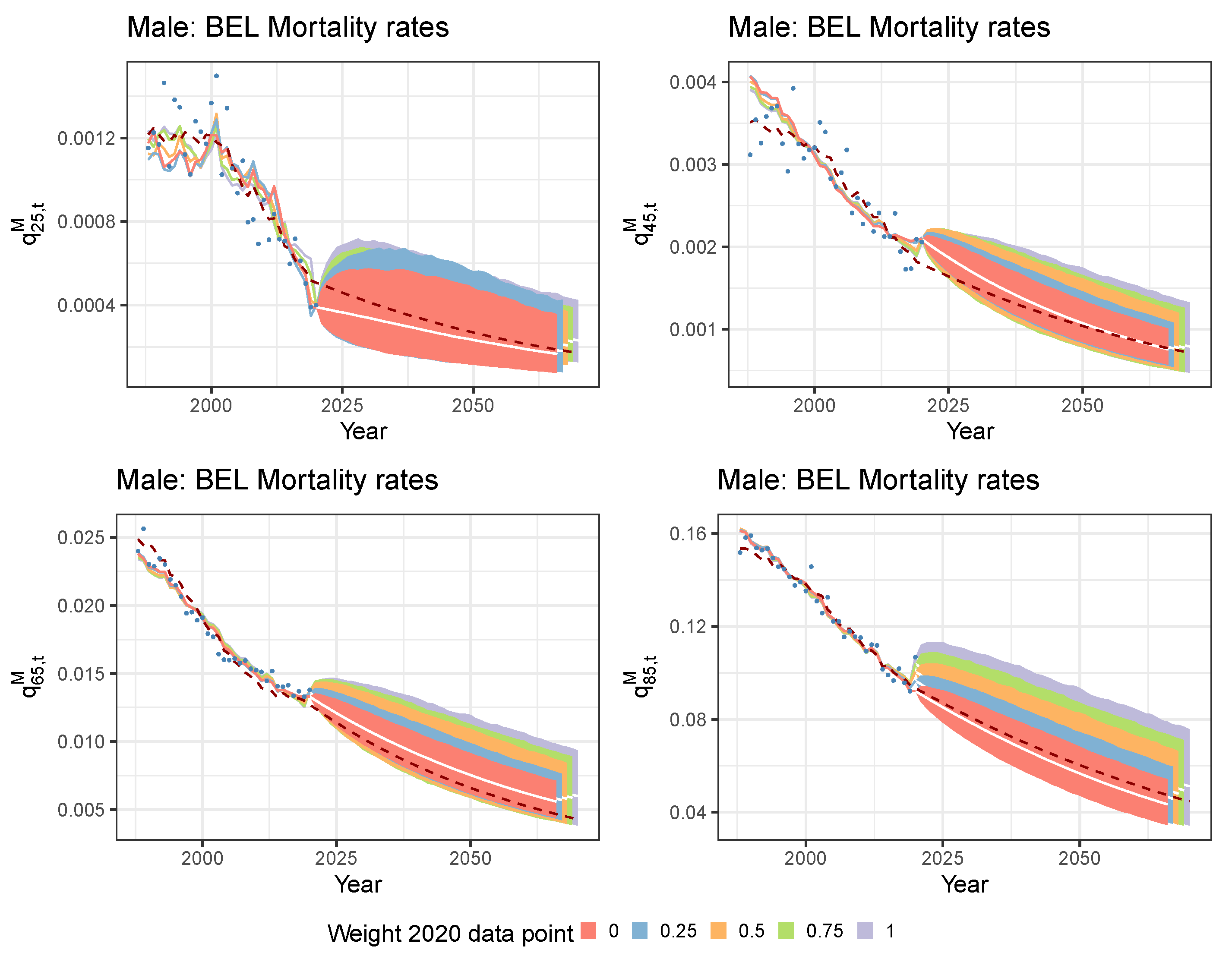

| Weight 2020 | ||||||
|---|---|---|---|---|---|---|
| 0 | −0.2315 | −0.1938 | 0.0071 | −0.0091 | 0.9027 | 0.9033 |
| 0.25 | −0.2236 | −0.1872 | 0.0025 | −0.0142 | 0.9306 | 0.9600 |
| 0.50 | −0.2159 | −0.1807 | −0.0028 | −0.0180 | 0.9424 | 0.9730 |
| 0.75 | −0.2083 | −0.1743 | −0.0083 | −0.0216 | 0.9487 | 0.9790 |
| 1 | −0.2009 | −0.1681 | −0.0138 | −0.0250 | 0.9527 | 0.9825 |
| IA∣BE 2020 | −0.2285 | −0.1882 | 0.0140 | −0.0240 | 0.9682 | 0.9226 |
| Cohort Life Expectancy in 2020 | Males | Females | |||
|---|---|---|---|---|---|
| 0 | 65 | 0 | 65 | ||
| Recalibration 2020 weight = 0 | Best. Est. | 89.36 | 19.70 | 91.42 | 22.78 |
| Recalibration 2020 weight = 0.25 | Best. Est. | 89.07 | 19.65 | 91.11 | 22.65 |
| Recalibration 2020 weight = 0.50 | Best. Est. | 88.77 | 19.58 | 90.78 | 22.56 |
| Recalibration 2020 weight = 0.75 | Best. Est. | 88.45 | 19.52 | 90.46 | 22.48 |
| Recalibration 2020 weight = 1 | Best. Est. | 88.13 | 19.45 | 90.13 | 22.41 |
| IA∣BE 2020 | Best. Est. | 89.91 | 20.38 | 91.54 | 23.14 |
| Weight 2020 | ||||||
|---|---|---|---|---|---|---|
| 0 | −0.2177 | −0.1881 | −0.0474 | −0.0300 | 0.9588 | 0.9124 |
| 0.25 | −0.2139 | −0.1836 | −0.0305 | −0.0277 | 0.9545 | 0.9607 |
| 0.50 | −0.2094 | −0.1809 | −0.0319 | −0.0303 | 0.9243 | 0.8567 |
| 0.75 | −0.2061 | −0.1791 | −0.0424 | −0.0337 | 0.8539 | 0.7110 |
| 1 | −0.2037 | −0.1774 | −0.0587 | −0.0324 | 0.8248 | 0.5297 |
| Cohort Life Expectancy in 2020 | Males | Females | |||
|---|---|---|---|---|---|
| 0 | 65 | 0 | 65 | ||
| Recalibration 2020 weight = 0 | Best. Est. | 89.95 | 20.31 | 92.15 | 23.32 |
| Recalibration 2020 weight = 0.25 | Best. Est. | 89.25 | 19.89 | 91.58 | 22.99 |
| Recalibration 2020 weight = 0.50 | Best. Est. | 88.60 | 19.57 | 91.12 | 22.82 |
| Recalibration 2020 weight = 0.75 | Best. Est. | 88.05 | 19.37 | 90.71 | 22.71 |
| Recalibration 2020 weight = 1 | Best. Est. | 87.57 | 19.19 | 90.32 | 22.58 |
| IA∣BE 2020 | Best. Est. | 89.91 | 20.38 | 91.54 | 23.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robben, J.; Antonio, K.; Devriendt, S. Assessing the Impact of the COVID-19 Shock on a Stochastic Multi-Population Mortality Model. Risks 2022, 10, 26. https://doi.org/10.3390/risks10020026
Robben J, Antonio K, Devriendt S. Assessing the Impact of the COVID-19 Shock on a Stochastic Multi-Population Mortality Model. Risks. 2022; 10(2):26. https://doi.org/10.3390/risks10020026
Chicago/Turabian StyleRobben, Jens, Katrien Antonio, and Sander Devriendt. 2022. "Assessing the Impact of the COVID-19 Shock on a Stochastic Multi-Population Mortality Model" Risks 10, no. 2: 26. https://doi.org/10.3390/risks10020026
APA StyleRobben, J., Antonio, K., & Devriendt, S. (2022). Assessing the Impact of the COVID-19 Shock on a Stochastic Multi-Population Mortality Model. Risks, 10(2), 26. https://doi.org/10.3390/risks10020026






