Abstract
This paper presents a methodology for making decisions in the stock market using the AHP-TOPSIS multi-criteria technique. The problem is related to the stock market’s investment process considering the criteria of liquidity, risk, and profitability. The proposed methodology includes integrating economic and financial theories of investment in equity portfolios with the AHP-TOPSIS multi-criteria technique, which allows for evaluating a finite number of alternatives hierarchically under qualitative and quantitative criteria. The methodology has been tested in a real case of selecting a portfolio of high and medium marketability stocks for the Colombian market from April 2012 to April 2017. The computational results show the importance and efficiency of successfully integrating traditional equity portfolio investment criteria and multi-criteria methodologies to find an appropriate balance between profitability and risk in the investment decision-making process in shares in the Colombian stock market. The proposed methodology could be applied to other emerging markets, similar to Colombia.
1. Introduction
Investing in the financial market has become an increasingly routine activity by individuals who find an opportunity to increase their capital in this market (Escobar 2015). The incursion into these financial activities occurs through the purchase and sale of financial instruments, which generate value in specific market situations—situations that are typically inherent to risk and market volatilities because, in general, assets and financial instruments are frequently affected by a myriad of variables that can very quickly lead the investor from a state of economic prosperity to total misfortune (Escobar 2015). In this sense, investment decisions require intricate knowledge of market conditions (Escobar 2014), in addition to a strong understanding of indicators, techniques, and notions such that final determinations are the most efficient in terms of earnings. Given that portfolio selection problems involve a set of decisions linked to a variety of alternatives, conceptual frameworks such as multi-criteria selection methods are required. These methods cover a significant number of alternatives (classified and ranked by a number of criteria (N)) under a structured and scientific method that provides the optimal choice while taking into account the preferences of the decision-maker (Zopounidis 1999).
The use of theory for the optimal selection of efficient portfolios begins with Markowitz (1952) and benefits from essential contributions such as those by Sharpe (1964) and Stephen (1976), among other authors who have made significant advances concerning the problems that stand out in portfolio selection decisions. The use of multi-criteria decision analysis (MCDA) considers the great variety of criteria or objectives that are part of the optimization process that the investor must perform. Zopounidis (1999) examines the contribution of multi-criteria analysis in solving financial decision problems. In this work, the author presents a methodological framework of multi-criteria analysis and mentions some methods that relate directly to financial problems, such as selecting portfolios under the Markowitz framework and optimizing the Sharpe model, among other financial problems. Finally, the author provides a vast list of studies highlighting the use of these decision methods on financial and corporate problems and, in particular, on portfolio management problems. Research has also been highlighted where financial decision-making is carried out using multi-criteria methods in the most recent decades (see Xidonas et al. 2021; Mendonça et al. 2020). This work points out the significant contribution of this type of analysis on the optimal selection problem of financial portfolios. It emphasizes the mean-variance model (also known as the Markowitz model), which has an important flaw—incorporating all of the criteria that managers truly require for investment decisions goes beyond analyzing just two variables. It is essential to highlight the level of subjectivity present in this work since the preferences of the decision-maker must be taken into account, especially their profile against risk, which will lead to their choices; however, the scientific and mathematical rigor of the multi-criteria methods tries to bias as little as possible the optimal choice(s).
The present work proposes a hybrid method between two multi-criteria techniques applied directly to the optimal selection of financial portfolios in search of a more robust and complete optimization process. One of the criteria or objectives that are more decisive for the investor is considered through this process. This type of agent is given more powerful tools than those available in economic and financial theory—away from the pragmatism implied by traditional methods based on intuition and experience. The present work also supposes a structural change in the decision-making process that distances itself from the prevailing economic theory method. However, this work does not ignore the theory’s significant advances; it starts from the base of these theoretical developments to arrive at the optimal selection of assets and, subsequently, a set of portfolios, which is the purpose of ongoing research.
This work is organized as follows. Section 2 contains a literature review on the beginning and progress of portfolio selection theory and the use and respective contributions made by multi-criteria methods concerning the field of economics, particularly finance. Section 3 presents the proposed methodology detailing the theoretical tools used to construct the criteria and indicators used in multi-criteria decision methods. Section 4 provides the results obtained during the process. Finally, Section 5 offers the conclusions obtained from the results.
2. Literature Review
In the 1950s and 1960s, no specific measure existed to assess the concept of risk in the investment community. However, Markowitz’s (1952) work and subsequent developments provided the academic community with a theoretical foundation and investors during this time with a starting point for formulating models focused on asset allocation. In particular, modern portfolio theory first provided a measure of expected risk associated with returns—a variable that, in turn, has been taken as a contribution to the current work. Markowitz (1952) showed the variance in the expected return as a reasonable risk measure under a series of rational assumptions, and being nonrestrictive, provided all relevant facts for the rapid dissemination and acceptance within the academic community.
After the initial formulation proposed in Markowitz (1952), modern portfolio theory (MPT) required developments of a theoretical nature and practical approaches that directly benefited investors when making capital allocations and creating portfolios, using the MPT conceptual framework. This fact was shown as the capital asset pricing model emerged (Sharpe 1964; Lintner 1965, 1969; Mossin 1966; French 2002). According to the previously described mean-variance model, this model’s formulation allowed investors to understand the relationship between the return on assets and risk. More profoundly, the pricing model distinguished the effects of systematic risk (undiversifiable risk) and nonsystematic risk (diversified risk). Closely related to this discussion is the possibility of affirming that the pricing model provided an essential distinction about returns. Formulating the model allows for determining returns generated by the market (the beta coefficient), while excess returns are the alpha coefficient. The close link between the MPT and CAPM popularized market-weighted indices because this method emphasized diversification in the financial assets market.
Finally, in Samuelson (1967), the efficient market hypothesis is developed, which argues that asset prices entirely reflect all available information. The direct implications of this hypothesis are the impossibility of consistently outperforming the market itself, and on a risk-adjusted basis, because asset prices in the market should only react to new information, initially distorting the work that can make an investor. Fama (1970) published a review of the hypothesis, adding evidence and expanding and refining the theory developed in the previous decade, including defining three forms of market efficiencies: weak, semistrong, and strong.
Early published works using multi-criteria methods for selecting stock portfolios have been proposed by Hababou and Martel (1998), Bouri et al. (2002), and Costa and Soares (2004). Hababou and Martel (1998) introduce the multi-criteria method PROMETHEE II to select a portfolio. The proposed methodology involved four steps: (1) defining a list of potential solutions to the considered problem; (2) defining a list of critical criteria; (3) evaluating the performance of each solution according to each criterion; and (4) aggregating these performances by using the PROMETHEE II multi-criteria method. Bouri et al. (2002) include the investor’s attitude to solvency and liquidity solving a stock portfolio problem with a multi-criteria issue, which should be tackled using appropriate techniques. Costa and Soares (2004) present a model to select a portfolio of stocks based on the fund managers’ fieldwork results and using direct rating, MACBETH, and optimization techniques.
Zopounidis (1999) provides a complete compilation of the contribution of multi-criteria analysis in resolving decision problems in the financial field, particularly in real contexts, because—as the author argues—generally, an organization’s financial decisions include optimization processes involving several variables and criteria that require a priori methodological frameworks to be resolved. Such use of multi-criteria decision methods has been an essential tool for solutions to financial decisions.
Alptekin (2009) proposed evaluating mutual and pension stock funds by using the TOPSIS method. The method considers all of these fund performance measurement techniques and provides a more appropriate performance measurement. Fasanghari and Montazer (2010) investigate a Multiple Criteria Decision Making (MCDM) problem based on a fuzzy expert system for selecting shares dealing with the uncertainty of stock portfolio performance problem and apply rules used by expert investors. The proposed methodology has been applied to the Tehran Stock Exchange (TSE) market.
Zopounidis and Doumpos (2002) review MCDA methods applied to the context of financial problems, including a section that emphasizes portfolio performance problems, highlighting their multi-dimensional nature—a field in which the MCDA paradigm provides essential support for treating and solving these problems. The previous conclusion is reached through an exhaustive literature review that organizes the work through the methods used and the approach given to them, finds a transversal incursion in the financial field, and concludes that developing and improving these methods should go along with technological advances related to the computerized systems used for the respective calculations.
The relevance of the use of MCDA is further reinforced by Xidonas et al. (2009), which focuses on asset selection through a specific method. This work argues that the MCDA paradigm provides a broad methodological approach to address portfolio selection problems effectively. Additionally, in search of delimiting the problem and methods used in the present work, Bahmani et al. (1987) apply the analytic hierarchy process (AHP) method to the asset selection process for a given investment. The method’s use is supported by the nature of the criteria that the authors consider for such asset selection because among the factors are wealth, age, experience, investor characteristics, and investment alternatives, among others. He also argues that the AHP method adds a new perspective to the portfolio selection analysis and serves as an alternative mechanism to maximizing expected utility. This study concludes that the AHP model is an excellent tool for solving complex problems in real financial contexts, demonstrating its effectiveness and efficiency in an investment selection process.
Xidonas et al. (2011) introduce a combined approach for the construction and selection of portfolios, considering the inherent multi-dimensional nature of the problem, allowing the use of multi-criteria methods. The proposed approach considers a multiple-criteria decision-making (MCDM) method, based on multi-objective mathematical programming (MMP), called IPSSIS (integrated portfolio synthesis and selection information system). Marasović and Babić (2011) propose a two-step multi-criteria approach considering the well-known PROMETHEE II. The former methodology was applied to the Zagreb stock exchange (ZSE) market.
Similarly, Charouz and Ramík (2010) apply the AHP method to a portfolio management process and argue the relevance of the approach used to convert assets into cash. Setbacks such as contracts, internal requirements, and other relevant criteria are assumed to exist when making the most appropriate decision. In addition to the classical AHP model, the authors apply an alternative version that corrects some of the theoretical deficiencies (called FVK) and reaches approximately equivalent results. This method’s significant contribution lies in that it provides the portfolio manager with rapid information about its advantages when choosing between assets based on each alternative’s characteristics and the additional advantage of comparing them.
Yodmun and Witayakiattilerd (2016) consider a stock portfolio problem using a fuzzy scheme. In particular, the shares are classified according to the type of sector. The shares are ranked according to the best weight from a fuzzy quantitative approach. Furthermore, the stocks are ranked according to their group from a fuzzy analytic hierarchy process (FAHP) and the TOPSIS approach.
The work proposed by Escobar (2015) presents a very current situation close to the problem to be addressed because it applies the AHP method to the national context through a focus on the Colombian stock market and the problem of asset selection in search of forming an efficient portfolio when taking into account specific criteria, such as risk and profitability. Using a relatively complete sample of stock prices, he generates portfolios based on these decision criteria, which he weights using the AHP method and, under this approach, reaches a portfolio that proves to be the most efficient in terms of the mean-variance model. He concludes that using these alternative methods, supported by computational experiments, generates greater efficiency in the decision-making process because it eliminates guesswork by implementing analytical techniques and tools applied to complex contexts concerning the available alternatives.
Mahmoodzadeh et al. (2007) and Joghi (2016) carry out innovative developments in which two multi-criteria decision methods are coupled in search of more efficient results to various financial problems that require more robust approaches. The first approach applies the AHP method to calculate each alternative’s relative weight and alternative investments. When obtaining these weights, they use the preference by similarity to the ideal solution (TOPSIS) method to evaluate the projects and choose the ideal solution. The second work performs a similar procedure but applies the hybrid model to the portfolio selection problem to execute an analogous methodology, as it uses the AHP method to find the relative weight of each criterion. In this case, these criteria are indicators of profitability, risk, and liquidity, among others. Then, the ideal portfolio is achieved through the TOPSIS method. Finally, the method is tested using real asset data to demonstrate its validity and relevance in portfolio selection problems.
Aouni et al. (2018) reviewed the papers dealing with methods to address portfolio selection problems based on mean and variance. We also analyze these methodologies, allowing the portfolio solution problem within a multiple-criteria context, thus extending the mean-variance approach features that have had an impact on portfolio theory. Recently, several works related to multi-criteria methods for investment on stock portfolio selection have been proposed by Pätäri et al. (2018), Abdelaziz and Mallek (2018), Alali and Tolga (2019), Galankashi et al. (2020), Nguyen et al. (2020), and Frej et al. (2021).
Pätäri et al. (2018) compare the efficiency of four MCDM methods identifying the best-performing approach applied to two comprehensive samples of U.S. stocks. The compared methods are median-scaling (MS), TOPSIS, analytic hierarchy process (AHP), and additive data envelopment analysis (ADDEA). The results show that all evaluated approaches could successfully be applied to the equity portfolio selection problem.
Abdelaziz and Mallek (2018) focused on solving the multi-criteria portfolio optimization problem by applying two different models derived from the theory of optimal stopping problems. An interactive method against solution-based algorithms is applied. Alali and Tolga (2019) propose an approach based on the well-known multi-criteria decision-making method, called TODIM, to the portfolio problem. The proposed approach uses variance, correlation, and returns applied to different empirical US stock data periods. The validation period demonstrated that obtained portfolios by TODIM configurations yield significantly better results than equally weighted portfolios and inferior results than the theory proposed by the Sharpe ratio.
Galankashi et al. (2020) propose an approach based on the well-known fuzzy analytic network process (FANP) to select the portfolio problem on the Tehran Stock Exchange market. A literature review allowed selection of the main criteria for portfolio selection, and then a chosen criterion was applied within the FANP scheme to rank ten different portfolios. The results indicated that profitability, growth, market, and risk are the most critical portfolio selection criteria.
Nguyen et al. (2020) propose a ranking for the agriculture stocks belonging to the Vietnam Stock Exchange Market. The former approach uses a combined approach of the AHP with a grey relational analysis (GRA), multi-objective optimization ratio analysis (MOORA), and TOPSIS. The obtained results suggest that the integrated model is efficient in making decisions on different agriculture sectors. Other alternative schemes such as COPRAS, KEMIRA, and EDAS could be employed to evaluate other companies’ financial performance in different sectors. Finally, Frej et al. (2021) developed a BCR-based approach for selecting portfolios under asymmetric information of the market. The proposed methodology is applied to the Brazilian market to illustrate its practical applicability.
Based on the literature review, many authors and practical investors have studied the stock portfolio problem and written many papers, news articles, documents, and theses in the last century. Several articles deal with the stock portfolio optimization problem, while other papers address a specific problem by proposing numerous criteria for assessing and selecting portfolios. Despite this, the same authors point out that there are still many opportunities to improve and expand the research that exists. While most studies have focused on financial criteria, other qualitative criteria must be considered. Some authors have narrowed the gap between the proposed approaches to real case applications in stock markets, indicating that research on the subject has been growing very fast but is largely detached from real-market applications. However, managers, decision-makers, and investors face different factors in portfolio assessment. The portfolio selection criteria should be specifically applicable for use by investors. According to financial theory, there is no single-criterion decision for real-world problems. Therefore, multi-criteria methods must be considered where different criteria should be concurrently considered. However, existing multi-criteria approaches have some limitations. First, some approaches do not consider the internal relations between criteria because combining techniques can be scary.
Therefore, to address the gap in published works, this paper proposes a methodology for making decisions in the stock market using the AHP-TOPSIS multi-criteria technique, which allows for hierarchically evaluating a finite number of alternatives under qualitative and quantitative criteria. Indeed, the integration of AHP with TOPSIS has been applied to other financial decisions with successful applications (Alptekin 2009; Mahmoodzadeh et al. 2007; Joghi 2016). The main contribution of this work is the proposed structure of the methodology with the consideration and integration of two approaches. This approach proposes a model that fits into the reality of the emergent markets and, at the same time, contributes to the prioritization of specific criteria for portfolio selection. Similarly, the actual application case results measure the solution strategy’s efficiency, allowing its scalability to other financial markets with characteristics similar to Colombia.
3. Proposed Methodology
The stages under the proposed methodology and the development of the multi-criteria decision-making indicators are detailed below. The methodology has been divided into four stages.
3.1. Stage I
The first step is selecting a sample of medium- and high-marketability shares on which the base indicators, e.g., profitability, standard deviation, variance, coefficient of variation, and asymmetry coefficient, are calculated. It is worth mentioning that a relationship between some of these statistical estimators with financial and economic theory exists because they provide a priori information on some series’ behavior in a given period, such as risk and return.
Subsequently, the cost of capital and systematic risk are calculated according to the theory proposed by Sharpe (1964). Finally, the beta and critical ratios are calculated according to the theory proposed by Elton et al. (1976). This paper proposes a share selection rule that includes the following steps:
Step 1: Calculate the beta coefficient () for each share x, according to the methodology proposed by Sharpe (1970), and then calculate the beta ratio using the following expression:
Step 2: Calculate the critical ratio using the following expression:
where represents the total number of shares considered, is the expected return of stock , is the variance in the profitability of the market index, is the variance in the profitability of stock , and represents the profitability of the risk-free share of the country in which the shares for the investment are listed.
Step 3: Compare the beta ratio of each share with the critical ratio , in such a way that . If this condition is met, it is convenient to invest in the asset.
After these analyses, from the total sample of assets, a smaller sample is selected that meets the conditions of:
- Trading during the entire study period;
- Maintaining a positive average profitability;
- Meeting the described conditions in the beta ratio theory, which suggests the feasibility of investing in the share.
3.2. Stage II
After individual stocks are selected, an ordered classification is used to prioritize those that maintain a balance between profitability and risk because it is desirable to use stocks that are closer to the behavior of the stock market index. In this work, the decision of the number of shares—a size that did not exceed the computational capacity and that would not demand valuable time for the final analysis—was chosen because it is worth remembering that, in addition to economic and financial theory, multi-criteria decision-making methods are used.
The number of portfolios should involve all possible combinations between the selected shares, which is how the following expression is used, as extracted from Alexeev and Tapon (2012):
where is the number of shares selected and represents the possible combinations. With seven different shares selected, portfolios of at least two shares must exist, even one that includes all of the stocks.
In this stage, the number of portfolios to analyze is calculated by considering the number of stocks. In particular, the stocks to make the portfolios are selected and are fixed according to stage 1. Portfolios of two to seven shares are conformed. These portfolios are analyzed and refined in the following stages using the multi-criteria methods, generating an assessment of the different selection criteria for each.
3.3. Stage III
At this stage, the criteria to be applied to all portfolios have been selected for evaluation using multi-criteria methods. Such criteria need to address crucial aspects so that an investor’s decision is optimal, thereby increasing profitability and mitigating the risk present in any financial decision. Such aspects should cover topics previously mentioned and issues related to liquidity, non-diversifiable risk, and investment viability, among others, that provide tools to the investor and, in particular, lead to achieving the desired results from using the methodologies proposed in the present work.
The criteria selected to evaluate the portfolios were the following:
- C1: Average profitability;
- C2: Conditional value at risk;
- C3: Weighted cost of capital;
- C4: Idiosyncratic volatility index;
- C5: Stock market index;
- C6: Profitability-weighted cost of capital.
Criterion C1 is derived from the mean-variance model proposed by Markowitz (1952, 1959). In this model, portfolio efficiency is considered, a rule that is reached by minimizing the variance in the portfolio ( ). The general model is as follows:
Minimize:
Subject to:
Constraint (6) indicates that the total portfolio return is equivalent to the return on each share multiplied by its percentage invested. Constraint (7) indicates that the sums of the percentages to be invested in each share must be equivalent to 100%. In this case, the formalization of the performance indicator of each asset or portfolio is taken as:
where:
- = Average market return of the stock or portfolio .
- = Return of stock at time .
- = Period of the stock or portfolio return.
The estimation of the variance-covariance matrix represents a fundamental element in determining efficiency in terms of both assets and portfolios because it contains information on the volatility of financial assets and joint movements between assets or portfolios. The notion of an efficient frontier refers to the set of points on the return-risk plane, in which all possible combinations of assets remain, forming portfolios that maintain a minimum risk in the face of a given expected return. This border will allow us to know the best previously diversified portfolios. Once these portfolios are known, investors will choose according to their preferences.
Regarding criterion C2, the conditional value at risk (CVaR) is a variant of the known value at risk (VaR), which is a useful indicator in the field of financial economics because it is intuitive and understandable through its exposure of the amount of money that can be lost for a certain level of probability and during a specific period. These characteristics have caused this tool to be generalized in terms of its usefulness in the financial field. Sarykalin et al. (2008) define the VaR of the variable X with a confidence level α є [0.1] as:
where, by definition, is the lowest α percentile of the random variable X. A significant disadvantage of this measure lies in the fact that it does not comply with the property of subadditivity, characteristic of a coherent risk measure described by Artzner et al. (1999). This property’s importance lies in the problem that would be incurred when comparing the VaR of a diversified portfolio with the sum of the VaR of the assets separately from such a portfolio because the latter may be lower. This disadvantage allowed room for the formulation of the CVaR (Rockafellar and Uryasev 2000). Additionally, known as the expected loss that corrects the VaR deficiency, the CVaR also does not generally lose the previous measure’s simplicity. The CVaR manages to capture or quantify the expected losses if the worst-case threshold is crossed. In other words, this measure obtains a more pessimistic estimate for the investor’s potential losses because it is a complete tool and theoretically more robust than the VaR. Sarykalin et al. (2008) define the CVaR for random variables with a possible discontinuous distribution function and a confidence level α є [0.1] as the average of the generalized distribution of the α tail:
where:
The C3 criterion equivalent to the weighted cost of capital () was calculated according to the theory proposed by Sharpe (1964):
where is the risk-free rate, is the systematic risk indicator, and is the market risk premium.
An additional factor immersed in the choice of shares or assets when selecting a portfolio is the fraction of risk not explained by the beta factor of the pricing model—a component of which extensive evidence has been found on its relationship with movements in the returns on assets (Bali and Cakici 2008). This study analyzes the effect of this variability component and the variation in returns using a measure called IVOL, which is an estimate of idiosyncratic volatility (criterion C4) that follows directly from the CAPM pricing model, defined as:
where is the idiosyncratic return of the i-th value; the return of this value is defined as follows:
where is the risk-free rate, is the coefficient of variability of the value relative to the market, and represents the market return.
In exploring influential factors in the choice of assets and portfolios, the shares’ liquidity property was considered because it is desirable that these financial instruments can be quickly exchanged for money. In the research process, the stock exchange index (Índice de Bursatilidad Accionaria—IBA) was found; this indicator was adopted by the Financial Superintendence of Colombia and captured the shares’ liquidity that makes up the Colombian stock market through a numerical scale from 0 to 10. It is calculated by a weighting of the following four aspects:
- (1)
- Average value traded per round;
- (2)
- Relationship between the number of shares traded and the number of shares outstanding;
- (3)
- Several trades over the number of rounds completed;
- (4)
- The number of rounds in which the number of rounds was traded.
This indicator is considered criterion C5. It is essential to mention that, for the stock market index related to the liquidity of the stocks, the analysis must be performed for each stock, taking the place it occupies in the IBA ranking. The weighted average of each share combination is a numerical value that reflects the portfolio’s liquidity. Finally, criterion C6 is calculated as the difference between criteria C1 and C3. Indeed, we consider that the average return of the stock/portfolio (C1) must be greater than its cost of capital (C3) under a given risk level, indicating economic value generation. Note that the required rate of return must be the minimum return that an investor will accept for owning a company’s stock (C3) as compensation for a given level of risk associated with holding the share.
Importantly, for each portfolio configuration, the media-variance models (5)–(7) were applied to optimize each stock’s weights in each portfolio to maximize the benefit and, in turn, minimize the associated risk. The average of the daily returns determined the profitability of each portfolio by weighing each stock. In contrast, the CVaR was calculated using the parametric or nonparametric method (historical method) depending on the results obtained using a specific normality test applied to the data. In our study, the Shapiro–Wilk (Shapiro and Wilk 1965) and Jarque–Bera (Jarque and Bera 1987) tests were selected, which validate whether specific data follow a normal distribution.
The Shapiro–Wilk test consists of, first, ordering the sample , size , in ascending order to obtain a sample vector , where is the j-th sample vector. Then, the contrast statistics are calculated.
where denotes the sample variance,
We obtain the value of the statistic and calculate the critical value of the test based on its distribution to make decisions about the normality of the sample. Finally, calculating the critical probability is contrasted with the null hypothesis of normality.
The Jarque–Bera test is asymptotic; in large samples, based on the residues of the ordinary least squares (OLS) method. It calculates the asymmetry and kurtosis of the OLS residues in the first instance. This test’s basic principle is to determine the degree to which the coefficients of asymmetry and kurtosis deviate from the residuals when using these same asymmetry and kurtosis coefficients of the normal distribution.
Skewness:
Kurtosis coefficient:
Statistical:
A procedure similar to that described in the previous test was performed and contrasted the values of the critical probability against the null hypothesis of normality.
In this stage, the six portfolios that presented the best balance between return and risk were selected by superimposing the criteria of profitability (C1), risk (C2), and liquidity (C5). These criteria were selected before the others and after consulting experts in the financial field and stock transactions. This fact could be reflected in the criteria weighting matrix, where they are superimposed on C3, C4, C6.
The Shapiro–Wilk and Jarque-Bera normality tests were utilized to show that the distribution is normal; this must not, however, be confused with the C1–C6 selection criteria.
3.4. Stage IV
This stage includes everything related to using the hybrid multi-criteria method chosen to address this work, which already uses the portfolios analyzed in Stage III as input. In particular, the use of the AHP–TOPSIS multi-criteria methodology has been proposed due to its applicability in the context of the considered problem.
The literature review shows a large number of multi-criteria methods or techniques. Simultaneously, a wide variety was found in their combinations, particularly the use of the analytic network process (ANP, Saaty 1990), the most general form of the AHP method. However, we decided to select the AHP method due to its greater use in the financial literature; this could be corroborated with a simple bibliometric analysis in the main scientific databases. Furthermore, AHP structures the considered decision problem into a hierarchy with a goal, decision criteria, and alternatives. Moreover, the application of ANP is complicated and requires much more effort from the participants than AHP. However, AHP is very popular, and ANP is less prominent (Othman et al. 2011).
Saaty (1990) developed the AHP, a model that allows decision-makers to represent multiple factors’ interactions in complex situations. This model requires that decision-makers develop a hierarchical structure for explicit factors in the problem to be addressed to provide judgments about each’s relative importance. The use of the relative judgment scale developed by Saaty (1990) is decisive in developing the model because it allows us to separately compare and provide a hierarchy of different factors representing both the alternatives and the criteria. The scale is as follows.
The previous scale serves as a tool for the decision-maker to compare alternatives and assigns a numerical value from 1 to 9, articulating their analytical process preferences. It should be noted that the even values are not considered in the table but have relevance and space within the analysis because they represent intermediate values in the scale. In addition to this crucial tool, Saaty (1990) proposes a logical sequence of steps to develop the model, and the steps are as follows.
Step 1: Determine an objective (best stocks portfolio) and the evaluation factors, identify the objectives or purposes at a higher level, the factors or criteria at the second level (return, liquidity, and risk criteria), and the alternatives at the third level (portfolios).
Step 2: Find the relative importance of the criteria (return, liquidity, and risk criteria) in relation to the objective outlined in the previous step. For this, a pairwise comparison matrix is constructed using the relative importance scale, in which the comparison judgments are detailed in Table 1. Assuming criteria, the pairwise comparison among criteria yields a square matrix that we call A1N×N, where indicates the relative importance of criterion with respect to criterion ; in addition , when and .

Table 1.
AHP Scale for Pairwise Comparison on stock performance. Source: owner elaboration based on Saaty (1990).
Subsequently, the normalized relative weight of each criterion must be found to calculate the geometric mean of the i-th row and to normalize the geometric means of the rows in the comparison matrix.
where:
- = Geometric average of criterion .
- = Normalized relative weight of criterion .
After these calculations, matrices A3 and A4 were calculated, such that A3 = A1 × A2 and A4 = A3/A2, where A2 = [W1, W2, …, Wi, …, WN]T. Subsequently, the maximum eigenvalue must be calculated, which is the average of matrix A4; consequently, the consistency index is calculated as , in which a lower index value results in a smaller deviation of consistency. Subsequently, the random index (RI) is obtained for the number of criteria used in constructing the model. After this process, the consistency ratio CR = CI/CR is calculated, for which a consistency ratio of 0.1 or less is considered generally acceptable because it considers the analyst’s knowledge to be minimally consistent with the study problem (Bahloul and Abid 2011).
Step 3: This step consists of comparing the resulting alternatives (portfolios) in pairs concerning which is the best (dominant) in satisfying each criterion (return, liquidity, and risk criteria), that is, whether each alternative satisfies the criteria included in the model. If there are candidate alternatives, then there are judgment matrices of size , given that there are criteria. The pairwise comparison matrices are constructed using one of the aforementioned relative importance scales, and the process is similar to that in Step 2.
Step 4: This last step is to obtain the composite weights of the alternatives such that the product is made between the normalized relative weight Wi of each criterion obtained in Step 2, with its corresponding value for the normalized weight for each alternative obtained in Step 3 and, finally, summed over all of the criteria for each portfolio. A list of percentages is then obtained in which each portfolio has a value that reflects its relative weight in the total of portfolios, suggesting a final classification.
With the AHP method, the technique for the order of the preference using a similar ideal solution (TOPSIS) proposed by Chen and Hwang (1992) is addressed. This work shows that the chosen portfolio’s basic principle should be that which has the shortest distance to the ideal solution to maximize the benefit and simultaneously minimize the total cost. This portfolio should have the longest distance to the negative ideal solution that minimizes the benefit and maximizes the total cost (Joghi 2016). The TOPSIS method has been applied through the following steps.
Step 1: The normalized decision matrix is calculated, and each normalized value is calculated using the following expression:
where refers to the normalized value for the normalization of portfolio against criterion ; while refers to the value of the indicator of each alternative against criterion .
Step 2: The weighted normalized decision matrix is calculated, and each normalized value is calculated using the following expression:
where corresponds to the weight of the criterion (return, liquidity, and risk) , and:
Step 3: The ideal solution and the negative ideal solution are determined for which is associated with criteria that provide benefits (return), and is associated with criteria that provide costs (liquidity and risk).
where is associated with the criteria providing profits, and is associated with the criteria providing costs.
Step 4: The separation measures are calculated using an m-dimensional Euclidean distance, and the separation of each portfolio of the ideal solution is calculated from the following expression:
Similarly, the separation of each portfolio from the negative ideal solution is calculated using the following expression:
It is worth mentioning that, for the calculation of (27) and (28), the Euclidean distance measure is used, which basically refers to the square root of the difference of the squared vectors.
Step 5: The relative proximity to the ideal solution is calculated; each element of matrix Ai with respect to A* is defined by the following expression:
Step 6: Finally, the order of the preference (order of portfolios) is classified. The values of the relative closeness index are in the interval (0,1), where a value close to 1 indicates being closer to the ideal solution for the alternatives.
At first, the portfolio selection problem is carried out, doing a debugging of actions through stages 1, 2, and 3. Subsequently, after the formation of the portfolios, the AHP methodology is applied to identify, under the multi-criteria methods, the best portfolio.
3.5. Stage V
Another notable comparison in the methodology is to analyze the autoregressive integrated moving average (ARIMA) series of portfolio performance to model the portfolios’ volatility during the study period considered. In this manner, in a search for a contrast of methods, the ARIMA modeling of the portfolio returns was used; in particular, by using the ARCH/GARCH methodology to model the volatility of these portfolios given that this modeling method captures the dynamic behavior of portfolios and the models’ conditional variance (Bollerslev 1986).
Theoretically, represents the variance in the portfolio and, in turn, its volatility, and represents the error term. Both and are expected to be <1; however, the volatility of the portfolios might not respond symmetrically to the shocks produced by the series of returns.
There is no dominant criterion in the stock portfolio selection problem for deciding the best stocks to select. Profitability, risk, and liquidity criteria are important in the decision-making process. Usually, the criteria do not converge to a single decision, making it necessary to use multi-criteria techniques that integrate all the criteria. The proposed methodology allows the decision-maker to make long-term investments considering an adequate balance for all criteria.
4. Obtained Results
The proposed methodology’s efficiency has been tested using historical data on Colombian stock market prices. Initially, 25 series of stock prices with medium and high marketability of the Colombian stock market were used during the period from April 2012 to April 2017; we also used the COLCAP index’s price during the same study period. These price series are characterized by daily periodicity with official day-end prices. Of the total sample, the company’s shares CEMEX LATAM HOLDINGS SA and the preferred shares of the companies CEMENTO ARGOS SA and GRUPO ARGOS SA were not taken into account because their stocks began trading on the exchange after April 2012. This drawback could affect the validity and consistency of the subsequent results obtained. The COLCAP index had a negative average variation of 0.017% during the study period, with the most significant decline during November 2015 and January 2016, followed by a slight recovery in the subsequent months and stabilization in the last year. Eighty percent of the shares had average returns higher than the COLCAP index, and 64% of the shares showed positive average returns. Based on these data, the sample was reduced to 22 shares in search of more robust and consistent results.
After applying Stage I of the methodology, the shares in Table 2 were obtained.

Table 2.
Selected stocks after applying Stage 1 of the proposed methodology. Source: owner.
According to Stage II, a prioritization is performed from the total list of the 25 shares to achieve an adequate balance and profitability. In this case, seven shares were selected to form portfolios (see Table 3). In total, 120 portfolios with two to seven stocks were analyzed.

Table 3.
Selected stocks for the portfolios. Source: owner.
After constructing the indicators for the 120 portfolios, Table 4 shows the ordered classification of the portfolios with the highest and lowest values in each indicator, discriminated by the number of shares that constitute each portfolio. This table shows the six portfolios that maintained the strongest balance between the indicators, which is called the criteria. The nomenclature used to identify a portfolio is EX-Y, where E means shares, X is the number of shares, and Y is the number of the portfolio (see Table 4).

Table 4.
Portfolio classification according to criteria. Source: owner.
As a result of the previous table, the portfolios with the most balanced criteria of the total constructed portfolios were selected (P1–P6). These six portfolios were the input for applying Phase IV, which includes multi-criteria decision methods. Table 5 summarizes the results obtained for each portfolio.

Table 5.
Obtained results of the portfolios for the six criteria. Source: owner.
In this table, it is relevant to highlight that the profitability criteria (C1), liquidity (C5), and profitability-cost of capital (C6) are preferable to the extent that their values are high. Otherwise, with the risk criteria (C2), cost of capital (C3), and volatility (C4), low values are preferable. As mentioned in Stage IV, after obtaining the alternatives, we proceeded to build the pairwise comparison matrices, starting with each criterion and ending with the comparison matrix between the decision criteria using the relative numerical scale by Saaty (2008).
This matrix of criteria maintains a conservative configuration in which the criteria corresponding to profitability, risk, and volatility are prioritized over the criteria related to the cost of capital, idiosyncratic volatility, and profitability/cost of capital ratio. This assessment is supported by the rating performed by experts on the subject, especially in the financials and stock markets. Thus, using the AHP scale, the following table is reached.
Significantly, the values obtained in Table 6 can be modified according to the investor’s evaluation of the risk and profitability criteria. In this case, the general idea proposed by Escobar (2015) was followed to define the values in Table 6. This matrix is interpreted by comparing each column’s criterion with its corresponding criterion of each row, such that the main diagonal is composed of unit values, whereas the components on this diagonal are the pairwise comparisons of the criteria. Analogously, the components under this diagonal are the inverses of the pairwise comparison of the criteria. This matrix’s normalization provides the relative weights of each criterion—an indispensable factor for the subsequent use of the TOPSIS method. These values should be contrasted against the random consistency index. This index is fundamental to providing validity and consistency to the analysts’ judgments.

Table 6.
Matrix of criteria. Source: owner.
After normalizing the decision matrix composed of the alternatives and weighing it using the relative weights of the AHP method, the ideal solutions—both positive and negative—are found and organized. After this step, each alternative’s distance to the ideal solution—both positive and negative—is calculated. Then, the relative proximity to each alternative’s ideal solution is estimated. Finally, the alternatives were classified, and Table 7 was obtained.

Table 7.
Final classification TOPSIS method. Source: owner.
This table shows that the alternative corresponding to the portfolio made up of the two shares (CEMARGOS CB and EEB CB), with 34.5% and 65.5% participation, respectively, is the most successful choice according to this hybrid multi-criteria decision method, given the configuration and preference detailed in the criteria comparison matrix. It is also important to mention that the alternatives corresponding to portfolios 2 and 5 are the subsequent choices that yield the results closest to the positive ideal and farthest from the negative ideal. This fact becomes important when comparing the results obtained using this AHP–TOPSIS hybrid method with the results that would have been obtained using only the AHP method. Although the first three choices are the same, their order varies, especially with the optimal choice—using only the AHP method, the alternative that the investor should choose would be the one corresponding to portfolio 5.
The suggested approach’s optimal portfolio is a two-stock, non-diversified portfolio. One of the financial advantages of a more concentrated portfolio (two stocks) is that the potential returns are higher if the risk is low. Investment portfolios with the best returns for investors are typically not highly diversified. Those who focus their investments in a few firms or industries have a higher chance of amassing vast sums of money. A smaller portfolio allows investors to concentrate on a smaller number of high-quality investments. Furthermore, the more extensive a portfolio’s assets are, the more expensive it is because purchasing and selling various holdings results in more transaction fees and brokerage charges. Diversification’s spreading-out technique, more fundamentally, works both ways, lowering both risk and profit.
Another notable comparison is using ARIMA modeling of portfolio performance to model volatility during the study period. This analysis shows that the three most volatile alternatives are the same as those included in the hybrid method and the result of the AHP–TOPSIS analysis. This is a considerable distance from the other alternatives, as observed in the following graph (Figure 1).
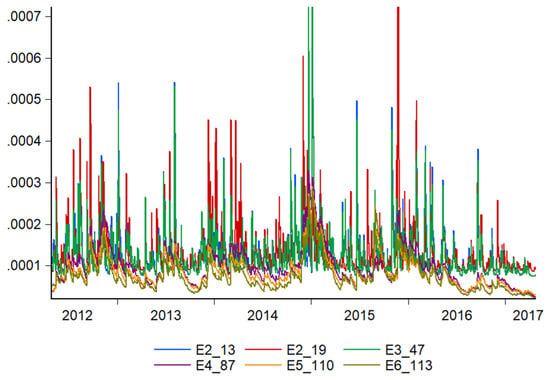
Figure 1.
Model for volatility of portfolios. Source: owner.
5. Concluding Remarks
This work has integrated various aspects, and notions focused on financial problems and specific investments in the financial market, which is currently becoming an activity frequented by individuals with excess capital who wish to increase their profits. When accessing these types of markets, investors find themselves in a rather complex environment regarding knowledge, experience, and financial barriers. In this work, an AHP-TOPSIS methodology is proposed for investment in the stock market. The incorporation of various theories and their conjunction has given rise to this work. In particular, we started with a base model of an economic and financial nature, such as the mean-variance model, continuing with multi-criteria decision methods that have served as methodological support, and notions that functioned as indicators as criteria for constructing the formed portfolios.
The use of multi-criteria decision methods for solving this type of problem is an innovative development concerning the vast techniques used for the optimal conformation of financial portfolios. This practice maintains a logical, mathematical rigor and ensures specific parameters and consistency of the results. Simultaneously, the integrated use of methods brings together each method’s advantages and complements each method’s gaps. Although the hierarchical analytical process (AHP) provides an effective structured technique based on mathematical concepts and ease of use, it also clarifies the alternatives. For its part, the technique for ordering preferences by using similarity towards the ideal solution (TOPSIS) is known for its great simplicity and ability to maintain the same number of steps regardless of the problem’s size. It has also been an optimal tool to complement other multi-criteria decision methods, according to Velasquez and Hester (2013).
As mentioned, these methods are not entirely isolated from subjectivity since preferences on the part of investors can become more or less conservative. However, all the theoretical support used provides logical solidity and consistency. The configuration of preferences highlighted and prioritized profitability, risk, and asset marketability, which led to the optimal portfolios having been those that kept values in these indicators closer to ideal. Each portfolio’s volatility modeling also supported this result. The most variable portfolios were the same as those initially found under the AHP-TOPSIS analysis and later by the AHP analysis; in this sense, a crucial result is achieved that supports the research using qualitative methodologies and taking into account the subjectivity of the investor’s preferences. These results are similar to that provided by pure data (through modeling ARIMA), to the extent that those portfolios with the highest performance were similar to those optimally selected under the hybrid AHP-TOPSIS method.
An exciting field of future research remains open by considering a combination of multi-criteria decision methods that can be carried out, or the improvement of the methods used here, such as the TOPSIS technique’s refinement, by incorporating the Mahalanobis distance. Magaña and Zúñiga (2007) researched a selection process for advanced manufacturing (TMA). This statistical measure, in particular, offers the possibility of admitting in its construction the correlations that exist between the variables involved since a variance-covariance matrix is integrated into the expression. This element is excluded in the expression of the Euclidean distance. According to Magaña and Zúñiga (2007), this application shows more reliable results since it integrates the collinearity factor between variables. In this sense, the incorporation of criteria with greater explanatory power in situations related to the formation of portfolios provides more accurate results in search of significant benefits to the investor and less exposure to losses. Furthermore, changes in the objective function (5) and one of the selected criteria (Stage III), by replacing these indicators with the Sharpe Ratio, could be considered to validate the efficiency of the proposed approach.
Author Contributions
Conceptualization, J.A.V. and J.W.E.; methodology, J.A.V., J.W.E. and D.F.M.; software, J.A.V.; validation, J.A.V., J.W.E. and D.F.M.; formal analysis, J.W.E.; investigation, J.W.E. and D.F.M.; resources, J.W.E. and D.F.M.; data curation, J.A.V.; writing—original draft preparation, J.W.E.; writing—review and editing, J.A.V. and J.W.E.; visualization, J.W.E.; supervision, J.W.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdelaziz, Fouad Ben, and Ray Saadaoui Mallek. 2018. Multi-criteria optimal stopping methods applied to the portfolio optimisation problem. Annals of Operations Research 267: 29–46. [Google Scholar] [CrossRef]
- Alali, Fatih, and A. Cagri Tolga. 2019. Portfolio allocation with the TODIM method. Expert Systems with Applications 124: 341–48. [Google Scholar] [CrossRef]
- Alexeev, Vitali, and Francis Tapon. 2012. Equity Portfolio Diversification: How Many Stocks Are Enough? Evidence from Five Developed Markets. Available online: https://ssrn.com/abstract=2182295 (accessed on 28 January 2021).
- Alptekin, Nesrin. 2009. Performance evaluation of Turkish type a mutual funds and pension stock funds by using TOPSIS method. International Journal of Economics and Finance Studies 1: 11–22. [Google Scholar]
- Aouni, Belaid, Michalis Doumpos, Blanca Pérez-Gladish, and Ralph E. Steuer. 2018. On the increasing importance of multiple criteria decision aid methods for portfolio selection. Journal of the Operational Research Society 69: 1525–42. [Google Scholar] [CrossRef]
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bahloul, Slah, and Fathi Abid. 2011. A Combined Analytic Hierarchy Process and Goal Programming Approach to International Portfolio Selection in the Presence of Investment Barriers. Available online: https://ssrn.com/abstract=1806969 (accessed on 24 March 2021).
- Bahmani, Nick, David Yamoah, Potkin Basseer, and Farahmand Rezvani. 1987. Using the analytic hierarchy process to select investment in a heterogenous environment. Mathematical Modelling 8: 157–62. [Google Scholar] [CrossRef][Green Version]
- Bali, Turan G., and Nusret Cakici. 2008. Idiosyncratic volatility and the cross section of expected returns. Journal of Financial and Quantitative Analysis 43: 29–58. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouri, Abdelfettah, Jean-Marc Martel, and Habib Chabchoub. 2002. A multi-criterion approach for selecting attractive portfolio. Journal of Multi-Criteria Decision Analysis 11: 269–77. [Google Scholar] [CrossRef]
- Charouz, Jaroslav, and Jaroslav Ramík. 2010. A multicriteria decision making at portfolio management. Ekonomika A Management 2010: 44–52. [Google Scholar]
- Chen, Shu-Jen, and Ching-Lai Hwang. 1992. Fuzzy multiple attribute decision making methods. In Fuzzy Multiple Attribute Decision Making. Berlin and Heidelberg: Springer, pp. 289–486. [Google Scholar]
- Costa, Carlos A. Bana E., and João Oliveira Soares. 2004. A multicriteria model for portfolio management. The European Journal of Finance 10: 198–211. [Google Scholar] [CrossRef]
- Elton, Edwin J., Martin J. Gruber, and Manfred W. Padberg. 1976. Simple criteria for optimal portfolio selection. The Journal of Finance 31: 1341–57. [Google Scholar] [CrossRef]
- Escobar, John Willmer. 2014. Metodología para la conformación de portafolio de acciones utilizando la técnica Multicriterio de Borda. INGE CUC 10: 60–66. [Google Scholar]
- Escobar, John Willmer. 2015. Metodología para la toma de decisiones de inversión en portafolio de acciones utilizando la técnica multicriterio AHP. Contaduría y Administración 60: 346–66. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fasanghari, Mehdi, and Gholam Ali Montazer. 2010. Design and implementation of fuzzy expert system for Tehran Stock Exchange portfolio recommendation. Expert Systems with Applications 37: 6138–47. [Google Scholar] [CrossRef]
- Frej, Eduarda Asfora, Petr Ekel, and Adiel Teixeira de Almeida. 2021. A benefit-to-cost ratio based approach for portfolio selection under multiple criteria with incomplete preference information. Information Sciences 545: 487–98. [Google Scholar] [CrossRef]
- French, Craig W. 2002. Jack Treynor’s toward a Theory of Market Value of Risky Assets. Available online: https://ssrn.com/abstract=628187 (accessed on 13 February 2021).
- Galankashi, Masoud Rahiminezhad, Farimah Mokhatab Rafiei, and Maryam Ghezelbash. 2020. Portfolio selection: A fuzzy-ANP approach. Financial Innovation 6: 1–34. [Google Scholar]
- Hababou, Moez, and Jean-Marc Martel. 1998. A multicriteria approach for selecting a portfolio manager. INFOR: Information Systems and Operational Research 36: 161–76. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1987. A test for normality of observations and regression residuals. International Statistical Review/Revue Internationale de Statistique 55: 163–72. [Google Scholar] [CrossRef]
- Joghi, E. K. 2016. An AHP-TOPSIS based Approach to Portfolio Selection. Global Journal of Management Studies and Researches 3: 31–35. [Google Scholar]
- Lintner, John. 1965. Security prices, risk, and maximal gains from diversification. The Journal of Finance 20: 587–615. [Google Scholar]
- Lintner, John. 1969. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets: A reply. The Review of Economics and Statistics 51: 222–24. [Google Scholar] [CrossRef]
- Magaña, Maria Mojarro, and Julio Macías Zúñiga. 2007. Mejoramiento de la técnica Topsis mediante la integración de la distancia de Mahalanobis. Revista Ingenieria Industrial 2: 64–74. [Google Scholar]
- Mahmoodzadeh, S., Jamal Shahrabi, Mahmood Pariazar, and M. S. Zaeri. 2007. Project selection by using fuzzy AHP and TOPSIS technique. World Academy of Science, Engineering and Technology 30: 333–38. [Google Scholar]
- Marasović, Branka, and Zoran Babić. 2011. Two-step multi-criteria model for selecting optimal portfolio. International Journal of Production Economics 134: 58–66. [Google Scholar] [CrossRef]
- Markowitz, Harry J. 1952. Portfolio Selection. The Journal of Finance 71: 77–91. [Google Scholar]
- Markowitz, Harry J. 1959. Portfolio Selection, Efficient Diversification of Investments, Cowles Foundation Monograph 16. New York: Wiley. [Google Scholar]
- Mendonça, Gustavo H. M., Fernando G. D. C. Ferreira, Rodrigo T. N. Cardoso, and Flávio V. C. Martins. 2020. Multi-attribute decision making applied to financial portfolio optimization problem. Expert Systems with Applications 158: 113527. [Google Scholar] [CrossRef]
- Mossin, Jan. 1966. Equilibrium in a capital asset market. Econometrica: Journal of the Econometric Society 34: 768–83. [Google Scholar] [CrossRef]
- Nguyen, Phi-Hung, Jung-Fa Tsai, G. Venkata Ajay Kumar, and Yi-Chung Hu. 2020. Stock Investment of Agriculture Companies in the Vietnam Stock Exchange Market: An AHP Integrated with GRA-TOPSIS-MOORA Approaches. The Journal of Asian Finance, Economics, and Business 7: 113–21. [Google Scholar] [CrossRef]
- Othman, Mohamad Rizza, Günter Wozny, and Jens-Uwe Repke. 2011. Selection of sustainable chemical process design using ANP: A biodiesel case study. Paper presented at International Symposium on the Analytic Hierarchy Process, Sorrento, Italy, June 15–18. [Google Scholar]
- Pätäri, Eero, Ville Karell, Pasil Luukka, and Julian S. Yeomans. 2018. Comparison of the multicriteria decision-making methods for equity portfolio selection: The US evidence. European Journal of Operational Research 265: 655–72. [Google Scholar] [CrossRef]
- Rockafellar, R. Tyrrell, and Stanislav Uryasev. 2000. Optimization of conditional value-at-risk. Journal of Risk 2: 21–42. [Google Scholar] [CrossRef]
- Saaty, Thomas L. 1990. How to make a decision: The analytic hierarchy process. European Journal of Operational Research 48: 9–26. [Google Scholar] [CrossRef]
- Saaty, Thomas L. 2008. Decision making with the analytic hierarchy process. International Journal of Services Sciences 1: 83–98. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1967. Efficient portfolio selection for Pareto-Lévy investments. Journal of Financial and Quantitative Analysis 2: 107–22. [Google Scholar] [CrossRef]
- Sarykalin, Sergey, Gaia Serraino, and Stan Uryasev. 2008. Value-at-Risk vs. Conditional Value-at-Risk in Risk Management and Optimization. INFORMS TutORials in Operations Research 2008: 270–94. [Google Scholar] [CrossRef]
- Shapiro, Samuel Sanford, and Martin B. Wilk. 1965. An analysis of variance test for normality (complete samples). Biometrika 52: 591–611. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance 19: 425–42. [Google Scholar]
- Sharpe, William F. 1970. Portfolio Theory and Capital Markets. New York: McGraw-Hill, vol. 217. [Google Scholar]
- Stephen, Ross. 1976. The arbitrage theory of capital asset pricing. Journal of Economic Theory 13: 341–60. [Google Scholar]
- Velasquez, Mark, and Patrick T. Hester. 2013. An analysis of multi-criteria decision making methods. International Journal of Operations Research 10: 56–66. [Google Scholar]
- Xidonas, Panagiotis, George Mavrotas, and John Psarras. 2009. A multicriteria methodology for equity selection using financial analysis. Computers & Operations Research 36: 3187–203. [Google Scholar]
- Xidonas, Panagiotis, George Mavrotas, Constantin Zopounidis, and John Psarras. 2011. IPSSIS: An integrated multicriteria decision support system for equity portfolio construction and selection. European Journal of Operational Research 210: 398–409. [Google Scholar] [CrossRef]
- Xidonas, Pans, Haris Doukas, and Christis Hassapis. 2021. Grouped data, investment committees & multicriteria portfolio selection. Journal of Business Research 129: 205–22. [Google Scholar] [CrossRef]
- Yodmun, Satit, and Wichai Witayakiattilerd. 2016. Stock selection into portfolio by fuzzy quantitative analysis and fuzzy multicriteria decision making. Advances in Operations Research 2016: 9530425. [Google Scholar] [CrossRef]
- Zopounidis, Constantin. 1999. Multicriteria decision aid in financial management. European Journal of Operational Research 119: 404–15. [Google Scholar] [CrossRef]
- Zopounidis, Constantin, and Michael Doumpos. 2002. Multi-criteria decision aid in financial decision making: Methodologies and literature review. Journal of Multi-Criteria Decision Analysis 11: 167–86. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).