Optimal Asset Allocation Subject to Withdrawal Risk and Solvency Constraints
Abstract
:1. Introduction
2. General Optimization Problem
2.1. Model Setup under Withdrawals and Solvency Constraints
2.2. General Formulation and Dynamic Programming Principle
2.3. An Alternative Dynamic Program with Exponential Utility Function
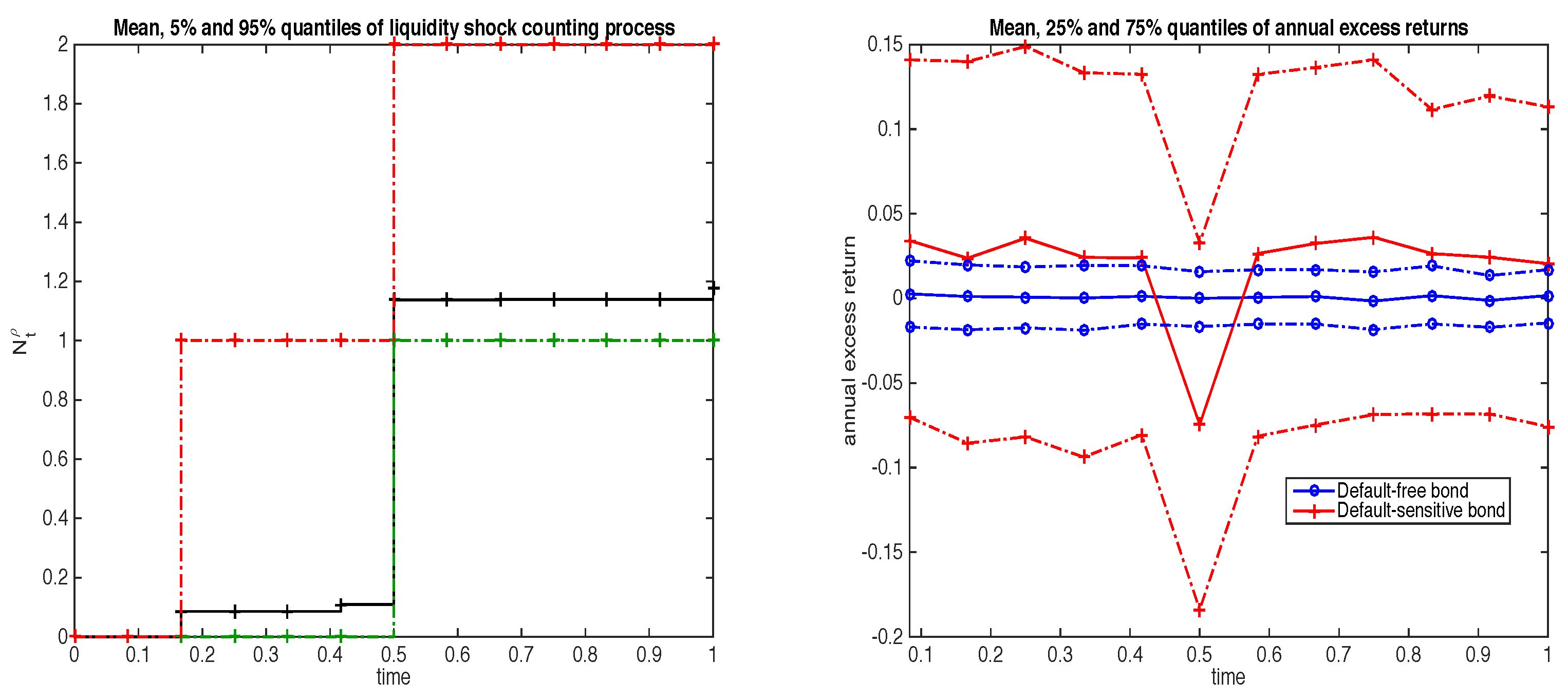
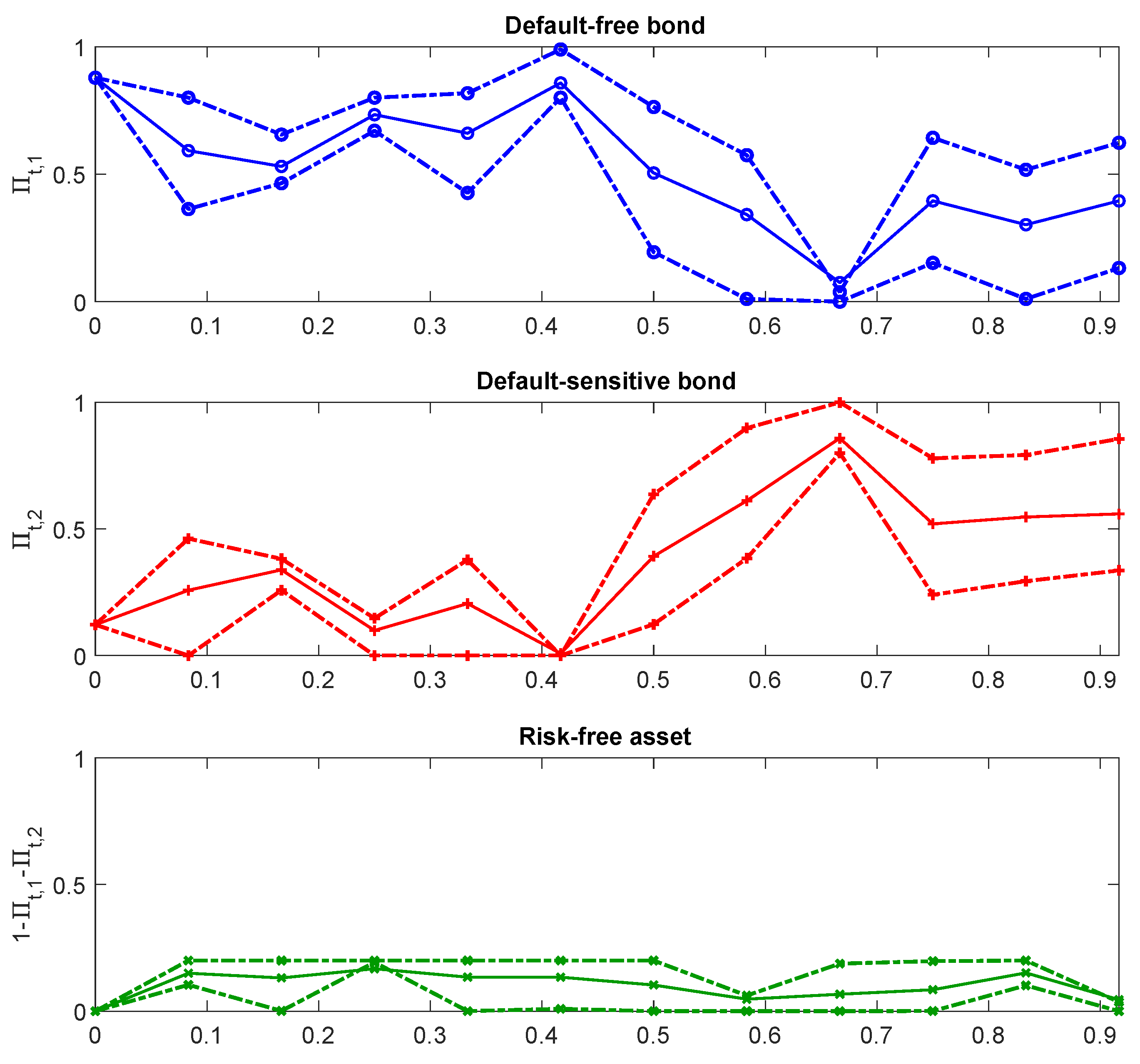
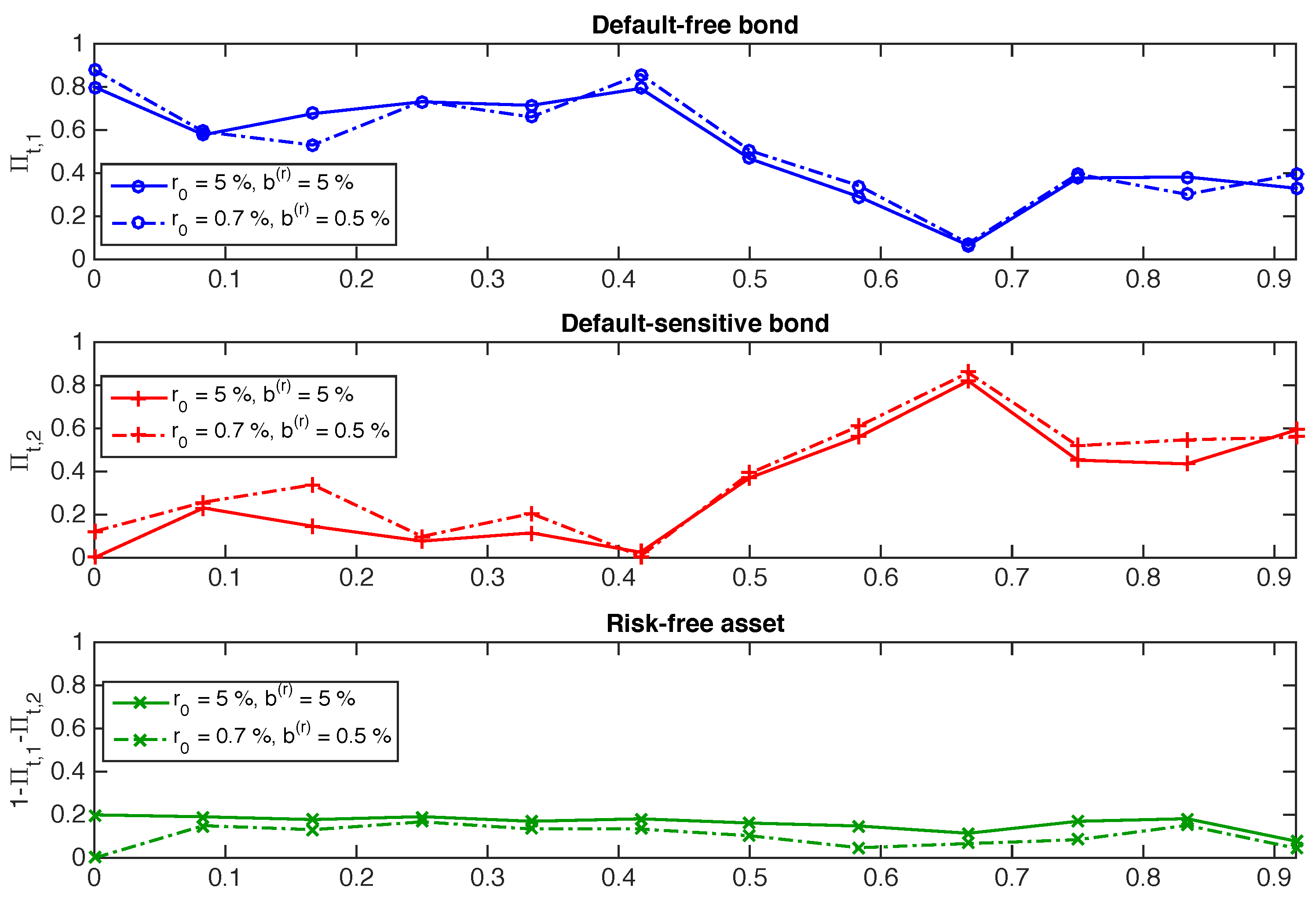
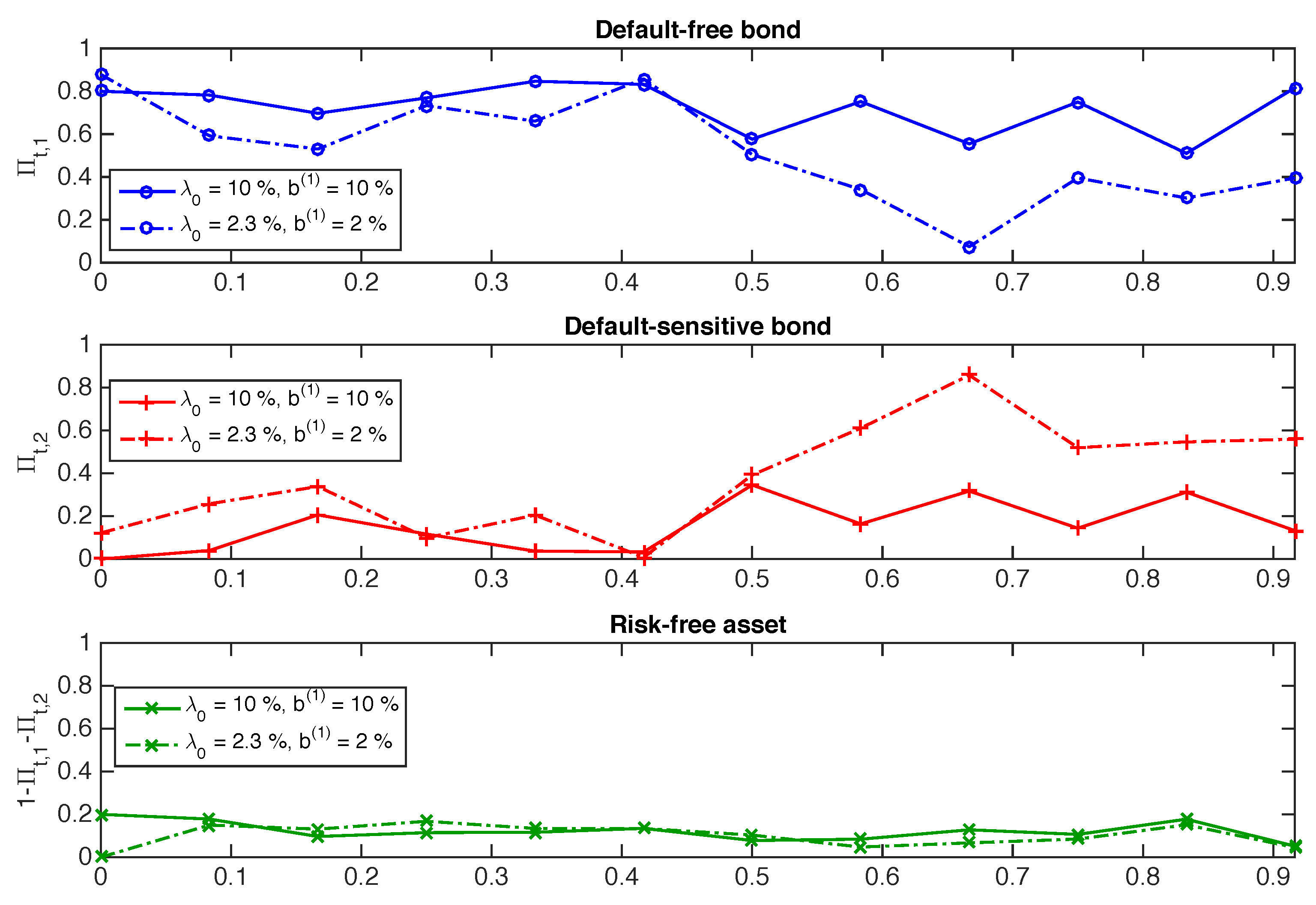
3. Application and Numerical Illustrations in the Presence of Liquidity Risk
- (1)
- the cash with a stochastic instantaneous return rate whose price at is given by ;
- (2)
- a default-free zero-coupon bond with maturity whose price is given by
- (3)
- a default-sensitive zero-coupon bond with maturity , which is impacted by both credit and liquidity risks. The endogenous credit risk is characterized by the default intensity and the pre-default price of the bond is given byAppendix A details the financial modeling of the default-free bond and of the pre-default price of the default-sensitive bond, along with specification of the market risk processes r and under both historical measure and risk-neutral measure . Moreover, following Ericsson and Renault (2006), we assume that random liquidity shocks on the market exist. According to the literature, e.g., Chen et al. (2017), the liquidity intensity depends on the global credit quality of the market and, specifically, is positively correlated with the credit risk level. We suppose that the liquidity shocks arrive according to a Cox process , where and the random times represent the occurrence times of liquidity shocks. The liquidity intensity of the Cox process is defined as , where are the scale parameters governing the sensitivity of to , the constant lower bound, and the elasticity parameter, respectively, which is similar to the extended credit CEV model in Carr and Linetsky (2006).In such an illiquid market, the bonds are sold at a discounted price that is proportional to the level of illiquidity described by the aggregated liquidity impact process with and valued in , which are independent random marks associated with the liquidity shock time (so that ). In other words, the realized transaction price of the defaultable zero-coupon bond subject to liquidity risk is then given by
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stochastic Dynamics of Financial Assets
Appendix B
Appendix B.1. Value Function and Bellman Equation
Appendix B.2. Computation of and
Appendix B.3. Numerical Procedure
- Discretizing the state space by simulating state processes. We generate n independent sample paths of the exogenous state processes r and (and accordingly modify paths of N) on the time grid . At each time t, the state space grid is been defined as the collection of sample values taken by these processes. Knowing that optimal strategies are constrained in a bounded domain, the state space for the state variable X is approximated by collecting, at each time , sample values of X generated from (26) using sampled paths of r and , and by employing, at each rebalancing date, uniformly distributed sampled strategies on the bounded domain.
- Solving the Bellman equation on the discretized state space
- The time-T value of cost-to-go function is initialized on each point of the time-T state space grid using (A16).
- For each time iteration t, and for any point in the time-t state space grid, is obtained as the solution of (A17). The coefficients of the quadratic optimization problems and are approximated using previously computed values of interpolated on the corresponding state space grid and using regression on the sample path of Z.
- Assessing the performance of optimal strategies. For each sample path of the state processes r and , we compute the value of the optimal asset portfolio by using, at each rebalancing date, the optimal strategy that best represents the state variable current value. The employed strategy is found by interpolating pre-computed optimal strategies on the current state space grid. Based on these sample paths, we can then compute sample paths of the optimal asset portfolio together with any relevant statistics.
Appendix C. Other Sensitivity Analyses
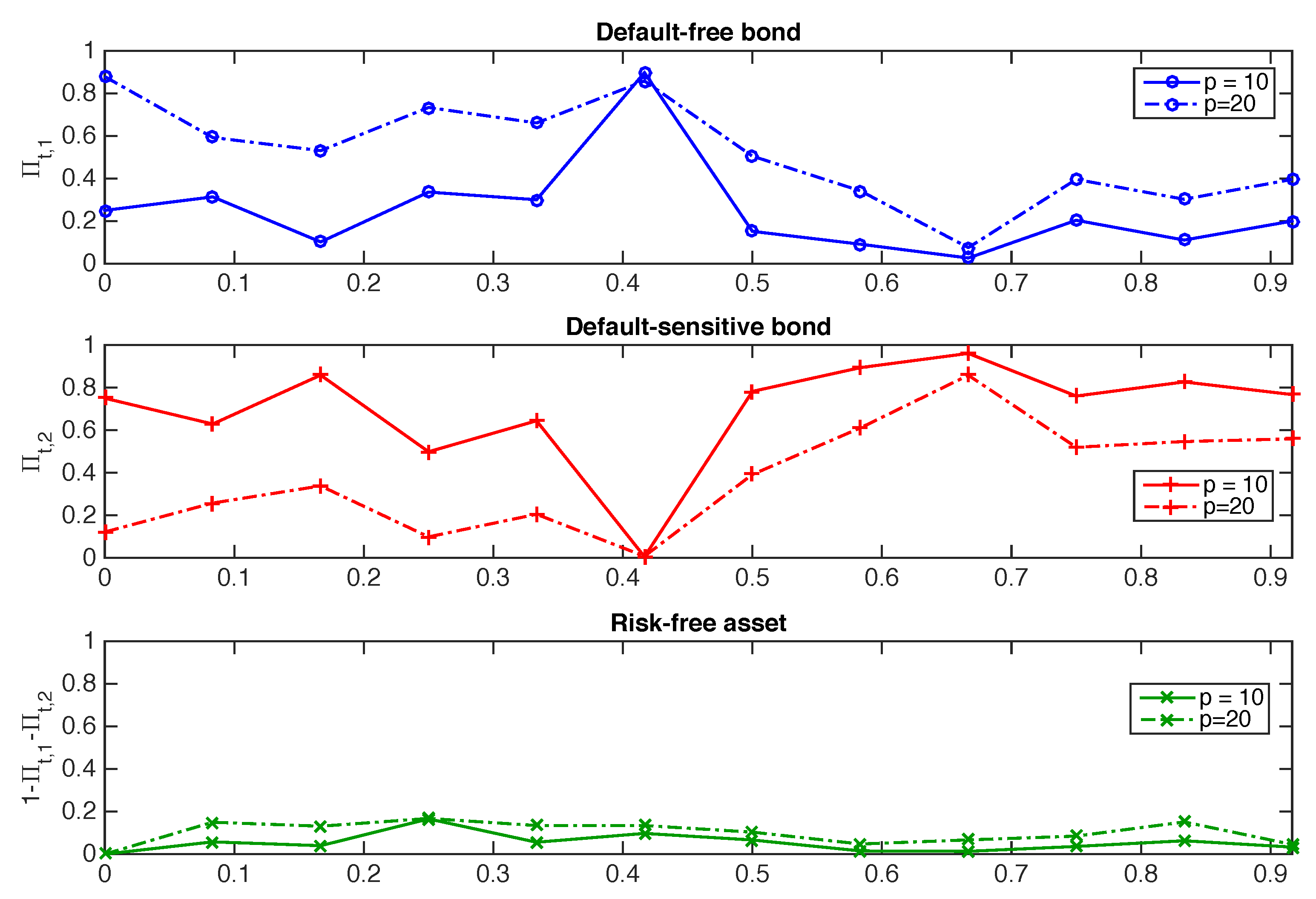

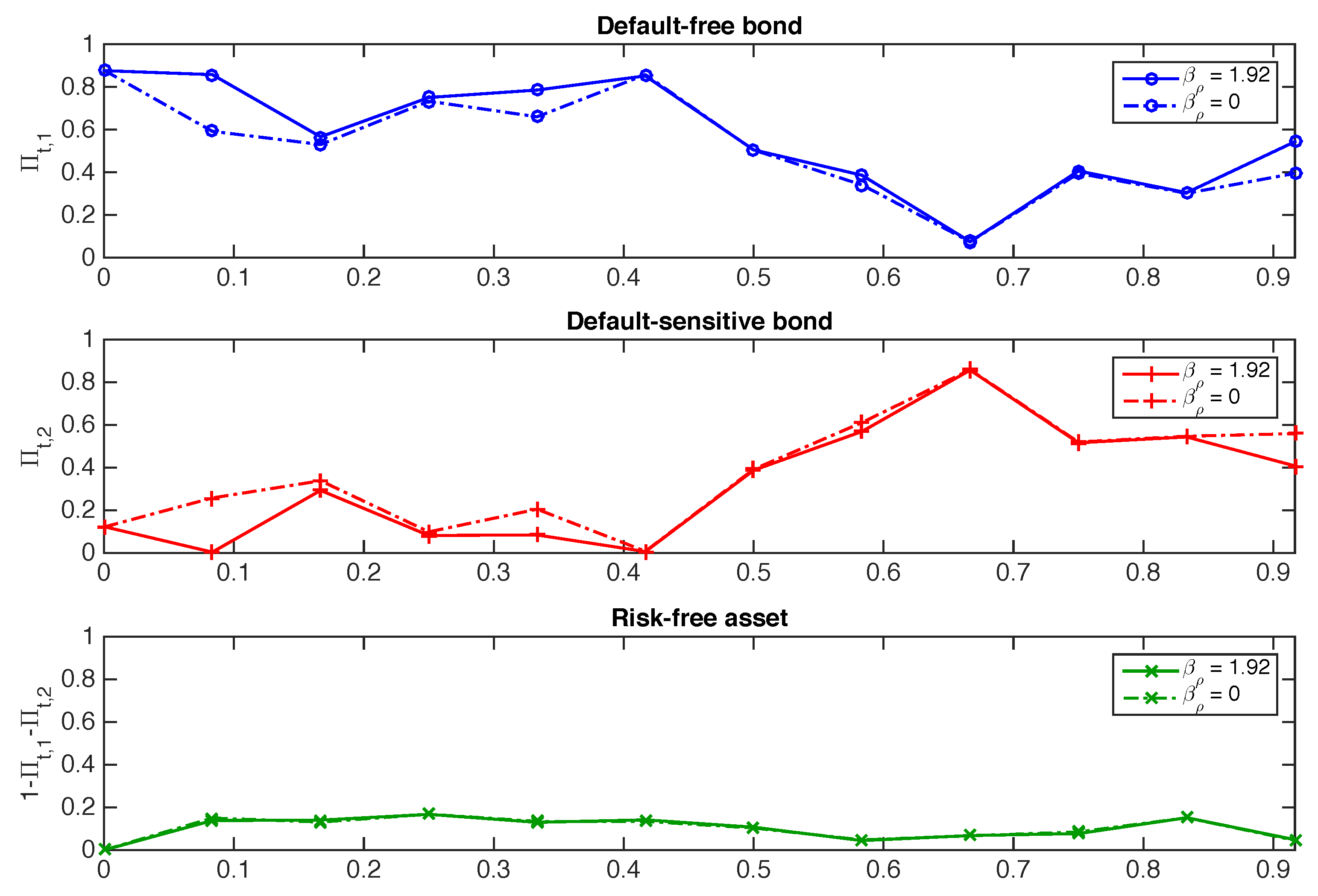
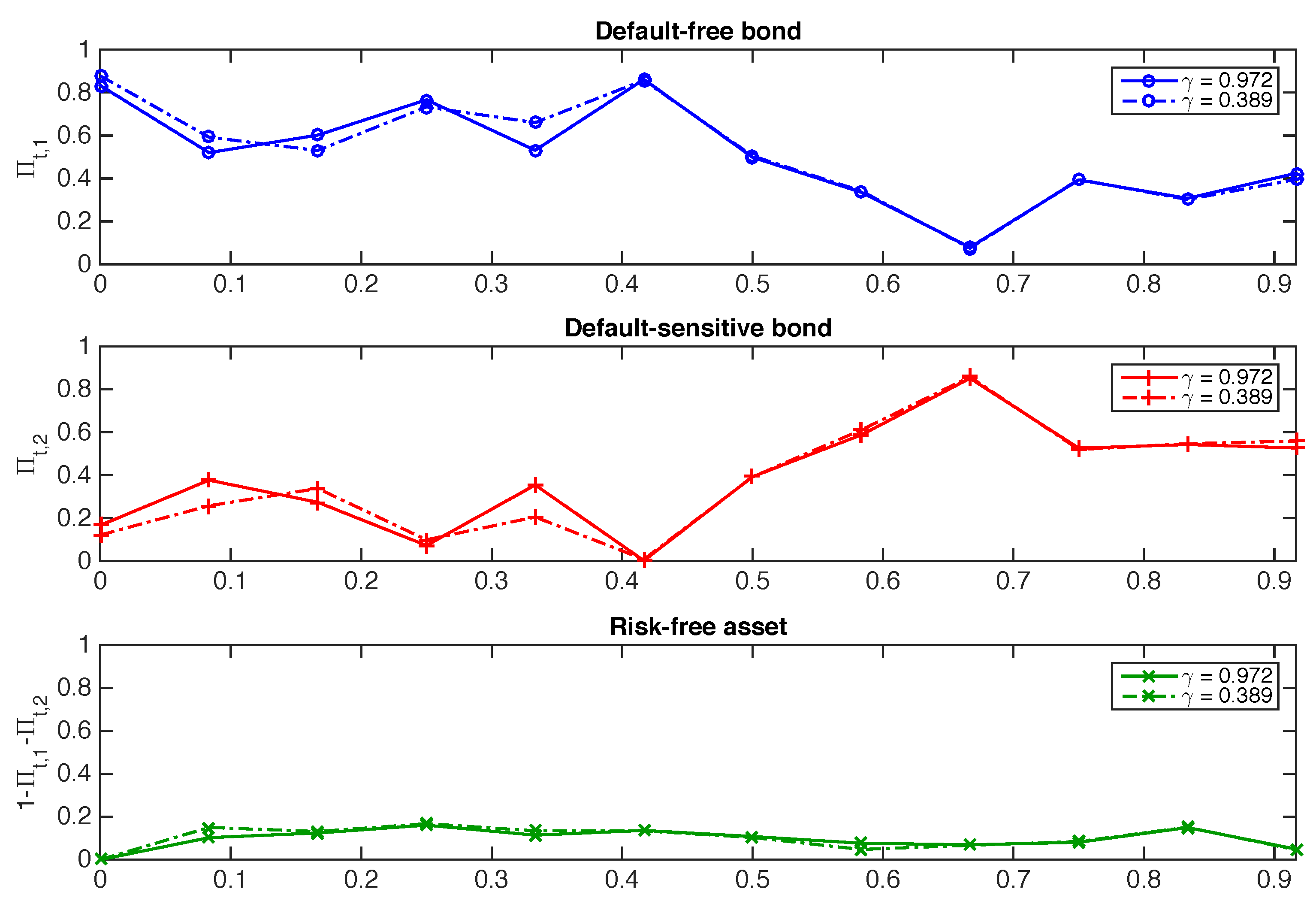

| 1 | The investment portfolio value may become negative if almost all customers decide to withdraw money from their contract and if the value of the invested assets falls, but this happens with a very low probability (see, e.g., the case study considered in Section 3 and Figure 3). |
| 2 | See Section 2.3 for a more detailed discussion. |
| 3 | |
| 4 | Meaning that when simulating these Cox processes from a standard Poisson process, only one single deterministic path of the Poisson process is used. |
| 5 | Even if Poisson noise is frozen to a deterministic path, the differences in sampled paths is due to its stochastic intensity . |
| 6 | The intensity of the liquidity shock is observed just before the jump and therefore the optimal allocation takes it into account. |
| 7 | We used the same to numerically solve Bellman equations. |
References
- Alfonsi, Aurelien. 2005. On the discretization schemes for the CIR (and Bessel squared) processes. Monte Carlo Methods and Applications 11. [Google Scholar] [CrossRef]
- Allen, Franklin, and Douglas Gale. 2004. Financial Intermediaries and Markets. Econometrica 72: 1023–61. [Google Scholar] [CrossRef] [Green Version]
- Bao, Jack, Jun Pan, and Jiang Wang. 2011. The Illiquidity of Corporate Bonds. The Journal of Finance 66: 911–46. [Google Scholar] [CrossRef] [Green Version]
- Berry-Stölzle, Thomas R. 2008. The impact of illiquidity on the asset management of insurance companies. Insurance: Mathematics and Economics 43: 1–14. [Google Scholar] [CrossRef]
- Blanchard, Romain, and Laurence Carassus. 2018. Multiple-priors optimal investment in discrete time for unbounded utility function. The Annals of Applied Probability 28: 1856–92. [Google Scholar] [CrossRef] [Green Version]
- Boyle, Phelim, and Weidong Tian. 2007. Portfolio management with constraints. Mathematical Finance 17: 319–43. [Google Scholar] [CrossRef]
- Brandt, Michael W., Amit Goyal, Pedro Santa-Clara, and Jonathan R. Stroud. 2005. A Simulation Approach to Dynamic Portfolio Choice with an Application to Learning About Return Predictability. Review of Financial Studies 18: 831–73. [Google Scholar] [CrossRef] [Green Version]
- Brunnermeier, Markus K., and Lasse Heje Pedersen. 2008. Market Liquidity and Funding Liquidity. Review of Financial Studies 22: 2201–38. [Google Scholar] [CrossRef] [Green Version]
- Cao, Charles, and Lubomir Petrasek. 2014. Liquidity risk in stock returns: An event-study perspective. Journal of Banking & Finance 45: 72–83. [Google Scholar] [CrossRef]
- Carr, Peter, and Vadim Linetsky. 2006. A jump to default extended CEV model: An application of Bessel processes. Finance and Stochastics 10: 303–30. [Google Scholar] [CrossRef]
- Chen, Hui, Rui Cui, Zhiguo He, and Konstantin Milbradt. 2017. Quantifying Liquidity and Default Risks of Corporate Bonds over the Business Cycle. The Review of Financial Studies 31: 852–97. [Google Scholar] [CrossRef]
- Chen, Tsung-Kang, Hsien-Hsing Liao, and Pei-Ling Tsai. 2011. Internal liquidity risk in corporate bond yield spreads. Journal of Banking & Finance 35: 978–87. [Google Scholar] [CrossRef]
- Cousin, Areski, Ying Jiao, Christian Y. Robert, and Olivier David Zerbib. 2016. Asset allocation strategies in the presence of liability constraints. Insurance: Mathematics and Economics 70: 327–38. [Google Scholar] [CrossRef]
- Dick-Nielsen, Jens, Peter Feldhütter, and David Lando. 2012. Corporate bond liquidity before and after the onset of the subprime crisis. Journal of Financial Economics 103: 471–92. [Google Scholar] [CrossRef] [Green Version]
- Duffie, Darrell. 2005. Credit risk modeling with affine processes. Journal of Banking & Finance 29: 2751–802. [Google Scholar] [CrossRef]
- El Karoui, Nicole. 1981. Les aspects probabilistes du contrôle stochastique. In Ninth Saint Flour Probability Summer School—1979 (Saint Flour, 1979). Lecture Notes in Math. Berlin and New York: Springer, vol. 876, pp. 73–238. [Google Scholar]
- El Karoui, Nicole, Monique Jeanblanc, and Vincent Lacoste. 2005. Optimal portfolio management with American capital guarantee. Journal of Economic Dynamics and Control 29: 449–68. [Google Scholar] [CrossRef]
- Ericsson, Jan, and Olivier Renault. 2006. Liquidity and Credit Risk. The Journal of Finance 61: 2219–50. [Google Scholar] [CrossRef]
- Favero, Carlo, Marco Pagano, and Ernst-Ludwig von Thadden. 2009. How Does Liquidity Affect Government Bond Yields? Journal of Financial and Quantitative Analysis 45: 107–34. [Google Scholar] [CrossRef] [Green Version]
- Feng, Runhuan, and Jan Vecer. 2016. Risk based capital for guaranteed minimum withdrawal benefit. Quantitative Finance 17: 471–78. [Google Scholar] [CrossRef]
- Föllmer, Hans, and Peter Leukert. 1999. Quantile hedging. Finance and Stochastics 3: 251–73. [Google Scholar] [CrossRef]
- Föllmer, Hans, and Peter Leukert. 2000. Efficient hedging: Cost vs. shortfall risk. Finance and Stochastics 4: 117–46. [Google Scholar]
- Frauendorfer, Karl, and Michael Schürle. 2003. Management of non-maturing deposits by multistage stochastic programming. European Journal of Operational Research 151: 602–16. [Google Scholar] [CrossRef] [Green Version]
- Goyenko, Ruslan, Avanidhar Subrahmanyam, and Andrey Ukhov. 2010. The Term Structure of Bond Market Liquidity and Its Implications for Expected Bond Returns. Journal of Financial and Quantitative Analysis 46: 111–39. [Google Scholar] [CrossRef] [Green Version]
- Goyenko, Ruslan Y., and Andrey D. Ukhov. 2009. Stock and Bond Market Liquidity: A Long-Run Empirical Analysis. Journal of Financial and Quantitative Analysis 44: 189–212. [Google Scholar] [CrossRef] [Green Version]
- Gundel, Anne, and Stefan Weber. 2007. Robust utility maximization with limited downside risk in incomplete markets. Stochastic Processes and Their Applications 117: 1663–88. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Ying, Olivier Klopfenstein, and Peter Tankov. 2017. Hedging under multiple risk constraints. Finance and Stochastics 21: 361–96. [Google Scholar] [CrossRef] [Green Version]
- Kalkbrener, Michael, and Jan Willing. 2004. Risk management of non-maturing liabilities. Journal of Banking & Finance 28: 1547–68. [Google Scholar] [CrossRef]
- Kling, Alexander, Frederik Ruez, and Jochen Russ. 2013. The Impact of stochastic volatility on pricing, hedging, and hedge efficiency of withdrawal benefit guarantees in variable annuities. ASTIN Bulletin 41: 511–45. [Google Scholar] [CrossRef]
- Lin, X. Sheldon, and Shuai Yang. 2020. Fast and efficient nested simulation for large variable annuity portfolios: A surrogate modeling approach. Insurance: Mathematics and Economics 91: 85–103. [Google Scholar] [CrossRef]
- Nyström, Kaj. 2008. On deposit volumes and the valuation of non-maturing liabilities. Journal of Economic Dynamics and Control 32: 709–56. [Google Scholar] [CrossRef]
- Pan, Jian, and Qingxian Xiao. 2017. Optimal asset–liability management with liquidity constraints and stochastic interest rates in the expected utility framework. Journal of Computational and Applied Mathematics 317: 371–87. [Google Scholar] [CrossRef]
- Pham, Huyên. 2009. Continuous-time stochastic control and optimization with financial applications. In Stochastic Modelling and Applied Probability. Berlin: Springer, vol. 61, pp. xviii, 232. [Google Scholar] [CrossRef]
- Shevchenko, Pavel V., and Xiaolin Luo. 2017. Valuation of variable annuities with Guaranteed Minimum Withdrawal Benefit under stochastic interest rate. Insurance: Mathematics and Economics 76: 104–17. [Google Scholar] [CrossRef] [Green Version]
- Steinorth, Petra, and Olivia S. Mitchell. 2015. Valuing variable annuities with guaranteed minimum lifetime withdrawal benefits. Insurance: Mathematics and Economics 64: 246–58. [Google Scholar] [CrossRef] [Green Version]
- Wang, Jindong, and Wei Xu. 2020. Risk based capital for variable annuity under stochastic interest rate. ASTIN Bulletin 50: 959–99. [Google Scholar] [CrossRef]

| Short term interest | Default intensity | ||
| 1 | |||
| ZC bond | ZC bond | ||
| 10 | 10 | ||
| Surrender risk | Liquidity shock | ||
| 0 | 100 | ||
| 0 | |||
| 1 | |||
| Other parameters | Initial value | ||
| M | 100 | ||
| C | |||
| 1 | |||
| p | 20 | ||
| T | 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cousin, A.; Jiao, Y.; Robert, C.Y.; Zerbib, O.D. Optimal Asset Allocation Subject to Withdrawal Risk and Solvency Constraints. Risks 2022, 10, 15. https://doi.org/10.3390/risks10010015
Cousin A, Jiao Y, Robert CY, Zerbib OD. Optimal Asset Allocation Subject to Withdrawal Risk and Solvency Constraints. Risks. 2022; 10(1):15. https://doi.org/10.3390/risks10010015
Chicago/Turabian StyleCousin, Areski, Ying Jiao, Christian Yann Robert, and Olivier David Zerbib. 2022. "Optimal Asset Allocation Subject to Withdrawal Risk and Solvency Constraints" Risks 10, no. 1: 15. https://doi.org/10.3390/risks10010015
APA StyleCousin, A., Jiao, Y., Robert, C. Y., & Zerbib, O. D. (2022). Optimal Asset Allocation Subject to Withdrawal Risk and Solvency Constraints. Risks, 10(1), 15. https://doi.org/10.3390/risks10010015





