Impact of Climate Change on Heat Wave Risk
Abstract
:1. Introduction
2. From Ruin Theory to Climate Risk
3. Modeling Temperature and Heat Wave Risk
3.1. Modeling Temperature Evolution by an Ornstein–Uhlenbeck Process
3.2. Properties of the Risk Measure for OU Processes
3.2.1. First Properties
- Monotonicity:
- Translation increase of risk: ,
- Positive homogeneity: ,
- Homothetic property at a fixed barrier:
- –
- Increase of risk when :
- –
- Decrease of risk when :
- Monotonicity:
- Translation increase of risk: ,
- Positive homogeneity: ,
- Homothetic property at a fixed barrier:
- –
- Increase of risk when :
- –
- Decrease of risk when :
3.2.2. Convex Order Property
3.2.3. Differentiability Property
4. Numerical Studies
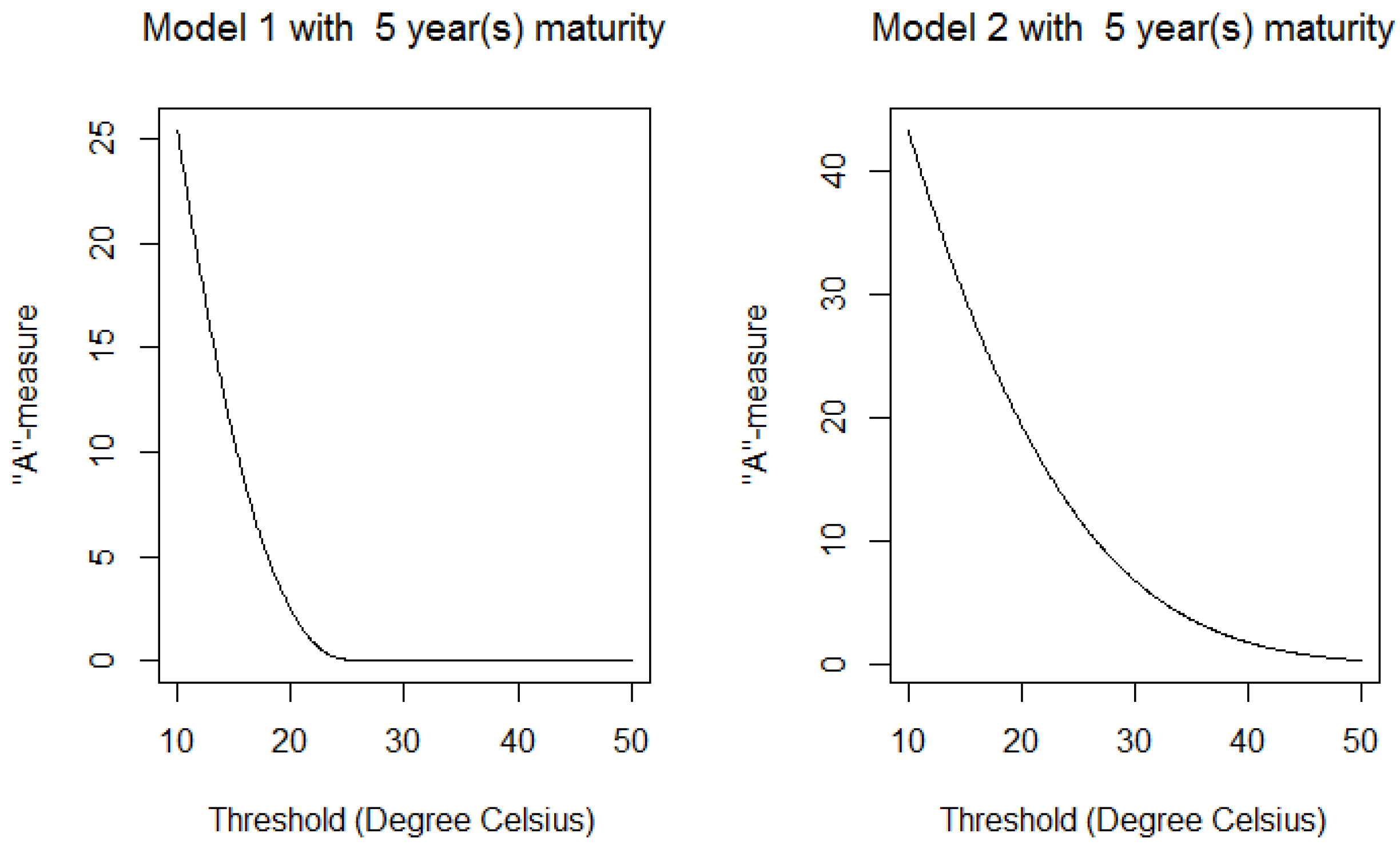
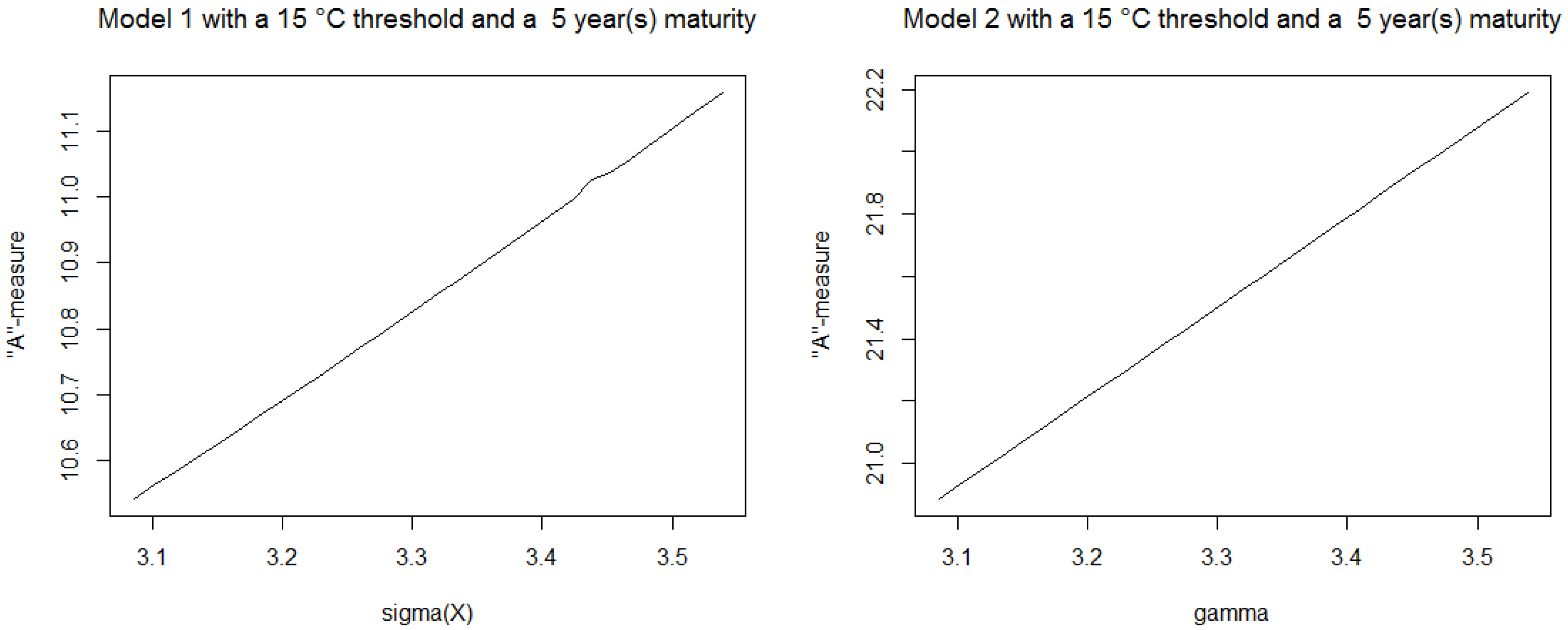
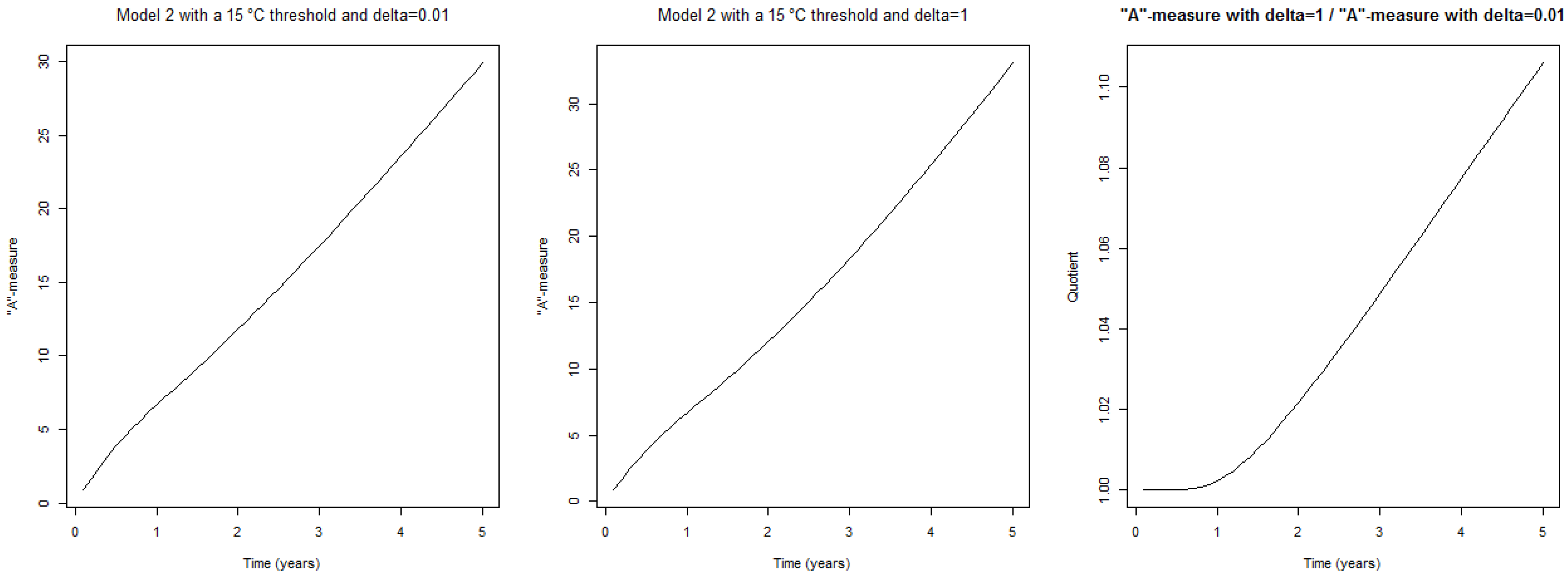
4.1. A-Measure
- The first one (Model 1) is the classical OU-process Equation (5):
- The second one (Model 2) is the OU-process, , proposed by Benth and Šaltytė Benth [10], which follows:so:where:
- is a deterministic function modeling the trend and seasonality of temperature;
- is a deterministic function describing the daily volatility of temperature variations.
| 0 | 1 | 4 | ||||||
| 4 | 2 |

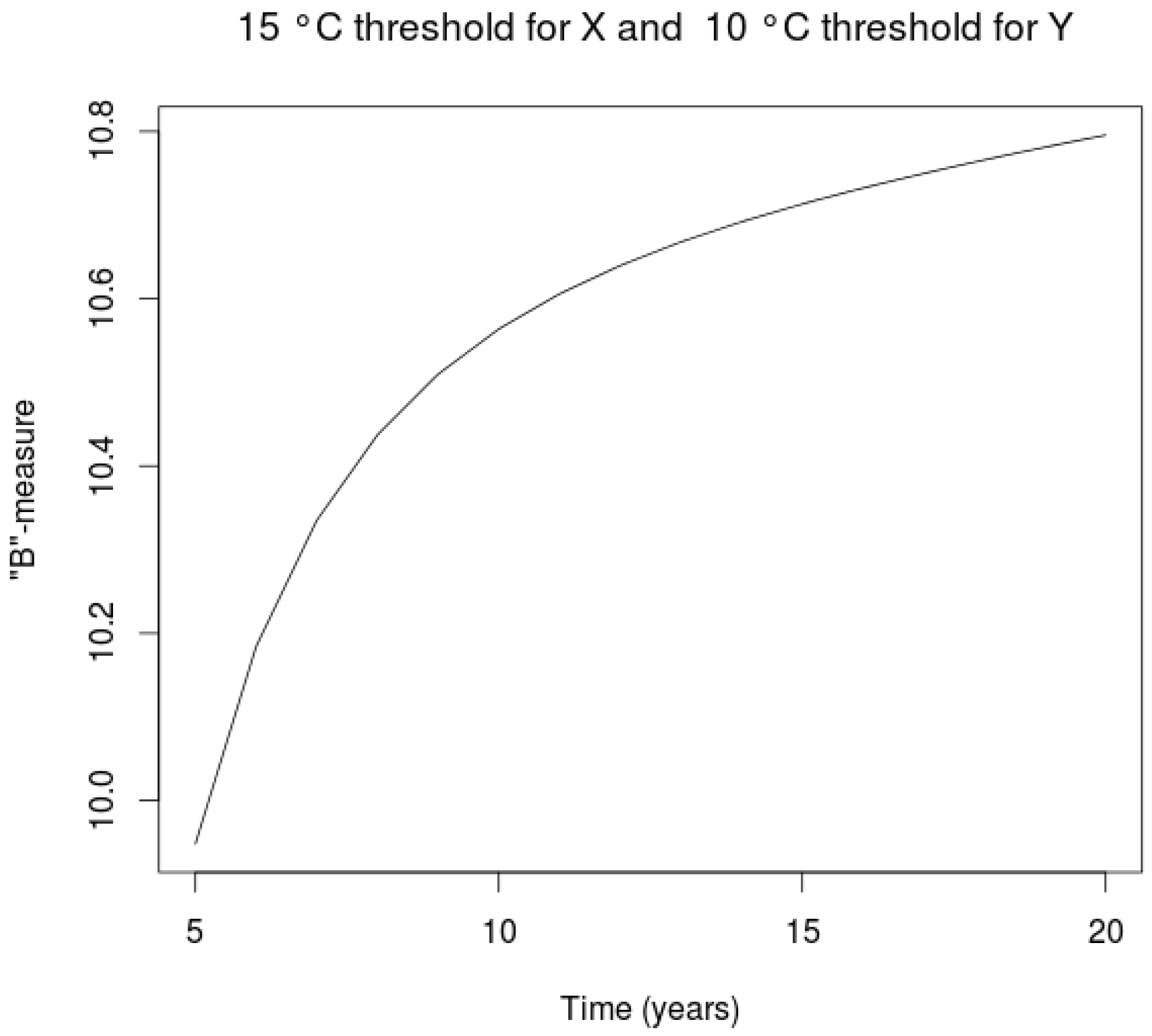
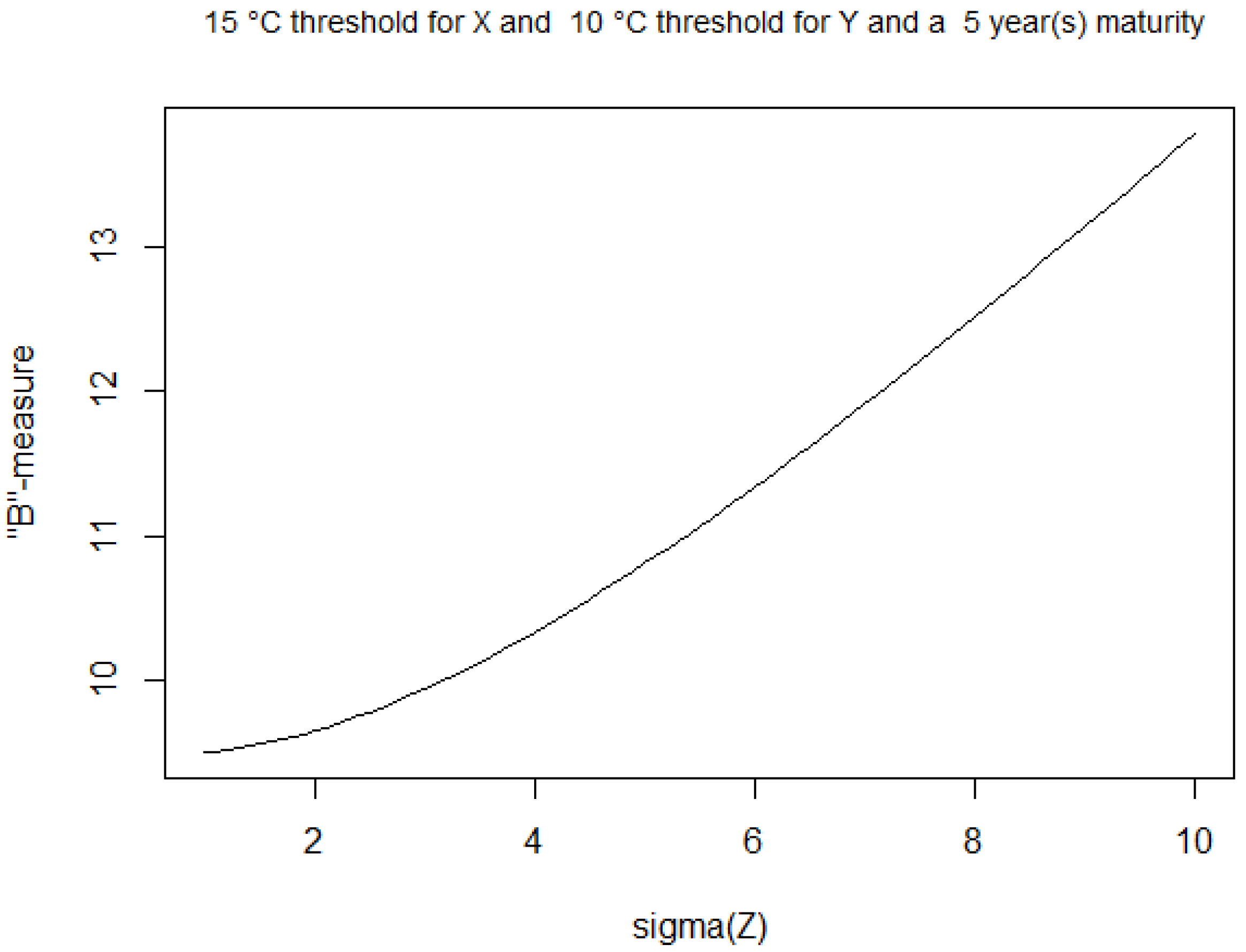
4.2. B-Measure


5. Remarks and Extensions
- A heat wave is defined by “Météo France” as a sequence of at least three consecutive days for which the highest temperature is larger than a high-level temperature and the lowest temperature is greater than a low-level temperature (both high- and the low-level temperatures depend on the geographical zone). For , define and . In this context, it could be also interesting to look at the expectation of the quantity, like:with f a function to be defined.
- For some events, the extreme behavior of several quantities at the same time can breed a major risk. For example, both high wind and high temperature have to be taken into account in wildfire risk. Therefore, we could imagine quantities, like, for two processes, and , and relative constants, and :where f is a function to be defined.
Acknowledgments
Conflicts of Interest
References
- IPCC. Stockholm, Sweden, 23–26 September 2013; Geneva, Switzerland: Intergovernmental Panel on Climate Change, 2013.
- M.L. Weitzman. “On modeling and interpreting the economics of catastrophic climate change.” Rev. Econ. Stat. 91 (2009): 1–19. [Google Scholar] [CrossRef]
- S. Loisel. “Differentiation of some functionals of risk processes, and optimal reserve allocation.” J. Appl. Probab. 42 (2005): 379–392. [Google Scholar] [CrossRef]
- R. Dishel. “A Weather Risk Management Choice: Hedging with Degree-Day Derivatives.” In Insurance and Weather Derivatives. Edited by H. Genam. London, UK: Risks Books, 1999, pp. 180–195. [Google Scholar]
- F. Dornier, and M. Queruel. “Caution to the wind.” Energ. Risk 13 (2000): 30–32. [Google Scholar]
- J. Hull, and A. White. “The pricing of options on assets with stochastic volatility.” J. Financ. 42 (1987): 281–300. [Google Scholar] [CrossRef]
- C.D. Brody, J. Syroka, and M. Zervos. “Dynamical pricing of weather derivatives.” Quant. Financ. 2 (2002): 189–198. [Google Scholar] [CrossRef]
- P. Alaton, B. Djehinche, and D. Stillberger. “On modelling and pricing of weather derivatives.” Appl. Math. Financ. 9 (2002): 1–20. [Google Scholar] [CrossRef]
- F.E. Benth, and J. Šaltytė Benth. “Stochastic modelling of temperature variations with a view towards weather derivatives.” Appl. Math. Financ. 12 (2005): 53–85. [Google Scholar] [CrossRef]
- F.E. Benth, and J. Šaltytė Benth. “The volatility of temperature and pricing of weather derivatives.” Quant. Financ. 7 (2007): 553–561. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biard, R.; Blanchet-Scalliet, C.; Eyraud-Loisel, A.; Loisel, S. Impact of Climate Change on Heat Wave Risk. Risks 2013, 1, 176-191. https://doi.org/10.3390/risks1030176
Biard R, Blanchet-Scalliet C, Eyraud-Loisel A, Loisel S. Impact of Climate Change on Heat Wave Risk. Risks. 2013; 1(3):176-191. https://doi.org/10.3390/risks1030176
Chicago/Turabian StyleBiard, Romain, Christophette Blanchet-Scalliet, Anne Eyraud-Loisel, and Stéphane Loisel. 2013. "Impact of Climate Change on Heat Wave Risk" Risks 1, no. 3: 176-191. https://doi.org/10.3390/risks1030176
APA StyleBiard, R., Blanchet-Scalliet, C., Eyraud-Loisel, A., & Loisel, S. (2013). Impact of Climate Change on Heat Wave Risk. Risks, 1(3), 176-191. https://doi.org/10.3390/risks1030176





