The Effects of Soccer Specific Exercise on Countermovement Jump Performance in Elite Youth Soccer Players
Abstract
1. Introduction
2. Materials and Methods
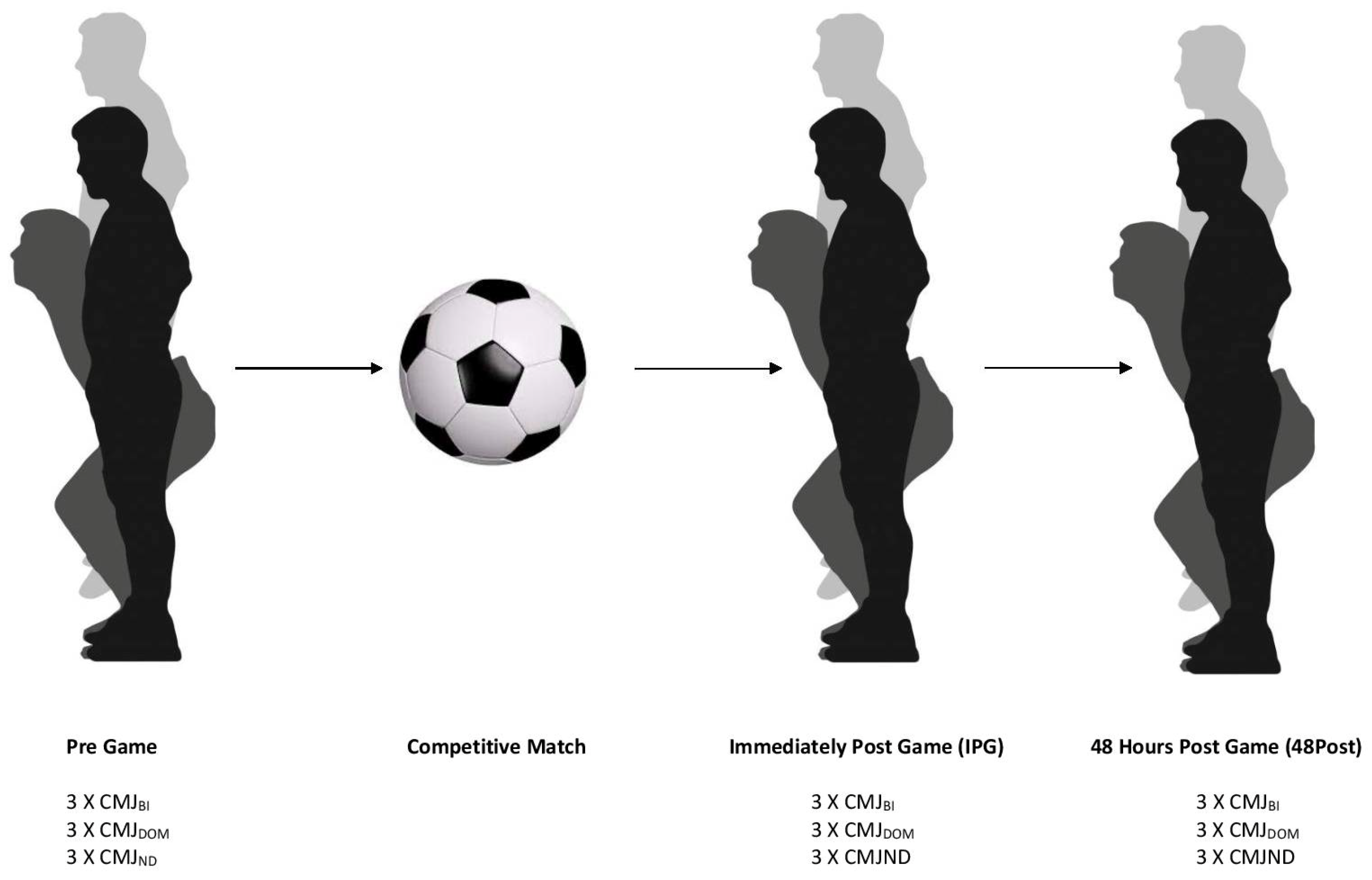
2.1. Study A
2.2. Study B
2.3. Data Analysis
2.4. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Robineau, J.; Jouaux, T.; Lacroix, M.; Babault, N. Neuromuscular Fatigue Induced by a 90-Minute Soccer Game Modeling. J. Strength Cond. Res. 2012, 26, 555–562. [Google Scholar] [CrossRef] [PubMed]
- Gathercole, R.; Sporer, B.; Stellingwerff, T.; Sleivert, G. Alternative Countermovement-Jump Analysis to Quantify Acute Neuromuscular Fatigue. Int. J. Sport. Physiol. Perform. 2015, 10, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Balsalobre-Fernández, C.; Glaister, M.; Lockey, R.A. The Validity and Reliability of an IPhone App for Measuring Vertical Jump Performance. J. Sport. Sci. 2015, 33, 1574–1579. [Google Scholar] [CrossRef] [PubMed]
- Cormie, P.; McBride, J.M.; McCaulley, G.O. Power-Time, Force-Time, and Velocity-Time Curve Analysis of the Countermovement Jump: Impact of Training. J. Strength Cond. Res. 2009, 23, 177–186. [Google Scholar] [CrossRef]
- Liebermann, D.G.; Katz, L. On the Assessment of Lower-Limb Muscular Power Capability. Isokinet. Exerc. Sci. 2003, 11, 87–94. [Google Scholar] [CrossRef]
- Chavda, S.; Bromley, T.; Jarvis, P.; Williams, S.; Bishop, C.; Turner, A.N.; Lake, J.P.; Mundy, P.D. Force-Time Characteristics of the Countermovement Jump: Analyzing the Curve in Excel. Strength Cond. J. 2018, 40, 67–77. [Google Scholar] [CrossRef]
- Cormack, S.J.; Newton, R.U.; McGuigan, M.R.; Doyle, T.L.A. Reliability of Measures Obtained during Single and Repeated Countermovement Jumps. Int. J. Sport. Physiol. Perform. 2018, 3, 131–144. [Google Scholar] [CrossRef]
- Nicol, C.; Avela, J.; Komi, P.V. The Stretch-Shortening Cycle. Sport. Med. 2006, 36, 977–999. [Google Scholar] [CrossRef]
- Granacher, U.; Puta, C.; Gabriel, H.H.W.; Behm, D.G.; Arampatzis, A. Editorial: Neuromuscular Training and Adaptations in Youth Athletes. Front. Physiol. 2018, 9, 1264. [Google Scholar] [CrossRef]
- Oliver, J.L.; Lloyd, R.S.; Whitney, A. Monitoring of In-Season Neuromuscular and Perceptual Fatigue in Youth Rugby Players. Eur. J. Sport Sci. 2015, 15, 514–522. [Google Scholar] [CrossRef]
- Merrigan, J.J.; Stone, J.D.; Hornsby, W.G.; Hagen, J.A. Identifying Reliable and Relatable Force–Time Metrics in Athletes—Considerations for the Isometric Mid-Thigh Pull and Countermovement Jump. Sports 2020, 9, 4. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, R.A.; Drake, D. The Effect of Acute Fatigue on Countermovement Jump Performance in Rugby Union Players during Preseason. J. Sport. Med. Phys. Fit. 2017, 57, 1261–1266. [Google Scholar] [CrossRef] [PubMed]
- Watkins, C.M.; Barillas, S.R.; Wong, M.A.; Archer, D.C.; Dobbs, I.J.; Lockie, R.G.; Coburn, J.W.; Tran, T.T.; Brown, L.E. Determination of Vertical Jump as a Measure of Neuromuscular Readiness and Fatigue. J. Strength Cond. Res. 2017, 31, 3305–3310. [Google Scholar] [CrossRef] [PubMed]
- Murtagh, C.F.; Nulty, C.; Vanrenterghem, J.; O’Boyle, A.; Morgans, R.; Drust, B.; Erskine, R.M. The Neuromuscular Determinants of Unilateral Jump Performance in Soccer Players Are Direction-Specific. Int. J. Sport. Physiol. Perform. 2018, 13, 604–611. [Google Scholar] [CrossRef] [PubMed]
- Lepers, R.; Maffiuletti, N.A.; Rochette, L.; Brugniaux, J.; Millet, G.Y. Neuromuscular Fatigue during a Long-Duration Cycling Exercise. J. Appl. Physiol. 2002, 92, 1487–1493. [Google Scholar] [CrossRef] [PubMed]
- McLellan, C.P.; Lovell, D.I.; Gass, G.C. Markers of Postmatch Fatigue in Professional Rugby League Players. J. Strength Cond. Res. 2011, 25, 1030–1039. [Google Scholar] [CrossRef] [PubMed]
- Legg, J.; Pyne, D.; Semple, S.; Ball, N. Variability of Jump Kinetics Related to Training Load in Elite Female Basketball. Sports 2017, 5, 85. [Google Scholar] [CrossRef]
- Flandin, G.; Friston, K. Statistical Parametric Mapping (SPM). Scholarpedia 2008, 3, 6232. [Google Scholar] [CrossRef]
- Roe, G.; Darrall-Jones, J.; Till, K.; Phibbs, P.; Read, D.; Weakley, J.; Jones, B. Between-Days Reliability and Sensitivity of Common Fatigue Measures in Rugby Players. Int. J. Sport. Physiol. Perform. 2016, 11, 581–586. [Google Scholar] [CrossRef]
- Heishman, A.D.; Daub, B.D.; Miller, R.M.; Freitas, E.D.S.; Frantz, B.A.; Bemben, M.G. Countermovement Jump Reliability Performed with and without an Arm Swing in NCAA Division 1 Intercollegiate Basketball Players. J. Strength Cond. Res. 2018, 34, 1. [Google Scholar] [CrossRef]
- Lake, J. The ‘ODSF System’: A Guide to Selecting Your Force-Time Metrics. Hawkin Dynamics, 16 March 2020. Available online: https://www.hawkindynamics.com/blog/select-your-force-time-metrics-with-this-simple-system (accessed on 12 January 2022).
- Dugdale, J.H.; Arthur, C.A.; Sanders, D.; Hunter, A.M. Reliability and Validity of Field-Based Fitness Tests in Youth Soccer Players. Eur. J. Sport Sci. 2018, 19, 745–756. [Google Scholar] [CrossRef] [PubMed]
- Owen, C.; Till, K.; Phibbs, P.; Read, D.J.; Weakley, J.; Atkinson, M.; Cross, M.; Kemp, S.; Sawczuk, T.; Stokes, K.; et al. A multidimensional approach to identifying the physical qualities of male English regional academy rugby union players; considerations of position, chronological age, relative age and maturation. Eur. J. Sport Sci. 2022, 22, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hughes, S.; Warmenhoven, J.; Haff, G.G.; Chapman, D.W.; Nimphius, S. Countermovement Jump and Squat Jump Force-Time Curve Analysis in Control and Fatigue Conditions. J. Strength Cond. Res. 2022, 36, 2752–2761. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 14 November 2022).
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis, 2nd ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Atkinson, G.; Nevill, A.M. Statistical Methods for Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sport. Med. 1998, 26, 217–238. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.C. An application of hierarchical kappa-type statistics in the assessment of majority agreement among multiple observers. Biometrics 1977, 33, 363–374. [Google Scholar] [CrossRef]
- Lakens, D. Calculating and Reporting Effect Sizes to Facilitate Cumulative Science: A Practical Primer for T-Tests and ANOVAs. Front. Psychol. 2013, 4, 863. [Google Scholar] [CrossRef] [PubMed]
- Sawczuk, T.; Jones, B.; Scantlebury, S.; Weakley, J.; Read, D.; Costello, N.; Darrall-Jones, J.D.; Stokes, K.; Till, K. Between-Day Reliability and Usefulness of a Fitness Testing Battery in Youth Sport Athletes: Reference Data for Practitioners. Meas. Phys. Educ. Exerc. Sci. 2017, 22, 11–18. [Google Scholar] [CrossRef]
- Meylan, C.; McMaster, T.; Cronin, J.; Mohammad, N.I.; Rogers, C.; Deklerk, M. Single-Leg Lateral, Horizontal, and Vertical Jump Assessment: Reliability, Interrelationships, and Ability to Predict Sprint and Change-of-Direction Performance. J. Strength Cond. Res. 2009, 23, 1140–1147. [Google Scholar] [CrossRef]
- Lloyd, R.S.; Radnor, J.M.; Croix, M.B.A.d.; Cronin, J.B.; Oliver, J.L. Changes in Sprint and Jump Performances after Traditional, Plyometric, and Combined Resistance Training in Male Youth Pre- and Post-Peak Height Velocity. J. Strength Cond. Res. 2016, 30, 1239–1247. [Google Scholar] [CrossRef]
- Peña-González, I.; Fernández-Fernández, J.; Cervelló, E.; Moya-Ramon, M. Effect of biological maturation on strength-related adaptations in young soccer players. PLoS ONE 2019, 14, e0219355. [Google Scholar] [CrossRef]
- Viru, A.; Loko, J.; Harro, M.; Volver, A.; Laaneots, L.; Viru, M. Critical periods in the development of performance capacity during childhood and adolescence. Eur. J. Phys. Educ. 1999, 4, 75–119. [Google Scholar] [CrossRef]
- Radnor, J.M.; Oliver, J.L.; Waugh, C.M.; Myer, G.D.; Moore, I.S.; Lloyd, R.S. The Influence of Growth and Maturation on Stretch-Shortening Cycle Function in Youth. Sport. Med. 2017, 48, 57–71. [Google Scholar] [CrossRef] [PubMed]
- Vandervoort, A.A.; Sale, D.G.; Moroz, J. Comparison of Motor Unit Activation during Unilateral and Bilateral Leg Extension. J. Appl. Physiol. 1984, 56, 46–51. [Google Scholar] [CrossRef] [PubMed]
- Krustrup, P.; Zebis, M.; Jensen, J.M.; Mohr, M. Game-Induced Fatigue Patterns in Elite Female Soccer. J. Strength Cond. Res. 2010, 24, 437–441. [Google Scholar] [CrossRef]
- Thorlund, J.; Aagaard, P.; Madsen, K. Rapid Muscle Force Capacity Changes after Soccer Match Play. Int. J. Sport. Med. 2009, 30, 273–278. [Google Scholar] [CrossRef]
- Knicker, A.J.; Renshaw, I.; Oldham, A.R.H.; Cairns, S.P. Interactive Processes Link the Multiple Symptoms of Fatigue in Sport Competition. Sport. Med. 2011, 41, 307–328. [Google Scholar] [CrossRef] [PubMed]
- Bonnard, M.; Sirin, A.V.; Oddsson, L.; Thorstensson, A. Different Strategies to Compensate for the Effects of Fatigue Revealed by Neuromuscular Adaptation Processes in Humans. Neurosci. Lett. 1994, 166, 101–105. [Google Scholar] [CrossRef]
- So, R.C.H.; Tse, M.A.; Wong, S.C.W. Application of Surface Electromyography in Assessing Muscle Recruitment Patterns in a Six-Minute Continuous Rowing Effort. J. Strength Cond. Res. 2007, 21, 724. [Google Scholar] [CrossRef]
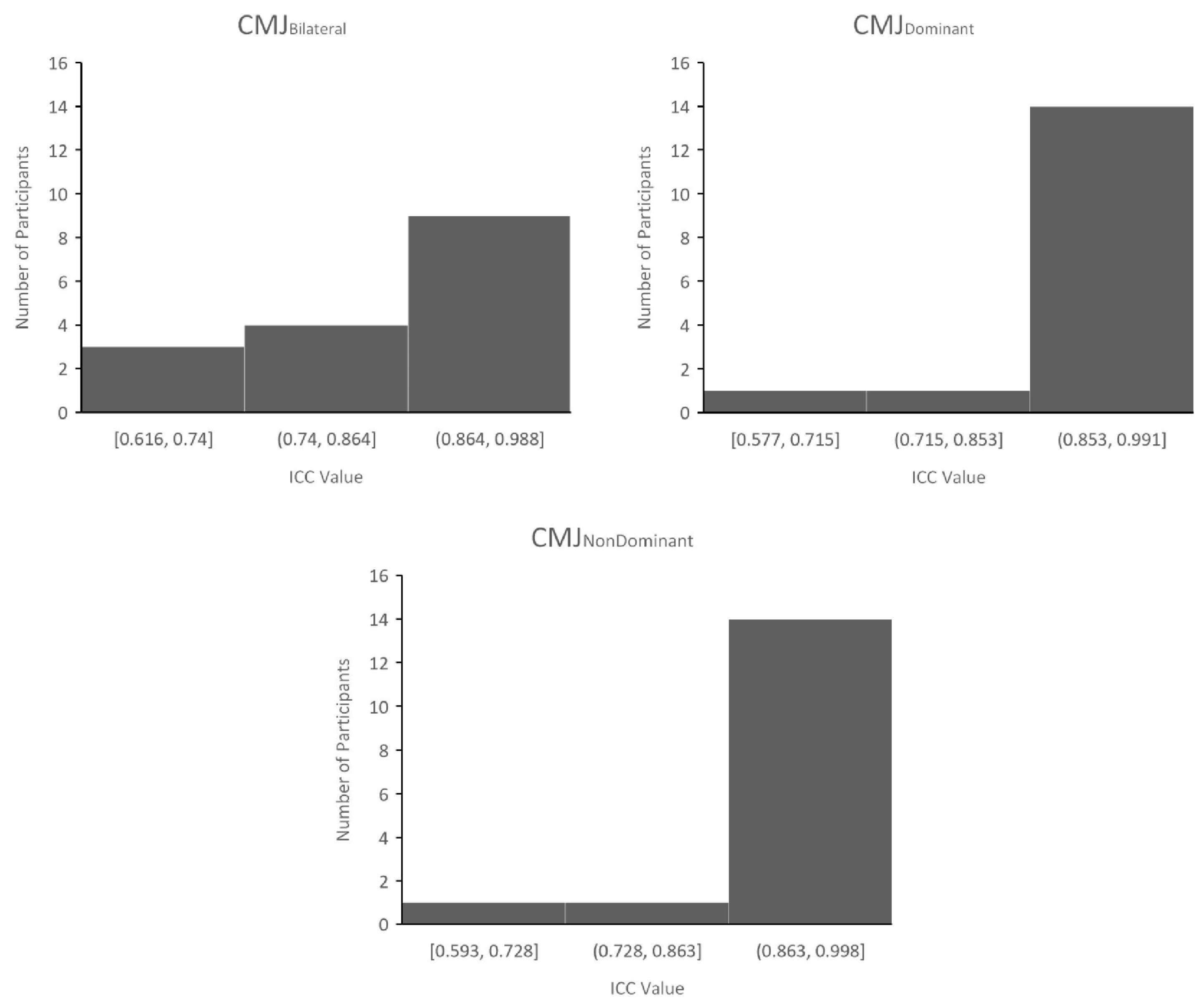
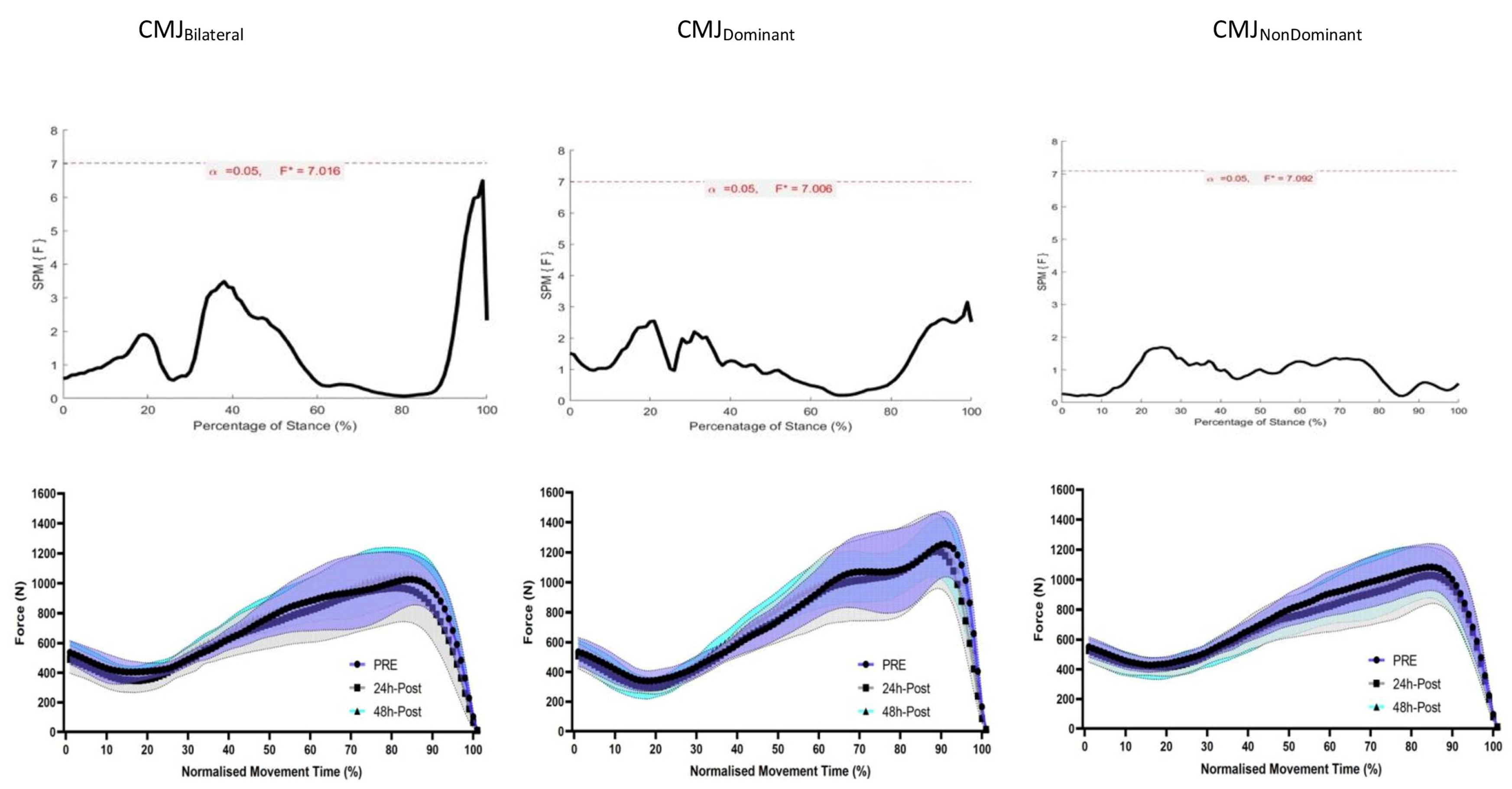
| Bland–Altman | ||||||||
|---|---|---|---|---|---|---|---|---|
| Outcome | Test 1 | Test 2 | CV (%) | ICC (95% CI) | Bias | Lower LOA | Upper LOA | |
| CMJBI | Jump Height (m) | 0.30 ± 0.05 | 0.29 ± 0.05 | 13.16 | 0.49 (0.07 to 0.88) | 0.01 ± 0.07 | −0.12 | 0.13 |
| mRSI | 0.29 ± 0.06 | 0.30 ± 0.08 | 15.78 | 0.54 (0.31 to 0.92) | −0.01 ± 0.09 | −0.17 | 0.16 | |
| Force at Min. Displacement (N) | 1133.46 ± 200.47 | 1064.35 ± 181.47 | 13.52 | 0.68 (0.67 to 0.960 | −69.10 ± 249.64 | −562.86 | 424.65 | |
| Countermovement Depth (m) | 0.33 ± 0.06 | 0.32 ± 0.06 | 11.37 | 0.70 (0.54 to 0.87) | −0.01 ± 0.05 | −0.12 | 0.11 | |
| Time to Takeoff (s) | 1.08 ± 0.21 | 1.05 ± 0.14 | 8.89 | 0.59 (0.52 to 0.94) | 0.02 ± 0.17 | −0.35 | 0.30 | |
| Ecc Time (s) | 0.30 ± 0.12 | 0.28 ± 0.07 | 19.24 | 0.66 (0.04 to 0.89) | 0.02 ± 0.11 | −0.20 | 0.23 | |
| Peak Ecc Power (W) | 738.25 ± 291.74 | 660.24 ± 201.77 | 18.90 | 0.75 (0.60 to 0.95) | −78.01 ± 221.79 | −526.44 | 370.42 | |
| Mean Ecc Power (W) | 541.40 ± 192.60 | 484.59 ± 142.42 | 19.52 | 0.75 (0.65 to 0.96) | −56.81 ± 149.32 | −347.32 | 260.68 | |
| Ecc Impulse (kg⋅m/s) | 233.40 ± 59.59 | 215.46 ± 56.03 | 13.84 | 0.82 (0.45 to 0.94) | 17.93 ± 53.60 | −97.61 | 133.48 | |
| Con Time (s) | 0.34 ± 0.08 | 0.33 ± 0.06 | 12.37 | 0.63 (0.45 to 0.98) | 0.01 ± 0.08 | −0.13 | 0.16 | |
| Peak Con Power (W) | 2936.52 ± 492.26 | 2847.97 ± 443.69 | 8.62 | 0.67 (0.46 to 0.98) | 88.54 ± 420.62 | −722.77 | 899.87 | |
| Mean Con Power (W) | 1401.67 ± 249.65 | 1353.64 ± 274.98 | 12.06 | 0.53 (0.37 to 0.97) | −48.03 ± 306.70 | −668.64 | 572.57 | |
| Con Impulse (kg⋅m/s) | 356.90 ± 65.50 | 335.33 ± 59.68 | 8.14 | 0.66 (0.48 to 0.96) | 21.56 ± 48.30 | −76.60 | 119.74 | |
| Ecc:Con Ratio | 1 ± 0.21 | 1 ± 0.14 | 14.20 | 0.12 (0.06 to 0.73) | 0.01 ± 0.24 | −0.47 | 0.45 | |
| CMJDOM | Jump Height (m) | 0.14 ± 0.04 | 0.13 ± 0.03 | 18.40 | 0.53 (0.24 to 0.85) | 0.00 ± 0.06 | −0.10 | 0.10 |
| mRSI | 0.15 ± 0.04 | 0.16 ± 0.06 | 15.79 | 0.70 (0.54 to 0.95) | −22.95 ± 41.73 | −104.63 | 58.73 | |
| Force at Min. Displacement (N) | 940.33 ± 157.13 | 958.53 ± 183.71 | 8.99 | 0.80 (0.76 to 0.98) | −18.19 ± 140.25 | −284.83 | 248.43 | |
| Countermovement Depth (m) | 0.18 ± 0.06 | 0.20 ± 0.04 | 13.45 | 0.76 (0.30 to 0.91) | 0.01 ± 0.04 | −0.07 | 0.10 | |
| Time to Takeoff (s) | 0.94 ± 0.21 | 1.02 ± 0.19 | 13.84 | 0.60 (0.45 to 0.86) | 0.08 ± 0.23 | −0.39 | 0.55 | |
| Ecc Time (s) | 0.23 ± 0.10 | 0.30 ± 0.09 | 25.15 | 0.36 (0.23 to 0.80) | −0.06 ± 0.16 | −0.37 | 0.24 | |
| Peak Ecc Power (W) | 432.33 ± 150.86 | 437.19 ± 102.71 | 11.93 | 0.85 (0.78 to 0.96) | 4.86 ± 94.86 | −181.05 | 190.77 | |
| Mean Ecc Power (W) | 303.50 ± 117.23 | 307.89 ± 78.72 | 20.96 | 0.77 (0.69 to 0.96) | 4.37 ± 89.17 | −167.49 | 176.25 | |
| Ecc Impulse (kg⋅m/s) | 176.03 ± 59.13 | 219.32 ± 66.34 | 21.12 | 0.33 (0.17 to 0.65) | −14.36 ± 145.62 | −192.62 | 163.89 | |
| Con Time (s) | 0.32 ± 0.09 | 0.36 ± 0.09 | 12.67 | 0.71 (0.16 to 0.90) | −0.03 ± 0.08 | −0.21 | 0.14 | |
| Peak Con Power (W) | 1752.27 ± 415.52 | 1781.39 ± 335.05 | 11.11 | 0.77 (0.63 to 0.98) | 29.12 ± 324.92 | −606.89 | 665.14 | |
| Mean Con Power (W) | 885.77 ± 184.09 | 880.73 ± 220.75 | 12.89 | 0.74 (0.68 to 0.96) | 5.03 ± 170.87 | −329.52 | 329.52 | |
| Con Impulse (kg⋅m/s) | 293.96 ± 67.93 | 312.50 ± 56.57 | 10.70 | 0.79 (0.59 to 0.92) | −2.86 ± 104.21 | −47.22 | 41.49 | |
| Ecc:Con Ratio | 1 ± 0.18 | 1 ± 0.18 | 18.55 | 0.18 (0.06 to 0.71) | −0.11 ± 0.44 | −0.95 | 0.72 | |
| CMJND | Jump Height (m) | 0.15 ± 0.02 | 0.16 ± 0.06 | 21.35 | 0.36 (0.16 to 0.85) | −0.01 ± 0.06 | −0.11 | 0.09 |
| mRSI | 0.17 ± 0.04 | 0.19 ± 0.08 | 24.06 | 0.40 (0.26 to 0.86) | 0.01 ± 0.09 | −0.16 | 0.13 | |
| Force at Min. Displacement (N) | 969.52 ± 117.94 | 885.39 ± 131.54 | 10.93 | 0.34 (0.21 to 0.96) | 84.14 ± 156.70 | −223.45 | 391.72 | |
| Countermovement Depth (m) | 0.18 ± 0.05 | 0.20 ± 0.08 | 19.51 | 0.63 (0.36 to 0.70) | 0.02 ± 0.08 | −0.16 | 0.19 | |
| Time to Takeoff (s) | 0.91 ± 0.21 | 0.96 ± 0.21 | 9.87 | 0.76 (0.51 to 0.94) | −0.04 ± 0.17 | −0.41 | 0.31 | |
| Ecc Time (s) | 0.22 ± 0.10 | 0.25 ± 0.10 | 16.13 | 0.70 (0.42 to 0.93) | −0.02 ± 0.09 | −0.21 | 0.16 | |
| Peak Ecc Power (W) | 447.04 ± 130.76 | 469.99 ± 285.98 | 21.79 | 0.45 (0.18 to 0.66) | −18.93 ± 283.40 | −581.43 | 619.30 | |
| Mean Ecc Power (W) | 319.49 ± 92.94 | 300.14 ± 106.47 | 20.44 | 0.62 (0.22 to 0.86) | −16.38 ± 116.47 | −207.75 | 174.98 | |
| Ecc Impulse (kg⋅m/s) | 172.26 ± 65.64 | 165.63 ± 55.53 | 13.12 | 0.75 (0.28 to 0.92) | −3.77 ± 93.75 | −106.55 | 98.99 | |
| Con Time (s) | 0.31 ± 0.07 | 0.33 ± 0.08 | 8.96 | 0.84 (0.54 to 0.94) | −0.02 ± 0.06 | −0.14 | 0.09 | |
| Peak Con Power (W) | 1884.79 ± 271.91 | 1860.48 ± 435.77 | 7.63 | 0.86 (0.72 to 0.97) | 27.70 ± 391.97 | −468.16 | 523.56 | |
| Mean Con Power (W) | 958.19 ± 129.65 | 904.91 ± 226.59 | 11.57 | 0.72 (0.65 to 0.97) | 49.32 ± 225.54 | −288.40 | 387.04 | |
| Con Impulse (kg⋅m/s) | 296.24 ± 61.49 | 284.65 ± 62.80 | 9.35 | 0.85 (0.57 to 0.82) | 6.12 ± 89.73 | −73.89 | 86.15 | |
| Ecc:Con Ratio | 1 ± 0.15 | 1 ± 0.15 | 10.69 | 0.74 (0.26 to 0.91) | −0.03 ± 0.15 | −0.32 | 0.25 | |
| Mean | ||||||
|---|---|---|---|---|---|---|
| Outcome | Pre | IPG | 48Post | p | np2 | |
| CMJBI | Jump Height (m) | 0.28 ± 0.06 | 0.26 ± 0.07 | 0.26 ± 0.06 | 0.48 | 0.06 |
| mRSI | 0.29 ± 0.10 | 0.28 ± 0.09 | 0.27 ± 0.08 | 0.87 | 0.02 | |
| Force at Min. Displacement (N) | 1077.81 ± 360.89 | 1003.82 ± 397.44 | 1067.50 ± 262.22 | 0.30 | 0.10 | |
| Countermovement Depth (m) | 0.33 ± 0.07 | 0.34 ± 0.10 | 0.35 ± 0.07 | 0.83 | 0.01 | |
| Time to Takeoff (s) | 1.02 ± 0.16 | 0.97 ± 0.19 | 0.97 ± 0.10 | 0.32 | 0.10 | |
| Ecc Time (s) | 0.27 ± 0.10 | 0.26 ± 0.08 | 0.28 ± 0.08 | 0.68 | 0.03 | |
| Peak Ecc Power (W) | 683.99 ± 280.41 | 655.56 ± 293.10 | 757.82 ± 290.95 | 0.15 | 0.16 | |
| Mean Ecc Power (W) | 505.37 ± 212.54 | 480.29 ± 222.36 | 557.62 ± 215.67 | 0.13 | 0.18 | |
| Ecc Impulse (kg⋅m/s) | 212.10 ± 63.57 * | 192.40 ± 53.22^ | 226.74 ± 61.05 | 0.03 | 0.28 | |
| Con Time (s) | 0.32 ± 0.07 | 0.31 ± 0.05 | 0.31 ± 0.03 | 0.52 | 0.05 | |
| Peak Con Power (W) | 2651.86 ± 815.71 | 2551.26 ± 1103.45 | 2582.53 ± 814.17 | 0.59 | 0.04 | |
| Mean Con Power (W) | 1297.40 ± 502.62 | 1204.93 ± 585.76 | 1247.33 ± 394.02 | 0.48 | 0.07 | |
| Con Impulse (kg⋅m/s) | 318.75 ± 59.14 * | 292.66 ± 82.05^ | 317.66 ± 65.61 | 0.01 | 0.37 | |
| Ecc:Con Ratio | 1 ± 0.27 | 1 ± 0.18 | 1 ± 0.21 | 0.43 | 0.07 | |
| CMJDOM | Jump Height (m) | 0.13 ± 0.04 | 0.14 ± 0.05 | 0.12 ± 0.05 | 0.37 | 0.08 |
| mRSI | 0.15 ± 0.08 | 0.17 ± 0.09 | 0.14 ± 0.08 | 0.77 | 0.09 | |
| Force at Min. Displacement (N) | 896.35 ± 328.18 * | 823.67 ± 337.45 ^ | 945.25 ± 242.31 | 0.02 | 0.34 | |
| Countermovement Depth (m) | 0.20 ± 0.06 | 0.19 ± 0.10 | 0.19 ± 0.03 | 0.35 | 0.02 | |
| Time to Takeoff (s) | 0.97 ± 0.22 | 0.95 ± 0.26 | 0.93 ± 0.17 | 0.66 | 0.03 | |
| Ecc Time (s) | 0.26 ± 0.11 | 0.26 ± 0.14 | 0.22 ± 0.06 | 0.31 | 0.10 | |
| Peak Ecc Power (W) | 430.61 ± 149.13 | 388.56 ± 186.34 | 453.36 ± 146.59 | 0.10 | 0.19 | |
| Mean Ecc Power (W) | 303.51 ± 120.38 | 267.22 ± 138.71 ^ | 325.93 ± 106.50 | 0.03 | 0.27 | |
| Ecc Impulse (kg⋅m/s) | 181.74 ± 58.87 | 167.64 ± 69.42 | 170.31 ± 41.04 | 0.53 | 0.06 | |
| Con Time (s) | 0.37 ± 0.09 | 0.36 ± 69.42 | 0.34 ± 0.10 | 0.40 | 0.08 | |
| Peak Con Power (W) | 1581.17 ± 614.00 | 1583.98 ± 711.96 | 1586.23 ± 692.09 | 1.00 | 0.00 | |
| Mean Con Power (W) | 798.18 ± 373.50 | 772.83 ± 406.08 | 816.85 ± 378.58 | 0.40 | 0.08 | |
| Con Impulse (kg⋅m/s) | 299.26 ± 63.81 | 275.61 ± 98.46 | 291.77 ± 77.14 | 0.17 | 0.15 | |
| Ecc:Con Ratio | 3 ± 1.98 | 3 ± 2.51 | 3 ± 2.18 | 0.71 | 0.13 | |
| CMJND | Jump Height (m) | 0.13 ± 0.06 | 0.13 ± 0.06 | 0.14 ± 0.05 | 0.40 | 0.08 |
| mRSI | 0.16 ± 0.09 | 0.14 ± 0.07 | 0.17 ± 0.08 | 0.21 | 0.11 | |
| Force at Min. Displacement (N) | 877.68 ± 258.69 | 832.56 ± 252.16 | 892.33 ± 250.28 | 0.10 | 0.19 | |
| Countermovement Depth (m) | 0.15 ± 0.06 | 0.16 ± 0.06 | 0.17 ± 0.05 | 0.29 | 0.13 | |
| Time to Takeoff (s) | 0.91 ± 0.20 | 0.92 ± 0.16 | 0.90 ± 0.24 | 0.88 | 0.01 | |
| Ecc Time (s) | 0.23 ± 0.10 | 0.25 ± 0.06 | 0.23 ± 0.09 | 0.70 | 0.03 | |
| Peak Ecc Power (W) | 303.98 ± 257.85 | 379.32 ± 186.82 | 408.33 ± 167.62 | 0.21 | 0.16 | |
| Mean Ecc Power (W) | 223.08 ± 180.75 | 259.76 ± 137.85 | 286.62 ± 122.13 | 0.23 | 0.13 | |
| Ecc Impulse (kg⋅m/s) | 166.83 ± 63.48 | 170.25 ± 47.14 | 168.58 ± 64.71 | 0.96 | 0.00 | |
| Con Time (s) | 0.32 ± 0.08 | 0.34 ± 0.06 | 0.35 ± 0.13 | 0.48 | 0.07 | |
| Peak Con Power (W) | 1692.37 ± 742.40 | 1665.54 ± 784.90 | 1720.82 ± 646.90 | 0.67 | 0.02 | |
| Mean Con Power (W) | 831.34 ± 418.44 | 783.17 ± 389.85 | 850.03 ± 355.66 | 0.27 | 0.11 | |
| Con Impulse (kg⋅m/s) | 280.43 ± 79.54 | 281.23 ± 81.42 | 297.14 ± 100.08 | 0.47 | 0.07 | |
| Ecc:Con Ratio | 3 ± 2.48 | 3 ± 2.27 | 3 ± 2.78 | 0.43 | 0.07 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyons Donegan, M.; Eustace, S.; Morris, R.; Penny, R.; Tallis, J. The Effects of Soccer Specific Exercise on Countermovement Jump Performance in Elite Youth Soccer Players. Children 2022, 9, 1861. https://doi.org/10.3390/children9121861
Lyons Donegan M, Eustace S, Morris R, Penny R, Tallis J. The Effects of Soccer Specific Exercise on Countermovement Jump Performance in Elite Youth Soccer Players. Children. 2022; 9(12):1861. https://doi.org/10.3390/children9121861
Chicago/Turabian StyleLyons Donegan, Max, Steven Eustace, Rhys Morris, Ryan Penny, and Jason Tallis. 2022. "The Effects of Soccer Specific Exercise on Countermovement Jump Performance in Elite Youth Soccer Players" Children 9, no. 12: 1861. https://doi.org/10.3390/children9121861
APA StyleLyons Donegan, M., Eustace, S., Morris, R., Penny, R., & Tallis, J. (2022). The Effects of Soccer Specific Exercise on Countermovement Jump Performance in Elite Youth Soccer Players. Children, 9(12), 1861. https://doi.org/10.3390/children9121861






