Prediction of Whole Liver Graft Weight Based on Biometric Variables in Paediatric and Adult Liver Donors
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Patient Characteristics
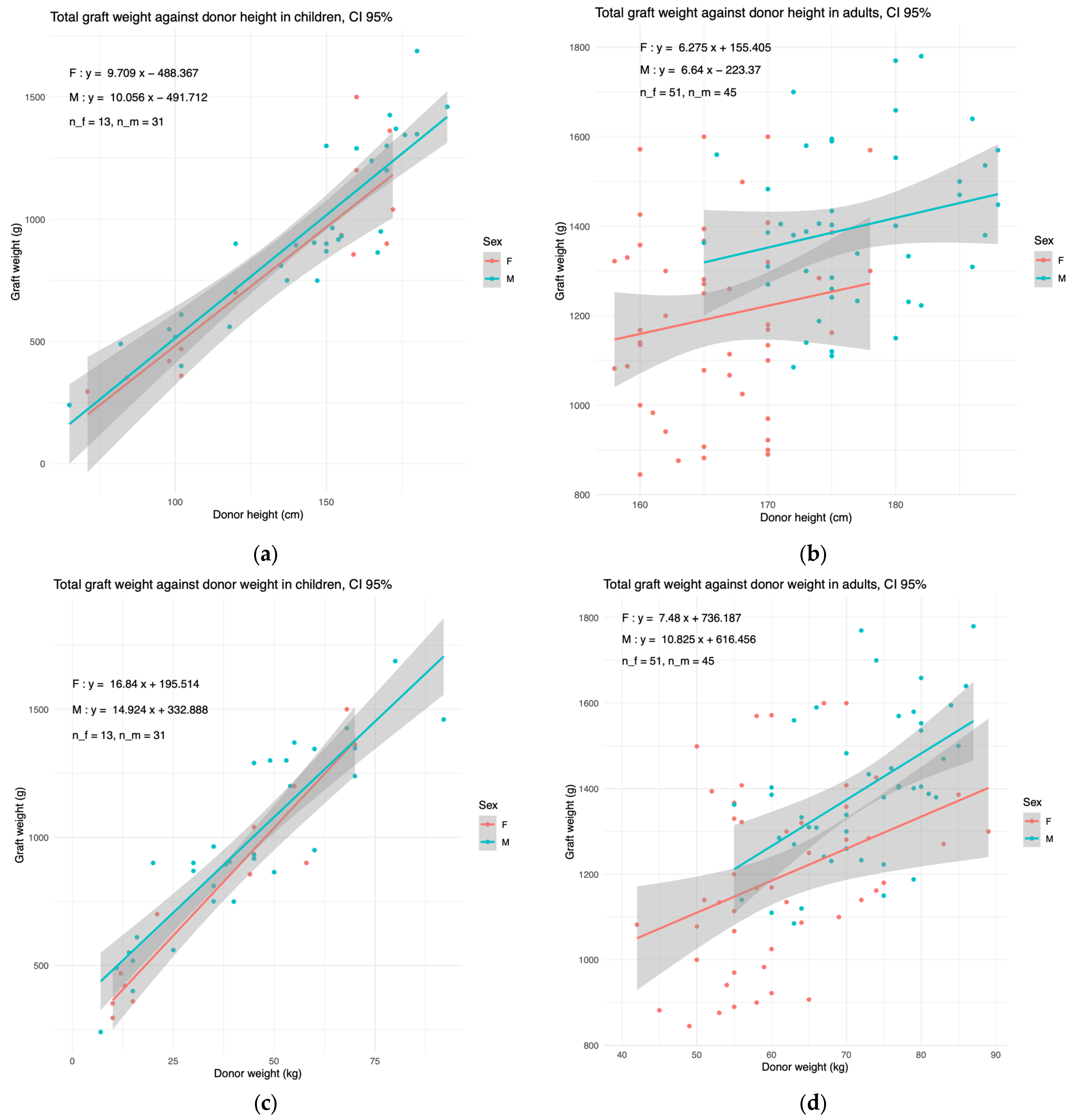
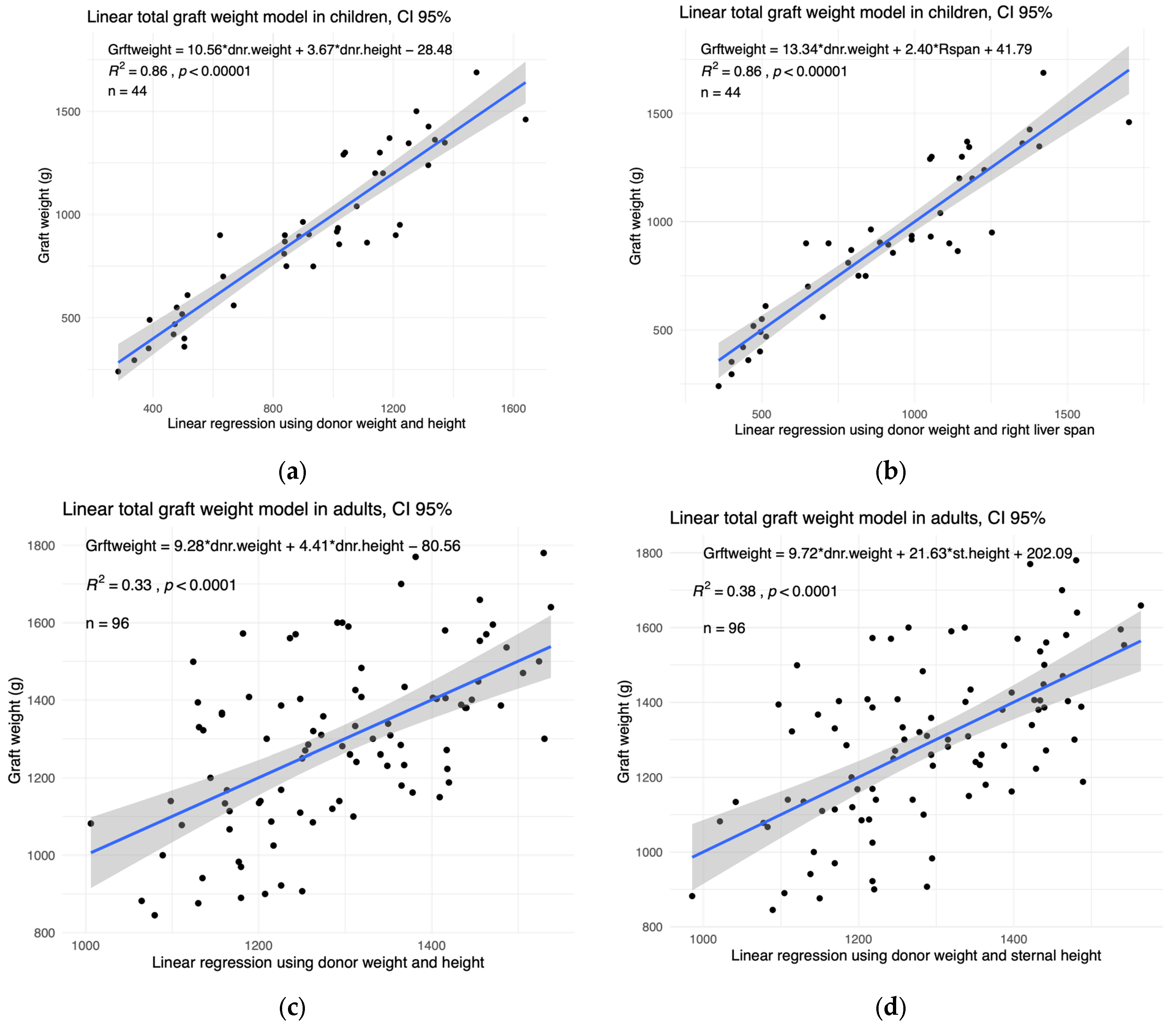
3.2. Training of Whole Graft Model
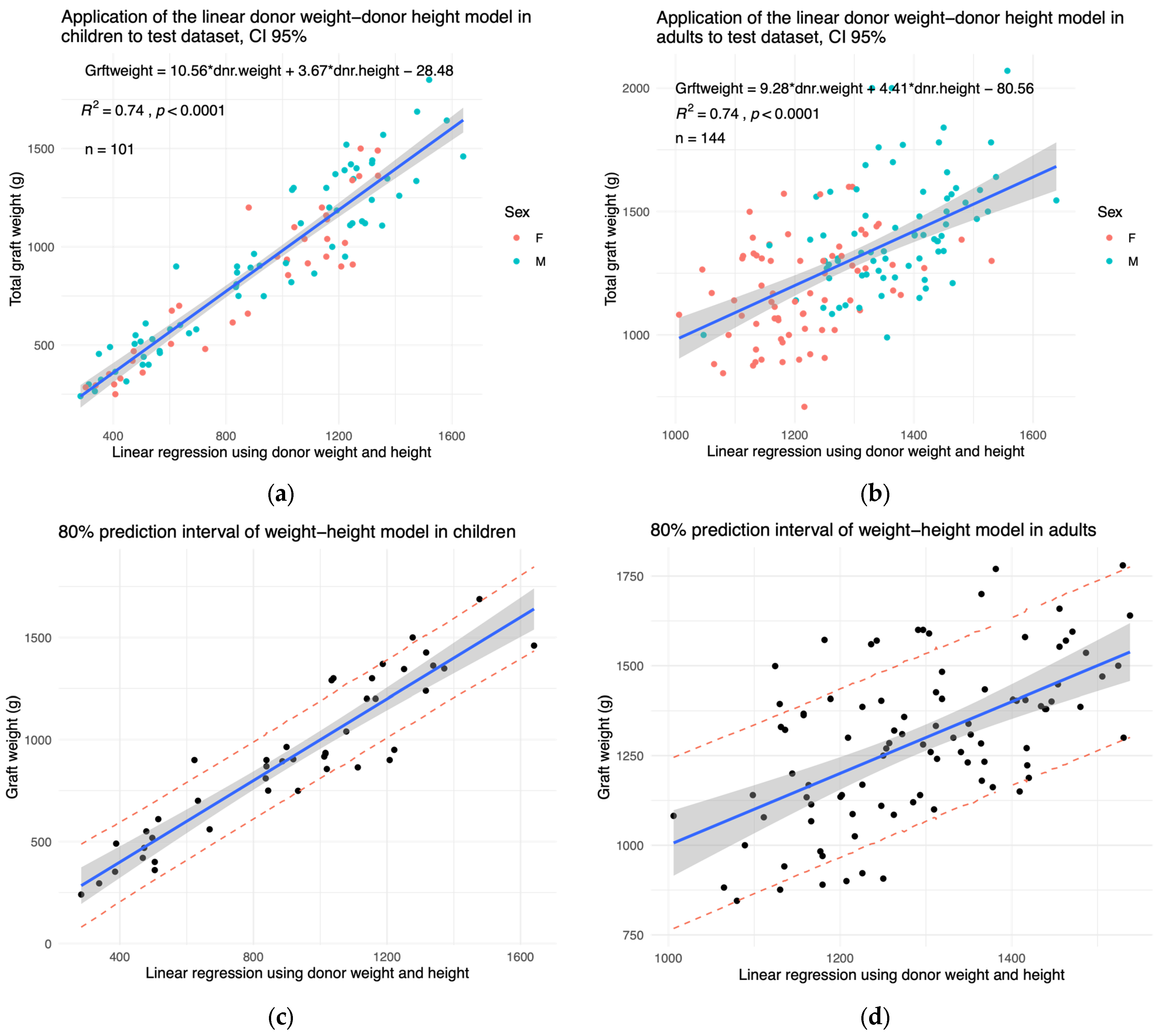
3.3. External Validation of Whole Graft Model
3.4. User Interface
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peng, J.K.; Hepgul, N.; Higginson, I.J.; Gao, W. Symptom prevalence and quality of life of patients with end-stage liver disease: A systematic review and meta-analysis. Palliat. Med. 2019, 33, 24–36. [Google Scholar] [CrossRef] [PubMed]
- Rawalm, N.; Yazigi, N. Paediatric Liver Transplantation. Pediat Clin. N. 2017, 64, 677–684. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Park, S.; Lee, S.; Han, K.; Lee, M.R.; Song, J.S.; Yu, H.C.; Do Yang, J. Estimation of right lobe graft weight for living donor liver transplantation using deep learning-based fully automatic computed tomographic volumetry. Sci. Rep. 2023, 13, 17746. [Google Scholar] [CrossRef] [PubMed]
- Vauthey, J.N.; Abdalla, E.K.; Doherty, D.A.; Gertsch, P.; Fenstermacher, M.J.; Loyer, E.M.; Lerut, J.; Materne, R.; Wang, X.; Encarnacion, A.; et al. Body surface area and body weight predict total liver volume in Western adults. Liver Transpl. 2002, 8, 233–240. [Google Scholar] [CrossRef] [PubMed]
- Tucker, O.N.; Heaton, N. The ‘small for size’ liver syndrome. Curr. Opin. Crit. Care 2005, 11, 150–155. [Google Scholar] [CrossRef] [PubMed]
- Golriz, M.; Majlesara, A.; El Sakka, S.; Ashrafi, M.; Arwin, J.; Fard, N.; Raisi, H.; Edalatpour, A.; Mehrabi, A. Small for Size and Flow (SFSF) syndrome: An alternative description for posthepatectomy liver failure. Clin. Res. Hepatol. Gastroenterol. 2016, 40, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Masuda, Y.; Yoshizawa, K.; Ohno, Y.; Mita, A.; Shimizu, A.; Soejima, Y. Small-for-size syndrome in liver transplantation: Definition, pathophysiology and management. Hepatobiliary Pancreat. Dis. Int. 2020, 19, 334–341. [Google Scholar] [CrossRef] [PubMed]
- Lim, M.C.; Tan, C.H.; Cai, J.; Zheng, J.; Kow, A.W.C. CT volumetry of the liver: Where does it stand in clinical practice? Clin. Radiol. 2014, 69, 887–895. [Google Scholar] [CrossRef] [PubMed]
- Urata, K.; Kawasaki, S.; Matsunami, H.; Hashikura, Y.; Ikegami, T.; Ishizone, S.; Momose, Y.; Komiyama, A.; Makuuchi, M. Calculation of child and adult standard liver volume for liver transplantation. Hepatology 1995, 21, 1317–1321. [Google Scholar] [CrossRef] [PubMed]
- Heinemann, A.; Wischhusen, F.; Püschel, K.; Rogiers, X. Standard Liver Volume inthe Caucasian Population. Liver Transpl. 1999, 5, 366–368. [Google Scholar] [CrossRef] [PubMed]
- Donadon, M.; Mimmo, A.; Costa, G.; Cimino, M.; Viganò, L.; Palmisano, A.; Torzilli, G. Measurement of Total Liver Volume Using the Energy Expenditure: A New Formula. World J. Surg. 2018, 42, 3350–3356. [Google Scholar] [CrossRef] [PubMed]
- Agence de la Biomédecine. 2024 Activité de Prélèvement et de Greffe D’organes en 2023 et Baromètre D’opinion. 2024. Available online: https://presse.agence-biomedecine.fr/chiffres-greffe-2023 (accessed on 25 September 2024).

| Number of Values | Number of NA | Min | Max | Median | IQR | Mean | |
|---|---|---|---|---|---|---|---|
| Age (years) | 44 | 0 | 0 | 18 | 12 | 10 | 11 |
| Height (cm) | 44 | 0 | 65 | 190 | 151 | 54 | 141 |
| Weight (kg) | 44 | 0 | 7 | 92 | 42 | 36 | 40 |
| BMI (kg/m2) | 44 | 0 | 11 | 27 | 18 | 4 | 18 |
| Graft weight (g) | 44 | 0 | 240 | 1688 | 900 | 654 | 912 |
| Right liver span (mm) | 43 | 1 | 89 | 184 | 137 | 49 | 137 |
| Left liver span (mm) | 7 | 37 | 48 | 120 | 64 | 25 | 74 |
| Chest perimeter (cm) | 43 | 1 | 43 | 102 | 70 | 22 | 70 |
| Sternal height (cm) | 43 | 1 | 7 | 24 | 16 | 5.5 | 16 |
| Abdominal perimeter (cm) | 43 | 1 | 43 | 99 | 63 | 14 | 64 |
| Sex M | 31 | 0 | NA | NA | NA | NA | NA |
| Number of Values | Number of NA | Min | Max | Median | IQR | Mean | |
|---|---|---|---|---|---|---|---|
| Age (years) | 96 | 0 | 19 | 59 | 32 | 23 | 34 |
| Height (cm) | 96 | 0 | 158 | 188 | 170 | 10 | 171 |
| Weight (kg) | 96 | 0 | 42 | 89 | 66 | 17 | 67 |
| BMI (kg/m2) | 96 | 0 | 17 | 30 | 23 | 4 | 23 |
| Graft weight (g) | 94 | 2 | 845 | 1780 | 1300 | 268 | 1293 |
| Right liver span (mm) | 94 | 2 | 100 | 220 | 157 | 36 | 157 |
| Left liver span (mm) | 13 | 83 | 45 | 166 | 86 | 33 | 89 |
| Chest perimeter (cm) | 94 | 2 | 54 | 130 | 91 | 11 | 90 |
| Sternal height (cm) | 94 | 2 | 15 | 29 | 20 | 3 | 20 |
| Abdominal perimeter (cm) | 94 | 2 | 66 | 160 | 82 | 15 | 84 |
| Sex M | 45 | 0 | NA | NA | NA | NA | NA |
| Number of Values | Number of NA | Min | Max | Median | IQR | Mean | |
|---|---|---|---|---|---|---|---|
| Age (years) | 101 | 0 | 0 | 18 | 12 | 9 | 11 |
| Height (cm) | 101 | 0 | 65 | 190 | 154 | 51 | 141 |
| Weight (kg) | 101 | 0 | 7 | 92 | 44 | 35 | 41 |
| BMI (kg/m2) | 101 | 0 | 12 | 27 | 19 | 5 | 19 |
| Graft weight (g) | 101 | 0 | 240 | 1850 | 910 | 724 | 898 |
| Right liver span (mm) | 18 | 83 | 99 | 202 | 160 | 21 | 159 |
| Sex M | 66 | 0 | NA | NA | NA | NA | NA |
| Number of Values | Number of NA | Min | Max | Median | IQR | Mean | |
|---|---|---|---|---|---|---|---|
| Age (years) | 144 | 0 | 19 | 73 | 29 | 21 | 33 |
| Height (cm) | 144 | 0 | 150 | 195 | 170 | 13 | 171 |
| Weight (kg) | 144 | 0 | 42 | 95 | 66 | 17 | 67 |
| BMI (kg/m2) | 144 | 0 | 15 | 29 | 23 | 6 | 22 |
| Graft weight (g) | 144 | 0 | 709 | 2070 | 1300 | 984 | 1301 |
| Right liver span (mm) | 34 | 110 | 90 | 210 | 150 | 32 | 152 |
| Sex M | 73 | 0 | NA | NA | NA | NA | NA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuksin, M.; Bidault Jourdainne, V.; Rossignol, G.; Aegerter, P.; Hery, G.; Teglas, J.-P.; Fouquet, V.; Branchereau, S.; Guérin, F. Prediction of Whole Liver Graft Weight Based on Biometric Variables in Paediatric and Adult Liver Donors. Children 2024, 11, 1248. https://doi.org/10.3390/children11101248
Kuksin M, Bidault Jourdainne V, Rossignol G, Aegerter P, Hery G, Teglas J-P, Fouquet V, Branchereau S, Guérin F. Prediction of Whole Liver Graft Weight Based on Biometric Variables in Paediatric and Adult Liver Donors. Children. 2024; 11(10):1248. https://doi.org/10.3390/children11101248
Chicago/Turabian StyleKuksin, Maria, Valeska Bidault Jourdainne, Guillaume Rossignol, Philippe Aegerter, Géraldine Hery, Jean-Paul Teglas, Virginie Fouquet, Sophie Branchereau, and Florent Guérin. 2024. "Prediction of Whole Liver Graft Weight Based on Biometric Variables in Paediatric and Adult Liver Donors" Children 11, no. 10: 1248. https://doi.org/10.3390/children11101248
APA StyleKuksin, M., Bidault Jourdainne, V., Rossignol, G., Aegerter, P., Hery, G., Teglas, J.-P., Fouquet, V., Branchereau, S., & Guérin, F. (2024). Prediction of Whole Liver Graft Weight Based on Biometric Variables in Paediatric and Adult Liver Donors. Children, 11(10), 1248. https://doi.org/10.3390/children11101248







