Non-Invasive Prediction of Atrial Fibrosis Using a Regression Tree Model of Mean Left Atrial Voltage
Abstract
1. Introduction
2. Materials and Methods
2.1. Clinical Variables
2.2. Echocardiographic Protocol
2.3. Ultra-High-Density Mapping and Quantitative Map Analysis
2.4. Statistical Analysis
3. Results
3.1. Study Population: Clinical and Electroanatomical Characteristics
3.2. Echocardiographic Characteristics
3.3. Mean Voltage Regression Tree
3.4. Comparative Analysis Between Groups
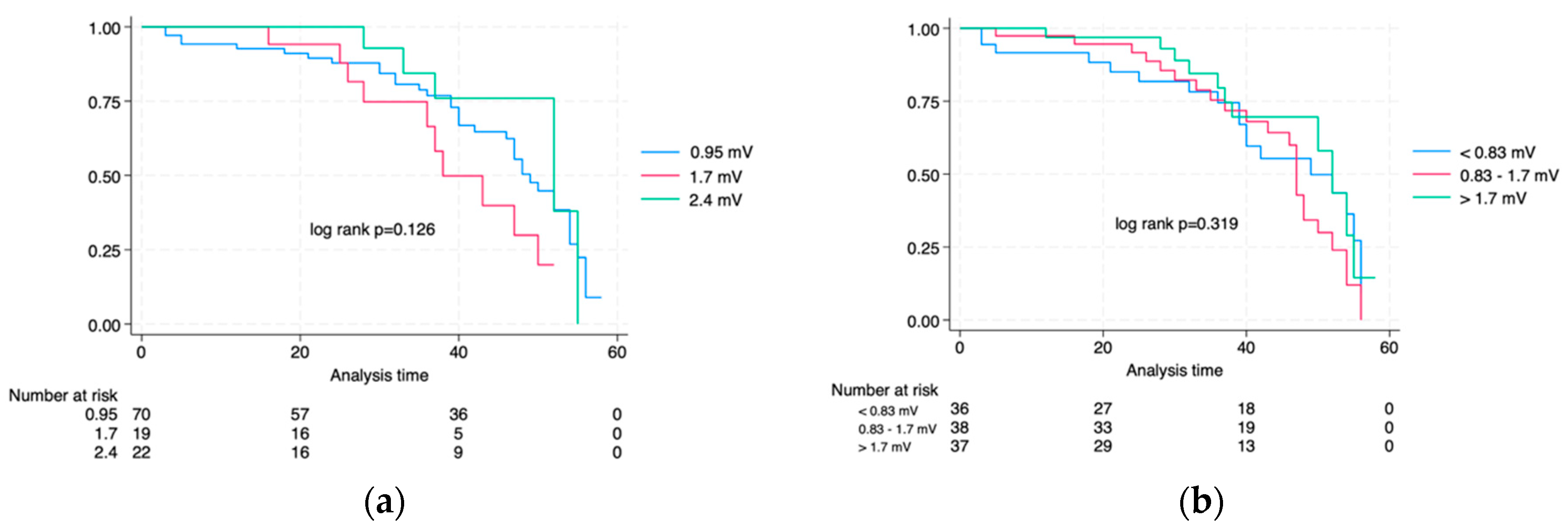
3.5. Survival Analysis
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MLAV | Mean Left Atrial Voltage |
| ML | Machine Learning |
| AF | Atrial Fibrillation |
| PVI | Pulmonary Vein Isolation |
| uHDvM | Ultra-High-Density Voltage Mapping |
| CART | Classification and Regression Trees |
| AI | Artificial Intelligence |
| MRI | Magnetic Resonance |
| CUN | Clínica Universidad de Navarra |
| LV | Left Ventricle |
| LA | Left Atria |
| LAmax | LA Maximum Volume |
| LAmin | LA Minimum Volume |
| LApreA | LA preA Volume |
| LAEF | LA Total Emptying Fraction |
| LApEF | LA Passive Emptying Function |
| LAactEF | LA Active Emptying Function |
| LASres | LA Reservoir Strain |
| LAScd | LA Conduction Strain |
| LASct | LA Active Strain |
References
- Svennberg, E.; Han, J.K.; Caiani, E.G.; Engelhardt, S.; Ernst, S.; Friedman, P.; Garcia, R.; Ghanbari, H.; Hindricks, G.; Man, S.H.; et al. State of the Art of Artificial Intelligence in Clinical Electrophysiology in 2025: A Scientific Statement of the European Heart Rhythm Association (EHRA) of the ESC, the Heart Rhythm Society (HRS), and the ESC Working Group on E-Cardiology. EP Eur. 2025, 27, euaf071. [Google Scholar] [CrossRef]
- Soleimanian Gharehchopogh, F.; Mohammadi, P.; Hakimi, P. Application of Decision Tree Algorithm for Data Mining in Healthcare Operations: A Case Study. Int. J. Comput. Appl. 2012, 52, 21–26. [Google Scholar] [CrossRef]
- Goette, A.; Corradi, D.; Dobrev, D.; Aguinaga, L.; Cabrera, J.A.; Chugh, S.S.; de Groot, J.R.; Soulat-Dufour, L.; Fenelon, G.; Hatem, S.N.; et al. Atrial cardiomyopathy revisited—Evolution of a concept: A clinical consensus statement of the European Heart Rhythm Association (EHRA) of the ESC, the Heart Rhythm Society (HRS), the Asian Pacific Heart Rhythm Society (APHRS), and the Latin American Heart Rhythm Society (LAHRS). Europace 2024, 26, euae204. [Google Scholar] [CrossRef] [PubMed]
- Boyle, P.M.; Del Álamo, J.C.; Akoum, N. Fibrosis, atrial fibrillation and stroke: Clinical updates and emerging mechanistic models. Heart 2021, 107, 99–105. [Google Scholar] [CrossRef]
- Sim, I.; Bishop, M.; O’Neill, M.; Williams, S.E. Left atrial voltage mapping: Defining and targeting the atrial fibrillation substrate. J. Interv. Card. Electrophysiol. 2019, 56, 213–227. [Google Scholar] [CrossRef] [PubMed]
- Ballesteros, G.; Ravassa, S.; Bragard, J.; Ramos, P.; López, B.; Vives, E.; Neglia, R.; Wise, B.; González, A.; Moreno, M.U.; et al. Association of left atrium voltage amplitude and distribution with the risk of atrial fibrillation recurrence and evolution after pulmonary vein isolation: An ultrahigh-density mapping study. J. Cardiovasc. Electrophysiol. 2019, 30, 1231–1240. [Google Scholar] [CrossRef] [PubMed]
- Bijvoet, G.P.; Nies, H.M.J.M.; Holtackers, R.J.; Linz, D.; Adriaans, B.P.; Nijveldt, R.; Wildberger, J.E.; Vernooy, K.; Chaldoupi, S.M.; Mihl, C. Correlation between Cardiac MRI and Voltage Mapping in Evaluating Atrial Fibrosis: A Systematic Review. Radiol. Cardiothorac. Imaging 2022, 4, e220061. [Google Scholar] [CrossRef]
- Pilichowska-Paszkiet, E.; Baran, J.; Sygitowicz, G.; Sikorska, A.; Stec, S.; Kułakowski, P.; Zaborska, B. Noninvasive assessment of left atrial fibrosis. Correlation between echocardiography, biomarkers, and electroanatomical mapping. Echocardiography 2018, 35, 1326–1334. [Google Scholar] [CrossRef]
- Tao, Y.; Zhang, D.; Pang, N.; Geng, S.; Tan, C.; Tian, Y.; Hong, S.; Liu, X. Multi-modal artificial intelligence algorithm for the prediction of left atrial low-voltage areas in atrial fibrillation patient based on sinus rhythm electrocardiogram and clinical characteristics: A retrospective, multicentre study. Eur. Heart J.—Digit. Health 2025, 6, 200–208. [Google Scholar] [CrossRef]
- Van Gelder, I.C.; Rienstra, M.; Bunting, K.V.; Casado-Arroyo, R.; Caso, V.; Crijns, H.J.G.M.; De Potter, T.J.R.; Dwight, J.; Guasti, L.; Hanke, T.; et al. 2024 ESC Guidelines for the management of atrial fibrillation developed in collaboration with the European Association for Cardio-Thoracic Surgery (EACTS). Eur. Heart J. 2024, 45, 3314–3414. [Google Scholar] [CrossRef]
- Mitchell, C.; Rahko, P.S.; Blauwet, L.A.; Canaday, B.; Finstuen, J.A.; Foster, M.C.; Horton, K.; Ogunyankin, K.O.; Palma, R.A.; Velazquez, E.J. Guidelines for Performing a Comprehensive Transthoracic Echocardiographic Examination in Adults: Recommendations from the American Society of Echocardiography. J. Am. Soc. Echocardiogr. 2019, 32, 1–64. [Google Scholar] [CrossRef]
- Nagueh, S.F.; Smiseth, O.A.; Appleton, C.P.; Byrd, B.F.; Dokainish, H.; Edvardsen, T.; Dokainish, H.; Edvardsen, T.; Flachskampf, F.A.; Gillebert, T.C.; et al. Recommendations for the Evaluation of Left Ventricular Diastolic Function by Echocardiography: An Update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging. J. Am. Soc. Echocardiogr. 2016, 29, 277–314. [Google Scholar] [CrossRef]
- Shi, J.; Xu, S.; Chen, L.; Wu, B.; Yang, K.; Chen, S.; Zhou, D.; Zhang, B.; Xuan, T.; Hu, X. Impact of Left Atrial Sphericity Index on the Outcome of Catheter Ablation for Atrial Fibrillation. J. Cardiovasc. Transl. Res. 2021, 14, 912–920. [Google Scholar] [CrossRef]
- Olsen, F.J.; Bertelsen, L.; De Knegt, M.C.; Christensen, T.E.; Vejlstrup, N.; Svendsen, J.H.; Jensen, J.S.; Biering-Sørensen, T. Multimodality Cardiac Imaging for the Assessment of Left Atrial Function and the Association with Atrial Arrhythmias. Circ. Cardiovasc. Imaging 2016, 9, e004947. [Google Scholar] [CrossRef]
- Ballesteros, G.; Ramos, P.; Neglia, R.; Menéndez, D.; García-Bolao, I. Ablación de fibrilación auricular guiada por un nuevo sistema de navegación no fluoroscópica. Rev. Esp. Cardiol. 2017, 70, 706–712. [Google Scholar] [CrossRef]
- García-Bolao, I.; Ballesteros, G.; Ramos, P.; Menéndez, D.; Erkiaga, A.; Neglia, R.; Jiménez Martín, M.; Vives-Rodríguez, E. Identification of pulmonary vein reconnection gaps with high-density mapping in redo atrial fibrillation ablation procedures. EP Eur. 2018, 20, f351–f358. [Google Scholar] [CrossRef]
- Ravassa, S.; Ballesteros, G.; López, B.; Ramos, P.; Bragard, J.; González, A.; Moreno, M.U.; Querejeta, R.; Vives, E.; García-Bolao, I.; et al. Combination of Circulating Type I Collagen-Related Biomarkers Is Associated With Atrial Fibrillation. J. Am. Coll. Cardiol. 2019, 73, 1398–1410. [Google Scholar] [CrossRef] [PubMed]
- Fatema, K.; Barnes, M.E.; Bailey, K.R.; Abhayaratna, W.P.; Cha, S.; Seward, J.B.; Tsang, T.S.M. Minimum vs. maximum left atrial volume for prediction of first atrial fibrillation or flutter in an elderly cohort: A prospective study. Eur. J. Echocardiogr. 2008, 10, 282–286. [Google Scholar] [CrossRef]
- Smiseth, O.A.; Larsen, C.K.; Hopp, E. Left atrial volume as risk marker: Is minimum volume superior to maximum volume? Eur. Heart J.—Cardiovasc. Imaging 2024, 25, 1575–1576. [Google Scholar] [CrossRef] [PubMed]
- Matei, L.L.; Ghilencea, L.N.; Bejan, G.C.; Stoica, S.; Dragoi-Galrinho, R.; Siliste, C.; Vinereanu, D. Minimum Left Atrial Volume Evaluated by 3D Echocardiography Predicts Atrial Fibrillation Recurrences After a First Radiofrequency Catheter Ablation for Paroxysmal Episodes. Maedica 2021, 16, 345–352. [Google Scholar] [CrossRef] [PubMed]
- Dodson, J.A.; Neilan, T.G.; Shah, R.V.; Farhad, H.; Blankstein, R.; Steigner, M.; Michaud, G.F.; John, R.; Abbasi, S.A.; Jerosch-Herold, M.; et al. Left Atrial Passive Emptying Function Determined by Cardiac Magnetic Resonance Predicts Atrial Fibrillation Recurrence After Pulmonary Vein Isolation. Circ. Cardiovasc. Imaging 2014, 7, 586–592. [Google Scholar] [CrossRef] [PubMed]


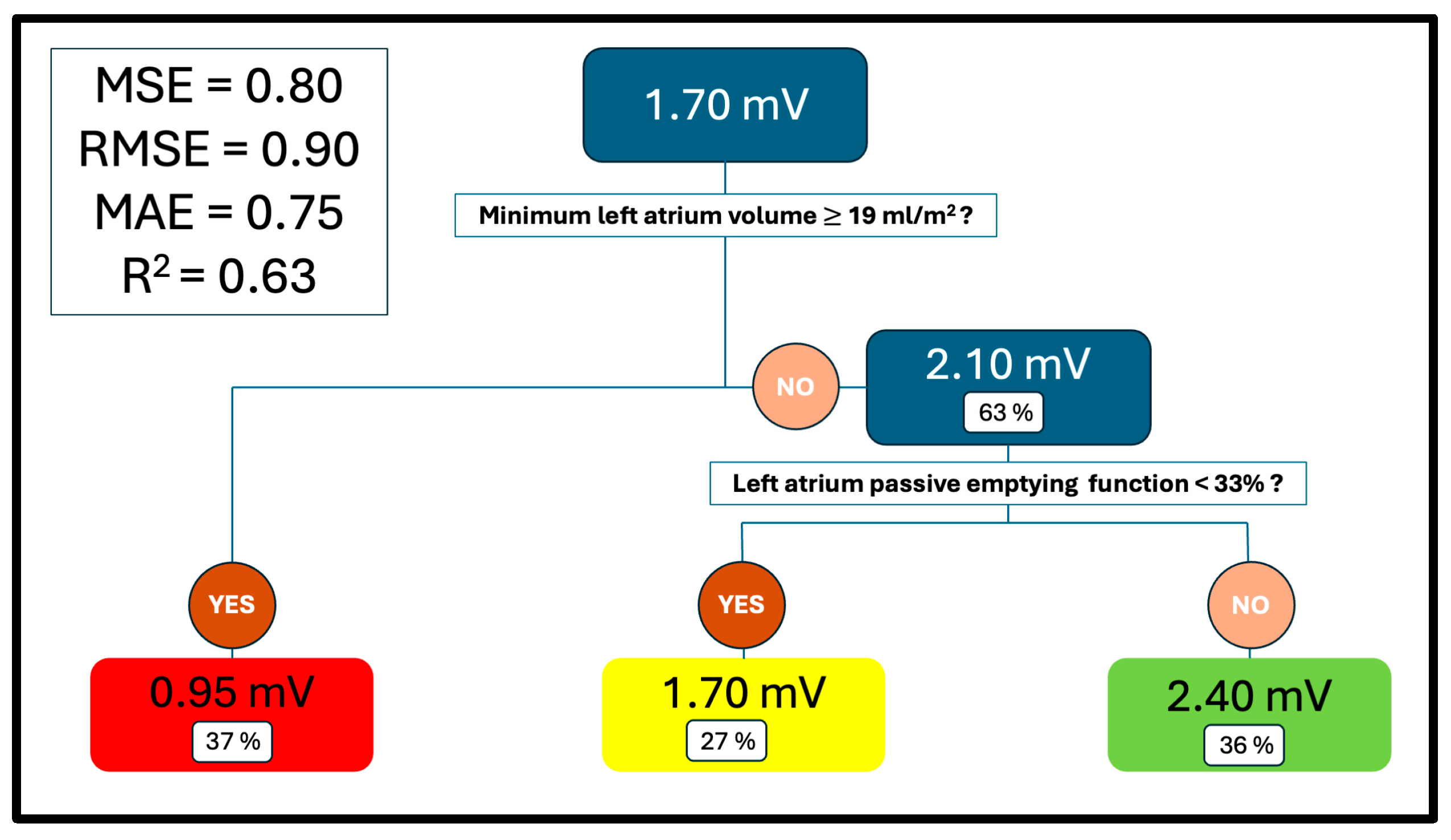
| Variables | Overall | “0.95” Group | “1.70” Group | “2.40” Group | p | Standardised Differences 2 | ||
|---|---|---|---|---|---|---|---|---|
| 0.95 vs. 1.70 | 0.95 vs. 2.40 | 1.7 vs. 2.40 | ||||||
| n, % | 113 (100.00) | 72 (63.72) | 19 (16.81) | 22 (19.47) | ||||
| Mean voltage ± SD | 1.41 ± 0.85 | 1.15 ± 0.71 | 1.63 ± 0.70 | 2.06 ± 1.01 | <0.001 * | −0.68 (M) | −1.04 (L) | −0.49 (S) |
| Age, year ± SD | 63.69 ± 10.19 | 65.63 ± 9.63 | 62.89 ± 9.60 | 58.05 ± 10.68 | 0.008 * | −0.19 (I) | 0.08 (I) | 0.27 (S) |
| Male sex, n (%) | 82 (72.57) | 54 (75.00) | 13 (68.42) | 15 (68.18) | 0.744 | 0.06 (I) | 0.07 (I) | 0.01 (S) |
| Cardiovascular risk factors | ||||||||
| Tobacco | ||||||||
| Never smoker, n (%) | 54 (47.79) | 35 (48.61) | 7 (36.84) | 12 (54.55) | 0.726 | 0.10 (S) | 0.12 (S) | 0.23 (S) |
| Previous smoker, n (%) | 5 (4.42) | 4 (5.56) | 1 (5.26) | 0 (0.00) | ||||
| Smoker, n (%) | 54 (47.79) | 33 (45.83) | 11 (57.89) | 10 (45.45) | ||||
| Hypertension, n (%) | 63 (55.75) | 43 (59.72) | 10 (52.63) | 10 (45.45) | 0.477 | 0.06 (I) | 0.12 (S) | 0.07 (I) |
| Diabetes mellitus, n (%) | 10 (8.84) | 8 (11.11) | 1 (5.26) | 1 (4.55) | 0.707 | 0.08 (I) | 0.09 (I) | 0.02 (I) |
| Dyslipidaemia, n (%) | 51 (45.13) | 37 (51.39) | 5 (26.3) | 9 (40.91) | 0.134 | 0.2 (S) | 0.09 (I) | 0.15 (S) |
| Body mass index, kg/m2 ± SD | 27.61 ± 3.97 | 27.93 ± 3.57 | 29.15 ± 4.23 | 25.24 ± 4.16 | <0.003 * | 0.06 (I) | −0.40 (S) | −0.41 (S) |
| Comorbidities | ||||||||
| Stroke, n (%) | 9 (7.96) | 8 (11.11) | 1 (5.26) | 0 (0.00) | 0.205 | 0.08 (I) | 0.17 (S) | 0.17 (S) |
| Carotid artery disease, n (%) | 4 (3.54) | 4 (5.56) | 0 (0.00) | 0 (0.00) | 0.454 | 0.11 (S) | 0.12 (S) | - |
| COPD, n (%) 1 | 7 (6.19) | 4 (5.56) | 3 (15.79) | 0 (0.00) | 0.102 | 0.17 (S) | 0.14 (S) | 0.35 (M) |
| OSA, n (%) 1 | 12 (10.62) | 9 (12.50) | 2 (10.53) | 1 (4.55) | 0.613 | 0.03 (I) | 0.11 (S) | 0.12 (S) |
| CPAP use, n (%) 1 | 5 (4.42) | 3 (4.17) | 2 (10.53) | 0 (0.00) | 0.244 | 0.11 (S) | 0.1 (S) | 0.24 (S) |
| CKD, n (%) 1 | 9 (7.96) | 8 (11.11) | 0 (0.00) | 1 (4.55) | 0.370 | 0.16 (S) | 0.09 (I) | 0.15 (S) |
| Hypothyroidism, n (%) | 15 (13.27) | 10 (13.89) | 3 (15.79) | 2 (9.09) | 0.850 | 0.02 (I) | 0.06 (I) | 0.1 (S) |
| Neoplasia, n (%) | 16 (14.16) | 10 (13.89) | 3 (15.79) | 3 (13.64) | - | 0.02 (I) | <0.01 (I) | 0.03 (I) |
| Previous cardiovascular history | ||||||||
| Heart failure, n (%) | 16 (14.16) | 13 (18.06) | 2 (10.53) | 1 (4.55) | 0.283 | 0.08 (I) | 0.16 (S) | 0.12 (S) |
| Non-preserved LVEF, n (%) 1 | 12 (10.62) | 9 (12.50) | 2 (10.53) | 1 (4.55) | 0.613 | 0.03 (I) | 0.11 (S) | 0.12 (S) |
| Ischaemic heart disease, n (%) | 10 (8.85) | 9 (12.50) | 1 (5.26) | 0 (0.00) | 0.214 | 0.01 (I) | 0.18 (S) | 0.17 (S) |
| Pacemaker/ICDs, n (%) | 5 (4.42) | 4 (5.56) | 0 (0.00) | 1 (4.55) | 0.822 | 0.11 (S) | 0.15 (S) | 0.15 (S) |
| Medication | ||||||||
| Beta blockers, n (%) | 61 (53.98) | 41 (56.94) | 9 (47.37) | 11 (50.00) | 0.694 | 0.08 (I) | 0.06 (I) | 0.03 (I) |
| Non-dihydropyridine antagonist, n (%) | 3 (2.65) | 3 (4.17) | 0 (0.00) | 0 (0.00) | - | 0.10 (S) | 0.10 (S) | - |
| Digoxin, n (%) | 5 (4.42) | 5 (6.94) | 0 (0.00) | 0 (0.00) | 0.522 | 0.12 (S) | 0.13 (S) | - |
| RAAS-related inhibitors, n (%) 1 | 54 (47.79) | 37 (51.39) | 6 (31.58) | 7 (31.82) | 0.237 | 0.11 (S) | 0.16 (S) | 0.04 (I) |
| Mineralocorticoid antagonist receptor, n (%) | 7 (6.19) | 7 (9.72) | 0 (0.00) | 0 (0.00) | 0.119 | 0.15 (S) | 0.16 (S) | - |
| Flecainide, n (%) | 22 (19.47) | 10 (13.89) | 4 (21.05) | 8 (36.36) | 0.060 | 0.08 (I) | 0.24 (S) | 0.17 (S) |
| Propafenone, n (%) | 2 (1.77) | 2 (2.78) | 0 (0.00) | 0 (0.00) | - | 0.08 (I) | 0.08 (I) | - |
| Amiodarone, n (%) | 13 (11.50) | 10 (13.89) | 2 (10.53) | 1 (4.55) | 0.577 | 0.04 (I) | 0.12 (S) | 0.12 (S) |
| AF characteristics | ||||||||
| Paroxysmal AF, n (%) | 80 (70.80) | 45 (62.50) | 14 (73.68) | 21 (95.42) | 0.010 * | 0.10 (S) | 0.31 (M) | 0.31 (M) |
| Typical atrial flutter, n (%) | 29 (25.66) | 17 (23.61) | 8 (42.11) | 4 (18.18) | 0.188 | 0.17 (S) | 0.06 (I) | 0.26 (S) |
| EHRA ± SD 1 | 2 ± 0.37 | 1.9 ± 0.46 | 2 ± 0.00 | 2 ± 0.00 | 0.527 | −0.30 (S) | −0.30 (S) | −0.01 (I) |
| CHA2DS2 VASc ± SD 1 | 1.82 ± 1.43 | 2.07 ± 1.54 | 1.68 ± 1.11 | 1.14 ± 1.08 | 0.024 * | 0.29 (S) | 0.70 (M) | 0.49 (S) |
| Re-procedure, n (%) | 21 (18.58) | 14 (19.44) | 3 (15.79) | 4 (18.18) | 0.934 | 0.04 (I) | 0.01 (I) | 0.03 (I) |
| AF diagnosis before PVI, months ± SD | 40.99 ± 52.78 | 39.53 ± 54.63 | 60.74 ± 64.63 | 28.73 ± 25.87 | 0.351 | −0.35 (S) | 0.25 (S) | 0.65 (M) |
| Follow-up after PVI, months ± SD | 33.84 ± 16.40 | 35.01 ± 17.26 | 32.15 ± 13.38 | 31.45 ± 16.16 | 0.600 | 0.19 (I) | 0.21 (S) | 0.05 (I) |
| Recurrence, n (%) | 52 (46.02) | 37 (51.39) | 10 (52.63) | 5 (22.73) | 0.041 * | <0.01 (I) | 0.26 (S) | 0.31 (M) |
| Variables | Overall | “0.95” Group | “1.70” Group | “2.40” Group | p | Standardised Differences 2 | ||
|---|---|---|---|---|---|---|---|---|
| 0.95 vs. 1.70 | 0.95 vs. 2.40 | 1.7 vs. 2.40 | ||||||
| HR, bpm ± SD 1 | 67.47 ± 17.43 | 69.19 ± 18.98 | 62.63 ± 10.85 | 66.00 ± 16.37 | 0.431 | 0.42 (S) | 0.18 (I) | −0.24 (S) |
| SBP, mm Hg ± SD 1 | 117.29 ± 16.72 | 116.64 ± 18.04 | 117.68 ± 16.1 | 119.14 ± 12.51 | 0.830 | −0.06 (I) | −0.16 (I) | −0.10 (I) |
| DBP, mm Hg ± SD 1 | 75.35 ± 11.27 | 74.60 ± 10.93 | 76.16 ± 15.29 | 77.19 ± 8.00 | 0.660 | −0.12 (I) | −0.27 (S) | −0.08 (I) |
| Body surface, m2 ± SD | 1.93 ± 0.23 | 1.93 ± 0.21 | 1.99 ± 0.29 | 1.88 ± 0.21 | 0.297 | −0.24 (S) | 0.24 (S) | 0.43 (S) |
| AF, n (%) 1 | 44 (38.94) | 42 (58.33) | 0.00 (0.00) | 2 (9.09) | <0.001 * | 0.41 (M) | 0.42 (M) | 0.21 (S) |
| LV dimensions and function parameters | ||||||||
| IVS, mm ± SD 1 | 1.05 ± 0.19 | 1.11 ± 0.19 | 0.98 ± 0.15 | 0.95 ± 0.17 | <0.001 * | 0.76 (M) | 0.89 (L) | 0.19 (I) |
| EDD, mm/m2 ± SD 1 | 2.52 ± 0.31 | 2.53 ± 0.31 | 2.46 ± 0.30 | 2.54 ± 0.34 | 0.662 | 0.23 (S) | −0.03 (I) | −0.25 (S) |
| LVPW, mm ± SD 1 | 1.12 ± 0.21 | 1.16 ± 0.22 | 1.03 ± 0.17 | 1.04 ± 0.17 | 0.013 * | 0.66 (M) | 0.61 (M) | −0.06 (I) |
| ESD, mm/m2 ± SD 1 | 1.71 ± 0.31 | 1.73 ± 0.31 | 1.70 ± 0.28 | 1.65 ± 0.36 | 0.554 | 0.10 (I) | 0.24 (S) | 0.16 (I) |
| EDLV volume, mL/m2 ± SD 1 | 45.31 ± 12.84 | 45.58 ± 13.58 | 41.07 ± 11.70 | 47.97 ± 10.90 | 0.233 | 0.36 (S) | −0.19 (I) | −0.61 (M) |
| ESLV volume, mL/m2 ± SD 1 | 18.60 ± 7.11 | 19.50 ± 7.62 | 15.42 ± 5.12 | 18.58 ± 6.41 | 0.090 | 0.63 (M) | 0.13 (I) | −0.54 (M) |
| LVEF, % ± SD 1 | 58.38 ± 7.32 | 57.32 ± 7.60 | 60.37 ± 3.98 | 60.13 ± 8.24 | 0.022 * | −0.50 (M) | −0.35 (S) | 0.04 (I) |
| Global longitudinal strain ± SD | 18.72 ± 4.13 | 17.67 ± 4.23 | 19.82 ± 2.71 | 20.73 ± 3.85 | 0.007 * | −0.61 (M) | −0.76 (M) | −0.27 (S) |
| Mitral and tricuspid valve Doppler parameters | ||||||||
| E Vmax, cm/s ± SD | 81.56 ± 21.19 | 86.72 ± 21.80 | 68.04 ± 15.31 | 76.38 ± 17.38 | 0.001 * | 0.99 (L) | 0.52 (M) | −0.51 (M) |
| A Vmax, cm/s ± SD | 61.71 ± 18.50 | 57.72 ± 21.09 | 66.58 ± 18.95 | 63.05 ± 12.47 | 0.248 | −0.44 (S) | −0.31(S) | 0.22 (S) |
| E/A ratio ± SD | 1.38 ± 0.62 | 1.69 ± 0.74 | 1.08 ± 0.35 | 1.20 ± 0.38 | 0.005 * | 1.05 (L) | 0.83 (L) | −0.33 (S) |
| e′, cm/s ± SD | 10.48 ± 3.00 | 10.42 ± 2.61 | 9.83 ± 2.34 | 11.26 ± 4.39 | 0.506 | 0.24 (S) | −0.23 (S) | −041 (S) |
| E/e′ ratio ± SD | 8.26 ± 3.34 | 8.81 ± 3.73 | 7.11 ± 1.83 | 7.43 ± 2.53 | 0.083 | 0.58 (M) | 0.43 (S) | −0.14 (I) |
| a′ Vmax, cm/s ± SD | 8.9 ± 2.98 | 7.63 ± 3.19 | 9.89 ± 2.91 | 9.84 ± 2.08 | 0.010 * | −0.74 (M) | −0.82 (L) | 0.02 (I) |
| TR Vmax, m/s ± SD 1 | 2.31 ± 0.52 | 2.28 ± 0.52 | 1.98 ± 0.97 | 2.54 ± 0.33 | 0.225 | 0.39 (S) | −0.60 (M) | −0.77 (M) |
| LA diameters | ||||||||
| Anteroposterior, mm ± SD | 42.32 ± 6.99 | 44.73 ± 6.44 | 39.58 ± 6.78 | 36.82 ± 4.64 | <0.001 * | 0.78 (M) | 1.41 (L) | 0.48 (S) |
| Maximum, mm ± SD | 63.08 ± 8.54 | 65.93 ± 7.98 | 60.63 ± 8.73 | 55.95 ± 4.64 | <0.001 * | 0.63 (M) | 1.53 (L) | 0.67 (M) |
| Minimum, mm ± SD | 44.70 ± 6.09 | 46.17 ± 6.05 | 40.26 ± 5.00 | 43.77 ± 5.12 | <0.001 * | 1.06 (L) | 0.43 (S) | −0.69 (M) |
| LA volumes | ||||||||
| Maximum volume, mL/m2 ± SD | 41.60 ± 11.97 | 47.28 ± 10.68 | 31.67 ± 8.36 | 32.87 ± 6.28 | <0.001 * | 1.63 (L) | 1.64 (L) | −0.16 (I) |
| Minimum volume, mL/m2 ± SD | 26.39 ± 12.48 | 33.53 ± 10.67 | 15.00 ± 3.06 | 14.83 ± 2.78 | <0.001 * | 2.36 (L) | 2.40 (L) | 0.06 (I) |
| preA volume, mL/m2 ± SD | 27.09 ± 9.79 | 34.01 ± 10.76 | 22.74 ± 5.75 | 21.79 ± 4.51 | <0.001 * | 1.31 (L) | 1.48 (L) | 0.18 (I) |
| LA sphericity index (LASI) | ||||||||
| LASI ± SD | 61.96 ± 18.40 | 63.22 ± 20.45 | 64.33 ± 15.15 | 56.21 ± 11.99 | 0.214 | −0.06 (I) | 0.42 (S) | 0.59 (M) |
| LA function | ||||||||
| Total empty function, % ± SD | 38.59 ± 16.55 | 29.72 ± 13.56 | 50.95 ± 12.37 | 54.5 ± 5.64 | <0.001 * | −1.64 (L) | −2.39 (L) | −0.37 (S) |
| Passive empty function, % ± SD | 57.70 ± 35.1 | 71.0 ± 36.38 | 24.21 ± 7.92 | 43.18 ± 14.17 | <0.001 * | 1.78 (L) | 1.01 (L) | −1.65 (L) |
| Active empty function, % ± SD | 30.13 ± 17.1 | 27.58 ± 23.88 | 32.63 ± 12.33 | 30.95 ± 9.30 | 0.040 * | −0.27 (S) | −0.19 (I) | 0.15 (I) |
| LA strain | ||||||||
| Reserve, % ± SD | 25.36 ±13.13 | 19.78 ±11.92 | 32.51 ± 8.68 | 36.30 ± 9.67 | <0.001 * | −1.22 (L) | −1.52 (L) | −0.41 (S) |
| Conduit, % ± SD | 17.25 ± 8.10 | 15.55 ± 7.72 | 17.51 ± 6.01 | 22.14 ± 8.96 | <0.001 * | −0.28 (S) | −0.79 (M) | −0.61 (M) |
| Contraction, % ± SD | 13.05 ± 5.64 | 10.34 ± 4.85 | 15.03 ± 6.21 | 14.88 ± 4.82 | <0.001 * | −0.84 (L) | −0.94 (L) | 0.03 (I) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibero, J.; García-Bolao, I.; Ballesteros, G.; Ramos, P.; Albarrán-Rincón, R.; Moriones, L.; Bragard, J.; Díaz-Dorronsoro, I. Non-Invasive Prediction of Atrial Fibrosis Using a Regression Tree Model of Mean Left Atrial Voltage. Biomedicines 2025, 13, 1917. https://doi.org/10.3390/biomedicines13081917
Ibero J, García-Bolao I, Ballesteros G, Ramos P, Albarrán-Rincón R, Moriones L, Bragard J, Díaz-Dorronsoro I. Non-Invasive Prediction of Atrial Fibrosis Using a Regression Tree Model of Mean Left Atrial Voltage. Biomedicines. 2025; 13(8):1917. https://doi.org/10.3390/biomedicines13081917
Chicago/Turabian StyleIbero, Javier, Ignacio García-Bolao, Gabriel Ballesteros, Pablo Ramos, Ramón Albarrán-Rincón, Leire Moriones, Jean Bragard, and Inés Díaz-Dorronsoro. 2025. "Non-Invasive Prediction of Atrial Fibrosis Using a Regression Tree Model of Mean Left Atrial Voltage" Biomedicines 13, no. 8: 1917. https://doi.org/10.3390/biomedicines13081917
APA StyleIbero, J., García-Bolao, I., Ballesteros, G., Ramos, P., Albarrán-Rincón, R., Moriones, L., Bragard, J., & Díaz-Dorronsoro, I. (2025). Non-Invasive Prediction of Atrial Fibrosis Using a Regression Tree Model of Mean Left Atrial Voltage. Biomedicines, 13(8), 1917. https://doi.org/10.3390/biomedicines13081917







