Environmental Odour Quantification by IOMS: Parametric vs. Non-Parametric Prediction Techniques
Abstract
:1. Introduction
2. Material and Methods
2.1. Odour Samples
2.2. Analytical Methods
2.2.1. Dynamic Olfactometry
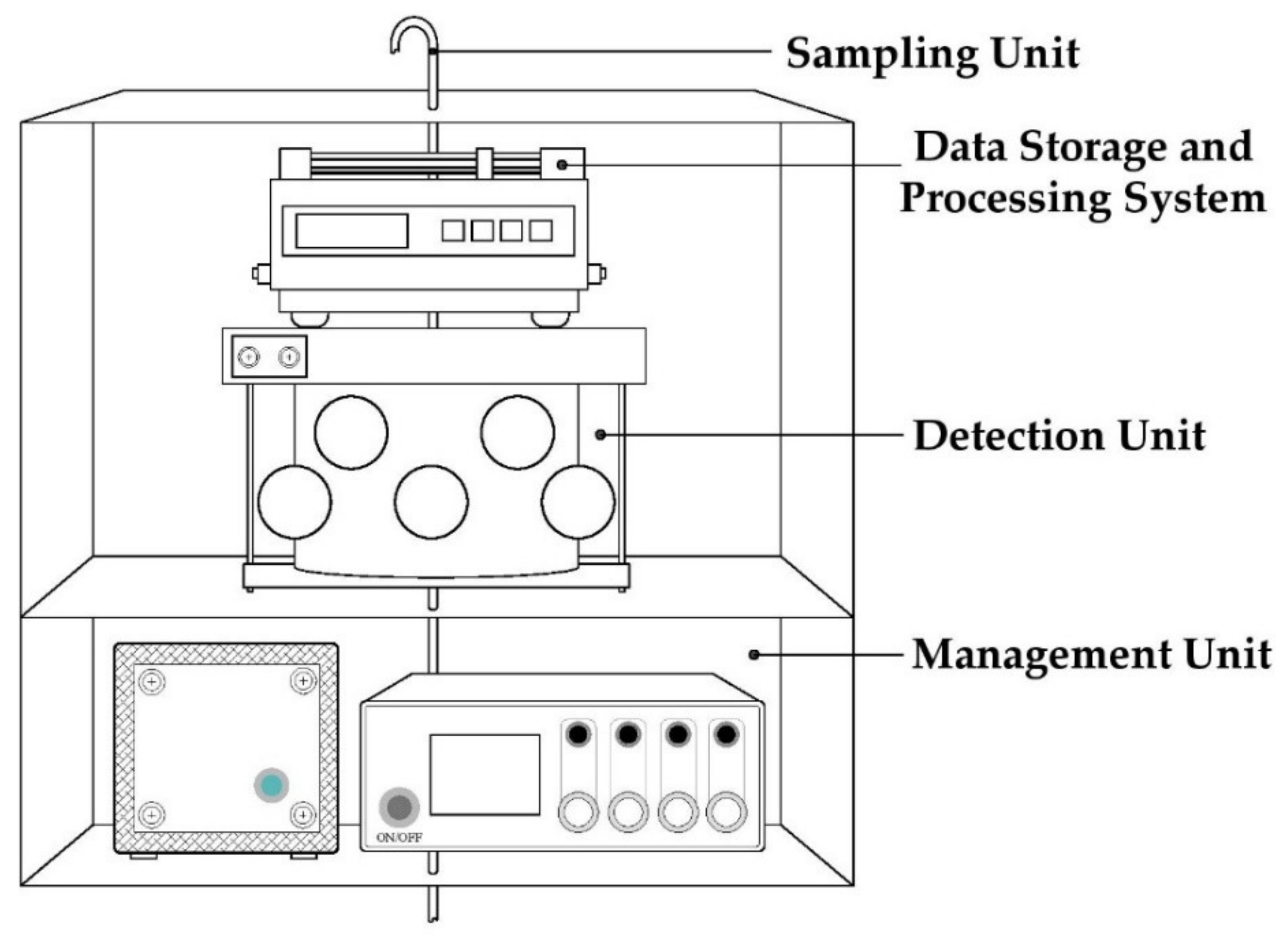
2.2.2. SeedOA Instrumental Odour Monitoring System
2.3. Odour Quantification Monitoring Models (OQMM) Development
2.3.1. ANN
2.3.2. MARSPlines
- -
- β0 = intercept parameter;
- -
- βm = weighted sum of one or more basis functions (hm(X));
- -
- M = sum over the non-constant terms of the model.
2.3.3. MLR
- -
- C = residual terms of the model and the distribution assumption;
- -
- β0, β1, β2… βn = regression coefficients.
2.3.4. PLS
- -
- C = residual terms of the model and the distribution assumption;
- -
- β0, β1, β2… βn = weights/coefficients.
2.3.5. RSR
- -
- w, x, and z are the predictor variables;
- -
- β0… β9 are the coefficients.
2.4. Statistical Analysis
- -
- , is the sum of squared residuals (SSR);
- -
- , is the sum squared total error (SST),
- -
- x represents the predicted data,
- -
- is the actual data;
- -
- is the mean value of the dataset;
- -
- n is the total number of observations.
2.5. Comparison Analysis
3. Results and Discussions
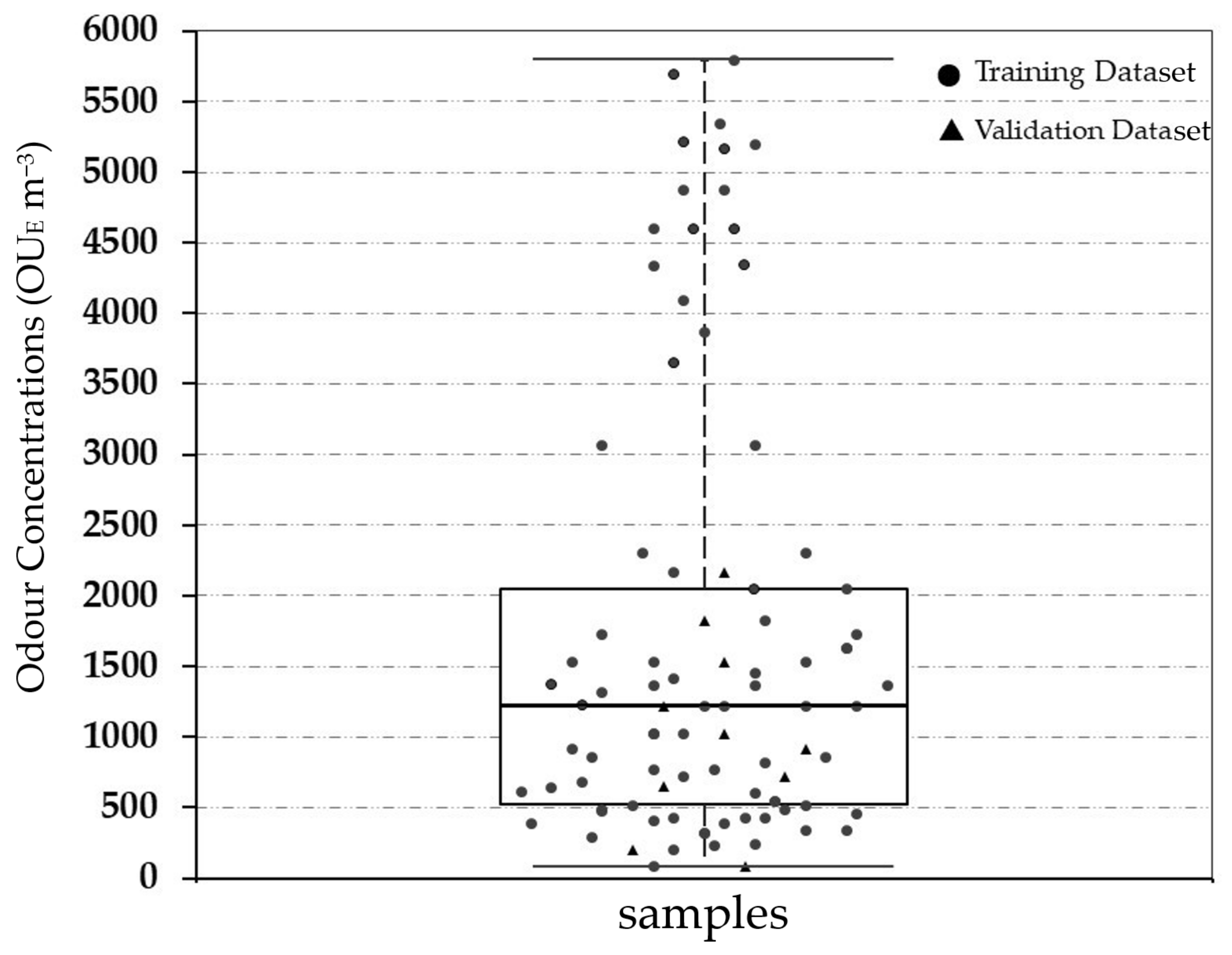
3.1. Odour Concentration Quantification by Dynamic Olfactometry
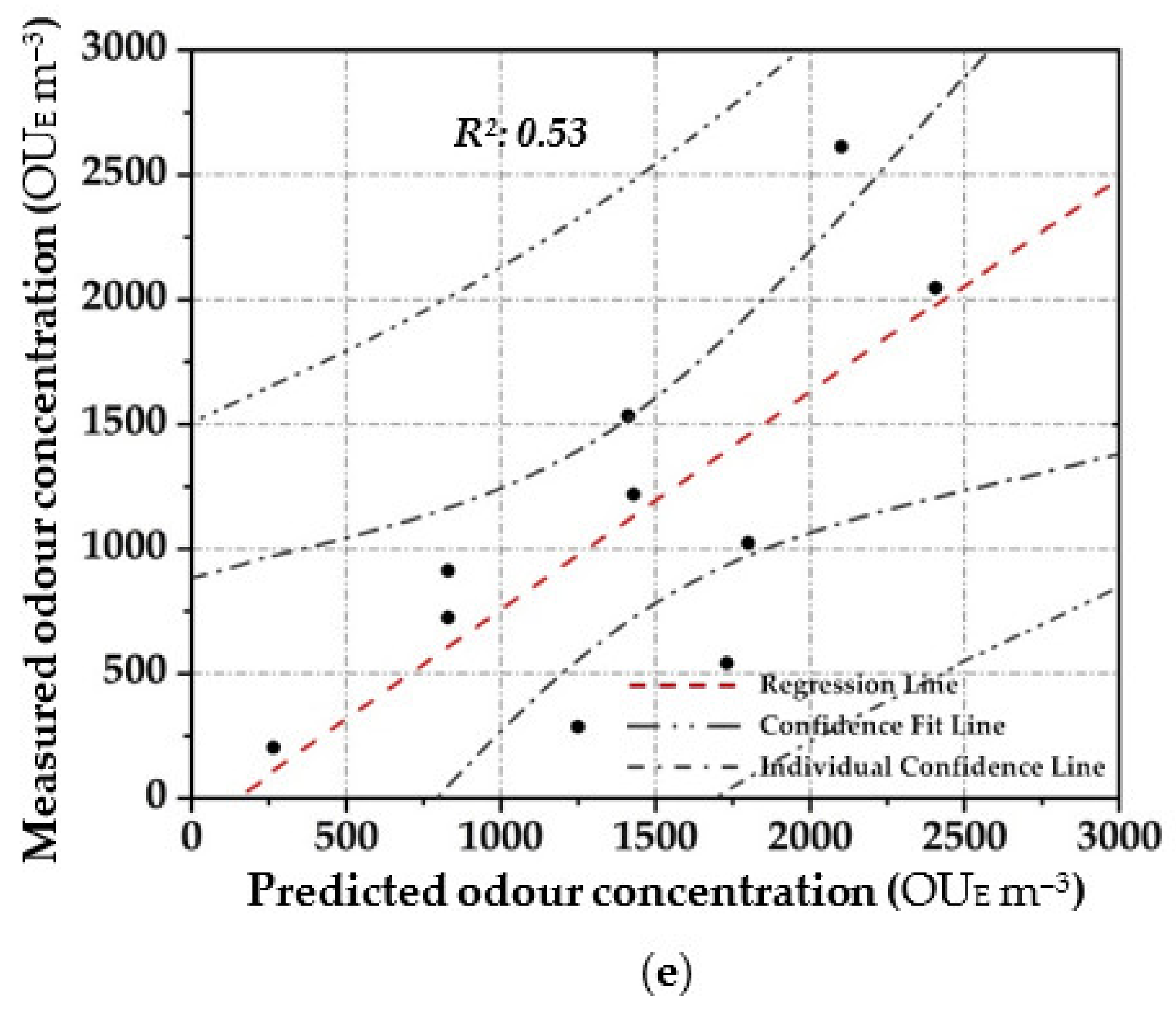
3.2. Odour Quantification Monitoring Models (OQMMs)
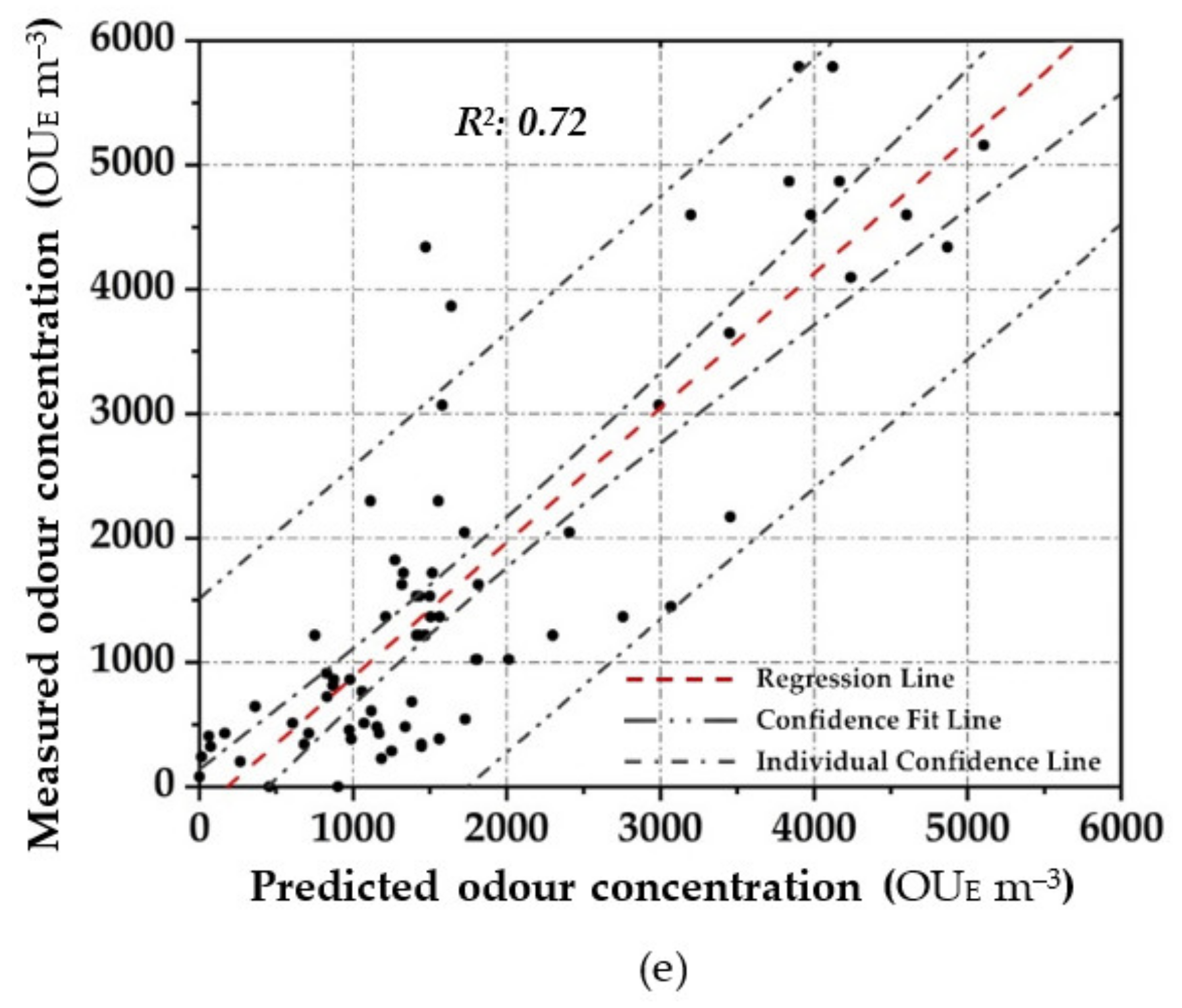
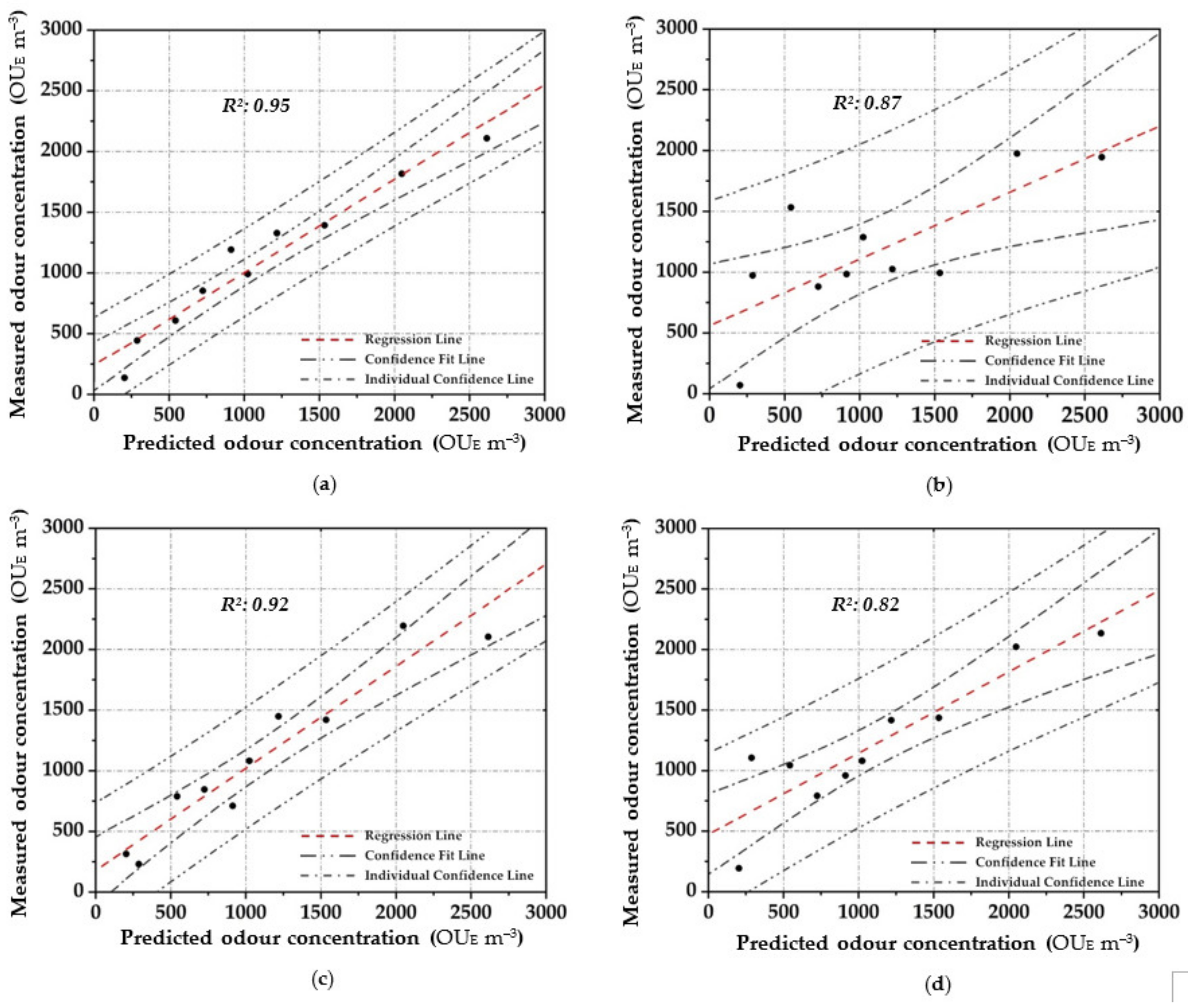
3.3. Comparative Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brancher, M.; Griffiths, K.D.; Franco, D.; de Melo Lisboa, H. A review of odour impact criteria in selected countries around the world. Chemosphere 2017, 168, 1531–1570. [Google Scholar] [CrossRef] [PubMed]
- Kerckhoffs, J.; Hoek, G.; Portengen, L.; Brunekreef, B.; Vermeulen, R.C.H. Performance of Prediction Algorithms for Modeling Outdoor Air Pollution Spatial Surfaces. Environ. Sci. Technol. 2019, 53, 1413–1421. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kimbrough, S.; Krabbe, S.; Baldauf, R.; Barzyk, T.; Brown, M.; Brown, S.; Croghan, C.; Davis, M.; Deshmukh, P.; Duvall, R.; et al. The Kansas City transportation and local-scale air quality study (KC-TRAQS): Integration of low-cost sensors and reference grade monitoring in a complex metropolitan area. Part 1: Overview of the project. Chemosensors 2019, 7, 26. [Google Scholar] [CrossRef] [Green Version]
- Belgiorno, V.; Naddeo, V.; Zarra, T. Odour Impact Assessment Handbook; John & Wiley Sons, Inc.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Wu, C.; Liu, J.; Liu, S.; Li, W.; Yan, L.; Shu, M.; Zhao, P.; Zhou, P.; Cao, W. Assessment of the health risks and odor concentration of volatile compounds from a municipal solid waste landfill in China. Chemosphere 2018, 202, 1–8. [Google Scholar] [CrossRef]
- Fernández-González, J.M.; Díaz-López, C.; Martín-Pascual, J.; Zamorano, M. Recycling organic fraction of municipal solid waste: Systematic literature review and bibliometric analysis of research trends. Sustainability 2020, 12, 4798. [Google Scholar] [CrossRef]
- Piringer, M.; Schauberger, G. Environmental odour: Emission, dispersion, and the assessment of annoyance. Atmosphere 2020, 11, 896. [Google Scholar] [CrossRef]
- Stafford, L.D.; Fleischman, D.S.; Le Her, N.; Hummel, T. Exploring the emotion of disgust: Differences in smelling and feeling. Chemosensors 2018, 6, 9. [Google Scholar] [CrossRef] [Green Version]
- Chang, H.; Zhao, Y.; Tan, H.; Liu, Y.; Lu, W.; Wang, H. Parameter sensitivity to concentrations and transport distance of odorous compounds from solid waste facilities. Sci. Total Environ. 2019, 651, 2158–2165. [Google Scholar] [CrossRef]
- Han, Z.; Qi, F.; Li, R.; Wang, H.; Sun, D. Health impact of odor from on-situ sewage sludge aerobic composting throughout different seasons and during anaerobic digestion with hydrolysis pretreatment. Chemosphere 2020, 249, 126077. [Google Scholar] [CrossRef]
- Zarra, T.; Giuliani, S.; Naddeo, V.; Belgiorno, V. Control of odour emission in wastewater treatment plants by direct and undirected measurement of odour emission capacity. Water Sci. Technol. 2012, 66, 1627–1633. [Google Scholar] [CrossRef] [Green Version]
- Hettinger, T.P.; Frank, M.E. Stochastic and temporal models of olfactory perception. Chemosensors 2018, 6, 44. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Xiao, W.; Shang, T.; Zhang, S.; Han, X.; Wang, Y.; Sun, H. An electronic nose technology to quantify pyrethroid pesticide contamination in tea. Chemosensors 2020, 8, 30. [Google Scholar] [CrossRef]
- Wilson, A.D. Applications of electronic-nose technologies for noninvasive early detection of plant, animal and human diseases. Chemosensors 2018, 6, 45. [Google Scholar] [CrossRef] [Green Version]
- Zarra, T.; Galang, M.G.; Ballesteros, F.; Belgiorno, V.; Naddeo, V. Environmental odour management by artificial neural network—A review. Environ. Int. 2019, 133, 105189. [Google Scholar] [CrossRef]
- Fasolino, I.; Grimaldi, M.; Zarra, T.; Naddeo, V. Odour control strategies for a sustainable nuisances action plan. Glob. Nest J. 2016, 18, 734–741. [Google Scholar] [CrossRef] [Green Version]
- Zarra, T.; Reiser, M.; Naddeo, V.; Belgiorno, V.; Kranert, M. Odour Emissions Characterization from Wastewater Treatment Plants by Different Measurement Methods. Chem. Eng. Trans. 2014, 40, 37–42. [Google Scholar] [CrossRef]
- Galang, M.G.K.; Zarra, T.; Naddeo, V.; Belgiorno, V.; Ballesteros, F. Artificial neural network in the measurement of environmental odours by e-nose. Chem. Eng. Trans. 2018, 68, 247–252. [Google Scholar] [CrossRef]
- Laor, Y.; Parker, D.; Pagé, T. Measurement, prediction, and monitoring of odors in the environment: A critical review. Rev. Chem. Eng. 2014, 30, 139–166. [Google Scholar] [CrossRef]
- Oliva, G.; Zarra, T.; Pittoni, G.; Senatore, V.; Galang, M.G.; Castellani, M.; Belgiorno, V.; Naddeo, V. Next-generation of instrumental odour monitoring system (IOMS) for the gaseous emissions control in complex industrial plants. Chemosphere 2021, 271, 129768. [Google Scholar] [CrossRef]
- Gobbi, E.; Falasconi, M.; Zambotti, G.; Sberveglieri, V.; Pulvirenti, A.; Sberveglieri, G. Rapid diagnosis of Enterobacteriaceae in vegetable soups by a metal oxide sensor based electronic nose. Sens. Actuators B Chem. 2015, 207, 1104–1113. [Google Scholar] [CrossRef]
- Abdulrazzaq, N.N.; Al-Sabbagh, B.H.; Rees, J.M.; Zimmerman, W.B. Measuring vapor and liquid concentrations for binary and ternary systems in a microbubble distillation unit via gas sensors. Chemosensors 2018, 6, 31. [Google Scholar] [CrossRef] [Green Version]
- Guillot, J.M. E-noses: Actual limitations and perspectives for environmental odour analysis. Chem. Eng. Trans. 2016, 54, 223–228. [Google Scholar] [CrossRef]
- Naddeo, V.; Zarra, T.; Oliva, G.; Kubo, A.; Ukida, N.; Higuchi, T. Odour measurement in wastewater treatment plant by a new prototype of e.nose: Correlation and comparison study with reference to both European and Japanese approaches. Chem. Eng. Trans. 2016, 54, 85–90. [Google Scholar]
- Conti, C.; Guarino, M.; Bacenetti, J. Measurements techniques and models to assess odor annoyance: A review. Environ. Int. 2020, 134, 105261. [Google Scholar] [CrossRef] [PubMed]
- Szulczyński, B.; Gębicki, J. Electronic nose—An instrument for odour nuisances monitoring. E3S Web Conf. 2019, 100. [Google Scholar] [CrossRef] [Green Version]
- Martinelli, E.; Magna, G.; Polese, D.; Vergara, A.; Schild, D.; Di Natale, C. Stable odor recognition by a neuro-adaptive electronic nose. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pelosi, P.; Zhu, J.; Knoll, W. From gas sensors to biomimetic artificial noses. Chemosensors 2018, 6, 32. [Google Scholar] [CrossRef] [Green Version]
- Zarra, T.; Galang, M.G.K.; Ballesteros, F.C.; Belgiorno, V.; Naddeo, V. Instrumental odour monitoring system classification performance optimization by analysis of different pattern-recognition and feature extraction techniques. Sensors 2021, 21, 114. [Google Scholar] [CrossRef] [PubMed]
- Naddeo, V.; Zarra, T.; Giuliani, S.; Belgiorno, V. Odour impact assessment in industrial areas. Chem. Eng. Trans. 2012, 30, 85–90. [Google Scholar] [CrossRef]
- Gardner, J.W.; Bartlett, P.N. A brief history of electronic noses. Sensors Actuators B Chem. 1994, 18, 210–211. [Google Scholar] [CrossRef]
- Hidayat, S.N.; Triyana, K.; Fauzan, I.; Julian, T.; Lelono, D.; Yusuf, Y.; Ngadiman, N.; Veloso, A.C.A.; Peres, A.M. The electronic nose coupled with chemometric tools for discriminating the quality of black tea samples in situ. Chemosensors 2019, 7, 29. [Google Scholar] [CrossRef] [Green Version]
- Rasekh, M.; Karami, H.; Wilson, A.D.; Gancarz, M. Classification and Identification of Essential Oils from Herbs and Fruits Based on a MOS Electronic-Nose Technology. Chemosensors 2021, 9, 142. [Google Scholar] [CrossRef]
- Gancarz, M.; Malaga-Toboła, U.; Oniszczuk, A.; Tabor, S.; Oniszczuk, T.; Gawrysiak-Witulska, M.; Rusinek, R. Detection and measurement of aroma compounds with the electronic nose and a novel method for MOS sensor signal analysis during the wheat bread making process. Food Bioprod. Process. 2021, 127, 90–98. [Google Scholar] [CrossRef]
- Kwiatkowski, A.; Chludziński, T.; Saidi, T.; Welearegay, T.G.; Jaimes-Mogollón, A.L.; El Bari, N.; Borys, S.; Bouchikhi, B.; Smulko, J.; Ionescu, R. Assessment of electronic sensing techniques for the rapid identification of alveolar echinococcosis through exhaled breath analysis. Sensors 2020, 20, 2666. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Le Calvé, S.; Newport, D. A review of optical interferometry techniques for VOC detection. Sens. Actuators A Phys. 2020, 302. [Google Scholar] [CrossRef]
- Kabir, E.; Raza, N.; Kumar, V.; Singh, J.; Tsang, Y.F.; Lim, D.K.; Szulejko, J.E.; Kim, K.H. Recent Advances in Nanomaterial-Based Human Breath Analytical Technology for Clinical Diagnosis and the Way Forward. Chem 2019, 5, 3020–3057. [Google Scholar] [CrossRef]
- Sethi, S.; Nanda, R.; Chakraborty, T. Clinical application of volatile organic compound analysis for detecting infectious diseases. Clin. Microbiol. Rev. 2013, 26, 462–475. [Google Scholar] [CrossRef] [Green Version]
- Slimani, S.; Bultel, E.; Cubizolle, T.; Herrier, C.; Rousselle, T.; Livache, T. Opto-electronic nose coupled to a silicon micro pre-concentrator device for selective sensing of flavored waters. Chemosensors 2020, 8, 60. [Google Scholar] [CrossRef]
- Yurko, G.; Roostaei, J.; Dittrich, T.; Xu, L.; Ewing, M.; Zhang, Y.; Shreve, G. Real-Time Sensor Response Characteristics of 3 Commercial Metal Oxide Sensors for Detection of BTEX and Chlorinated Aliphatic Hydrocarbon Organic Vapors. Chemosensors 2019, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Korsa, M.T.; Domingo, J.M.C.; Nsubuga, L.; Hvam, J.; Niekiel, F.; Lofink, F.; Rubahn, H.G.; Adam, J.; Hansen, R.D.O. Optimizing piezoelectric cantilever design for electronic nose applications. Chemosensors 2020, 8, 114. [Google Scholar] [CrossRef]
- Cao, J.; Liu, T.; Chen, J.; Yang, T.; Zhu, X.; Wang, H. Drift Compensation on Massive Online Electronic-Nose Responses. Chemosensors 2021, 9, 78. [Google Scholar] [CrossRef]
- Licen, S.; Barbieri, G.; Fabbris, A.; Briguglio, S.C.; Pillon, A.; Stel, F.; Barbieri, P. Odor control map: Self organizing map built from electronic nose signals and integrated by different instrumental and sensorial data to obtain an assessment tool for real environmental scenarios. Sens. Actuators B Chem. 2018, 263, 476–485. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Distante, C.; Leo, M.; Siciliano, P.; Persaud, K.C. On the study of feature extraction methods for an electronic nose. Sens. Actuators B Chem. 2002, 87, 274–288. [Google Scholar] [CrossRef]
- Teniou, A.; Rhouati, A.; Marty, J.L. Mathematical Modelling of Biosensing Platforms Applied for Environmental Monitoring. Chemosensors 2021, 9, 50. [Google Scholar] [CrossRef]
- Abbatangelo, M.; Núñez-Carmona, E.; Sberveglieri, V.; Comini, E.; Sberveglieri, G. k-NN and k-NN-ANN combined classifier to assess mox gas sensors performances affected by drift caused by early life aging. Chemosensors 2020, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Ding, S.; Zhu, H.; Jia, W.; Su, C. A survey on feature extraction for pattern recognition. Artif. Intell. Rev. 2012, 37, 169–180. [Google Scholar] [CrossRef]
- Okur, S.; Sarheed, M.; Huber, R.; Zhang, Z.; Heinke, L.; Kanbar, A.; Wöll, C.; Nick, P.; Lemmer, U. Identification of Mint Scents Using a QCM Based E-Nose. Chemosensors 2021, 9, 31. [Google Scholar] [CrossRef]
- Szulczyński, B.; Armiński, K.; Namieśnik, J.; Gębicki, J. Determination of odour interactions in gaseous mixtures using electronic nose methods with artificial neural networks. Sensors 2018, 18, 519. [Google Scholar] [CrossRef] [Green Version]
- Lokuge, W.; Wilson, A.; Gunasekara, C.; Law, D.W.; Setunge, S. Design of fly ash geopolymer concrete mix proportions using Multivariate Adaptive Regression Spline model. Constr. Build. Mater. 2018, 166, 472–481. [Google Scholar] [CrossRef]
- Ojha, P.K.; Roy, K. PLS regression-based chemometric modeling of odorant properties of diverse chemical constituents of black tea and coffee. RSC Adv. 2018, 8, 2293–2304. [Google Scholar] [CrossRef] [Green Version]
- Dahlén, J.; Karlsson, S.; Bäckström, M.; Hagberg, J.; Pettersson, H. Determination of nitrate and other water quality parameters in groundwater from UV/Vis spectra employing partial least squares regression. Chemosphere 2000, 40, 71–77. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Pan, Y. Enhancing electronic nose performance by feature selection using an improved grey wolf optimization based algorithm. Sensors 2020, 20, 4065. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.J.; Jonassen, K.E.N.; Løkke, M.M.; Adamsen, A.P.S.; Feilberg, A. Multivariate prediction of odor from pig production based on in-situ measurement of odorants. Atmos. Environ. 2016, 135, 50–58. [Google Scholar] [CrossRef]
- Orzi, V.; Riva, C.; Scaglia, B.; D’Imporzano, G.; Tambone, F.; Adani, F. Anaerobic digestion coupled with digestate injection reduced odour emissions from soil during manure distribution. Sci. Total Environ. 2018, 621, 168–176. [Google Scholar] [CrossRef]
- Matias-Guiu, P.; Garza-Moreira, E.; Rodríguez-Bencomo, J.J.; López, F. Rapid sensory analysis using response surface methodology: Application to the study of odour interactive effects in model spirits. J. Inst. Brew. 2018, 124, 100–105. [Google Scholar] [CrossRef] [Green Version]
- Keller, A.; Gerkin, R.C.; Guan, Y.; Dhurandhar, A.; Turu, G.; Szalai, B.; Mainland, J.D.; Ihara, Y.; Yu, C.W.; Wolfinger, R.; et al. Predicting human olfactory perception from chemical features of odor molecules. Science 2017, 355, 820–826. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geană, E.I.; Ciucure, C.T.; Apetrei, C. Electrochemical sensors coupled with multivariate statistical analysis as screening tools for wine authentication issues: A review. Chemosensors 2020, 8, 59. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C. Multivariate adaptive regression splines and neural network models for prediction of pile drivability. Geosci. Front. 2016, 7, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Giuliani, S.; Zarra, T.; Nicolas, J.; Naddeo, V.; Belgiorno, V.; Romain, A.C. An alternative approach of the e-nose training phase in odour impact assessment. Chem. Eng. Trans. 2012, 30, 139–144. [Google Scholar] [CrossRef]
- Giuliani, S.; Zarra, T.; Naddeo, V.; Belgiorno, V. Measurement of odour emission capacity in wastewater treatment plants by multisensor array system. Environ. Eng. Manag. J. 2013, 12, 173–176. [Google Scholar]
- Viccione, G.; Zarra, T.; Giuliani, S.; Naddeo, V.; Belgiorno, V. Performance study of e-nose measurement chamber for environmental odour monitoring. Chem. Eng. Trans. 2012, 30, 109–114. [Google Scholar] [CrossRef]
- Galang, M.G.K.; Ballesteros, F. Estimation of waste mobile phones in the Philippines using neural networks. Glob. Nest J. 2018, 20, 767–772. [Google Scholar] [CrossRef] [Green Version]
- Khaldi, S.; Dibi, Z. Neural Network Technique for Electronic Nose Based on High Sensitivity Sensors Array. Sens. Imaging 2019, 20, 1–19. [Google Scholar] [CrossRef]
- Oduro, S.D.; Metia, S.; Duc, H.; Hong, G.; Ha, Q.P. Multivariate adaptive regression splines models for vehicular emission prediction. Vis. Eng. 2015, 3. [Google Scholar] [CrossRef] [Green Version]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Vedrtnam, A.; Singh, G.; Kumar, A. Optimizing submerged arc welding using response surface methodology, regression analysis, and genetic algorithm. Def. Technol. 2018, 14, 204–212. [Google Scholar] [CrossRef]
- Wang, H.; Gu, J.; Wang, S.; Saporta, G. Spatial partial least squares autoregression: Algorithm and applications. Chemom. Intell. Lab. Syst. 2019, 184, 123–131. [Google Scholar] [CrossRef]
- Al-Salem, S.M.; Al-Nasser, A.; Al-Dhafeeri, A.T. Multi-variable regression analysis for the solid waste generation in the State of Kuwait. Process. Saf. Environ. Prot. 2018, 119, 172–180. [Google Scholar] [CrossRef]
- Kang, J.H.; Song, J.H.; Yoo, S.S.; Lee, B.J.; Ji, H.W. Prediction of odor concentration emitted from wastewater treatment plant using an artificial neural network (ANN). Atmosphere 2020, 11, 784. [Google Scholar] [CrossRef]
- Samadi, M.; Afshar, M.H.; Jabbari, E.; Sarkardeh, H. Application of Multivariate Adaptive Regression Splines and Classification and Regression Trees to Estimate Wave-Induced Scour Depth around Pile Groups. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 447–459. [Google Scholar] [CrossRef]


| Statistical Category | Prediction Technique | Indicators |
|---|---|---|
| Parametric | Multiple Linear Regression (MLR) | Dependent–independent variable relationship |
| Partial Least Square (PLS) | Ideal number of components | |
| Response Surface Regression (RSR) | Significant variables | |
| Non-parametric | Multivariate Adaptive Regression Splines (MARSpline) | Ideal number of basic functions |
| Artificial Neural Network (ANN) | Ideal number of hidden neurons |
| Description | Number of Observation Points | ||||
|---|---|---|---|---|---|
| Training Dataset | Validation Dataset | OUE m−3 | |||
| Raw Samples | Data Points (kΩ) | Raw Samples | Data Points (kΩ) | ||
| Odorous Air | 82 | 2460 | 10 | 300 | 82 |
| Statistical Category | Prediction Technique | OQMM | |||
|---|---|---|---|---|---|
| Training | Validation | ||||
| R2 | RMSE (OUE m−3) | R2 | RMSE (OUE m−3) | ||
| Parametric | PLS | OQMM1.1 | OQMM2.1 | ||
| RSR | OQMM1.2 | OQMM2.2 | |||
| MLR | OQMM1.3 | OQMM2.3 | |||
| Non-Parametric | ANN | OQMM1.4 | OQMM2.4 | ||
| MARSPline | OQMM1.5 | OQMM2.5 | |||
| Statistical Category | Prediction Technique for OQMM Elaboration | Training | Validation | ||
|---|---|---|---|---|---|
| R2 | RMSE (OUE m−3) | R2 | RMSE (OUE m−3) | ||
| Parametric | PLS | 0.92 | 451 | 0.92 | 219 |
| RSR | 0.90 | 487 | 0.82 | 348 | |
| MLR | 0.72 | 837 | 0.53 | 583 | |
| Non-Parametric | ANN | 0.97 | 289 | 0.95 | 216 |
| MARSPline | 0.83 | 651 | 0.87 | 482 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarra, T.; Galang, M.G.K.; Belgiorno, V.; Naddeo, V. Environmental Odour Quantification by IOMS: Parametric vs. Non-Parametric Prediction Techniques. Chemosensors 2021, 9, 183. https://doi.org/10.3390/chemosensors9070183
Zarra T, Galang MGK, Belgiorno V, Naddeo V. Environmental Odour Quantification by IOMS: Parametric vs. Non-Parametric Prediction Techniques. Chemosensors. 2021; 9(7):183. https://doi.org/10.3390/chemosensors9070183
Chicago/Turabian StyleZarra, Tiziano, Mark Gino K. Galang, Vincenzo Belgiorno, and Vincenzo Naddeo. 2021. "Environmental Odour Quantification by IOMS: Parametric vs. Non-Parametric Prediction Techniques" Chemosensors 9, no. 7: 183. https://doi.org/10.3390/chemosensors9070183
APA StyleZarra, T., Galang, M. G. K., Belgiorno, V., & Naddeo, V. (2021). Environmental Odour Quantification by IOMS: Parametric vs. Non-Parametric Prediction Techniques. Chemosensors, 9(7), 183. https://doi.org/10.3390/chemosensors9070183








