Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity
Abstract
1. Introduction
2. Related Work
3. Proposed Sensing Device
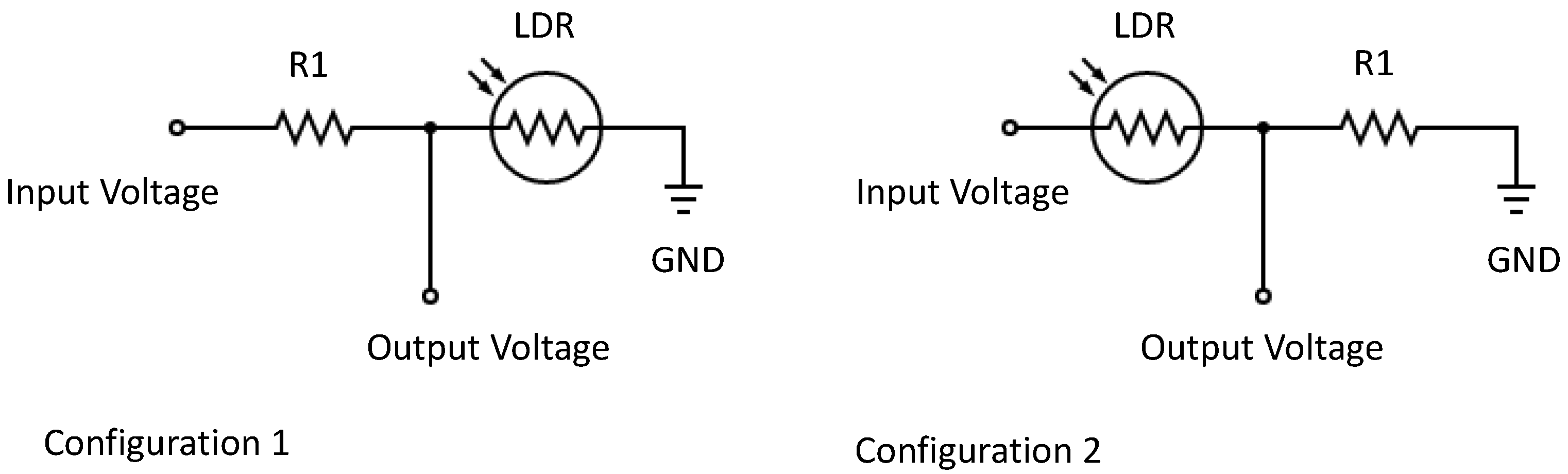
3.1. Operation Principle
3.2. Sensing Elements
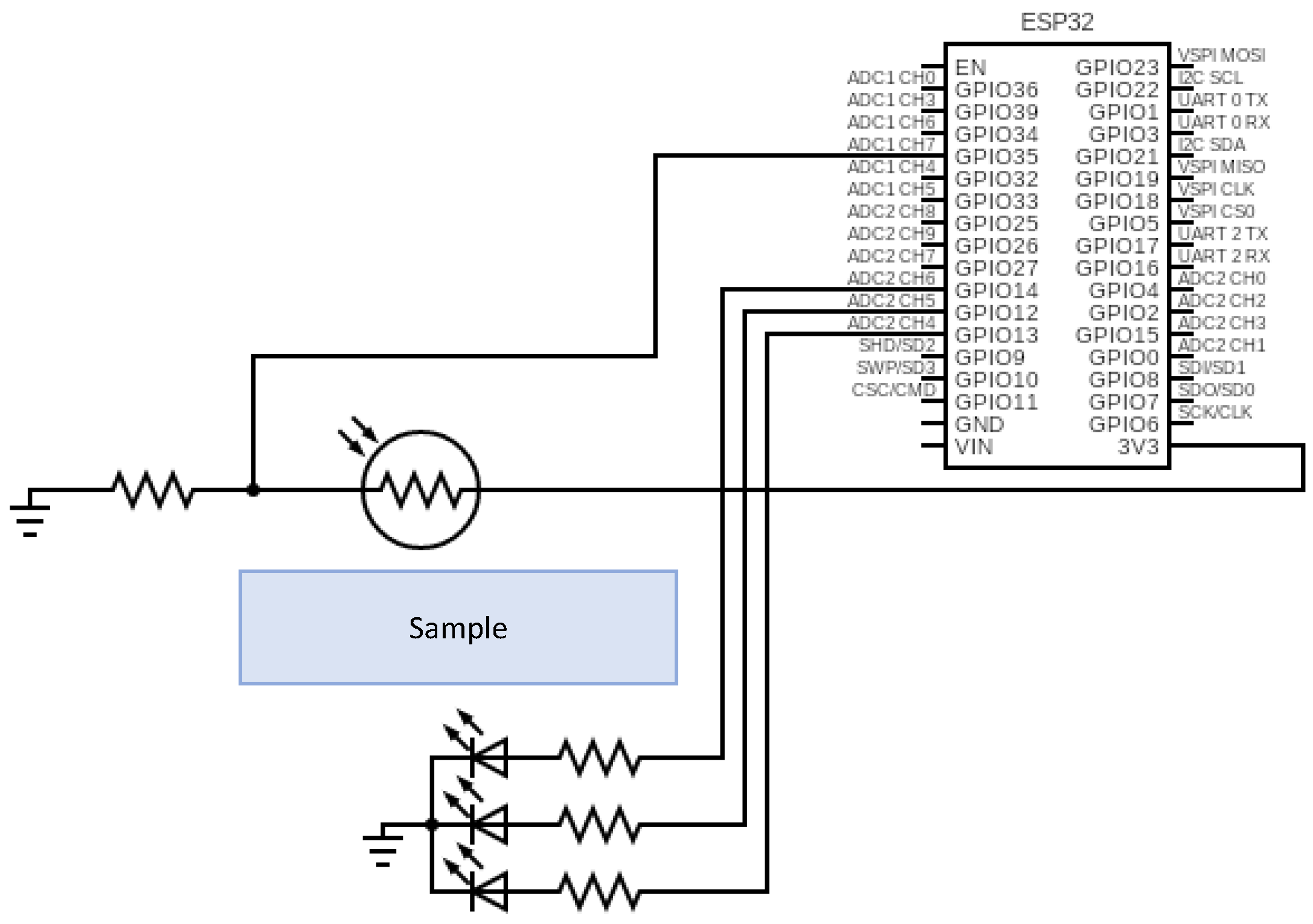
3.3. Node
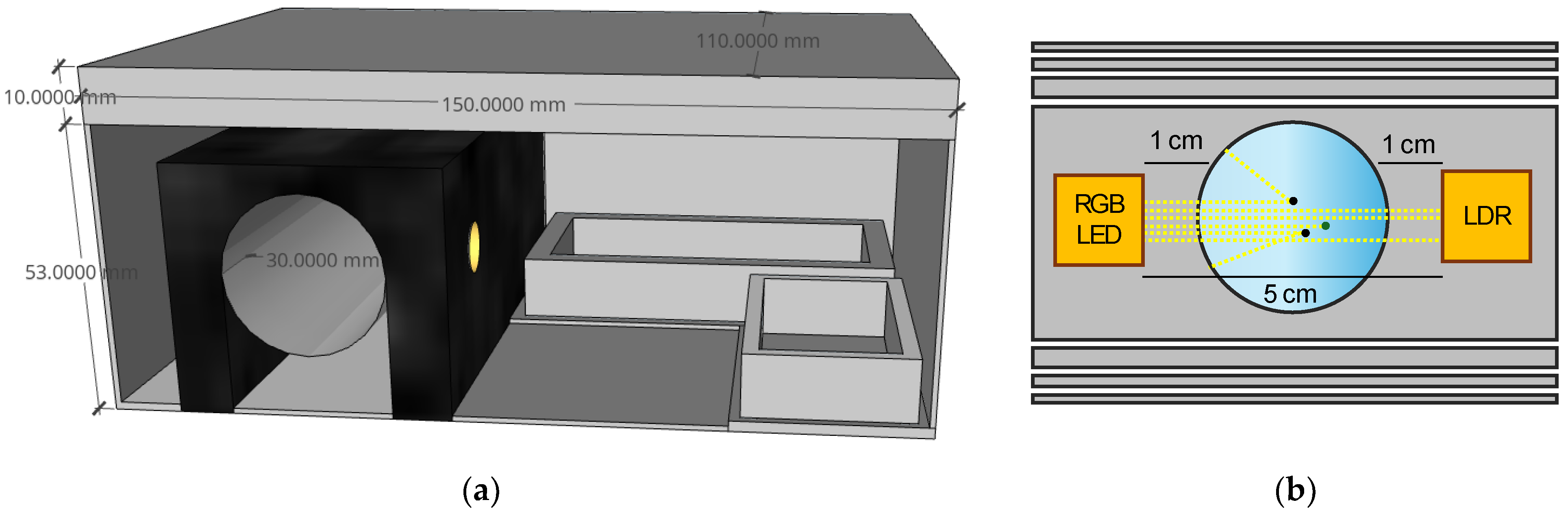
3.4. Sensor Assembly
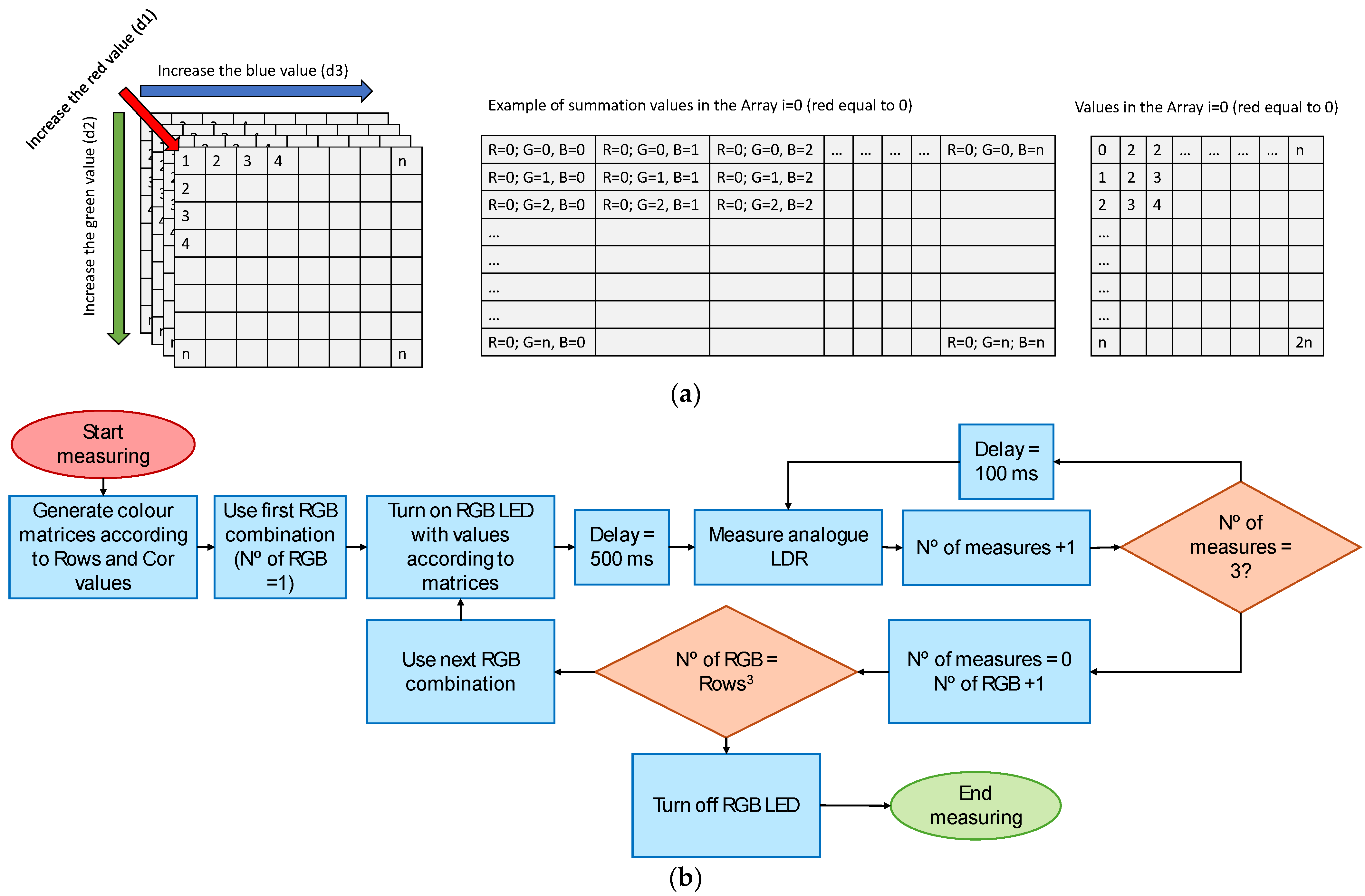
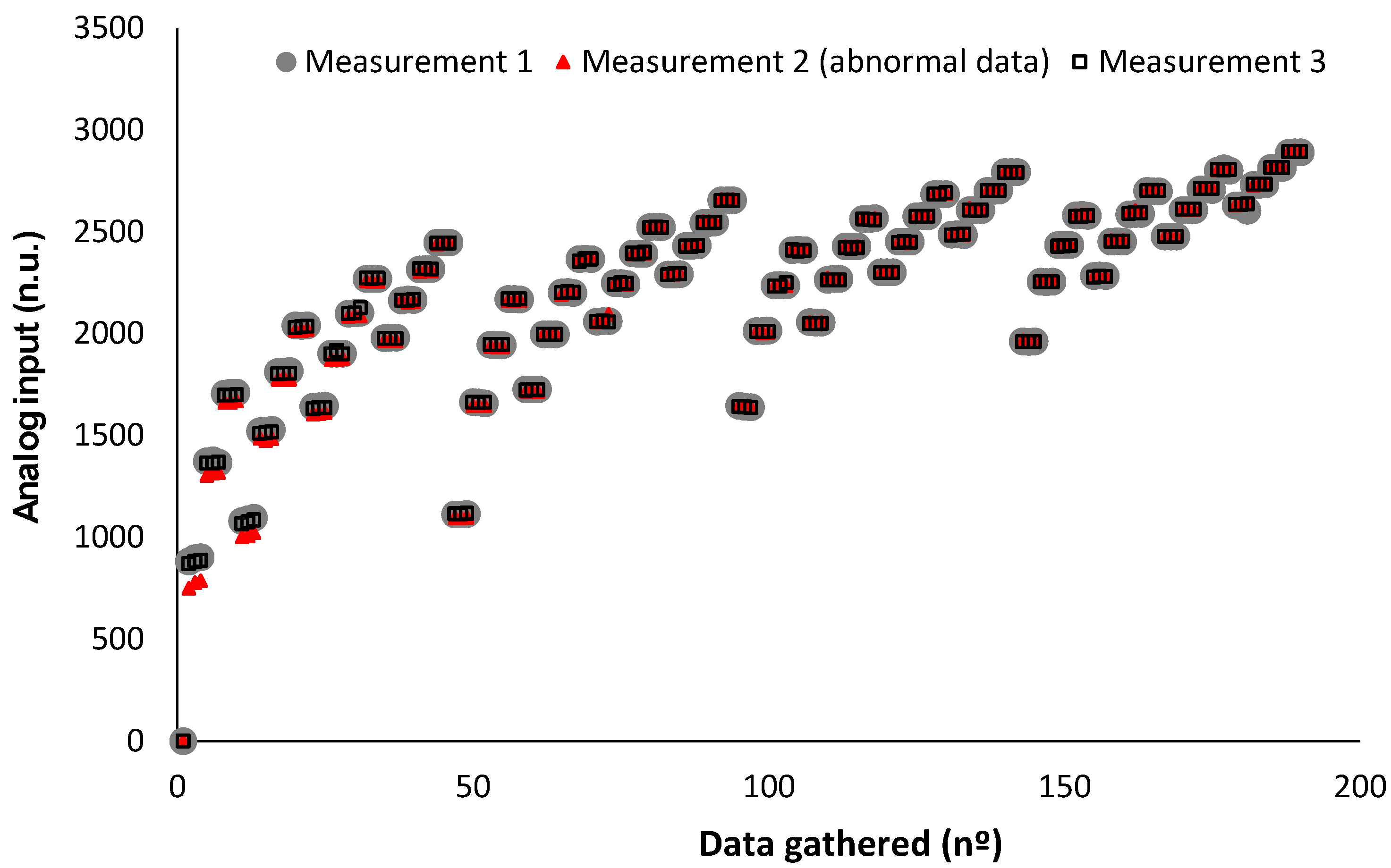
3.5. Sensor Operation
| Algorithm 1: Allocate and Initialize the Array |
| int myArray[rows][rows][rows]; for (int d1 = 0; d1 < rows; d1++) { for (int d2 = 0; d2 < rows; d2++) { for (int d3 = 0; d3 < rows; d3++) { myArray[d1][d2][d3] = (d1 + d2 + d3); } } } |
| Algorithm 2: Using the Array to Power the RGB LED |
| for (int i = 0; i < rows; i++) { for (int j = 0; j < rows; j++) { for (int k = 0; k < rows; k++) { // Value from 0 to 255 for the R, G, and B component int valueRed = cor * (myArray[i][j][k] − myArray[0][j][k]); int valueGreen = cor * (myArray[i][j][k] − myArray[i][0][k]); int valueBlue = cor * (myArray[i][j][k] − myArray[i][j][0]); //Emmited light colour analogWrite(pinRed, valueRed); analogWrite(pinGreen, valueGreen); analogWrite(pinBlue, valueBlue); cont++; Serial.print(“Colnº:”); Serial.print(cont);Serial.print(“de”); Seri-al.print(maxcol); Serial.print(“RGB:”); Serial.print(valueRed); Serial.print(vaueGreen); Serial.println(valueBlue); delay(500); |
| Algorithm 3: Measuring the LDR Voltage |
| for (int i = 0; i < 3; i++) { delay(100); Read = adc1_get_voltage(ADC1_CHANNEL_7); //get the val of channel0 Serial.println(Read); } //delay for the LDR analogWrite(pinRede, 0); analogWrite(pinGreen, 0); analogWrite(pinGreen, 0); delay(delaydark); } } } |
4. Test Bench
4.1. Sample Generation
4.2. Measuring Equipment
4.3. Conducted Tests
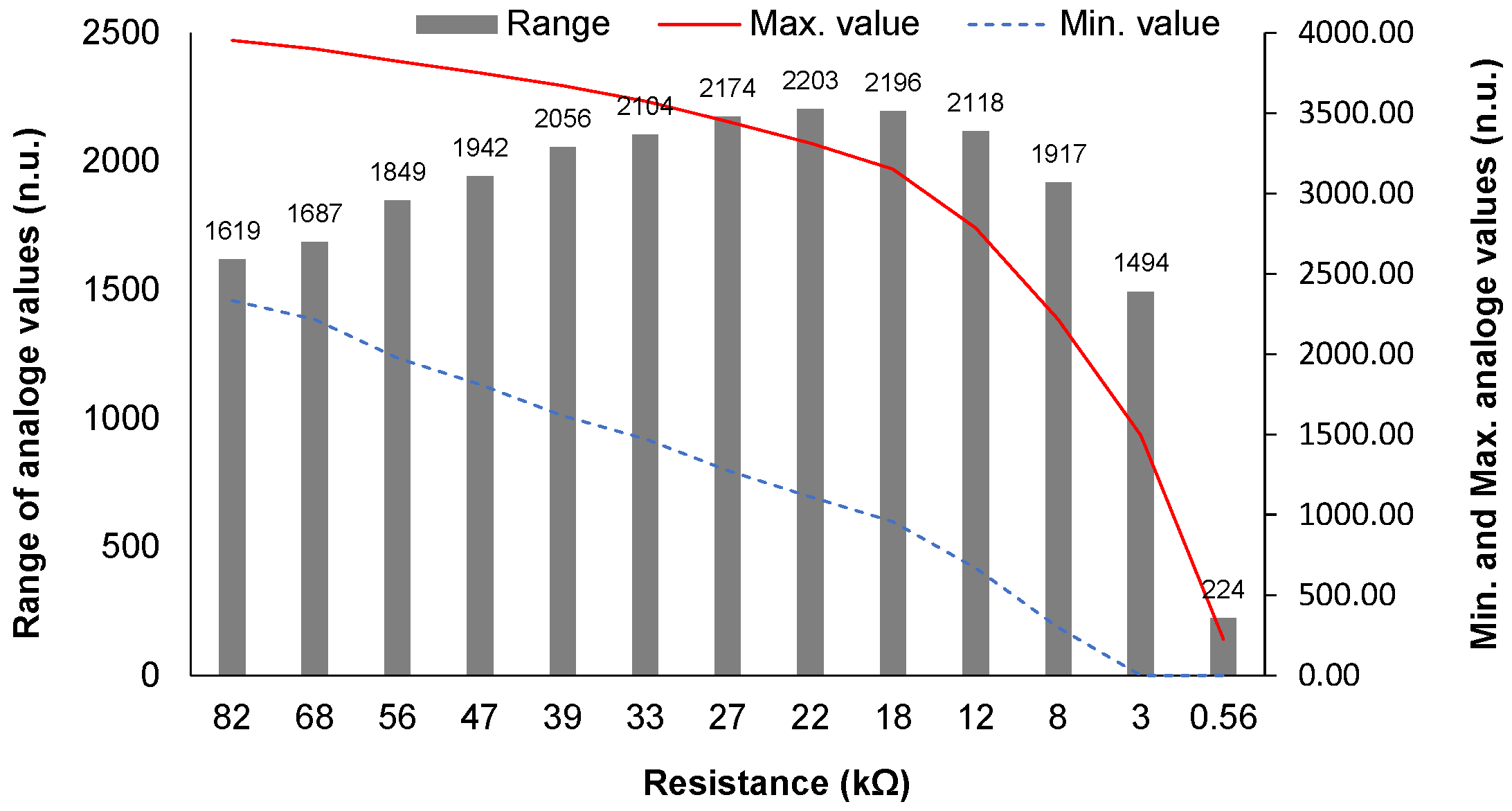
4.3.1. Test to Select the Resistance
4.3.2. Test to Select the Delaydark
4.3.3. Calibration Test
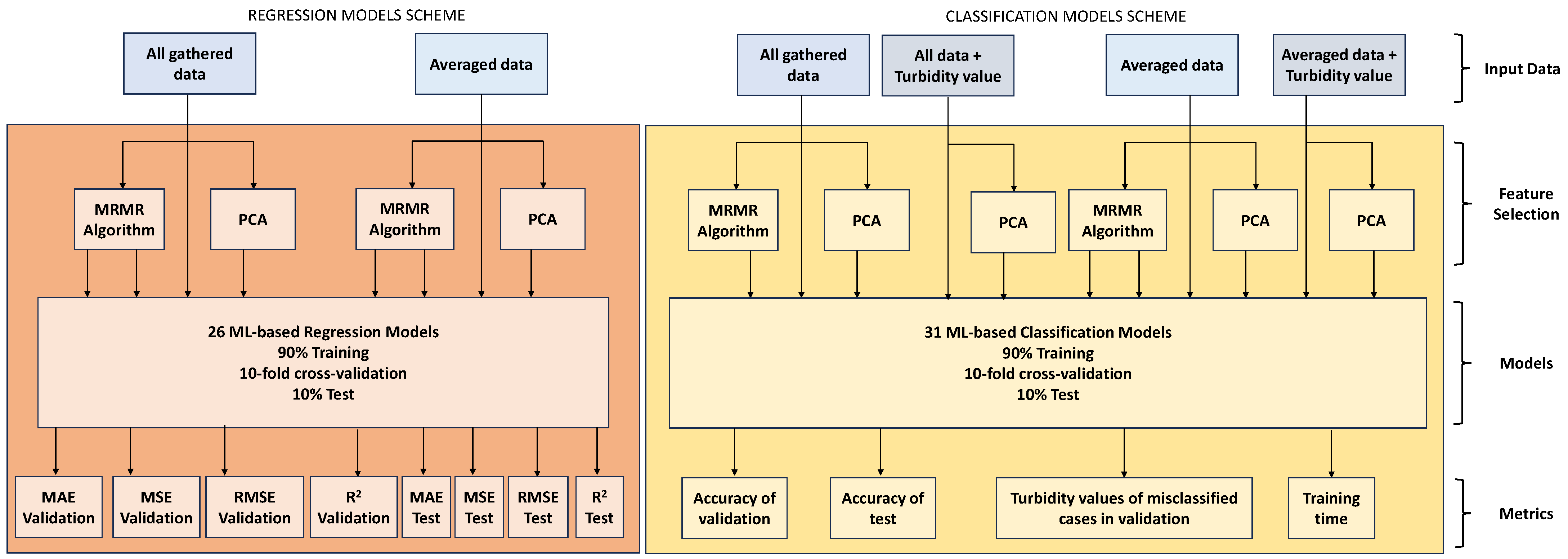
4.4. Data Processing and Performed Analyses
5. Results and Discussion
5.1. Results of Preliminary Test
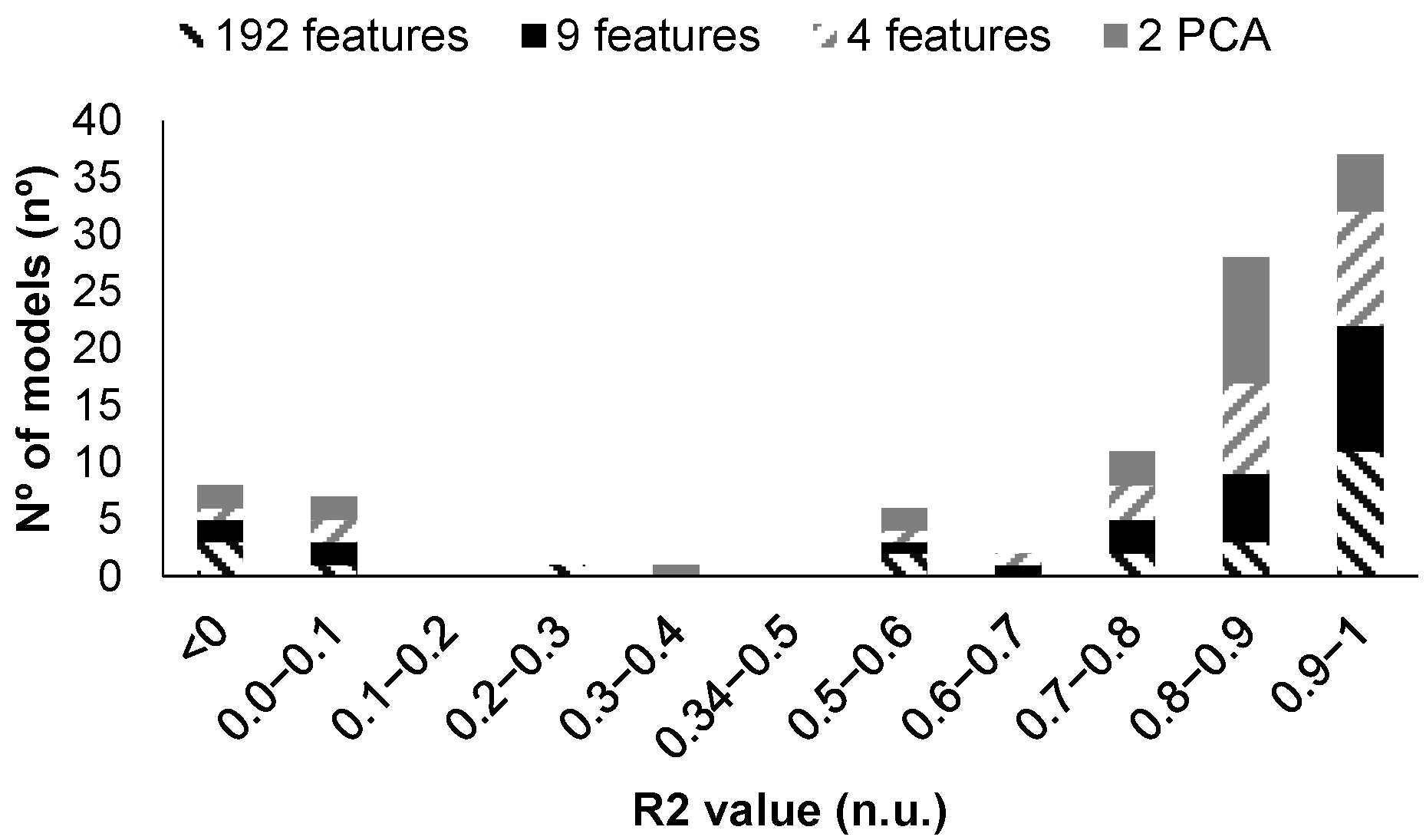
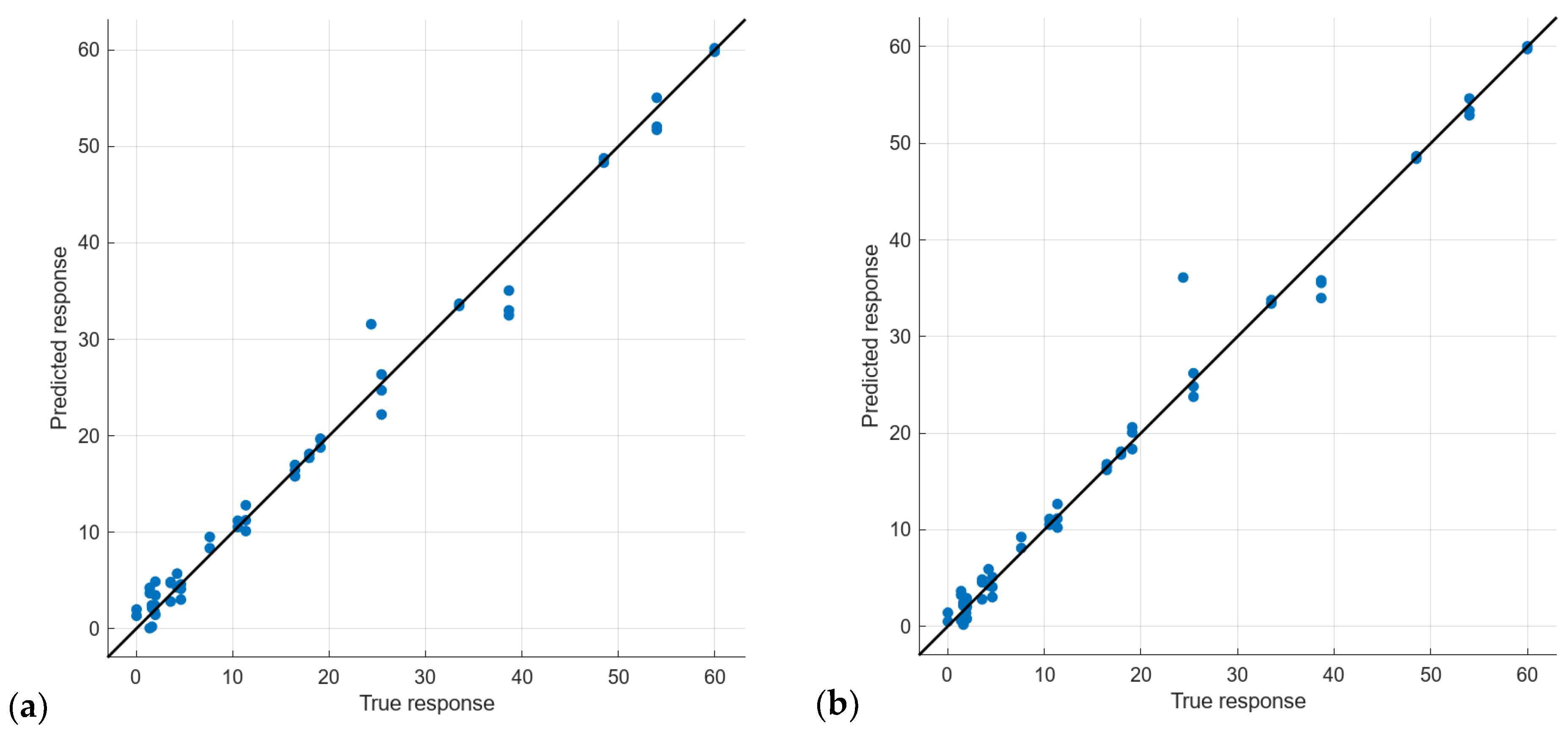
5.2. Calibration Results: Quantify Turbidity
5.3. Calibration Results: Characterise Turbidity
5.4. Discussion
5.4.1. General Findings
5.4.2. Comparison with Existing Proposals
5.4.3. Limitations of Presented Tests
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Omer, N.H. Water quality parameters. In Water Quality-Science, Assessments and Policy; Intech Open: London, UK, 2019; Volume 18, pp. 1–34. [Google Scholar]
- Tomperi, J.; Isokangas, A.; Tuuttila, T.; Paavola, M. Functionality of turbidity measurement under changing water quality and environmental conditions. Environ. Technol. 2022, 43, 1093–1101. [Google Scholar] [CrossRef] [PubMed]
- Feng, J.; Chen, H.; Zhang, H.; Li, Z.; Yu, Y.; Zhang, Y.; Bilal, M.; Qiu, Z. Turbidity estimation from GOCI satellite data in the turbid estuaries of China’s coast. Remote Sens. 2020, 12, 3770. [Google Scholar] [CrossRef]
- Ortega, J.C.; Figueiredo, B.R.; da Graca, W.J.; Agostinho, A.A.; Bini, L.M. Negative effect of turbidity on prey capture for both visual and non-visual aquatic predators. J. Anim. Ecol. 2020, 89, 2427–2439. [Google Scholar] [CrossRef] [PubMed]
- Freitas, L.M.; de Dirceu, M.M.; Leão, Z.M.A.N.; Kikuchi, R.K.P. Effects of turbidity and depth on the bioconstruction of the Abrolhos reefs. Coral Reefs 2019, 38, 241–253. [Google Scholar] [CrossRef]
- Blain, C.O.; Shears, N.T. Seasonal and spatial variation in photosynthetic response of the kelp Ecklonia radiata across a turbidity gradient. Photosynth. Res. 2019, 140, 21–38. [Google Scholar] [CrossRef]
- Fernández-Ortega, J.; Barberá, J.A.; Andreo, B. Coupling major ions and trace elements to turbidity dynamics for allogenic contribution assessment in a binary karst system (Sierra de Ubrique, S Spain). Environ. Earth Sci. 2023, 82, 536. [Google Scholar] [CrossRef]
- Steadmon, M.; Ngiraklang, K.; Nagata, M.; Masga, K.; Frank, K.L. Effects of water turbidity on the survival of Staphylococcus aureus in environmental fresh and brackish waters. Water Environ. Res. 2023, 95, e10923. [Google Scholar] [CrossRef]
- Bowers, D.G.; Roberts, E.M.; Hoguane, A.M.; Fall, K.A.; Massey, G.M.; Friedrichs, C.T. Secchi disk measurements in turbid water. J. Geophys. Res. Ocean. 2020, 125, e2020JC016172. [Google Scholar] [CrossRef]
- Liang, S.; Miyake, T.; Shimizu, K. Optical parameters estimation in inhomogeneous turbid media using backscattered light: For transcutaneous scattering measurement of intravascular blood. Biomed. Opt. Express 2024, 15, 237–255. [Google Scholar] [CrossRef]
- Kuntao, Y.; Musha, J.E.; Zhai, S. Influence of particle shape on polarization characteristics of backscattering light in turbid media. Chin. J. Lasers 2020, 47, 1. [Google Scholar] [CrossRef]
- Simmons, S.M.; Azpiroz-Zabala, M.; Cartigny, M.J.B.; Clare, M.A.; Cooper, C.; Parsons, D.R.; Pope, E.L.; Sumner, E.J.; Talling, P.J. Novel acoustic method provides first detailed measurements of sediment concentration structure within submarine turbidity currents. J. Geophys. Res. Ocean. 2020, 125, e2019JC015904. [Google Scholar] [CrossRef]
- Sahin, C.; Ozturk, M.; Aydogan, B. Acoustic doppler velocimeter backscatter for suspended sediment measurements: Effects of sediment size and attenuation. Appl. Ocean Res. 2020, 94, 101975. [Google Scholar] [CrossRef]
- Golubkov, M.S.; Golubkov, S.M. Secchi Disk Depth or Turbidity, Which Is Better for Assessing Environmental Quality in Eutrophic Waters? A Case Study in a Shallow Hypereutrophic Reservoir. Water 2023, 16, 18. [Google Scholar] [CrossRef]
- Snazelle, T.T. Field Comparison of Five In Situ Turbidity Sensors; No. 2020–1123; US Geological Survey: Reston, VA, USA, 2020. [Google Scholar]
- Pamula, A.S.; Gholizadeh, H.; Krzmarzick, M.J.; Mausbach, W.E.; Lampert, D.J. A remote sensing tool for near real-time monitoring of harmful algal blooms and turbidity in reservoirs. JAWRA J. Am. Water Resour. Assoc. 2023, 59, 929–949. [Google Scholar] [CrossRef]
- Gad, M.; Saleh, A.H.; Hussein, H.; Farouk, M.; Elsayed, S. Appraisal of surface water quality of nile river using water quality indices, spectral signature and multivariate modeling. Water 2022, 14, 1131. [Google Scholar] [CrossRef]
- Fay, C.D.; Nattestad, A. Advances in optical based turbidity sensing using led photometry (Pedd). Sensors 2021, 22, 254. [Google Scholar] [CrossRef] [PubMed]
- Parra, L.; Rocher, J.; Escrivá, J.; Lloret, J. Design and development of low cost smart turbidity sensor for water quality monitoring in fish farms. Aquac. Eng. 2018, 81, 10–18. [Google Scholar] [CrossRef]
- Magrì, S.; Ottaviani, E.; Prampolini, E.; Federici, B.; Besio, G.; Fabiano, B. Application of machine learning techniques to derive sea water turbidity from Sentinel-2 imagery. Remote Sens. Appl. Soc. Environ. 2023, 30, 100951. [Google Scholar] [CrossRef]
- Youssef-Douss, R.; Derbel, W.; Krichen, E.; Benazza-Benyahia, A. Estimation of water turbidity by image-based learning approaches. In Proceedings of the International Conference on Artificial Intelligence and Green Computing, Beni Mellal, Morocco, 15–17 March 2023; Springer Nature: Cham, Switzerland, 2023; pp. 63–77. [Google Scholar]
- Ma, Y.; Song, K.; Wen, Z.; Liu, G.; Shang, Y.; Lyu, L.; Du, J.; Yang, Q.; Li, S.; Tao, H.; et al. Remote sensing of turbidity for lakes in northeast China using Sentinel-2 images with machine learning algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9132–9146. [Google Scholar] [CrossRef]
- Viciano-Tudela, S.; Sendra, S.; Parra, L.; Jimenez, J.M.; Lloret, J. Proposal of a Gas Sensor-Based Device for Detecting Adulteration in Essential Oil of Cistus ladanifer. Sustainability 2023, 15, 3357. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Wang, T.; Li, W.; Lu, Q.; Sun, H.; Huang, L.; Liang, X.; Liu, F.; Liu, F.; et al. Machine learning-assisted volatile organic compound gas classification based on polarized mixed-potential gas sensors. ACS Appl. Mater. Interfaces 2023, 15, 6047–6057. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, X.; Xiang, W.; Wang, T.; Otis, C.; Sarge, L.; Lei, Y.; Li, B. Forward-looking roadmaps for long-term continuous water quality monitoring: Bottlenecks, innovations, and prospects in a critical review. Environ. Sci. Technol. 2022, 56, 5334–5354. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Zhang, S.; Wu, J. Detecting, extracting, and monitoring surface water from space using optical sensors: A review. Rev. Geophys. 2018, 56, 333–360. [Google Scholar] [CrossRef]
- Saboe, D.; Ghasemi, H.; Gao, M.M.; Samardzic, M.; Hristovski, K.D.; Boscovic, D.; Burge, S.R.; Burge, R.G.; Hoffman, D.A. Real-time monitoring and prediction of water quality parameters and algae concentrations using microbial potentiometric sensor signals and machine learning tools. Sci. Total Environ. 2021, 764, 142876. [Google Scholar] [CrossRef]
- Burge, S.R.; Hristovski, K.D.; Burge, R.G.; Hoffman, D.A.; Saboe, D.; Chao, P.; Taylor, E.; Koenigsberg, S.S. Microbial potentiometric sensor: A new approach to longstanding challenges. Sci. Total Environ. 2020, 742, 140528. [Google Scholar] [CrossRef]
- Rocher, J.; Jimenez, J.M.; Tomas, J.; Lloret, J. Low-Cost Turbidity Sensor to Determine Eutrophication in Water Bodies. Sensors 2023, 23, 3913. [Google Scholar] [CrossRef]
- Wang, Y.; Rajib, S.S.M.; Collins, C.; Grieve, B. Low-cost turbidity sensor for low-power wireless monitoring of fresh-water courses. IEEE Sens. J. 2018, 18, 4689–4696. [Google Scholar] [CrossRef]
- Cadondon, J.G.; Ong, P.M.B.; Vallar, E.A.; Shiina, T.; Galvez, M.C.D. Chlorophyll-a pigment measurement of spirulina in algal growth monitoring using portable pulsed LED fluorescence lidar system. Sensors 2022, 22, 2940. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Peng, Y.; Du, Z.; Lin, H.; Yu, Q. Calibrations of suspended sediment concentrations in high-turbidity waters using different in situ optical instruments. Water 2020, 12, 3296. [Google Scholar] [CrossRef]
- Bright, C.; Mager, S.; Horton, S. Response of nephelometric turbidity to hydrodynamic particle size of fine suspended sediment. Int. J. Sediment Res. 2020, 35, 444–454. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, Y.; Xie, D.; Huang, R.; Zeng, G.; Liu, X.; Deng, H.; Wang, H.; Lin, Z. Machine learning constructs color features to accelerate development of long-term continuous water quality monitoring. J. Hazard. Mater. 2024, 461, 132612. [Google Scholar] [CrossRef]
- Huang, J.; Qian, R.; Gao, J.; Bing, H.; Huang, Q.; Qi, L.; Song, S.; Huang, J. A novel framework to predict water turbidity using Bayesian modeling. Water Res. 2021, 202, 117406. [Google Scholar] [CrossRef]
- Duarte, D.P.; Nogueira, R.N.; Bilro, L. Low cost color assessment of turbid liquids using supervised learning data analysis–Proof of concept. Sens. Actuators A Phys. 2020, 305, 111936. [Google Scholar] [CrossRef]
- Yan, J.; Jin, M.; Xu, Z.; Chen, L.; Zhu, Z.; Zhang, H. Recognition of suspension liquid based on speckle patterns using deep learning. IEEE Photonics J. 2020, 13, 1–7. [Google Scholar] [CrossRef]
- Héran, D.; Ryckewaert, M.; Abautret, Y.; Zerrad, M.; Amra, C.; Bendoula, R. Combining light polarization and speckle measurements with multivariate analysis to predict bulk optical properties of turbid media. Appl. Opt. 2019, 58, 8247–8256. [Google Scholar] [CrossRef]
- Loutfi, H.; Pellen, F.; Le Jeune, B.; Le Brun, G.; Abboud, M. Polarized laser speckle images produced by calibrated polystyrene microspheres suspensions: Comparison between backscattering and transmission experimental configurations. Laser Phys. 2023, 33, 086001. [Google Scholar] [CrossRef]
- Bello, V.; Bodo, E.; Merlo, S. Speckle Pattern Acquisition and Statistical Processing for Analysis of Turbid Liquids. IEEE Trans. Instrum. Meas. 2023, 72, 7005004. [Google Scholar] [CrossRef]
- Parra, L.; Viciano-Tudela, S.; Carrasco, D.; Sendra, S.; Lloret, J. Low-cost microcontroller-based multiparametric probe for coastal area monitoring. Sensors 2023, 23, 1871. [Google Scholar] [CrossRef] [PubMed]
- RGB LED Datasheet. Available online: https://datasheetspdf.com/datasheet/KY-016.html (accessed on 15 January 2024).
- LDR NSL-19M51 Datasheet. Available online: https://www.advancedphotonix.com/wp-content/uploads/2022/03/DS-NSL-19M51.pdf (accessed on 15 January 2024).
- Node ESP32 Datasheet. Available online: https://www.espressif.com/en/products/socs/esp32 (accessed on 15 January 2024).
- Turbiditymeter Lutron Datasheet TU-2016. Available online: https://www.sunwe.com.tw/lutron/TU-2016.pdf (accessed on 15 January 2024).
- Analytical Balance FR-3200 Datasheet. Available online: https://www.alldatasheet.com/view.jsp?Searchword=FR3200&sField=2 (accessed on 15 January 2024).
- Matlab Software. Available online: https://es.mathworks.com/products/matlab.html (accessed on 15 January 2024).
- Azman, A.A.; Rahiman MH, F.; Taib, M.N.; Sidek, N.H.; Bakar, I.A.A.; Ali, M.F. A low cost nephelometric turbidity sensor for continual domestic water quality monitoring system. In Proceedings of the 2016 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Selangor, Malaysia, 22 October 2016; pp. 202–207. [Google Scholar]
- Maier, P.M.; Keller, S. Machine learning regression on hyperspectral data to estimate multiple water parameters. In Proceedings of the 2018 9th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Amsterdam, The Netherlands, 23–26 September 2018; pp. 1–5. [Google Scholar]
- Schima, R.; Krüger, S.; Bumberger, J.; Paschen, M.; Dietrich, P.; Goblirsch, T. Mobile monitoring—Open-source based optical sensor system for service-oriented turbidity and dissolved organic matter monitoring. Front. Earth Sci. 2019, 7, 184. [Google Scholar] [CrossRef]
- Trevathan, J.; Read, W.; Sattar, A. Implementation and calibration of an iot light attenuation turbidity sensor. Internet Things 2022, 19, 100576. [Google Scholar] [CrossRef]
- Facco, D.S.; Guasselli, L.A.; Ruiz, L.F.C.; Simioni, J.P.D.; Dick, D.G. Comparison of PBIA and GEOBIA classification methods in classifying turbidity in reservoirs. Geocarto Int. 2022, 37, 4762–4783. [Google Scholar] [CrossRef]
- Souza, A.P.; Oliveira, B.A.; Andrade, M.L.; Starling, M.C.V.; Pereira, A.H.; Maillard, P.; Nogueira, K.; dos Santos, J.A.; Amorim, C.C. Integrating remote sensing and machine learning to detect turbidity anomalies in hydroelectric reservoirs. Sci. Total Environ. 2023, 902, 165964. [Google Scholar] [CrossRef] [PubMed]
- Feizi, H.; Sattari, M.T.; Mosaferi, M.; Apaydin, H.A.L.İ.T. An image-based deep learning model for water turbidity estimation in laboratory conditions. Int. J. Environ. Sci. Technol. 2023, 20, 149–160. [Google Scholar] [CrossRef]
- Lopez-Betancur, D.; Moreno, I.; Guerrero-Mendez, C.; Saucedo-Anaya, T.; González, E.; Bautista-Capetillo, C.; González-Trinidad, J. Convolutional Neural Network for Measurement of Suspended Solids and Turbidity. Appl. Sci. 2022, 12, 6079. [Google Scholar] [CrossRef]
- Rocher, J.; Parra, L.; Jimenez, J.M.; Lloret, J.; Basterrechea, D.A. Development of a Low-Cost Optical Sensor to Detect Eutrophication in Irrigation Reservoirs. Sensors 2021, 21, 7637. [Google Scholar] [CrossRef]
- Sader, M. Turbidity Measurement: A Simple, Effective Indicator of Water Quality Change; OTT Hydromet: Sterling, VA, USA, 2017. [Google Scholar]
- Bright, C.E.; Mager, S.M.; Horton, S.L. Predicting suspended sediment concentration from nephelometric turbidity in organic-rich waters. River Res. Appl. 2018, 34, 640–648. [Google Scholar] [CrossRef]



| Rows (nº) | Total Light Combinations (nº) | Required Time for Complete Measurement (s) |
|---|---|---|
| 3 | 27 | 13.5 |
| 4 | 64 | 32 |
| 5 | 125 | 62.5 |
| 6 | 216 | 108 |
| 7 | 343 | 171.5 |
| 8 | 512 | 256 |
| 9 | 729 | 364.5 |
| 10 | 1000 | 500 |
| Rows (nº) | Cor Value (nº) | Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 84 | 0 | 84 | 168 | |||||||
| 4 | 63 | 0 | 63 | 126 | 189 | ||||||
| 5 | 50 | 0 | 50 | 100 | 150 | 200 | |||||
| 6 | 42 | 0 | 42 | 84 | 126 | 168 | 210 | ||||
| 7 | 35 | 0 | 35 | 70 | 105 | 140 | 175 | 210 | |||
| 8 | 31 | 0 | 31 | 62 | 93 | 124 | 155 | 186 | 217 | ||
| 9 | 27 | 0 | 27 | 54 | 81 | 108 | 135 | 162 | 189 | 216 | |
| 10 | 25 | 0 | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | 225 |
| Id | Label | Added Solid | Dilution | Turbidity in t = 0 min (NTUs) | Turbidity in t = 1 min (NTUs) |
|---|---|---|---|---|---|
| 1 | a | fresh green vegetal organic matter | 60 | 53 | 38.66 |
| 2 | a | 33.33 | 25.66 | 19.1 | |
| 3 | a | 20 | 11.37 | 10.53 | |
| 4 | a | 11.11 | 5.25 | 4.23 | |
| 5 | a | 3.45 | 1.99 | 1.62 | |
| 6 | b | decaying vegetal organic matter | 15 | 53 | 54 |
| 7 | b | 10 | 26.69 | 24.37 | |
| 8 | b | 5 | 11.72 | 11.36 | |
| 9 | b | 2.5 | 8.45 | 7.62 | |
| 10 | b | 0.72 | 2.62 | 1.9 | |
| 11 | c | soil and ashes | 10 | 50 | 48.51 |
| 12 | c | 8 | 25.86 | 25.44 | |
| 13 | c | 5 | 16.98 | 16.46 | |
| 14 | c | 2.5 | 4.59 | 3.73 | |
| 15 | c | 0.84 | 2.65 | 1.97 | |
| 16 | d | soil | 15 | 66 | 60 |
| 17 | d | 10 | 37.25 | 33.5 | |
| 18 | d | 5 | 18.39 | 17.94 | |
| 19 | d | 2.5 | 6.21 | 3.56 | |
| 20 | d | 1.25 | 1.83 | 2.51 | |
| 21 | - | - | - | 0.74 | 0.02 |
| Id | Type of Model | Preset | Id | Type of Model | Preset |
|---|---|---|---|---|---|
| 1 | LR | Linear | 14 | Ensemble | Boosted Trees |
| 2 | LR | Interactions Linear | 15 | Ensemble | Bagged Trees |
| 3 | LR | Robust Linear | 16 | GPR | Squared Exponential GPR |
| 4 | Stepwise LR | Stepwise Linear | 17 | GPR | Matern 5/2 GPR |
| 5 | Tree | Fine Tree | 18 | GPR | Exponential GPR |
| 6 | Tree | Medium Tree | 19 | GPR | Rational Quadratic GPR |
| 7 | Tree | Coarse Tree | 20 | NN | Narrow Neural Network |
| 8 | SVM | Linear SVM | 21 | NN | Medium Neural Network |
| 9 | SVM | Quadratic SVM | 22 | NN | Wide Neural Network |
| 10 | SVM | Cubic SVM | 23 | NN | Bilayered Neural Network |
| 11 | SVM | Fine Gaussian SVM | 24 | NN | Trilayered Neural Network |
| 12 | SVM | Medium Gaussian SVM | 25 | Kernel | SVM Kernel |
| 13 | SVM | Coarse Gaussian SVM | 26 | Kernel | Least Squares Regression Kernel |
| Id | Type of Model | Preset | Id | Type of Model | Preset |
|---|---|---|---|---|---|
| 1 | Tree | Fine Tree | 17 | KNN | Cosine KNN |
| 2 | Tree | Medium Tree | 18 | KNN | Cubic KNN |
| 3 | Tree | Coarse Tree | 19 | KNN | Weighted KNN |
| 4 | Discriminant | Linear Discriminant | 20 | Ensemble | Boosted Trees |
| 5 | Discriminant | Quadratic Discriminant | 21 | Ensemble | Bagged Trees |
| 6 | Naive Bayes | Gaussian Naive Bayes | 22 | Ensemble | Subspace Discriminant |
| 7 | Naive Bayes | Kernel Naive Bayes | 23 | Ensemble | Subspace KNN |
| 8 | SVM | Linear SVM | 24 | Ensemble | RUSBoosted Trees |
| 9 | SVM | Quadratic SVM | 25 | NN | Narrow Neural Network |
| 10 | SVM | Cubic SVM | 26 | NN | Medium Neural Network |
| 11 | SVM | Fine Gaussian SVM | 27 | NN | Wide Neural Network |
| 12 | SVM | Medium Gaussian SVM | 28 | NN | Bilayered Neural Network |
| 13 | SVM | Coarse Gaussian SVM | 29 | NN | Trilayered Neural Network |
| 14 | KNN | Fine KNN | 30 | Kernel | SVM Kernel |
| 15 | KNN | Medium KNN | 31 | Kernel | Logistic Regression Kernel |
| 16 | KNN | Coarse KNN |
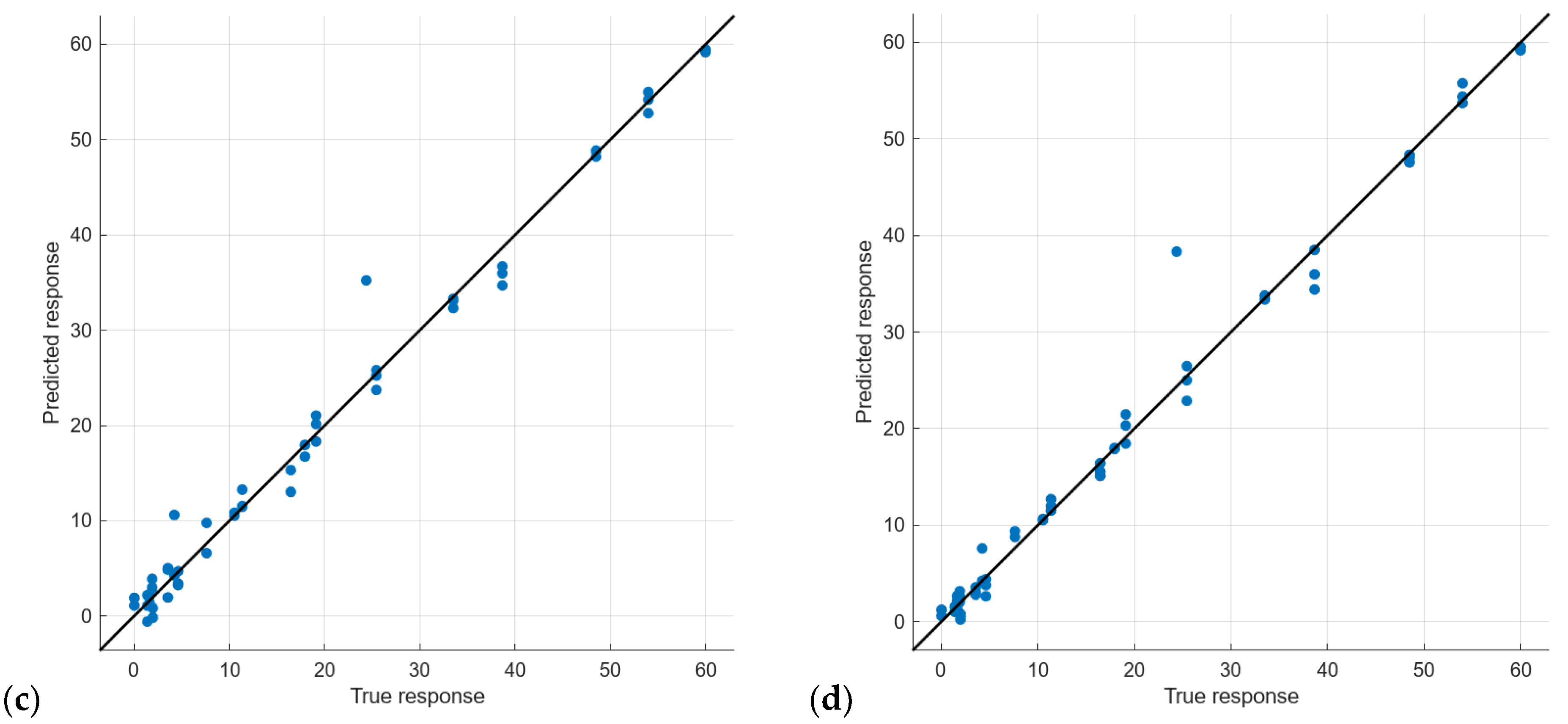
| Model Id | Used Features | Label in Figure 10 | RMSE Validation | MSE Validation | MAE Validation | RMSE Test | MSE Test | MAE Test |
|---|---|---|---|---|---|---|---|---|
| 17 | 192 | (a) | 1.92 | 3.68 | 1.20 | 0.70 | 0.50 | 0.47 |
| 19 | PCA | (b) | 1.97 | 3.86 | 1.03 | 0.81 | 0.66 | 0.61 |
| 16 | 192 | (c) | 2.18 | 4.76 | 1.35 | 1.44 | 2.09 | 1.20 |
| 18 | PCA | (d) | 2.21 | 4.89 | 1.07 | 1.33 | 1.78 | 0.90 |
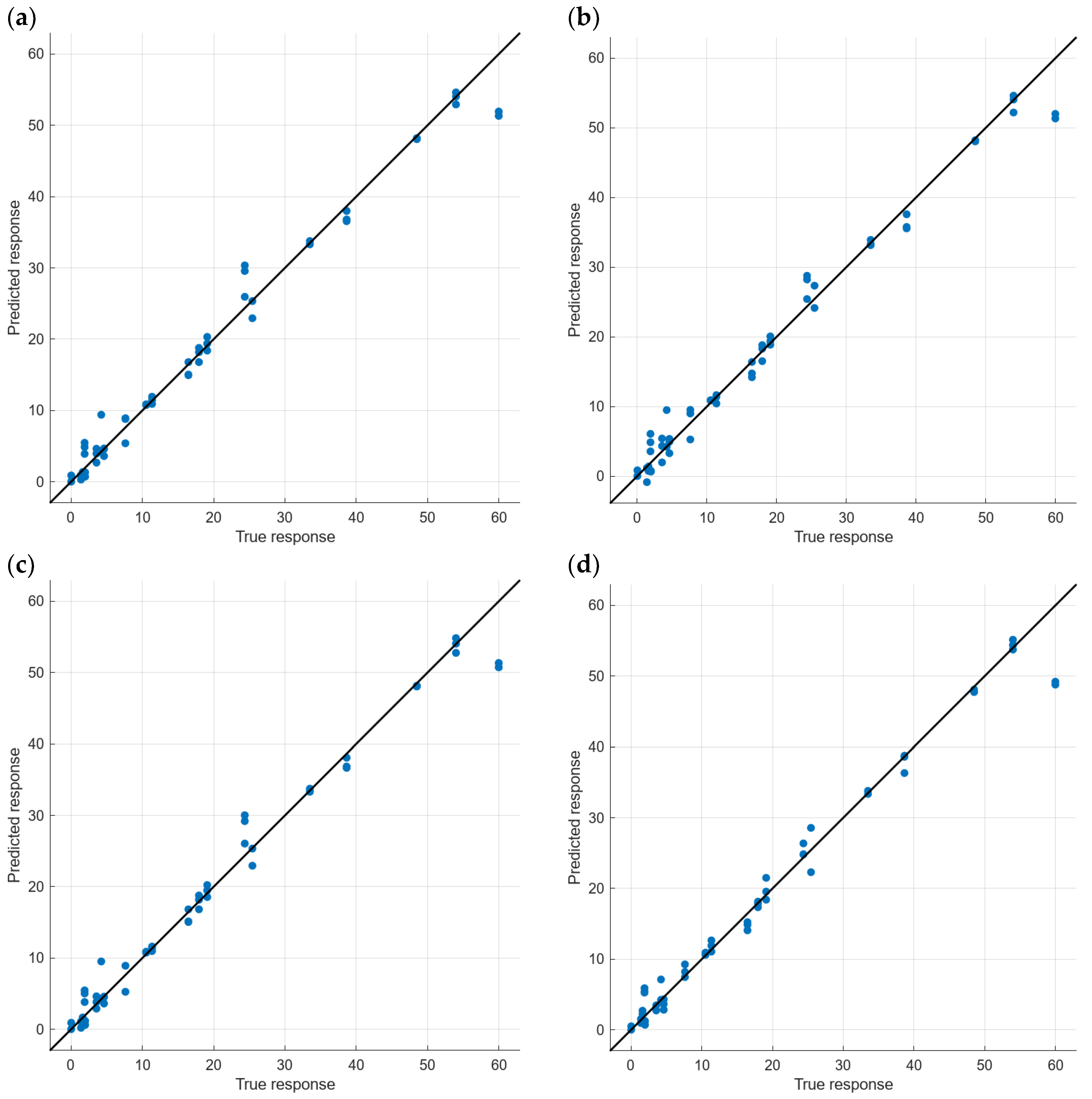
| Model Id | Used Features | Label in Figure 11 | RMSE Validation | MSE Validation | MAE Validation | RMSE Test | MSE Test | MAE Test |
|---|---|---|---|---|---|---|---|---|
| 17 | 192 | (a) | 2.29 | 5.25 | 1.34 | 0.70 | 0.75 | 0.86 |
| 19 | PCA | (b) | 2.30 | 5.30 | 1.48 | 0.90 | 1.02 | 1.01 |
| 16 | 192 | (c) | 2.35 | 5.51 | 1.34 | 0.63 | 0.68 | 0.83 |
| 18 | PCA | (d) | 2.49 | 6.19 | 1.31 | 0.55 | 0.47 | 0.68 |
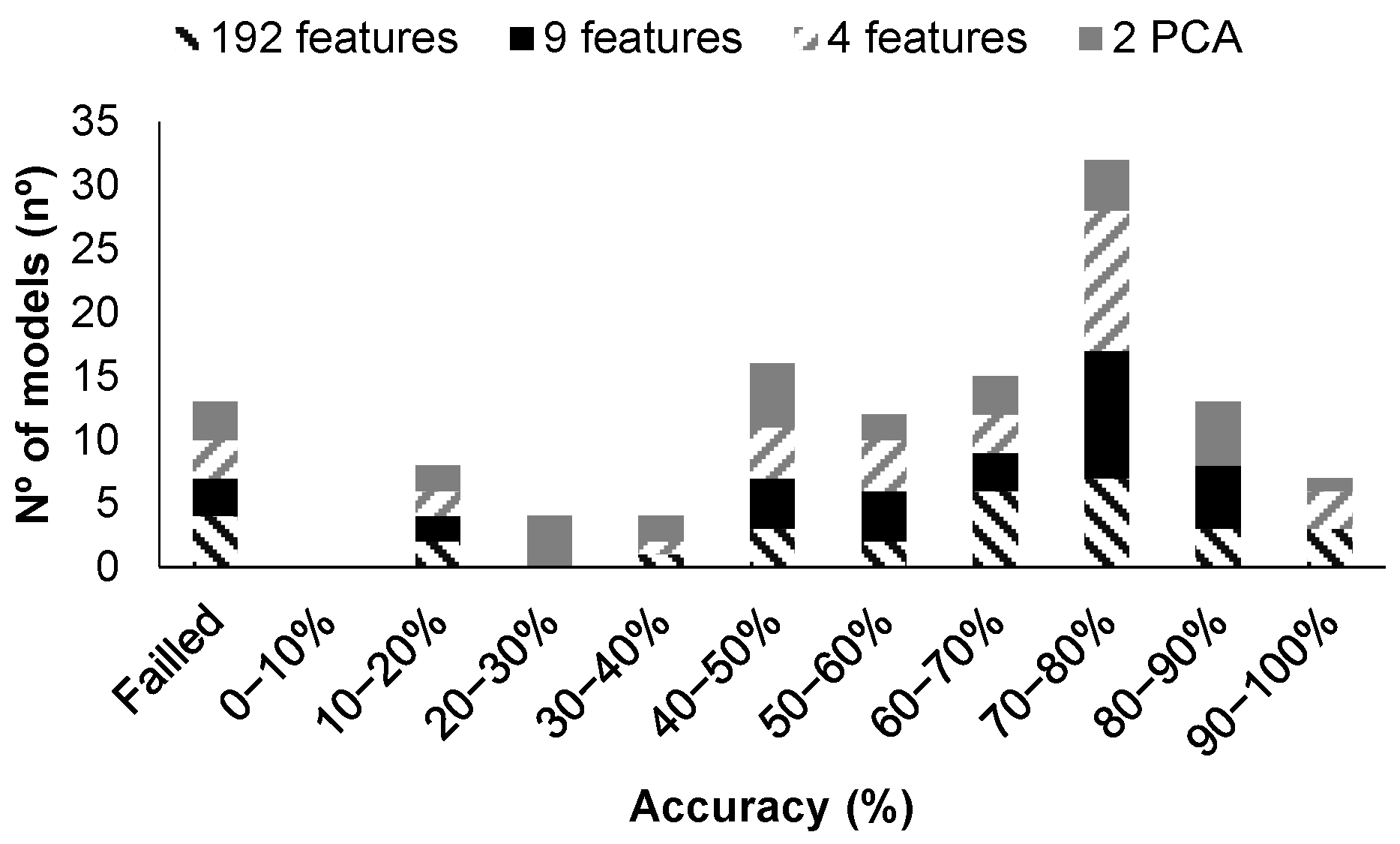
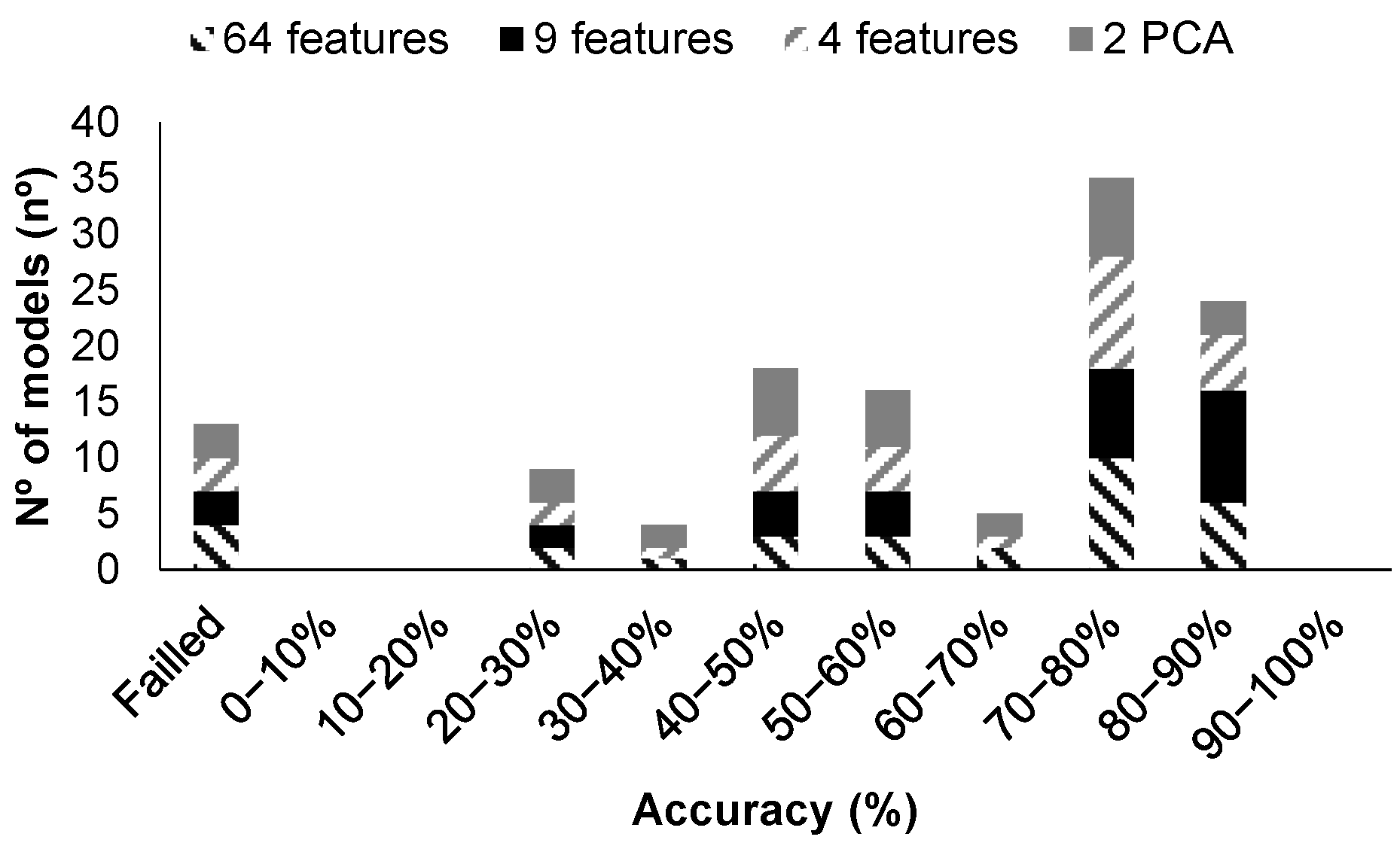
| Model Id | Averaged or All Data | Used Turbidity | Used Features | Turbidity of Misclassified Data Validation (NTUs) | Figure and Label | Accuracy Test (%) | Training Time (s) |
|---|---|---|---|---|---|---|---|
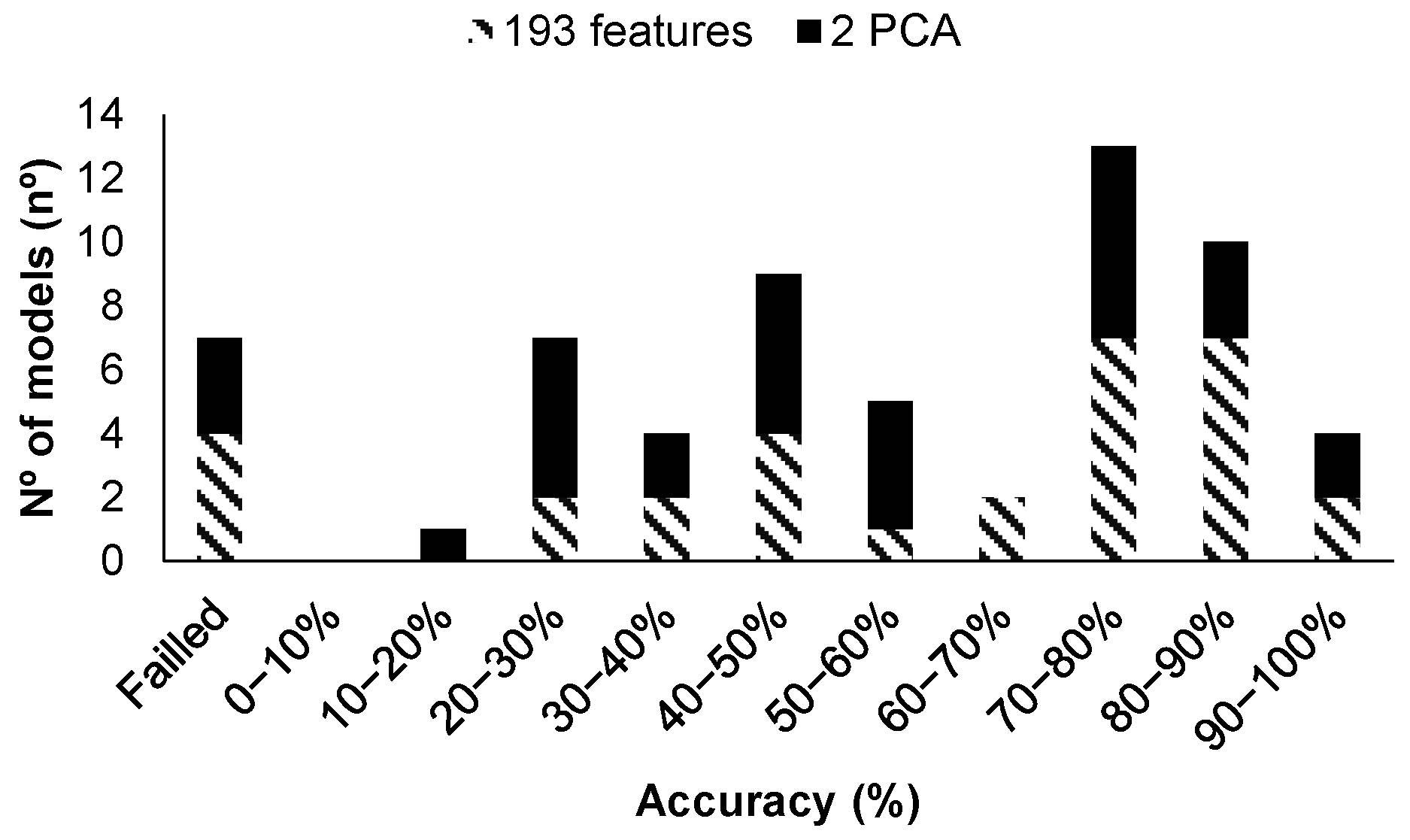
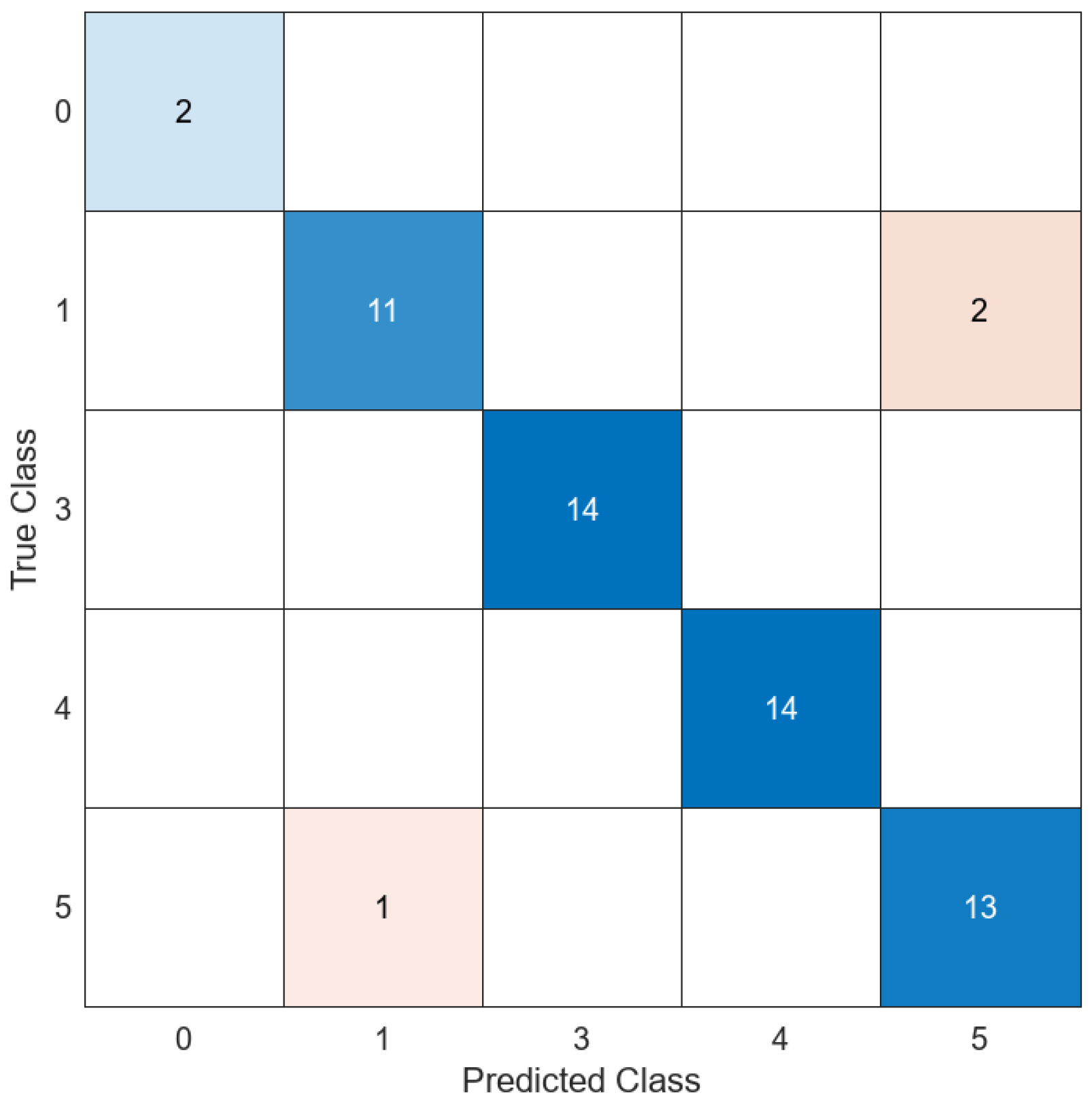
| 14 | All | No | 192 | <5 | Figure 16 | 83.33 | 1.6975015 |
| 21 | Averaged | No | 3 | <50 | Figure 17a | 100 | 2.545574 |
| 21 | Averaged | No | 64 PCA | <50 | Figure 17b | 100 | 3.1462531 |
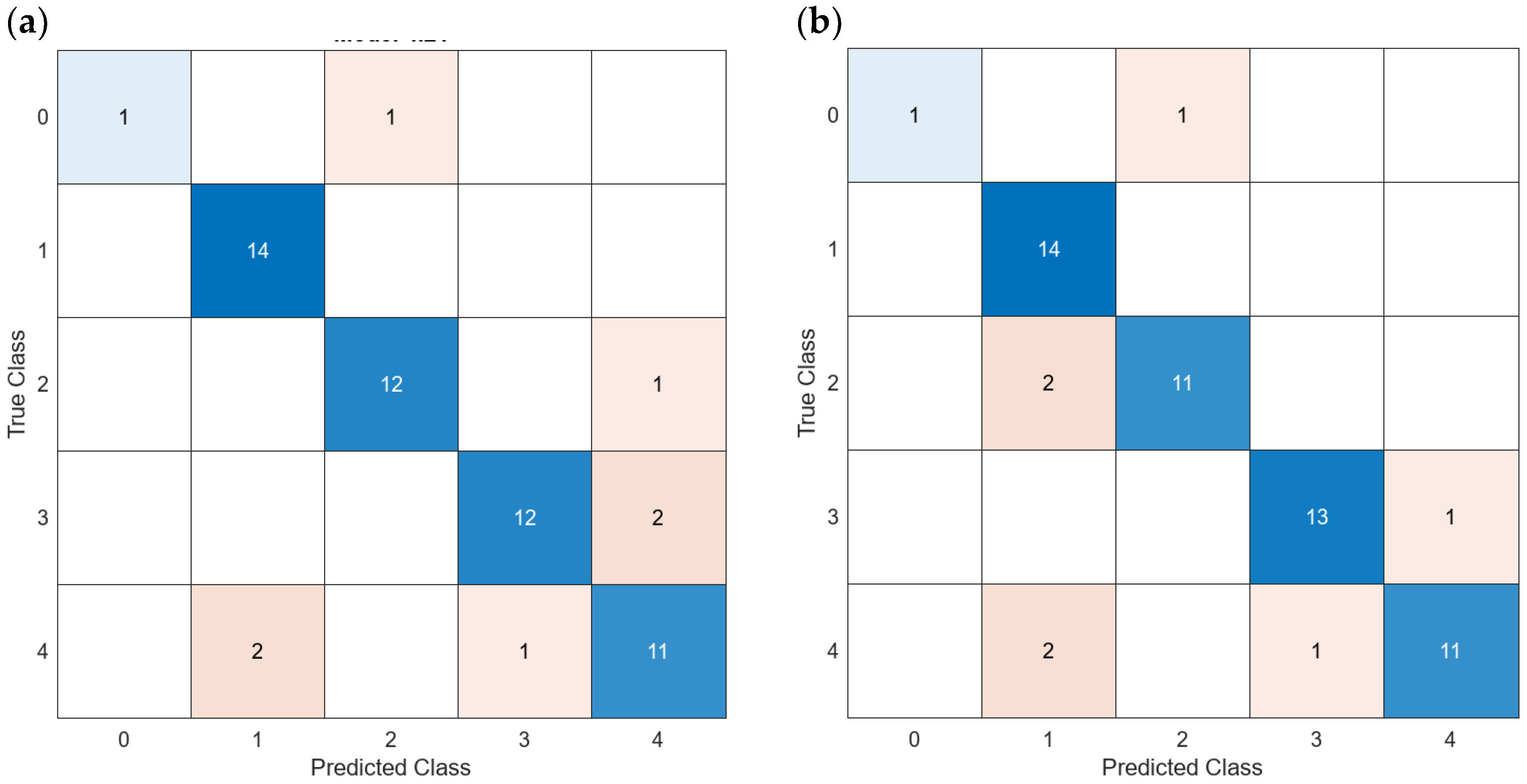
| 14 | All | Yes | 192 | 4.62 | Figure 18a | 100 | 2.6324913 |
| 23 | All | Yes | 192 | 4.62 | Figure 18b | 100 | 5.2588926 |
| 14 | All | Yes | 192 PCA | 4.62 | Figure 18c | 100 | 1.9605995 |
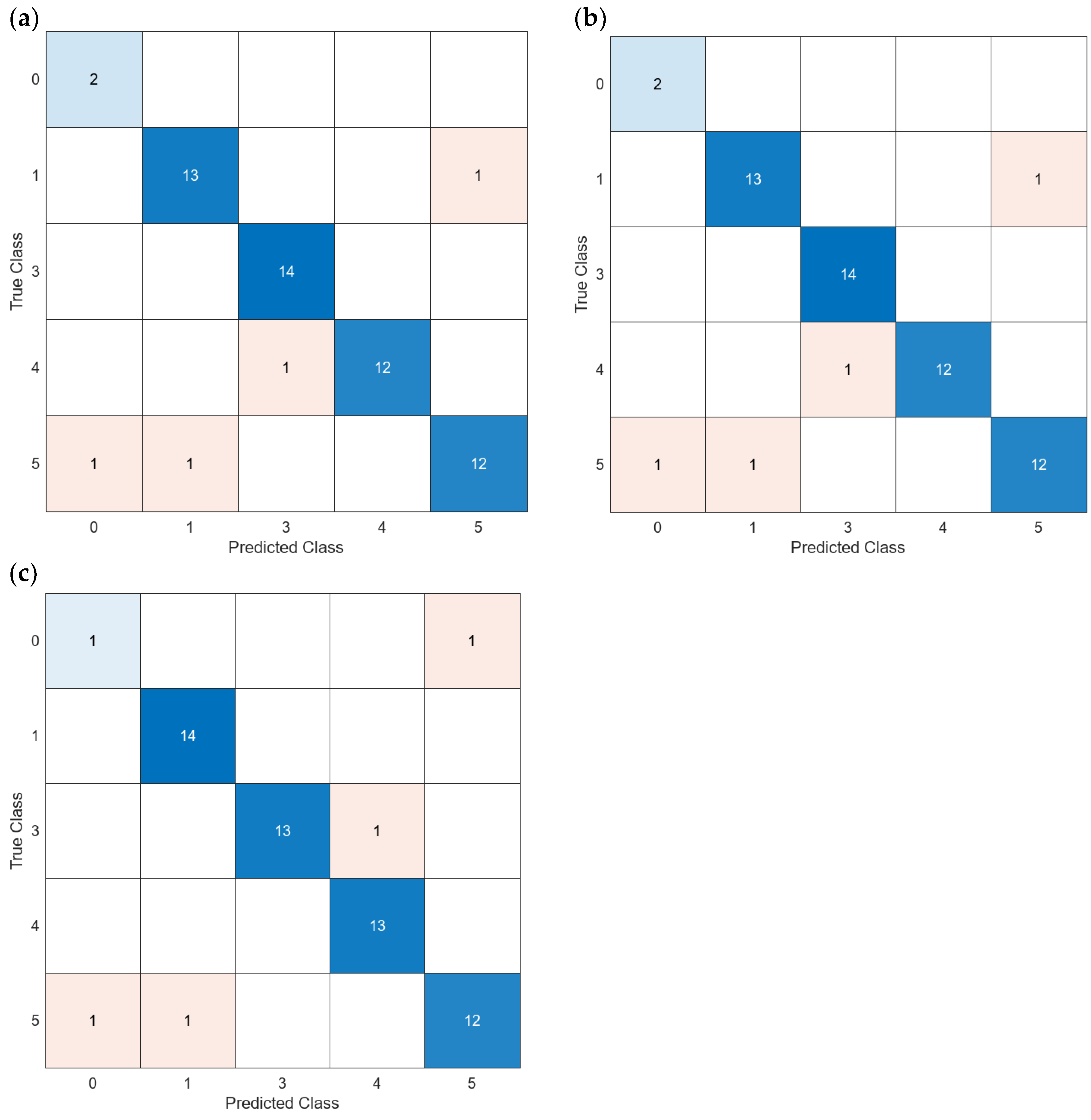
| 27 | Averaged | Yes | 65 | 11.36 | Figure 19a | 83.33 | 1.8494421 |
| 14 | Averaged | Yes | 65 PCA | 4.62 | Figure 19b | 100 | 1.1472791 |
| Year | Used Lights | Min. Max. Values (NTUS) | Samples < 5 NTU | Adjust Resistances | Regression Model | R2 | MAE (NTU) | MSE (%) | RMSE (%) | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|
| 2016 | Red LED | 10–85 | No | Simple Regression | 0.959 | 8.02 | [48] | |||
| 2018 | IR LED | 0–200 | No | Simple Regression | 10 | [30] | ||||
| 2019 | Cubert UHD 285 | 0–4 * | Yes | SVM + PCA | 0.902 | 0.2 | [49] | |||
| 2019 | IR LED | 0–80 * | No | Simple Regression | 0.943 | [50] | ||||
| 2020 | Visible IR light | 0–4000 | No | Yes | EMG | [25] | ||||
| 2022 | IR | 20–4000 | No | Simple Regression | 10 | 10 | [51] | |||
| 2023 | IR + RGB LED | 2.73–176.7 | Yes | Yes | NN | 0.983 | 2.85 | 7.45 | [29] | |
| 2024 | RGB LED | 0.2–60 | Yes | Yes | Exponential GPR + PCA | 0.979 | 0.68 | 0.47 | 0.55 | Proposed |
| Year | Used Lights | Nº of Classes | Classification Model | Accuracy (%) | Maximum Values Misclassified | Ref. |
|---|---|---|---|---|---|---|
| 2018 | IR + RGB | 4 Turbidity sources | Based on regression models and algorithms | - | [19] | |
| 2021 | IR + RGB | 2 Turbidity sources | Based on regression models and algorithms | - | [56] | |
| 2023 | IR + RGB | 2 Turbidity sources | NN | 90.9 | - | [29] |
| 2022 | Landsat 8 | 5 Levels of turbidity | Random Forest | 85 | - | [52] |
| 2023 | Sentinel 2 | 2 Levels of turbidity | Isolated Forest | 89.58 | [53] | |
| 2023 | Image in Laboratory | 5 Levels of turbidity | Deep Learning | 97.5 | [54] | |
| 2022 | Image in laboratory with different lights | 9 Levels or turbidity | CNN | 100 | [55] | |
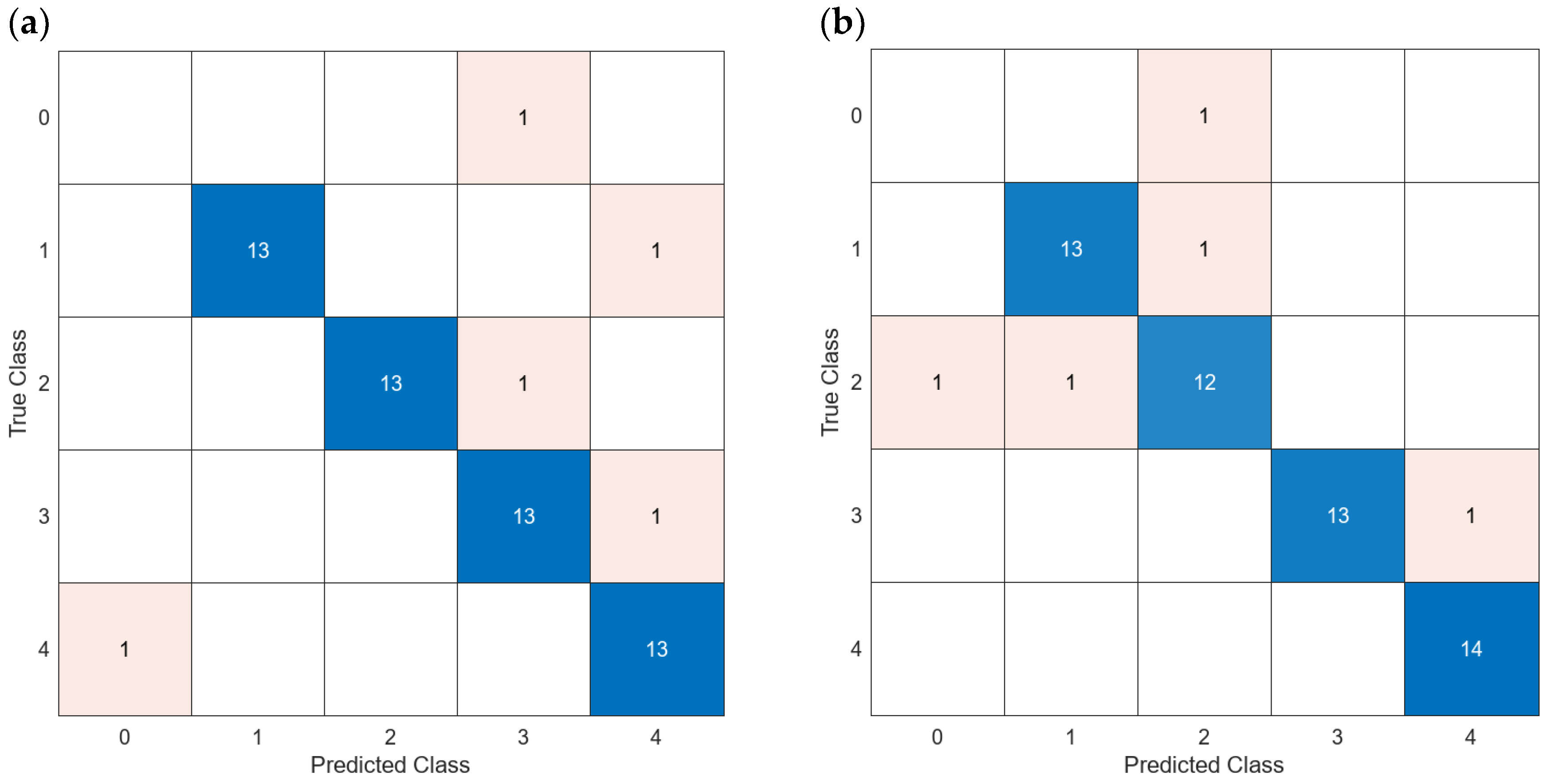
| 2024 | 64 visible lights | 4 Turbidity sources | Fine KNN | 91.23 | <5 NTUs | Proposal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors 2024, 12, 34. https://doi.org/10.3390/chemosensors12030034
Parra L, Ahmad A, Sendra S, Lloret J, Lorenz P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors. 2024; 12(3):34. https://doi.org/10.3390/chemosensors12030034
Chicago/Turabian StyleParra, Lorena, Ali Ahmad, Sandra Sendra, Jaime Lloret, and Pascal Lorenz. 2024. "Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity" Chemosensors 12, no. 3: 34. https://doi.org/10.3390/chemosensors12030034
APA StyleParra, L., Ahmad, A., Sendra, S., Lloret, J., & Lorenz, P. (2024). Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors, 12(3), 34. https://doi.org/10.3390/chemosensors12030034









