Abstract
We propose and discuss an effective tool for substance detection and identification using a broadband THz pulse that is based on frequency conversion near the substance absorption frequencies. With this aim, we analyze the evolution of spectral intensities at the doubled absorption frequencies in order to prove their similarity to those at which the absorption of THz pulse energy occurs. This analysis is provided for both artificial THz signals and the real signals reflected from the substances under consideration. We demonstrate the feasibility of the proposed approach in the detection and identification of substances with an inhomogeneous surface, which is the most difficult case for practice, by using the method of spectral dynamic analysis and integral correlation criteria.
1. Introduction
Terahertz time-domain spectroscopy (THz TDS) is a material analysis method which is currently widely applied for both basic research and security problems, as well as for industrial applications. It is well known that THz TDS is used for the detection and identification of explosives and dangerous substances [1,2,3,4,5,6,7,8]. It is currently considered as a powerful new tool for research in the chemical sciences and molecular structure investigations [9,10,11], biomedical and pharmaceutical applications [12,13], non-destructive control [14,15,16], and quality control in the agri-food industry [17,18,19].
As a rule, substance identification is carried out through the comparison of the absorption frequencies of the substance under investigation with those belonging to the database, containing absorption frequencies of the substances and measured in the THz frequency range. In the current study, this identification technique is referred to as the standard THz TDS method. While this technology has shown significant progress over the past decade, it has well-known disadvantages. For instance, if the substance under investigation is hidden under non-opaque covering (paper, plastic, cardboard, clothes, etc.), the packaging material can significantly attenuate and distort the spectrum of the transmitted or reflected THz signal [20,21]. The presence of water vapor absorption frequencies can also lead to errors when using THz TDS for the remote control of substances under real conditions [22,23]. The essential limitations of the standard THz TDS method were shown in [24,25].
THz TDS and THz spectroscopic imaging, together with different chemometrics methods, are currently widely used in chemistry, biochemistry, medicine and biology to determine the concentration of pharmaceutical or chemical ingredients in multi-component mixtures [26,27,28,29]. The partial least-squares (PLS) algorithms, principal component analysis (PCA), and support vector machine (SVM) are the most common methods used for the quantitative analysis of multi-component mixtures in transmission mode.
However, there are also several restrictions in the application of chemometrics methods for security screening in the THz frequency range under real conditions. First, these methods require a large number of samples (the so-called training set) for reliable quantitative analysis of the mixture. At the same time, processing multiple measurements decreases the performance of real-time security screening. Secondly, security screening in the THz frequency range is typically carried out in the reflection mode. However, in our knowledge, chemometrics methods deal with the THz signals measured in the transmission mode. As a rule, the spectrum of the main pulse (a pulse, which duration is approximately equal to that of the incident pulse) of the reflected THz signal contains much less pronounced absorption frequencies in comparison with the spectrum of the THz pulse transmitted through the substance. This circumstance also makes it difficult to identify the components of the mixture under real conditions using standard THz TDS methods together with chemometrics methods.
Another factor which can significantly complicate substance identification when using pulsed THz TDS under real conditions is the random inhomogeneities of the sample surface (its roughness or/and curvature), which lead to essential distortion of the spectrum of the THz pulse reflected from this sample [30,31,32,33]. To decrease these spectrum distortions, several methods were proposed in [30,31]. It was shown in [30] that the scattering effect caused by the rough surface can be significantly decreased by summing and averaging multiple measurements over a sample area (about 1800 realizations per 2 min). In [31], for the same purpose, the authors proposed increasing the number of viewing angles (about 900 realizations). It should be stressed that these techniques allow one to reliably identify only one absorption frequency with maximal spectral amplitude. Obviously, averaging over several hundred realizations decreases the performance of real-time security screening; moreover, absorption frequencies possessing smaller spectral amplitudes are not used in these techniques, which also decreases the accuracy and reliability of this method and limits its applicability under real conditions.
In [34,35], a new method was proposed for the detection and identification of a substance using THz TDS. It is based on the appearance of induced absorption frequencies in the substance spectrum due to the frequency up-conversion mechanism. However, this physical mechanism can also be accompanied by a negative feature. So, in [36] we showed that this mechanism can lead to the appearance of spurious absorption frequencies under the action of a broadband THz pulse. Nevertheless, this feature of the THz pulse’s interaction with a substance can be used with success for substance detection and its identification.
In the current study, we demonstrate for the first time the possibility of detecting and identifying dangerous substances based on doubling the absorption frequency when analyzing such a complex case as the reflection of a THz pulse from a sample with an inhomogeneous surface. Additionally, we show such a possibility when the substance under investigation does not demonstrate the presence of the absorption frequencies in the spectrum of the main reflected THz pulse with a duration about 10–15 ps. To achieve substance detection and its identification in this case, we use only one reflected THz pulse with a long duration (180–200 ps). The substance detection and identification are carried out on the basis of the joint application of the spectral dynamics analysis method (SDA-method) and the integral correlation criteria (ICC) [24,25,37,38].
For the illustration of the physical mechanism of appearance of the doubled absorption frequency (doubled frequency) corresponding to certain absorption frequency (basic frequency), belonging to the spectrum of the THz pulse transmitted through or reflected by a substance, we first carry out a simulation of the interaction of a broadband THz pulse with a substance. To this end, we consider the artificial signal, which consists of several sub-pulses that partially intersect. Our aim is to demonstrate the appearance of such a frequency in the spectrum of the artificial signal, transmitted through the optical thin layer of a medium with the quadratic susceptibility, and, more importantly, a high correlation between the time evolutions of the spectral amplitudes computed at the basic and doubled frequencies. For the same purpose, we consider another artificial signal with a structure without sub-pulses following the main pulse and with two minima in its spectrum. The results obtained during the simulation are very important because they demonstrate the possibility of using doubled absorption frequencies to detect and identify the substances instead of the absorption frequencies of a medium.
Then, we analyze the THz pulse, reflected from a tablet, containing the plastic explosive PWM C4, and possessing an inhomogeneous (rough and concave) surface. Let us note that, when conducting a security screening under real conditions, one may encounter various types of inhomogeneous surfaces, including rough and/or curved surfaces. A concave surface is a type of curved surface, and, unlike a rough surface, it is smooth and does not lead to the scattering of reflected THz radiation. However, concavity also distorts the spectrum of the reflected THz pulse, which makes substance identification difficult [37,38]. Therefore, in the current study, we consider both types of surface as common in real life.
We show that for both types of the inhomogeneous surface, the reflected THz pulse with long duration (about 180 ps) contains doubled absorption frequencies, which are observed in different time intervals—in the main pulse, and the first and the second sub-pulses. The identification of a PWM C4 sample with a rough surface is demonstrated using doubled absorption frequencies instead of basic ones.
It should be stressed that we do not perform multiple measurements over the sample surface as well as at various viewing angles. Earlier, in [37,38], we detected and identified substances with such a surface using only the absorption frequencies inherent in this substance. The proposed novel method substantially increases the probability of detecting and identifying a substance by increasing the number of used absorption frequencies (basic frequencies and doubled ones), and due to this fact the substance spectrum at high THz frequencies is distorted less than at low frequencies. Thus, the current study can be considered as a continuation of the research started in [36,37,38].
Another sample is a tablet containing the explosive HMX with a smooth surface. As is well-known, the spectrum of the HMX main pulse reflected from the tablet does not contain pronounced absorption frequencies. Therefore, the standard THz TDS method is ineffective in this case. Using the high similarity between the spectral line dynamics at the basic and doubled HMX absorption frequencies, it is possible to identify this substance.
We note that frequency doubling is widely used in non-linear radio locators (non-linear junction detectors, NLJD) for the detection of semiconductor elements [39,40,41,42,43]. The frequency range used in such locators is 400 MHz–1 GHz, and there are various commercially available devices—see, for example, [44]. Because we propose using a second harmonic generation of the THz pulse under its interaction with a medium, this approach therefore seems to be similar to a non-linear locator mentioned above, but in the THz range of frequencies.
This paper is arranged as follows. Section 2 briefly describes the physical mechanism of the doubled and additional emission/absorption frequencies appearing in the spectra of the artificial signals. In Section 3, we present the basic formulas for the SDA-method and integral correlation criteria. Section 4 describes the substance detection and identification on the base of the pulsed THz TDS operating in the reflection mode at doubled absorption frequencies. In Section 5, we briefly discuss the characteristics of proposed method for the detection of a substance. In Section 6, we formulate the main results of the paper.
The measurements for reflected THz signals PWM C4 and HMX_STF were obtained at the Military University of Technology (Warsaw, Poland). THz signals transmitted through the samples with pure RDX and HMX were measured at the Center for Terahertz Research, Rensselaer Polytechnic Institute (Troy, NY, USA).
2. Physical Mechanism of the Absorption Frequency Doubling for the Pulse with a Broadband Spectrum
In this section, we illustrate the appearance of the doubled absorption frequencies in the spectra of the broadband signals, which simulate a real broadband THz pulse transmitted through/reflected by the substance. Our aim is to show a high correlation (high similarity) between the spectral line dynamics computed at the basic and doubled frequencies for these artificial signals. This allows one to use the doubled frequencies for the detection and identification of substances instead of the spectral intensity evolution at true (basic) frequencies. We emphasize that the conclusion about whether the doubled absorption frequency is inherent in the substance or whether it is a spurious absorption frequency resulting from the frequency up-conversion process can be drawn using the scheme for providing physical experiments proposed in [36]. In Figure 1 we depict this scheme using dimensionless units for both axes.
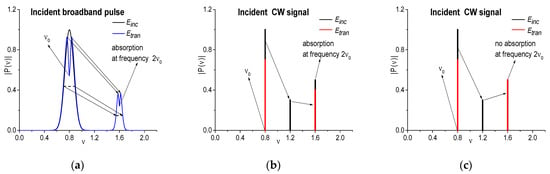
Figure 1.
Scheme of verification of the substance absorption frequencies observed under the action of the incident broadband THz pulse. The black line in (a) denotes the spectrum of the incident broadband THz pulse () and the blue line denotes the spectrum of the pulse ( ) transmitted through the substance: two spectral lines near the frequencies (basic absorption frequency) and (doubled absorption frequency). The black lines in (b,c) denote the spectrum of the incident THz CW radiation ( ) with scanned carrier frequency, and the red lines denote the spectrum of the THz CW radiation ( ) transmitted through the substance. In (b) the absorption at the frequency is present, and in (c) it is absent. The modulus of the spectral amplitude is denoted as .
Let us suppose that the frequency (basic frequency) is the absorption frequency of a medium. The incident THz pulse with a Gaussian shape and with the carrier frequency —the pulse shape is filled by oscillations of the electric field strength at this frequency (black line in Figure 1a)—falls on a medium. Because of the quadratic susceptibility of a medium, the spectrum of the electric field strength of the transmitted pulse contains a spectral line near the frequency (doubled absorption frequency) with a minimum at this frequency as well as the spectral line near the frequency (Figure 1a, blue line). A more explicit description of the pulse shape transform can be provided depending on the choice of the model of the medium. In particular, in [45], we developed the finite-difference scheme for the computer simulation of the THz pulse’s interaction with a medium whose response is described in the framework of density matrix formalism, and demonstrated some examples of the reflection and transmission of the THz pulse through a layer of the medium.
It should be emphasized that the spectra shown in Figure 1a were artificially constructed to illustrate the experimental scheme only. They were not obtained as a result of the Fourier transform of any real broadband THz signal. At the same time, the spectra were constructed in such a way that the total energy of the transmitted pulse coincides with the energy of the incident one. This means that the THz pulse energy absorbed by a medium is emitted in a different frequency range.
The observer will see the pulse spectrum similar to that in Figure 1a and identify two minima at the corresponding frequencies as the absorption frequencies of a medium. Our question refers to the doubled absorption frequency: is this absorption frequency inherent to a medium or does it appear due to the frequency up-conversion process? To answer this question, we need to apply narrowband THz CW radiation with scanned carrier frequency (black line in Figure 1b). If the absorption of the THz radiation occurs, then the spectral intensity of the transmitted THz CW radiation at the frequency has a lower value (red line in Figure 1b) than the spectral intensity of the incident THz radiation. When its carrier frequency coincides with the frequency , the spectral intensity of the THz radiation transmitted through a medium also has a lower value at this frequency (red line in Figure 1b) than the spectral intensity of the incident radiation (black line in Figure 1b). In this case, the doubled absorption frequency is a true absorption frequency of a medium. If the spectral intensity of the incident THz radiation at the frequency does not change after its transmission through a medium (black and red lines in Figure 1c), then the minimum at the doubled frequency in the spectrum of the transmitted broadband THz pulse (blue line in Figure 1a) is induced by the frequency doubling process, and it is a spurious frequency. Let us stress that the results of physical experiments provided in such a way for an aspirin tablet, a piece of soap, a paper sheet, a polyethylene bag, a chocolate bar and dangerous materials confirmed this phenomenon [36].
Let us briefly discuss the physical mechanisms of the doubled frequency appearance as well as some parameters, in particular the maximal electric field strength and dispersion of the first order susceptibility of a medium for the THz range of frequencies. In Figure 2, we depict schematically the electrical pulse action on a medium. We depict a well-known relationship between the electric displacement () vector and the electric field strength () vector for scalar wave (see, for example [46], p. 2). The induced polarization of a medium depends both linearly () and non-linearly () on the electric field strength. The constant of proportionality is known as the linear susceptibility. In turn, the quantity is known as the second-order non-linear optical susceptibility. They depend on the frequency at which the electric field strength acts on a medium.
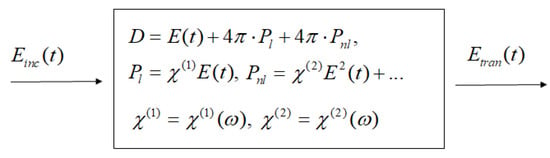
Figure 2.
Scheme of the THz pulse interaction with a substance. is the incident electric field strength, is the electric induction, is the electric field strength in a medium and is an electric field strength transmitted through a medium.
In the frameworks of Drude’s model, it is possible to write a dispersion law of the dielectric permittivity of a medium accounting for a two-level system ([47], p. 113):
where is the plasma frequency and is the resonance frequency, corresponding to the transition between two neighbor energy levels of an atom or molecule. The parameter characterizes the decay of harmonic oscillations (we consider a model of the harmonic oscillator). The frequency is a current frequency of the wave packet, and is the dielectric permittivity of a medium corresponding to the case . It should be stressed that the dielectric permittivity depends strongly on wave type. For example, the authors of [48] demonstrated the following dependence of the linear dielectric permittivity in the terahertz range of frequencies for the crystal of lithium niobate (): changes from 6.5 to 8 for the ordinary wave and from 4.95 to 5.1 for the extraordinary wave at changing frequency up to 2.8 THz. Thus, for the extraordinary wave, the dielectric permittivity dispersion is much less than that for the ordinary wave. One can expect similar dependences for other substances.
From Equation (1), the following expression with respect to the refractive index of a medium and its extinction coefficient can be written:
respectively, where is the carrier frequency detuning from the resonant frequency of a medium. Because the nonlinear response
of a medium at an action of the pulse with broadband spectrum is computed as
then we will see the spectrum of the pulse, transmitted through a medium as it is depicted in Figure 1a. Evidently, the spectral power near the doubled frequency depends on the second-order susceptibility and amplitude of the incident electric field strength.
More explicit expression for the dielectric permittivity can be obtained in the framework of the matrix density formalism. The response of a two-level system is governed by the Bloch equations [49]. If the population relaxation time is much less than the pulse duration , then the response of a medium can be expressed through the susceptibility of the two-level system [50]:
where is the dipole (polarization) relaxation time and are the densities of the lower and upper energy levels of the two-levels system, respectively. We see that the response of a medium near resonant frequency (both Expressions (1) and (5)) depends on both the corresponding relaxation time and the frequency detuning.
As follows from [50], if the carrier frequency of the incident electric field does not coincide with the resonant frequency, then the propagation of the laser pulse is governed by the Ginzburg–Landau equation. In the case under consideration, it should be expected that the propagation of parts of the THz pulse will also be governed by this equation.
We also used matrix density formalism to obtain a description of the broadband THz pulse interaction with the multi-level medium [45,51]. The THz pulse propagation is governed by Maxwell’s equations. The maximal electric field strength was equal to , slightly greater than this value. Other parameters of this interaction were given in these papers. It should be stressed that in [52], the authors explored the maximal electric field strength of the THz pulse equal to and they observed an effect associated with cubic susceptibility, which is many orders less than the quadratic susceptibility of a medium. Increasing the maximal value of the electric field strength of the THz pulse was presented in [53], and one can expect that this value will be further increased, as was demonstrated in [54]. In this paper, the authors reported reaching an electric field strength exceeding .
As is well-known regarding non-linear optics, the second harmonic generation (and others frequency conversion processes also) can been observed on the surface of a crystal that possesses even third-order susceptibility (this means that this crystal has a centrosymmetric structure). Such a bulk crystal cannot be used for frequency doubling if this crystal is used in the transmission mode under THz pulse action. Therefore, the quadratic susceptibility of a solid explored in reflection mode will always occur, and the frequency doubling will occur for a coherent source of the THz radiation. Its efficiency depends on the THz pulse’s maximal intensity. However, there is another physical mechanism of the frequency up-conversion of the broadband THz pulse that was described in [45,51]. Because the THz pulse interacts with a medium by exploring vibration energy levels of molecules (gaseous medium) or phonons (solid), the difference between the energy levels is many times less than that for electronic levels. Therefore, the broadband THz pulse excites a few energy levels, as one can see in various physical experiments. In turn, the THz pulse can excite high energy levels due to the cascade mechanism, and the emission frequencies from these energy levels lie far from the spectrum of the incident pulse. Among these frequencies may be the frequencies which are doubled with respect to the absorption frequencies of a substance. This mechanism of frequency conversion does not depend on the quadratic susceptibility of a medium, but rather it depends on the spectrum width of the pulse. In practice, both physical mechanisms can occur simultaneously. Because the energy efficiency of the frequency conversion is not of interest for us (we need to observe enough high intensity of the radiation at the doubled frequency), we expect that an efficiency of about 0.1% (or potentially less) will be enough to observe radiation at the doubled frequency if the system of detection operates in the reflection mode. It should be kept in mind also that the doubled frequencies, which are of interest for the problem of the detection and identification of substances, lie outside of the incident pulse spectrum. Therefore, to observe them, it is necessary only that their spectral intensity is greater than the noise intensity, which essentially decreases the requirements for the efficiency of the process of frequency doubling.
To illustrate a possible method for using doubled frequencies for the detection and identification of the substances, we first consider the artificial signal that transmutes a medium possessing a quadratic nonlinear response. Assuming its instantaneous response and using dimensionless variables, we can express a simplified relation, which can be applied to achieve our aim, between the incident electric field strength and the electric field strength transmitted through a layer of a medium:
where is the dimensionless strength of the electric field of the pulse transmitted through a medium and written in the so-called approximation of the optical thin layer. denotes the dimensionless strength of the electric field of the incident pulse. For brevity, we use the previous notations for the electric field strength. The dimensionless parameter characterizes the quadratic susceptibility of a medium, where , are physical parameters; in particular, a value of is equal to the maximal electric field strength. For definiteness, below we choose its value equal to: = 1.0, 0.1, 0.01 and 0.001. We note that if we consider the frequency doubling, then its value depends also on the length of a medium, the pulse duration and the radius of the THz beam. As follows from non-linear optics for the optical pulse, the corresponding value of the coupling coefficient can be both greater than unity and less then unity. Obviously, this parameter influences the response of a medium: with an increase in its value, the doubled frequencies will have greater brightness.
2.1. The Doubled Emission Frequencies
In this section, we simulate the frequency doubling of the incident broadband artificial THz pulse :
with a medium in the framework of the optical thin layer. We will call each of the terms in Equation (7) the sub-pulses. Here, represents the amplitudes, denotes the center position and is the half-width of the sub-pulses, . The carrier frequencies are equal to: , , , , respectively. We will call them the basic frequencies. It should be stressed that the time coordinate , the frequency and the amplitude are dimensionless variables in Section 2. In Table 1, the parameters of the artificial signal are shown.

Table 1.
Parameters of the artificial signal [36].
As one can see, this signal consists of intersecting sub-pulses, three of which possess narrow spectra (they do not overlap each other), and one has a broad spectrum. The spectra of sub-pulses partially with overlap each other. The spectrum contains four spectral maxima at the basic frequencies ν = 0.8, 1.2, 1.4, 1.8. We stress that such a signal is similar to a real broadband THz pulse reflected by a substance. As is well-known, it consists of the main pulse, reflected from the outer surface of the sample, and several sub-pulses following it due to the multi-reflection from the inner surfaces of the sample.
The signals , and their Fourier spectra are shown in Figure 3a–d. In the spectrum of the signal Figure 3d, one can see the maxima at the doubled basic frequencies ν = 1.6, 2.4, 2.8, 3.6. Let us note that the spectrum Figure 3d also contains the spectral peaks at the frequencies 0.4, 0.6, 2.2, 3.2, which can be represented as linear combinations of the basic frequencies: ν = 0.4 = 1.2 − 0.8 = 1.8 − 1.4; ν = 0.6 = 1.8 − 1.2; ν = 2.2 = 1.4 + 0.8; ν = 3.2 = 1.2 + 1.8. Additionally, in Figure 3d, one can see the frequencies located near the zero-value frequency. Thus, we observe a rectification of the THz signal, and the corresponding frequencies, the appearance of which is caused by the THz pulse’s shape, belong to the GHz and MHz range of frequencies. They may be used as a new range of frequencies for the identification and detection of substances using the THz pulse, increasing the probability of the detection and true identification of a substance. Obviously, it is necessary that the substance possesses quadratic susceptibility, and the THz pulse intensity must be enough to allow the appearance of such a response. Another remark refers to analyzing this phenomenon for the THz signal reflected by or transmitted through the substance. As is known, the properties of the sample surface and the bulk sample are different [47,54,55]. In the THz frequency range, the influence of an inhomogeneous surface on the spectral characteristics of a substance, as well as the differences between them and the spectral characteristics of the bulk sample, are considered, for example, in [31,32].
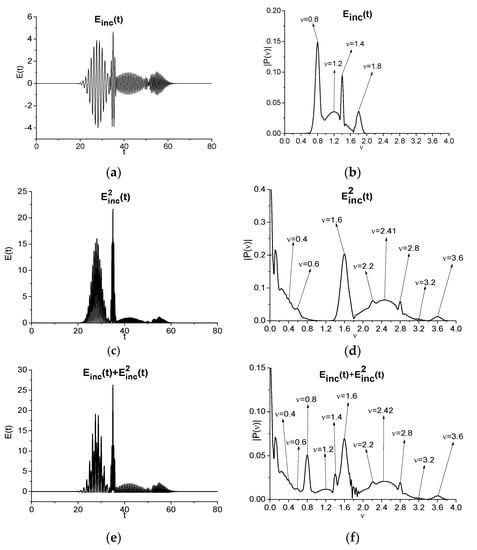
Figure 3.
Artificial signals (a), (c) and their Fourier spectra (b,d); normalized (Equation (8)) signal ) with parameter = 1.0 (e) and its spectrum (f).
Therefore, this can lead to observing the quadratic effects only for one of these schemes of the THz pulse interaction with a substance.
Figure 3e,f show the transmitted signal and its spectrum with parameter . We see that the spectral maxima of the transmitted signal coincide with the spectral maxima of the corresponding signals in Figure 3b and in Figure 3d. Below, we will analyze the evolution of the time-dependent spectral amplitudes (spectral line dynamics) at the basic and doubled frequencies for the signals and . The correlation between these spectral intensities is of most interest for us.
We notice that when depicting the spectrum in Figure 3f, a normalization of the energy of the transmitted signal is performed in such a way that its total energy coincides with the energy of the incident signal . This can be achieved in the following way. Let us denote by the energy of the incident signal, and by the energy of the transmitted signal. These are computed as follows:
Then, the normalization is carried out as follows:
Here, is the maximal value of the time coordinate up to which the signal is specified. In Section 2.1 and Section 2.2, we choose its value equal to = 100.
Unlike [36], our aim is to show the high degree of similarity between the evolutions of the spectral amplitudes at the basic and doubled frequencies. The evolution of the spectral amplitudes , (their computation is described in [24,25]) at the frequencies ν = (0.8, 1.6), (1.2, 2.4), (1.4, 1.8), (1.8, 3.6) is depicted in Figure 4a–d, respectively. We see that the shapes of these spectral dynamics are very similar. This follows also from the analysis of the corresponding correlation coefficients between them, which are close to unity: = 0.969, 0.915, 0.904, 0.889 (Figure 4a–d). The correlation coefficients are computed using the expression:
where and are the average values of the sets of spectral amplitudes and , respectively, . Parameter is a number of time moments, and it depends on the construction parameters of the dynamics—the window length T and its shift Δ along the signal . Continuing the research started in [37,38], we take these parameter values as T = 2.8 and Δ = 0.2 dimensionless units.
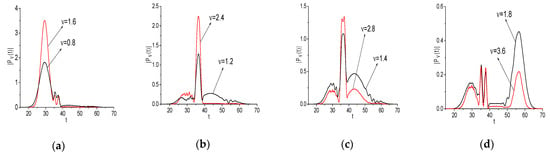
Figure 4.
Evolution of the spectral amplitude modulus , at the basic and doubled frequencies ν = (0.8, 1.6) (a), (1.2, 2.4) (b), (1.4, 1.8) (c), (1.8, 3.6) (d). Black lines correspond to the signal , red lined – to the signal [36].
In Figure 4, it can be seen at that the evolution of the spectral amplitude modulus at the doubled frequencies (red lines) and that at the basic frequencies (black lines) are similar to each other. Because in this figure we depict the spectral intensity of the signal without accounting for both the value of the parameter , which defines a real amplitude of such an intensity, and the normalization of the full energy of the pulse and , we see that in Figure 4a–c the spectral brightness at the doubled frequency is higher than that at the basic frequency (black lines). Therefore, the observed relationship between the frequency evolutions is only for illustration. Let us note that for a verification of the computation for the spectral lines, we showed in [36] that the integral intensity of the spectral intensity dynamics at the chosen frequency computed for the time interval is equal to the spectral brightness of the spectrum computed for this time interval.
In Figure 4b, one can see that the intensity of the spectral line dynamics at the doubled frequency = 2.4 (signal ) is significantly lower in comparison with that at the frequency = 1.2 (signal ) in the time interval t = [40, 50]. We argue that this is a consequence of both the decrease in the second pulse belonging to the signal (compare Figure 3a,c) and the broadening of the spectrum for this signal (Figure 3b,d).
In Figure 5, the spectrum of the signal (8) computed with = 0.1 is presented in the frequency ranges = [0.2, 4.0] Figure 5a and = [2.0, 4.0] Figure 5b (magnified view). We can see that the doubled frequencies and a linear combination of the basic frequencies are presented in Figure 5a,b in the same way as they are observed in Figure 3c. A section of the doubled frequencies is more pronounced in Figure 5.
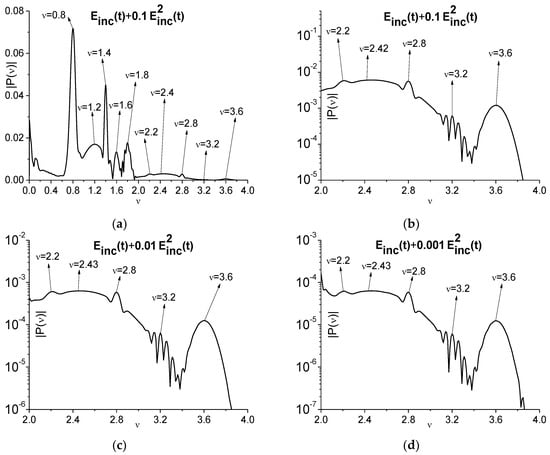
Figure 5.
Fourier spectrum of the signal with =0.1 (a,b) and 0.01 (c), 0.001 (d) in the frequency ranges = [0.2, 4]. (a), and [2.0, 4.0] (b–d).
The spectrum of the signal computed with = 0.01 and 0.001 is shown in the frequency range = [2.0, 4.0] in Figure 5c,d, respectively. The spectral maxima at the frequencies = 2.2, 2.43, 2.8, 3.2, 3.6 are preserved in the transmitted spectrum at a decreasing value of .
The evolutions of the spectral amplitude modulus , at the frequencies ν = (0.8, 1.6), (1.2, 2.4), (1.4, 1.8), (1.8, 3.6) depicted in Figure 6a–d (black and red lines, respectively) for = 0.1 show a high correlation: the correlation coefficients are also close to unity. The same result is valid for = 0.01 and 0.001.
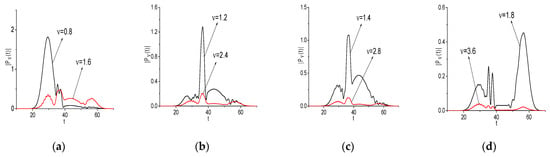
Figure 6.
Evolution of the spectral amplitudes modulus at the basic and doubled frequencies ν = (0.8, 1.6) (a), (1.2, 2.4) (b), (1.4, 1.8) (c), (1.8, 3.6) (d) with = 0.1. Black lines correspond to the signal , red lined—to the signal .
Thus, a high degree of similarity between the evolution of the spectral amplitudes at the basic and doubled emission frequencies is shown for different values of = 1.0, 0.1, 0.01 and 0.001.
2.2. The Doubled Absorption Frequencies
In this section, we consider an artificial signal with a structure not containing sub-pulses following the main pulse, and its spectrum contains two spectral minima at the frequencies = 0.5, 0.8 (Figure 7a,b, respectively). The spectra of the signals and are depicted in Figure 7c,d. These spectra contain minima at the frequencies, which correspond to the linear combinations of the basic frequencies: = 0.2 = 0.5 × 2 − 0.8, = 1.4 = 0.5 × 2 + 0.8/2, = 1.8 = 0.5 × 2 + 0.8. In each of the linear combinations, the doubled frequency = 0.5 × 2 is present. However, this doubled absorption frequency is not observed in Figure 7d, because at this frequency there is a large spectral intensity in the pulse spectrum. At the same time, in Figure 7c,d, one can also see the appearance of the spectral maximum at the doubled basic frequency = 1.6 = 0.8 × 2, which corresponds to the substance emission at this frequency. It should be noted that more explicit computation of the signal is based on the spectral representation of the incident signal; then it is necessary to multiply the spectral harmonics, and then the result must be transformed in the time domain.
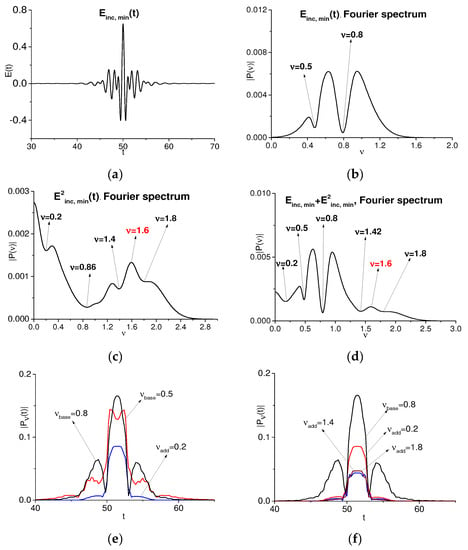
Figure 7.
Artificial signal (a), its spectrum (b), and the spectra of the signals (c), , = 1 (d); the spectral lines dynamics at the basic frequencies = 0.5, 0.8 and additional frequencies = 0.2 (e), 0.2, 1.4, 1.8 (f) [36].
The spectral line dynamics computed at the basic frequencies = 0.5, 0.8 and at the additional frequencies = 0.2, 1.4, 1.8 are depicted in Figure 7e,f, and one can see high similarity between the spectral line dynamics at these frequencies and that computed for a frequency of 0.8. This means that a frequency of 0.8 is involved in the appearance of the additional frequencies. A frequency of 0.5 is also involved in this process, as we can see in Figure 7e,f, where the additional spectral lines appear in the time interval when both spectral dynamics are large enough. The corresponding correlation coefficients are shown in Table 2. As we can see, all of them are greater than 0.9.

Table 2.
Correlation coefficients between the spectral line dynamics at the basic frequency and the linear combinations of the basic frequencies .
A similar computation was performed for the parameter = 0.1. For convenience, in Figure 8, the spectrum of the signal is depicted in the linear Figure 8a and logarithmic Figure 8b scale. One can see that the linear combination of the basic frequencies resulting in = 0.2 does not appear in the spectrum of the signal . In turn, the doubled basic frequency = 1.6 = 0.8 × 2 as well as the linear combinations of the frequencies: = 1.42 (close to 1.4) and 1.8 are preserved in Figure 8a,b. The corresponding correlation coefficients between the evolutions of the spectral amplitudes at the basic and doubled/additional frequencies are close to unity, which confirms our conclusion about their generation. It should be noted that spectra in Figure 7 and Figure 8 are normalized in accordance with Equation (8).
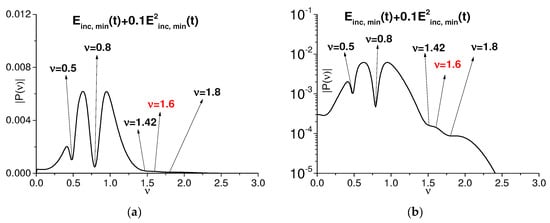
Figure 8.
Fourier spectrum of the signal at = 0.1 in the linear (a) and logarithmic scale along the abscissa axis (b).
Thus, we see that in certain cases, it is necessary to increase the amplitude of the incident THz pulse to observe an action of the quadratic susceptibility on the spectrum of the pulse transmitted through a substance. Below we show that these frequencies can be used for the detection and identification of substances, instead of the absorption frequencies of a medium.
3. SDA Method and Integral Correlation Criteria
Since for the substance detection and its identification based on using the doubled absorption frequency of the substance, we apply the SDA-method and ICC, below we briefly repeat the corresponding formulas.
Let us denote the discrete set of the spectral amplitude modulus at a chosen frequency for the standard transmitted signal belonging to a database as , The corresponding set of the spectral amplitude modulus at the frequency of the reflected (or transmitted) THz signal under investigation is denoted as , . Its part, which contains components and begins at the time moment , is denoted as . The formulas for the computation of the spectral line (or spectral intensity) dynamics can be found, for example, in [24]. Parameters and depend on the parameters for the Fourier–Gabor transform—the window length T and its shift Δ along the signal. Below we assign these parameters values of T = 2.8 ps and Δ = 0.2 ps, respectively.
Both sets, and , must be averaged at each of the time moments to avoid the influence of constant components of sets and on correlation coefficient. Moving the set along the set , we get at each time moment the correlation coefficient
where
which is used for the computation of the integral correlation criteria (ICC)
or
Here, and are the weight coefficients. For example, they can be chosen to be equal to units () or to be , , or and , which is equal to inverse values of the spectal brightness at the corresponding frequencies. The last two pairs of weight coefficients take into account the substance absorbance at these frequencies. We also apply in identification a modification of the ICC Equation (12):
In Equation (13), we use only one weight coefficient, , accounting for the spectral brightness of the standard signal. This allows us to increase algorithm performance and decrease the influence of the random fluctuation of the THz signal.
Let us note that the frequency is considered to be detected in the spectrum of the signal under investigation, if the corresponding ICC value computed for the pair of the frequencies (,), where frequency is the absorption frequency belonging to a spectrum of the standard signal from a database, is greater than the values of all other ICC for the signal frequencies belonging to the frequency detection range (FDR). The boundaries of the FDR are the frequencies of the spectral maxima located near the spectral minimum under consideration . In turn, the frequency is not considered to be detected if there is at least one frequency (where belongs to the FDR, and ) for which the ICC line computed for the pair of frequencies (, ) lies below the ICC line computed for the pair (, ).
4. Substance Detection and Identification in the Reflection Mode Based on Using Doubled Absorption Frequencies
Below we study the manifestations of the frequency doubling in the THz pulse reflected from the sample with an inhomogeneous surface, and show the possibility of substance detection and identification using the doubled absorption frequencies. Let us note that below, time and the frequency are the physical variables, and they are measured in picoseconds (ps) and in terahertz (THz), respectively. In this section and henceforth, the values of are written in a dimensionless form, as is usually provided in the literature [47].
4.1. THz Signal Reflected from the Tablet with a Rough Surface
As an example of a sample with a rough surface, we consider a tablet containing the plastic explosive PWM C4, which is a mixture of RDX and plasticizer in the ratio 9:1. For a better understanding, we briefly describe the corresponding physical experiments [37,38], in which the Teraview 3000 setup in the reflection mode of its configuration [56] was used. The 600 mg sample was located at a distance of 30 cm from the detector. The measurements were performed in a dry air environment with a relative humidity less than 2%; therefore, the influence of the water vapor absorption was absent.
The THz signal reflected from the tablet with PWM C4 had a duration of about 180 ps. For brevity, we denote it as the PWM_40 signal, which is shown in Figure 9a. Its structure is clearly seen—the reflected THz signal contains the pronounced main pulse reflected from the outer surface of the sample, and several sub-pulses appearing due to multiple reflection from the inner surfaces of the tablet. The main pulse and the pronounced sub-pulses , and are shown in the time intervals t = [0, 30] ps, [35, 65] ps, [65, 95] ps and [140, 160] ps (Figure 9b–e, respectively). As the sub-pulse we chose a remote part of the PWM_40 signal with sub-pulse features—a higher amplitude of oscillations over a short time interval compared to the adjacent parts of the pulse. This part of the PWM_40 signal is located in the time interval t = [140, 160] ps in Figure 9e, and its structure is similar to the second sub-pulse.
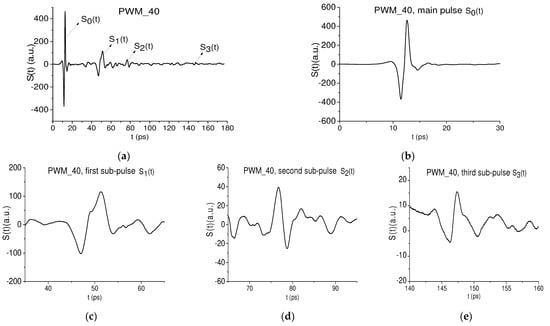
Figure 9.
THz signal PWM_40 reflected from the rough surface and depicted in the time intervals t = [0, 180] ps (a), t = [0, 30] ps (b), [35, 65] ps (c), [65, 95] ps (d), and [140, 160] ps (e).
It is worth noting that the sub-pulses Figure 9c and Figure 9e have the same phase as the main pulse Figure 9b. At the same time, the sub-pulse Figure 9d demonstrates the inversion of its phase in comparison with the main pulse .
4.1.1. Observing Doubled Absorption Frequency Belonging to the Main Pulse, t = [0, 25] ps
As a rule, the main pulse of the reflected THz signal is only used in the standard THz TDS. Therefore, at first, we analyze the spectrum of the PWM_40 main pulse and demonstrate the presence of the doubled absorption frequencies in the high frequency range ν > 3.0 THz. In Figure 10a,b this spectrum and the reference spectrum are depicted in the frequency range ν = [0, 2.5] THz. The pronounced RDX absorption frequencies are absent in Figure 10a. One can see only one weak minimum at the frequency ν = 0.88 THz, while the minimum at the doubled frequency ν = 1.76 = 2 × 0.88 THz is absent in the spectrum Figure 10a. Let us recall that according to [2,3], the main absorption frequencies of RDX, measured in the transmission mode, are the following: ν = 0.82, 1.05, 1.50 (1.54), 1.95 (1.96), 2.19 (2.20), 3.08 (3.0) THz.
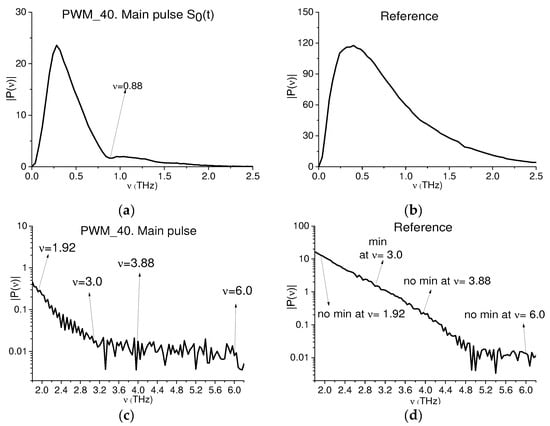
Figure 10.
Fourier spectrum of the PWM_40 main pulse (a,c) and reference spectrum (b,d) in the frequency ranges ν = [0.0, 2.5] THz (a,b) and [1.8, 6.2] THz (c,d). The spectral amplitudes in (c,d) are shown in the logarithmic scale, and the spectral resolution in (a–d) is equal to Δν = 0.04 THz.
Essentially, in Figure 10b, the spectral minima corresponding to the water vapor absorption frequencies belonging to the frequency range ν = [0.1, 2.0] THz [22,23] are absent, which confirms the absence of water vapor during the measuring.
For convenience, in Figure 10c,d, the corresponding Fourier spectra are shown in the frequency range ν = [1.8, 6.2] THz in the logarithmic scale. We see that the spectrum Figure 10c contains minima at the frequencies ν = 1.92, 3.0 THz, which are close to the well-known absorption frequencies of RDX ν = 1.95, 3.08 THz ([2,3]), and at the frequencies ν = 3.88, 6.0 THz, which are close to the doubled frequencies ν = 1.92 × 2, 3.0 × 2 THz. Accounting for the spectral resolution of the computation, this demonstrates good coincidence. It is important that the spectral minima at the frequencies ν = 1.92, 3.88, 6.0 THz are absent in the reference spectrum. However, it contains a weak spectral minimum at the frequency ν = 3.0 THz (Figure 10d). Because water vapor absorption was absent when providing the measurements, the appearance of a spectral minimum at this frequency in the reference spectrum (Figure 10d) may be caused by noise and the influence of the surface’s inhomogeneity. Thus, the spectral minimum at the frequency ν = 3.0 THz in the PWM_40 spectrum Figure 10c is also not caused by water vapor absorption, and it could be the absorption frequency of the substance RDX. In Section 4.1.4, we show how to verify the spectral minimum of interest as the absorption frequency of the substance RDX by means of the ICC Equation (13).
The minima appearance at the frequencies ν = 3.88, 6.0 THz in the spectrum Figure 10a may be caused by the frequency doubling process. To verify this assumption, in Figure 11a–d, the PWM_40 spectral line dynamics at the frequencies ν = 1.92, 3.88 THz and ν =3.0 THz, 6.0 THz are shown in the time interval t = [5, 25] ps. One can see a high similarity between the evolutions of spectral intensity at the frequencies ν = 1.92, 3.88 THz Figure 11a,b and ν = 3.0, 6.0 THz Figure 11c,d.
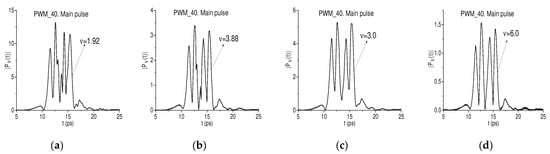
Figure 11.
Time-dependent evolution of the PWM_40 amplitude modulus at the frequencies ν = 1.92 THz (a), 3.88 THz (b), 3.0 THz (c), 6.0 THz (d) in the time interval t = [5, 25] ps. The window shift Δ = 0.05.
It should be stressed that the structure of the spectral dynamics depends on the size of the time window T and its shift Δ. If the dynamics’ structure is complex, it is necessary to change these parameters in order to reveal characteristic features of the dynamics. In this case, (Figure 11), we reduced the window shift from Δ = 0.2 ps up to Δ = 0.05 ps. This allowed us to detect the difference in the shapes of the dynamics. One can see that the spectral dynamics at the frequencies ν = 1.92, 3.88 THz in Figure 11a,b differ from those in Figure 11c,d—they have two additional maxima in the time interval t = [12.5, 14.6] ps.
Moreover, the generation of the doubled absorption frequencies occurs in other time intervals. This is easily seen in Figure 12a, in which the correlation coefficient between the long PWM_40 spectral line dynamics at the frequency ν = 1.92 THz and the short spectral line dynamics, computed for the PWM_40 main pulse at the doubled frequency ν = 3.88 THz, is depicted (we will denote this frequency pair as ν = (1.92, 3.88). THz). To obtain the correlation coefficient , we shift the short spectral line dynamics at the doubled frequency ν = 3.88 THz along the spectral line dynamics computed in the long time interval t = [0, 180] ps at the basic frequency ν = 1.92 THz. In Figure 12b, a similar computation is shown for the frequency pair ν = (3.0, 6.0) THz. One can see in Figure 12a,b that the pronounced maxima of the correlation coefficients (0.986 and 0.99, respectively) are achieved in the time interval t = [0, 20] ps, corresponding to the main pulse of the reflected THz signal PWM_40.
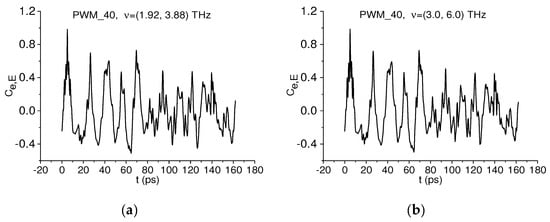
Figure 12.
Correlation coefficient between the PWM_40 spectral line dynamics computed for the frequency pairs ν = (1.92, 3.88) THz (a), (3.0, 6.0) THz (b).
Thus, in the spectrum of the PWM_40 main pulse, the presence of two pairs with doubled absorption frequencies ν = (1.92, 3.88) THz and (3.0, 6.0) THz is demonstrated. Both doubled absorption frequencies ν = 3.88, 6.0 THz lie in the high frequency range of the spectrum: ν > 3.0 THz.
4.1.2. Finding Doubled Absorption Frequency Belonging to the First Sub-Pulse, t = [40, 65] ps
As we mentioned above, the standard THz-TDS method does not consider the sub-pulses following the main pulse. However, they also contain information about the absorption frequencies of the substance. With this aim, below we analyze the first sub-pulse of the PWM_40 signal in the time interval t = [40, 65] ps and demonstrate the existence of three pairs containing the basic absorption frequency ν and its doubled frequency 2ν.
In Figure 13a,b, the Fourier spectra of PWM_40 first sub-pulse and reference are shown in the frequency range ν = [1.8, 6.2] THz using the logarithmic scale. We see in Figure 13a the minima at the frequencies ν = 1.92, 2.2, 3.0 THz, which are close to the well-known RDX absorption frequencies ν = 1.95, 2.2, 3.0 THz [2,3]. The spectrum Figure 13a also contains the minima at the frequencies ν = 3.88, 4.4, 6.04 THz, which are close to the doubled absorption frequencies mentioned above. Since the spectral minima at all of these frequencies are absent in the reference spectrum Figure 13b, the appearance of the minima at the frequencies ν = 3.88, 4.4, 6.04 THz in Figure 13a may therefore be caused by the frequency doubling. Below, in Section 4.1.4, we verify this assumption. Obviously, the data in Figure 13 are rather noisy due to the influence of the tablet surface and the small spectral amplitudes of the incident THz signal in this frequency range.
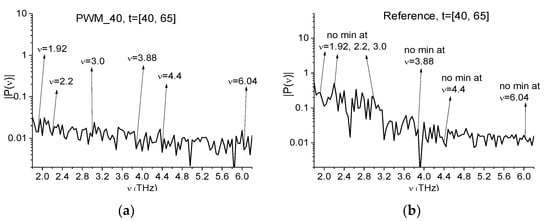
Figure 13.
Fourier spectra of the PWM_40 first sub-pulse (a) and reference (b) in the frequency range ν = [1.8, 6.2] THz in the logarithmic scale along the abscissa axis.
In Figure 14a–c the time-dependent evolution of the spectral amplitude modulus is shown at the basic frequencies ν = 1.92, 2.2, 3.0 THz; and in Figure 14d–f—at the doubled frequencies ν = 3.88, 4.4, 6.04 THz, respectively, in the time interval t = [40, 65] ps. One can see that the shapes of the corresponding spectral line dynamics Figure 14a,d, Figure 14b,e, and Figure 14c,f are very similar to each other.
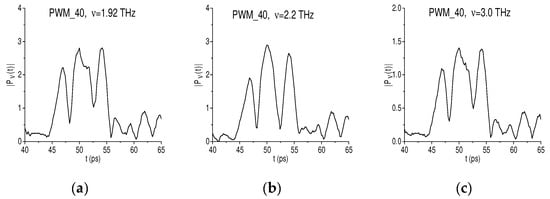
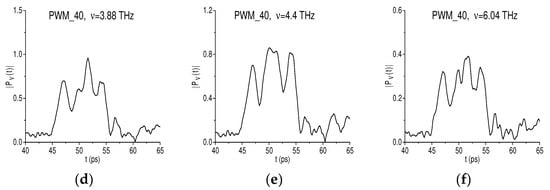
Figure 14.
Time-dependent evolution of the spectral amplitude modulus of the PWM_40 signal at the frequencies ν = 1.92 THz (a), 2.2 (b), 3.0 THz (c), 3.88 THz (d), 4.4 THz (e), and 6.04 THz (f) in the time interval t = [40, 65] ps.
This conclusion is confirmed by the correlation coefficient between the PWM_40 dynamics evolution computed for the frequency pairs ν = (1.92, 3.88) THz, (2.2, 4.4) THz and (3.0, 6.04) THz. The pronounced maxima of the correlation coefficients are achieved in the time interval t = [30, 60] ps, which corresponds to the first sub-pulse, and they are equal to 0.907, 0.941 and 0.936, respectively.
Thus, the presence of doubled absorption frequencies ν = 3.88, 4.0, 6.0 THz is shown in the first sub-pulse of the PWM_40 signal. All of them lie in the high-frequency range of the spectrum: ν > 3.0 THz.
4.1.3. Observing Doubled Absorption Frequency in the Time Intervals after the First Sub-Pulse
The doubled absorption frequency can be also observed in the time intervals t = [70, 95] ps and [140, 160] ps, containing the second and third sub-pulses of the PWM_40 signal. Figure 15a,b shows the Fourier spectra of the second sub-pulse (t = [70, 95] ps) and reference spectrum belonging to the frequency range ν = [1.8, 6.2] THz. For convenience, the spectrum Figure 15b is shown in the logarithmic scale.
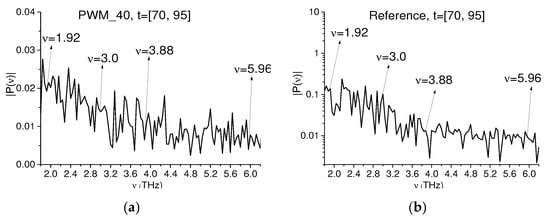
Figure 15.
Fourier spectra of the PWM_40 s-sub-pulse in a linear scale (a) and reference spectrum in a logarithmic scale (b) in the time interval t = [70, 95] ps.
The spectrum Figure 15a contains the spectral minima at the frequencies ν = 1.92, 3.0 THz and ν = 3.88, 5.96 THz, which are close to the doubled frequencies ν = 1.92 × 2, 3.0 × 2 THz. It should be noted that the differences in the minima values of the spectra for the first and the second sub-pulses can be caused by the phase inversion of the second sub-pulse (see Figure 9c,d), because it leads to changing pulse spectrum. Since the spectral minima at the frequencies ν = 1.92, 3.0, 3.88, 5.96 THz are absent in the reference spectrum Figure 15b, these spectral minima may therefore be caused by the absorption frequency doubling.
We emphasize that the spectral line dynamics computed in the time interval t = [70, 95] ps for the frequencies ν = 1.92 THz (a), 3.88 THz (b) are similar. As in the previous cases, the pronounced maxima of the corresponding correlation coefficients are achieved in the time interval t = [70, 95] ps, and they are equal to a value of = 0.86 for the pair of frequencies ν = (1.92, 3.88) THz and = 0.56 for the pair ν = (3.0, 5.96) THz. Thus, in the spectrum of the PWM_40 s sub-pulse, one can also see the presence of the doubled absorption frequencies ν = 3.88, 5.96 THz. Analysis of the third sub-pulse spectrum shows the absence of the spectral minima at the frequencies ν = 1.92, 3.0 THz.
It is important to note that for the reliable detection and identification of a substance, we recommend using a value of the correlation coefficient which is greater than 0.9, and it has to be computed for two different time intervals containing the main pulse and sub-pulse or two sub-pulses. A correlation coefficient value less than 0.9 but more than 0.5 can be used as an additional criterion for detection. The lower value of the correlation coefficient for the second sub-pulse can be caused by the inversion of the absolute phase of this sub-pulse. As a consequence, the spectrum of this sub-pulse differs from the spectra of other pulses (the main one and the sub-pulses).
Finally, we see that for the time-dependent spectral intensities computed at the doubled absorption frequencies in time intervals corresponding to the main pulse, the first and the second sub-pulses have similar shapes and can be used for the detection and identification of the substance. The simultaneous use of all these pulses increases the probability of substance detection and its identification.
4.1.4. Detection of the PWM C4 Substance with a Rough Surface Using a Doubled Absorption Frequency in Different Time Intervals
Below we show how one can detect the PWM C4 substance with a rough surface using the doubled absorption frequency of the THz signal PWM_40 and the basic absorption frequency of the standard THz signal RDX_Air [24] by means of the ICC Equation (13). The RDX_Air signal was measured in the transmission mode using the tablet containing 10% pure RDX and 90% PE in ambient air. We stress that the measurements were performed at 22 °C and a relative humidity of about 30%, and the distance between the sample and detector was about 20 cm. The absorption frequencies of the RDX_Air signal are in a good agreement with the frequencies given in [2,3], and are used below for the detection and identification.
As we can see above, the THz signal under investigation as well as its spectrum are noisy, which leads to additional difficulties for identification. In this connection, we note that in [57] we discussed an effective method for the detection and identification of a dangerous substance using a highly noisy THz signal. We showed that the SDA method together with several types of ICCs allow us to localize the useful signal in the noisy THz signal and to detect the absorption frequencies of a dangerous substance in this part of the signal even for SNR up to a value of 1.005. The verification was carried out for a real highly noisy THz signal transmitted through a substance MA. In this section, we demonstrate in the same way how one can detect the PWM C4 substance with a rough surface using the doubled absorption frequency ν = 3.88 THz and the basic absorption frequency ν = 1.92 THz of the standard signal RDX_Air.
The spectrum of the RDX_Air standard signal is depicted in Figure 16a, and the corresponding spectral line dynamics computed at the frequency ν = 1.92 THz is shown in Figure 16b. As mentioned above, the frequency ν = 3.88 THz is found in the main pulse and the first and second sub-pulses (the corresponding time intervals are t = [0, 25], [40, 65], [70, 95] ps), respectively. We will use this frequency instead of the PWM_40 basic absorption frequency ν = 1.92 THz (Figure 9, Figure 13 and Figure 15) in the detection of the substance RDX in the PWM C4 sample. For this aim, we compute three spectral line dynamics of the PWM_40 signal in these time intervals. In order to compute the values of the ICC , we shift the standard RDX_Air spectral line dynamics (Figure 16b) to the PWM_40 spectral line dynamics in each of the time intervals.
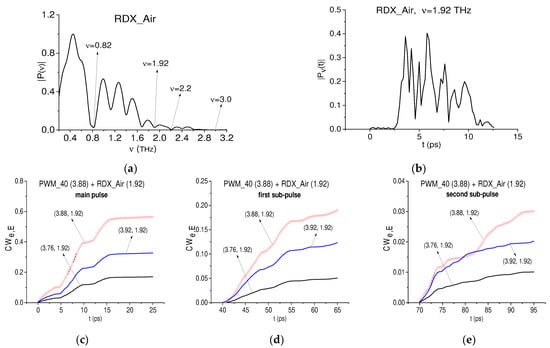
Figure 16.
Fourier spectrum of the standard THz signal RDX_Air (a) and spectral line dynamics at the frequency ν = 1.92 THz (b). Evolution of the ICC computed for the PWM_40 spectral line dynamics at the doubled absorption frequency ν = 3.88 THz and the standard RDX_Air spectral line dynamics at the frequency ν = 1.92 THz in the time intervals t = [0, 25] ps (c), [40, 65] ps (d), [70, 95] ps (e).
The evolution of the corresponding ICC is shown in the time intervals t = [0, 25] ps, [40, 65] ps and [70, 95] ps (Figure 16c–e, respectively). The FDR (see Section 3) is common for all three time intervals, and is equal to ν = [3.76, 3.92] THz. In all cases, we see pronounced integral correlation between the spectral line dynamics of PWM_40 and RDX_Air signals for the frequency pair ν = (3.88, 1.92) THz. The ICC lines corresponding to this pair lie above all ICC lines, computed for the pairs = (, 1.92) THz within the selected FDR, where ≠ 3.88, and it belongs to the FDR. According to the detection rule (Section 3), the frequency ν = 3.88 THz is detected as the RDX absorption frequency in the PWM_40 signal.
We stress that the doubled frequency ν = 6.0 ± 0.04 THz can be used for substance detection in the same way. In turn, the pair ν = (2.2, 4.4) THz can be used for the detection of RDX in the first sub-pulse only.
4.2. THz Signal Reflected from the Sample with Concave Surface
In this section, we analyze the THz signal reflected from the PWM_C4 tablet with a smooth concave surface. The curvature radius of the surface is 1.5 mm. By analogy with the case of the rough surface, we denote this THz signal as the PWM_1.5 signal, and it is shown in Figure 17a. The magnified view of the main pulse and the first sub-pulse is presented in Figure 17b,c. As mentioned above, the first sub-pulse Figure 17c also demonstrates the inversion of the phase in comparison with the main pulse Figure 17b. The reference signal is the same as for the PWM_40 THz signal.
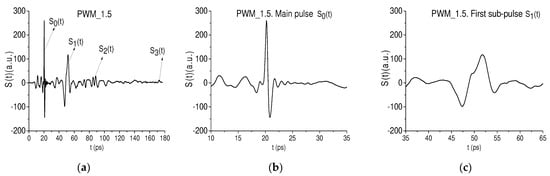
Figure 17.
THz signal PWM_1.5 reflected from the concave surface in the time intervals t = [0, 180] ps (a), t = [10, 35] ps (b), and [35, 65] ps (c).
4.2.1. Observing the Doubled Absorption Frequency in the Main Pulse (Concave Surface)
Figure 18a,b shows the Fourier spectrum of the PWM_1.5 main pulse, computed in the time interval t = [10, 35] ps, in the frequency ranges ν = [0, 2.5] THz in the linear scale and [2.5, 6.25] THz in the logarithmic scale. As above, the corresponding spectral resolution is equal to Δν = 0.04 THz. We see that the absorption frequencies of RDX (or close to them) ν = 0.82 ± 0.04, 1.05 ± 0.04, 1.5 ± 0.04, 1.92 ± 0.04, 2.2 ± 0.04 THz [2,3] as well as at the frequency ν = 1.16 THz are absent in Figure 18a. This is a consequence of the influence of the inhomogeneous surface on the spectrum of the THz pulse reflected by this surface. At the same time, in Figure 18b, one can see two spectral minima at the frequencies ν = 3.04, 6.08 THz, which are close to the RDX absorption frequency ν = 3.0 THz and its doubled frequency ν = 6.0 THz. Let us recall that in Section 4.1, we showed the absence of water vapor absorption frequencies in the range ν = [0.1, 2.5] THz belonging to the reference spectrum. Thus, the spectral minimum at the frequency ν = 6.08 THz may be caused by the absorption frequency doubling in the PWM_1.5 main pulse.
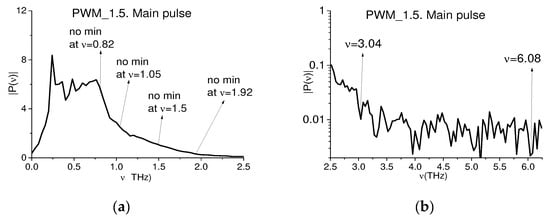
Figure 18.
Fourier spectrum of the main pulse of the concave PWM_1.5 signal in the frequency ranges ν = [0, 2.5] THz in the linear scale (a) and [2.5, 6.25] THz in the logarithmic scale (b).
Figure 19a,b demonstrates a time-dependent evolution of the PWM_1.5 spectral amplitude modulus at the basic absorption frequency ν = 3.04 THz and its doubled frequency ν = 6.08 THz. The correlation coefficient between the long PWM_1.5 spectral line dynamics at the basic frequency ν = 3.04 THz and the corresponding short dynamics at the doubled frequency ν = 6.08 THz (the frequency pair is ν = (3.04, 6.08) THz) is depicted in Figure 19c. We see that its maximal value is equal to = 0.98, and it is achieved in the time interval t = [0, 25] ps containing the PWM_1.5 main pulse. There is also high similarity between the spectral line dynamics at the doubled frequency ν = 6.08 THz and at the basic absorption frequency ν = 3.04 THz.
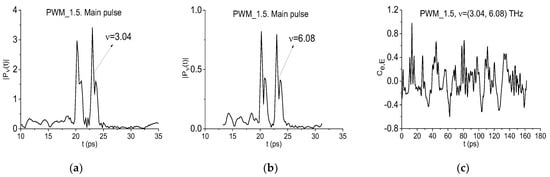
Figure 19.
Time-dependent evolution of the PWM_1.5 intensity at the frequencies ν = 3.04 THz (a) and 6.08 THz (b) in the time interval t = [10, 35] ps. Correlation coefficient between the PWM_1.5 dynamics for the frequency pair ν = (3.04, 6.08) THz (c).
Let us note that in contrast to the case of the rough surface, only one pair containing the base absorption frequency and the spectral minimum at the doubled frequency is found in the spectrum of the PWM_1.5 main pulse. Thus, different types of surface inhomogeneity have different effects on the appearance of the doubled absorption frequencies in the spectrum of the main pulse.
4.2.2. Observing Doubled Absorption Frequency in the First Sub-Pulse (Concave Surface)
In this section, we study the presence of doubled absorption frequency in the first sub-pulse and demonstrate the existence of three pairs of frequencies, which correspond to the basic absorption frequencies ν and the doubled frequencies 2ν.
With this aim, Figure 20a,b shows the Fourier spectrum of the PWM_1.5 first sub-pulse in the linear scale and the reference spectrum in the logarithmic scale in the frequency range ν = [1.8, 6.2] THz. Both spectra are computed in the time interval t = [40, 65] ps.
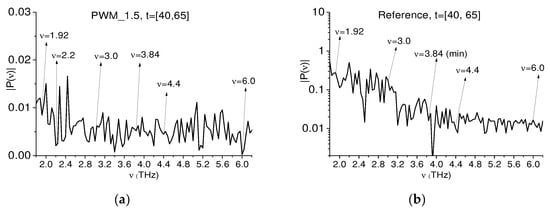
Figure 20.
Spectra of the PWM_1.5 first sub-pulse (a) and reference in the logarithmic scale (b) computed in the time interval t = [40, 65] ps in the frequency range ν = [1.8, 6.2] THz.
In the spectrum Figure 20a, one can see three spectral minima at the frequencies ν = 1.92, 2.2, 3.0 THz that are close or equal to the absorption frequencies of the substance RDX ν = 1.95, 2.2, 3.0 THz, respectively [2,3]. It also contains three spectral minima at the doubled frequencies ν = 3.84, 4.4, 6.0 THz. In turn, in the reference spectrum Figure 20b, one can see that this frequency is located near the weak spectral minimum at the frequency ν = 3.84 THz. Since the measurements were obtained in a dry atmosphere, this minimum is not caused by water vapor absorption. Consequently, this minimum appears because of noise or the math operation. Therefore, the PWM_1.5 spectrum minimum at the frequency ν = 3.84 THz (also as at the frequencies ν = 4.4, 6.0 THz) may occur because of the absorption frequencies doubling.
As above, we compute the correlation coefficient between the long PWM_1.5 spectral line dynamics at the basic frequencies ν = 1.92, 2.2, 3.0 THz and the corresponding short dynamics at the doubled frequencies ν = 3.84, 4.4, 6.0 THz, which are obtained in the time interval t = [40, 65] ps. The pronounced maxima of the correlation coefficient are achieved in the time interval t = [40, 65] ps, and they are equal to = 0.86, 0.996, 0.81 for the pairs ν = (1.92, 3.88) THz, (2.2, 4.4) THz, (3.0, 6.0) THz, respectively. All three spectral line dynamics at the doubled frequencies ν = 3.0, 4.4, 6.0 THz demonstrate high similarity with the corresponding spectral dynamics at the basic absorption frequencies ν = 1.92, 2.2, 3.0 THz, respectively. Therefore, three doubled absorption frequencies are present in the spectrum of the PWM_1.5 first sub-pulse.
4.2.3. Observing Doubled Absorption Frequency in the Time Intervals after the First Sub-Pulse (Concave Surface)
In the same way, it is possible to demonstrate the presence of two frequency pairs containing doubled absorption frequencies in the spectrum of the second and third sub-pulses of the PWM_1.5 signal located in the time intervals t = [70, 95] ps and [160, 185] ps, see Figure 21a,b, respectively. They are ν = (1.96, 3.96) THz and (3.04, 6.04) THz for the second sub-pulse and ν = (1.96, 3.92) THz and (3.0, 6.04) THz for the third sub-pulse. The correlation coefficient and integral correlation computed for the frequency pairs ν = (1.96, 3.96 ± 0.04) THz and ν = (3.0 ± 0.04, 6.0 ± 0.04) THz confirm the presence of the doubled absorption frequency in the reflected THz signal PWM_1.5 in these time intervals.
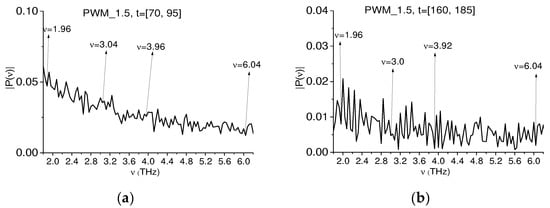
Figure 21.
Fourier spectra of the PWM_1.5 s (a) and third (b) sub-pulses in the time intervals t = [70, 95] ps (a), [160, 185] ps (b), respectively.
Thus, despite the differences in the types of surface inhomogeneity in the samples PWM_40 and PWM_1.5, in the spectrum of the main pulse, the first and second sub-pulses of the corresponding THz signals, the doubled absorption frequencies were found, and it was shown that they can be used to identify these substances. If the tablet has a concave surface, then even the third sub-pulse can be used to identify the substance, because its spectrum also contains doubled absorption frequencies. This fact increases the reliability of the identification of PWM C4 with a concave surface.
4.3. Observing Doubled Absorption Frequencies in the THz Pulse Reflected from the Substance HMX
Below we present another example of observing doubled absorption frequency in the reflected THz signal. For this purpose, we use the tablet with containing HMX in a mixture with plasticizer at a ratio of 9:1. The weight of the tablet is 800 mg, and its surface is smooth. We denote it as HMX_STF, for brevity. As seen for the THz signals PWM_40 and PWM_1.5, the measurements were performed in a dry air environment with a relative humidity less than 2%. Note that earlier in [51], the detection and identification of HMX in reflection mode were carried out using the basic absorption frequencies of the substance on the basis of the joint application of the SDA method and several types of ICCs. We showed that it is possible to detect and identify HMX without using the main pulse.
In Figure 22a, the reflected THz signal HMX_STF is presented in the long-time interval t = [0, 180] ps. It also contains the main pulse Figure 22b and the pronounced first sub-pulse Figure 22c, which has an inverted phase in comparison with the main pulse.
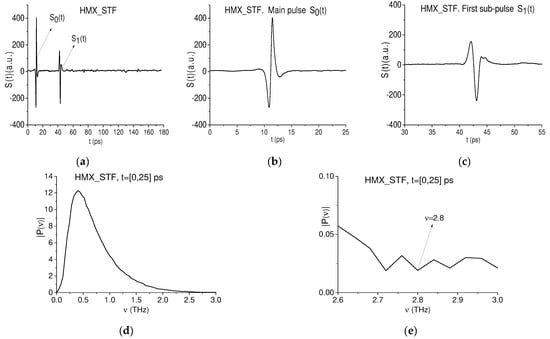
Figure 22.
Reflected THz signal HMX_STF (a) [51] in the long-time interval t = [0, 180] ps; the main pulse in the time interval t = [0, 25] ps (b); the first sub-pulse in the time interval t = [30, 55] ps (c). Fourier spectrum of the HMX_STF main pulse in the frequency ν = [0.0, 3.0] THz (d), [2.6, 3.0] THz (e).
In accordance with [2,3], HMX has the following absorption frequencies: ν = 1.78, 2.51, 2.82 THz in the frequency range ν < 3 THz. The first two of these are absent in the Fourier spectrum of the HMX_STF main pulse (Figure 22d). However, the third one at the frequency ν = 2.8 THz is present (see Figure 22e). The spectral minima, which are close to the doubled absorption frequency ν = 2∙2.8 THz, are also absent in the main pulse spectrum. Thus, frequency doubling is not observed in the HMX_STF main pulse. Nevertheless, the first sub-pulse contains information about absorption frequencies of the reflected THz signal HMX_STF, and below we investigate its Fourier spectrum.
The Fourier spectrum of the first sub-pulse located in the time interval t = [30, 70] ps is shown in Figure 23a,b in the frequency ranges ν = [1.6, 3.0] THz and [3.2, 6.0] THz, respectively. We see the spectral minima at the frequencies ν = 1.75, 2.5, 2.83 THz Figure 23a and at the frequencies ν = 3.5, 4.95, 5.65 THz Figure 23b, which are close to the doubled absorption frequencies. The spectral minima in the reference spectrum Figure 23c are absent for ν = 4.95, 5.65 THz, but a very weak spectral minimum is present at the frequency ν = 3.5 THz, which may be caused by noise. Thus, the HMX_STF spectral minima at the frequencies ν = 3.5, 4.95, 5.65 THz Figure 23b may be the doubled absorption frequencies.
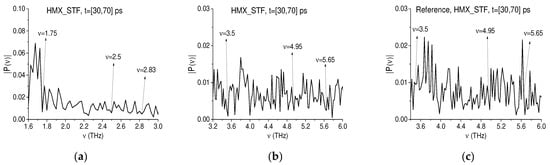
Figure 23.
Fourier spectrum of the HMX_STF first sub-pulse in the frequency ranges ν = [1.6, 3.0] THz (a) and [3.2, 6.0] THz (b). The reference spectrum is depicted in the frequency range ν = [3.2, 6.0] THz (c).
In Figure 24a–c, the spectral line dynamics are shown at the basic absorption frequencies ν = 1.75, 2.5, 2.83 THz and in Figure 24d–f they are shown at the doubled absorption frequencies ν = 3.5, 4.95, 5.65 THz, respectively. These figures demonstrate their high similarity.
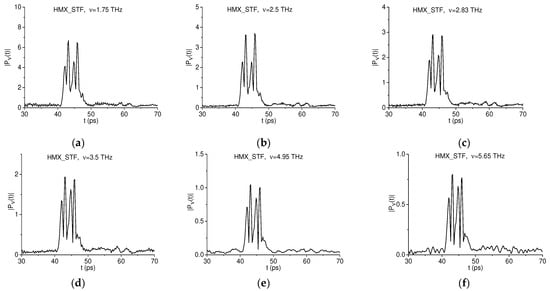
Figure 24.
Time-dependent evolution of the HMX_STF spectral amplitudes at the frequencies ν = 1.75 THz (a), 2.5 THz (b), and 2.83 THz (c) and at the corresponding doubled absorption frequencies ν = 3.5 THz (d), 4.95 THz (e), and 5.65 THz (f).
The high similarity is also confirmed by the correlation coefficient between the long dynamics at the basic absorption frequencies and the short dynamics at the doubled frequencies computed in the HMX_STF first sub-pulse for the pairs of frequencies ν = (1.75, 3.5) THz, (2.5, 4.95) THz and (2.83, 5.65) THz. Their pronounced maxima are achieved in the time interval t = [30, 70] ps, and their values are very close to unity: = 0.983, 0.98 and 0.987, correspondingly.
Thus, the doubled absorption frequencies ν = 3.5, 4.95, 5.65 THz are observed in the spectrum of the first sub-pulse of the signal HMX_STF, and they can be used for the detection and identification of HMX instead of the basic absorption frequencies ν = 1.75, 2.5, 2.83 THz.
4.4. Influence of Water Vapor on Observing Doubled Absorption Frequencies under Real Conditions
The results obtained in the previous sections can be very useful for the detection and identification of a substance under laboratory conditions when the relative humidity is low enough during the measurement and does not influence the spectral characteristics of the registered THz signal. However, under real conditions (at a non-zero relative humidity), it is necessary to take into account the water vapor absorption of the THz radiation. Obviously, in this case, we have to choose such basic absorption frequencies and their doubled frequencies which do not coincide with the water vapor absorption frequencies.
The absorption spectrum of water molecules in the THz frequency range 0.3 < ν < 7 THz obtained from the HITRAN database [58] is presented in Figure 25a. One can see that the water vapor absorption increases at higher frequencies, especially for ν > 3 THz. However, in this spectral range, there are gaps with low or zero water vapor absorption. In Figure 25b–d, this spectrum is shown in the short frequency ranges ν = [3.8, 4.0] THz, [4.2, 4.5] THz and [5.9, 6.15] THz, in which the PWM_40 doubled absorption frequencies ν = 3.88, 4.4, 6.04 THz are depicted by red arrows, respectively. We see that the absorption frequencies of water vapor ν = 3.858, 4.464, and 6.08 THz Figure 25b–d are closest to them. However, their absorption intensities (except for the frequency ν = 6.08 THz), 0.144, 0.048 and 7.93 J/cm3·s Figure 25b–d [23,48], are low enough. One can see that the absorption intensity at the frequency ν = 6.08 THz is approximately 55 times greater than at the frequency ν = 3.858 THz Figure 25b, and 165 times greater than at the frequency ν = 4.464 THz Figure 25d. In this situation, the PWM_40 doubled frequency ν = 6.04 THz Figure 25d may not be suitable for detection under real conditions: it depends on the distance between the receiver of the THz signal and the sample. At the same time, it may be used for this purpose under laboratory conditions in a dry air environment or with low humidity in the atmosphere, at approximately less than 10%. The PWM_40 doubled frequency ν = 3.88 THz Figure 25b can be used for substance detection both under laboratory and real conditions at a low relative humidity (less than 30–40%).
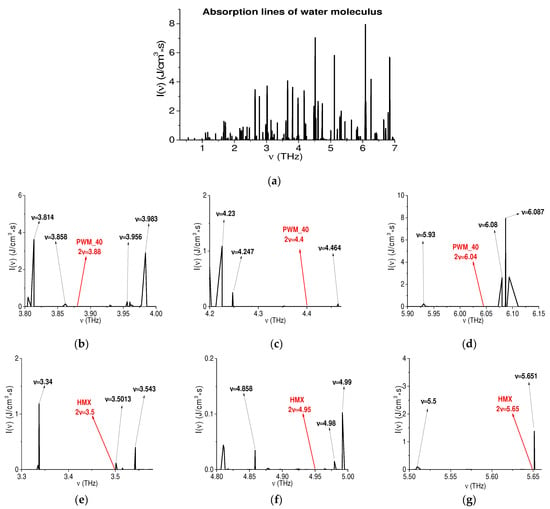
Figure 25.
Absorption spectrum of water molecules in the frequency ranges ν = [0.3, 7.0] THz (a), [3.8, 4.0] THz (b), [4.2, 4.5] THz (c), [5.9, 6.15] THz (d), [3.3, 3.58] THz (e), [4.8, 5.05] THz (f), [5.5, 5.65] THz (g) and location of the PWM_40 doubled absorption frequencies and those of HMX_STF (red arrows) in these frequency ranges.
Let us note that the water vapor absorption intensity at the frequency ν = 4.464 THz in Figure 25c is extremely low; therefore, the doubled frequency ν = 4.4 THz can also be used for the detection and identification of PWM C4 with a rough surface, both in a dry air environment and under real conditions.
In Figure 25e–g, the absorption spectrum of water molecules is presented in the short frequency ranges ν = [3.3, 3.58] THz, [4.8, 5.05] THz and [5.5, 5.65] THz, in which the HMX_STF doubled absorption frequencies ν = 3.5, 4.95, 5.65 THz are shown with red arrows, respectively. The absorption frequencies of water vapor ν = 3.5013, 4.98, 5.651 THz are closest to them. Their absorption intensities are 0.116, 0.0145 and 1.38 (g) J/cm3·s Figure 25e–g, respectively. Thus, the water absorption intensity at the frequency ν = 5.651 THz Figure 25g is approximately 95 times greater than that at the frequency ν = 4.98 THz Figure 25f, and 12 times greater than that at the frequency ν = 3.5013 THz Figure 25e. Therefore, the HMX_STF doubled frequency ν =5.65 THz is not recommended for the detection of the substance under real conditions, because it is located very close to the water vapor absorption frequency ν =5.651 THz (the difference Δν = 0.001 THz = 1.0 GHz), and can be attenuated by it. However, it can be used for this purpose under laboratory conditions in a dry air environment. Another doubled frequency, ν =3.5 THz (Δν = 3.5013 THz-3.5 THz = 0.0013 THz = 1.3 GHz), can be used for the detection and identification of this substance in a dry air environment or at low relative humidity (up to 12–15%) because the water absorption intensity is low enough. The doubled frequency ν = 4.95 THz (Δν = 4.98 THz-4.95 THz = 0.03 THz = 30 GHz) can be both in a dry air environment and under real conditions due to the very low water vapor absorption intensity at this frequency.
We notice additionally that the verification of the proposed approach was first carried out in [36], where the doubled absorption frequencies were successfully used for the detection and identification of the dangerous substance 2,4-DNT with a smooth surface under real conditions using the THz signal measured at 4.2–12.0% relative humidity. We showed that the doubled absorption frequencies of this substance at the frequencies ν > 3.0 THz were not attenuated or masked by the water vapor absorption when increasing the relative humidity, and they can be used for substance detection with the help of the ICCs. Moreover, it is important to note that the high frequencies (ν > 3.0 THz) are less distorted not only by water vapor absorption, but also by different coverings and an inhomogeneous surface in comparison with the lower (ν < 3.0 THz) frequencies. Therefore, their use is very promising for security screening under real conditions in the THz frequency range.
5. Discussion of the Characteristics of the Proposed Method for the Detection of a Substance
Let us estimate several quantitative parameters of the discussed method. The performance of this method depends on the number of realizations when measuring the THz signal reflected by/transmitted through the substance, as well on the duration of the THz signal. As a rule, the number of realizations for one measurement is equal to 32, while the measuring time interval of the reflected THz signal does not exceed 180 ps. We note that as a rule, other authors analyze the signal in a time interval equal to 20 ps, involving only the main pulse. Our experience of using THz setup shows that the time required for the measurements does not exceed 0.1–5 s, depending on the THz pulse duration.
Computer processing of the THz signal can be carried out in real-time due to the simplicity of the algorithm for obtaining spectral dynamics, the definition of the location of the useful THz pulse in the noise signal, and the computation of ICCs. Moreover, computation can be performed using the algorithm of parallelization thanks to the Fourier–Gabor algorithm. Therefore, we can estimate the measurement and processing time as 0.5–6 s (or shorter if we treat a THz pulse with a duration of less than 60–80 ps). All computations are carried out on a laptop computer.
The detection efficiency (detectability) is determined using a number of criteria. We believe that it is necessary to use the comparison of the spectra (as is standard), the correlation criteria computed for the basic absorption frequencies (using a database and the signal under investigation) as well as the doubled absorption frequencies and the basic absorption frequencies from the database in the time intervals containing the main and the first sub-pulse. The combination of these criteria leads to reaching a detectability of more than 90% under real conditions. However, we believe that this value can be increased by machine learning.
In the literature, there are several other well-known approaches for the detection and identification of hazardous substances under laboratory and real conditions. Among them we emphasize portable gas chromatography–mass spectrometry (GC-MS), which has important capabilities for a variety of different scientific and industrial applications. Recently, portable GC-MS systems were also deployed for the detection and identification of toxic chemicals under real conditions. As reported in [59], a sensitive and definitive analysis using portable GC-MS systems generally last no longer than approximately 15 min, but in some systems, this process is as short as 3 min, with a unit-mass resolution in the range of 43–500 atomic mass units.
Various types of gas analyzers are also widely used for scientific, industrial and security applications. A highly sensitive photo-acoustic (PA) multi-gas analyzer [60] achieved an averaging processing time of 60 s with a detection limit of 10–94 ppb (μm3/mm3) for multi-component gas mixtures.
Note that both of these approaches take a long time to process the measured signal. So, we believe that they cannot be used in real time, unlike the method discussed in the article.
The sensitivity of the proposed method can be evaluated by the following facts. In the current article, the proposed method allows us to detect the explosives in tablets weighing 600 mg (PWM C4) and 800 mg (HMX) in reflection mode. In [61], the SDA method allowed us to detect powdered soup and chocolate in small paper bags, weighing less than 1 g. In [36], an aspirin tablet weighing about 200 mg (with diameter 5 mm and thickness 2 mm) was used for joint applications of the SDA method and ICCs. We believe that these examples illustrate the potential of the developed method and demonstrate that it can be used with success for security screening and quality control.
6. Conclusions
Using artificial signals, we showed the appearance of the doubled emission or absorption frequencies in the spectrum of the broadband pulse transmitted through a medium possessing a quadratic nonlinear response and absorption at a certain frequency. A high similarity between the spectral line dynamics at the basic emission/absorption frequencies and at doubled frequencies was demonstrated by means of the computation of the correlation coefficient between them.
In the broadband THz pulses reflected by the PWM C4 tablet with a inhomogeneous surface, the doubled absorption frequencies were observed in the main pulse as well as in the first and second sub-pulses of the signals PWM_40 (a tablet with a rough surface) and PWM_1.5 (a tablet with a concave surface). For PWM C4 with a concave surface, the doubled absorption frequency was observed even in the third sub-pulse.
An example of detecting PWM C4 with a rough surface using a doubled absorption frequency instead of the basic frequency is provided, using different time intervals containing the main pulse, the first and the second sub-pulses of the PWM_40 reflected THz signal based on using ICC Equation (13). To this end, the THz pulse transmitted through the RDX sample under real conditions was used as a standard THz signal.
In the THz signal reflected by the HMX tablet with a smooth surface, the doubled absorption frequencies, which correspond to the basic absorption frequencies inherent in the spectrum of the transmitted signal, are observed only in the first sub-pulse. Because this substance does not possess pronounced absorption frequencies in the spectrum of the main reflected THz pulse, the up-conversion of the absorption frequencies make it possible to detect this dangerous substance.
All doubled absorption frequencies in the examples under consideration are observed in the high frequency range (ν > 3.0 THz) of the THz pulse spectrum. This result is very important in practice, because the higher frequencies (ν > 3.0 THz) are less distorted by an inhomogeneous surface and noise in comparison with the lower frequencies.
Comparison with absorption frequencies of water vapor demonstrated that the doubled absorption frequencies of PWM and HMX substance, lying in the frequency range 3.0 < ν < 5.6 THz, can be used for substance detection and identification both under laboratory (dry air) and real conditions, because they do not coincide with the frequencies of water vapor absorption.
The doubled absorption frequencies, which lie in the frequency range ν > 5.6 THz, can coincide with the corresponding water absorption frequencies possessing enough small absorption coefficient. Therefore, these frequencies have restrictions on their use. Other frequencies are located near the water absorption frequencies possessing a high absorption coefficient. In this case, the doubled absorption frequencies can be used for substance detection under laboratory conditions only, and for their application under real conditions, the bandwidth of the THz pulse must be limited to avoid the intersection of its spectral line with the corresponding absorption frequency of water.
Using doubled absorption frequency may be an additional effective tool for the detection and identification of substances (and molecules) based on the joint application of the SDA method and integral correlation criteria. The discussed method demonstrates a high probability of substance identification. Therefore, it can be very useful for the design of systems for THz security screening and for the analysis of quality in 3D printing product manufacturing from non-metallic bases.
Author Contributions
Conceptualization, V.A.T.; investigation, S.A.V.; data curation, V.A.T., S.A.V. and Z.C.; writing—original draft preparation, S.A.V.; writing—review and editing, V.A.T., Y.Y. and S.A.V.; visualization, S.A.V. and Z.C.; supervision, V.A.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Program of Joint Fund of the National Natural Science Foundation of China, grant number U2001218; and by the International (regional) Cooperation and Exchange Program of the National Natural Science Foundation of China, grant number 51875215.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All relevant data are within the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leahy-Hoppa, M.R.; Fitch, M.J.; Zheng, X.; Hayden, L.M.; Osiander, R. Wideband terahertz spectroscopy of explosives. Chem. Phys. Lett. 2007, 434, 227–230. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Y.; Zhao, H.; Bastiaans, G.J.; Zhang, X.-C. Absorption coefficients of selected explosives and related compounds in the range of 0.1–2.8 THz. Opt. Express 2007, 15, 12060. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.B.; Zhong, H.; Karpowicz, N.; Chen, Y.; Zhang, X.C. Terahertz spectroscopy and imaging for defense and security applications. Proc. IEEE 2007, 95, 1514–1527. [Google Scholar] [CrossRef]
- Michalopoulou, Z.H.; Mukherjee, S.; Hor, Y.L.; Su, K.; Liu, Z.; Barat, R.B.; Gary, D.E.; Federici, J.F. RDX detection with THz spectroscopy. J. Infrared Millim. Terahertz Waves 2010, 31, 1171–1181. [Google Scholar] [CrossRef]
- Choi, K.; Hong, T.; Sim, K.I.; Ha, T.; Park, B.C.; Chung, J.H.; Cho, S.G.; Kim, J.H. Reflection terahertz time-domain spectroscopy of RDX and HMX explosives. J. Appl. Phys. 2014, 115, 023105. [Google Scholar] [CrossRef]
- Palka, N.; Szala, M. Transmission and reflection terahertz spectroscopy of insensitive melt-cast high-explosive materials. J. Infrared Millim. Terahertz Waves 2016, 37, 977–992. [Google Scholar] [CrossRef] [Green Version]
- He, T.; Shen, J.L. Applications of terahertz spectroscopy in illicit drugs detection. Spectrosc. Spect. Anal. 2013, 33, 2348–2353. [Google Scholar]
- Wang, C.H.; Terracciano, A.C.; Masunov, A.E.; Xu, M.; Vasu, S.S. Accurate prediction of terahertz spectra of molecular crystals of fentanyl and its analogs. Sci. Rep. 2021, 11, 4062. [Google Scholar] [CrossRef]
- McIntosh, A.I.; Yang, B.; Goldup, S.M.; Watkinson, M.; Donnan, R.S. Terahertz spectroscopy: A powerful new tool for the chemical sciences? Chem. Soc. Rev. 2012, 41, 2072–2082. [Google Scholar] [CrossRef]
- Nickel, D.V.; Ruggiero, M.T.; Korter, T.M.; Mittleman, D.M. Terahertz disorder-localized rotational modes and lattice vibrational modes in the orientationally-disordered and ordered phases of camphor. Phys. Chem. Chem. Phys. 2015, 17, 6671–7078. [Google Scholar] [CrossRef]
- Damari, R.; Weinberg, O.; Krotkov, D.; Demina, N.; Akulov, K.; Golombek, A.; Schwartz, T.; Fleischer, S. Strong coupling of collective intermolecular vibrations in organic materials at terahertz frequencies. Nat. Commun. 2019, 10, 3248. [Google Scholar] [CrossRef] [PubMed]
- D’Arco, A.; Di Fabrizio, M.; Dolci, V.; Petrarca, M.; Lupi, S. THz pulsed imaging in biomedical applications. Condens. Matter 2020, 5, 25. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.C. Terahertz pulsed spectroscopy and imaging for pharmaceutical applications: A review. Int. J. Pharm. 2011, 417, 48–60. [Google Scholar] [CrossRef] [PubMed]
- Kawase, K.; Shibuya, T.; Hayashi, S.I.; Suizu, K. THz imaging techniques for nondestructive inspections. Comptes Rendus Phys. 2010, 11, 510–518. [Google Scholar] [CrossRef]
- Ahi, K.; Anwar, M. Advanced terahertz techniques for quality control and counterfeit detection. Proc. SPIE 2016, 9856, 98560G. [Google Scholar]
- Ahi, K.; Shahbazmohamadi, S.; Asadizanjani, N. Quality control and authentication of packaged integrated circuits using enhanced-spatial-resolution terahertz time-domain spectroscopy and imaging. Opt. Lasers Eng. 2018, 104, 274–284. [Google Scholar] [CrossRef]
- Wang, K.; Sun, D.W.; Pu, H. Emerging non-destructive terahertz spectroscopic imaging technique: Principle and applications in the agri-food industry. Trends Food Sci. Technol. 2017, 67, 93–105. [Google Scholar] [CrossRef]
- Karaliūnas, M.; Nasser, K.E.; Urbanowicz, A.; Kašalynas, I.; Bražinskienė, D.; Asadauskas, S.; Valušis, G. Non-destructive inspection of food and technical oils by terahertz spectroscopy. Sci. Rep. 2018, 8, 18025. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, R.; Huang, Y.; Xie, L.; Ying, Y. Terahertz spectroscopic imaging with discriminant analysis for detecting foreign materials among sausages. Food Control 2019, 97, 100–104. [Google Scholar] [CrossRef]
- Kemp, M.C. Explosives detection by terahertz spectroscopy—A bridge too far? IEEE Trans. Terahertz Sci. Technol. 2011, 1, 282–292. [Google Scholar] [CrossRef]
- Kato, M.; Tripathi, S.R.; Murate, K.; Imayama, K.; Kawase, K. Non-destructive drug inspection in covering materials using a terahertz spectral imaging system with injection-seeded terahertz parametric generation and detection. Opt. Express 2016, 24, 6425–6432. [Google Scholar] [CrossRef]
- Federici, J.F. Review of moisture and liquid detection and mapping using terahertz imaging. J. Infrared Millim. Terahertz Waves 2012, 33, 97–126. [Google Scholar] [CrossRef]
- Huang, Y.; Sun, P.; Zhang, Z.; Jin, C. Numerical method based on transfer function for eliminating water vapor noise from terahertz spectra. Appl. Opt. 2017, 56, 5698–5704. [Google Scholar] [CrossRef] [PubMed]
- Trofimov, V.A.; Varentsova, S.A. An effective method for substance detection using the broad spectrum THz signal: A “Terahertz nose”. Sensors 2015, 15, 12103–12132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trofimov, V.A.; Varentsova, S.A. Essential limitations of the standard THz TDS method for substance detection and identification and a way of overcoming them. Sensors 2016, 16, 502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taday, P.F. Applications of terahertz spectroscopy to pharmaceutical sciences. Philos. Trans. A Math. Phys. Eng. Sci. 2004, 362, 351–364. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Li, Z.; Hu, F.R.; Mo, W. Quantitative analysis of mixtures using terahertz time-domain spectroscopy and different PLS algorithms. Adv. Mater. Res. 2013, 804, 23–28. [Google Scholar] [CrossRef]
- Jiang, D.; Zhao, S.; Shen, J. Quantitative analysis of the mixtures of illicit drugs using terahertz time-domain spectroscopy. Proc. SPIE 2008, 6840, 68400U. [Google Scholar]
- Sleiman, J.B.; Perraud, J.B.; Bousquet, B.; Guillet, J.P.; Palka, N.; Mounaix, P. Discrimination and identification of RDX/PETN explosives by chemometrics applied to terahertz time-domain spectral imaging. Proc. SPIE 2015, 9651, 965109. [Google Scholar]
- Shen, Y.C.; Taday, P.F.; Pepper, M. Elimination of scattering effects in spectral measurement of granulated materials using terahertz pulsed spectroscopy. Appl. Phys. Lett. 2008, 92, 051103. [Google Scholar] [CrossRef] [Green Version]
- Henry, S.; Kniffin, G.; Schecklman, S.; Zurk, L.; Chen, A. Measurement and modeling of rough surface effects on terahertz spectroscopy and imaging. Proc. SPIE 2010, 7601, 760108. [Google Scholar]
- Malevich, V.L.; Sinitsyn, G.V.; Sochilin, G.B.; Rosanov, N.N. Manifestations of radiation scattering in the method of pulsed terahertz spectroscopy. Opt. Spectrosc. 2018, 124, 889–894. [Google Scholar] [CrossRef]
- Sheikh, F.; Gao, Y.; Kaiser, T. A study of diffuse scattering in massive MIMO channels at terahertz frequencies. IEEE Trans. Antennas Propag. 2019, 68, 997–1008. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Zakharova, I.G.; Zagursky, D.Y.; Varentsova, S.A. New approach for detection and identification of substances using THz TDS. Proc. SPIE 2017, 10441, 1044107. [Google Scholar]
- Trofimov, V.A.; Zakharova, I.G.; Varentsova, S.A. New method of substance detection and identification using the substance emission frequency up-conversion in the THz frequency range. Proc. SPIE 2018, 10639, 106392C. [Google Scholar]
- Trofimov, V.A.; Wang, N.N.; Qiu, J.H.; Varentsova, S.A. Spurious absorption frequency appearance due to frequency conversion processes in pulsed THz TDS problems. Sensors 2020, 20, 1859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trofimov, V.A.; Varentsova, S.A.; Szustakowski, M.; Palka, N. Influence of surface of explosive on its detection and identification using the SDA method for analysis of the reflected THz signal. Proc. SPIE 2013, 8734, 87340Q. [Google Scholar]
- Trofimov, V.A.; Varentsova, S.A. High effective time-dependent THz spectroscopy method for the detection and identification of substances with inhomogeneous surface. PLoS ONE 2018, 13, e0201297. [Google Scholar] [CrossRef] [Green Version]
- Barsumian, B.R.; Jones, T.H. Pulse Transmitting Non-Linear Junction Detector. U.S. Patent 6,163,259, 19 December 2000. [Google Scholar]
- Holmes, S.J.; Stephen, A.B. Non-Linear Junction Detector. U.S. Patent 6,897,777, 24 May 2005. [Google Scholar]
- Mazzaro, G.J.; Martone, A.F.; McNamara, D.M. Detection of RF electronics by multitone harmonic radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 477–490. [Google Scholar] [CrossRef]
- Aniktar, H.; Baran, D.; Karav, E.; Akkaya, E.; Birecik, Y.S.; Sezgin, M. Getting the bugs out: A portable harmonic radar system for electronic countersurveillance applications. IEEE Microw. Mag. 2015, 16, 40–52. [Google Scholar] [CrossRef]
- Aniktar, H.; Baran, D. An efficient implementation of intermodulation radar with an integrated EMI sensor. IEEE Sens. J. 2021, 21, 23492–23497. [Google Scholar] [CrossRef]
- Information Security Associates. Boomerang Series Non-Linear Junction Detector Data Sheet. Available online: http://isa-technology.com/products/items/boomarang4.html (accessed on 8 April 2022).
- Trofimov, V.A.; Varentsova, S.A.; Zakharova, I.G.; Zagursky, D.Y. Conservative finite-difference scheme for the problem of THz pulse interaction with multilevel layer covered by disordered structure based on the density matrix formalism and 1D Maxwell equation. PLoS ONE 2018, 13, e0201572. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R.W. Nonlinear Optics, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008; p. 611. [Google Scholar]
- Zhang, X.C.; Xu, J. Introduction to THz Wave Photonics; Springer: Berlin/Heidelberg, Germany, 2010; p. 330. [Google Scholar]
- Loata, G.C.; Thomson, M.D.; Loffler, T.; Roskos, H.G. Radiation field screening in photoconductive antennae studied via pulsed terahertz emission spectroscopy. Appl. Phys. Lett. 2007, 91, 232506. [Google Scholar] [CrossRef]
- Siegman, A.E. Laser; University Science Books: Mill Valley, CA, USA, 1986. [Google Scholar]
- Agrawal, G.P. Optical pulse propagation in doped fiber amplifiers. Phys. Rev. A 1991, 44, 7493–7501. [Google Scholar] [CrossRef] [PubMed]
- Trofimov, V.A.; Zakharova, I.G.; Zagursky, D.Y.; Varentsova, S.A. Detection and identification of substances using noisy THz signal. Proc. SPIE 2017, 10194, 101942O. [Google Scholar]
- Hofmann, M.C.; Brant, N.C.; Hwang, H.Y.; Yeh, K.-L.; Nelson, K.A. Terahertz Kerr effect. Appl. Phys. Lett. 2009, 95, 231105. [Google Scholar] [CrossRef] [Green Version]
- Lengyel, K.; Péter, Á.; Kovács, L.; Corradi, G.; Pálfalvi, L.; Hebling, J.; Unferdorben, M.; Dravecz, G.; Hajdara, I.; Szaller, Z.; et al. Growth, defect structure, and THz application of stoichiometric lithium niobite. Appl. Phys. Rev. 2015, 2, 040601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.C.; Shkurinov, A.; Zhang, Y. Extreme terahertz science. Nat. Photonics 2017, 11, 16–18. [Google Scholar] [CrossRef]
- Landau, L.D.; Akhiezer, A.I.; Lifshitz, E.M. General Physics: Mechanics and Molecular Physics; Pergamon Press: Oxford, UK; New York, NY, USA, 1967; p. 372. [Google Scholar]
- TeraView Corporation. Available online: www.teraview.com (accessed on 9 May 2022).
- Trofimov, V.A.; Varentsova, S.A. Detection and identification of drugs under real conditions by using noisy terahertz broadband pulse. Appl. Opt. 2016, 55, 9605–9618. [Google Scholar] [CrossRef]
- HITRAN Database. Available online: www.hitran.org (accessed on 8 April 2022).
- Leary, P.E.; Kammrath, B.W.; Lattman, K.J.; Beals, G.L. Deploying portable gas chromatography—Mass spectrometry (GC-MS) to military users for the identification of toxic chemical agents in theater. Appl. Spectrosc. 2019, 73, 841–858. [Google Scholar] [CrossRef]
- Chen, K.; Liu, S.; Zhang, B.; Gong, Z.; Chen, Y.; Zhang, M.; Deng, H.; Guo, M.; Ma, F.; Zhu, F.; et al. Highly sensitive photoacoustic multi-gas analyzer combined with mid-infrared broadband source and near-infrared laser. Opt. Lasers Eng. 2020, 124, 105844. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Varentsova, S.A. About efficiency of identification of materials using spectrum dynamics of medium response under the action of THz radiation. Proc. SPIE 2009, 7311, 73110U. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).