Point-of-Care Using Vis-NIR Spectroscopy for White Blood Cell Count Analysis †
Abstract
1. Introduction
White Blood Cells and Blood Spectroscopy
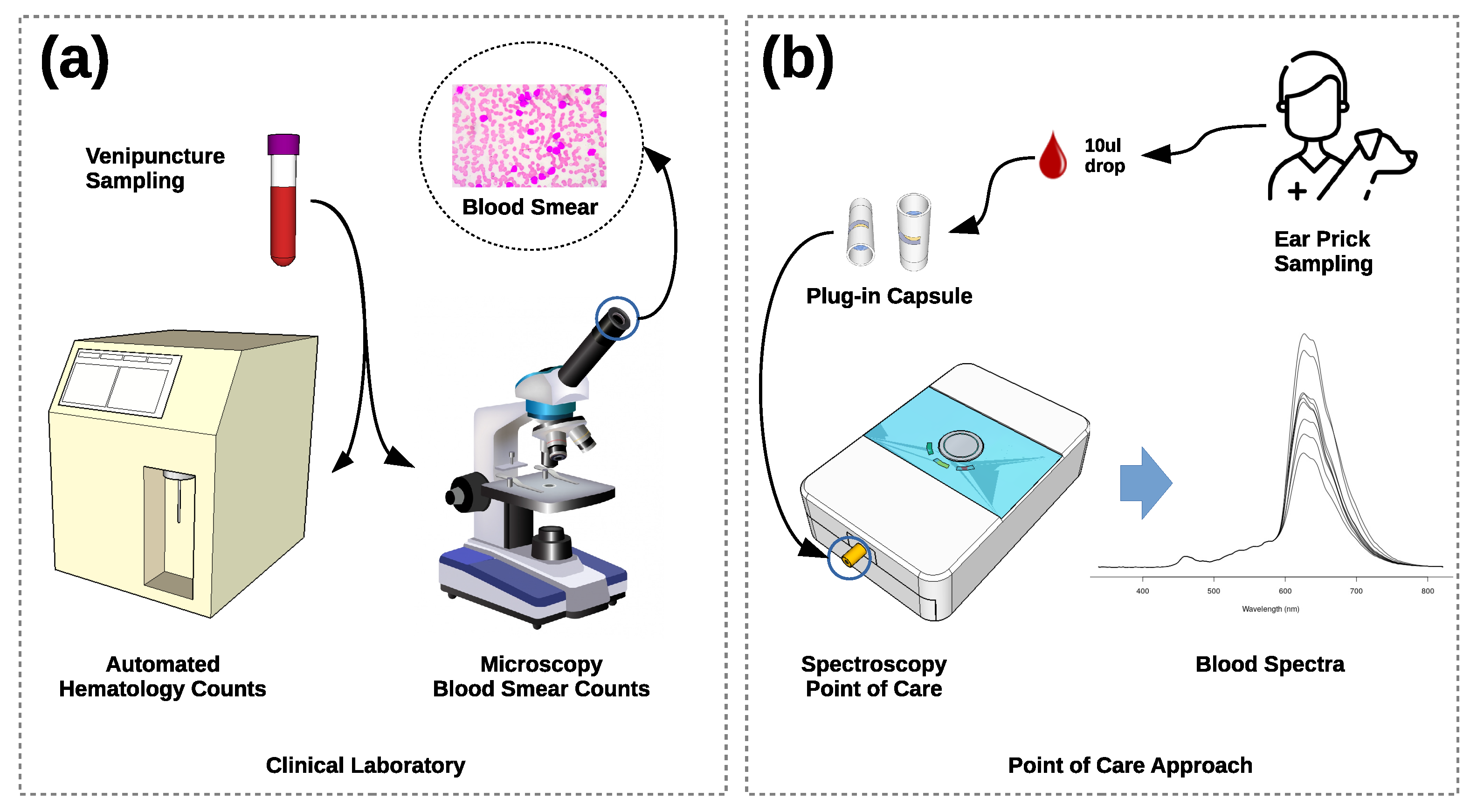
2. Methods
2.1. Hemogram Analysis
2.2. Spectroscopy
2.3. Benchmarking
- Partial least squares (PLS): maximizes the covariance between the spectra and blood WBC composition by determining the eigenvectors of . This method forces the latent structures of spectra and composition (PLS scores—) to be equal (NIPALS algorithm) [37] for the determination of each correspondent basis and [38]. It proceeds with deflation and sequential orthogonal eigenvectors of the remaining information in [37,39]. The number of deflations or latent variables are optimized by cross-validation/hold-out samples minimal predicted sum of squares (PRESS) [40]. PLS uses an oblique projection to determine the coefficients in [37,39].
- Local PLS (LocPLS): uses KNN clustering to create local sub-groups, where local PLS models are optimized. The KNN clusters are obtained in the PCA scores space. The number of clusters and number of principal components (PC) is optimized by cross-validation/hold-out samples [41];
- Artificial neural networks (ANN): were introduced in spectroscopy as an approach to deal with non-linearity. ANN is a piece-wise linear combination of non-linear activation functions at each node (or neuron) of the network, being parameters optimized by back-propagation. Most ANNs in spectroscopy use PCA or PLS scores as input, being designated PCA-ANN and PLS-ANN [42,43]. The number of LV and ANN architecture (variables and layers) have to be optimized. In this research, we applied the most used template: (i) input layer—coordinates in the LV; (ii) hidden layer—optimized between two and three layers; and (iii) one output node—the estimation of WBC. The tangent and identity functions were used as hidden and output layer activation, respectively. ANN was regressed by back-propagation using the Levenberg–Marquardt algorithm;
- Least-squares support vector machines (LS-SVM): was introduced in spectroscopy to deal with the high non-linearity of feature spaces due to interference. SVM maps similarity between samples using the kernel function, mapping it into a new feature space, where the Gaussian radial basis function (RBF) maps the PLS scores (). The LS-SVM replaces the e-sensitive loss function by the square loss function to optimize the Karush–Kuhn–Tucker (KKT) linear system obtained by Lagrangian multipliers methodology [44]. At each U comprising an increasing number of LVs, the LS-SVM optimizes the RBF kernel width parameter () and the regularization parameter of the KKT linear system () [45]. The number of LV used to compute the kernel matrix is obtained by cross-validation/hold-out sample validation. LS-SVM was implemented using the kernlab library for R [46].
2.4. Covariance Mode Search
- Feature space optimization: information about a constituent is present in the spectra in different scales and wavelengths. Selecting the correct features and transforms (e.g., singular value decomposition, Fourier or wavelets transforms) is essential to extract the information into a feature space that holds proportionality to the concentration of the constituents; and
- Covariance mode search: searching a group of samples within the feature space that belong to the same interference pattern. Such means that spectral features hold the same information as composition , with a stable covariance .
2.5. Validation
2.6. Spectral Data Augmentation
3. Results and Discussion
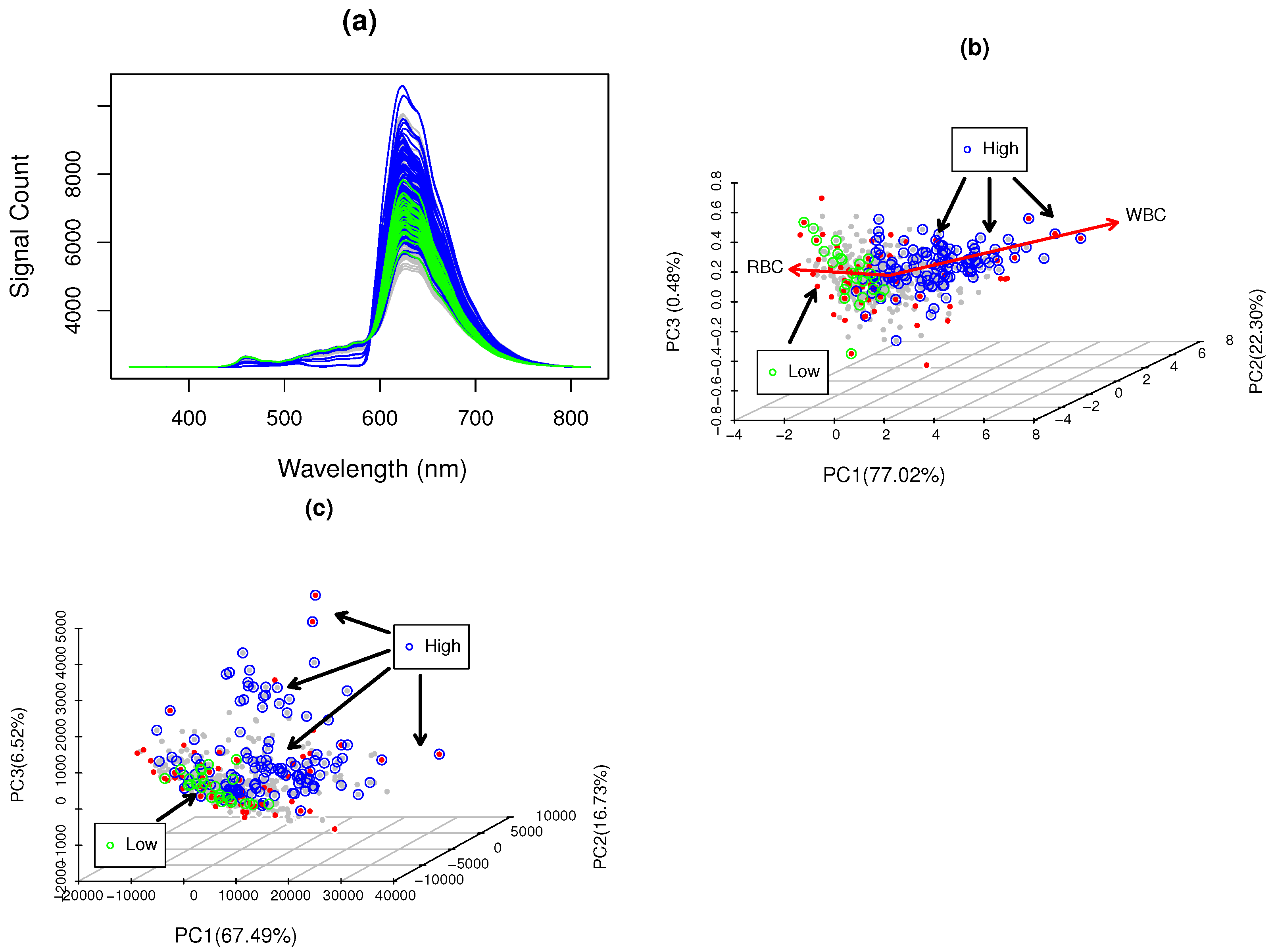
3.1. WBC Blood Spectroscopy
3.2. WBC Quantification
3.3. Bias-Variance Analysis
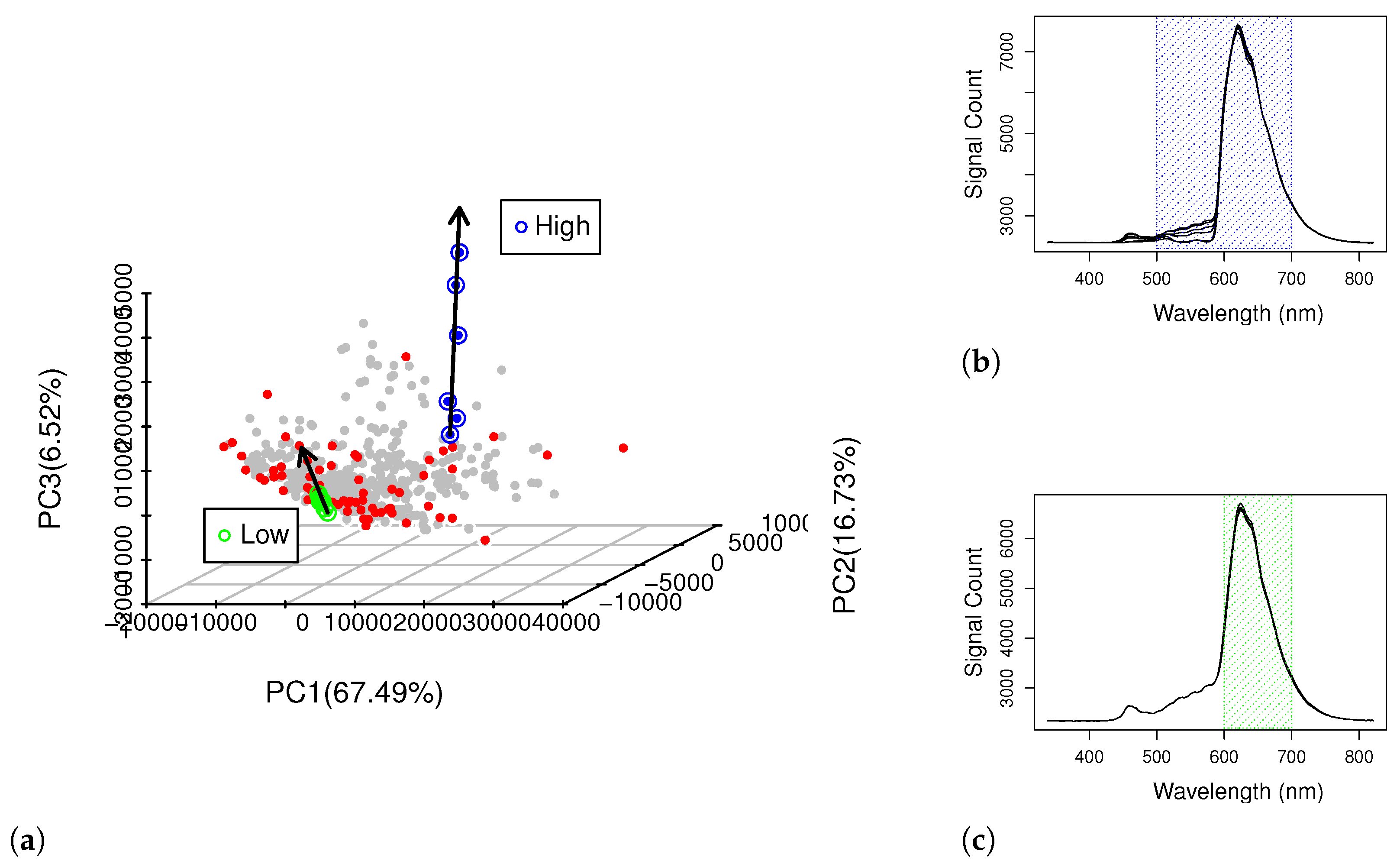
3.4. CovM Interpretation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural networks |
| ASVCP | American Society for Veterinary Clinical Pathology |
| Accep | Acceptable |
| ATE | Allowable total error |
| Bil | Billirubin |
| BLL | Beer–Lambert law |
| CovM | Covariance mode |
| CV | Cross-validation |
| Des | Desired |
| EDTA | Ethylenediamine tetraacetic acid |
| Hgb | Total hemoglobin |
| HO | Hold-out samples |
| HTC | Hematocrit |
| IoT | Internet of Things |
| KKT | Karush–Kuhn–Tucker |
| LocPLS | Local partial least squares |
| LV | Latent variable |
| LS-SVM | Least-squares suppport vector machines |
| MAPE | Mean average percentage error |
| Opt | Optimal |
| PC | Principal component |
| PCA | Principal component analysis |
| PCA-ANN | Principal component analysis—Artificial neural networks |
| PLS | Partial least squares |
| PLS-ANN | Partial least squares—Artificial neural networks |
| POC | Point-of-care |
| R | Pearsons correlation coefficient |
| RBC | Red blood cells |
| RBF | Radial basis function |
| RI | Reference interval |
| ROI | Region of interest |
| RWD | Real-world knowledgebase dataset |
| SE | Standard error |
| SIM | Similarity |
| SLAI | Self-learning artificial intelligence |
| SSD | Synthetic spectroscopy dataset |
| SVM | Support Vector Machines |
| TE | Total error |
| UV-Vis | Ultra-violet visible |
| Vis-NIR | Visible near infrared |
| WBC | White blood cells |
References
- Pasquini, C. Near infrared spectroscopy: A mature analytical technique with new perspectives—A review. Anal. Chim. Acta 2018, 1026, 8–36. [Google Scholar] [CrossRef] [PubMed]
- Olinger, J.M.; Griffiths, P.R. Quantitative effects of an absorbing matrix on near-infrared diffuse reflectance spectra. Anal. Chem. 1988, 60, 2427–2435. [Google Scholar] [CrossRef]
- Sparén, A.; Hartman, M.; Fransson, M.; Johansson, J.; Svensson, O. Matrix effects in quantitative assessment of pharmaceutical tablets using transmission Raman and Near-Infrared (NIR) Spectroscopy. Appl. Spectrosc. 2015, 69, 580–589. [Google Scholar] [CrossRef] [PubMed]
- Nishat, S.; Jafry, A.T.; Martinez, A.W.; Awan, F.R. Paper-based microfluidics: Simplified fabrication and assay methods. Sens. Actuators B Chem. 2021, 336, 129681. [Google Scholar] [CrossRef]
- Zhou, T.; Lu, D.; She, Q.; Chen, C.; Chen, J.; Huang, Z.; Feng, S.; You, R.; Lu, Y. Hypersensitive detection of IL-6 on SERS substrate calibrated by dual model. Sens. Actuators B Chem. 2021, 336, 129597. [Google Scholar] [CrossRef]
- Jiang, K.; Wu, J.; Qiu, Y.; Go, Y.Y.; Ban, K.; Park, H.J.; Lee, J.H. Plasmonic colorimetric PCR for rapid molecular diagnostic assays. Sens. Actuators B Chem. 2021, 337, 129762. [Google Scholar] [CrossRef]
- Lewińska, I.; Speichert, M.; Granica, M.; Tymecki, Ł. Colorimetric point-of-care paper-based sensors for urinary creatinine with smartphone readout. Sens. Actuators B Chem. 2021, 340, 129915. [Google Scholar] [CrossRef]
- Burns, D.; Ciurczak, E. Handbook of Near Infrared Analysis, 2nd ed.; Marcel Dekker, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Barroso, T.G.; Martins, R.C.; Fernandes, E.; Cardoso, S.; Rivas, J.; Freitas, P.P. Detection of BCG bacteria using a magnetoresistive biosensor: A step towards a fully electronic platform for tuberculosis point-of-care detection. Biosens. Bioelectron. 2018, 100, 259–265. [Google Scholar] [CrossRef]
- Lin, K.; Cheng, D.L.P.; Huang, Z. Optical diagnosis of laryngeal cancer using high wavenumber Raman spectroscopy. Biosens. Bioelectron. 2012, 35, 213–217. [Google Scholar] [CrossRef]
- Monteiro-Silva, F.; Jorge, P.A.S.; Martins, R.C. Optical Sensing of Nitrogen, Phosphorus and Potassium: A Spectrophotometrical Approach toward Smart Nutrient Deployment. Chemosensors 2019, 7, 51. [Google Scholar] [CrossRef]
- Barroso, T.; Ribeiro, L.; Gregório, H.; Santos, F.; Martins, R.C. Point-of-care Vis-SWNIR spectroscopy towards reagent-less hemogram analysis. Sens. Actuators B Chem. 2021, 343, 130138. [Google Scholar] [CrossRef]
- Martins, R.C.; Barroso, T.; Jorge, P.; Cunha, M.; Santos, F. Unscrambling spectral interference and matrix effects in Vitis vinifera Vis-NIR spectroscopy: Towards analytical grade ‘in vivo’ sugars and acids quantification. Comput. Electron. Agric. 2022, 194, 106710. [Google Scholar] [CrossRef]
- Martins, R.C. Big Data Self-Learning Artificial Intelligence Methodology for the Accurate Quantification and Classification of Spectral Information under Complex Variability and Multi-Scale Interference. WO/2018/060967, 5 April 2018. [Google Scholar]
- Philo, J.; Adams, M.; Schuster, T.M. Association-dependent absorption spectra of oxyhemoglobin A and its subunits. J. Biol. Chem. 1981, 256, 7917–7924. [Google Scholar] [CrossRef]
- Tan, H.; Liao, S.; Pan, T.; Zhang, J.; Chen, J. Rapid and simultaneous analysis of direct and indirect bilirubin indicators in serum through reagent-free visible-near-infrared spectroscopy combined with chemometrics. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2020, 233, 118215. [Google Scholar] [CrossRef] [PubMed]
- Burton, A.G.; Jandrey, K.E. Leukocytosis and Leukopenia. In Textbook of Small Animal Emergency Medicine; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2018; Chapter 64; pp. 405–412. [Google Scholar] [CrossRef]
- Chabot-Richards, D.S.; George, T.I. White Blood Cell Counts: Reference Methodology. Clin. Lab. Med. 2015, 35, 11–24. [Google Scholar] [CrossRef]
- Rishniw, M.; Pion, P.D. Evaluation of performance of veterinary in-clinic hematology analyzers. Vet. Clin. Pathol. 2016, 45, 604–614. [Google Scholar] [CrossRef]
- Nabity, M.B.; Harr, K.E.; Camus, M.S.; Flatland, B.; Vap, L. ASVCP guidelines: Allowable total error hematology. Vet. Clin. Pathol. 2018, 47, 9–21. [Google Scholar] [CrossRef]
- Terent’yeva, Y.G.; Yashchuk, V.M.; Zaika, L.A.; Snitserova, O.M.; Losytsky, M.Y. The manifestation of optical centers in UV–Vis absorption and luminescence spectra of white blood human cells. Methods Appl. Fluoresc. 2016, 4, 044010. [Google Scholar] [CrossRef]
- Ramesh, J.; Kapelushnik, J.; Mordehai, J.; Moser, A.; Huleihel, M.; Erukhimovitch, V.; Levi, C.; Mordechai, S. Novel methodology for the follow-up of acute lymphoblastic leukemia using FTIR microspectroscopy. J. Biochem. Biophys. Methods 2002, 51, 251–261. [Google Scholar] [CrossRef]
- Ramesh, J.; Huleihel, M.; Mordehai, J.; Moser, A.; Erukhimovich, V.; Levi, C.; Kapelushnik, J.; Mordechai, S. Preliminary results of evaluation of progress in chemotherapy for childhood leukemia patients employing Fourier-transform infrared microspectroscopy and cluster analysis. J. Lab. Clin. Med. 2003, 141, 385–394. [Google Scholar] [CrossRef]
- Liu, W.; Howarth, M.; Greytak, A.B.; Zheng, Y.; Nocera, D.G.; Ting, A.Y.; Bawendi, M.G. Compact biocompatible quantum dots functionalized for cellular imaging. J. Am. Chem. Soc. 2007, 130, 1274–1284. [Google Scholar] [CrossRef] [PubMed]
- Sahu, R.K.; Zelig, U.; Huleihel, M.; Brosh, N.; Talyshinsky, M.; Ben-Harosh, M.; Mordechai, S.; Kapelushnik, J. Continuous monitoring of WBC (biochemistry) in an adult leukemia patient using advanced FTIR-spectroscopy. Leuk. Res. 2006, 30, 687–693. [Google Scholar] [CrossRef] [PubMed]
- Zelig, U.; Mordechai, S.; Shubinsky, G.; Sahu, R.K.; Huleihel, M.; Leibovitz, E.; Nathan, I.; Kapelushnik, J. Pre-screening and follow-up of childhood acute leukemia using biochemical infrared analysis of peripheral blood mononuclear cells. Biochim. Biophys. Acta Gen. Subj. 2011, 1810, 827–835. [Google Scholar] [CrossRef] [PubMed]
- Chaber, R.; Kowal, A.; Jakubczyk, P.; Arthur, C.; Łach, K.; Wojnarowska-Nowak, R.; Kusz, K.; Zawlik, I.; Paszek, S.; Cebulski, J. A Preliminary Study of FTIR Spectroscopy as a Potential Non-Invasive Screening Tool for Pediatric Precursor B Lymphoblastic Leukemia. Molecules 2021, 26, 1174. [Google Scholar] [CrossRef]
- Kochan, K.; Bedolla, D.E.; Perez-Guaita, D.; Adegoke, J.A.; Veettil, T.C.P.; Martin, M.; Roy, S.; Pebotuwa, S.; Heraud, P.; Wood, B.R. Infrared Spectroscopy of Blood. Appl. Spectrosc. 2021, 75, 611–646. [Google Scholar] [CrossRef]
- Agbaria, A.H.; Beck, G.; Lapidot, I.; Rich, D.H.; Kapelushnik, J.; Mordechai, S.; Salman, A.; Huleihel, M. Diagnosis of inaccessible infections using infrared microscopy of white blood cells and machine learning algorithms. Analyst 2020, 145, 6955–6967. [Google Scholar] [CrossRef]
- Martins, R.C.; Sousa, N.; Osorio, R. Optical System for Parameter Characteization of an Element of Body Fluid or Tissue. US10209178B2, 19 February 2019. [Google Scholar]
- Barroso, T.G.; Ribeiro, L.; Gregório, H.; Santos, F.; Martins, R.C. Visible Near-Infrared Platelets Count: Towards Thrombocytosis Point-of-Care Diagnosis. Chem. Proc. 2021, 5, 78. [Google Scholar] [CrossRef]
- Brown, M.; Wittwer, C. Flow Cytometry: Principles and Clinical Applications in Hematology. Clin. Chem. 2000, 46, 1221–1229. [Google Scholar] [CrossRef]
- INESCTEC. AgIoT—Modular Solution and Open Source IoT Solution for Agrofood Domain; INESCTEC: Porto, Portugal, 2020. [Google Scholar]
- Martens, H.; Stark, E. Extended multiplicative signal correction and spectral interference subtraction: New preprocessing methods for near infrared spectroscopy. J. Pharm. Biomed. Anal. 1991, 9, 625–635. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Behrens, T.; Schmidt, K.; Stevens, A.; Demattê, J.; Scholten, T. The spectrum-based learner: A new local approach for modelling soil vis-nir spectra of complex datasets. Geoderma 2013, 195–196, 268–279. [Google Scholar] [CrossRef]
- Fachada, N.; Figueiredo, M.A.; Lopes, V.V.; Martins, R.C.; Rosa, A.C. Spectrometric differentiation of yeast strains using minimum volume increase and minimum direction change clustering criteria. Pattern Recognit. Lett. 2014, 45, 55–61. [Google Scholar] [CrossRef]
- Ergon, R. Re-interpretation of NIPALS results solves PLSR inconsistency problem. J. Chemo. 2009, 23, 72–75. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalsky, B. Partial least squares regression: A tutorial. Anal. Chim. Acta 1988, 185, 1–17. [Google Scholar] [CrossRef]
- Phatak, A.; Jong, S. The geometry of partial least squares. J. Chemom. 1997, 11, 311–338. [Google Scholar] [CrossRef]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Chemom. 2014, 6, 10. [Google Scholar] [CrossRef]
- Shen, G.; Lesnoff, M.; Baeten, V.; Dardenne, P.; Davrieux, F.; Ceballos, H.; Belalcazar, J.; Dufour, D.; Yang, Z.; Han, L.; et al. Local partial least squares based on global PLS scores. J. Chemom. 2019, 33, e3117. [Google Scholar] [CrossRef]
- Janik, L.; Cozzolino, D.; Dambergs, R.; Cynkar, W.; Gishen, M. The prediction of total anthocyanin concentration in red-grape homogenates using visible-near-infrared spectroscopy and artificial neural networks. Anal. Chim. Acta 2013, 594, 107–118. [Google Scholar] [CrossRef]
- Fernandes, A.; Franco, C.; Mendes-Ferreira, A.; Mendes-Faia, A.; Costa, P.; Melo-Pinto, P. Brix, pH and anthocyanin content determination in whole Port wine grape berries by hyperspectral imaging and neural networks. Comput. Electron. Agric. 2015, 115, 88–96. [Google Scholar] [CrossRef]
- Suykens, J.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted least squares support vector machines: Robustness and sparse approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Chauchard, F.; Cogdill, R.; Roussel, S.; Roger, J.; Bellon-Maurel, V. Application of LS-SVM to non-linear phenomena in NIR spectroscopy: Development of a robust and portable sensor for acidity prediction in grapes. Chemom. Intell. Lab. Syst. 2004, 71, 141–150. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: http://www.r-project.org/ (accessed on 20 August 2022).
- Nalepa, J.; Marcinkiewicz, M.; Kawulok, M. Data Augmentation for Brain-Tumor Segmentation: A Review. Front. Comput. Neurosci. 2019, 13, 83. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Jensen, A.L.; Kjelgaard-Hansen, M. Method comparison in the clinical laboratory. Vet. Clin. Pathol. 2006, 35, 276–286. [Google Scholar] [CrossRef] [PubMed]
- Cook, A.M.; Moritz, A.; Freeman, K.P.; Bauer, N. Objective evaluation of analyzer performance based on a retrospective meta-analysis of instrument validation studies: Point-of-care hematology analyzers. Vet. Clin. Pathol. 2017, 46, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Cook, A.M.; Moritz, A.; Freeman, K.P.; Bauer, N. Quality requirements for veterinary hematology analyzers in small animals—A survey about veterinary experts’ requirements and objective evaluation of analyzer performance based on a meta-analysis of method validation studies: Bench top hematology analyzer. Vet. Clin. Pathol. 2016, 45, 466–476. [Google Scholar] [CrossRef]
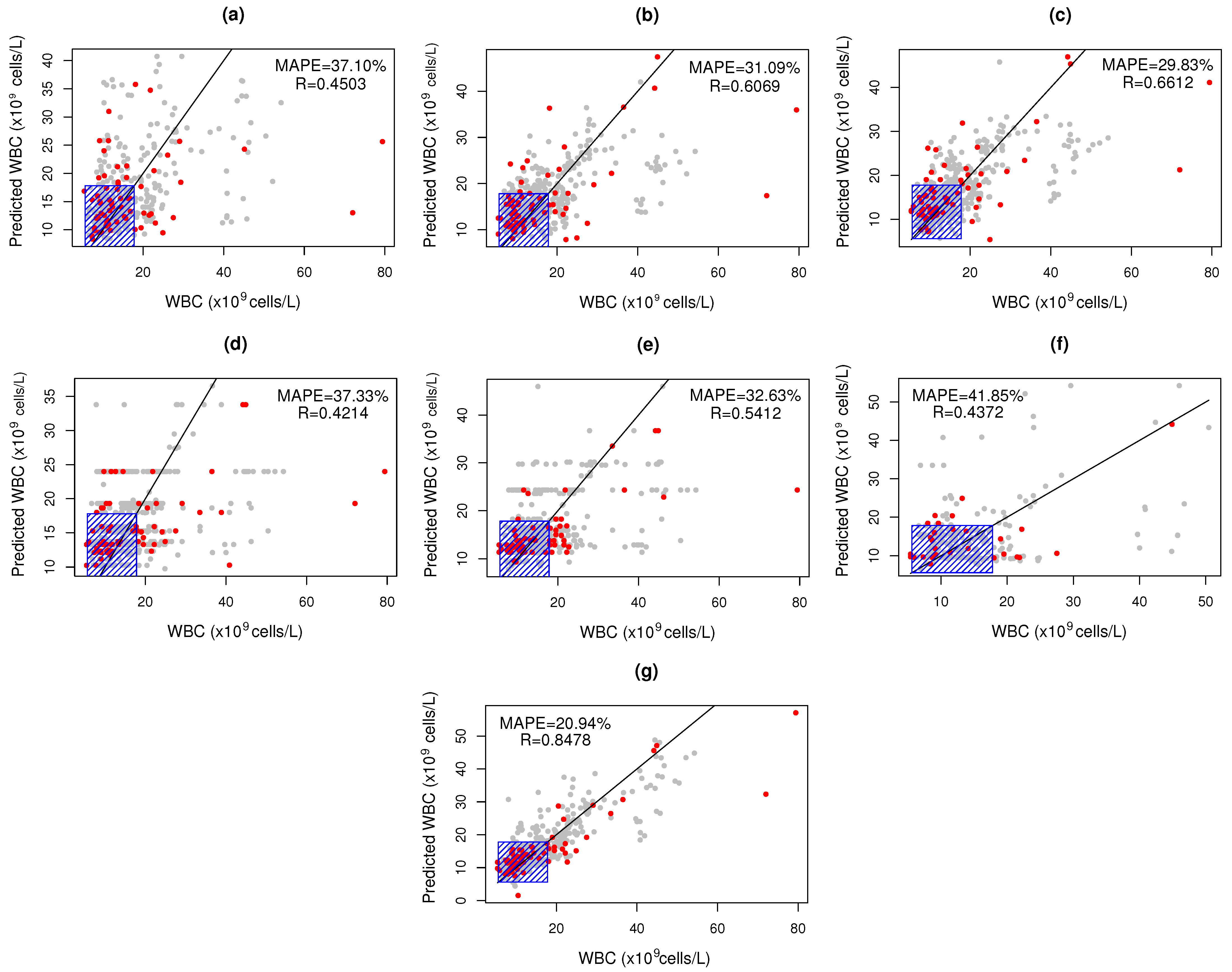
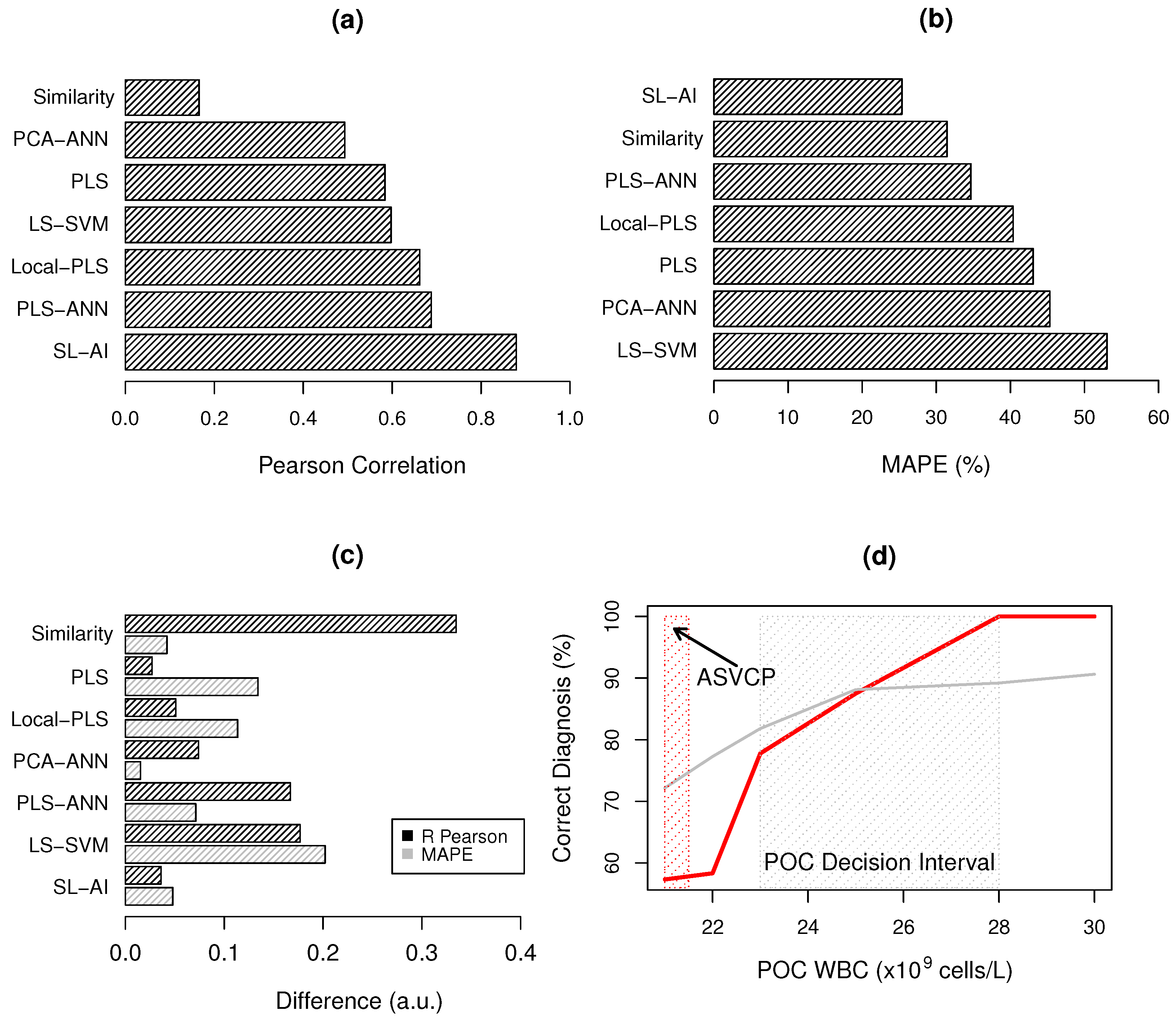
| Method | Parameters | Dataset | R | SE ( Cells/L) | MAPE (%) |
|---|---|---|---|---|---|
| SIM | nPC = 3 | Mixture | 0.5005 | 8.16 | 35.66 |
| n = 3 | Real | 0.1658 | 15.66 | 31.45 | |
| PLS | LV = 6 | Mixture | 0.6109 | 6.87 | 29.66 |
| Real | 0.5838 | 10.92 | 43.08 | ||
| LocPLS | LV = 5 | Mixture | 0.6110 | 6.52 | 28.51 |
| Real | 0.6619 | 10.10 | 40.37 | ||
| PCA-ANN | LV = 3 | Mixture | 0.4197 | 8.01 | 46.85 |
| (8:18:12) | Real | 0.4934 | 12.39 | 45.32 | |
| PLS-ANN | LV = 3 | Mixture | 0.5210 | 7.60 | 41.79 |
| (18:20:15) | Real | 0.6879 | 9.02 | 34.67 | |
| LS-SVM | Mixture | 0.4207 | 7.80 | 32.83 | |
| Real | 0.5976 | 7.50 | 53.04 | ||
| SLAI | LV = 1 | Mixture | 0.8432 | 4.67 | 20.57 |
| nCov = 100 | Real | 0.8789 | 6.92 | 25.37 |
| Real | Mixture | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Method | % Inside RI | % Outside RI | % Inside RI | % Outside RI | ||||||||
| Opt | Des | Accep | Opt | Des | Accep | Opt | Des | Accep | Opt | Des | Accep | |
| SIM | 13.30 | 20.00 | 30.00 | 0.00 | 14.29 | 14.29 | 16.72 | 33.77 | 40.54 | 9.75 | 26.89 | 34.14 |
| PLS | 18.87 | 30.18 | 41.51 | 14.28 | 21.42 | 28.57 | 16.13 | 32.75 | 48.13 | 28.57 | 40.36 | 55.10 |
| LocPLS | 24.53 | 41.51 | 47.17 | 14.25 | 28.57 | 42.85 | 16.62 | 30.52 | 48.63 | 19.38 | 36.73 | 52.34 |
| ANNPCA | 14.00 | 24.00 | 36.00 | 0.00 | 5.88 | 11.76 | 15.67 | 28.85 | 45.03 | 24.24 | 34.34 | 44.44 |
| ANNPLS | 10.15 | 27.27 | 41.82 | 8.33 | 16.60 | 33.30 | 17.04 | 31.82 | 45.86 | 32.35 | 39.22 | 40.25 |
| LS-SVM | 4.72 | 14.24 | 23.81 | 25.00 | 25.00 | 25.00 | 19.19 | 33.83 | 44.94 | 20.00 | 30.00 | 36.60 |
| SLAI | 24.53 | 41.50 | 58.49 | 21.42 | 28.57 | 42.87 | 27.36 | 50.99 | 66.92 | 29.59 | 52.04 | 72.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barroso, T.G.; Ribeiro, L.; Gregório, H.; Monteiro-Silva, F.; Neves dos Santos, F.; Martins, R.C. Point-of-Care Using Vis-NIR Spectroscopy for White Blood Cell Count Analysis. Chemosensors 2022, 10, 460. https://doi.org/10.3390/chemosensors10110460
Barroso TG, Ribeiro L, Gregório H, Monteiro-Silva F, Neves dos Santos F, Martins RC. Point-of-Care Using Vis-NIR Spectroscopy for White Blood Cell Count Analysis. Chemosensors. 2022; 10(11):460. https://doi.org/10.3390/chemosensors10110460
Chicago/Turabian StyleBarroso, Teresa Guerra, Lenio Ribeiro, Hugo Gregório, Filipe Monteiro-Silva, Filipe Neves dos Santos, and Rui Costa Martins. 2022. "Point-of-Care Using Vis-NIR Spectroscopy for White Blood Cell Count Analysis" Chemosensors 10, no. 11: 460. https://doi.org/10.3390/chemosensors10110460
APA StyleBarroso, T. G., Ribeiro, L., Gregório, H., Monteiro-Silva, F., Neves dos Santos, F., & Martins, R. C. (2022). Point-of-Care Using Vis-NIR Spectroscopy for White Blood Cell Count Analysis. Chemosensors, 10(11), 460. https://doi.org/10.3390/chemosensors10110460









