Simulation of Stimuli-Responsive Polymer Networks
Abstract
1. Introduction
2. Macroscopic Models, Finite Element and Phase Field Methods
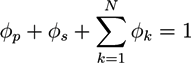
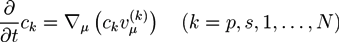
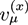 is the µth component of the local velocity of phase k. In this article, we use the summation convention for Greek indices that appear twice.
is the µth component of the local velocity of phase k. In this article, we use the summation convention for Greek indices that appear twice. 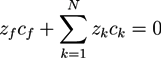
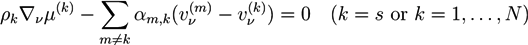
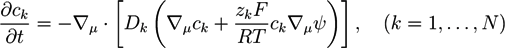
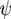 . For systems that show chemical reactions or a non-ideal mixing behavior of the solvent, extended versions of Equation (5) have been used, which include a term for the chemical activity or other source terms for the ions [49]. In [39], a convection term −∇μ(ckVμ), with a flow velocity V, is added to the right side of Equation (5). The electric potential
. For systems that show chemical reactions or a non-ideal mixing behavior of the solvent, extended versions of Equation (5) have been used, which include a term for the chemical activity or other source terms for the ions [49]. In [39], a convection term −∇μ(ckVμ), with a flow velocity V, is added to the right side of Equation (5). The electric potential 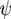 obeys the Poisson equation:
obeys the Poisson equation:
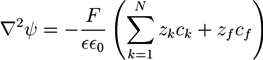
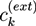 between the ion concentrations ck in the hydrogel and the respective concentrations
between the ion concentrations ck in the hydrogel and the respective concentrations 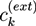 at the external boundary of the hydrogel:
at the external boundary of the hydrogel:
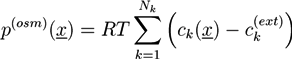
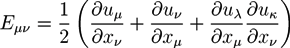
2.1. Phase Field Theory
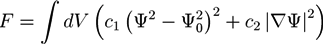
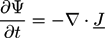
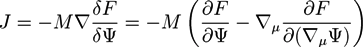
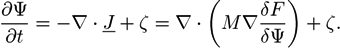
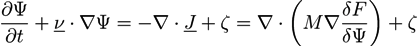
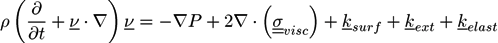
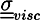 is the viscous stress tensor, ksurf and considers the surface tension from the interfaces [59]. The term kext represents external forces, such as gravity, while
is the viscous stress tensor, ksurf and considers the surface tension from the interfaces [59]. The term kext represents external forces, such as gravity, while 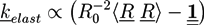 denotes the elastic response of polymers to a flow field, leading to viscoelastic behavior [67]. An alternative description of viscoelasticity is the Oldroyd-B model [68], which has been used, together with the PF method, to study the elongation and burst of viscoelastic droplets [69] and the coalescence of polymer drops and interfaces [61,70].
denotes the elastic response of polymers to a flow field, leading to viscoelastic behavior [67]. An alternative description of viscoelasticity is the Oldroyd-B model [68], which has been used, together with the PF method, to study the elongation and burst of viscoelastic droplets [69] and the coalescence of polymer drops and interfaces [61,70].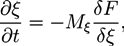
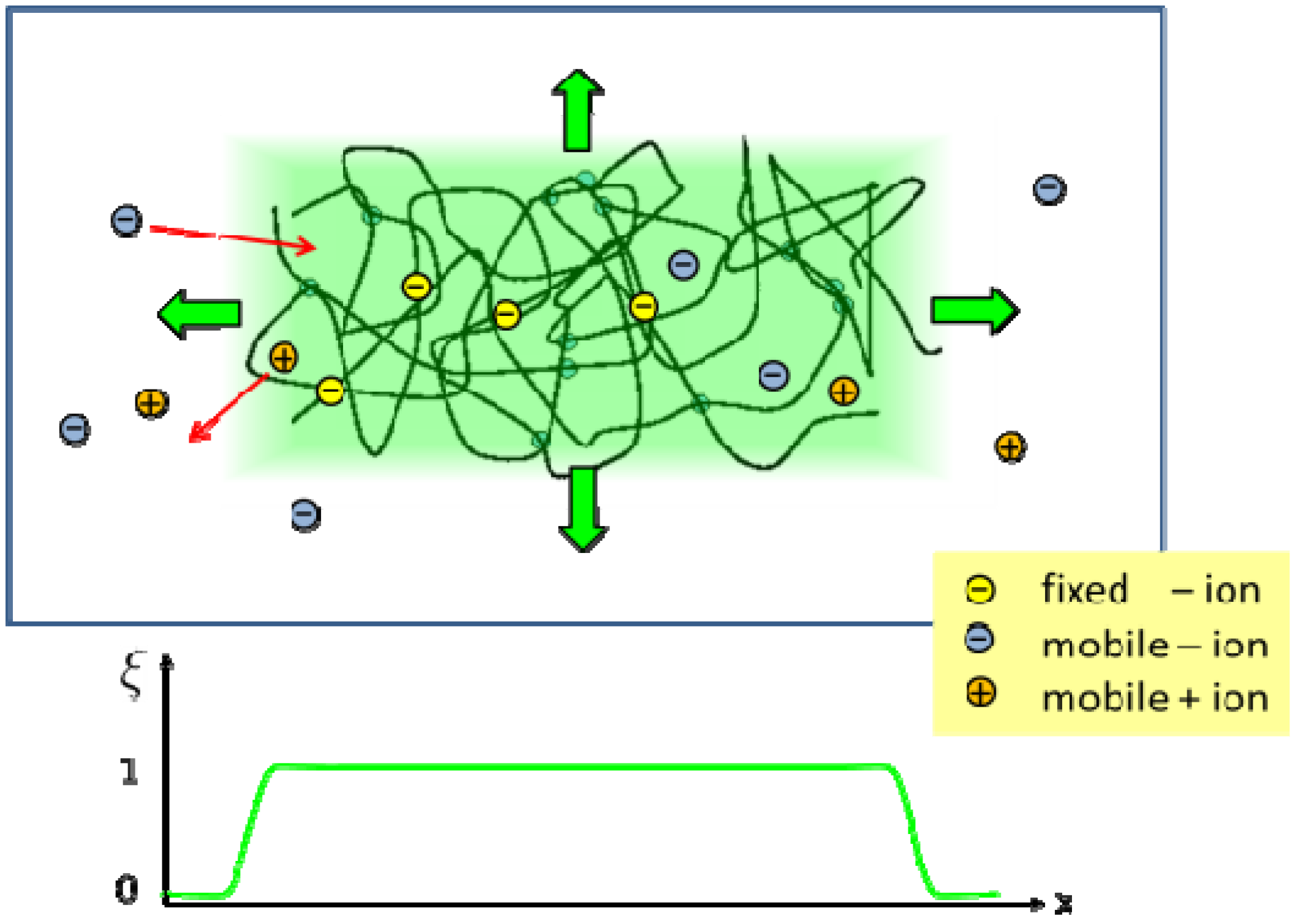
2.2. Phase Field Model of a Hydrogel
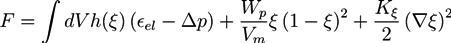
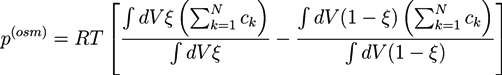
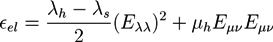
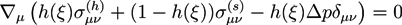
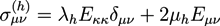 and
and 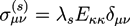 . The concentration of fixed charges is defined by:
. The concentration of fixed charges is defined by:
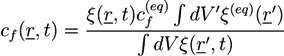
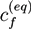 and ξ(eq) are the concentration of fixed ions and the phase field variable at the initial equilibrium state. Note that ∫ dV cf(r, t) = ∫ dV
and ξ(eq) are the concentration of fixed ions and the phase field variable at the initial equilibrium state. Note that ∫ dV cf(r, t) = ∫ dV 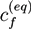 at all times. In the bath region, the concentration of fixed charges is zero inside the bath region while it is a finite constant inside the hydrogel region. The fields ξ, ck, cf,
at all times. In the bath region, the concentration of fixed charges is zero inside the bath region while it is a finite constant inside the hydrogel region. The fields ξ, ck, cf, 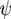 , and Eμv are coupled via Equations (19)–(23), which are solved simultaneously.
, and Eμv are coupled via Equations (19)–(23), which are solved simultaneously. 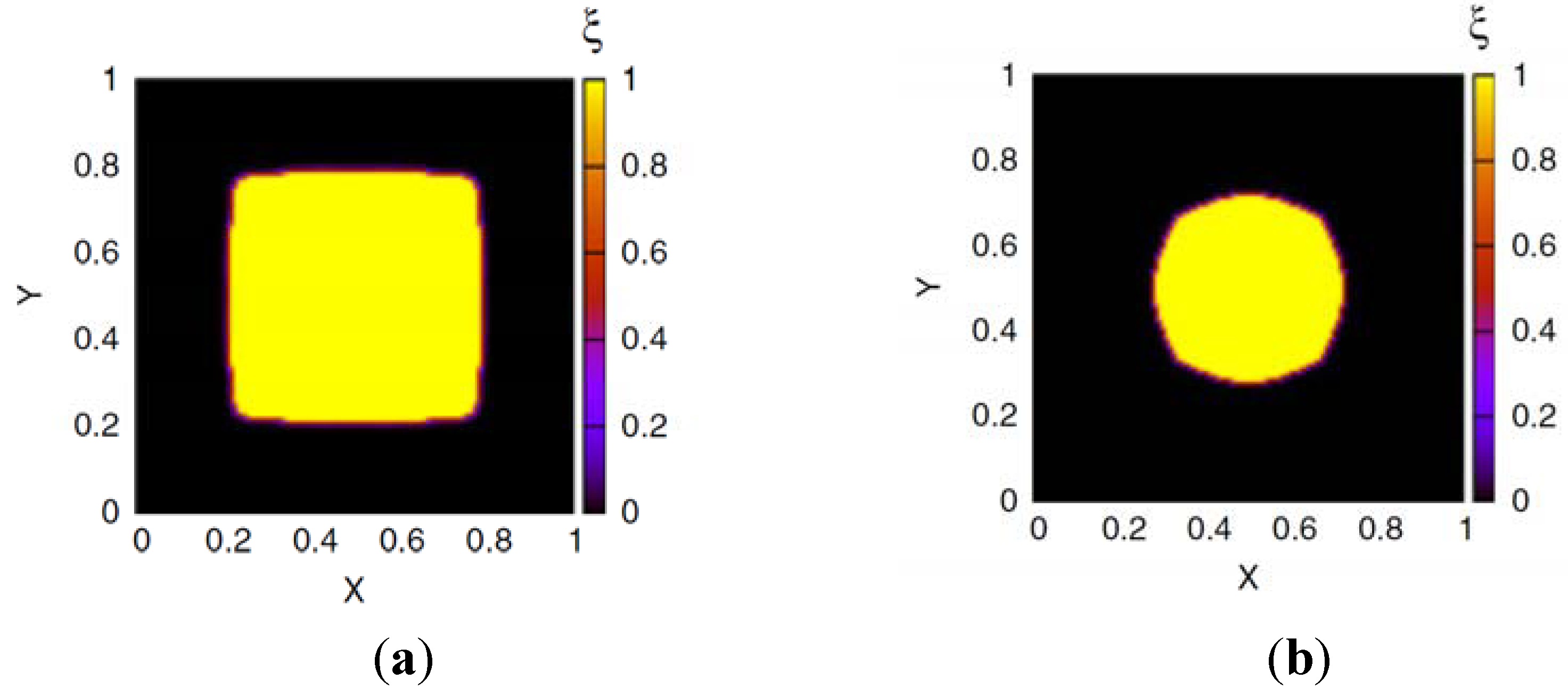
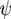 in the hydrogel region are determined by the Donnan equilibrium and electric neutrality conditions
in the hydrogel region are determined by the Donnan equilibrium and electric neutrality conditions
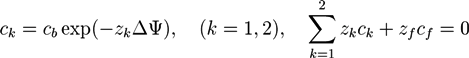
3. Self-Consistent Field Theory
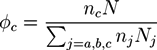
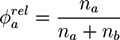
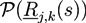 . A and B monomers have a local density
. A and B monomers have a local density 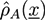 that can be divided into the density
that can be divided into the density  from type a homopolymers and the density
from type a homopolymers and the density 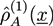 from the A part of the copolymers. Analogously, one has
from the A part of the copolymers. Analogously, one has  for the density of B monomers.
for the density of B monomers. 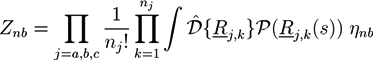
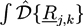 over all configurations of the kth polymer of type j. Path integrals are useful mathematical tools. They can be considered as the limit for N → ∞ of a 3N-dimensional integral that considers all configurations of a polymer with fixed length L and N atoms of diameter L/N. In practice, most path integrals cannot be solved numerically. One exception is the path integral of a single Gaussian chain. The basic idea of the self-consistent field theory is to transform Equation (27) such that only path integrals of single Gaussian chains have to be solved. In Equation (27), non-bonded interactions between polymers are considered by:
over all configurations of the kth polymer of type j. Path integrals are useful mathematical tools. They can be considered as the limit for N → ∞ of a 3N-dimensional integral that considers all configurations of a polymer with fixed length L and N atoms of diameter L/N. In practice, most path integrals cannot be solved numerically. One exception is the path integral of a single Gaussian chain. The basic idea of the self-consistent field theory is to transform Equation (27) such that only path integrals of single Gaussian chains have to be solved. In Equation (27), non-bonded interactions between polymers are considered by:
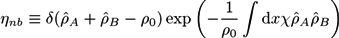
Self-Consistent Field Theory for Reversibly Crosslinked Polymer Networks
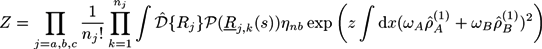
 with the gyration radius Rg of a free Gaussian polymer of length N. Dimensionless densities are given by
with the gyration radius Rg of a free Gaussian polymer of length N. Dimensionless densities are given by 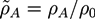 , while we use dimensionless free energies of the form
, while we use dimensionless free energies of the form 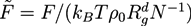 for a system with d dimensions. We use zred = zρ0/χ for the crosslink strength. The dimensionless mean field free energy can be divided into three terms [21]:
for a system with d dimensions. We use zred = zρ0/χ for the crosslink strength. The dimensionless mean field free energy can be divided into three terms [21]:
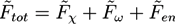
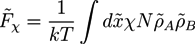
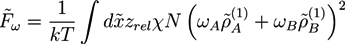
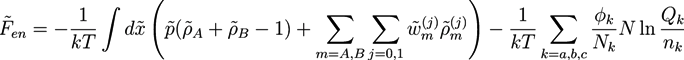
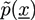 and
and 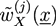 with X = A, B and j = 0, 1 are introduced in the HS transformation. The quantity Qk is the partition function of a single polymer chain of type k fluctuating in the auxiliary fields (see [20]). It can be calculated numerically by solving modified diffusion equations. In the saddle point approximation, the auxiliary fields
with X = A, B and j = 0, 1 are introduced in the HS transformation. The quantity Qk is the partition function of a single polymer chain of type k fluctuating in the auxiliary fields (see [20]). It can be calculated numerically by solving modified diffusion equations. In the saddle point approximation, the auxiliary fields 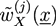 and
and 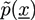 and, finally, the desired monomer densities
and, finally, the desired monomer densities 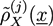 can be determined by considering that the variations of the free energy with respect to
can be determined by considering that the variations of the free energy with respect to 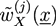 ,
, 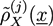 , and
, and 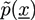 must vanish. An algorithm is described in [21].
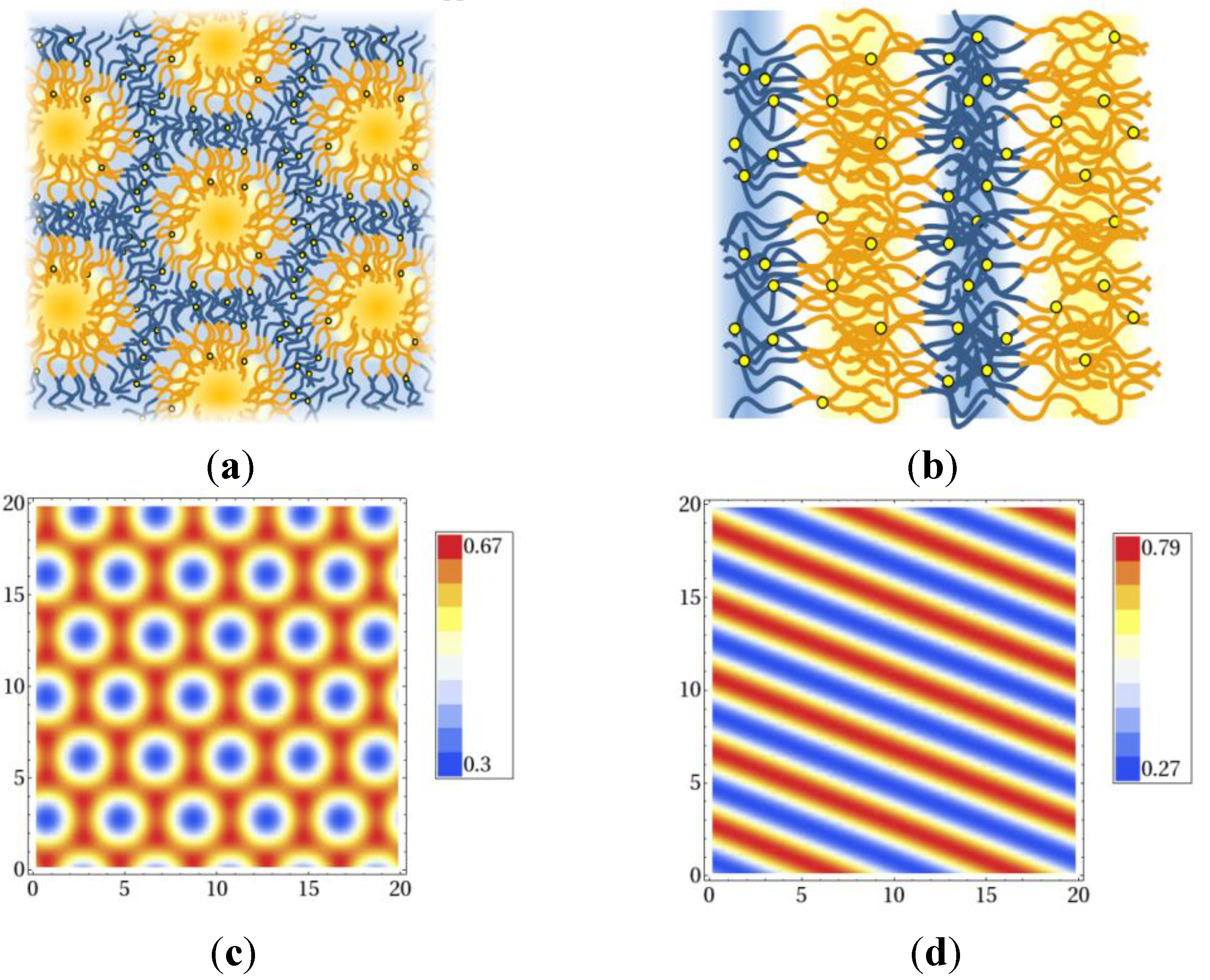
must vanish. An algorithm is described in [21].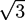 . The geometry supports the formation of a hexagonal as well as a lamellar phase. We have varied Lx in the range of 3.0 ≤ Lx ≤ 4.8 and determined the phase with the lowest free energy density. We find that for
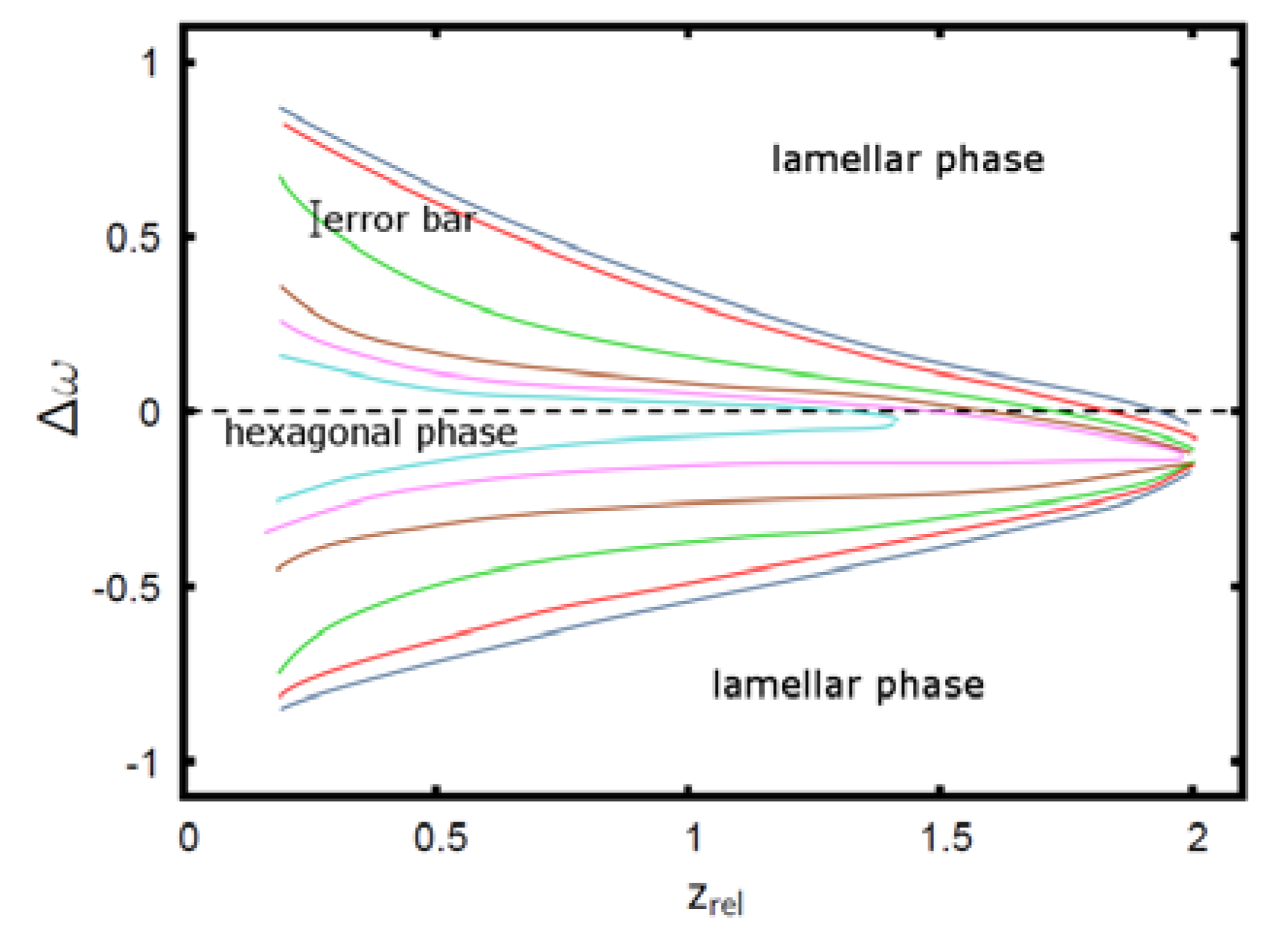
. The geometry supports the formation of a hexagonal as well as a lamellar phase. We have varied Lx in the range of 3.0 ≤ Lx ≤ 4.8 and determined the phase with the lowest free energy density. We find that for  and zrel > 0, only lamellar structures are stable. Otherwise, the hexagonal phase is stable if zrel and |∆w| are suitably small. In Figure 5, the phase boundaries between the hexagonal and the lamellar phase are shown for various A fractions of the homopolymers in the range of
and zrel > 0, only lamellar structures are stable. Otherwise, the hexagonal phase is stable if zrel and |∆w| are suitably small. In Figure 5, the phase boundaries between the hexagonal and the lamellar phase are shown for various A fractions of the homopolymers in the range of 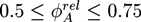 .
. 
4. Monte Carlo and Molecular Dynamic Simulations of Polymer Networks
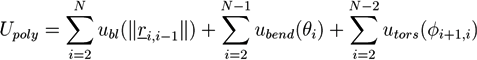
Monte Carlo Simulation of Filament Networks with Reversibly Binding Crosslinkers
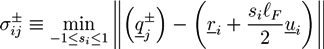
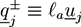 . The centers of the adhesive sites are localized on the crosslinker axis a distance la away from the crosslinker’s center of mass. We use lC = 2D and la = 1.35D, so that the adhesion sites lie inside the hemispheres of the crosslinkers.
. The centers of the adhesive sites are localized on the crosslinker axis a distance la away from the crosslinker’s center of mass. We use lC = 2D and la = 1.35D, so that the adhesion sites lie inside the hemispheres of the crosslinkers. 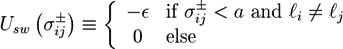
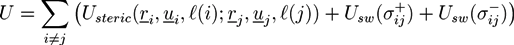
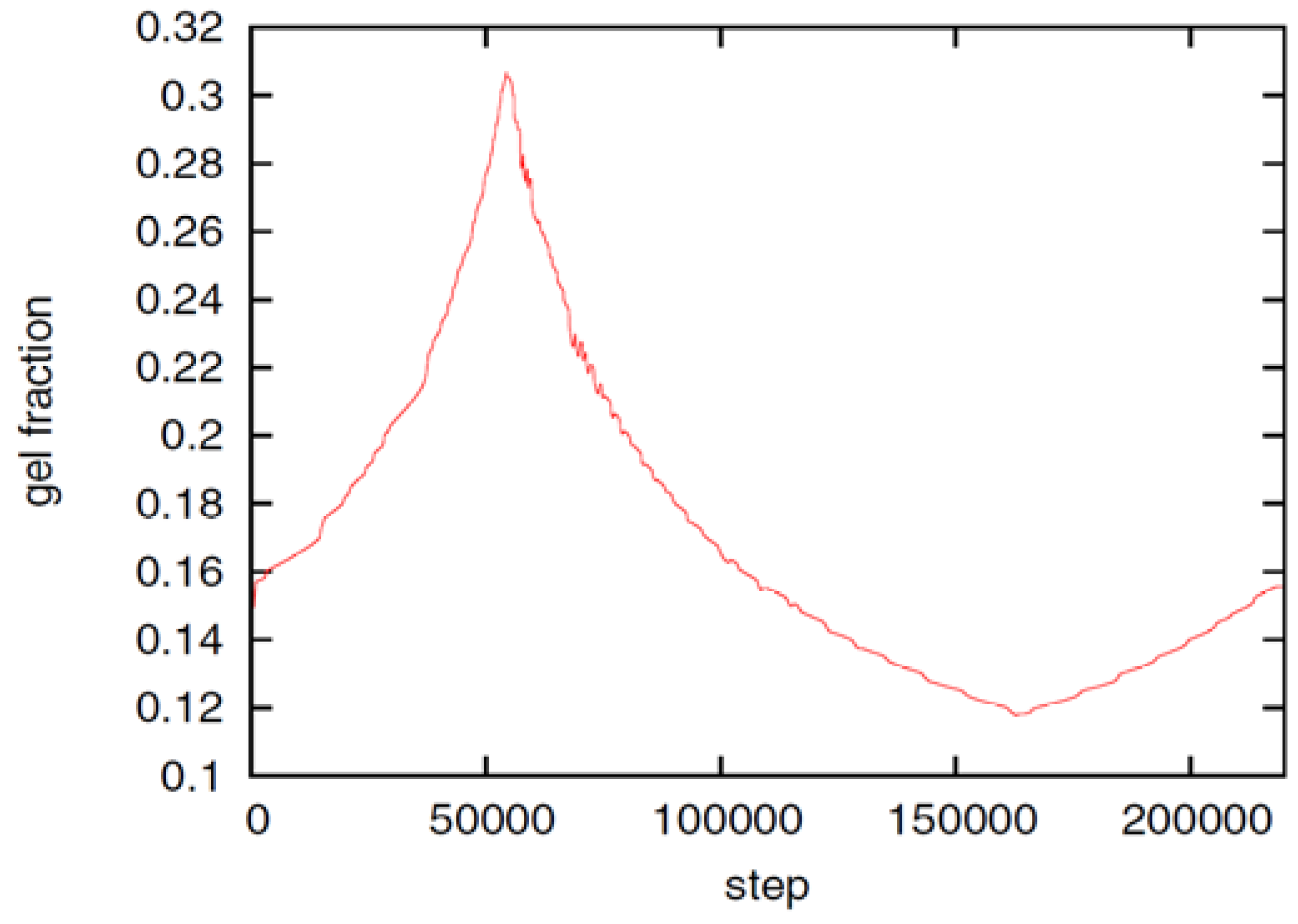
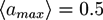 at the percolation threshold. In Figure 6a, phase diagram of the system is shown as a function of the adhesion strength ∊ /T and the filament volume fraction ϕ for fixed crosslinker-filament ratio nlr = 2. A percolated network forms if the filament volume fraction and the adhesion strength are large enough. This means, that a percolated network can be created and destroyed, reversibly, by changing the hydrogel volume or the temperature. Furthermore, the system forms bundles for suitably low filament volume fractions. This can be explained as follows: The system favors crosslinkers that are bound to filaments on both ends. Parallel filaments can be interconnected by a large number of crosslinks forming a ladder-like structure. At low filament concentrations, only aligned groups of filaments make it possible that large numbers of crosslinkers can bind on both ends. At high filament concentrations, crosslinkers can bind on both ends, even if the filament network is disordered. The phase diagram shows that percolated network may form with and without pronounced bundling and bundling can form with and without the formation of a percolated network.
at the percolation threshold. In Figure 6a, phase diagram of the system is shown as a function of the adhesion strength ∊ /T and the filament volume fraction ϕ for fixed crosslinker-filament ratio nlr = 2. A percolated network forms if the filament volume fraction and the adhesion strength are large enough. This means, that a percolated network can be created and destroyed, reversibly, by changing the hydrogel volume or the temperature. Furthermore, the system forms bundles for suitably low filament volume fractions. This can be explained as follows: The system favors crosslinkers that are bound to filaments on both ends. Parallel filaments can be interconnected by a large number of crosslinks forming a ladder-like structure. At low filament concentrations, only aligned groups of filaments make it possible that large numbers of crosslinkers can bind on both ends. At high filament concentrations, crosslinkers can bind on both ends, even if the filament network is disordered. The phase diagram shows that percolated network may form with and without pronounced bundling and bundling can form with and without the formation of a percolated network. 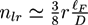 so that the percolation threshold is independent of the filament length if rlF is kept fixed.
so that the percolation threshold is independent of the filament length if rlF is kept fixed. 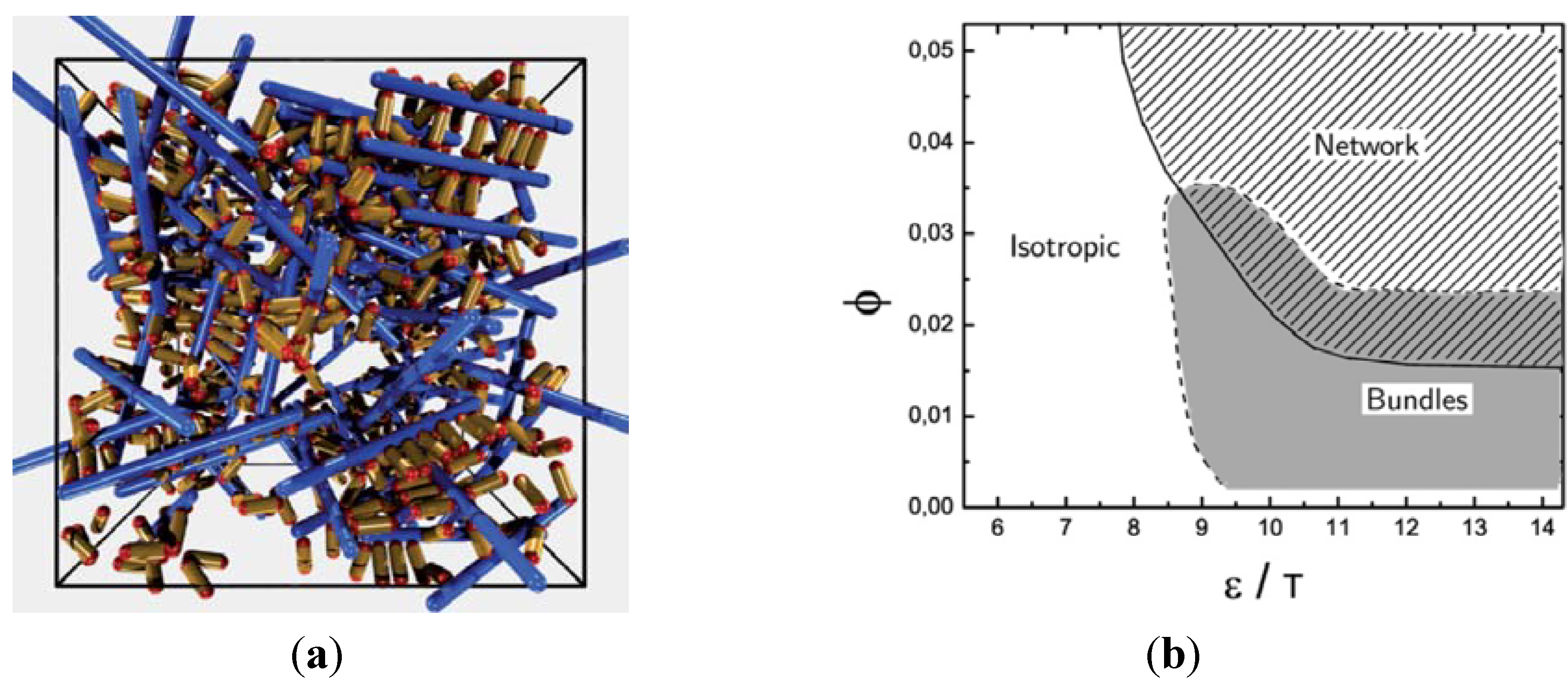
5. Summary and Conclusions
Acknowledgments
Conflict of Interest
References
- Jagur-Grodzinski, J. Polymeric gels and hydrogels for biomedical and pharmaceutical applications. Polym. Adv. Technol. 2010, 21, 27–47. [Google Scholar]
- Adelsberger, J.; Metwalli, E.; Diethert, A.; Grillo, I.; Bivigou-Koumba, A.M.; Laschewsky, A.; Müller-Buschbaum, P.; Papadakis, C.M. Kinetics of collapse transition and cluster formation in a thermoresponsive micellar solution of P(S-b-NIPAM-b-S) induced by a temperature jump. Macromol. Rapid Commun. 2012, 33, 254–259. [Google Scholar] [CrossRef]
- Huck, W.T.S. Materials chemistry: Polymer networks take a bow. Nature 2011, 472, 425–426. [Google Scholar] [CrossRef]
- Suzuki, A.; Ishii, T.; Maruyama, Y. Optical switching in polymer gels. J. Appl. Phys. 1996, 80, 131–136. [Google Scholar] [CrossRef]
- Deligkaris, K.; Tadele, T.S.; Olthuis, W.; van den Berg, A. Hydrogel-based devices for biomedical applications. Sensor. Actuat. B-Chem. 2010, 147, 765–774. [Google Scholar] [CrossRef]
- Na, K.; Lee, E.S.; Bae, Y.H. Self-organized nanogels responding to tumor extracellular pH: pH-dependent drug release and in vitro cytotoxicity against MCF-7 cells. Bioconjugate Chem. 2007, 18, 1568–1574. [Google Scholar] [CrossRef]
- Bassik, N.; Abebe, B.T.; Laflin, K.E.; Gracias, D.H. Photolithographically patterned smart hydrogel based bilayer actuators. Polymer 2010, 51, 6093–6098. [Google Scholar] [CrossRef]
- Holtz, J.H.; Asher, S.A. Polymerized colloidal crystal hydrogel films as intelligent chemical sensing materials. Nature 1997, 389, 829–832. [Google Scholar] [CrossRef]
- Nagai, D.; Suzuki, A.; Maki, Y.; Takeno, H. Reversible chain association/dissociation via a CO2 responsive crosslinking/decrosslinking system. Chem. Commun. 2011, 47, 8856–8858. [Google Scholar] [CrossRef]
- Çaykara, T.; Doğmuş, M. The effect of solvent composition on swelling and shrinking properties of poly(acrylamide-co-itaconic acid) hydrogels. Eur. Polym. J. 2004, 40, 2605–2609. [Google Scholar] [CrossRef]
- Casolaro, M.; Casolaro, I. Multiple stimuli-responsive hydrogels for metal-based drug therapy. Polymers 2012, 4, 964–985. [Google Scholar] [CrossRef]
- Tan, L.; Liu, Y.; Ha, W.; Ding, L.-S.; Peng, S.-L.; Zhang, S.; Li, B.-J. Stimuli-induced gel–sol transition of multi-sensitive supramolecular β-cyclodextrin grafted alginate/ferrocene modified pluronic hydrogel. Soft Matter 2012, 8, 5746–5749. [Google Scholar] [CrossRef]
- Guenther, M.; Kuckling, D.; Corten, C.; Gerlach, G.; Sorber, J.; Suchaneck, G.; Arndt, K.-F. Chemical sensors based on multiresponsive block copolymer hydrogels. Sens. Actuators B 2007, 126, 97–106. [Google Scholar] [CrossRef]
- Seliktar, D. Designing cell-compatible hydrogels for biomedical applications. Science 2012, 336, 1124–1128. [Google Scholar] [CrossRef]
- Richter, A.; Howitz, S.; Kuckling, D.; Arndt, K.F. Influence of volume phase transition phenomena on the behavior of hydrogel-based valves. Sens. Actuators B: Chem. 2004, 99, 451–458. [Google Scholar] [CrossRef]
- Serra, L.; Doménech, J.; Peppas, N.A. Drug transport mechanisms and release kinetics from molecularly designed poly(acrylic acid-g-ethylene glycol) hydrogels. Biomaterials 2006, 27, 5440–5451. [Google Scholar] [CrossRef]
- Wu, C.; Ying, A.; Ren, S. Fabrication of polymeric micelles with core–shell–corona structure for applications in controlled drug release. Colloid. Polym. Sci. 2013, 291, 827–834. [Google Scholar] [CrossRef]
- Yue, J.; Wang, R.; Liu, S.; Wu, S.; Xie, Z.; Huang, Y.; Jing, X. Reduction-responsive shell-crosslinked micelles prepared from Y-shaped amphiphilic block copolymers as a drug carrier. Soft Matter 2012, 8, 7426–7435. [Google Scholar] [CrossRef]
- Yan, X.; Weng, F.; Zheng, B.; Huang, F. Stimuli-responsive supramolecular polymeric materials. Chem. Soc. Rev. 2012, 41, 6042–6065. [Google Scholar] [CrossRef]
- Li, D.; Yang, H.L.; Emmerich, H. Phase field model simulations of hydrogel dynamics under chemical stimulation. Colloid Polym. Sci. 2011, 289, 513–521. [Google Scholar] [CrossRef]
- Li, D.; Gruhn, T.; Emmerich, H. Mean field theory for a reversibly crosslinked polymer network. J. Chem. Phys. 2012, 137, 024906. [Google Scholar] [CrossRef]
- Gruhn, T.; Li, D.; Emmerich, H. Calculating structural properties of reversibly crosslinked polymer systems using self-consistent field theory. Prog. Colloid Polym. Sci. 2013, in press. [Google Scholar]
- Gruhn, T.; Emmerich, H. Phase behavior of polymer blends with reversible crosslinks—A self-consistent field theory study. J. Mater. Res. 2013. [Google Scholar] [CrossRef]
- Chelakkot, R.; Lipowsky, R.; Gruhn, T. Self-assembling network and bundle structures in systems of rods and crosslinkers – A Monte Carlo study. Soft Matter 2009, 5, 1504–1513. [Google Scholar] [CrossRef]
- Chelakkot, R.; Gruhn, T. Length dependence of crosslinker induced network formation of rods: a Monte Carlo study. Soft Matter 2012, 8, 11746–11754. [Google Scholar] [CrossRef]
- Saunders, J.R.; Abu-Salih, S.; Khaleque, T; Hanula, S; Moussa, W. Modeling theories of intelligent hydrogel polymers. J. Comput. Theor. Nanosci. 2008, 5, 1942–1960. [Google Scholar] [CrossRef]
- Shahinpoor, M.; Kim, K.J. Ionic polymer-metal composites—III. Modeling and simulation as biomimetic sensors, actuators, transducers and artificial muscles. Smart Materials and Structures 2004, 13, 1362–1388. [Google Scholar] [CrossRef]
- Wu, S.; Li, H.; Chen, J.P.; Lam, K.Y. Modeling investigation of hydrogel volume transition. Macromol. Theory Simul. 2004, 13, 13–29. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J. Statistical mechanics of cross-linked polymer networks I. Rubberlike elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J. Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Doi, M.; Matsumoto, M.; Hirose, Y. Deformation of ionic polymer gels by electric fields. Macromolecules 1992, 25, 5504–5511. [Google Scholar] [CrossRef]
- Erman, B.; Flory, P.J. Critical phenomena and transitions in swollen polymer networks and in linear macromolecules. Macromolecules 1986, 19, 2342–2353. [Google Scholar] [CrossRef]
- English, A.E.; Mafé, S.; Manzanares, J.; Yu, X.; Grosberg, A.Y. Equilibrium swelling properties of polyampholytic hydrogels. J. Chem. Phys. 1996, 104, 8713–8720. [Google Scholar] [CrossRef]
- Okay, O.; Sariisik, S.B. Swelling behavior of poly(acrylamide-co-sodium acrylate) hydrogels in aqueous salt solutions: Theory versus experiments. Eur. Polym. J. 2000, 36, 393–399. [Google Scholar] [CrossRef]
- Çaykara, T.; Bozkaya, U.; Kantoğlu, Ö. Network Structure and Swelling Behavior of Poly(acrylamide/crotonic acid) Hydrogels in Aqueous Salt Solutions. J. Polym. Sci. Part B 2003, 41, 1656–1664. [Google Scholar] [CrossRef]
- Kramarenko, E.Y.; Khokhlov, A.R.; Yoshikawa, K. A three-state model for counterions in a dilute solution of weakly charged polyelectrolytes. Macromol. Theory Simul. 2000, 9, 249–256. [Google Scholar] [CrossRef]
- Keener, J.P.; Sircar, S.; Fogelson, A.L. Kinetics of swelling gels. Siam. J. Appl. Math. 2011, 71, 854–875. [Google Scholar] [CrossRef]
- Feng, L.; Jia, Y.; Chen, X.; Li, X.; An, L. A multiphasic model for the volume change of polyelectrolyte hydrogels. J. Chem. Phys. 2010, 133, 114904. [Google Scholar] [CrossRef]
- Chen, J.; Ma, G. Modelling deformation behaviour of polyelectrolyte gels under chemo-electro-mechanical coupling effects. Int. J. Numer. Meth. Engng. 2006, 68, 1052–1071. [Google Scholar] [CrossRef]
- Hon, Y.C.; Lu, M.W.; Xue, W.M.; Zhou, X. Numerical algorithm for triphasic model of charged and hydrated soft tissues. Comput. Mech. 2002, 29, 1–15. [Google Scholar] [CrossRef]
- Sun, D.N.; Gu, W.Y.; Guo, X.E.; Lai, W.M.; Mow, V.C. A mixed finite element formulation of triphasic mechano-electrochemical theory for charged, hydrated biological soft tissues. Int. J. Numer. Meth. Engng. 1999, 45, 1375–1402. [Google Scholar] [CrossRef]
- Freiboth, S.; Class, H.; Helmig, R.; Graf, T.; Ehlers, W.; Schwarz, W.; Vrettos, C. A model for multiphase flow and transport in porous media including a phenomenological approach to account for deformation—A model concept and its validation within a code intercomparison study. Comput. Geosci. 2009, 13, 281–300. [Google Scholar] [CrossRef]
- Zhou, X.; Hon, Y.C.; Sun, S.; Mak, A.F.T. Numerical simulation of the steady-state deformation of a smart hydrogel under an external electric field. Smart Mater. Struct. 2002, 11, 459–467. [Google Scholar] [CrossRef]
- De, S.K.; Aluru, N.R. A chemo-electro-mechanical mathematical model for simulation of pH sensitive hydrogels. Mech. Mater. 2004, 36, 395–410. [Google Scholar] [CrossRef]
- Hon, Y.C.; Lu, M.W.; Xue, W.M.; Zhou, X. A new formulation and computation of the triphasic model for mechano-electrochemical mixtures. Comput. Mech. 1999, 24, 155–165. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Hisada, T. Non-linear finite element analysis of mechanical electrochemical phenomena in hydrated soft tissues based on triphasic theory. Int. J. Numer. Meth. Engng. 2006, 65, 147–173. [Google Scholar] [CrossRef]
- Wallmersperger, T.; Ballhause, D.; Kröplin, B.; Günther, M.; Gerlach, G. Coupled multi-field formulation in space and time for the simulation of intelligent hydrogels. J. Intel. Mat. Syst. Str. 2009, 20, 1483–1492. [Google Scholar] [CrossRef]
- Li, H.; Luo, R.; Lam, K.Y. Multiphysics modeling of electrochemomechanically smart microgels responsive to coupled pH/electric stimuli. Macromol. Biosci. 2009, 9, 287–297. [Google Scholar] [CrossRef]
- Li, H.; Luo, R. Modeling and characterization of glucose-sensitive hydrogel: Effect of Young’s modulus. Biosens. Bioelectron. 2009, 24, 3630–3636. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Wang, Z.; Lam, K.Y. Multiphysics modelling of volume phase transition of ionic hydrogels responsive to thermal stimulus. Macromol. Biosci. 2005, 5, 904–914. [Google Scholar] [CrossRef]
- Sun, S.; Mak, A.F.T. The dynamical response of a hydrogel fiber to electrochemical stimulation. J. Polym. Sci. Part B 2001, 39, 236–246. [Google Scholar] [CrossRef]
- Luo, R.; Li, H.; Lam, K.Y. Modeling and simulation of chemo-electro-mechanical behavior of pH-electric-sensitive hydrogel. Anal. Bioanal. Chem. 2007, 389, 863–873. [Google Scholar] [CrossRef]
- Wang, Q.X.; Li, H.; Lam, K.Y. Meshless Simulation of Equilibrium Swelling/Deswelling of PH-Sensitive Hydrogels. J. Polym. Sci. Part B 2006, 44, 326–337. [Google Scholar] [CrossRef]
- Li, H.; Ng, Y.; Cheng, J.Q.; Lam, K.Y. Hermite–Cloud: A novel true meshless method. Comput. Mech. 2003, 33, 30–41. [Google Scholar] [CrossRef]
- Li, H.; Mulay, S.S. 2D simulation of the deformation of pH-sensitive hydrogel by novel strong-form meshless random differential quadrature method. Comput. Mech. 2011, 48, 729–753. [Google Scholar] [CrossRef]
- Li, H.; Ng, T.Y.; Yew, Y.K.; Lam, K.Y. Modeling and simulation of the swelling behavior of ph-stimulus-responsive hydrogels. Biomacromolecules 2005, 6, 109–120. [Google Scholar] [CrossRef]
- Anders, D.; Weinberg, K. A variational approach to the decomposition of unstable viscous fluids and its consistent numerical approximation. ZAMM Z. Angew. Math. Mech. 2011, 91, 609–629. [Google Scholar] [CrossRef]
- Tian, H.; Shao, J.; Ding, Y.; Li, Y.; Li, X. Numerical studies of electrically induced pattern formation by coupling liquid dielectrophoresis and two-phase flow. Electrophoresis 2011, 32, 2245–2252. [Google Scholar]
- Boffetta, G.; Mazzino, A.; Musacchio, S.; Vozella, L. Rayleigh-Taylor instability in a viscoelastic binary fluid. J. Fluid mech. 2010, 643, 127–136. [Google Scholar] [CrossRef]
- Xu, H.; Bellehumeur, C.T. Modeling the morphology development of ethylene copolymers in rotational molding. J. Appl. Polym. Sci. 2006, 102, 5903–5917. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.; Liu, C.; Shen, J. Diffuse-interface simulations of drop coalescence and retraction in viscoelastic fluids. J. Non-Newton. Fluid Mech. 2005, 129, 163–176. [Google Scholar] [CrossRef]
- Emmerich, H. Advances of and by phase-field modelling in condensed-matter physics. Adv. Phys. 2008, 57, 1–87. [Google Scholar] [CrossRef]
- Cahn, J.; Hilliard, J. Free energy of a nonuniform system. 1. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Flory, P. Thermodynamics of high polymer solutions. J. Chem. Phys. 1942, 10, 51–61. [Google Scholar] [CrossRef]
- Huggins, M. Theory of solutions of high polymers. J. Am. Chem. Soc. 1942, 64, 1712–1719. [Google Scholar] [CrossRef]
- Li, Y.C.; Shi, R.P.; Wang, C.P.; Liu, X.J.; Wang, Y. Predicting microstructures in polymer blends under two-step quench in two-dimensional space. Phys. Rev. E 2011, 83, 041502. [Google Scholar]
- Bird, R.; Curtiss, C.; Hassager, O.; Armstrong, R. Dynamics of Polymeric Liquids; Volume 2, Wiley: New York, NY, USA, 1987. [Google Scholar]
- Oldroyd, J. The effect of interfacial stabilizing films on the elastic and viscous properties of emulsions. Proc. R. Soc. A 1955, 232, 567–577. [Google Scholar] [CrossRef]
- Beaucourt, J.; Biben, T.; Verdier, C. Elongation and burst of axisymmetric viscoelastic droplets: a numerical study. Phys. Rev. 2005, E71, 066309. [Google Scholar]
- Yue, P.; Zhou, C.; Feng, J.J. A computational study of the coalescence between a drop and an interface in newtonian and viscoelastic fluids. Phys. Fluids 2006, 18, 102102. [Google Scholar] [CrossRef]
- Hohenberg, P.; Halperin, B. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Badalassi, V.; Ceniceros, H.; Banerjee, S. Computation of multiphase systems with phase field models. J. Comput. Phys. 2003, 190, 371–397. [Google Scholar] [CrossRef]
- Müller-Krumbhaar, H.; Emmerich, H.; Brener, E.; Hartmann, M. Dewetting hydrodynamics in 1+1 dimensions. Phys. Rev. E 2001, 63, 026304. [Google Scholar] [CrossRef]
- Allen, S.; Cahn, J. Microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Wang, D.; Shi, T.; Chen, J.; An, L.; Jia, Y. Simulated morphological landscape of polymer single crystals by phase field model. J. Chem. Phys. 2008, 129, 194903. [Google Scholar] [CrossRef]
- Xu, H.; Matkar, R.; Kyu, T. Phase-field modeling on morphological landscape of isotactic polystyrene single crystals. Phys. Rev. E 2005, 72, 011804. [Google Scholar] [CrossRef]
- Ricka, J.; Tanaka, T. Swelling of ionic gels: Quantitative performance of the Donnan theory. Macromolecules 1984, 17, 2916–2921. [Google Scholar] [CrossRef]
- Edwards, S.F. The statistical mechanics of polymers with excluded volume. Proc. Phys. Soc. 1965, 85, 613–624. [Google Scholar] [CrossRef]
- Helfand, E.; Yukiko, T. Theory of the interface between immiscible polymers. II. J. Chem. Phys. 1972, 56, 3592–3601. [Google Scholar] [CrossRef]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help to test theories and to interpret experiments. J. Polym. Sci., Part B: Polym. Phys. 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Wang, J.; Müller, M.; Wang, Z.-G. Nucleation in A/B/AB blends: Interplay between microphase assembly and macrophase separation. J. Chem. Phys. 2009, 130, 154902. [Google Scholar] [CrossRef]
- Müller, M.; Schmid, F. Incorporating fluctuations and dynamics in self-consistent field theories for polymer blends. Adv. Polym. Sci. 2005, 185, 1–56. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Ganesan, V.; Drolet, F. Field-theoretic computer simulation methods for polymers and complex fluids. Macromolecules 2002, 35, 16–39. [Google Scholar] [CrossRef]
- Schmid, F. Self-consistent-field theories for complex fluids. J. Phys.: Condens. Matter 1998, 10, 8105–8138. [Google Scholar] [CrossRef]
- Benhamou, M.; Derouiche, A.; Bettachy, A.; Elhajjaji, F. Critical microphase properties of crosslinked polymer blends with quenched random impurities. Eur. Phys. J. E 2011, 34, 1–8. [Google Scholar] [CrossRef]
- Mao, X.; Goldbart, P.M.; Xing, X.; Zippelius, A. Soft random solids and their heterogeneous elasticity. Phys. Rev. E 2009, 80, 031140. [Google Scholar] [CrossRef]
- Ulrich, S.; Mao, X.; Goldbart, M.; Zippelius, A. Elasticity of highly cross-linked random networks. Europhys. Lett. 2006, 76, 677–682. [Google Scholar] [CrossRef]
- Helfand, E. Theory of inhomogeneous polymers: Fundamentals of the Gaussian random-walk model. J. Chem. Phys. 1975, 62, 999–1005. [Google Scholar] [CrossRef]
- Düchs, D.; Ganesan, V.; Fredrickson, G.H.; Schmid, F. Fluctuation effects in ternary AB+A+B polymeric emulsions. Macromolecules 2003, 36, 9237–9248. [Google Scholar] [CrossRef]
- Bates, F.S.; Maurer, W.W.; Lipic, P.M.; Hillmyer, M.A.; Almdal, K.; Mortensen, K.; Fredrickson, G.H.; Lodge, T.P. Polymeric bicontinuous microemulsions. Phys. Rev. Lett. 1997, 79, 849–852. [Google Scholar] [CrossRef]
- Hillmyer, M.A.; Maurer, W.W.; Lodge, T.P.; Bates, F.S.; Almdal, K.J. Model bicontinuous microemulsions in ternary homopolymer/block copolymer blends. Phys. Chem. 1999, 103, 4814–4824. [Google Scholar]
- Secchi, E.; Roversi, T.; Buzzaccaro, S.; Piazza, L.; Piazza, R. Biopolymer gels with “physical” cross-links: gelation kinetics, aging, heterogeneous dynamics, and macroscopic mechanical properties. Soft Matter 2013, 9, 3931–3944. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulations of Liquids, Reprint ed.; Oxford University Press: Oxford, Great Britain, 1993. [Google Scholar]
- Frenkel, D.; Smith, B. Understanding Molecular Simulation, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Kotelyanskii, M.; Theodorou, D.N. Simulation Methods for Polymers, 1st ed.; Marcel Dekker Inc.: New York, NY, USA, 2004. [Google Scholar]
- Masoud, H.; Alexeev, A. Controlled release of nanoparticles and macromolecules from responsive microgel capsules. ACS Nano 2012, 6, 212–219. [Google Scholar] [CrossRef]
- Netz, R.R. Polyelectrolytes in electric fields. J. Phys. Chem. B 2003, 107, 8208–8217. [Google Scholar] [CrossRef]
- Phadke, A.; Zhang, C.; Arman, B.; Hsu, C.-C.; Mashelkar, R.A.; Lele, A.K.; Tauber, M.J.; Arya, G.; Varghese, S. Rapid self-healing hydrogels. Proc. Natl. Acad. Sci. USA 2012, 109, 4383–4388. [Google Scholar] [CrossRef]
- Trewin, A.; Willock, D.J.; Cooper, A.I. Atomistic simulation of micropore structure, surface area, and gas sorption properties for amorphous microporous polymer networks. J. Phys. Chem. C 2008, 112, 20549–20559. [Google Scholar] [CrossRef]
- Jang, S.S.; Goddard, W.A., 3rd; Kalani, M.Y.S. Mechanical and transport properties of the poly(ethylene oxide)-poly(acrylic acid) double network hydrogel from molecular dynamic simulations. J. Phys. Chem. B 2007, 111, 1729–1737. [Google Scholar] [CrossRef]
- Wu, C.; Xu, W. Atomistic simulation study of absorbed water influence on structure and properties of crosslinked epoxy resin. Polymer 2007, 48, 5440–5448. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Lu, Z.-Y.; Zhang, Z.G.; Sun, C.-C.; Cui, T. Multiscale simulation study on the curing reaction and the network structure in a typical epoxy system. Macromolecules 2011, 44, 8650–8660. [Google Scholar] [CrossRef]
- Deshmukh, S.; Mooney, D.A.; McDermott, T.; Kulkarnib, S.; Don MacElroya, J.M. Molecular modeling of thermo-responsive hydrogels: observation of lower critical solution temperature. Soft Matter 2009, 5, 1514–1521. [Google Scholar] [CrossRef]
- Aydt, E.M.; Hentschke, R. Swelling of a model network: A Gibbs-ensemble molecular dynamics study. J. Chem. Phys. 2000, 112, 5480–5487. [Google Scholar] [CrossRef]
- Quesada-Pérez, M.; Maroto-Centeno, J.A.; Martín-Molina, A. Effect of the counterion valence on the behavior of thermo-sensitive gels and microgels: A Monte Carlo Simulation Study. Macromolecules 2012, 45, 8872–8879. [Google Scholar]
- Schneider, S.; Linse, P. Swelling of cross-linked polyelectrolyte gels. Eur. Phys. J. E 2002, 8, 457–460. [Google Scholar]
- Schneider, S.; Linse, P. Discontinuous volume transitions in cross-linked polyelectrolyte gels induced by short-range attractions and strong electrostatic coupling. Macromolecules 2004, 37, 3850–3856. [Google Scholar] [CrossRef]
- Guo, L.; Luijten, E. Reversible gel formation of triblock copolymers studied by molecular dynamics simulation. J. Polym. Sci. Part B 2005, 43, 959–969. [Google Scholar]
- Schneider, S.; Linse, P. Monte carlo simulation of defect-free cross-linked polyelectrolyte gels. J. Phys. Chem. B 2003, 107, 8030–8040. [Google Scholar] [CrossRef]
- Jamal, M.; Zarafshar, A.M.; Gracias, D.H. Differentially photo-crosslinked polymers enable self-assembling microfluids. Nature Commun. 2011, 2, 527. [Google Scholar] [CrossRef]
- Kim, J.; Hanna, J.A.; Byun, M.; Santangelo, C.D.; Hayward, R.C. Resigning Responsive Backled Surfaces by Halftone Gel Lithography. Science 2012, 335, 1201–1205. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gruhn, T.; Emmerich, H. Simulation of Stimuli-Responsive Polymer Networks. Chemosensors 2013, 1, 43-67. https://doi.org/10.3390/chemosensors1030043
Gruhn T, Emmerich H. Simulation of Stimuli-Responsive Polymer Networks. Chemosensors. 2013; 1(3):43-67. https://doi.org/10.3390/chemosensors1030043
Chicago/Turabian StyleGruhn, Thomas, and Heike Emmerich. 2013. "Simulation of Stimuli-Responsive Polymer Networks" Chemosensors 1, no. 3: 43-67. https://doi.org/10.3390/chemosensors1030043
APA StyleGruhn, T., & Emmerich, H. (2013). Simulation of Stimuli-Responsive Polymer Networks. Chemosensors, 1(3), 43-67. https://doi.org/10.3390/chemosensors1030043



