Identifying High-Risk Factors of Depression in Middle-Aged Persons with a Novel Sons and Spouses Bayesian Network Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Used for Experimentation
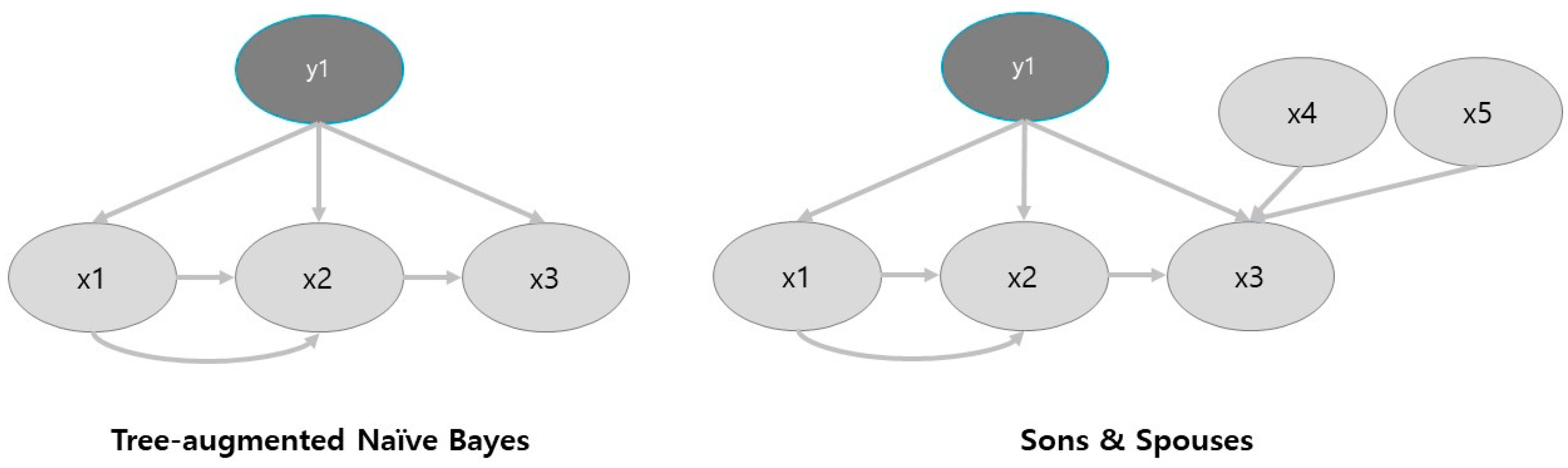
2.2. Machine Learning Approach Based on Bayesian Statistics
2.3. Artificial Intelligence Approach Based on a Genetic Algorithm
2.4. Benchmarked Classifiers
3. Results
3.1. Feature Selection through Sons and Spouses Network Formulation
3.2. Benchmarking the Performance of the Obtained Sons and Spouses Model
3.3. Identifying the Main Causes of Inducing and Reducing Depression with Genetic Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| ID | Name | Classification |
|---|---|---|
| Sex2 | Gender | 1. Male 2. Female |
| age2 | Age | 29~38 (30 s) 39~48 (40 s) 40~58 (50 s) |
| incm | Income Quartile (individual) | 1. Low 2. Middle low 3. Middle high 4. High |
| marri_2 | Marital status | 1. Married, live together 2. Married, live separated 3. Separated by death 4. Divorced 5. Unmarried |
| EC1_1 | Current economic status | 1. Yes (Employed) 2. No (Unemployed, economically inactive) |
| BD1_11 | Drinking frequency in one year | 0. N/A 1. I haven’t drunk at all in the last one year. 2. Less than once a month 3. About once a month 4. 2–4 times a month 5. Two or three times a week. 6. More than four times a week |
| BS1_1 | Smoking experience | 1. Less than 5 packs (100 pieces) 2. Five packs (100 pieces) or more 3. Non-smoker |
| HE_BMI | Body mass index | 1. Under Weigh (less than 18.5) 2. Normal Weight (18.5~22.9) 3. Over-Weight (23~29.9) 4. Mild Obesity (30~34.9) 5. Obese (35~39.9) 6. Severe Obesity (more than 39.9) |
| D_1_1 | Subjective health condition | 1.Very good 2.Good 3.Normal 4.Bad 5.Very bad |
| DI1_dg | Doctor’s diagnosis status for hypertension | 0. No 1. Yes |
| DI3_dg | Doctor’s diagnosis status for stroke | |
| DI5_dg | Doctor’s diagnosis status for myocardial infarction | |
| DI6_dg | Doctor’s diagnosis status for angina | |
| DM1_dg | Doctor’s diagnosis status for arthritis | |
| DM4_dg | Doctor’s diagnosis status for osteoporosis | |
| DJ2_dg | Doctor’s diagnosis status for pulmonary tuberculosis | |
| DJ4_dg | Doctor’s diagnosis status for asthma | |
| DE1_dg | Doctor’s diagnosis status for diabetes | |
| DE2_dg | Doctor’s diagnosis status for thyroid | |
| DC4_dg | Doctor’s diagnosis status for breast cancer | |
| DC5_dg | Doctor’s diagnosis status for cervical cancer | |
| DC7_dg | Doctor’s diagnosis status for thyroid cancer | |
| HE_HbA1c | Glycated hemoglobin | __% |
| HE_HB | hemoglobin | __g/dL |
| HE_hsCRP | High-sensitivity of C-reactive protein | __mg/L |
| OR1_2 | Oral examination in the last year | 0. No 1. Yes |
| LQ_5EQL | EuroQoL: Anxiety/Depression | 1. I’m not anxious/depressed 2. I’m anxious/depressed |
References
- Chang, Y.-S.; Fan, C.-T.; Lo, W.-T.; Hung, W.-C.; Yuan, S.-M. Mobile cloud-based depression diagnosis using an ontology and a Bayesian network. Future Gener. Comput. Syst. 2015, 43–44, 87–98. [Google Scholar] [CrossRef]
- Andrews, G.; Poulton, R.; Skoog, I. Lifetime risk of depression: Restricted to a minority or waiting for most? Br. J. Psychiatry 2005, 187, 495–496. [Google Scholar] [CrossRef] [PubMed]
- Mirowsky, J.; Ross, C.E. Age and Depression. J. Health Soc. Behav. 1992, 33, 187. [Google Scholar] [CrossRef] [PubMed]
- Leem, A.Y.; Han, C.H.; Ahn, C.M.; Lee, S.H.; Kim, J.Y.; Chun, E.M.; Yoo, K.H.; Jung, J.Y.; Shim, J.J.; Jung, T.H.; et al. Factors associated with stage of change in smoker in relation to smoking cessation based on the Korean National Health and Nutrition Examination Survey II-V. PLoS ONE 2017, 12, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Mirowsky, J. Age and the Gender Gap in Depression. J. Health Soc. Behav. 1996, 37, 362. [Google Scholar] [CrossRef]
- Miech, R.A.; Shanahan, M.J. Socioeconomic Status and Depression over the Life Course. J. Health Soc. Behav. 2000, 41, 162. [Google Scholar] [CrossRef]
- Gold, P.W.; Machado-Vieira, R.; Pavlatou, M.G. Clinical and biochemical manifestations of depression: Relation to the neurobiology of stress. Neural Plast. 2015, 2015, 7–9. [Google Scholar] [CrossRef]
- Cipriani, A.; Geddes, J.R.; Furukawa, T.A.; Barbui, C. Metareview on short-term effectiveness and safety of antidepressants for depression: An evidence-based approach to inform clinical practice. Can. J. Psychiatry 2007, 52, 553–562. [Google Scholar] [CrossRef]
- Pratt, L.A.; Brody, D.J.; Gu, Q. Antidepressant Use among Persons Aged 12 and Over: United States, 2011–2014. NCHS Data Brief 2017, 283, 1–8. [Google Scholar]
- Kim, M.J.; Kim, N.; Shin, D.; Rhee, S.J.; Hyung Keun Park, C.; Kim, H.; Cho, S.J.; Lee, J.W.; Kim, E.Y.; Yang, B.; et al. The epidemiology of antidepressant use in South Korea: Does short-term antidepressant use affect the relapse and recurrence of depressive episodes? PLoS ONE 2019, 14, 1–15. [Google Scholar] [CrossRef]
- How, M.L.; Cheah, S.M.; Chan, Y.J.; Khor, A.C.; Say, E.M.P. Artificial intelligence-enhanced decision support for informing global sustainable development: A human-centric Ai-Thinking approach. Information 2020, 11, 39. [Google Scholar] [CrossRef]
- Madden, M.G. On the classification performance of TAN and general Bayesian networks. Knowl. Based Syst. 2009, 22, 489–495. [Google Scholar] [CrossRef]
- Kim, C.; Costello, F.J.; Lee, K.C.; Li, Y.; Li, C. Predicting factors affecting adolescent obesity using general bayesian network and what-if analysis. Int. J. Environ. Res. Public Health 2019, 16, 4684. [Google Scholar] [CrossRef] [PubMed]
- Oh, J.; Yun, K.; Maoz, U.; Kim, T.S.; Chae, J.H. Identifying depression in the National Health and Nutrition Examination Survey data using a deep learning algorithm. J. Affect. Disord. 2019, 257, 623–631. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2011. [Google Scholar]
- Cliff, O.M.; Prokopenko, M.; Fitch, R. Minimising the kullback-leibler divergence for model selection in distributed nonlinear systems. Entropy 2018, 20, 51. [Google Scholar] [CrossRef]
- Barber, D. Bayesian Reasoning and Machine Learning. Bayesian Reason. Mach. Learn. 2011. [Google Scholar] [CrossRef]
- Prabhakaran, R.; Krishnaprasad, R.; Nanda, M.; Jayanthi, J. System Safety Analysis for Critical System Applications Using Bayesian Networks. Procedia Comput. Sci. 2016, 93, 782–790. [Google Scholar] [CrossRef][Green Version]
- Yuan, C.; Lim, H.; Lu, T.C. Most relevant explanation in bayesian networks. J. Artif. Intell. Res. 2011, 42, 309–352. [Google Scholar] [CrossRef]
- Larranaga, P. Structure learning of bayesian networks by genetic algorithms: A performance analysis of control parameters. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 912–926. [Google Scholar] [CrossRef]
- Olson, D.L.; Delen, D.; Meng, Y. Comparative analysis of data mining methods for bankruptcy prediction. Decis. Support Syst. 2012, 52, 464–473. [Google Scholar] [CrossRef]
- Huang, M.W.; Chen, C.W.; Lin, W.C.; Ke, S.W.; Tsai, C.F. SVM and SVM ensembles in breast cancer prediction. PLoS ONE 2017, 12, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Ballings, M.; van den Poel, D.; Hespeels, N.; Gryp, R. Evaluating multiple classifiers for stock price direction prediction. Expert Syst. Appl. 2015, 42, 7046–7056. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Chen, A.; Jin, X.; Che, H. Prediction of Type 2 Diabetes Risk and Its Effect Evaluation Based on the XGBoost Model. Healthcare 2020, 8, 247. [Google Scholar] [CrossRef]


| Node | Relative Binary Mutual Information | Posterior Mean Value | Max Bayes Factor for No Depression | Min Bayes Factor for No Depression | Max Bayes Factor for Depression | Min Bayes Factor for Depression |
|---|---|---|---|---|---|---|
| Subjective Health Condition | 9.74% | 1.59 | Very Good (1.0647) | Very Bad (0.6807) | Very Bad (0.6807) | Very Good (1.0647) |
| Income Quartile | 2.12% | 1.50 | High (1.0266) | Low (0.9530) | Low (0.9530) | High (1.0266) |
| Marital Status | 1.84% | 2.15 | Married Live Together (1.0127) | Divorced (0.9183) | Divorced (0.9183) | Married Live Together (1.0127) |
| Economic Status | 1.78% | 0.77 | Yes (1.0150) | No (0.9537) | No (0.9537) | Yes (1.0150) |
| Diagnosed Arthritis | 0.56% | 0.05 | No (1.0035) | Yes (0.9308) | Yes (0.9308) | No (1.0035) |
| Gender | 0.39% | 0.46 | Male (1.0128) | Female (0.9893) | Female (0.9893) | Male (1.0128) |
| Diagnosed Diabetes | 0.19 | 0.04 | No (1.0018) | Yes (0.9579) | Yes (0.9579) | No (1.0018) |
| SS | TAN | LOG | SVM | NN | DT | ADA | BA | RSS | RF | |
|---|---|---|---|---|---|---|---|---|---|---|
| F-Measure | ||||||||||
| Total | 91.81 | 91.00 | 90.70 | N/A | 90.00 | N/A | N/A | 90.50 | N/A | 90.20 |
| Accuracy | ||||||||||
| Total | 93.04 | 92.59 | 93.39 | 93.32 | 91.31 | 93.32 | 93.32 | 93.26 | 93.32 | 92.97 |
| AUC | ||||||||||
| Total | 76.97 | 75.20 | 75.90 | 50.00 | 65.40 | 49.80 | 73.30 | 74.20 | 73.90 | 71.30 |
| Precision | ||||||||||
| Total | 93.14 | 90.01 | 91.10 | N/A | 89.00 | N/A | N/A | 90.30 | N/A | 88.70 |
| Recall | ||||||||||
| Total | 90.60 | 92.60 | 93.40 | 93.30 | 91.30 | 93.30 | 93.30 | 90.50 | 93.30 | 93.30 |
| Most Probable Cause of Depression | ||||||||
|---|---|---|---|---|---|---|---|---|
| Age | Diagnosed Arthritis | Diagnosed Diabetes | Diagnosed Hypertension | Economic Status | Gender | Glycated Hemoglobin | Hemoglobin | |
| 1 | 50s | Yes | Yes | No | No | Male | ≤8(3/4) | ≤10(1/7) |
| 2 | 40s | Yes | No | Yes | No | Female | ≤8(3/4) | ≤16(6/7) |
| 3 | 50s | Yes | Yes | No | No | Male | >8(4/4) | ≤10(1/7) |
| 4 | 50s | Yes | Yes | No | No | Male | >8(4/4) | ≤10(1/7) |
| 5 | 50s | Yes | Yes | No | No | Female | ≤6(2/4) | ≤15(5/7) |
| Income Quartile | Marital Status | Oral Examination | Smoking Experience | Subjective Health Condition | Generalized Bayes Factor | |||
| 1 | Low | Unmarried | Yes | Less than 5 packs | Very Bad | 14.9738 | ||
| 2 | Low | Divorced | Yes | Non-smoker | Very Bad | 14.9738 | ||
| 3 | Low | Married Live Separated | Yes | Less than 5 packs | Not Bad | 14.9738 | ||
| 4 | Low | Married Live Separated | Yes | Non-smoker | Good | 14.9738 | ||
| 5 | Low | Unmarried | No | Less than 5 packs | Very Bad | 14.9738 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costello, F.J.; Kim, C.; Kang, C.M.; Lee, K.C. Identifying High-Risk Factors of Depression in Middle-Aged Persons with a Novel Sons and Spouses Bayesian Network Model. Healthcare 2020, 8, 562. https://doi.org/10.3390/healthcare8040562
Costello FJ, Kim C, Kang CM, Lee KC. Identifying High-Risk Factors of Depression in Middle-Aged Persons with a Novel Sons and Spouses Bayesian Network Model. Healthcare. 2020; 8(4):562. https://doi.org/10.3390/healthcare8040562
Chicago/Turabian StyleCostello, Francis Joseph, Cheong Kim, Chang Min Kang, and Kun Chang Lee. 2020. "Identifying High-Risk Factors of Depression in Middle-Aged Persons with a Novel Sons and Spouses Bayesian Network Model" Healthcare 8, no. 4: 562. https://doi.org/10.3390/healthcare8040562
APA StyleCostello, F. J., Kim, C., Kang, C. M., & Lee, K. C. (2020). Identifying High-Risk Factors of Depression in Middle-Aged Persons with a Novel Sons and Spouses Bayesian Network Model. Healthcare, 8(4), 562. https://doi.org/10.3390/healthcare8040562






