Comparison of Aggregated N-of-1 Trials with Parallel and Crossover Randomized Controlled Trials Using Simulation Studies
Abstract
1. Introduction
1.1. Selection Bias, Power, & Sample Size
1.2. Trial Design and Carryover Effects
1.3. Data Analysis in N-of-1 Trials
2. Methods
- Scenario 1—Weak heterogeneity and moderate error: and .
- Scenario 2—Homogeneity and moderate error: and .
- Scenario 3—Strong heterogeneity and moderate error: and .
- Scenario 4—Strong heterogeneity and large error: and .
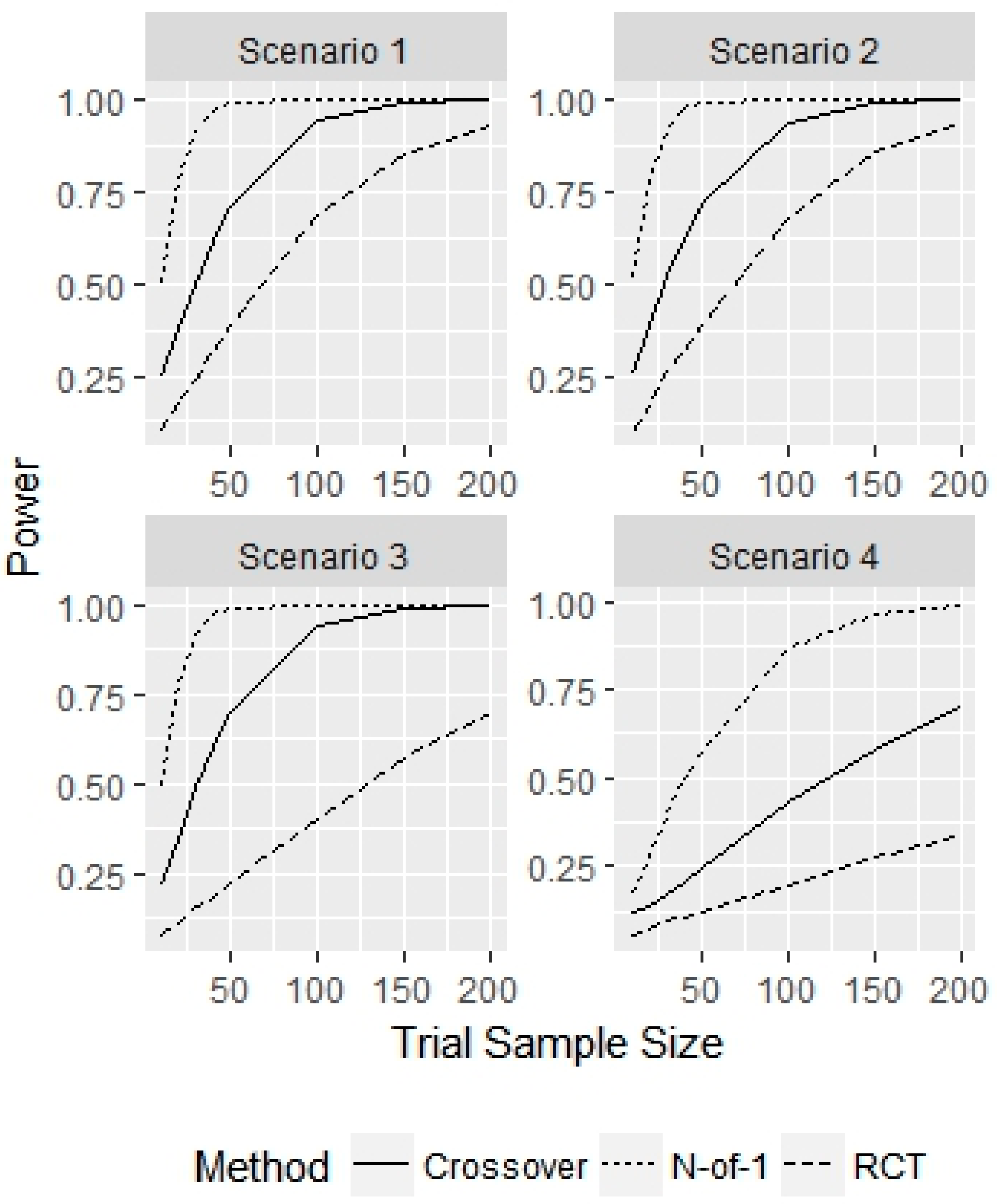
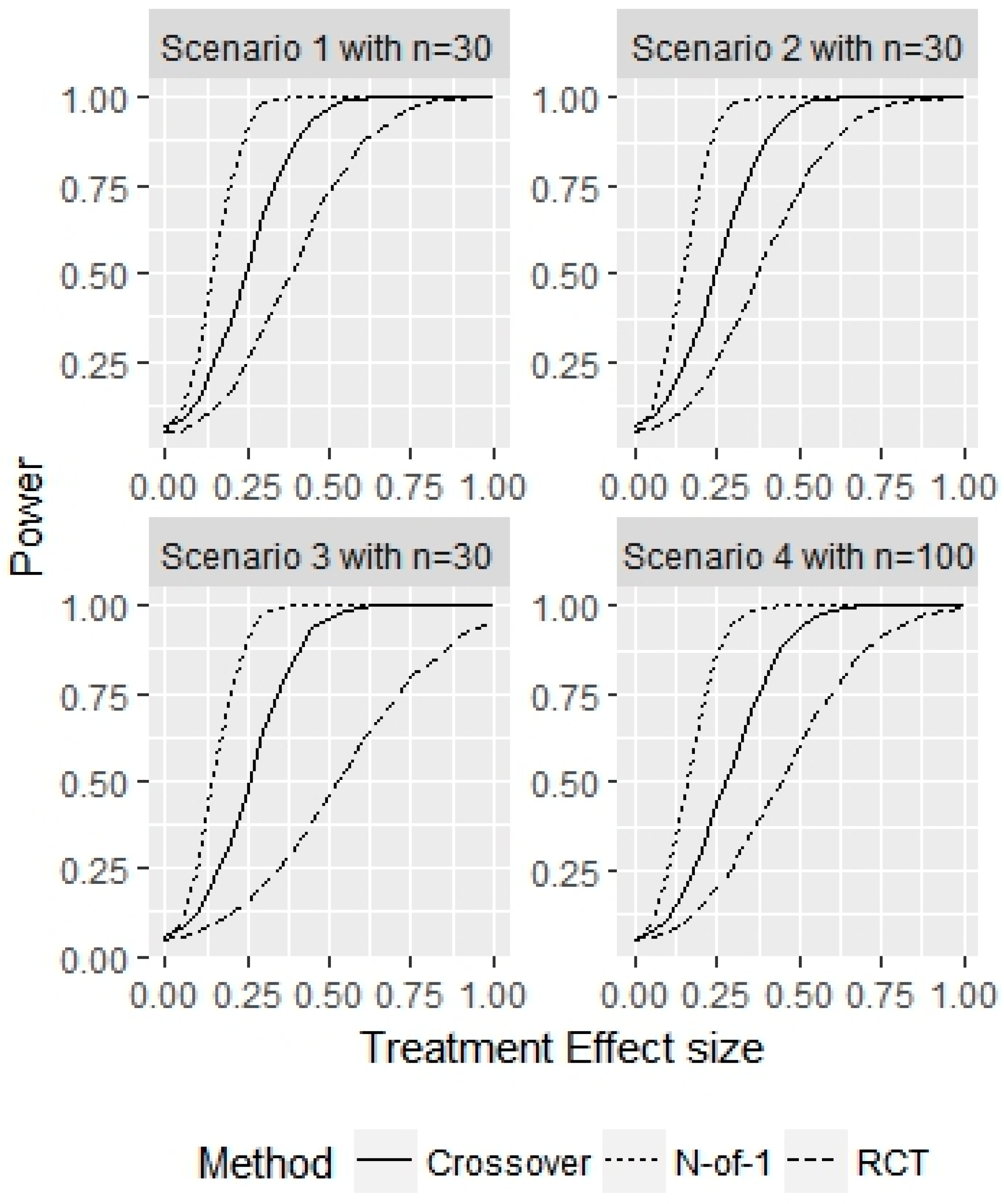
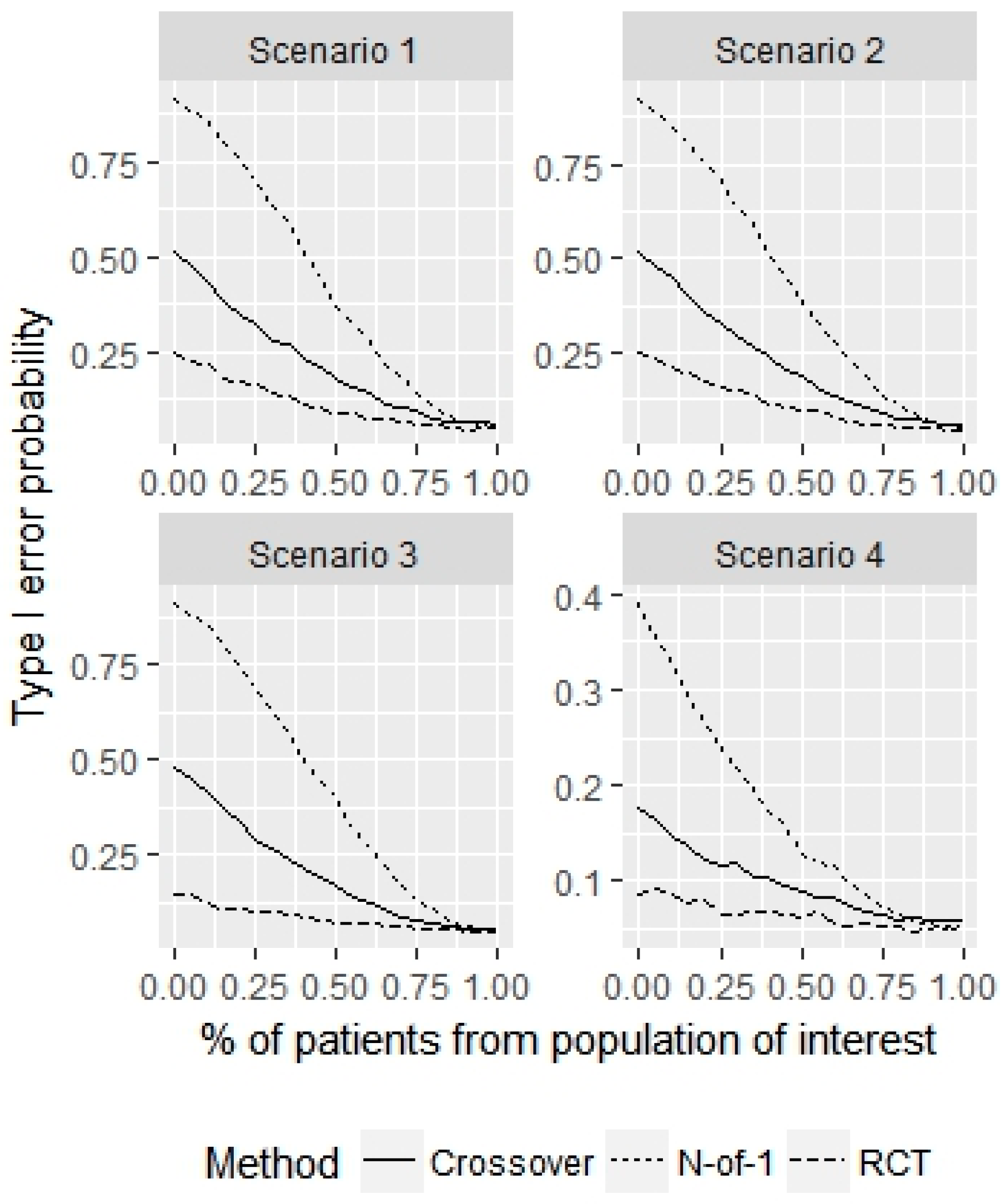
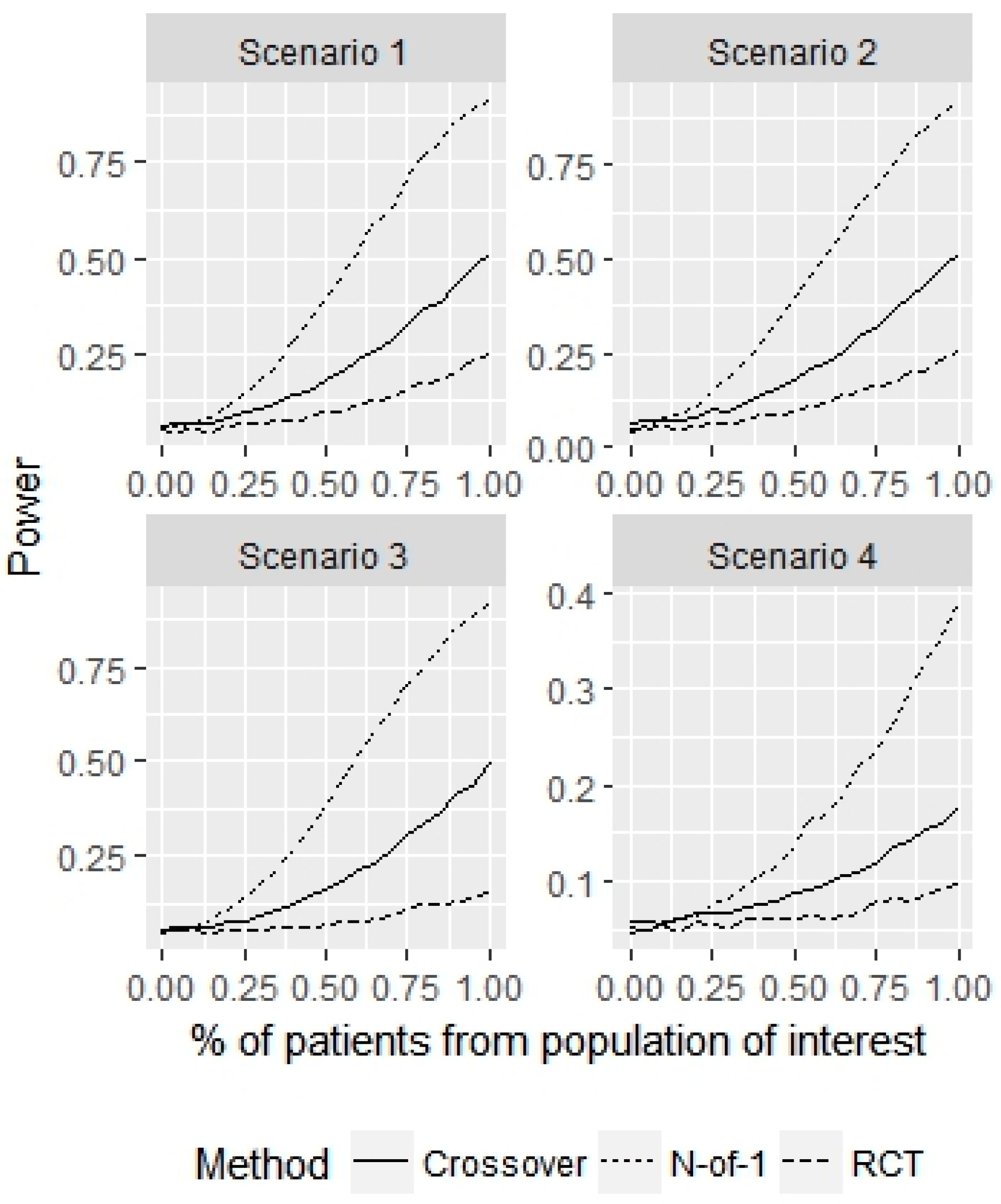
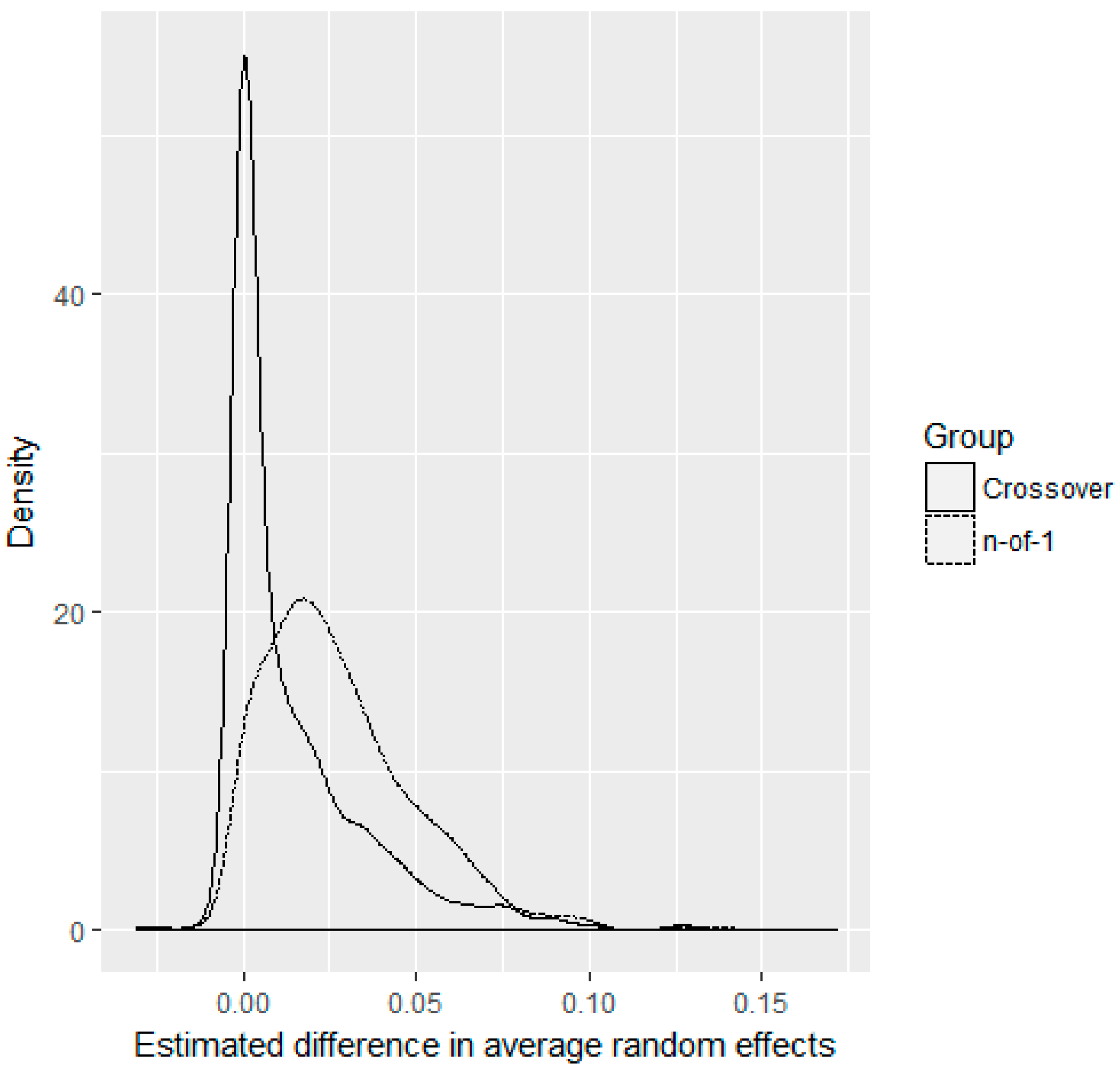
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guyatt, G.; Sackett, D.; Taylor, D.W.; Ghong, J.; Roberts, R.; Pugsley, S. Determining Optimal Therapy—Randomized Trials in Individual Patients. N. Engl. J. Med. 1986, 314, 889–892. [Google Scholar] [CrossRef]
- Punja, S.; Bukutu, C.; Shamseer, L.; Sampson, M.; Hartling, L.; Urichuk, L.; Vohra, S. N-of-1 trials are a tapestry of heterogeneity. J. Clin. Epidemiol. 2016, 76, 47–56. [Google Scholar] [CrossRef]
- Nikles, J.; Mitchell, G.; McKinlay, L.; Waugh, M.-C.; Epps, A.; Carmont, S.-A.; Schluter, P.J.; Lloyd, O.; Senior, H. A series of n-of-1 trials of stimulants in brain injured children. NeuroRehabilitation 2017, 40, 11–21. [Google Scholar] [CrossRef]
- Huber, A.M.; Tomlinson, G.A.; Koren, G.; Feldman, B.M. Amitriptyline to relieve pain in juvenile idiopathic arthritis: A pilot study using Bayesian metaanalysis of multiple N-of-1 clinical trials. J. Rheumatol. 2007, 34, 1125–1132. [Google Scholar]
- Nathan, P.C.; Tomlinson, G.; Dupuis, L.L.; Greenberg, M.L.; Ota, S.; Bartels, U.; Feldman, B.M. A pilot study of ondansetron plus metopimazine vs. ondansetron monotherapy in children receiving highly emetogenic chemotherapy: A Bayesian randomized serial N-of-1 trials design. Support. Care Cancer 2006, 14, 268–276. [Google Scholar] [CrossRef]
- Shaffer, J.A.; Falzon, L.; Cheung, K.; Davidson, K.W. N-of-1 randomized trials for psychological and health behavior outcomes: A systematic review protocol. Syst. Rev. 2015, 4, 87. [Google Scholar] [CrossRef]
- Dallery, J.; Cassidy, R.N.; Raiff, B.R. Single-case experimental designs to evaluate novel technology-based health interventions. J. Med. Internet Res. 2013, 15, e22. [Google Scholar] [CrossRef]
- Sung, L.; Tomlinson, G.A.; Greenberg, M.L.; Koren, G.; Judd, P.; Ota, S.; Feldman, B.M. Serial controlled N-of-1 trials of topical vitamin E as prophylaxis for chemotherapy-induced oral mucositis in paediatric patients. Eur. J. Cancer 2007, 43, 1269–1275. [Google Scholar] [CrossRef]
- Stunnenberg, B.C.; Raaphorst, J.; Groenewoud, H.M.; Statland, J.M.; Griggs, R.C.; Woertman, W.; Stegeman, D.F.; Timmermans, J.; Trivedi, J.; Matthews, E.; et al. Effect of Mexiletine on Muscle Stiffness in Patients with Nondystrophic Myotonia Evaluated Using Aggregated N-of-1 Trials. JAMA 2018, 320, 2344. [Google Scholar] [CrossRef]
- Marcucci, M.; Germini, F.; Coerezza, A.; Andreinetti, L.; Bellintani, L.; Nobili, A.; Rossi, P.D.; Mari, D. Efficacy of ultra-micronized palmitoylethanolamide (um-PEA) in geriatric patients with chronic pain: Study protocol for a series of N-of-1 randomized trials. Trials 2016, 17, 369. [Google Scholar] [CrossRef]
- Germini, F.; Coerezza, A.; Andreinetti, L.; Nobili, A.; Rossi, P.D.; Mari, D.; Guyatt, G.; Marcucci, M. N-of-1 Randomized Trials of Ultra-Micronized Palmitoylethanolamide in Older Patients with Chronic Pain. Drugs Aging 2017, 34, 941–952. [Google Scholar] [CrossRef]
- Punja, S.; Xu, D.; Schmid, C.H.; Hartling, L.; Urichuk, L.; Nikles, C.J.; Vohra, S. N-of-1 trials can be aggregated to generate group mean treatment effects: A systematic review and meta-analysis. J. Clin. Epidemiol. 2016, 76, 65–75. [Google Scholar] [CrossRef]
- Punja, S.; Nikles, C.J.; Senior, H.; Mitchell, G.; Schmid, C.H.; Heussler, H.; Witmans, M.; Vohra, S. Melatonin in Youth: N-of-1 trials in a stimulant-treated ADHD Population (MYNAP): Study protocol for a randomized controlled trial. Trials 2016, 17, 375. [Google Scholar] [CrossRef]
- McDonald, S.; Vieira, R.; Godfrey, A.; O’Brien, N.; White, M.; Sniehotta, F.F. Changes in physical activity during the retirement transition: A series of novel n-of-1 natural experiments. Int. J. Behav. Nutr. Phys. Act. 2017, 14, 167. [Google Scholar] [CrossRef]
- Alemayehu, C.; Nikles, J.; Mitchell, G. N-of-1 trials in the clinical care of patients in developing countries: A systematic review. Trials 2018, 19, 1–10. [Google Scholar] [CrossRef]
- Alemayehu, C.; Mitchell, G.; Aseffa, A.; Clavarino, A.; McGree, J.; Nikles, J. A series of N-of-1 trials to assess the therapeutic interchangeability of two enalapril formulations in the treatment of hypertension in Addis Ababa, Ethiopia: Study protocol for a randomized controlled trial. Trials 2017, 18, 470. [Google Scholar] [CrossRef]
- Samuel, J.P.; Tyson, J.E.; Green, C.; Bell, C.S.; Pedroza, C.; Molony, D.; Samuels, J. Treating Hypertension in Children With n-of-1 Trials. Pediatrics 2019, 143, e20181818. [Google Scholar] [CrossRef]
- Clough, A.J.; Hilmer, S.N.; Naismith, S.L.; Kardell, L.D.; Gnjidic, D. N-of-1 trials for assessing the effects of deprescribing medications on short-term clinical outcomes in older adults: A systematic review. J. Clin. Epidemiol. 2018, 93, 112–119. [Google Scholar] [CrossRef]
- Whitney, R.L.; Ward, D.H.; Marois, M.T.; Schmid, C.H.; Sim, I.; Kravitz, R.L. Patient Perceptions of Their Own Data in mHealth Technology–Enabled N-of-1 Trials for Chronic Pain: Qualitative Study. JMIR mHealth uHealth 2018, 6, e10291. [Google Scholar] [CrossRef]
- McDonald, S.; Quinn, F.; Vieira, R.; O’Brien, N.; White, M.; Johnston, D.W.; Sniehotta, F.F. The state of the art and future opportunities for using longitudinal n-of-1 methods in health behaviour research: A systematic literature overview. Health Psychol. Rev. 2017, 11, 307–323. [Google Scholar] [CrossRef]
- Scuffham, P.A.; Nikles, J.; Mitchell, G.K.; Yelland, M.J.; Vine, N.; Poulos, C.J.; Pillans, P.I.; Bashford, G.; del Mar, C.; Schluter, P.J.; et al. Using N-of-1 Trials to Improve Patient Management and Save Costs. J. Gen. Intern. Med. 2010, 25, 906–913. [Google Scholar] [CrossRef]
- Chapple, A.G.; Blackston, J.W. Finding Benefit in n-of-1 Trials. JAMA Intern. Med. 2019, 179, 453–454. [Google Scholar] [CrossRef]
- Kravitz, R.L.; Duan, N. Design and Implementation of N-of-1 Trials: A User’s Guide; Agency for Healthcare Research and Quality: Rockville, MD, USA, 2014. [Google Scholar]
- Higgins, J.P.; Green, S. Cochrane Handbook for Systematic Reviews of Interventions the Cochrane Collaboration; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Nicklas, T.A.; Morales, M.; Linares, A.; Yang, S.-J.; Baranowski, T.; De Moor, C.; Berenson, G. Children’s meal patterns have changed over a 21-year period: The Bogalusa heart study. J. Am. Diet. Assoc. 2004, 104, 753–761. [Google Scholar] [CrossRef]
- Zucker, D.R.; Ruthazer, R.; Schmid, C.H. Individual (N-of-1) trials can be combined to give population comparative treatment effect estimates: Methodologic considerations. J. Clin. Epidemiol. 2010, 63, 1312–1323. [Google Scholar] [CrossRef]
- Percha, B.; Baskerville, E.B.; Johnson, M.; Dudley, J.; Zimmerman, N. Designing robust N-of-1 studies for precision medicine. J. Med Internet Res. 2019, 21, e12641. [Google Scholar] [CrossRef]
- Bhaskaran, K.; Smeeth, L. What is the difference between missing completely at random and missing at random? Int. J. Epidemiol. 2014, 43, 1336–1339. [Google Scholar] [CrossRef]
- Vieira, R.; McDonald, S.; Araújo-Soares, V.; Sniehotta, F.F.; Henderson, R. Dynamic modelling of n-of-1 data: Powerful and flexible data analytics applied to individualised studies. Health Psychol. Rev. 2017, 11, 222–234. [Google Scholar] [CrossRef]
- Mengersen, K.; McGree, J.M.; Schmid, C.H. Statistical analysis of N-of-1 trials. In The Essential Guide to N-of-1 Trials; Springer: Berlin/Heidelberg, Germany, 2015; pp. 135–153. [Google Scholar]
- Senn, S. Sample size considerations for n-of-1 trials. Stat. Methods Med. Res. 2019, 28, 372–383. [Google Scholar] [CrossRef]
- Natesan, P.; Hedges, L. V Bayesian Unknown Change-Point Models to Investigate Immediacy in Single Case Designs. Psychol. Methods 2017, 22, 743–759. [Google Scholar] [CrossRef]
- Stunnenberg, B.C.; Woertman, W.; Raaphorst, J.; Statland, J.M.; Griggs, R.C.; Timmermans, J.; Saris, C.G.; Schouwenberg, B.J.; Groenewoud, H.M.; Stegeman, D.F.; et al. Combined N-of-1 trials to investigate mexiletine in non-dystrophic myotonia using a Bayesian approach; study rationale and protocol. BMC Neurol. 2015, 15, 43. [Google Scholar] [CrossRef][Green Version]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blackston, J.W.; Chapple, A.G.; McGree, J.M.; McDonald, S.; Nikles, J. Comparison of Aggregated N-of-1 Trials with Parallel and Crossover Randomized Controlled Trials Using Simulation Studies. Healthcare 2019, 7, 137. https://doi.org/10.3390/healthcare7040137
Blackston JW, Chapple AG, McGree JM, McDonald S, Nikles J. Comparison of Aggregated N-of-1 Trials with Parallel and Crossover Randomized Controlled Trials Using Simulation Studies. Healthcare. 2019; 7(4):137. https://doi.org/10.3390/healthcare7040137
Chicago/Turabian StyleBlackston, J. Walker, Andrew G. Chapple, James M. McGree, Suzanne McDonald, and Jane Nikles. 2019. "Comparison of Aggregated N-of-1 Trials with Parallel and Crossover Randomized Controlled Trials Using Simulation Studies" Healthcare 7, no. 4: 137. https://doi.org/10.3390/healthcare7040137
APA StyleBlackston, J. W., Chapple, A. G., McGree, J. M., McDonald, S., & Nikles, J. (2019). Comparison of Aggregated N-of-1 Trials with Parallel and Crossover Randomized Controlled Trials Using Simulation Studies. Healthcare, 7(4), 137. https://doi.org/10.3390/healthcare7040137





