Analysis of Time-Delay Epidemic Model in Rechargeable Wireless Sensor Networks
Abstract
1. Introduction
- Establish a mathematical epidemics model.
- Analyze the equilibrium point in the system, and study its stability.
- Achieve the optimal control to make the control of malware propagation more effective. According to previous studies, the classical mathematical models established by predecessors mainly include the following: SIS (Susceptible, Infected, Susceptible), SIR (Susceptible, Infected, Removed), and SIRS (Susceptible, Infected, Removed, Susceptible).
- A novel low-energy-status-based model is introduced to describe the propagation process of malicious software (virus) in WRSNs.
- The basic reproduction number is defined by the disease-free equilibrium solution and the epidemic equilibrium solution. The Routh criterion is applied to prove the local stability, and the Lyapunov universal function is constructed to prove the global attraction.
- Based on Pontryagin’s minimum principle, the optimal control variables satisfying the minimization of the objective function are obtained.
- The stability problem under time delay is specially revealed.
2. Modeling Analysis
3. Dynamic-Stability Analysis
3.1. Local Stability Analysis
3.2. Global-Stability Analysis
4. Optimal-Control Analysis
5. Time-Delay System Analysis
5.1. Local-Stability Analysis
5.2. Global-Stability Analysis
6. Simulation
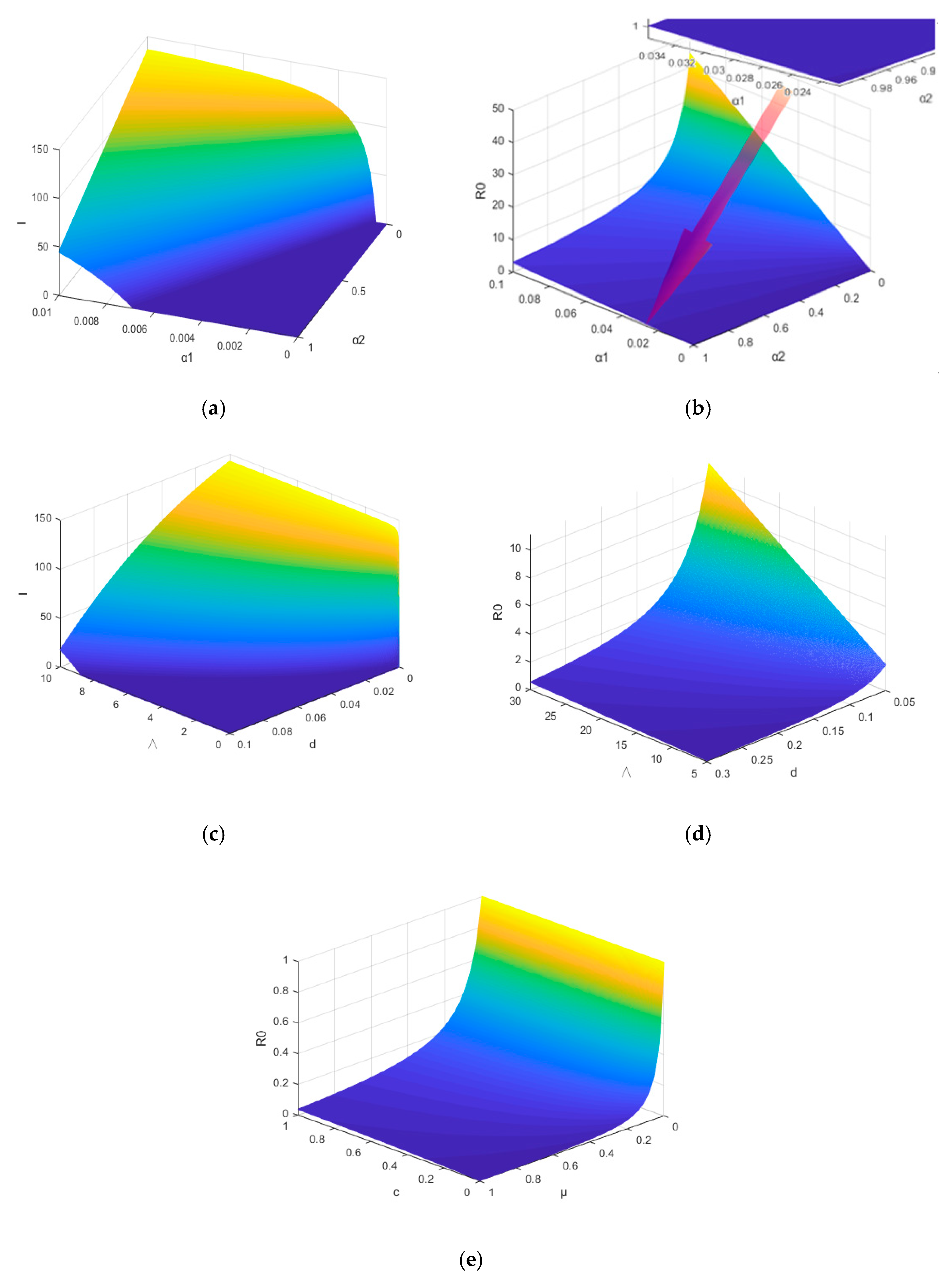
6.1. Parameter Dependence of R0 and I(∞)
6.2. Stability of Equilibrium Point
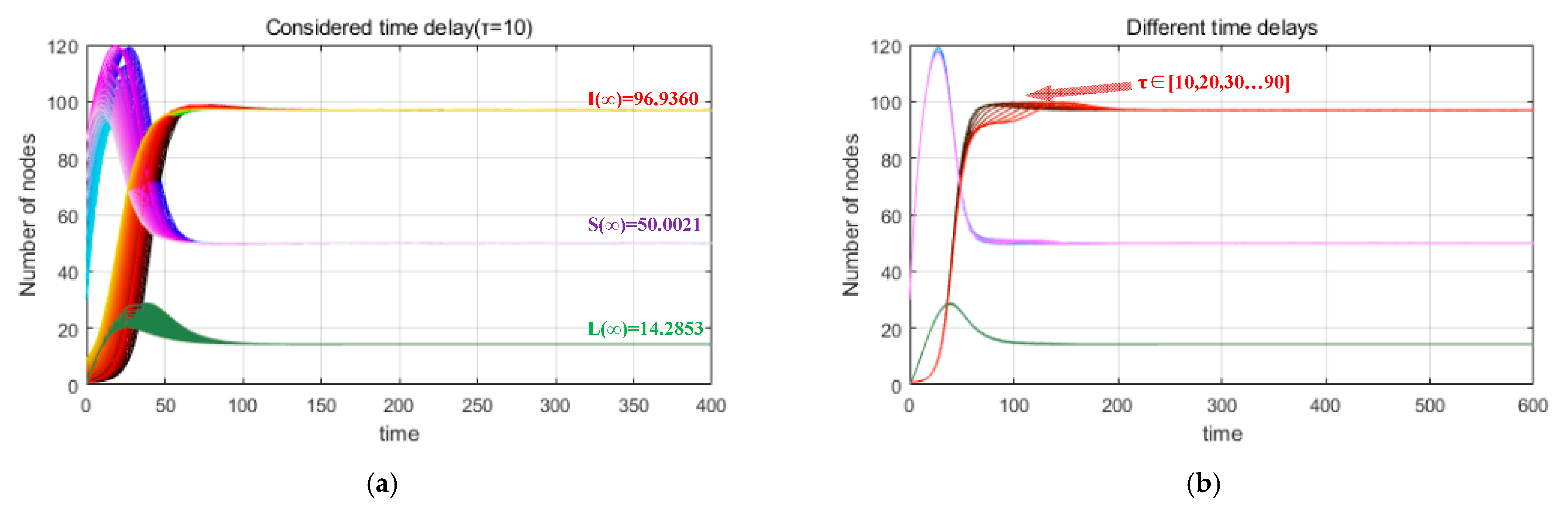
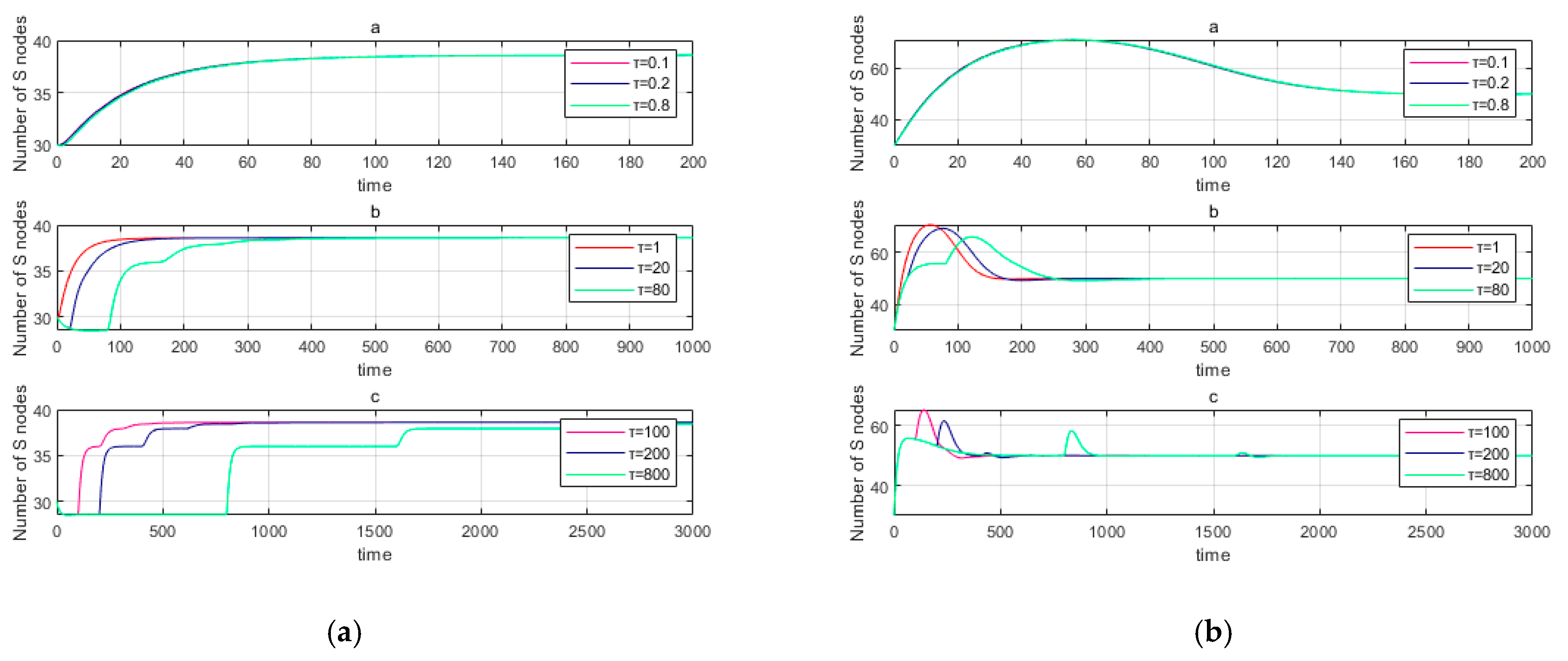
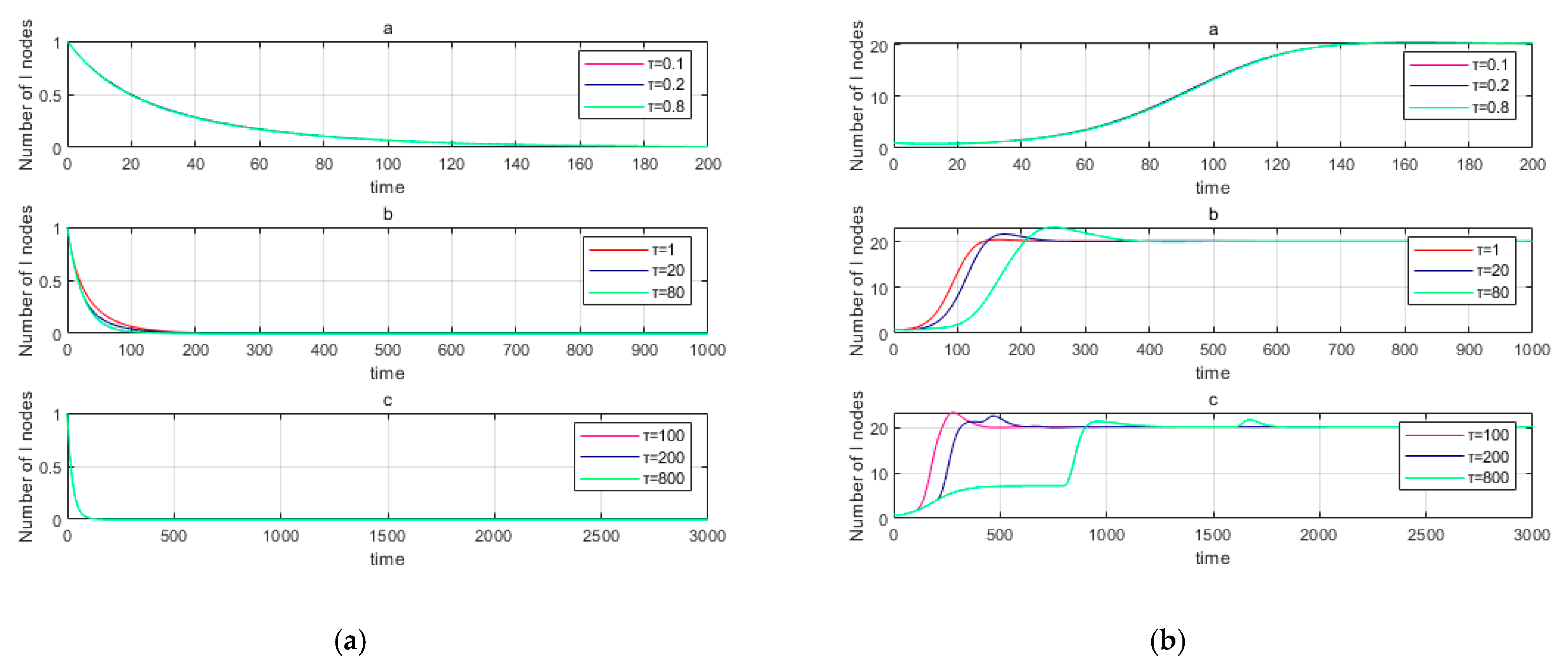
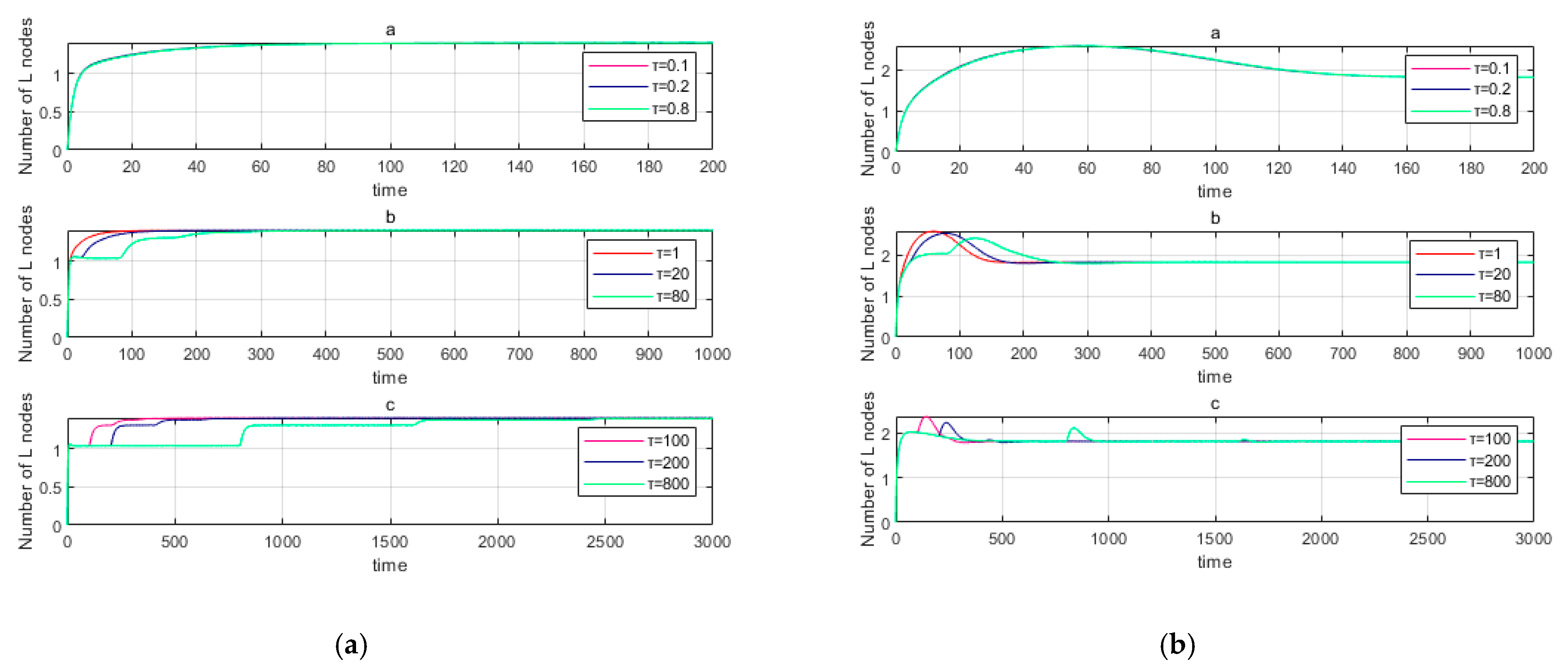
6.3. Influence of Time Delay on Malware Propagation
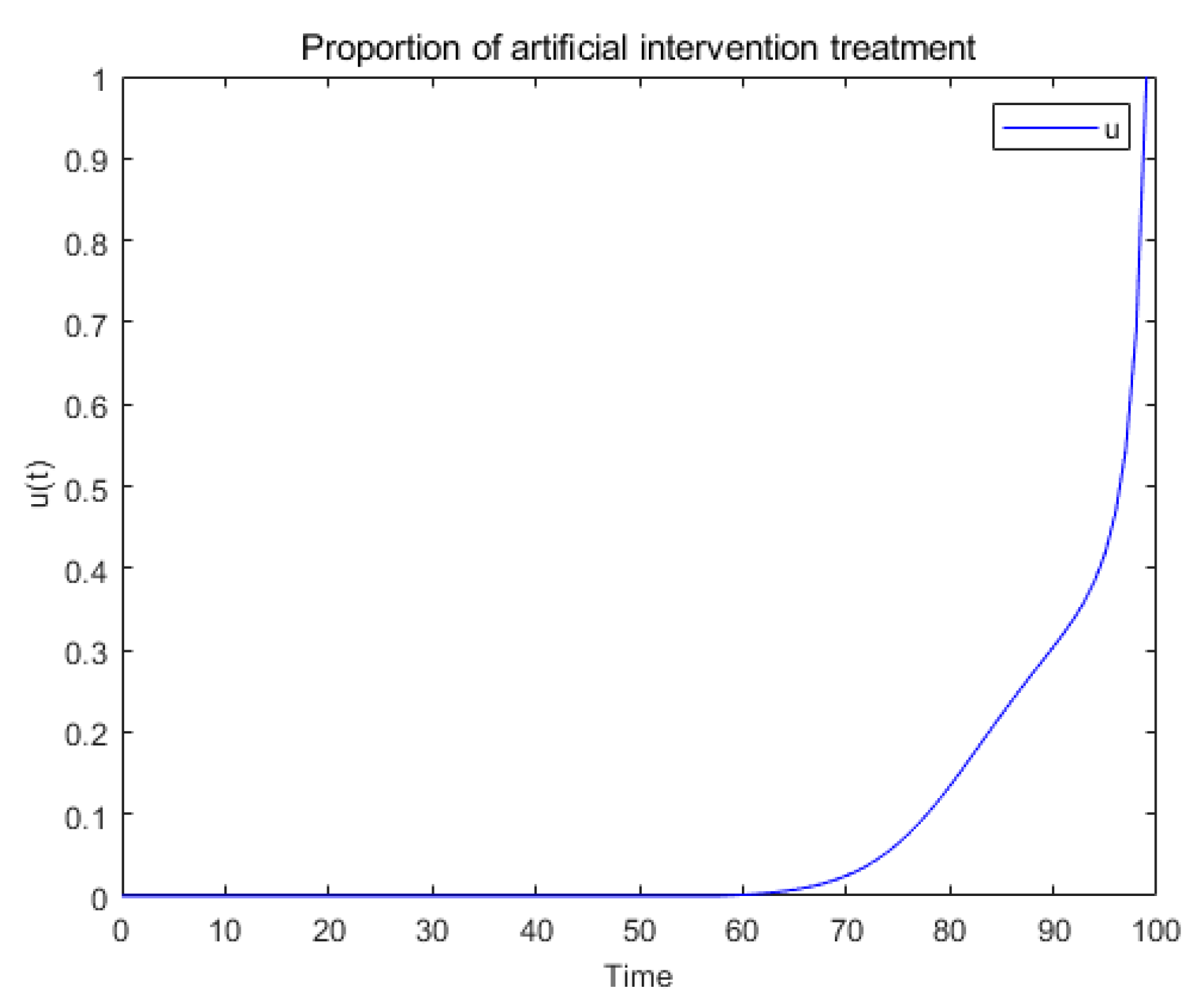
6.4. Realization of Optimal Control
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless Sensor Networks: A Survey on Recent Developments and Potential Synergies. J. Supercomput. 2014, 68, 1–48. [Google Scholar] [CrossRef]
- Liang, C.J.M.; Musăloiu-e, R.; Terzis, A. Typhoon: A Reliable Data Dissemination Protocol for Wireless Sensor Networks. In European Conference on Wireless Sensor Networks; Springer: Berlin/Heidelberg, Germany, 2008; pp. 268–285. [Google Scholar]
- Rashid, B.; Rehmani, M.H. Applications of Wireless Sensor Networks for Urban Areas: A Survey. J. Netw. Comput. Appl. 2016, 60, 192–219. [Google Scholar] [CrossRef]
- Yetgin, H.; Cheung, K.T.K.; El-Hajjar, M.; Hanzo, L.H. A Survey of Network Lifetime Maximization Techniques in Wireless Sensor Networks. IEEE Commun. Surv. Tutor. 2017, 19, 828–854. [Google Scholar] [CrossRef]
- Rasheed, A.; Mahapatra, R.N. The Three-Tier Security Scheme in Wireless Sensor Networks with Mobile Sinks. IEEE Trans. Parallel Distrib. Syst. 2010, 23, 958–965. [Google Scholar] [CrossRef]
- Reina, D.G.; Toral, S.L.; Johnson, P.; Barrero, F. A Survey on Probabilistic Broadcast Schemes for Wireless Ad Hoc Networks. Ad Hoc Netw. 2015, 25, 263–292. [Google Scholar] [CrossRef]
- Batista, F.K.; Martin del Rey, A.; Queiruga-Dios, A. A New Individual-Based Model to Simulate Malware Propagation in Wireless Sensor Networks. Mathematics 2020, 8, 410. [Google Scholar] [CrossRef]
- Lin, C.; Shang, Z.; Du, W.; Ren, J.; Wang, L.; Wu, G. CoDoC: A Novel Attack for Wireless Rechargeable Sensor Networks through Denial of Charge. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: New York, NY, USA, 2019; pp. 856–864. [Google Scholar]
- Encyclopedia on Ad Hoc and Ubiquitous Computing: Theory and Design of Wireless Ad Hoc, Sensor, And Mesh Networks; Agrawal, D.P., Xie, B., Eds.; World Scientific: Singapore, 2009. [Google Scholar]
- Song, Y.; Jiang, G.P. Model and Dynamic Behavior of Malware Propagation over Wireless Sensor Networks. In International Conference on Complex Sciences; Springer: Berlin/Heidelberg, Germany, 2009; pp. 487–502. [Google Scholar]
- Liu, G.; Peng, B.; Zhong, X. A Novel Epidemic Model for Wireless Rechargeable Sensor Network Security. Sensors 2021, 21, 123. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Guan, G. Dynamical Analysis of a Rumor Spreading Model with Self-Discrimination and Time Delay in Complex Networks. Physica A Stat. Mech. Appl. 2019, 533, 121953. [Google Scholar] [CrossRef]
- Zhu, L.; Zhao, H. Dynamical Analysis and Optimal Control for a Malware Propagation Model in an Information Network. Neurocomputing 2015, 149, 1370–1386. [Google Scholar] [CrossRef]
- Zhang, Z.; Si, F. Dynamics of a Delayed SEIRS-V Model on the Transmission of Worms in a Wireless Sensor Network. Adv. Differ. Equ. 2014, 2014, 1–15. [Google Scholar] [CrossRef][Green Version]
- Liu, J.; Zhang, Z. Hopf Bifurcation of a Delayed Worm Model with Two Latent Periods. Adv. Differ. Equ. 2019, 2019, 1–27. [Google Scholar] [CrossRef]
- Wang, C.; Chai, S. Hopf Bifurcation of an SEIRS Epidemic Model with Delays and Vertical Transmission in the Network. Adv. Differ. Equ. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y. Bifurcation Analysis for an SEIRS-V Model with Delays on the Transmission of Worms in a Wireless Sensor Network. Math. Probl. Eng. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, X. SIS Model of Rumor Spreading in Social Network with Time Delay and Nonlinear Functions. Commun. Theor. Phys. 2019, 72, 015002. [Google Scholar] [CrossRef]
- Zhang, Z.; Kundu, S.; Wei, R. A Delayed Epidemic Model for Propagation of Malicious Codes in Wireless Sensor Network. Mathematics 2019, 7, 396. [Google Scholar] [CrossRef]
- Zhu, L.; Zhou, X.; Li, Y. Global Dynamics Analysis and Control of a Rumor Spreading Model in Online Social Networks. Physica A Stat. Mech. Appl. 2019, 526, 120903. [Google Scholar] [CrossRef]
- Al-Darabsah, I. A Time-Delayed SVEIR Model for Imperfect Vaccine with a Generalized Nonmonotone Incidence and Application to Measles. Appl. Math. Model. 2020, 91, 74–92. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, X.; Zhang, H.; Shen, S.; Li, Y.; Zhou, Y. Dynamics Analysis and Optimal Control Strategy for a SIRS Epidemic Model with Two Discrete Time Delays. Phys. Scr. 2020, 95, 035213. [Google Scholar] [CrossRef]
- Liu, G.; Peng, B.; Zhong, X.; Lan, X. Differential Games of Rechargeable Wireless Sensor Networks against Malicious Programs Based on SILRD Propagation Model. Complexity 2020, 2020, 13. [Google Scholar] [CrossRef]
- Liu, G.; Peng, B.; Zhong, X.; Cheng, L.; Li, Z. Attack-Defense Game between Malicious Programs and Energy-Harvesting Wireless Sensor Networks Based on Epidemic Modeling. Complexity 2020, 2020, 3680518. [Google Scholar] [CrossRef]
- Liu, G.; Peng, B.; Zhong, X. Epidemic Analysis of Wireless Rechargeable Sensor Networks Based on an Attack–Defense Game Model. Sensors 2021, 21, 594. [Google Scholar] [CrossRef] [PubMed]
- Cooke, K.L.; van den Driessche, P. On zeroes of some transcendental equations. Funkc. Ekvacioj 1986, 29, 77–90. [Google Scholar]







| Authors | Model | Characteristics | Bifurcation | Enhancements |
|---|---|---|---|---|
| Zhu, L. et al. [12] | SBD (Susceptible-Believed-Denied) | Time delay of the rumor spreading | 1 | Establishment and analysis of SBD rumor-spreading model. |
| Zhu, L. et al. [13] | SIRS (Susceptible-Infected-Recovered-Susceptible) | Time delay of the immune validity | 2 | Consideration of immune validity period and the analysis of the optimal control. |
| Zhang, Z. et al. [14] | SEIRS-V (Susceptible-Exposed-Infected-Recovered-Susceptible and Vaccinated) | Time delay of the immune validity; the recovery and the vaccination | 2 | Introduction of the vaccinated nodes and the analysis of double time delays. |
| Liu, J. et al. [15] | SEIR (Susceptible-Exposed-Infected-Recovered) | Time delay of the exposure | 2 | Consideration of infectious-disease models with different incubation periods. |
| Wang, C. et al. [16] | SEIRS (Susceptible-Exposed-Infected-Recovered-Susceptible) | Time delay of the exposure and the immune validity | 2 | Consideration of immune validity period and the analysis of double time delays. |
| Zhang, Z. et al. [17] | SEIRS-V (Susceptible-Exposed-Infected-Recovered-Susceptible and Vaccinated) | Time delay of the immunity and the immune validity | 2 | Introduction of the vaccinated nodes and the analysis of double time delays. |
| Zhu, L. et al. [18] | SIS (Susceptible-Infected-Susceptible) | Time delay of the incubation | 2 | Time-delay analysis of recovery process based on SIS model. |
| Zhang, Z. et al. [19] | SEIQRS-V (Susceptible-Exposed-Infected-Quarantined -Recovered-Susceptible and Vaccinated) | Time delay of the exposure | 2 | Infectious-disease model considering the nodes’ distribution area. |
| Zhu, L. et al. [20] | SEIR (Susceptible-Exposed-Infected-Recovered) | Time delay of the incubation | 1 | Time-delay analysis of infection process based on SEIR system. |
| Al-Darabsah, I. et al. [21] | SEIRS-V (Susceptible-Exposed-Infected-Recovered-Susceptible and Vaccinated) | Time delay of the exposure | 1 | Time-delay analysis considering specific effective contact rate. |
| S(t) | The quantity of the susceptible node |
| I(t) | The quantity of the infected node |
| L(t) | The quantity of the low-energy node |
| ∧ | Injection rate of system |
| α1 | Transmission rate of malware |
| α2 | Self-disinfection rate of the infected nodes |
| c | Charging success rate |
| μ | Low-energy-node conversion rate |
| d | Node deactivation rate |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Li, J.; Liang, Z.; Peng, Z. Analysis of Time-Delay Epidemic Model in Rechargeable Wireless Sensor Networks. Mathematics 2021, 9, 978. https://doi.org/10.3390/math9090978
Liu G, Li J, Liang Z, Peng Z. Analysis of Time-Delay Epidemic Model in Rechargeable Wireless Sensor Networks. Mathematics. 2021; 9(9):978. https://doi.org/10.3390/math9090978
Chicago/Turabian StyleLiu, Guiyun, Junqiang Li, Zhongwei Liang, and Zhimin Peng. 2021. "Analysis of Time-Delay Epidemic Model in Rechargeable Wireless Sensor Networks" Mathematics 9, no. 9: 978. https://doi.org/10.3390/math9090978
APA StyleLiu, G., Li, J., Liang, Z., & Peng, Z. (2021). Analysis of Time-Delay Epidemic Model in Rechargeable Wireless Sensor Networks. Mathematics, 9(9), 978. https://doi.org/10.3390/math9090978








