Adomian Decomposition and Fractional Power Series Solution of a Class of Nonlinear Fractional Differential Equations
Abstract
1. Introduction and Preliminaries
2. Preliminary
2.1. Fractional Calculus
2.2. The ADM and FPSM
3. Applying the ADM and FPSM for Specific
3.1. Case 1:
3.2. Case 2:
3.3. Case 3:
3.4. Case 4:
4. Test Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The First Six Expressions of Υ i for Case 1
Appendix B. The First Six Expressions of Υ i for Case 2
Appendix C. The First Six Expressions of Υ i for Case 3
Appendix D. The First Six Expressions of Υ i for Case 4
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: Singapore, 2010. [Google Scholar]
- Magin, R. Fractional Calculus in Bioengineering; Begall House Publisher, Inc.: Connecticut, CT, USA, 2006. [Google Scholar]
- Wu, J.; Yuan, J.; Gao, W. Analysis of fractional factor system for data transmission in SDN. Appl. Math. Nonlinear Sci. 2019, 4, 191–196. [Google Scholar] [CrossRef]
- Şahin, R.; Yağcı, O. Fractional calculus of the extended hypergeometric function. Appl. Math. Nonlinear Sci. 2020, 5, 369–384. [Google Scholar] [CrossRef]
- Balcı, M.A. Fractional interaction of financial agents in a stock market network. Appl. Math. Nonlinear Sci. 2020, 5, 317–336. [Google Scholar] [CrossRef]
- Alqudah, M.A.; Mohammed, P.O.; Abdeljawad, T. Solution of singular integral equations via Riemann—Liouville fractional integrals. Math. Prob. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Srivastava, H.M.; Mohammed, P.O. A correlation between solutions of uncertain fractional forward difference equations and their paths. Front. Phys. 2020, 8. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Abdeljawad, T.; Jarad, F.; Chu, Y.-M. Existence and uniqueness of uncertain fractional backward difference equations of Riemann-Liouville type. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Günerhan, H.; Çelik, E. Analytical and approximate solutions of fractional partial differential-algebraic equations. Appl. Math. Nonlinear Sci. 2020, 5, 109–120. [Google Scholar] [CrossRef]
- Kurt, A.; Şenol, M.; Tasbozan, O.; Chand, M. Two reliable methods for the solution of fractional coupled Burgers’ equation arising as a model of Polydispersive sedimentation. Appl. Math. Nonlinear Sci. 2019, 4, 523–534. [Google Scholar] [CrossRef]
- Touchent, K.A.; Hammouch, Z.; Mekkaoui, T. A modified invariant subspace method for solving partial differential equations with non-singular kernel fractional derivatives. Appl. Math. Nonlinear Sci. 2020, 5, 35–48. [Google Scholar] [CrossRef]
- Onal, M.; Esen, A. A Crank-Nicolson approximation for the time fractional Burgers equation. Appl. Math. Nonlinear Sci. 2020, 5, 177–184. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Mohammed, P.O.; Guirao, J.L.G.; Hamed, Y.S. Some higher-degree lacunary fractional splines in the approximation of fractional differential equations. Symmetry 2021, 13, 422. [Google Scholar] [CrossRef]
- Ganjiani, M. Solution of nonlinear fractional differential equations using homotopy analysis method. Appl. Math. Model. 2010, 34, 1634–1641. [Google Scholar] [CrossRef]
- Gaoa, G.-H.; Sun, Z.-Z.; Zhang, H.-W. A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 2014, 259, 33–50. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, F.; Turner, I.; Anh, V. Finite element approximation for a modified anomalous subdiffusion equation. Appl. Math. Model. 2011, 35, 4103–4116. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation methods for linear and nonlinear variable order FPDEs. J. Comput. Phys. 2015, 293, 312–338. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H.; Wang, S. Positive Solution of a Nonlinear Fractional Differential Equation Involving Caputo Derivative. Discret. Dyn. Nat. Soc. 2012, 2012, 425408. [Google Scholar] [CrossRef]
- Bekir, A.; Güner, Ö. Exact solutions of nonlinear fractional differential equations by (G’/G)-expansion method. Chin. Phys. B 2013, 22, 110202. [Google Scholar] [CrossRef]
- Gao, G.; Sun, Z. A compact finite difference scheme for the fractional subdiffusion equations. J. Comput. Phys. 2011, 230, 586–595. [Google Scholar] [CrossRef]
- Duan, J.-S.; Chaolu, T.; Rach, R. Solutions of the initial value problem for nonlinear fractional ordinary differential equations by the Rach-Adomian-Meyers modified decomposition method. Appl. Math. Comput. 2012, 218, 8370–8392. [Google Scholar] [CrossRef]
- Modanli, M.; Abdulazeez, S.T.; Husien, A.M. A residual power series method for solving pseudo hyperbolic partial differential equations with nonlocal conditions. Numer. Methods Partial. Differ. Equ. 2021, 37, 2235–2243. [Google Scholar] [CrossRef]
- Lu, T.-T.; Zheng, W.-Q. Adomian decomposition method for first order PDEs with unprescribed data. Alex. Eng. J. 2021, 60, 2563–2572. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.A.T.; da Costa, J.S. Which Differintegration? IEE Proc. Vis. Image Signal Process. 2005, 152, 846–850. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Linear and Nonlinear Integral Equations; Higher Education Press: Beijing, China; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Wazwaz, A.M. A new algorithm for calculating Adomian polynomials for nonlinear operators. Appl. Math. Comput. 2000, 111, 33–51. [Google Scholar] [CrossRef]
- Cherrault, Y. Convergence of Adomian’s decomposition method. Math. Comp. Model. 1990, 14, 83–86. [Google Scholar] [CrossRef]
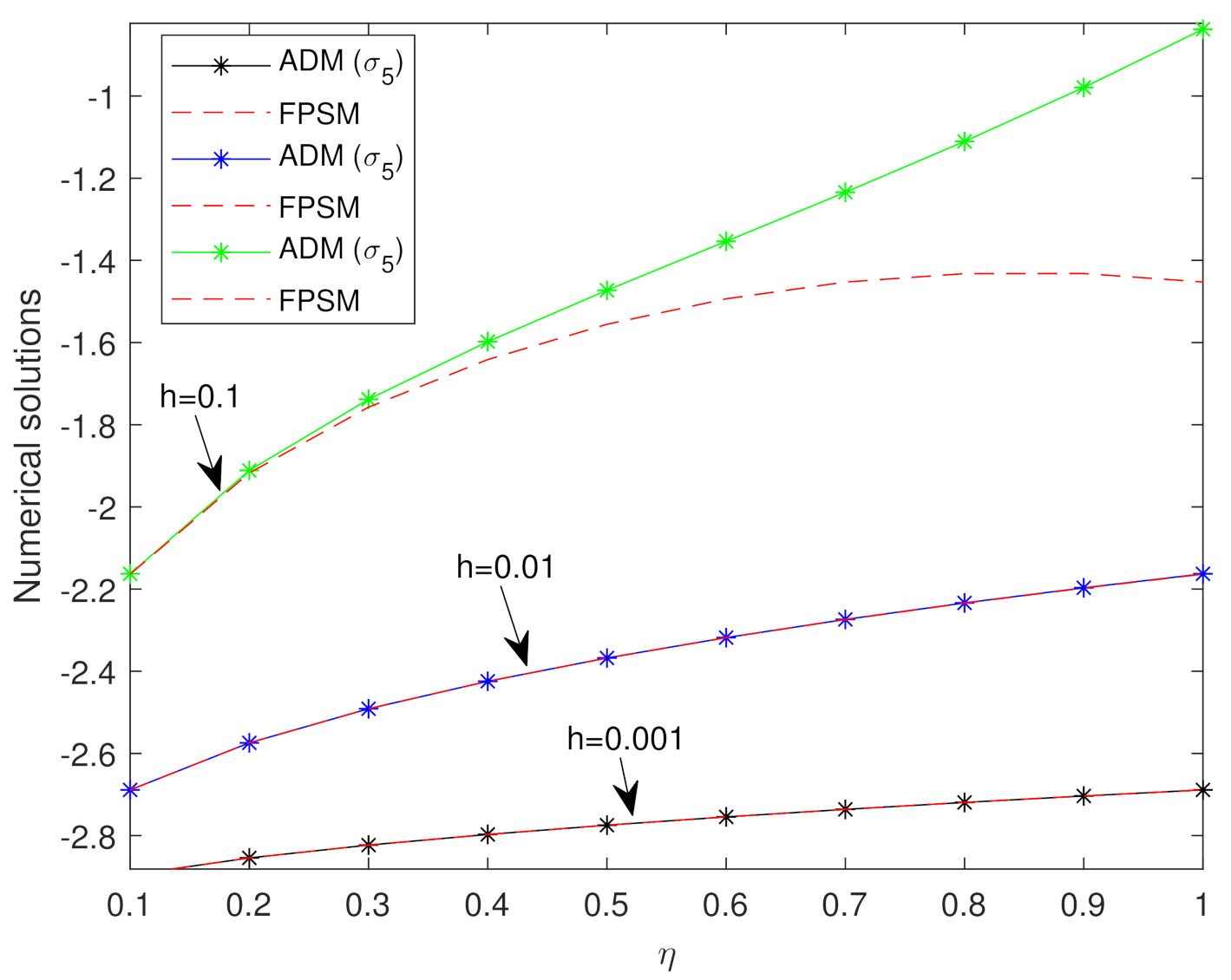
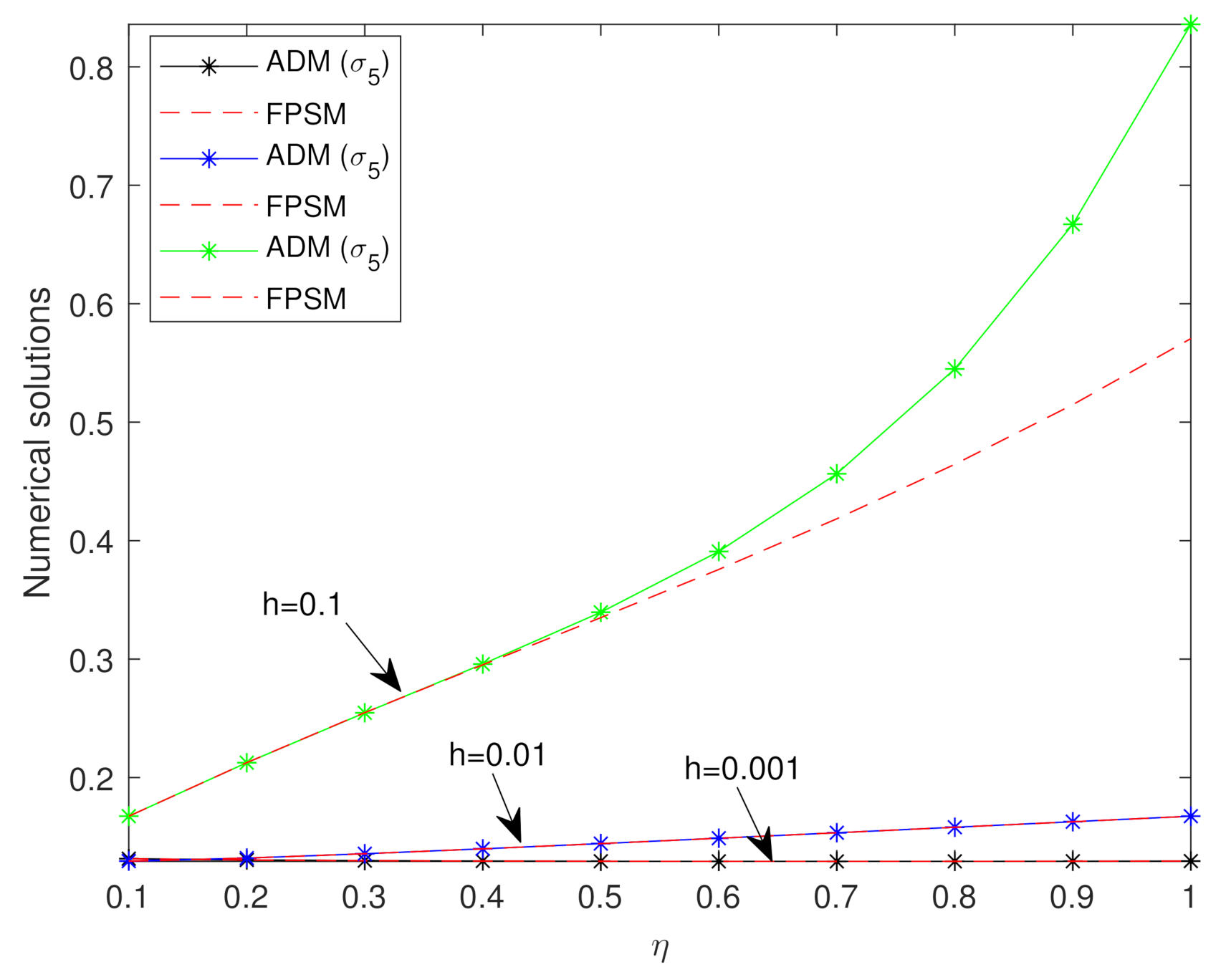

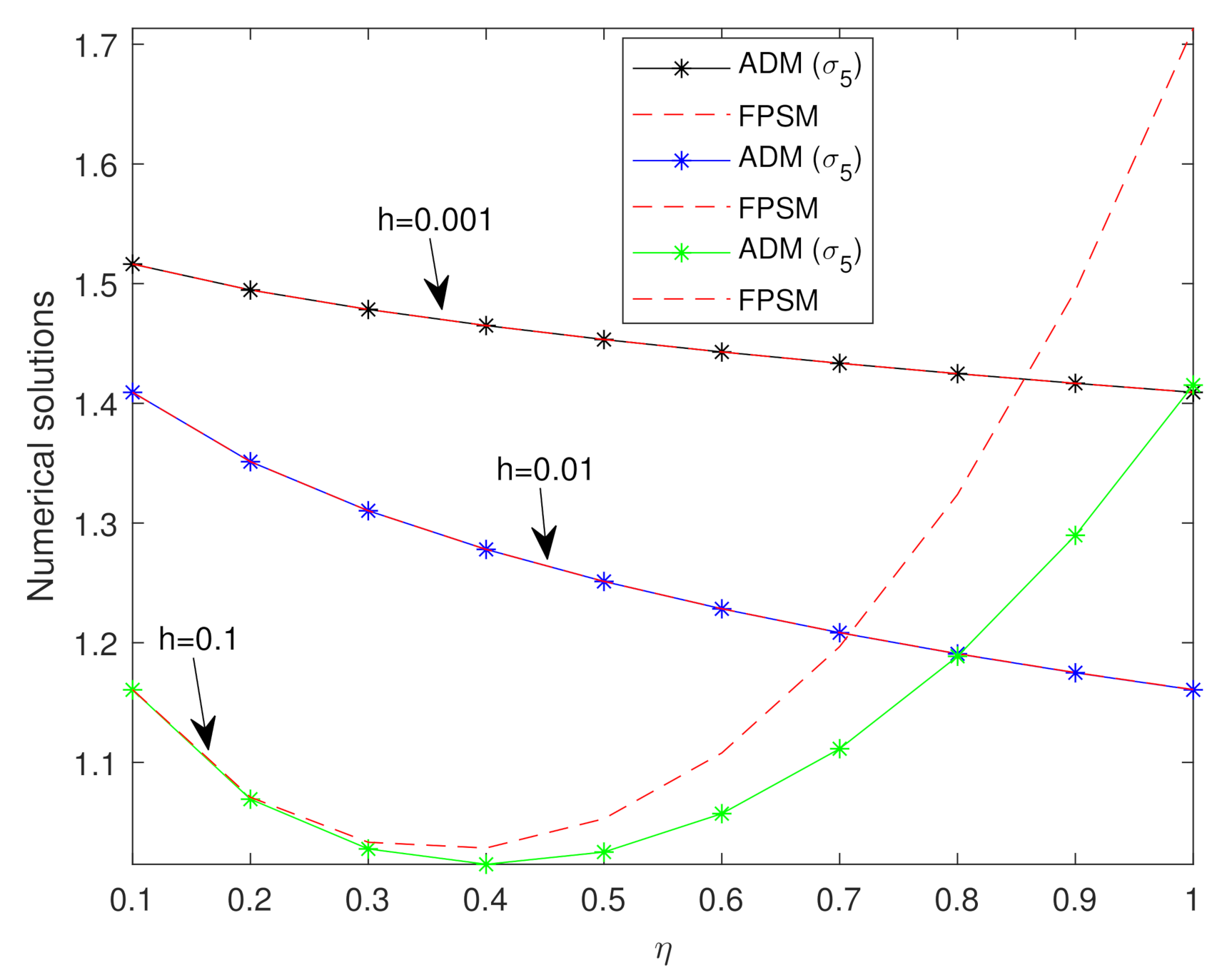
| ADM () | FPSM | Absolute Error | |
|---|---|---|---|
| ADM () | FPSM | Absolute Error | |
|---|---|---|---|
| ADM () | FPSM | Absolute Error | |
|---|---|---|---|
| ADM () | FPSM | Absolute Error | |
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, P.O.; Machado, J.A.T.; Guirao, J.L.G.; Agarwal, R.P. Adomian Decomposition and Fractional Power Series Solution of a Class of Nonlinear Fractional Differential Equations. Mathematics 2021, 9, 1070. https://doi.org/10.3390/math9091070
Mohammed PO, Machado JAT, Guirao JLG, Agarwal RP. Adomian Decomposition and Fractional Power Series Solution of a Class of Nonlinear Fractional Differential Equations. Mathematics. 2021; 9(9):1070. https://doi.org/10.3390/math9091070
Chicago/Turabian StyleMohammed, Pshtiwan Othman, José António Tenreiro Machado, Juan L. G. Guirao, and Ravi P. Agarwal. 2021. "Adomian Decomposition and Fractional Power Series Solution of a Class of Nonlinear Fractional Differential Equations" Mathematics 9, no. 9: 1070. https://doi.org/10.3390/math9091070
APA StyleMohammed, P. O., Machado, J. A. T., Guirao, J. L. G., & Agarwal, R. P. (2021). Adomian Decomposition and Fractional Power Series Solution of a Class of Nonlinear Fractional Differential Equations. Mathematics, 9(9), 1070. https://doi.org/10.3390/math9091070









