The Structure of n Harmonic Points and Generalization of Desargues’ Theorems

Abstract

In this paper, we consider the relation of more than four harmonic points in a line. For this purpose, starting from the dependence of the harmonic points, Desargues’ theorems, and perspectivity, we note that it is necessary to conduct a generalization of the Desargues’ theorems for projective complete $\mathrm{n}$-points, which are used to implement the definition of the generalization of harmonic points. We present new findings regarding the uniquely determined and constructed sets of H-points and their structure. The well-known fourth harmonic points represent the special case (n = 4) of the sets of H-points of rank 2, which is indicated by $P_4^2$.

1. Introduction

The idea of studying and investigating the possibility of construing more than four harmonic points was originally discussed in the article “The chords of the non-ruled quadratic in $PG\left(3,3\right)”$ (see [1]), where the forty-five chords of an “ellipsoid” in finite space $PG\left(3,3\right)$ are described, showing that they may be regarded as the edges of a notable graph that is in the group of automorphism of the symmetric group. The hexastigm is considered to be formed by six points of general positions in any projective 4-space. The six vertices of the hexastigm are joined in sets of two, three, or four, and each edge meets the opposite space in a diagonal point.

Three edges that together involve all six vertices are met by a unique line called a transversal. The correspondence between edges and transversals is seen in the fact that each transversal meets three edges, and each edge belongs to three transversals, which form a configuration ${15}_3$ of a harmonic conjugate with fifteen diagonal points with respect to the first and second vertices of the hexastigm.

Aiming to generalize the harmony of n-points in the projective geometry, we conducted a study in 1996 titled “Generalization of the Desargues’ theorems” [2] and more detailed presentation of set of harmonic points in 1998 titled “Harmonic points and Desargues’ Theorems” [3].

In 2014, we expanded on our research with the study “Generalized Desargues’ theorem” [4], where an arbitrary number of points on each one of the two distinct planes is considered, allowing the corresponding points on the two planes to coincide and three points on any of the planes to be collinear. In the work ([4], p. 3) we identified the generalized Desargues’ theorem in the following form:

Let p, p’ be two distinct planes, (1), (2), …, (𝑛), (𝑛 ∈ N), distinct points on p, and (1’), (2’), …, (𝑛’) distinct points on p’, both sets of points in general position.

(A) If all generalized lines (𝑖)(𝑖’) go through a common point, then all the intersections of the pairs of lines (𝑖)(𝑗), (𝑖’)(𝑗’) for 𝑖 ≠ 𝑗 are nonempty and lie on a common line (the common line of p and p’).

(B) If all the intersections of the pairs of lines (𝑖)(𝑗), (𝑖’)(𝑗’) for 𝑖 ≠ 𝑗 are nonempty, then all generalized lines (𝑖)(𝑖’) go through a common point.

([4], pp. 3–4)

The proof of the proposition is made by mathematical induction, and we assume that the given points (1), (2), etc. lie on the plane 𝑝; and (1’), (2’), etc., some corresponding points lie on another plane 𝑝’, allow for the possibility of some corresponding points coinciding. This restricts us from applying the generalization of the harmonic n-points, and we are also not able to prove the unicity of the mentioned generalized Desargues’ theorem.

In this paper, we explore the complete n-points (the triangle is considered to have 3-points as special case of complete n-points and dual-figure complete n-lines) and all of the cases in which the intersection line p is incident with diagonal points. This allows us to define generalized harmonic points, mainly based on the works [2,3].

First let us remember some basic concept of projective geometry which we will use as a tool in this paper.

Following Euclid, we usually denote points by upper case letters; we denote lines by lower case letters. If P I g is true, we shall also say that “’P is incident with g”, “’P lies on g”, “g passes through P”, and so on [5]. Instead of “P I g” we may also write “P ∈ g”. Now we introduce the axioms that are fundamental for the projective geometry [5]:

Axiom 1 (line axiom): For any two distinct points P and Q there is exactly one line that is incident with P and Q. This line is denoted by PQ.

Axiom 2 (Veblen-Young): Let A, B, C, and D be four points such that AB intersects the line CD. Then AC also intersects the line BD (Figure 1).

We find the following formulation of the Veblen-Young axiom which is more concise: if a line (in our case BD) intersects two “sides” (namely PA and PC) of a triangle (in our case APC) then the line also intersects the third side (namely AC) (Figure 1).

The Veblen-Young axiom is a truly ingenious way of saying that any two lines of a plane meet [5]. A projective plane is a nondegenerate projective space in which any two lines have at least one point in common.

We will continue working in this paper on the real projective plane. We can observe any set X called space, and the elements are the points of that space. The subsets of set X are called figures, thus figures in the projective plane consists of any subsets of the points and lines and the necessary incidence relations among them. The transformation of set X is called the bijective mapping f of set X to itself. We will treat projective transformations, to introduce specific concept of projective geometry, taken from [6]. A one-to-one correspondence is said to exist between the elements of two simple or complete figures, if there is associated with each element of one figure a unique element of the other figure, and reciprocally, with each element of the last a unique element of the first. Elements so paired are called homologous (correspondent, associated) and either one is said to correspond to other [6]. The perspectivity is a projective transformation and for two figures is said to be in perspective position, or are perspective, if they are in (1,1) correspondence and if homologous elements are incident. The most important of the figures with which we shall be concerned are:

Definition: A simple plane n-points is a set of n-points (vertices) of a plane taken in a definite order in which no three consecutive points are collinear, together with the n lines (sides) joining successive points. The dual is a simple plane n-line.

In each such figure there are 2n elements which fall into n pairs of opposite elements. If n is even the opposite elements are of the same kind (both points, or both lines); if n is odd they are not of the same kind. In general, the elements k and k + n are opposite if k $\le n$, while if k $>n$ the opposite elements are k and k − n. The diagonal lines of a simple n-point are the $\frac{1}{2}n\left(n-1\right)-n=\frac{1}{2}n\left(n-3\right)$ lines which join pairs of non-consecutive vertices.

Definition: A complete plane n-point is a set of n points (vertices) of a plane, no three of which are collinear, and the$\frac{n\left(n-1\right)}{2}$lines (sides) which join every pair of these points.

The dual is a complete plane n-line. The intersections’ points of the opposite sides are called diagonal points. The dual, the pairs of opposite vertices are joined by lines, which are called diagonal lines.

Definition: Two plane n-points are in perspective position if they are in a (1,1) correspondence such that pairs of homologous vertices are joined by lines concurrent at a point P, called the center of perspectivity. We will say that they are perspective from, or with, the center P.

In addition, we present the well-known four harmonic conjugate points in the projective plane [7]. Four harmonic collinear points: Four collinear points $\left(\mathrm{A},\mathrm{B},\mathrm{C},\mathrm{D}\right)$ are said to be a harmonic set, which is denoted as $\mathrm{H}\left(\mathrm{AB},\mathrm{CD}\right)$ if there exists a complete quadrangle (complete 4-points) $\left(\mathrm{E},\mathrm{F},\mathrm{G},\mathrm{F}\right)$ such that two of the points are diagonal points of the complete four points (quadrangle) and the other two points are on the opposite sides, determined by the third diagonal point (Figure 2).

We note that $\mathrm{H}\left(\mathrm{AB},\mathrm{CD}\right)$, $\mathrm{H}\left(\mathrm{BA},\mathrm{CD}\right)$, $\mathrm{H}\left(\mathrm{AB},\mathrm{DC}\right)$, and $\mathrm{H}\left(\mathrm{BA},\mathrm{DC}\right)$ all represent the same harmonic set of points. Several natural questions arise about harmonic sets of points:

• Does a harmonic set of more points exist?
• Given the determined number of collinear points, what number of a harmonic point sets can be constructed?
• If the answer is yes, is the harmonic set unique or does it depend on the complete n-points defining the points?
• How can we determine when a set of x collinear points is a harmonic set?

In this article, we begin by investigating these questions and present answers for each one.

In an exercise on basic theorems, we produced the generalized Desargues’ theorem for two complete n-points and the existence of a complete n-point [6]; thus, from these results, it follows that a harmonic set of x collinear points exists and can be constructed.

2. Generalization of the Desargues’ Theorems

Desargues’ theorem, the converse of Desargues’ theorem, and the theorem of the perspective quadrangle are the principal theorems in projective geometry ([5], pp. 31–32). A brief description of three principal theorems is presented below:

Theorem 1.

(Desargues’ theorem). If two triangles are perspective from a point, they are perspective from a line.

Theorem 2.

(the converse of Desargues’ theorem). If two triangles are perspective from a line, they are perspective from a point.

Theorem 3.

(perspective quadrangles). If two complete quadrangles are in (1-1) correspondence and so situated that five pairs of homologous sides intersect in points of the same straight line, then the point of intersection of the sixth pair of the homologous sides is also on this line, and the quadrangles are perspective to one another from a point and from a line.

It is important to note that the proof of Theorem 3 is based on the Desargues’ theorem and the converse of Desargues’ theorem. We know that for projective spaces of at list three dimension, are defined as the projective planes either by a set of incidence axioms or by algebraic constructions, Desargues’ theorems are always true [8].

In this study, we use a property of the projective geometry, the principle of duality, which proposes that once a theorem is proved, by the principal of duality (in the plane and in the space), the duality of the theorem is also valid [8].

Additionally, we bear in mind that Desargues’ theorem and its duality presented a relationship between the vertices and sides of the perspective triangles (three points).

We next consider the relationships between certain points and sides determined from complete n-point and/or its dual figure complete n-line; we present the proof of the propositions related to the complete n-point.

The simple question derived from Theorem 3 is when are two complete plane n-points perspective from a point and from a line?

We denote the complete plane $n$-points $A_1{A}_2 \dots A_n$, where $n$ is a natural number and $n>2$.

All of the sides $A_i{A}_j$ correspond to the order number $r\left(A_i{A}_j\right)\mathrm{defined}\mathrm{by}:$

$$r {\left(A_i{A}_j\right)}_n=j+\left(i-1\right)·n-\frac{i \left(i+1\right)}{2}, i,j=1, 2, 3,\dots , n. (\ast )$$

For example, the side $A_1{A}_2$ corresponds to the number $r\left(A_1{A}_2\right)=1;$ the side $A_1{A}_3$ corresponds to the number $r\left(A_1{A}_3\right)=2$; the side $r\left(A_{n-1}{A}_n\right)=\frac{n \left(n-1\right)}{2};$ etc.

Now, we define the perspectivity for two complete plane $n$-point [6]:

Two complete plane $n$-points are in the perspective position if they are in a $\left(1-1\right)$ correspondence such that pairs of homologous (correspondent) vertices are joined by lines concurrent at one point. Based on the principle of duality in projective geometry, we accept and consider definitions for the perspectivity of the two complete plane $n$-line. Is it important to determine when and what the conditions are when the two complete $n$-point are perspective? We find the answer in the following theorem [2]:

Let there be two given coplanar (or noncoplanar) complete plane $n$-point, $A_1{A}_2 \dots A_n$ and $B_1{B}_2 \dots B_n$, and let there be $X_{r\left(i,j\right)n}=A_i{A}_{j }·B_i{A}_j$ points of intersections of the correspondent sides, where:

$$r{\left(A_i{A}_j\right)}_n=j+\left(i-1\right)·n-\frac{i \left(i+1\right)}{2}; i, j=1, 2, 3, \dots , n,\mathrm{and}i<j.$$

GCD Theorem (Generalization of the Converse of Desargues’ theorem).

If two complete plane$n$-point are in$\left(1-1\right)$correspondence and so situated that$\left(2n-3\right)$intersections’ point$X_{r\left(i,j\right)n}$are collinear points, then the remaining.

$$\frac{\left(n-2\right)\left(n-3\right)}{2}$$

intersections’ points of homologous sides of the two complete$n$-point are collinear with the same line, and the two$n$-points are perspective from a point and from a line.

Proof of GCD Theorem.

We prove this theorem via mathematical induction.

Let there be two given coplanar (or noncoplanar) complete plane $n$-point, $A_1{A}_2 \dots A_n$ and $B_1{B}_2 \dots B_n$. (Figure 3).

(i) 

For $n=3$, the GCD theorem is equivalent to the Theorem 2 (the converse of Desargues’ theorem). For $n=4$, the GCD theorem is equivalent to Theorem 3 (perspective quadrangles).

(ii) 

We suppose that the GCD theorem is true for $n=k-1$.

(iii) 

We must prove that the GCD theorem is true for $n=k.$

We consider $X_{r\left(i,j\right)k}=A_i{A}_{j }·B_i{B}_j$ and intersections of the correspondent sides, where:

$$r{\left(A_i{A}_j\right)}_k=j+\left(i-1\right)·k-\frac{i \left(i+1\right)}{2}; i=1, 2, 3, \dots , k-2,\mathrm{and}j=2, 3, \dots , k-1.$$

Thus, by the hypothesis of this theorem, the points $X_{r\left(i,j\right)k} \mathrm{where}i,j=1, 2, 3, \dots k; i<j$ are colinear points with $p,$ and the straight lines $A_i{B}_j$ are concurrent lines with the point $O$.

The complete plane $k$-points $A_1{A}_2 \dots A_k$ and $B_1{B}_2 \dots B_k$ are in $\left(1-1\right)$ correspondence, and $\left(2k-3\right)$ sides pass through $A_1$ and $A_2$:

$$A_1\in A_1{A}_i , i=2, 3, \dots , k \mathrm{and} A_2\in A_2{A}_j , j=3, 4, \dots , k$$

meet the corresponding sides of the other complete $k$-point in the point of line $p$ formed by the corresponding vertices $B_1,B_2$ of the complete plane $k$-point $B_1{B}_2 \dots B_k$; i.e.,:

$$B_1\in B_1{B}_i , i=2, 3, \dots , k;B_2\in B_2{B}_j , j=3, 4, \dots , k.$$

We consider the complete plane $\left(k-1\right)$ points $A_1{A}_2 \dots A_{k-1}$ and $B_1{B}_2\dots B_{k-1}$.

According to hypothesis (ii), they are perspective from the axis $p\left(X_1, X_2, \dots ,\right)$ and we note that $2\left(k-1\right)-3=2k-5$ intersections’ points are the following collinear points:

$$\begin{gathered} A_1{A}_2 ⌒ B_1{B}_2=X_1 \\ \dots \dots \dots \dots \dots \dots \\ {A}_1{A}_{k-1} ⌒ B_1{B}_{k-1}=X_{k-2} \\ {A}_2{A}_3 ⌒ B_2{B}_3=X_k \\ \dots \dots \dots \dots \dots \dots \\ {A}_2{A}_{k-1} ⌒ B_2{B}_{k-1}=X_{2k-5} \\ \dots \dots \dots \dots \dots \dots \\ {A}_{k-2}{A}_{k-1} ⌒ B_{k-2}{B}_{k-1}=X_{\frac{\left(k-2\right)\left(k-1\right)}{2}} \end{gathered}$$

Lines $A_1{B}_1$, $i=1, 2, 3,\dots , \left(k-1\right)$ are concurrent with point $O$. Therefore, the others intersections’ points:

$$\begin{gathered} A_3{A}_4 ⌒ B_3{B}_4=X_{2k-2} \\ \dots \dots \dots \dots \dots \dots \\ {A}_3{A}_{k-1} ⌒ B_3{B}_{k-1}=X_{3k-7} \\ \dots \dots \dots \dots \dots \dots \\ {A}_{k-2}{A}_{k-1} ⌒ B_{k-2}{B}_{k-1}=X_{\frac{k\left(k-1\right)}{2}-2} \end{gathered}$$

are collinear with the same line $p$, and lines $A_i{B}_i$, $i=1, 2, 3, \dots ,k-1$, are concurrent with point $O$:

$$O\in A_i{B}_i , i=1, 2, \dots ,k-1$$

(1)

The two complete plane $\left(k-1\right)$-points, $A_1{A}_2 \dots A_{k-2}{A}_k$ and $B_1{B}_2 \dots B_{k-2}{B}_k,$ are perspective related to the $p\left(X_1, X_2, \dots \right)$ axis according to hypothesis (ii), because for two complete plane $\left(k-1\right)$-points, $A_1{A}_2\dots A_{k-2}{A}_k$ and $B_1{B}_2\dots B_{k-2}{B}_k$, we have $2\left(k-1\right)-3=2\left(k-5\right)$ collinear points:

$$\begin{gathered} A_1{A}_2 ⌒ B_1{B}_2=X_1 \\ \dots \dots \dots \dots \dots \dots \\ {A}_1{A}_{k-2} ⌒ B_1{B}_{k-2}=X_{k-3} \\ {A}_1{A}_k ⌒ B_1{B}_k=X_{k-1} \\ {A}_2{A}_3 ⌒ B_2{B}_3=X_k \\ \dots \dots \dots \dots \dots \dots \\ {A}_2{A}_{k-2} ⌒ B_2{B}_{k-2}=X_{2k-5} \\ {A}_2{A}_k ⌒ B_2{B}_k=X_{2k-3} \end{gathered}$$

Therefore, the other intersections’ points:

$$\begin{gathered} A_3{A}_4 ⌒ B_3{B}_4=X_{2k-1} \\ \dots \dots \dots \dots \dots \dots \\ {A}_3{A}_{k-2} ⌒ B_3{B}_{k-2}=X_{3k-8} \\ {A}_3{A}_k ⌒ B_3{B}_k=X_{3k-6} \\ \dots \dots \dots \dots \dots \dots \\ \dots \dots \dots \dots \dots \dots \\ {A}_{k-2}{A}_k ⌒ B_{k-2}{B}_k=X_{\frac{k\left(k-1\right)}{2}-1} \end{gathered}$$

are collinear with line $p$, and lines $A_i{B}_i; i=1, 2, \dots ,k-2, k$ are concurrent with point $O$:

$$O \in A_i{B}_i , i=1, 2, \dots ,k-2, k$$

(2)

We must prove that the points $A_{k-1}{A}_k ⌒ B_{k-1}{B}_k=X_{\frac{k\left(k-1\right)}{2}}$ are collinear with the points

$$X_i , i=1, 2, \dots \dots ,k-2, k.$$

In fact, the triangles $A_1{A}_{k-1}{A}_k$ and $B_1{B}_{k-1}{B}_k$ are perspective-related to point $O$; therefore, they are perspective from the line $p$ according to Theorem 1 (Desargues’ theorem).

Then, the pairs of homologous sides meet at collinear points:

$$\begin{gathered} A_1{A}_{k-1} ⌒ B_1{B}_{k-1}=X_{k-2} \\ {A}_1{A}_k ⌒ B_1{B}_k=X_{k-1} \\ {A}_{k-1}{A}_k ⌒ B_{k-1}{B}_k=X_{\frac{k\left(k-1\right)}{2}} \end{gathered}$$

However, the points $X_{k-2}$ and $X_{k-1}$ lie on the line $p$, and the point $X_{\frac{k\left(k-1\right)}{2}}$ must lie on the line $p$. Thus, considering relations (1) and (2), the two n-points are perspective from the point O, which proves that the GCD theorem is true for $\forall n\in \mathbb{N}$.

The GCD theorem is also valid when the line $\mathrm{p}$ passes through diagonal points of the complete n-point.

Now, in an analogical way, we can prove the generalized Desargues’ theorem (GD). For this purpose, in similar way, let there be two given coplanar (or noncoplanar) complete n-points, $A_1{A}_2 \dots A_n$ and $B_1{B}_2 \dots B_n$. Additionally, let there be $X_{r\left(i,j\right)n}=A_i{A}_{j }·B_i{A}_j$ points of intersections of the correspondent sides, where $r{\left(A_i{A}_j\right)}_n=j+\left(i-1\right)·n-\frac{i \left(i+1\right)}{2}; i, j=1, 2, 3, \dots , n,$ and $i<j,$ and let there be a P-intersection point of the lines determined by homologues vertices:

$$\mathrm{O}\ni A_i{B}_i, i=1,2,3, \dots , n.$$

□

GD Theorem (Generalized Desargues’ Theorem).

If two complete plane$n$-points are in perspective from a point P and the$\left(n-1\right)$-sides passing through one vertex meet the corresponding sides of the other$n$-point in the colinear points of a line, then the two complete$n$-points are perspective from a line.

Proof. 

Let there be two given coplanar (or noncoplanar) complete plane $n$-points, $A_1{A}_2 \dots A_n$ and $B_1{B}_2 \dots B_n.$ (Figure 4).

(i) 

For $n=3$, GD theorem is equivalent to Theorem 1 (Desargues’ theorem).

(ii) 

We suppose that GD theorem is true for $n=k-1$.

(iii) 

Thus, we can prove that the GD theorem is true for $n=k$.

The complete plane $k$-points $A_1{A}_2 \dots A_k$ and $B_1{B}_2\dots B_k$ are $\left(1-1\right)$ correspondence; $k$-pairs of homologous vertices are joined by lines concurrent at one point O; and $k-1$ pairs of homologous sides intersect at the collinear points of the line p:

Based on the hypothesis of the mathematic induction, the two complete plane $\left(k-1\right)$-points $A_1{A}_2 \dots A_{k-1}$ and $B_1{B}_2\dots B_{k-1}$ are perspective from the axis (line) $p\left( X_1, X_2, \dots \right)$ and from a center $O$, because for complete plane $\left(k-1\right)$-points $A_1{A}_2 \dots A_{k-1}$ and $B_1{B}_2\dots B_{k-1},$ we have $O\in A_i{B}_I,i=1,2,\dots ,k-1$ and $\left(k-1\right)-1=k-2$.

The collinear points are as follows:

$$\begin{gathered} A_1{A}_2 ⌒ B_1{B}_2=X_1 \\ \dots \dots \dots \dots \dots \dots \\ {A}_1{A}_{k-1} ⌒ B_1{B}_{k-1}=X_{k-2} \end{gathered}$$

Therefore, the others intersect points:

$$\begin{gathered} A_2{A}_3 ⌒ B_2{B}_3=X_k \\ \dots \dots \dots \dots \dots \dots \\ {A}_2{A}_{k-1} ⌒ B_2{B}_{k-1}=X_{2k-4} \\ {A}_3{A}_4 ⌒ B_3{B}_4=X_{2k-2} \\ \dots \dots \dots \dots \dots \dots \\ \dots \dots \dots \dots \dots \dots \\ {A}_{k-2}{A}_{k-1} ⌒ B_{k-2}{B}_{k-1}=X_{\frac{k\left(k-1\right)}{2}-2} \end{gathered}$$

are collinear points of the same line p.

Similarly, the two complete plane $\left(k-1\right)$-points $A_1{A}_2\dots A_{k-2}{A}_k$ and $B_1{B}_2\dots B_{k-2}{B}_k$ are perspective from the axis $p\left( X_1, X_2, \dots \right)$ and from a center (point) $O$ according to the hypothesis of the theorem for complete plane $\left(k-1\right)$-points $A_1{A}_2 \dots A_{k-2}{A}_k$ and $B_1{B}_2\dots B_{k-2}{B}_k$.

Thus, we obtain $O\in A_i{B}_i, i=1, 2, \dots ,k-2, k$ and (k − 1) − 1 = k − 2 collinear points:

$$\begin{gathered} A_1{A}_2 ⌒ B_1{B}_2=X_1 \\ \dots \dots \dots \dots \dots \dots \\ {A}_1{A}_{k-2} ⌒ B_1{B}_{k-2}=X_{k-3} \\ {A}_1{A}_k ⌒ B_1{B}_k=X_{k-1} \end{gathered}$$

Therefore, the other intersect points:

$$\begin{gathered} A_2{A}_3 ⌒ B_2{B}_3=X_k \\ \dots \dots \dots \dots \dots \dots \\ {A}_2{A}_{k-2} ⌒ B_2{B}_{k-2}=X_{2k-5} \\ {A}_2{A}_k ⌒ B_2{B}_k=X_{2k-3} \\ {A}_3{A}_4 ⌒ B_3{B}_4=X_{2k-2} \\ \dots \dots \dots \dots \dots \dots \\ \dots \dots \dots \dots \dots \dots \\ {A}_{k-2}{A}_k ⌒ B_{k-2}{B}_k=X_{\frac{k\left(k-1\right)}{2}-1} \end{gathered}$$

are collinear points with the same line $p$.

We must prove that the point $A_{k-1}{A}_k ⌒ B_{k-1}{B}_k=X_{\frac{k\left(k-1\right)}{2}}$ is collinear with the points $X_i, i=1, 2, \dots$ In fact, the triangles $A_1{A}_{k-1}{A}_k$ and $B_1{B}_{k-1}{B}_k$ are perspective-related to the point O; therefore, they are perspective from a line (on the basis of Desargues’ theorem). Thud, the pairs of homologous sides:

$$\begin{gathered} A_1{A}_{k-1} ⌒ B_1{B}_{k-1}=X_{k-2} \\ {A}_1{A}_k ⌒ B_1{B}_k=X_{k-1} \\ {A}_{k-1}{A}_k ⌒ B_{k-1}{B}_k=X_{\frac{k\left(k-1\right)}{2}} \end{gathered}$$

are collinear points.

Because the points $X_{k-2}$ and $X_{k-1}$ lie on the line $p$, point $X_{\frac{k\left(k-1\right)}{2}}$ also lies on the line $p$. Thus, we have proven that the GD theorem is true for $\forall n\in \mathbb{N}$.

The duality of the GD theorem is true based on the principle of duality.

Maintaining the synthetical logic of proof of the generalized Desargues’ theorems, it is not difficult the analytically prove them.

The proof of the generalized Desargues’ theorem is independent of the incidence of the axis of the perspectivity with diagonal points of the complete n-points (n-lines). This is an important fact in the next part of the paper, which discusses the generalization of the harmonic points of the line. □

3. The Structure of n-Harmonic Points

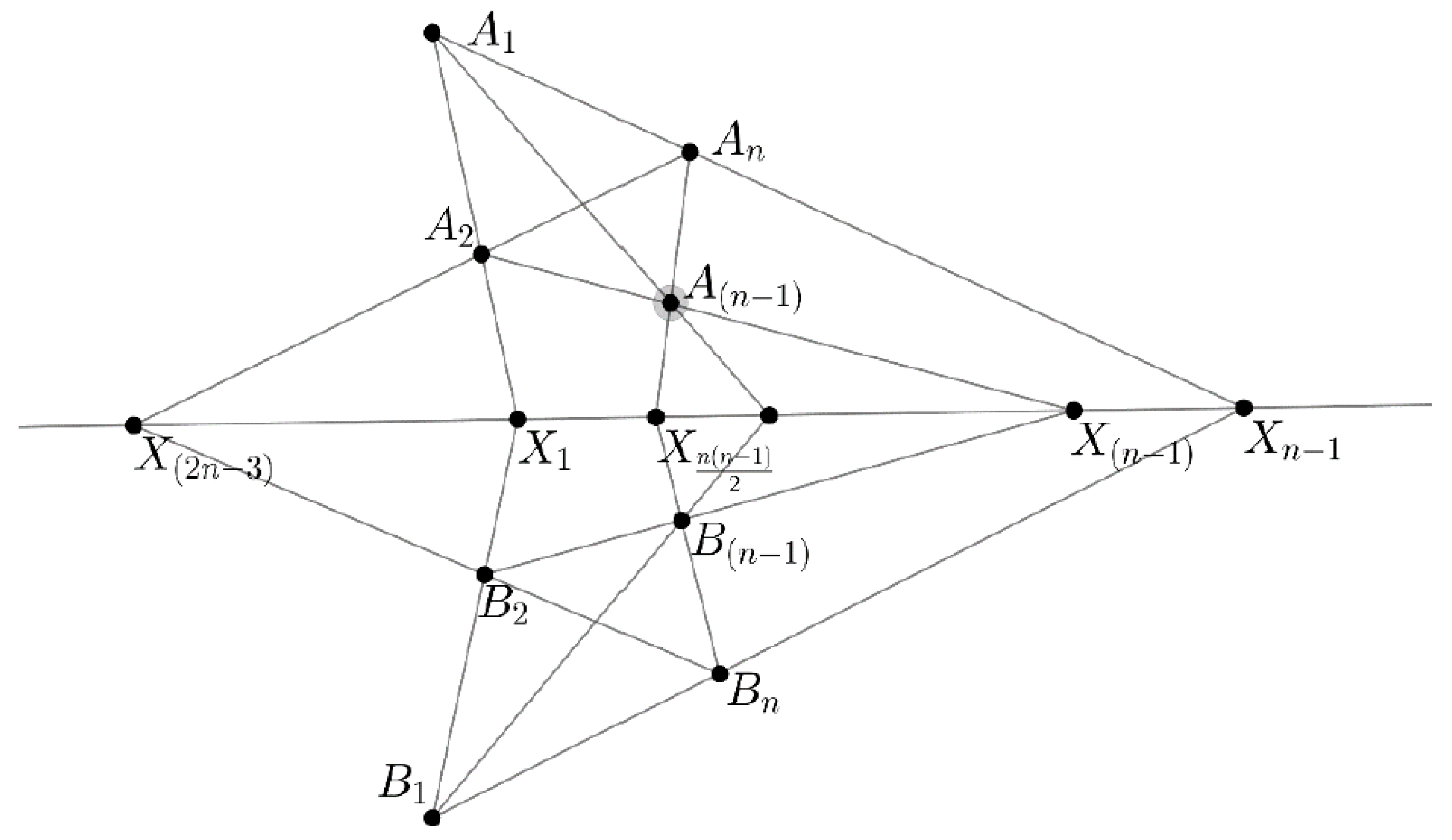
Let $A_1{A}_2\dots A_n$ be complete n-point and $p$ a coplanar line (Figure 5). Then, the following cases may occur:

• The line $p$ can be incident with at most two vertices of complete $n$-points.

If, e.g., the line $p$ is incident with vertices $A_s$ and $A_t$, then we can write $p\equiv A_{r\left(st\right)n}$, which means that the line p coincides with the side $A_{s } A_t$. The other sides of the $n$-point $A_1{A}_2\dots A_n$ are intersected by the line $p$ at $\frac{ \left(n-2\right)\left(n-3\right)}{2}$—different points.

Indeed, every side (in our case the line $p$) of the complete $n$-point has $\frac{\left(n-2\right)\left(n-3\right)}{2}$ opposite sides and $2\left(n-2\right)$ adjacent sides.

The line $p$ (which, in this case, is identical to a side of full $n$-point) is intersected by $2\left(n-2\right)$ adjacent sides at points $A_s$ and $A_t$, while with opposite sides (non-adjacent) at other points $P_u,$ $u=1,2,\dots , \frac{\left(n-2\right)\left(n-3\right)}{2}$, which in total are $\frac{\left(n-2\right)\left(n-3\right)}{2}+2$ points (Figure 5).

Similarly, we can discuss the other four cases:

• The line $p$ can be incident with one vertex of complete $n$-point.
• The line $p$ can be not incident with any vertices and diagonal points of complete $n$-point.
• The line $p$ is not incident with any vertices and is incident with one diagonal point of complete $n$-point.
• The line $p$ is not incident with any vertices but is incident with two diagonal points of complete $n$-point.

Thus, regarding the intersection points of the straight line and complete plane $n$-point, we can prove the following proposition:

The intersection points of the complete n-point and a straight line p can be $\frac{n\left(n-1\right)}{2}-2$, $\frac{n\left(n-1\right)}{2}-\left(n-1\right)$, or $\frac{n\left(n-1\right)}{2}-k$, where k is the number of diagonal points incidents with the line p, and k = 1, 2, 3, … n − 2.

Definition 1. 

A set of points in which the sides of complete plane$n$-point meet a straight line, where the line is not incident with any diagonal points and any vertices of complete$n$-point, is called a set of$H$-points of rank$0$, which is indicated by$P_{ n}^0.$

The number of points of set $P_{ n}^0$ is: $K\left|P_{ n}^0\right|=\frac{n\left(n-1\right)}{2}$.

Definition 2. 

A set of points in which the sides of a complete plane$n$-point meet a line, where the line is incident with the k diagonal points and not incident with any vertices of complete$n$-point, is called a set of$H$-points of rank$k$, which is indicated by$P_{ n}^k$.

The number of points of set $P_{ n}^k$ is: $K\left|P_{ n}^k\right|=\frac{n\left(n-1\right)}{2}-k$.

Example: A set of the points in which the sides of a complete n–point meet a line p, where the line p is incident with two diagonal points and not incident with any vertices of complete plane n–point, is called a set of $H$-points of rank $2$, and it is indicated by $P_{ n}^2.$

The number of points of set $P_{ n}^2$ is: $K\left|P_{ n}^2\right|=\frac{n\left(n-1\right)}{2}-2$.

In the case of $n=4$, this is the set $P_{ 2}^2$, which presents four harmonic points - a set of points in which the sides of a quadrangle meet a line, where the line is incident with two diagonal points of the quadrangle and not incident with any of vertices of it (the definition for harmonic points on page 3). Based on the principle of duality, we can define a set of $H$-lines of rank 0, and it is indicated by ${\delta }_n^0$.

The number of lines of set ${\delta }_n^0$ is: $K\left|{\delta }_{ n}^0\right|=\frac{n\left(n-1\right)}{2}$.

In addition, the set of $H$-lines of rank $k$ is indicated by ${\delta }_{ n}^k$.

The number of lines of set ${\delta }_n^k$ is: $K\left|{\delta }_n^k\right|=\frac{n\left(n-1\right)}{2}-k.$

Example: A set of $H$-lines of rank $2$ is indicated by ${\delta }_n^2$.

The number of lines of set ${\delta }_n^2$ is: $K\left|{\delta }_n^2\right|=\frac{n\left(n-1\right)}{2}-2$.

In the case of $n=4$, this is set ${\delta }_n^2$, which present four harmonic lines, that is, four concurrent lines, two of which are diagonal lines, while the other two are lines passing through the two vertices lying on the third diagonal line.

Now, it is important to study the relation between the sets $P_{ n}^k$ for different values of $n$ and $k$, $k<n+2$.

If the set $P_{n+1}^0$ is determined from the complete $\left(n+1\right)$-points, and, from these vertices’ isolates (exclude), the point n and the rested complete $n$-point determine the set $P_{n }^0$, then it is evident that the set $P_n^0$ is a subset of the set $P_{n+1}^0$.

Example: Let us observe the case of the points $A_1,A_2,A_3, A_4$, each of three of them are non collinear points. If the set $P_4^0$ is determined by complete 4-point $A_1{A}_2{A}_3{A}_4$ and the set $P_3^0$ is determined by complete 3-point $A_1{A}_2{A}_3$, then $P_3^0\subset P_4^0$.

In addition, if $P_5^0$ is determined by complete $5$-point, $A_1{A}_2{A}_3{A}_4{A}_5$, and the derived complete $4$-point, $A_1{A}_2{A}_3{A}_4$, then $P_4^0\subset P_5^0$, etc.

Therefore, the following relation is valid: $P_3^0\subset P_4^0\subset P_5^0\subset \dots \subset P_{\mathrm{n}}^0\subset P_{\mathrm{n}+1}^0\dots$ (*).

On the other hand, for the set $P_n^1$, the relation of the inclusion of (*) is different. Let there be $A_1{A}_2\dots A_n$ $n$-point, which determine the set $P_n^1$.

The definition of the set $P_n^1$ implies that there is a diagonal point, which means that two opposite sides of complete n-point $A_1{A}_2\dots A_n$ are incident with the same point of the set $P_n^1$. Let there be the sides $A_r{A}_s$ and $A_t{A}_v$, two opposite sides of $n$-point $A_1{A}_2\dots A_n$.

If we exclude one of the vertices $A_r,A_s, A_t$ or $A_v,$ then we obtain complete $\left(n-1\right)$-point; these determine the set $P_{n-1}^0$, which is $P_{n-1}^0\subset P_n^0$. In this case, considering relation (*), we have

$$P_3^0\subset P_4^0\subset \dots \subset P_{n-1}^0\subset P_n^0 (**)$$

We consider the complete $\left(n+1\right)$-point $A_1{A}_2\dots A_n{A}_{n+1,}$ which determine the set $P_{n+1}^2$. The set $P_{n+1}^2$ includes two diagonal points of complete $\left(n+1\right)$-point, $A_1{A}_2\dots A_n{A}_{n+1}$.

Let there be $D_1$ and $D_2$ diagonal points included in the set $P_{n+1}^2$ and:

$$D_1=A_m{A}_n\cdot A_p{A}_q, D_2=A_r{A}_s\cdot A_t{A}_v.$$

If from the complete $\left(n+1\right)$-point $A_1{A}_2{A}_3\dots A_n{A}_{n+1}$ we exclude one of the vertices $A_m,A_n,A_p,A_q,A_r,A_s,$ $A_t$ and $A_v$, then, we will obtain the complete $n$-point that determine the set $P_n^1$ and $P_n^1\subset P_{n+1}^2.$

Now, considering the relation (**), we have

$$P_3^0\subset P_4^0\subset \dots \subset P_{n-1}^0\subset P_n^1\subset P_{n+1}^2(***)$$

If from the complete (n + 1)-point $A_1{A}_2\dots A_n{A}_{n+1}$ that determine the set $P_{n+1}^2,$ we add the new vertex $A_{n+2}$, then we will obtain the set $P_{n+2}^2$ and the relation:

$$P_{n+1}^2\subset P_{n+2}^2$$

We can continue this process, and considering the relation (***), we obtain the following relation:

$$P_3^0\subset P_4^0\subset \dots \subset P_{n-1}^0\subset P_n^1\subset P_{n+1}^2\subset P_{n+2}^2\dots (****)$$

Let us observe the case of complete u-point $A_1{A}_2\dots A_u$ that determine the set $P_u^3, u>n+3$.

The set $P_u^3$ includes three diagonal points of complete u-point $A_1{A}_2\dots A_u$. Let there be $D_1,D_2$, and $D_3$, the diagonal points of $u$-point $A_1{A}_2\dots A_u$:

$$\begin{gathered} D_1=A_{r_1}{A}_{r_2}\cdot A_{r_3}{A}_{r_4}, \\ {D}_2=A_{s_1}{A}_{s_2}\cdot A_{s_3}{A}_{s_4},\mathrm{and} \\ {D}_3=A_{t_1}{A}_{t_2}\cdot A_{t_3}{A}_{t_4}, r_i\ne s_i\ne t_i, i=1,2,3,4. \end{gathered}$$

If, from complete u-point $A_1{A}_2\dots A_u$, we exclude one of the vertices, $A_{r_i}$, $A_{s_i}$, or $A_{t_i}, i=1,2,3,4$, then we obtain complete (u − 1)-point, which determine the set $P_{u-1}^3$ and the following relation:

$$P_{u-1}^2\subset P_u^3$$

Now, considering the relation (****), we obtain the following:

$$P_3^0\subset P_4^0\subset \dots \subset P_{n-1}^0\subset P_n^1\subset P_{n+1}^2\subset P_{n+2}^2\subset \dots \subset P_{u-1}^2\subset P_u^3 (*****)$$

This process, in the same way continues, and we obtain the following relations:

$$\begin{gathered} P_3^0\subset P_4^0\subset \dots \subset P_{n-1}^0\subset P_n^1\subset P_{n+1}^2\subset \dots \subset P_{u-1}^2\subset P_u^3\subset P_{u+1}^3\subset \dots \\ {P}_3^0\subset P_{k_1}^0\subset P_{k_{1+1}}^1\subset P_{k_{1+2}}^1\subset \dots \subset P_{k_{2-1}}^1\subset P_{k_2}^2\subset P_{k_{2+1}}^2\subset \dots \subset P_{k_{3-1}}^2\subset P_{k_3}^3\subset \dots \end{gathered}$$

where $k_1=3,4,5,6\dots k_2=5,6,7,\dots k_3=5,6,7,8,\dots$

We present all of these relations of sets of harmonic points in Figure 6.

Analyzing Figure 6, we note that a set of harmonic points $P_k^r$ is the subset of the set of $H$-points with a smaller rank or equal to $r+2$; thus, the relation is:

$$\begin{gathered} P_k^r\subset P_{k+1}^r, \\ {P}_k^r\subset P_{k+1}^{r+1} \mathrm{or} \\ {P}_k^r\subset P_{k+1}^{r+2}. \end{gathered}$$

In fact, if we add a new vertex to the complete k-point, we obtain a new complete $\left(k+1\right)$-point, which determine the following set:

• $P_{k+1}^r$ of rank $r$ if the number of the diagonal points is not increased.
• $P_{k+1}^{r+1}$ of rank $r+1$ if the number of the diagonal points is increased by one.
• $P_{k+1}^{r+2}$ of rank $r+2$ if the number of the diagonal points is increased by two.

As the number of diagonal points is incident with the line, it is not possible for it to be more than 2, because each point is determined by two lines.

Thus, if we add the vertex $A_{k+1}$ as an intersection of the two lines to the complete $k$-point $A_1{A}_2\dots A_k$, each of them incidents with a point of the set $P_k^r$ and one of vertices of the complete k-point $A_1{A}_2\dots A_k$. This provides us with the set of $H$-points of rank $r+2$: $P_{k+1}^{r+2}$;

If we add the vertex $A_{k+1}$ as an intersection of the two lines to the complete $k$-point $A_1{A}_2\dots A_k$, only one of them is incident with the points of the set $P_k^r$ and one of the vertices of the complete k-point $A_1{A}_2\dots A_k$. This provides us with the set of $H$-points of rank $r+1$: $P_{k+1}^{r+1}$;

If we add the vertex $A_{k+1}$ as an intersection of the two lines to the complete k-point $A_1{A}_2\dots A_k$, not one of them is incident with the points of the set $P_k^r$, thereby providing us with the set of $H$-points of rank $r: P_{k+1}^r$;

Considering Figure 6 and the relation of inclusion, for the harmonic points $P_k^r$, we can present the matrices’ form:

For example, if we consider the set $P_6^0$, the series of inclusive sets is $P_n^0, n=3,4,5$:

$$P_3^0\subset P_4^0\subset P_5^0\subset P_6^0$$

We can denote with the symbol (0000) that the first column presents the set $P_3^0$, the second column is the set $P_4^0$, the third column is the set $P_5^0$, and the fourth column is the $P_6^0$.

Each of the sets of H-points of rank 0 can be presented by matrices of one row and n-2 columns. The series of the inclusion of H- points of rank 1 is with two rows; for example, the set $P_6^1$ is presented by the following matrix:

$$\begin{gathered} P_3^0\subset P_4^0\subset P_5^0\subset P_6^1 \\ {P}_3^0\subset P_4^0\subset P_5^1\subset P_6^1 \\ {P}_3^0\subset P_4^1\subset P_5^1\subset P_6^1 \end{gathered}$$

Equivalent matrix:

$$\left(\begin{array}{ccc}\begin{array}{c}0\\ 0\\ 0\end{array}& \begin{array}{c}0\\ 0\\ 1\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 1\\ 1\end{array}& \begin{array}{c}1\\ 1\\ 1\end{array}\end{array}\end{array}\right)\mathrm{or}\left(\begin{array}{ccc}0& 0& 1\\ 0& 1& 1\\ 1& 1& 1\end{array}\right)$$

The number of elements in the matrix for the set $P_n^1$ is $n-3$. Thus, the matrix for the set $P_n^1$ is $\left(n-3\right)\times (n-2)$, or, if we exclude the set $P_3^0$, then the corresponding matrix for $P_n^1$ is in the form of $\left(n-3\right)\times \left(n-3\right)$.

The matrix of the inclusion for the set of H-points of rank 2 is reached. The matrix of the set $P_6^2$ is as follows:

$$\begin{gathered} P_3^0\subset P_4^0\subset P_5^0\subset P_6^2 \\ {P}_3^0\subset P_4^0\subset P_5^1\subset P_6^2 \\ {P}_3^0\subset P_4^1\subset P_5^1\subset P_6^2 \\ {P}_3^0\subset P_4^0\subset P_5^2\subset P_6^2 \\ {P}_3^0\subset P_4^1\subset P_5^2\subset P_6^2 \\ {P}_3^0\subset P_4^2\subset P_5^2\subset P_6^2 \end{gathered}$$

Equivalent matrix:

$$\left(\begin{array}{ccc}\begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}0\\ 0\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\\ \begin{array}{c}1\\ 2\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 1\\ \begin{array}{c}1\\ 2\\ \begin{array}{c}2\\ 2\end{array}\end{array}\end{array}& \begin{array}{c}2\\ 2\\ \begin{array}{c}2\\ 2\\ \begin{array}{c}2\\ 2\end{array}\end{array}\end{array}\end{array}\end{array}\right)\mathrm{or}\left(\begin{array}{ccc}\begin{array}{c}0\\ 0\\ \begin{array}{c}1\\ 0\\ \begin{array}{c}1\\ 2\end{array}\end{array}\end{array}& \begin{array}{c}0\\ 1\\ \begin{array}{c}1\\ 2\\ \begin{array}{c}2\\ 2\end{array}\end{array}\end{array}& \begin{array}{c}2\\ 2\\ \begin{array}{c}2\\ 2\\ \begin{array}{c}2\\ 2\end{array}\end{array}\end{array}\end{array}\right)$$

The number of rows for the set $P_n^2$ is $\frac{\left(n-2\right)\left(n-3\right)}{2}$. Thus, the matrix of inclusion for the h-points $P_n^2$ is $\left[\frac{\left(n-2\right)\left(n-3\right)}{2}\right]\times \left(n-2\right).$

If we exclude the set, $P_3^0,$ they will have the form $\left[\frac{\left(n-2\right)\left(n-3\right)}{2}\right]\times (n-3)$.

In the same way, we can construct the matrices for each of the sets of the H-points. The set of the four harmonic points obtained from complete 4-points and a line incident with two diagonal points is the subset of the largest set of H-points constructed before $P_n^k$, $k\le n-2$.

We can demonstrate the same for the harmonic H-lines. Now, we can prove the following propositions:

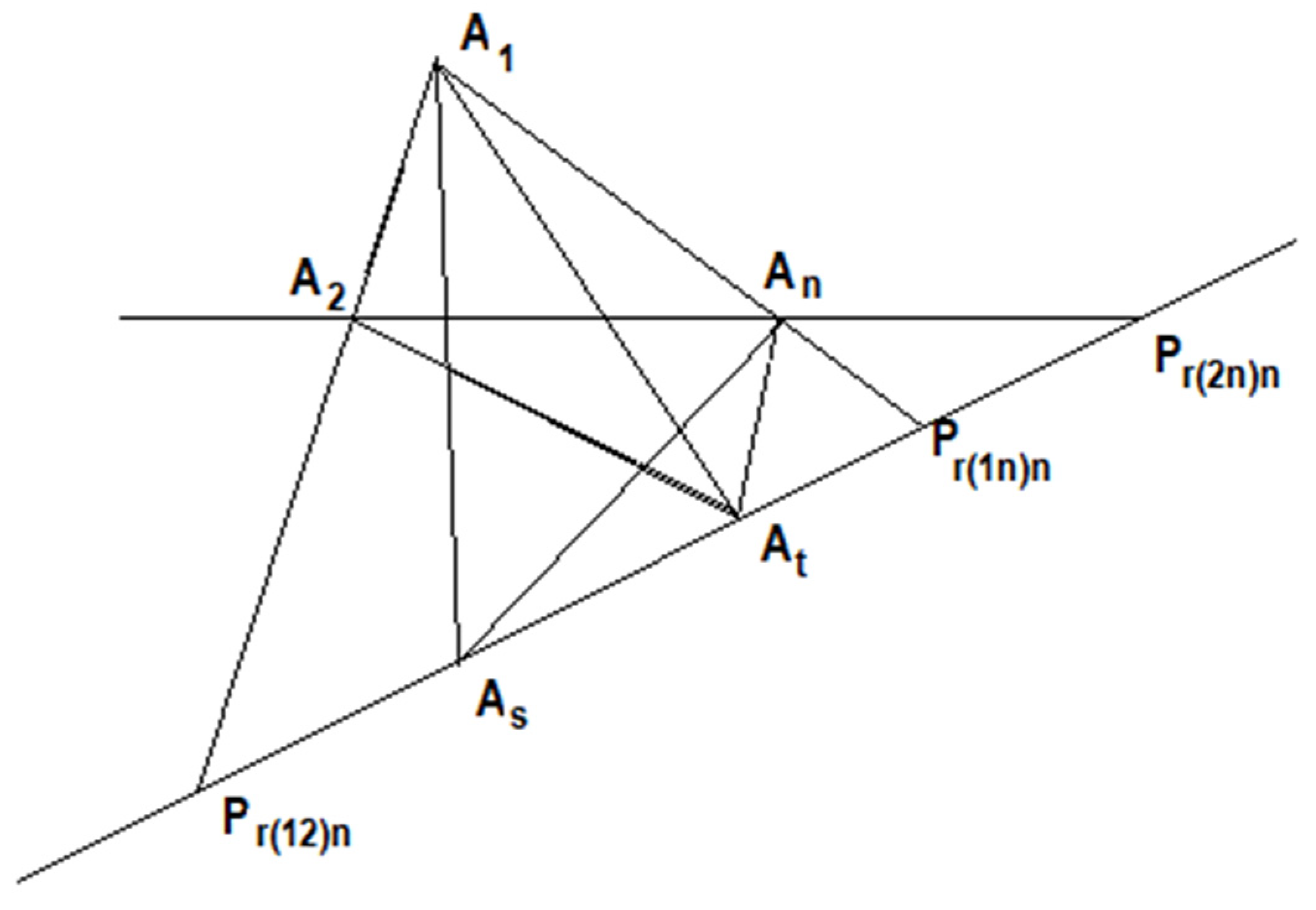
Proposition 1. 

The set of points$P_{ n}^0$is uniquely determined when$\left(2n-3\right)$collinear points are given.

Proof. 

If $\frac{n\left(n-1\right)}{2}$ points $T_1 ,T_2 , \dots ,T_{ \frac{n\left(n-1\right)}{2}}$ are on a line $p$ and form a set of $P_{ n}^0$ defined by a complete plane $n$-point $A_1{A}_2 \dots A_n$, then a second complete plane $n$-point $B_1{B}_2 \dots B_n$ in the same plane or in any plane passing through $p$, which has $\left(2n-3\right)$ sides passing through $T_i , i=1, 2, \dots , \left(2n-3\right)$ and through any two of the vertices $B_1,B_2,\dots ,B_n$, will have its the remaining sides passing through $T_j,j=2n-2, 2n-1,\dots , \frac{n\left(n-1\right)}{2}$.

This was evident from the GCD theorem (the generalized Converse of Desargues’ theorem).

Therefore, we draw arbitrarily in any plane through $p$, $\left(n-1\right)$-concurrent lines with a point. Let there be point $A_1$ and $\left(n-2\right)$-concurrent lines with a point; let there be point $A_2, A_2\in A_1{T}_1$—one through each of the given $T_1,T_2, \dots ,T_{2n-3}$ points. The remaining vertices $A_i, i>2$ are determined with:

$$A_i=A_1{Tr}_{1i}⌒A_2{Tr}_{2i}$$

where $r_{1i}=r{\left(A_1{A}_i\right)}_n=i-1$, $r_{2i}=r{\left(A_2{A}_i\right)}_n=n+i-3$, and $\frac{n\left(n-1\right)}{2}$ sides of the constructed $n$-point $A_1{A}_2\dots A_n$ meet the line $p$ in the desired points:

$$T_{i }, i=1, 2, \dots , 2n-3, 2n-2, \dots , \frac{n\left(n-1\right)}{2}.$$

The GCD theorem ensures that any other complete plane $n$-point $B_1{B}_2\dots B_n$ constructed in the same way as the complete plane $n$–point $A_1{A}_2\dots A_n$ will determine on $p$ the same points, $T_j, j=2n-2, 2n-1, \dots , \frac{n\left(n-1\right)}{2}.$ □

Proposition 2. 

The set of points$P_{ n}^1$is uniquely determined when$\left(2n-4\right)$collinear points are given.

Proof. 

As in Proposition 1, in this case, we have one pair of opposite sides intersecting at $T_i , i$ which is an index of $\left\{1, 2, \dots , 2n-4\right\}$.

Based on the GCD theorem, the points $T_j, j=2n-3, 2n-2, \dots , \frac{n\left(n-1\right)}{2}-1$, are uniquely determined. □

Proposition 3. 

The set of points$P_{ n}^2$is uniquely determined when$\left(2n-5\right)$collinear points are given.

Proof. 

As in Proposition 1, in this case, we have one pair of opposite sides intersecting at $T_I$ and a second pair of opposite sides intersecting at $T_j; i,j$, which is an index of $\left\{1, 2,\dots , 2n-5\right\}$. Based on GCD theorem, the points $T_j, j=2n-3, 2n-2, \dots , \frac{n\left(n-1\right)}{2}-1$ are uniquely determined. □

Now, we formulate the main proposition:

Theorem 4. 

For every set of$n$-collinear points, the set of$H$–points of rank$0$, rank$1,$or rank$2$are always uniquely determined.

Proof. 

Every natural number $\mathrm{n}$ has the form $n=2k$ or $n=2k-1$, $k\in {\mathbb{Z}}^{+}$.

If $n=2k$, then $n=2k=2\left( k+2 \right)-4$. For $\left( 2\left( k+2 \right)-4 \right)$ collinear points, Proposition 2 implies that the set of points $P_{ k+2}^1$ is uniquely determined.

If $n=2k-1$, then $n=2k-1=2\left( k+1 \right)-3$ or $n=2k-1=2\left( k+2 \right)-5$.

For $\left( 2\left( k+1 \right)-3 \right)$ collinear points, Proposition 1 implies that the set of points $P_{ k+2}^0$ is uniquely determined.

For $\left( 2\left( k+2 \right)-5 \right)$ collinear points, Proposition 3 implies that the set of points $P_{ k+2}^2$ is uniquely determined.

One interesting case is that when $n=3$. In this case, for each arbitrary three collinear points $A_1, A_2, A_3$, by the Theorem 4, implies that we may constructed sets $P_{ 3}^0$ and $P_{ 4}^2$. The set $P_{ 4}^2$ has four points that represent the well-known set of four harmonic points.

Thus, for arbitrary three collinear points $A_1, A_2, A_3$, we can determinate the fourth harmonic point:

$$A_4=H \left(A_1, A_3 ;A_2\right)\mathrm{that}\mathrm{is}H \left(A_1, A_3 ;A_2,A_4\right).$$

□

4. Conclusions

The ordering of points on a line according to a rule determined by the relation of the line and the sides of complete $n$-points is presented as the generalization of harmonic points. According to this rule of ordering the points of a line, it was necessary to generalize the well-known Desargues’ theorems. Both results will hopefully facilitate a debate in the mathematical community.

In this paper we are presented the generalization of the n-harmonic points in the real projective geometry. The elaboration of the generalization of the n-harmonic points in the finite projective geometry is issue to do in the future. Other issues to be studied is the properties of the n-harmonic points, like conjugatively of ordered number of points with other number of points of the set of $H$-points $P_n^k.$ The next researches maybe will give new results about these and other properties of the set of $H$-points $P_n^k$.

It is also necessary to study the algebraic structures of the sets of $H$-points $P_{ n}^k$ (and the sets of H-lines). In this paper, we examined only the relationship between these sets of $H$-points of different ranks.