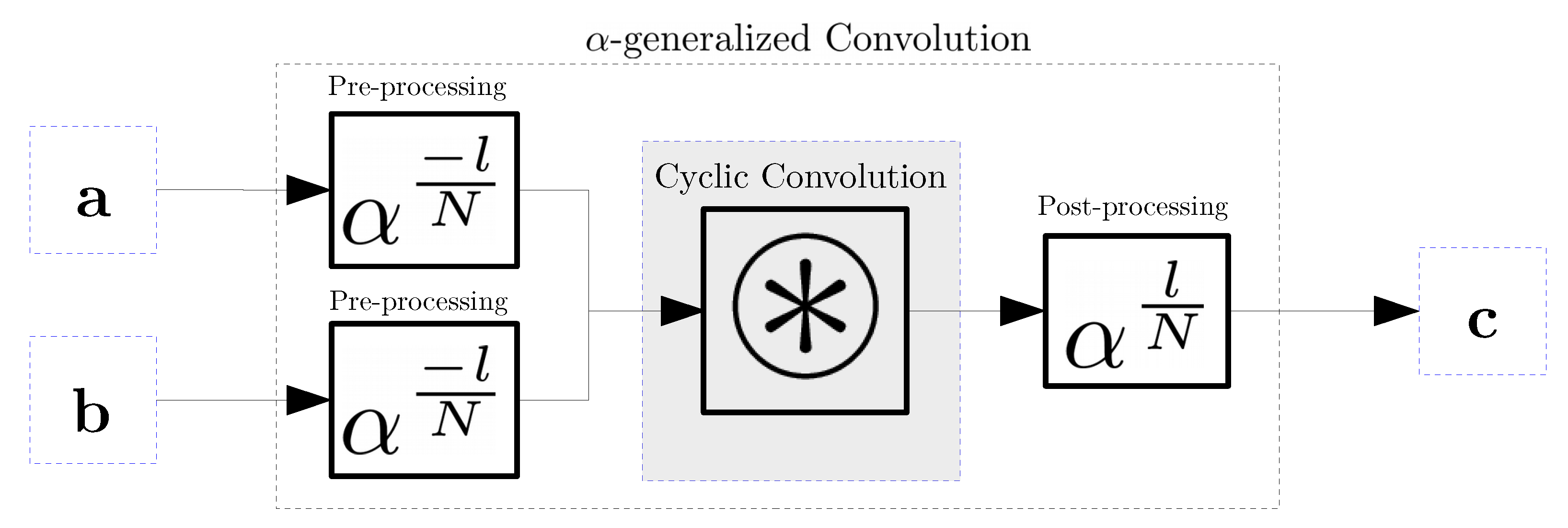
This is usually combined with a mechanism to efficiently move and exchange the plaintext contents across slots, by taking advantage of the properties of the available automorphisms in the used ring. In general, in the ring , we can define a set of automorphisms as different transformations with , which apply a change of variable over the elements in .
9.1. Efficient Slot Packing/Unpacking
The homomorphic packing/unpacking of plaintext values into slots is one of the most important examples of the evaluation of linear transformations on the ciphertexts, bootstrapping being one of the most representative applications [
14,
15,
16]. The way current cryptosystems implement this packing/unpacking is by means of a decomposition of the matrix multiplication into element-wise products between the different diagonals of the matrix and different rotated versions of the ciphertext (hence by adding the result of a set of multiplications between plaintexts and rotated ciphertexts).
The main bottleneck of this process is the number of switching key matrices required to rotate the ciphertexts. Working with n slots, a total of rotations, hence switching key matrices, is required in the worst case. Available strategies to reduce this number of matrices come at the cost of also increasing the runtimes per automorphism/switching key operation.
To the best of our knowledge, the best strategy for homomorphic packing/unpacking is presented in [
75] for the HEAAN cryptosystem. Their method, with an input of
n slots and parameterized by a radix
r, requires
constant vector multiplications,
rotations and a depth of
.
Thanks to the introduced multiquadratic RLWE with independent variables, we can also break the need of a number of rotations (automorphisms/switching key operations) equal to the number of slots, and we enable homomorphically packing/unpacking operations with a single switching key operation per independent ring variable.
Homomorphic Packing/Unpacking:
Considering a multiquadratic plaintext ring
(see Definition 11), we arrive to the following packing/unpacking matrices:
These matrices are similar to the ones introduced in
Section 8, but now having
and being defined over the plaintext ring, so satisfying
for
.
Both packing and unpacking matrices can be decomposed on a matrix of size over each independent variable. Additionally, these matrices can be very efficiently computed on a quadratic ring.
Consider, without loss of generality, that we have
By applying now the automorphism , we can efficiently extract both and by computing , and .
Once we have extracted and , the multiplication with the matrix can computed. This process can be recursively applied for each independent variable.
Hence, our proposed method enables homomorphic packing/unpacking on an input of
n slots which requires
rotations and depth
, but now working for BFV-type cryptosytems [
76].
9.2. Automorphisms in Multiquadratic Rings and Their Hypercube Structure
We show now how m-RLWE improves on the tradeoffs between space and computational cost when dealing with automorphisms, with respect to the univariate version.
Let
be a polynomial ring as the one described by Definition 9, and
be an element
; then, we denote by
the transformation over
which applies the change of variable
with
. For these particular rings, both transformations are, respectively, the identity
and the negation
. Reducing modulo
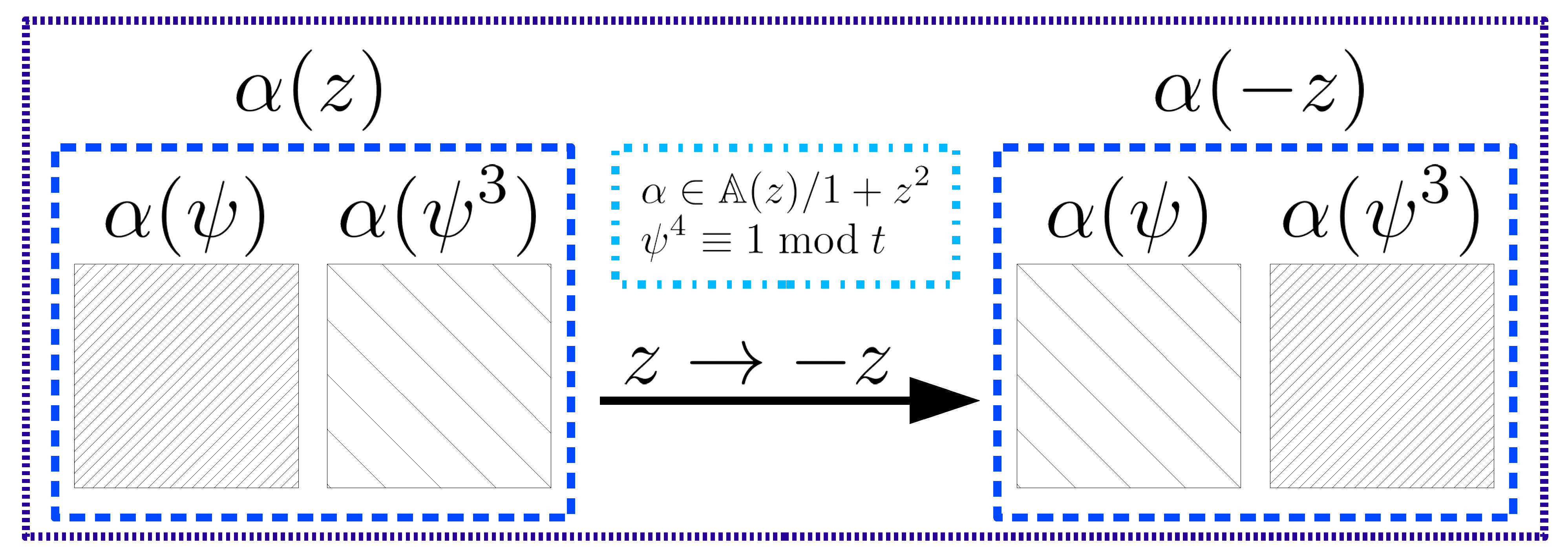
t (the modulo of the plaintext ring), the effect of the latter transformation over the slots would be equivalent to a block shift where each block is composed by one half of the total slots. This shift is graphically illustrated in
Figure 3 (also briefly described in
Table 4), where
is the 4th root of unity modulo
t (i.e.,
), and the two blocks of slots encoded respectively in
and
get shifted by applying
. With rings
we have similar automorphisms
and
.
Going back to the notation
with
for our ring, we can then apply combinations of these two transformations with the different variables
for
. Analogously to [
74], this gives a multidimensional structure on the automorphisms group considering the composition of transformations
where
,
and
.
This multidimensional structure of the automorphisms group can be seen as an
l-tuple with two different values per component (which gives a total of
different automorphisms). Hence, similarly to the shift property of a multidimensional DFT [
77], this group satisfies both the abelian and sharply transitive properties required to perform any type of permutation [
78].
Logarithmic Increase in Space and Computational Cost (Strategy 1):
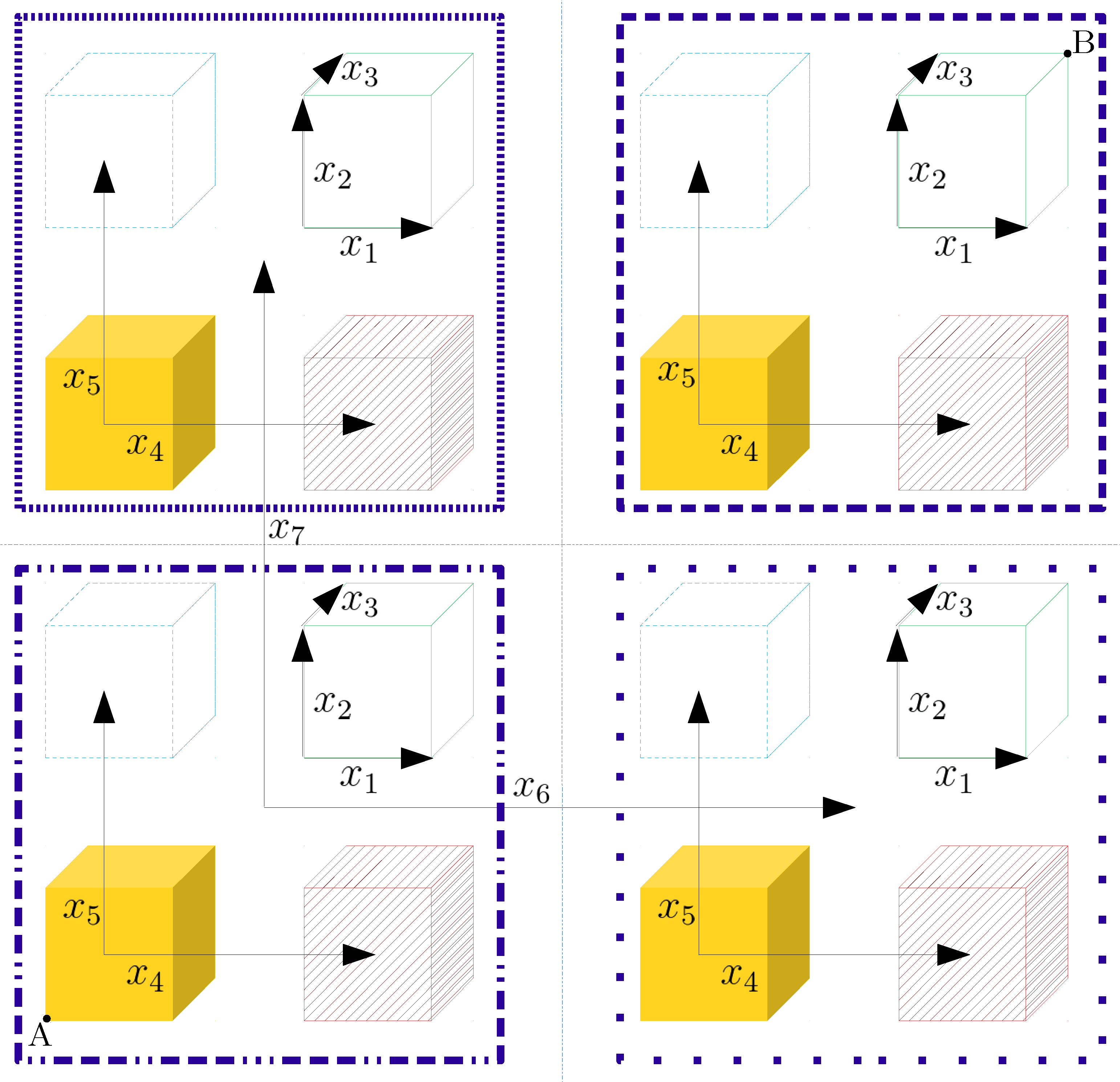
The effect of each of the automorphisms over the slots can be visually represented as a hypercube with as many dimensions as independent variables the rings have, that is, with a total of
dimensions. As a graphical example,
Figure 4 shows the slot structure corresponding to a multivariate ring with seven independent variables; in this case, each different vertex of the hypercube represents one of the
available slots, where the allowed transitions between vertices depend on the chosen strategy, as we describe next (see also
Table 5).
In case of storing n switching key matrices (corresponding to all the automorphisms), any vertex transition will be allowed through one single switching key operation. However, it is possible to store less switching key matrices (which, combined, represent the whole set of automorphisms), hence increasing the number of subsequent automorphisms/switching key operations for transitioning from one vertex to another.
Due to the specific structure of our multivariate rings, we propose an optimal strategy with
switching key matrices, each one corresponding to a different transformation
; with the additional advantage that these transformations are their own inverses. Following this strategy, we can also see the different slots (vertices in
Figure 4) as a binary vector of length
, where the available operations are bit-wise XOR operations with vectors
belonging to the standard basis of dimension
. In the example of
Figure 4 (with
), this method would be equivalent to working with seven independent vectors (of the standard basis) enabling only movements between vertices in the dimension associated to the vector.
It can be seen that with this strategy the farthest slot to a given one is always the slot represented as its ones’ complement, i.e., the opposite vertex. This implies a total of
automorphisms/switching key operations. Hence, in the worst case we have an increase in the computational cost by a factor of
when storing
switching key matrices and working with
n slots. This is a considerable reduction in the memory requirements when compared to the approximately
and
factors considered by Halevi and Shoup [
74] when working with
D slots (in one dimension).
As a quick comparison, for the practical values reported in [
74], i.e.,
, our strategy achieves an increase factor of 14 on the computational cost, which is not considerably higher than their results, but with huge savings in storage for our case: we store only 14 matrices, compared to the 51 matrices and three automorphisms/switching key operations achieved by [
74] for a similar value of
and one dimension with
following a baby-step/giant-step strategy.
Finally, it must be noted that when applying a switching key, noise constraints force the need of decomposing the coefficients of the involved polynomials in some specific base. This is true unless we resort to the strategy of Bajard et al. [
79] which takes advantage of the CRT decomposition over the polynomial coefficients. However, this strategy cannot be applied always, as it requires a highly composite modulo with primes of an adequate machine size (see [
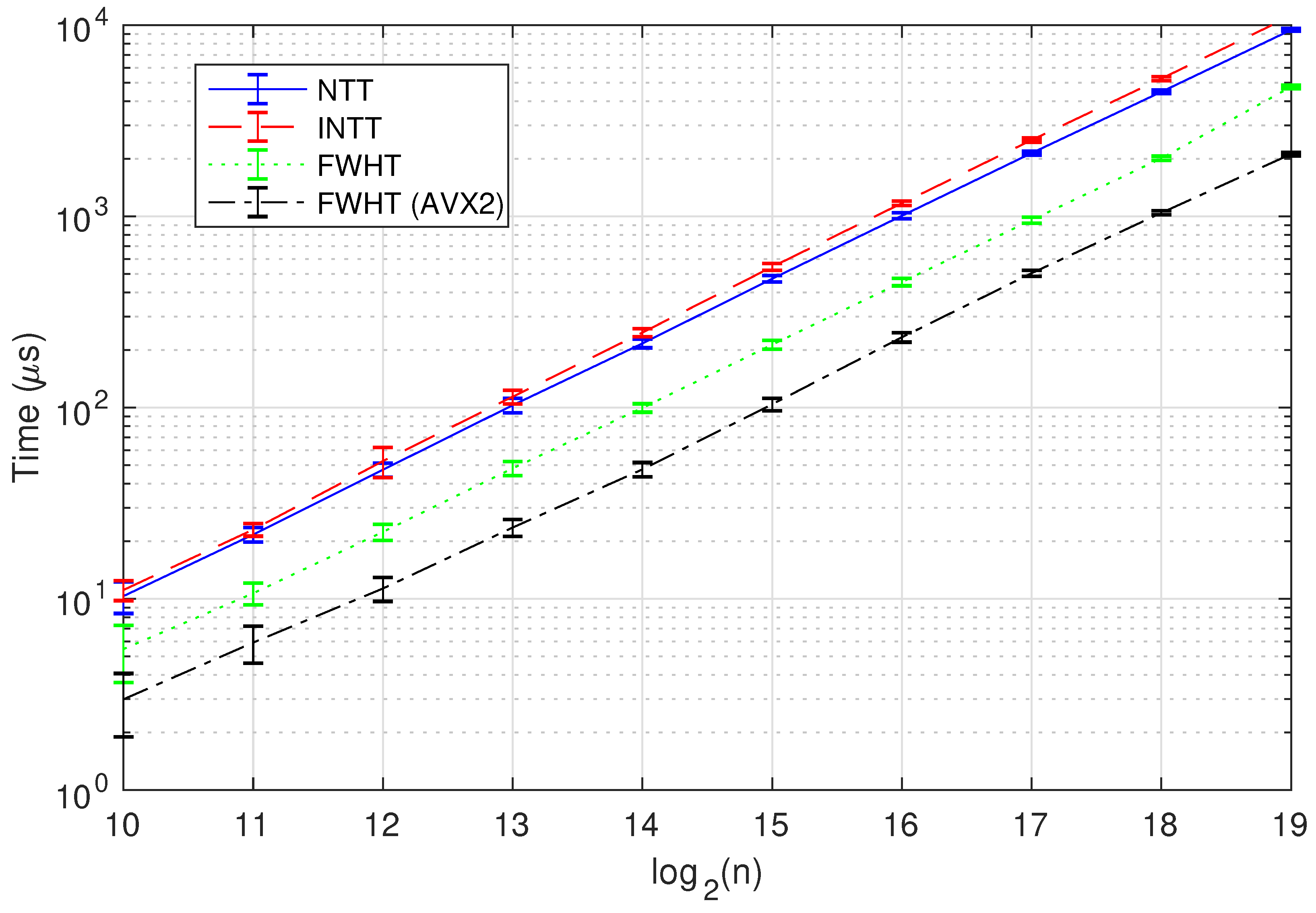
5]). As this base decomposition does not straightforwardly commute with the NTT/INTT (or CRT over the polynomial function) representation, the inverse and direct transforms have to be applied over the polynomials. Our setting in multivariate rings with FWHT enables a reduction on complexity for these transforms by a factor of
in terms of elemental products; i.e.,
this yields a net gain factor of in storage while keeping the same order of (multiplicative) computational complexity.
Efficiency/space tradeoffs:
In practical scenarios, the tradeoff between used memory and computational cost might require a different balance with less space efficiency than the achieved by the described strategy. Consequently, we also cover two additional strategies which lead to an improvement of the computational cost by a factor of 2.
Strategy 2: Our first approach adds to the previous
matrices those which are associated to “diagonal” vectors in our hypercube representation of the autormorphisms (see
Figure 4); that is, we work with automorphisms
where
and
, being
. Going back again to the binary representation of the slots, the additional automorphisms could be seen as the result of all pairwise XOR operations of different vectors of the standard basis of length
.
The number of needed switching key matrices is therefore increased to
In order to calculate the associated computational cost for this strategy, we resort to induction, working first with the odd natural numbers, and afterwards with the even natural numbers. Let the multivariate ring with where and , if we consider only the odd values of l we have:
For , any transition can be applied with only one automorphism/relinearization operation.
Assuming that l variables require k automorphisms/relinearization operations, it can be shown that adding two variables (i.e., ), automorphisms/relinearization operations are needed. We can graphically see this by resorting to the binary representation: moving between any two slots implies, in the worst case (consider one vector and its ones’ complement), one additional XOR operation.
Therefore, by induction, odd values of l require automorphisms/relinearization operations.
The argument is analogous for even l. First, we consider , where with only one automorphism/relinearization operation is enough to move between any of the slots. Next, the same reasoning as before could be applied between l and variables, resulting in a total of automorphisms/relinearization operations for l variables.
Taking into account both results, this strategy yields an increase in the number of automorphisms/switching key operations by a factor of . Hence, we can reduce by a half the computational cost compared to our previous strategy, with a quadratic increase in the memory requirements of instead of . For instance, with this would give an increase in cost by a factor of seven and a total of 105 stored matrices.
Strategy 3: The incurred increase in space requirements by Strategy 2 might not be acceptable for certain applications; therefore, our next approach preserves the cost improvement, but achieving a negligible increase in the number of required matrices: matrices instead of .
The idea behind this approach is adding to the switching key matrices for transformations of the form
for
the following one
As a graphical explanation, let us consider again the binary representation of the slots: in addition to working with those XOR operations with vectors belonging to the standard basis of length
, now we can also apply the ones’ complement of every “slot” in one operation (e.g., in
Figure 4 we could directly move with one automorphism/switching key operation from point A to point B).
Therefore, the worst case automorphism requiring matrices with our first strategy can now be computed with just one matrix. Moreover, as we know that for any , then the farthest slot position can be achieved by only automorphisms. Consequently, we can see that with matrices, we only need a maximum of automorphism/switching key operations. For instance, with this would give an increase in cost by a factor of seven and a total of 15 matrices in terms of use of memory.
9.4. On the Applicability to More General Multivariate Rings
It is worth noting that all the solutions exemplified above (
Section 9.2 and
Section 9.3) are sketched out with negacyclic rings. In this section, we give some insights on how to extend these results to the more general multivariate rings showcased in this manuscript.
An alternative set of polynomial ideals:
Bernstein et al. [
70] propose a different non-cyclotomic ring. The authors argue that with cyclotomic rings it is easy to have non-trivial ring homomorphisms (as the polynomial function usually splits in linear factors to perform FFT algorithms) and a relatively small Galois group. Consequently, the authors propose rings of the form
, with an irreducible polynomial function
and
p prime, where the Galois group is the permutation group
with
elements, and the modulo
q is inert in the ring. Hence,
is indeed a finite field. See [
80] for more details on the properties exhibited by functions of the form
.
These polynomial functions are also interesting for our purposes, but for very different reasons. Let
be a number field with
one of the roots of
. We know that [
80] polynomial functions
with
are irreducible, and for
the discriminant of
is squarefree. According to Theorem 6, this means that
K is monogenic and
.
Now, from Proposition 3, we have
so it is straightforward to find coprime discriminants for different values of
n.
For example, the discriminants of
are coprime. Therefore, we can define a multivariate RLWE sample over the ring of integers
for a multivariate number field of degree 5040 and 6 dimensions. In general, this gives an easy way to find multivariate number fields with many variables and a small expansion factor.
Operations over these rings are not as efficient as the ones with polynomial ideal , but still acceptable; i.e., in the worst case, multiplications modulo can be decomposed in multiplications modulo and , hence requiring two parallel efficient “cyclic” convolutions, and afterwards, adding the obtained results.
Automorphisms for more general multivariate rings:
The multivariate rings introduced in
Section 6 are, in general, separable but non-Galois field extensions. This implies that the number of available automorphisms is strictly smaller than the degree of the extension (see Corollary 4).
Corollary 4 (Corollary
from [
81])
. If is a finite extension that is either inseparable or not normal thenbeing the degree of the field extension.
Fortunately, this is not a problem in practice as we can make use of Theorem 11 to extend the mentioned separable multivariate number fields in
Section 6 to a Galois extension, where we have
; hence, automorphisms similar to the case of power-of-two cyclotomics (see
Section 9.3) can still be applied.
Theorem 11 (Theorem
from [
81])
. Every finite separable extension of a field can be enlarged to a finite Galois extension of the field. In particular, every finite extension of a field with characteristic 0 can be enlarged to a finite Galois extension. A toy example for a prime-degree field extension:
Consider the number field
(with
and
) isomorphic to the polynomial ring
and satisfying the conditions from
Section 6 (Proposition 4). We know that the roots of
are
. These roots are separable, but
is not the corresponding splitting field, and hence
is not a Galois field extension over the rationals
.
Even so, we know from Theorem 11 that this field can be extended to a Galois field where we have a Galois automorphism group which enables “rotations” of the slots. It suffices to add the root by means of a symbolic variable y over the cyclotomic polynomial , i.e., we enlarge the number field (see Theorem 11) to have with d and p different primes.
For this extended number field and considering a polynomial representation with (thanks to the field isomorphism ), we have the chain of transformations with and , which enables homomorphic “rotation” of the slots.
As an example, consider the polynomial
. We apply the change of variable
Consider now the following relation given by
It is worth noting that the ring is not, in general, the ring of integers of the field , but instead a subring of its ring of integers. This can be easily seen by inspecting the discriminants of and which are, respectively, and . As they are not coprime we cannot assert that the ring of integers of is the product of and , but if satisfies the conditions established in Proposition 4, is the ring of integers of .
Consequently, when working with rings following Definition 11 in
Section 6, if we want to (1) base the security on RLWE over a general number field and also (2) make use of the automorphisms, the reduction from Theorem 2 implies a loss in the lattice dimensionality; in the previous example of
, we end up working with a ring of degree
, but being the original RLWE sample defined over a number field of degree
p. Nevertheless, we can avoid this loss by basing the security in a generalization of RLWE called Order-LWE.
A much wider set of ring choices with Order-LWE:
Bolboceanu et al. [
51] propose a generalization of RLWE which, instead of considering the ring of integers
and its dual
, relies on the subrings called orders
and their corresponding duals
to define the underlying ideal lattices.
For a number field K of degree n, an order in K is a subring of containing a -basis of full-rank n of K such that . The ring of integers is the maximal order of K.
Order-LWE also presents worst-case hardness with respect to short vector problems, but in the invertible-ideal lattices of the considered order [
51].
This result enables a relaxation of many of the restrictions imposed for the rings in
Section 5 and
Section 6, by directly basing their hardness on Order-LWE. The previous example with the field
and order
can base its hardness on a lattice of dimension
by considering Order-LWE.
The use of the polynomial function
seems to contradict our initial requirements regarding the desired form of the polynomial ideal (see
Section 1). However, for efficient polynomial products we can substitute
by
by just multiplying both polynomial elements and polynomial function with the term
.
We plan to extend our results and optimizations to the corresponding relaxations offered by Order-LWE. In this direction, this work provides a wide set of concrete ring instantiations which could be considered to analyze the hardness of Order-LWE.