Revisiting Multivariate Ring Learning with Errors and Its Applications on Lattice-Based Cryptography

Abstract

The “Multivariate Ring Learning with Errors” problem was presented as a generalization of Ring Learning with Errors (RLWE), introducing efficiency improvements with respect to the RLWE counterpart thanks to its multivariate structure. Nevertheless, the recent attack presented by Bootland, Castryck and Vercauteren has some important consequences on the security of the multivariate RLWE problem with “non-coprime” cyclotomics; this attack transforms instances of m-RLWE with power-of-two cyclotomic polynomials of degree $n={\prod }_i{n}_i$ into a set of RLWE samples with dimension ${max}_i\left\{n_i\right\}$. This is especially devastating for low-degree cyclotomics (e.g., ${\Phi }_4\left(x\right)=1+x^2$). In this work, we revisit the security of multivariate RLWE and propose new alternative instantiations of the problem that avoid the attack while still preserving the advantages of the multivariate structure, especially when using low-degree polynomials. Additionally, we show how to parameterize these instances in a secure and practical way, therefore enabling constructions and strategies based on m-RLWE that bring notable space and time efficiency improvements over current RLWE-based constructions.

1. Introduction

Lattices have become a very promising tool for the development and improvement of new cryptographic constructions, notably those belonging to the field of homomorphic encryption. Instead of directly working with lattice assumptions, it is frequent to deal with assumptions whose underlying security can be based on the hardness of lattice problems. Among them, the family of Learning with Errors (LWE) [1,2] has become the preferred one due to its versatility. Lyubashevsky et al. [3,4] proposed a variant of LWE called Ring-LWE (or RLWE), whose hardness can be reduced from hardness problems over ideal lattices (instead of the general ones used in the LWE version). RLWE has proven to be more practical than LWE, as the underlying primitives can be usually more efficient; e.g., RLWE enables a notable reduction in the size of the public and secret keys in public key cryptosystems.

The RLWE problem enables homomorphic cryptography with a ring homomorphism supporting both addition and multiplication of ciphertexts. Among the possible quotient polynomial rings used for this purpose, the most practical ones are those where the ideal is a cyclotomic polynomial of the form $1+z^n$, with n a power of two. They present two advantages: (a) they enable efficient implementations of polynomial operations through fast radix algorithms of the Number Theoretic Transforms (NTTs) [5,6], and (b) the polynomial operations over the used ring correspond to basic blocks in practical applications in Computer Vision and Signal Processing [7,8,9], comprising, among others, linear convolutions, filtering, and linear transforms.

Recently, a multivariate version of RLWE (m-RLWE) was proposed as a means to efficiently deal with encrypted multidimensional structures, such as videos or images [9,10,11,12]. In this scenario, the use of a tensorial decomposition in “coprime” cyclotomic rings (see [3,4,13]) is a priori not applicable, as these structures require that the ideals have the same form (e.g., $(1+z^n)$). This is the context in which m-RLWE [10] was originally introduced.

Additionally, current hot problems in (fully) homomorphic encryption involve the optimization of elementary polynomial operations through fast transforms and, especially, the search for optimal strategies to execute homomorphic slot manipulations and trade off storage and computation needs for relinearization operations. These are fundamental blocks in homomorphic processing and in the implementation of the bootstrapping (see [14,15,16,17]) primitives enabling fully homomorphic encryption. As we will show, m-RLWE can bring significant efficiency improvements in all of them (see Section 8 and Section 9).

The use of the tensor of lattices and/or adding a multivariate structure to the involved rings has been the subject matter of several previous works, but with very different targets. We briefly survey here the closest ones: (a) In [18], the authors applied the standard tensor product of lattices to improve the hardness factor of the Shortest Vector Problem (SVP) under different assumptions. (b) In [13], the authors define an isomorphism between some cyclotomic fields and a tensor product of cyclotomic fields when the order m in ${\Phi }_m\left(z\right)$ can be factored into several (different) prime powers. (c) The “tensor” representation also appears in the definition of the GLWE problem (also called Module-LWE [19]) which was originally introduced in [20,21]. In fact, analogously to LWE versus RLWE, the introduced multivariate RLWE problem can be seen as a ring version of the GLWE problem, by means of adding for a second time a ring structure into the module. (d) Finally, the FHEW scheme features [22] a ring tensoring for a speed-up of the homomorphic accumulator, and also bivariate rings are used as a means to enhance the efficiency of polynomial products inside the refreshing procedure in [23].

It is discussed in [24] that the m-RLWE problem can be reduced from discrete Gaussian Sampling (equivalent to worst case Shortest Independent Vectors Problem, SIVP) over the tensor of rings. Unfortunately, a recent work [25] shows an effective attack against m-RLWE when the univariate subrings share common roots, therefore considerably lowering the security of the underlying problem. Hence, our main contribution in this work is to redefine the m-RLWE problem and find secure instantiations that preserve the efficient results on multivariate RLWE  [12], by basing their security on a subset of RLWE on general number fields (see the recent work by Peikert et al. [26], that generalizes the RLWE problem to any modulus and any ring over number fields).

We now briefly sketch the more conventional univariate RLWE problem, and its use for the implementation of efficient homomorphic encryption. Next, we informally introduce the definition of m-RLWE, the attack by Bootland, Castryck and Vercauteren [25], and the rationale of our solution, all exemplified in the bivariate case.

1.1. Univariate RLWE and Homomorphic Encryption

Gentry’s seminal work [27] introduced a new family of cryptosystems enabling Fully Homomorphic Encryption (FHE), which can compute an unbounded number of both encrypted additions and multiplications. Despite its theoretical relevance, current FHE schemes are still not entirely practical for real scenarios [28]. This motivated the use of a more efficient alternative as Somewhat Homomorphic Encryption (SHE), on which only a limited number of consecutive homomorphic operations is allowed. Precisely, as in many real scenarios the number of required operations is known beforehand, SHE turns out to be a perfect fit. Furthermore, many optimizations have been incorporated and, consequently, lattice-based SHE/FHE cryptosystems are being progressively adopted by researchers in the field [7,29,30,31]. In particular, RLWE-based cryptosystems show nowadays the best runtime performance.

Most of the efficiency improvements that RLWE has introduced into (somewhat/fully) homomorphic encryption rely on its particular algebraic structure [4], consisting in the use of polynomial cyclotomic rings. Actually, from a practical perspective, most of the recent libraries for homomorphic cryptography, such as the HElib [14,32], PALISADE [33], SEAL [34], Lattigo [35] and NFLlib [5], take advantage of this fact to optimize the runtime of the implemented lattice-based cryptosystems.

We exemplify in

Table 1. Univariate Ring Learning with Errors (RLWE) for homomorphic encryption.

A simple RLWE-based cryptosystem: Let $R_q$ be a cyclotomic polynomial ring ${\mathbb{Z}}_q\left[x\right]/\left({\mathsf{\Phi }}_{2n}\left(x\right)\right)$, where ${\mathsf{\Phi }}_{2n}\left(x\right)=1+x^n$ is the $2n$-th power-of-two cyclotomic polynomial with a maximum degree $\varphi \left(2n\right)=n$ (by $\varphi (·)$ we denote the Euler’s totient function). We refer the reader to Table 2 for a summary of the notation used in this work. The RLWE assumption states that given a pair $(a,b=as+e)$ where $a\leftarrow R_q$ is uniformly random and $e\leftarrow \psi$ is drawn from an error distribution (usually a discrete Gaussian distribution $\chi$), this sample is very hard to distinguish from the pair $(a,u)$ where $u\leftarrow R_q$ is also uniformly random.

By assuming this indistinguishability assumption, which reduces from hard problems on ideal lattices (see Theorem 2), it is very easy to define a simple cryptosystem based on RLWE. To this aim, the plaintext information can be encoded in the noise term by working with the ring $R_t={\mathbb{Z}}_t\left[x\right]/(1+x^n)$.

Let $m\in R_t$ be the plaintext, it can be encrypted by doing $(a^{\prime }=ta,b^{\prime }=a^{\prime }s+te+m)$, in such a way that the plaintext is encoded in the lower bits of the error term. This cryptosytem also allows for homomorphic operations.

Homomorphic cryptography: Consider two encryptions $(a_1,b_1=a_{1}s+t{e}_1+m_1)$ and $(a_2,b_2=a_{2}s+t{e}_2+m_2)$. If q is high enough compared to the maximum value of the noise terms, we can easily obtain a homomorphic addition of the plaintexts by doing $$\left(a_{\mathsf{add}}=a_1+a_2,b_{\mathsf{add}}=b_1+b_2=a_{\mathsf{add}}s+t(e_1+e_2)+(m_1+m_2)\right).$$ The process for a homomorphic multiplication is slightly more complicated, but it can still be done: $$\left(a_{\mathsf{mult}},b_{\mathsf{mult}},c_{\mathsf{mult}}\right)=\left(a_1{a}_2,a_1{b}_2+a_2{b}_1,b_1{b}_2\right).$$ Although we skip the details, the triple $(a_{\mathsf{mult}},b_{\mathsf{mult}},c_{\mathsf{mult}})$ can be seen as an encryption of the polynomial product $m_1{m}_{2}mod(1+x^n)$.

Efficient homomorphic encryption: This type of cryptosystems brings about some useful features by taking advantage of the plaintext/ciphertext ring structure: Operations in the ciphertext ring $R_q$ can be very efficiently performed by means of NTT/INTT transforms. If the plaintext ring $R_t$ factors into $\varphi \left(2n\right)=n$ linear factors, each ciphertext can directly encrypt vectors of n integers (or slots) and efficient SIMD (Single Instruction, Multiple Data) operations can be homomorphically performed. The use of the existing automorphisms in both the ciphertext/plaintext rings enables to exchange the contents between different slots. Hence, this is very convenient to homomorphically rotate the components of the encrypted vectors.

As we will show, the use of multivariate rings for both plaintext and ciphertext rings, instead of the conventional choice of univariate cyclotomics, introduces significant efficiency improvements in the above three aspects.

the use of univariate RLWE for homomorphic encryption.

1.2. Bivariate RLWE

Let $K_{\left(T\right)}=K_x⨂K_y$ be the tensor product of 2 cyclotomic number fields of dimensions $n_x=\varphi \left(m_x\right)$ and $n_y=\varphi \left(m_y\right)$, and $R=\mathbb{Z}[x,y]/({\Phi }_{m_x}\left(x\right),{\Phi }_{m_y}\left(y\right))$ the tensor of their corresponding ring of integers (see

Table 2. Notation and some basic concepts.

Notation	Description
Polynomial Rings, Matrices and Some Operators
$R\left[x\right]$, $R_q\left[x\right]$	They denote, respectively, the polynomial ring $\mathbb{Z}\left[x\right]/\left(f\right(x\left)\right)$ and ${\mathbb{Z}}_q\left[x\right]/\left(f\left(x\right)\right)$.
$R[x_1,\dots ,x_l]$, $R_q[x_1,\dots ,x_l]$	It represents the quotient multivariate polynomial ring with coefficients in $\mathbb{Z}$ (resp. ${\mathbb{Z}}_q$) and the l polynomial functions $f_i\left(x_i\right)$ with $1\le i\le l$. For simplicity, if there is no ambiguity, we omit the polynomial variable.
$a\left(x\right)$, $\mathit{a}$	The polynomial $a\left(x\right)$ is denoted as a when there is no ambiguity. It can also be denoted by a column vector $\mathit{a}$, whose components are the corresponding polynomial coefficients.
$\mathit{A}\otimes \mathit{B}$	It denotes the Kronecker product between matrices $\mathit{A}$ and $\mathit{B}$.
$\left[l\right]$, $\lfloor l\rfloor$, $\lceil l\rceil$	They denote, respectively, the set $\{1,2,\dots ,l\}$, the floor function and the ceiling function.
Lattices and algebraic number fields
K, $K_{\left(T\right)}$	K is a number field and $K_{\left(T\right)}$ is the result of the tensor product of several number fields.
${\mathcal{O}}_K$, ${\mathcal{O}}_K^{\vee }$	${\mathcal{O}}_K$ is the ring of integers of the number field K, while ${\mathcal{O}}_K^{\vee }$ refers to its dual. We also denote them, respectively, as R and $R^{\vee }$ referring to the polynomial representation considered in this work.
$K_{\mathbb{R}}$, $K_{\left(T\right),\mathbb{R}}$	$K_{\mathbb{R}}$ and $K_{\left(T\right),\mathbb{R}}$ are, respectively, $K_{\mathbb{R}}=K{\otimes }_{\mathbb{Q}}\mathbb{R}$ and $K_{\left(T\right)}{\otimes }_{\mathbb{Q}}\mathbb{R}$.
$\mathbb{T}$	$\mathbb{T}$ is, depending on the context, $K_{\left(T\right),\mathbb{R}}/R^{\vee }$ or directly $K_{\mathbb{R}}/R^{\vee }$.
$K=\mathbb{Q}\left({\zeta }_m\right)$	The m-th cyclotomic number field, where ${\zeta }_m$ is the m-th root of unity.
$K=\mathbb{Q}\left(\sqrt{d_i}\right)$	A quadratic number field.
$K=\mathbb{Q}(\sqrt{d_1},\dots ,\sqrt{d_l})$	A multiquadratic number field.
$K=\mathbb{Q}(a_1^{1/n_1},\dots ,a_l^{1/n_l})$	A multivariate number field, for which all the $a_i$ are squarefree and coprime.
${\Delta }_K$	Discriminant of the number field K.
$\mathcal{I}$, ${\mathcal{I}}^{\vee }$	$\mathcal{I}$ is a fractional ideal of K, while ${\mathcal{I}}^{\vee }$ is its dual. For an integer $q\ge 2$ we can have $\mathcal{I}/q\mathcal{I}$.
${\Phi }_m\left(x\right)$	The m-th cyclotomic polynomial.
$\varphi \left(m\right)$	Euler’s totient function, which outputs the degree of ${\Phi }_m\left(x\right)$.
${\Phi }_{2n}\left(x\right)=1+x^n$	The $2n$-th cyclotomic polynomial when n is a power of two. For this particular case $\varphi \left(2n\right)=n$.
$\eta \left(\mathcal{I}\right)$	Smoothing parameter of the lattice generated by $\mathcal{I}$.
${\lambda }_i\left(\mathcal{I}\right)$	It refers to the i-th successive minimum distance in the lattice generated by $\mathcal{I}$.
SVP, SIVP, DGS	They refer, respectively, to the Shortest Vector Problem, the Shortest Independent Vectors Problem and the Discrete Gaussian Sampling problem.
Error distributions
$\psi$	A continuous error distribution over $K_{\mathbb{R}}$.
$\chi$	A discrete error distribution over $R^{\vee }$ (also R).
$\Psi$	A family of continuous error distributions over $K_{\mathbb{R}}$.
${\rm Y}$	A distribution over a family of error distributions, each over $K_{\mathbb{R}}$.
$\Gamma (k,\theta )$	Gamma distribution with shape parameter k and scale parameter $\theta$.
$e\leftarrow \psi$, $e\leftarrow \chi$	They denote an element e drawn, respectively, from the error distribution $\psi$ and the error distribution $\chi$.
$a\leftarrow \mathbb{A}$	It denotes an element a chosen uniformly at random from the set $\mathbb{A}$.

for a summary of the notation used).

We define a Bivariate Ring LWE sample (see Definition 2 for the general formulation of m-RLWE) as the pair $(a,b=(a·s)/q+emod{R}^{\vee })$, where $a\leftarrow R_q$ is uniformly random and $e\leftarrow \psi$ comes from the error distribution $\psi$.

1.3. BCV Attack

Choices of polynomial functions $f_x\left(x\right)={\Phi }_{m_x}\left(x\right)$, $f_y\left(y\right)={\Phi }_{m_y}\left(y\right)$ as $f_x\left(x\right)=x^{n_x}+1$, $f_y\left(y\right)=y^{n_y}+1$ have been proposed in [10], as this structure presents computational advantages and can be very beneficial for practical applications.

BCV attack is able to exploit common roots on the involved rings to factorize the multivariate RLWE samples into RLWE samples of smaller dimension. For example, consider that $n_x=n_y=n$; by applying the substitution $x\to y$, we obtain n RLWE samples of dimension n each, hence decreasing the $n^2$ lattice dimension of the original m-RLWE sample.

1.4. Secure Multivariate RLWE Instantiations

Let $m=m_x{m}_y$ and $gcd(m_x,m_y)=1$; then, the m-th cyclotomic field $K=\mathbb{Q}\left({\zeta }_m\right)\cong \mathbb{Q}\left[x\right]/\left({\Phi }_m\left(x\right)\right)$ (with ${\zeta }_m$ the m-th root of unity) is isomorphic (see Theorem 1) to the bivariate field

$$K\cong \mathbb{Q}[x,y]/({\Phi }_{m_x}\left(x\right),{\Phi }_{m_y}\left(y\right)).$$

(1)

Consequently, by considering instantiations satisfying $gcd(m_x,m_y)=1$, the bivariate RLWE problem becomes equivalent to the equally sized RLWE problem. However, we would like to search for other instantiations where the polynomial ideals can have a similar form and, if possible, the same degree.

By restricting ourselves to the most common scenario of “power-of-two” cyclotomics (we must clarify here that we refer to polynomials with only two non-zero terms: the leading and the constant coefficient of the polynomial), polynomial ideals of the form $(x^{n_x}+d_x,y^{n_y}+d_y,z^{n_z}+d_z,\dots )$, could avoid BCV attack for some parameters $\{n_x,d_x,n_y,d_y,n_z,d_z,\dots \}$. E.g., the rings $\mathbb{Z}\left[x\right]/(x^{64}+1)$ and $\mathbb{Z}\left[y\right]/(y^{27}+5)$ do not have common roots, so trivial substitutions such as $x\to y$ cannot be applied. Additionally, whenever we reduce modulo q and work over $R_q$, we can impose (for the sake of efficiency) that both polynomials functions $x^{64}+1$ and $y^{27}+5$ factor in linear terms enabling the use of variants of the NTT. Additionally, slot encoding and slot manipulations are still possible in the plaintext ring by means of the pre-/post-processing, as presented in [7]. Analogously to the negayclic convolution, these pre-/post-processing steps preserve the properties of the NTT transform over a ring with an $\alpha$-generalized convolution [36].

This seems to effectively avoid a substitution attack; however, there might be some small ideal divisor for which, modulo some particular q, the noise does not increase substantially, and we can distinguish the resulting sample from uniform. This attack has been extensively studied by Peikert in [37] and we will discuss it in Section 7.1.

1.5. The Proposed Solution

The previous strategy preserves most of the advantages of the multivariate constructions while apparently avoiding the effects of BCV attack. However, the security of these instantiations is not based on any specific formulation of the RLWE problem, and there is no trivial way of parameterizing them. This raises the following questions:

• Can we find multivariate rings similar to $\mathbb{Z}[x,y,\dots ]/(x^{n_x}+d_x,y^{n_y}+d_y,\dots )$ while (a) still preserving the aforementioned advantages of this structure, and (b) basing its security on the hardness of the RLWE problem (see Definition 7); i.e., without a decrease in the ring dimension due to BCV attack (see Theorem 3)?
• If these multivariate rings exist, how can the values $\{n_x,n_y,\dots \}$, $\{d_x,d_y,\dots \}$ be chosen to easily define the ring of integers R and its dual $R^{\vee }$?

From this point forward, we focus on answering these two questions. To this aim, we identify number fields whose ring of integers (and their dual) have the sought structure (see Section 4). In particular, we divide this set of fields in two categories:

• Multiquadratic number fields (see Section 5). These structures ([38], Theorem 4.1 and its proof) enable efficient radix-2 transforms for faster polynomial arithmetic (see Section 8).
• More general number fields with polynomials functions $\{x^{n_x}+d_x$, $y^{n_y}+d_y$, $\dots \}$ (see Section 6). These structures support all the signal processing applications described in [8], and the matrix operations introduced by the original MHEAAN scheme [39] (not based on coprime cyclotomic polynomials [40]) while preserving the equivalent RLWE security.

1.5.1. Rationale on the Security of Our Solution

The weakness of some m-RLWE instantiations is rooted on the existence of (small norm) zero divisors in the tensor product of fields. For example, $\mathbb{Q}[x,y]/(x^2+1,y^2+1)$ has zero divisors as $x+y$ (e.g., $(x+y)(x-y)=0$), and hence m-RLWE samples defined on rings $\mathbb{Z}[x,y]/(x^2+1,y^2+1)$ can be easily factored, as the effective degree can be reduced with substitutions $\{x\to y,-x\to y\}$. Additionally, as these roots have small norm, the noise in the reduced samples is not increased enough to preserve security.

Instead of the previously proposed $\mathbb{Z}[x,y]/(x^2+1,y^2+1)$, we work with a quotient bivariate ring with polynomial ideals of the form $(x^{n_x}+d_x,y^{n_y}+d_y)$ (we use $\mathbb{Z}[x,y]/(x^2+1,y^2+3)$ as our example). The use of different polynomials functions avoids a trivial substitution attack. However, we need to rule out the possibility of (small norm) substitution attacks, such as the one from [25], modulo some q; even if they exist, finding them would require solving a hard subset-sum $modq$ (knapsack) problem.

As there is a security reduction from ideal lattices to RLWE defined on general number fields [26], we search for the ring of integers of multivariate number fields. This gives us a way to find secure parameters for the used ring, and also the right error distribution to guarantee that the noise increase after a substitution modulo q is enough to preserve the required security [37]. To exemplify this rationale, we compare the differences between a bivariate cyclotomic ring (which can be seen as a univariate cyclotomic ring), and our proposed solution.

Consider the ring $\mathbb{Z}\left[z\right]/\left({\Phi }_{12}\left(z\right)\right)$ with ${\Phi }_{12}\left(z\right)=z^4-z^2+1$. There is an isomorphism with the bivariate ring $\mathbb{Z}[x,y]/({\Phi }_4\left(x\right),{\Phi }_3\left(y\right))$ where ${\Phi }_4\left(x\right)=x^2+1$ and ${\Phi }_3\left(y\right)=y^2+y+1$. Therefore, our intuition is that if we found an effective substitution attack on our example ring $\mathbb{Z}[x,y]/(x^2+1,y^2+3)$, this would work analogously for the cyclotomic bivariate case $\mathbb{Z}[x,y]/({\Phi }_4\left(x\right),{\Phi }_3\left(y\right))$. In particular, if we apply the transformation $T\left(y\right)=2y+1$ in the ring $\mathbb{Z}\left[y\right]/(y^2+3)$, we obtain $\mathbb{Z}\left[y\right]/(y^2+y+1)$, which is the mentioned cyclotomic ring with ${\Phi }_3\left(y\right)$. Consequently, for this particular case, it is clear that the existence of an attack in our example ring implies an attack to the bivariate cyclotomic ring.

For more general multivariate rings, we can apply a similar idea. In general, for a secure bivariate ring such as $\mathbb{Z}[x,y]/(x^{n_x}+d_x,y^{n_y}+d_y)$, we can search for a transformation $y\to T\left(y\right)$ where the new polynomial function can share at least some roots with $x^{n_x}+d_x$. If this transformation can be effectively applied, we could use it to attack multivariate cyclotomic rings.

Thus, this strengthens the belief that an attack on secure m-RLWE instantiations defined on a general number field should provide us with either an attack to RLWE on the product of prime-powers cyclotomic rings, and/or a better understanding on the weaknesses of general cyclotomic rings. For a discussion on the practical security of RLWE on the proposed number fields we refer the reader to Section 7.1.

1.5.2. Division Algebras and Non-Norm Condition

In [41], the authors propose an alternative variant of LWE over cyclic algebras, which they denote as CLWE (Cyclic Algebra LWE). The main difference with respect to RLWE relies on the fact that, instead of adding a ring structure, they incorporate into Module-LWE a cyclic algebra structure, constructing a non-commutative variant of LWE.

The security of CLWE is supported by the hardness of finding short vectors in certain structured lattices induced by ideals in a cyclic algebra $\mathcal{A}$. Additionally, they explicitly address BCV attack by means of the “non-norm” condition (see  [42], Proposition 3.5).

Let a cyclic algebra $\mathcal{A}=(L/K,\theta ,\gamma )$ where K is a number field of degree k and L is a Galois extension of K of degree n such that $Gal(L/K)=\langle \theta \rangle$. For a non-zero $\gamma \in K$, the cyclic algebra is defined as $\mathcal{A}=L\oplus uL\oplus \dots \oplus u^{n-1}L$ where $u\in \mathcal{A}$ and $u^n=\gamma$.

The non-norm condition on $\gamma$ (see  [42], Proposition 3.5) avoids BCV attack by stating that the lowest power of $\gamma$ which appears in $N_{L/K}\left(L\right)$ is ${\gamma }^n$, where $N_{L/K}$ represents the relative norm of L into K (see [41] for more details).

This defense against BCV attack also relies on avoiding the existence of zero divisors, which are needed for the attack to succeed. In our case, as we already work in a number field, we can adhere to the security conditions established by Peikert [37] to avoid this type of attacks.

It is worth mentioning that we see both approaches as potentially complementary, in such a way that the underlying field K considered in the (cyclic) division algebra could be one of the multivariate fields discussed in Section 5 and Section 6.

1.5.3. Contributions

The first contribution of this work is the definition and parameterization of secure instantiations of the multivariate Ring Learning With Errors problem [8,24], supported by the extended reduction [26] of the original proof by Lyubashevsky et al. [3,4]. The proposed instantiations address the vulnerability leveraged on BCV attack to m-RLWE [25], while still preserving all the efficiency improvements that m-RLWE brings. Moreover we show that is possible to securely instantiate the m-RLWE problem, because the canonical embedding of R has a polynomial skewness (${\lambda }_n/{\lambda }_1$). Our two main results are summarized in Theorem 5 and Corollary 1 for multiquadratic rings (see Section 5), and Theorems 7 and 8 together with Corollaries 2 and 3, which refer to more general multivariate rings (see Section 6). They show valid parameter choices so that the reduction for RLWE over general number fields [26] (Theorem 2) applies to the hardness of multivariate RLWE, and without a reduction in the lattice dimension. More flexible parameter choices require to relax this assumption from RLWE to the Order-LWE assumption (see Section 9.4). Finally, Theorem 3 gives a worst-case security guarantee for RLWE with any multivariate cyclotomic ring, by stating that it is at least as hard as univariate RLWE, but introducing a decrease in the lattice dimension of the univariate RLWE assumption by a factor of L (see Section 4).

The second contribution is to showcase the possible applications. They are numerous and achieve improved space-time tradeoffs in the most critical lattice operations. Therefore enabling more efficient homomorphic processing and closing the gap to the realization of practical fully homomorphic encryption. This is the main list of applications:

• We introduce the $\mathit{\alpha }$-generalized Walsh–Hadamard Transform as the basic block that can replace Number Theoretic Transforms in multivariate rings [43], achieving an improvement on the computational complexity of degree-n polynomial products by a factor $log\left(n\right)$ in terms of elemental multiplications, with additional savings in memory usage (see Section 8). It is worth noting that the results of Section 8 were previously introduced in [43], where we also exemplify its use for the implementation of Oblivious Linear function Evaluation.
• We enable net improvements in cryptographic primitives built on top of m-RLWE, such as efficient time and space computation of automorphisms, relinearizations, packing, unpacking and homomorphic slot manipulation, and, consequently, bootstrapping, improving on current achievable trade-offs in RLWE (see Section 9).
• We instantiate a simple cryptosystem based on m-RLWE (see Section 7.2), and exemplify with it the use of the multivariate structure of m-RLWE to improve on complex number embedding, enabling fully packed complex numbers, compared to the exponentially decreasing packing ratio of current approaches working with multivariate rings [39,40] (see Section 10). This enables applications in homomorphically encrypted approximate arithmetic, complex processing, and efficient multidimensional signal manipulation.

1.5.4. Structure

The rest of the paper is organized as follows: Section 2 describes BCV attack to multivariate RLWE. Section 3 introduces some algebraic number theory notions and the main definitions for the m-RLWE problem. Section 4 describes the followed strategy to achieve secure instantiations of multivariate RLWE, including the well-known tensor of “coprime” cyclotomic rings. Section 5 focuses on the analysis of multiquadratic rings. Section 6 studies a set of more general multivariate rings. Section 7 includes a discussion on the achieved resilience against known attacks together with example instantiations that showcase the practicality of multivariate RLWE, and discusses some practical applications. Additionally, the included Section 8 particularizes the problem to rings enabling an $\mathit{\alpha }$-generalized Walsh–Hadamard Transform, and compares its performance with fast NTT algorithms currently used in state-of-the-art RLWE cryptosystems. Section 9 introduces the strategies for homomorphic packing/unpacking and the space/time tradeoffs improving on current RLWE relinearization and bootstrapping operations. Section 10 briefly discusses how to work with complex slots, comparing to current approaches that work with bivariate rings. Finally, Section 11 draws some conclusions.

2. Worst Case Security of Multivariate RLWE

We first introduce the notation used in this section (see Table 2 for more details on the notation used in this work). Polynomials are denoted with regular lowercase letters, omitting the polynomial variable (i.e., a instead of $a\left(x\right)$) when there is no ambiguity.

We follow a recursive definition of multivariate modular rings: $R_q\left[x_1\right]={\mathbb{Z}}_q\left[x_1\right]/\left(f_1\left(x_1\right)\right)$ denotes the polynomial quotient ring in the variable $x_1$ modulo $f_1\left(x_1\right)$ with coefficients belonging to ${\mathbb{Z}}_q$. Analogously, $R_q[x_1,x_2]=\left(R_q\left[x_1\right]\right)\left[x_2\right]/\left(f_2\left(x_2\right)\right)$ is the quotient bivariate polynomial ring with coefficients belonging to ${\mathbb{Z}}_q$ reduced modulo univariate $f_1\left(x_1\right)$ and $f_2\left(x_2\right)$. In general, $R_q[x_1,\dots ,x_l]$ (resp. $R[x_1,\dots ,x_l]$) represents the quotient multivariate polynomial ring with coefficients in ${\mathbb{Z}}_q$ (resp. $\mathbb{Z}$) and the l polynomial functions $f_i\left(x_i\right)$ with $1\le i\le l$. The polynomial a can also be denoted by a column vector $\mathit{a}$ whose components are the corresponding polynomial coefficients.

For the sake of clarity, we present the definition of multivariate RLWE with power-of-two cyclotomic polynomials, as originally introduced in [10], but all the results in this section can be generalized to any cyclotomic function:

Definition 1

(Multivariate RLWE with power-of-two polynomial functions as $x_i^{n_i}+1$). Given a multivariate polynomial ring $R_q[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=1+x_j^{n_j}$ for $j=1,\dots ,l$ where $n={\prod }_j{n}_j$ (with all $n_j$ a power of two) and an error distribution $\chi [x_1,\dots ,x_l]$ that generates small-norm random multivariate polynomials in $R_q[x_1,\dots ,x_l]$, the multivariate polynomial RLWE problem relies upon the computational indistinguishability between samples $(a_i,b_i=a_i·s+e_i)$ and $(a_i,u_i)$, where $a_i,u_i\leftarrow R_q[x_1,\dots ,x_l]$ are chosen uniformly at random from the ring $R_q[x_1,\dots ,x_l]$; $s,e_i\leftarrow \chi [x_1,\dots ,x_l]$ are drawn from the error distribution.

The original works of multivariate RLWE [8,10] assume that the search and decision m-RLWE problems (see Definitions 3 and 4) in dimension $n={\prod }_{i=1}^m{n}_i$ are as hard as the corresponding RLWE problems in dimension n. However, Bootland, Castryck and Vercauteren [25] introduced an attack that can exploit polynomial functions that allow repeated “low-norm” roots in the multivariate ring. As a result, when the subrings of the tensor have common roots, this attack is able to factor the m-RLWE samples into RLWE samples of smaller dimension, hence reducing the security of these m-RLWE samples to that of solving a set of independent RLWE samples which are easiest to break. For e.g., the ring $\mathbb{Z}[x,y]/(x^{2n}+1,y^n+1)$, changes of variable $y\to x^{2i}$ with $i\in {\mathbb{Z}}_{2n}^{*}$ factors the m-RLWE sample into n different RLWE samples with rings of polynomial function $x^{2n}+1$ and an increase in the error variance of n (maximum degree of $y^n+1$).

The instantiations of (multivariate) RLWE with “coprime” cyclotomic rings are not affected by this attack, as they do not introduce these “common” roots (see Section 4.1).

We now give a more formal description of the attack, particularized for bivariate RLWE (2-RLWE) with power of two cyclotomics (Definition 1). Let $(a,b=as+e)\in R_q^2[x,y]$ and $R_q[x,y]={\mathbb{Z}}_q[x,y]/\left(x^{n_x}+1,y^{n_y}+1\right)$ with $n_x\ge n_y$ and $k=\frac{n_x}{n_y}$ without loss of generality.

Now we define the map $\tilde{\Theta }$:

$$\begin{array}{c}\hfill \tilde{\Theta }:{\mathbb{Z}}_q[x,y]/(x^{n_x}+1,y^{n_y}+1)\to {\left({\mathbb{Z}}_q\left[x\right]/(x^{n_x}+1)\right)}^{n_y}\\ \hfill a(x,y)\to \left(a(x,x^k),a(x,x^{3k}),\dots ,a(x,x^{(2n_y-1)k})\right)\end{array}$$

This map is a ring homomorphism, and if q is odd it is also invertible (see [25]). This transforms the pair $(a,b)\in R_q[x,y]$ into $(\tilde{\Theta }\left(a\right),\tilde{\Theta }\left(b\right)\in R_q^{n_y}\left[x\right]$. If we denote each of the components by ${\tilde{\Theta }}_i$, for $i=1,\dots ,n_y$, we have

$$\left({\tilde{\Theta }}_i\left(a\right),{\tilde{\Theta }}_i\left(b\right)={\tilde{\Theta }}_i\left(a\right){\tilde{\Theta }}_i\left(s\right)+{\tilde{\Theta }}_i\left(e\right)\right)\in R_q^2\left[x\right],$$

(2)

for $i=1,\dots n_y$. This results in $n_y$ different RLWE samples of dimension $n_x$ and whose noise has a variance $n_y$ times higher than the original 2-RLWE sample (the result of adding $n_y$ independent variables).

The attack works by trying to break the obtained $n_y$ RLWE samples. Once this is done, as the map is invertible, it is possible to reconstruct the original secret key with the different $n_y$ smaller keys.

This attack can be generalized to an m-RLWE sample (Definition 1) by recursively applying “versions” of this map $(l-1)$ times. This recursion converts an m-RLWE sample into $\frac{n}{n_1}$ RLWE samples (assuming, without loss of generality, that $n_1\ge n_2\ge \dots \ge n_l$) with dimension $n_1$ and an error variance $\frac{n}{n_1}$ times higher.

3. Multivariate Ring Learning with Errors

This section revisits the main definitions from algebraic number theory and multivariate RLWE, including a generalized version of the multivariate polynomial RLWE problem which admits any type of cyclotomic polynomial as ideals. For the sake of clarity, we particularize to power-of-two cyclotomic functions (Definition 1) when exemplifying some of the results, but this does not affect to the generality of the discussion.

3.1. Algebraic Number Theory Background

This section presents the fundamental concepts of lattices and algebraic number theory and extends them to the more general case of a tensor of number fields on which m-RLWE is based.

3.1.1. The Space $H_{\left(T\right)}={⨂}_i{H}_i$

When dealing with cyclotomic fields, it is useful to work with the subspace $H\subseteq {\mathbb{R}}^{s_1}\times {\mathbb{C}}^{2s_2}$ with $s_1+2s_2=n$, where the tuple $(s_1,s_2)\in {\mathbb{N}}^2$ is called the signature of the number field, and H satisfies

$$H=\{(x_1,\dots ,x_n)\in {\mathbb{R}}^{s_1}\times {\mathbb{C}}^{2s_2}\mathrm{such\; that} x_{s_1+s_2+j}={\overline{x}}_{s_1+j},\forall j\in \left[s_2\right]\}\subseteq {\mathbb{C}}^n.$$

(3)

The subspace H is composed of vectors from ${\mathbb{R}}^{s_1}\times {\mathbb{C}}^{2s_2}$, whose first $s_1$ elements $(x_1,\dots ,x_{s_1})$ are real numbers, and the last part is composed of $s_2$ complex numbers $(x_{s_1+1},\dots ,x_{s_1+s_2})$ together with their complex conjugates $(x_{s_1+s_2+1},\dots ,x_{s_1+2s_2})=({\overline{x}}_{s_1+1},\dots ,{\overline{x}}_{s_1+s_2})$.

An orthonormal basis ${\left\{{\mathit{h}}_j\right\}}_{j\in \left[n\right]}$ for H can be defined as

$${\mathit{h}}_j=\left\{\begin{array}{cc}{\mathit{e}}_j& ifj\in \left[s_1\right]\\ \frac{1}{\sqrt{2}}({\mathit{e}}_j+{\mathit{e}}_{j+s_2})& if{s}_1<j\le s_1+s_2\\ \frac{\sqrt{-1}}{\sqrt{2}}({\mathit{e}}_{j-s_2}-{\mathit{e}}_j)& if{s}_1+s_2<j\le s_1+2s_2,\end{array}\right.$$

where ${\mathit{e}}_j$ are the vectors of the standard basis in ${\mathbb{R}}^n$. Each element $a={\sum }_{j\in \left[n\right]}{a}_j{\mathit{h}}_j\in H$ (with $a_j\in \mathbb{R}$) has its own $l_p$ norm. For our purposes, we define the subspace $H_{\left(T\right)}={⨂}_{i\in \left[l\right]}{H}_i$ as the tensor product of l subspaces $H_i$ (each subspace $H_i$ defined as in Equation (3) but with $s_1+2s_2=n_i$).

In particular, if we see each element belonging to each $H_i$ as a different linear transformation, we are actually working with the Kronecker product of the subspaces $H_i$. We can therefore express an orthonormal basis for $H_{\left(T\right)}$ given by ${\left\{{\mathit{h}}_j\right\}}_{j\in \left[n\right]}$ as the result of the Kronecker product of the original basis of each $H_i$, by defining any invertible mapping for j and $\{j_1,\dots ,j_l\}$, where ${\mathit{h}}_j={⨂}_{i\in \left[l\right]}{\mathit{h}}_{j_i}^{\left(i\right)}$ are the basis vectors for $H_{\left(T\right)}$, and $n={\prod }_{i\in \left[l\right]}{n}_i$; each ${\left\{{\mathit{h}}_{j_i}^{\left(i\right)}\right\}}_{j_i\in \left[n_i\right]}$ is the orthonormal basis of each $H_i\subseteq {\mathbb{C}}^{n_i}$ for $i\in \left[l\right]$.

3.1.2. Lattice Background

A lattice in our multivariate setting is defined as an additive subgroup of $H_{\left(T\right)}$. We only consider full rank lattices, obtained as the set of all integer linear combinations of a set of n linear independent basis vectors $B=\{{\mathit{b}}_1,\dots ,{\mathit{b}}_n\}\subset H_{\left(T\right)}$

$$\Lambda =\mathcal{L}\left(B\right)=\left\{\sum _{i\in \left[n\right]}{z}_i{\mathit{b}}_i\mathrm{such\; that} \mathit{z}\in {\mathbb{Z}}^n\right\}$$

The minimum distance ${\lambda }_1(\Lambda )$ of a lattice $\Lambda$ for the norm $\left|\right|.\left|\right|$ is given by the length of the shortest non-zero lattice vector, that is, ${\lambda }_1(\Lambda )={\min }_{\mathit{x}\in \Lambda /\mathit{x}\ne \mathbf{0}}\left|\right|\mathit{x}\left|\right|$.

The dual lattice of $\Lambda \subset H_{\left(T\right)}$ is defined as ${\Lambda }^{*}=\{\mathit{x}\in H_{\left(T\right)}|\langle \Lambda ,\mathit{x}\rangle \subseteq \mathbb{Z}\}$ and it satisfies ${\left({\Lambda }^{*}\right)}^{*}=\Lambda$.

3.1.3. Gaussian Measures

The results on nonspherical Gaussian distributions presented in [4] can be extended to our case. Hence, we revisit here some of the concepts for Gaussian measures, adapted to our tensor setting.

We consider the Gaussian function ${\rho }_r:H_{\left(T\right)}\to (0,1]$ with $r>0$ as ${\rho }_r\left(\mathit{x}\right)=\exp (-\pi {\left|\right|\mathit{x}\left|\right|}^2/r^2)$. A continuous Gaussian probability distribution $D_r$ can be obtained by normalizing the previous function to obtain a probability density function as $r^{-n}{\rho }_r\left(\mathit{x}\right)$. Extending this to the non spherical Gaussian case, we consider the vector $\mathit{r}={⨂}_{i\in \left[l\right]}{\mathit{r}}_i$ where $\mathit{r}=(r_1,\dots ,r_n)\in {\left({\mathbb{R}}^{+}\right)}^n$ and ${\mathit{r}}_i=(r_{i,1},\dots ,r_{i,n_i})\in {\left({\mathbb{R}}^{+}\right)}^{n_i}$ and whose components satisfy $r_{i,j+s_1+s_2}=r_{i,j+s_1}$. Finally, a sample from $D_{\mathit{r}}$ is given by ${\sum }_{j\in \left[n\right]}{x}_j{\mathit{h}}_j$ where each $x_j$ is drawn independently from a Gaussian distribution $D_{r_j}$ over $\mathbb{R}$; $r_j$ equals ${\prod }_{i\in \left[l\right]}{r}_{i,j_i}$ (where l is the number of “unidimensional” spaces $H_i$ in the tensor, that is $n={\prod }_{i\in \left[l\right]}{n}_i$) and we are using any invertible mapping between ${\left\{j\right\}}_{j\in \left[n\right]}$ and ${\left\{j_i\right\}}_{j_i\in \left[n_i\right],i\in \left[l\right]}$.

3.2. Main Definitions for Multivariate Ring-LWE

Let $K_{\left(T\right)}={⨂}_{i\in \left[l\right]}{K}_i$ be the tensor product of l cyclotomic fields of dimension $n_i=\varphi \left(m_i\right)$ each, and $R={⨂}_{i\in \left[l\right]}{\mathcal{O}}_{K_i}$ ($R^{\vee }={⨂}_{i\in \left[l\right]}{\mathcal{O}}_{K_i}^{\vee }$) the tensor of their corresponding (dual of the) ring of integers. We have the following definitions:

Definition 2

(Multivariate Ring LWE distribution). For $s\in R_q^{\vee }$ and an error distribution ψ over $K_{\left(T\right),\mathbb{R}}$, a sample from the m-RLWE distribution $A_{s,\psi }$ over $R_q\times \mathbb{T}$ is generated by $a\leftarrow R_q$ uniformly at random, $e\leftarrow \psi$, and outputting $(a,b=(a·s)/q+emod{R}^{\vee })$ (where $\mathbb{T}=K_{\left(T\right),\mathbb{R}}/R^{\vee }$ and $K_{\left(T\right),\mathbb{R}}=K_{\left(T\right)}{\otimes }_{\mathbb{Q}}\mathbb{R}$).

Definition 3

(Multivariate Ring LWE, Search). Let Ψ be a family of distributions over $K_{\left(T\right),\mathbb{R}}$. $m{-RLWE}_{q,\mathsf{\Psi }}$ denotes the search version of the m-RLWE problem. It is defined as follows: given access to arbitrarily many independent samples from $A_{s,\psi }$ for some arbitrary $s\in R_q^{\vee }$ and $\psi \in \Psi$, find s.

Definition 4

(Multivariate Ring LWE, Average-Case Decision). Let Υ be a distribution over a family of error distributions, each over $K_{\left(T\right),\mathbb{R}}$. The average-case decision version of the m-RLWE problem, denoted $m{-R-DLWE}_{q,{\rm Y}}$, is to distinguish with non-negligible advantage between arbitrarily many independent samples from $A_{s,\psi }$, for a random choice of $(s,\psi )\leftarrow U\left(R_q^{\vee }\right)\times {\rm Y}$ (where $U\left(R_q^{\vee }\right)$ represents the uniform distribution over $R_q^{\vee }$), and the same number of uniformly random and independent samples from $R_q\times \mathbb{T}$.

For an asymptotic treatment of the m-RLWE problems, we let $K_{\left(T\right)}$ come from an infinite sequence of tensors of number fields $\mathbb{K}=\left\{K_{\left(T\right),n}\right\}$ of increasing dimension n ($n={\prod }_i\varphi \left(m_i\right)$ is the number of basis elements that form the integral basis), and let q, $\Psi$, and ${\rm Y}$ depend on n as well.

3.2.1. Error Distributions

We include here two definitions about the error distributions.

Definition 5

(extension of Lyubashevsky et al. [4], Definition 3.4). For a positive real $\alpha >0$, the family ${\Psi }_{\le \alpha }$ is the set of all elliptical Gaussian distributions $D_{\mathit{r}}$ (over $K_{\left(T\right),\mathbb{R}}$), where each parameter $r_i\le \alpha$ with $i\in \left[n\right]$.

Definition 6

(extension of Lyubashevsky et al. [4], Definition 3.5). Let $K_{\left(T\right)}={⨂}_{i\in \left[l\right]}{K}_i$ where the $K_i$ are the $m_i$-th cyclotomic number field having degree $n_i=\varphi \left(m_i\right)$. For a positive real $\alpha >0$, a distribution sampled from ${{\rm Y}}_{\alpha }$ is given by an elliptical Gaussian distribution $D_{\mathit{r}}$ (over $K_{\left(T\right),\mathbb{R}}$) whose parameters are $r_j\in \left[n\right]$ using the unidimensional index (see Section 3.1.3), and each $r_j$ satisfies $r_j^2={\alpha }^2(1+\sqrt{n}{x}_j)$ where different $x_j$,$x_k$ that do not correspond to conjugate positions are chosen independently from the distribution $\Gamma (2,1)$.

Practical applications [7,9,10] usually deal with variants of the problem:

• discrete b: Instead of working with an error distribution $\psi$ over $K_{\left(T\right),\mathbb{R}}$, the m-RLWE distribution $A_{s,\chi }$ can use $\chi$ as a discrete error distribution over $R^{\vee }$, so that the element b belongs to $R_q^{\vee }$.
• small key: Instead of a uniform s, s can be a “short key” equivalently sampled from the error distribution (this is known as “normal form” in [13]), with equivalent security. Given a list of lm-RLWE samples, s can be substituted with the error e of any sample $(a,b)$ whose term a is invertible in $R_q$, which occurs with constant probability by Claim 1 below.
• power of 2 cyclotomic: Instead of sampling a and s from $R_q$ and $R_q^{\vee }$ respectively, both are usually sampled from $R_q$ (this is usually known as the non-dual variant). In general, the works which consider s in $R_q$ deal with cyclotomic fields where $m_i$ is a power of two. It can be shown that for this particular type of cyclotomic fields both definitions are equivalent.
• modulus switching: The original definitions of the problem are presented with a prime modulus q that splits the space into small independent coordinates. With the same hardness guarantees, it is possible to modulus-switch to other compute-friendly modulus at the price of a slight increase of the error.

Lyubashevsky et al. [13] show that the variant of RLWE with discrete and short error (${R-DLWE}_{q,\chi }$) is as hard as the original ${R-DLWE}_{q,\psi }$, by following the technique from [44]. These results can be adapted to our more general case as follows:

Claim 1.

The fraction of invertible elements in $R_q={⨂}_{i\in \left[l\right]}{\mathcal{O}}_{K_i}/\left(q\right)$, for prime $q=1mod{m}_i$ for all i and with $n={\prod }_i\varphi \left(m_i\right)$, is ${(1-\frac{1}{q})}^n$. Thus, if $q\ge n$, this probability is constant.

Proof. 

Since $R_q$ is in bijection with the ring ${(\mathbb{Z}/q\mathbb{Z})}^n$ via the tensor embedding mod q, so an element is invertible iff. its image does not contain any zero. Hence, there are ${(q-1)}^n$ invertible elements out of $q^n$.    □

3.2.2. Pseudorandomness of m-RLWE

To show that the m-RLWE distribution is pseudorandom (that is, there exists a reduction from the search problem to the decision variant of the hardness problem) we rely on the results from [4], applied to the case of multivariate elements. The main needed properties are those related to the decomposition of $\left(q\right)$ into n prime ideals ($q\equiv 1mod{m}_i$ for all i) and the use of the automorphisms that permute the prime ideals.

4. Proposed Approach for Secure Multivariate Rings

Despite the efficiency benefits of multivariate RLWE, its security can be much smaller than originally expected for those instances vulnerable to BCV attack [25]. This motivates us to redefine the set of instantiations that preserve the security in the tensor lattice dimension.

This section enumerates those secure instantiations of multivariate RLWE. With this in mind, we first briefly revise the choice of “coprime” order cyclotomics explicitly included in [13]. Afterwards, we discuss the possibility of using a more general set of number fields, enabling other multivariate rings that can be more convenient for practical applications.

4.1. Multivariate RLWE as a Subset of RLWE

It is well known that for two cyclotomic number fields $\mathbb{Q}\left({\zeta }_a\right)$ and $\mathbb{Q}\left({\zeta }_b\right)$ with coprime orders $gcd(a,b)=1$, their product is the cyclotomic number field $\mathbb{Q}\left({\zeta }_{ab}\right)$ (see Lemma $11.8$ in [45]). For convenience, we include an adapted version of this property ([13], Equation (1.1)) using the polynomial representation of the cyclotomic number fields.

Theorem 1

(Tensorial decomposition of cyclotomic number fields).   The m-th cyclotomic field $K=\mathbb{Q}\left({\zeta }_m\right)\cong \mathbb{Q}\left[x\right]/\left({\Phi }_m\left(x\right)\right)$ (with ${\zeta }_m$ the m-th root of unity) is isomorphic to the multivariate field

$$K\cong \mathbb{Q}[x_1,\dots ,x_l]/({\Phi }_{m_1}\left(x_1\right),\dots ,{\Phi }_{m_l}\left(x_l\right)),$$

(4)

where $m={\prod }_i{m}_i$ is decomposed in its prime-power decomposition with $gcd(m_j,m_k)=1$ for all $j\ne k$.

This fact gives an alternative basis to the power basis $\{1,x,\dots ,x^{\varphi \left(m\right)-1}\}$ for the ring of integers $R=\mathbb{Z}\left[x\right]/\left({\Phi }_m\left(x\right)\right)$; this basis is the “powerful” basis of K composed of elements ${\prod }_i{x}_i^{j_i}$ with $0\le j_i<\varphi \left(m_i\right)$. It does not coincide with the power basis under the mentioned field isomorphism and considering the map $x^{\frac{m}{m_i}}\to x_i$ for $i=1,\dots ,l$ (see [13]). This “powerful” basis has some very nice properties [13] which make it more appealing than the more “conventional” power basis. Additionally the authors of [13] provide a detailed analysis on how the performance of ring operations can be improved by means of this multivariate structure.

Besides [13], the use of the multivariate structure in Equation (4) has been exploited to enhance polynomial operations in both the HElib [14,32] and the MHEAAN [40] libraries. This gives us a first approach to deal with multivariate instantiations which do not suffer a decrease on the underlying lattice dimension. However, this structure is not flexible enough to convey the same benefits that general multivariate structures can achieve; in particular, it cannot preserve the interesting structure of power-of-two cyclotomics ($1+x^n$).

4.2. More General RLWE Instantiations

We look now beyond cyclotomics, into more general and flexible number fields and their parameterization. We first introduce the definitions of RLWE over any number field [26], and then give the intuition on the properties required to resist the BCV attack. A detailed discussion on the choice of good parameters and the security of RLWE on these number fields follows in Section 5, Section 6 and Section 7.1.

4.2.1. RLWE Over Any Number Field

Peikert et al. [26] have recently generalized the RLWE problem to any number field. Let K be a number field with ring of integers $R={\mathcal{O}}_K$; let $R^{\vee }$ be the fractional codifferent ideal of K, and let $\mathbb{T}=K_{\mathbb{R}}/R^{\vee }$. Let $q\ge 2$ be a (rational) integer modulus, and for any fractional ideal I of K, let ${\mathcal{I}}_q=\mathcal{I}/q\mathcal{I}$ (for any fractional ideal $\mathcal{I}\subset K$ there is $a\in {\mathcal{O}}_K$ such that $a\mathcal{I}\subseteq {\mathcal{O}}_K$ is an integral ideal of ${\mathcal{O}}_K$). We include now the relevant definitions of RLWE over any number field that we use in our formulation.

Definition 7

(Ring-LWE Distribution, Definition $2.14$ in [26]). For $s\in R_q^{\vee }$ and an error distribution ψ over $K_{\mathbb{R}}$, the $R-LWE$ distribution $A_{s,\psi }$ over $R_q\times \mathbb{T}$ is sampled by independently choosing a uniformly random $a\leftarrow R_q$ and an error term $e\leftarrow \psi$, and outputting $\left(a,b=(a·s)/q+emod{R}^{\vee }\right)$.

Definition 8

(Ring-LWE, Average-Case Decision, Definition $2.15$ in [26]). Let Υ be a distribution over a family of error distributions, each over $K_{\mathbb{R}}$. The average-case Ring-LWE decision problem, denoted $R-{LWE}_{q,{\rm Y}}$, is to distinguish (with non-negligible advantage) between independent samples from $A_{s,\psi }$ for a random choice of $(s,\psi )\leftarrow U\left(R_q^{\vee }\right)\times {\rm Y}$, and the same number of uniformly random and independent samples from $R_q\times \mathbb{T}$.

Theorem 2

(Theorem $6.2$ from [26]).  Let K be an arbitrary number field of degree n, $\mathcal{I}$ any fractional ideal of K, and $R={\mathcal{O}}_K$. Let $\alpha =\alpha \left(n\right)\in (0,1)$, and let $q=q\left(n\right)\ge 2$ be an integer such that $\alpha q\ge 2·\omega \left(1\right)$. There is a polynomial-time quantum reduction from $K-{DGS}_{\gamma }$ to (average-case, decision) $R-{LWE}_{q,{{\rm Y}}_{\alpha }}$, for any

$$\gamma =max\left\{\eta \left(\mathcal{I}\right)·\sqrt{2}/\alpha ·\omega \left(1\right),\sqrt{2n}/{\lambda }_1\left({\mathcal{I}}^{\vee }\right)\right\}.$$

$K-{DGS}_{\gamma }$ corresponds to the Discrete Gaussian Sampling (DGS) problem, but restricted to (fractional) ideal lattices in K.

The ${{\rm Y}}_{\alpha }$ distribution considered here is narrower than the one from Theorem 6. We refer the reader to Definition $6.1$ from [26] for its concrete expression.

Additionally, it is worth highlighting some observations on the choice of a particular number field in RLWE, as stated in [26]:

• The geometry of the dual ideal $R^{\vee }$ affects the error rate $\alpha$ (chosen to be smaller than the minimum distance ${\lambda }_1\left(R^{\vee }\right)$). As $\alpha$ decreases, worst-case hardness theorems give weaker guarantees (i.e., larger approximation factors), and known attacks on Ring-LWE become more efficient.
• A similar phenomenon arises for rings with large “expansion factors” (see [46]) which imposes smaller $\alpha$ for achieving correct decryption; hence, good rings for practical applications have small expansion factors.
• Besides the two previous relations, there is no practical evidence on which particular number field is better in terms of security.

4.2.2. Ad-Hoc Countermeasures to BCV Attack

BCV attack [25] shows that a reduced RLWE sample is at least as hard as an m-RLWE sample. To prove the converse, we can use an oracle for m-RLWE. With access to such oracle and a set of RWLE samples with different keys, we can construct an m-RWLE sample (with a slight increase in the noise variance) by means of the reverse map of BCV attack (i.e., ${\tilde{\Theta }}^{-1}$). Once this oracle returns the secret key of the m-RLWE sample, the original keys of the RLWE sample can be recovered by means of the map $\tilde{\Theta }$.

We can therefore express the security of m-RLWE in terms of RLWE, but the decrease of the involved dimension considerably reduces the applicability of the problem with “non-coprime” polynomial functions. The security of ${\prod }_{j\ne k}\varphi (gcd(m_j,m_k))$ independent RLWE samples with dimension $\frac{{\prod }_{i\in \left[l\right]}\varphi \left(m_i\right)}{{\prod }_{j\ne k}\varphi (gcd(m_j,m_k))}$ could be reduced to that of one m-RLWE sample (according to Definition 2) with dimensions $\{\varphi \left(m_1\right),\dots ,\varphi \left(m_l\right)\}$:

Theorem 3

(${\tilde{\Theta }}^{-1}$ transform from [25]). Let L independent univariate RLWE samples $(a_i,b_i)\in R_q\times \mathbb{T}$ for $i\in \left[L\right]$ and dimension n. We can transform (this transformation is invertible when q is prime) these L samples by means of the (inverse) of BCV attack into one m-RLWE sample with l dimensions $\{\varphi \left(m_1\right),\dots ,\varphi \left(m_l\right)\}$ (see Definition 2) satisfying $L={\prod }_{j\ne k}\varphi \left(gcd(m_j,m_k)\right)$ and having for the RLWE sample $n=\frac{{\prod }_{i\in \left[l\right]}\varphi \left(m_i\right)}{L}$. This transformation slightly increases the variance of the error distribution by a factor L.

The decrease in the lattice dimension by a factor $L={\prod }_{j\ne k}\varphi \left(gcd(m_j,m_k)\right)$ brings about the question of whether we can modify some of the multivariate RLWE constructions where $L>1$ to avoid BCV attack.

4.2.3. Followed Strategy

By considering instantiations satisfying $gcd(m_j,m_k)=1$ for all $j\ne k$, we straightforwardly go back again to the RLWE problem defined on univariate cyclotomic rings. On the contrary, we would like to find other instantiations where the polynomial ideals can have a similar form and degree. We will hence focus on polynomial functions as follows: $\{x^{n_x}+d_x,y^{n_y}+d_y,z^{n_z}+d_z,\dots \}$, which can avoid BCV attack for certain parameters, while enabling NTT-like fast transforms and preserving the advantages of the originally introduced m-RLWE constructions.

However, the security of these instantiations is apparently not based on any specific formulation of the RLWE problem, so we do not have a clear way of choosing the right parameters.

In the next two sections, we will show that this is not really true and that there are many number fields satisfying Definition 7, and whose ring of integers (and their dual) has the aforementioned structure. In particular, we focus on multiquadratic number fields (Section 5) and more general multivariate rings (Section 6).

5. Multiquadratic Rings

Let $K=\mathbb{Q}\left(\sqrt{d_i}\right)$ be a field with prime $d_i$ (hence squarefree) satisfying $d_i=1mod4$; its ring of integers is ${\mathcal{O}}_K=\mathbb{Z}\left[\frac{1+\sqrt{d_i}}{2}\right]$ with basis $\{1,\frac{1+\sqrt{d_i}}{2}\}$ and discriminant ${\Delta }_K=d_i$, then we can also represent ${\mathcal{O}}_K$ as a polynomial ring $\mathbb{Z}\left[x\right]/(x^2-x+\frac{1-d_i}{4})$ (${\mathcal{O}}_K$ is free of rank 2), according to (see Proposition 1):

Proposition 1

(Proposition $2.24$ from [47] ). Let $K=\mathbb{Q}\left(\sqrt{d}\right)$ be a quadratic field with d a squarefree integer. If $d\equiv 2,3(mod4)$, then ${\mathcal{O}}_K=\mathbb{Z}\left[\sqrt{d}\right]\simeq \mathbb{Z}\left[x\right]/(x^2-d)$ and ${\mathcal{O}}_K$ is free of rank 2 over $\mathbb{Z}$ with basis $\{1,\sqrt{d}\}$. If $d\equiv 1(mod4)$, then ${\mathcal{O}}_K=\mathbb{Z}\left[\frac{1+\sqrt{d}}{2}\right]\simeq \mathbb{Z}\left[x\right]/(x^2-x+\frac{1-d}{4})$ and ${\mathcal{O}}_K$ is free of rank 2 over $\mathbb{Z}$ with basis $\{1,\frac{1+\sqrt{d}}{2}\}$.

Let us extend the field to $\mathbb{Q}(\sqrt{d_1},\dots ,\sqrt{d_l})$ (a multiquadratic field), with all $d_i$ pairwise coprime, but still sticking to the case $d_i=1mod4$. Taking into account that ${\mathcal{O}}_K{\mathcal{O}}_{K^{\prime }}={\mathcal{O}}_F$ when $gcd({\Delta }_K,{\Delta }_{K^{\prime }})=1$, where F is the compositum over $\mathbb{Q}$ (see [48]) of two subfields $K=\mathbb{Q}\left(\sqrt{d_1}\right)$ and $K^{\prime }=\mathbb{Q}\left(\sqrt{d_2}\right)$ (see [49]), we have that ${\mathcal{O}}_F=\mathbb{Z}\left[\frac{1+\sqrt{d_1}}{2},\frac{1+\sqrt{d_2}}{2}\right]$. This can be generalized to the case of a field with l “coprime” squares, whose resulting ring of integers is

$${\mathcal{O}}_K=\mathbb{Z}\left[\frac{1+\sqrt{d_1}}{2}\right]·\dots ·\mathbb{Z}\left[\frac{1+\sqrt{d_l}}{2}\right].$$

(5)

Therefore, as all $d_i$ are different primes, the discriminants of $\mathbb{Q}\left(\sqrt{d_i}\right)$ are also coprime, which implies that the ring of integers can be expressed as the product of the respective univariate rings of integers. However, the definition of RLWE (see Definition 8) works on the dual of the ring of integers, due to its geometric properties. The dual can be obtained through Theorem 4:

Theorem 4

(Theorem $3.7$ from [50] ). Let $K=\mathbb{Q}\left(\alpha \right)$ and let $f\left(T\right)$ be the minimal polynomial of α in $\mathbb{Q}\left[T\right]$. Write

$$f\left(T\right)=(T-\alpha )(c_0\left(\alpha \right)+c_1\left(\alpha \right)T+\dots +c_{n-1}\left(\alpha \right)T^{n-1}),c_i\left(\alpha \right)\in K.$$

The dual basis to $\{1,\alpha ,\dots ,{\alpha }^{n-1}\}$ relative to the trace product is

$$\left\{\frac{c_0\left(\alpha \right)}{f^{\prime }\left(\alpha \right)},\frac{c_1\left(\alpha \right)}{f^{\prime }\left(\alpha \right)},\dots ,\frac{c_{n-1}\left(\alpha \right)}{f^{\prime }\left(\alpha \right)}\right\}.$$

In particular, if $K=\mathbb{Q}\left(\alpha \right)$ and $\alpha \in {\mathcal{O}}_K$ then

$${(\mathbb{Z}+\mathbb{Z}\alpha +\dots +\mathbb{Z}{\alpha }^{n-1})}^{\vee }=\frac{1}{f^{\prime }\left(\alpha \right)}(\mathbb{Z}+\mathbb{Z}\alpha +\dots +\mathbb{Z}{\alpha }^{n-1}).$$

For simplicity, if a ring of integers $R=\mathbb{Z}\left[x\right]/\left(f\right(x\left)\right)$ satisfies Theorem 4, we usually denote its dual as $R^{\vee }=\frac{1}{f^{\prime }\left(x\right)}\mathbb{Z}\left[x\right]/\left(f\left(x\right)\right)$, being $f^{\prime }\left(x\right)$ the corresponding scale factor introduced in the power basis. Particularized to the quadratic case, Theorem 4 says that whenever the ring of integers has a power basis, the basis of the dual is

$${\left\{1,\frac{1+\sqrt{d_i}}{2}\right\}}^{\vee }=\left\{\frac{1}{f^{\prime }\left(\alpha \right)},\frac{1}{f^{\prime }\left(\alpha \right)}\frac{1+\sqrt{d_i}}{2}\right\},$$

(6)

where $f\left(x\right)=x^2-x+\frac{1-d}{4}$ and $\alpha =\frac{1+\sqrt{d}}{2}$, so $f^{\prime }\left(x\right)=2x-1$; evaluated at $x=\alpha =\frac{1+\sqrt{d_i}}{2}$, it satisfies $f^{\prime }\left(\alpha \right)=\sqrt{d_i}$.

As dual commutes tensoring, this result can be straightforwardly extended to the compositum case with several $d_i$. Additionally, we see that we can go from the dual to ${\mathcal{O}}_K$ by just scaling with $\sqrt{d_i}$ (or multiplying with the polynomial $2x-1$).

Following our requirements, we need a ring of the form $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^2-d_1,\dots ,x_l^2-d_l)$, which is an order of the field $\mathbb{Q}(\sqrt{d_1},\dots ,\sqrt{d_l})$, but not necessarily its ring of integers and a Dedekind domain. Actually, a recent work [51] discusses the hardness of a generalization of Ring-LWE called Order-LWE, which can be leveraged to have more freedom in the choice of the multivariate rings (see Section 9 for more details on the advantages of Order-LWE). We also refer the reader to [52] for a recent study on the connections between several algebraic LWE variants.

However, in this section we only want to base the security on RLWE defined on a number field of the form $\mathbb{Q}(\sqrt{d_1},\dots ,\sqrt{d_l})$ (see Definition 7) and its ring of integers satisfying $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^2-x_1+\frac{1-d_1}{4},\dots ,x_l^2-x_l+\frac{1-d_l}{4})$. We will therefore show that we can define an invertible map modulo q from the ring ${\mathcal{O}}_K$ (and its dual ${\mathcal{O}}_K^{\vee }$) to the ring $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^2-d_1,\dots ,x_l^2-d_l)$, while still basing its security on the original RLWE formulation from Definition 7. Additionally, this map does not significantly increase the noise; in fact, it also decorrelates it in the coefficient domain, enabling direct sampling of the noise in the coefficient representation with an independent error distribution.

The map, applied to each variable $x_i$, works as follows:

• We apply the change of variable $x\to \frac{x+1}{2}$.
• We multiply the sample by a factor 2.

This mapping can be applied whenever the inverse of 2 exists modulo q. The multiplication by 2 is applied afterwards to avoid the potentially high distortion introduced by the factor $\frac{1}{2}$ into the noise.

Canonical Embedding:

Let $K=\mathbb{Q}(\sqrt{d}$), and note that $\frac{1}{2x-1}$ evaluated at $x=\frac{1+\sqrt{d}}{2}$ equals $\frac{1}{\sqrt{d}}$. We define the Embedding map $\mathcal{E}$ going from ${\mathcal{O}}_K^{\vee }\cong \frac{1}{\sqrt{d}}\mathbb{Z}\left[x\right]/(x^2-x+\frac{1-d}{4})$ to ${\mathbb{C}}^2$, as the substitutions $\{x\to \frac{1+\sqrt{d}}{2},\sqrt{d}\to \sqrt{d}\}$ and $\{x\to \frac{1-\sqrt{d}}{2},\sqrt{d}\to -\sqrt{d}\}$. This gives this transformation matrix for $\mathcal{E}$

$$\frac{1}{\sqrt{d}}\left(\begin{array}{cc}1& \frac{1+\sqrt{d}}{2}\\ -1& \frac{\sqrt{d}-1}{2}\end{array}\right).$$

(7)

The inverse map ${\mathcal{E}}^{-1}$ is defined as the product with the matrix

$$\left(\begin{array}{cc}\frac{\sqrt{d}-1}{2}& -\frac{1+\sqrt{d}}{2}\\ 1& 1\end{array}\right).$$

(8)

Sampling the error directly in the coefficient domain:

Finally, if we define the noise in the embedding of the dual ring as two independent Gaussian variables $e_0,e_1$ with variance ${\sigma }^2$, we have in the ring $\frac{1}{x}\mathbb{Z}\left[x\right]/(x^2-d)$ after following the whole “processing chain”:

$$\frac{1}{x}\left(\underset{2{\sigma }^2}{\underbrace{(e_0+e_1)}}x+\underset{2d{\sigma }^2}{\underbrace{\sqrt{d}(e_0-e_1)}}\right)mod{x}^2-d.$$

Hence, the noise is not correlated in the coefficient domain and we can easily sample the error distribution considering an appropriate variance per coefficient.

For simplicity, we have focused on a quadratic field, but the embedding matrix can be extended to the multiquadratic case by means of the Kronecker product.

5.1. Multiquadratic RLWE

Let us define the multiquadratic version of m-RLWE, where all the polynomial functions have the form $f_i\left(x_i\right)=d_i+x_i^2$, as 

Definition 9

(Multivariate polynomial RLWE with quadratic polynomial ideals). Given a multivariate polynomial ring $R_q^{\vee }[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=d_j+x_j^2$ for $j=1,\dots ,l$ where $l={log}_{2}n$ (with n a power of two) and an error distribution $\chi [x_1,\dots ,x_l]$ that generates small-norm random multivariate polynomials in $R_q^{\vee }[x_1,\dots ,x_l]$, the multivariate polynomial RLWE relies upon the computational indistinguishability between samples $(a_i,b_i=a_i·s+e_i)$ and $(a_i,u_i)$, where $a_i\leftarrow R_q[x_1,\dots ,x_l]$, $u_i\leftarrow R_q^{\vee }[x_1,\dots ,x_l]$ are chosen uniformly at random from the rings $R_q[x_1,\dots ,x_l]$ and $R_q^{\vee }[x_1,\dots ,x_l]$; and $s,e_i\leftarrow \chi [x_1,\dots ,x_l]$ are drawn from the error distribution (see Section 5).

Given an adequate parameter setting, the security reduction from Theorem 2 applies to this multiquadratic version of the RLWE problem.

Theorem 5

(Parameter setting—hardness of multiquadratic RLWE). The polynomial-time quantum reduction from Theorem 2 applies to the multiquadratic RLWE assumption from Definition 9 (with $f_i\left(x_i\right)=d_i+x_i^2$) whenever:

• All $d_i$ are squarefree integers.
• All $d_i$ are pairwise coprime, i.e., $gcd(d_i,d_j)=1$ for all $i\ne j$.
• All $d_i$ satisfy $-d_i=1mod4$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Corollary 1

(Parameter setting—hardness of multiquadratic RLWE, derived fom Theorem 5).   The polynomial-time quantum reduction from Theorem 2 applies to the multiquadratic RLWE assumption from Definition 9 (with $f_i\left(x_i\right)=d_i+x_i^2$) whenever:

• All $d_i$ are different prime numbers.
• All $d_i$ satisfy $-d_i=1mod4$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Section 7.1 gives further insights on the security and practicality of the chosen parameterization, and exemplifies it with a concrete instantiation. In particular, Proposition 5 gives a sufficient condition to consider the problem secure against known attacks. It is worth mentioning that even when the Principal Ideal Problem is easy in multiquadratics [53], to the best of our knowledge, this has not been proven enough to solve RLWE.

5.2. Comparison with Gaussian Integers

We now compare the multiquadratic RLWE with the particular case of power-of-two cyclotomics m-RLWE (see Definition 1) where all the used polynomial functions have the same form $f_i\left(x_i\right)=1+x_i^2$:

Definition 10

(multivariate polynomial RLWE with ${\Phi }_4(·)$ as polynomial functions). Given a multivariate polynomial ring $R_q[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=1+x_j^2$ for $j=1,\dots ,l$ where $l={log}_{2}n$ (with n a power of two) and an error distribution $\chi [x_1,\dots ,x_l]$ that generates small-norm random multivariate polynomials in $R_q[x_1,\dots ,x_l]$, the multivariate polynomial RLWE relies upon the computational indistinguishability between samples $(a_i,b_i=a_i·s+e_i)$ and $(a_i,u_i)$, where $a_i,u_i\leftarrow R_q[x_1,\dots ,x_l]$ are chosen uniformly at random from the ring $R_q[x_1,\dots ,x_l]$; and $s,e_i\leftarrow \chi [x_1,\dots ,x_l]$ are drawn from the error distribution.

The comparison of our secure multiquadratic RLWE samples with RLWE samples from Definition 10 is specially relevant, as the latter are severely affected by BCV attack. Samples from Definition 10 can be reduced to a dimension of 2, by applying the map $\tilde{\Theta }$ a total of $({log}_{2}n-1)$ times, yielding $n/2$ RLWE samples with $f\left(x\right)=1+x^2$ and error variance $n/2$ times higher than the original m-RLWE sample; this can be very easily solved. Consequently, despite of the efficiency of the polynomial operations on the rings instantiated according to Definition 10, they are not valid for cryptographic applications. Meanwhile, the samples from a secure instantiation of multiquadratic RLWE (Definition 9) preserve the lattice dimension n and withstand BCV attack.

Another advantage of the multiquadratic RLWE problem is that it also enables very efficient polynomial operations, without decreasing security. In particular, it is possible to apply a variant of the Fast Walsh–Hadamard Transform (over finite rings instead of the usual real numbers), featuring a convolution property that relates the coefficient-wise representation with the transformed domain. This transform can be very efficiently computed with FFT-like algorithms whose computational cost is only $\mathcal{O}(nlogn)$ additions and $\mathcal{O}\left(n\right)$ products, hence considerably speeding up practical implementations [43]. For more details, we refer the reader to Section 8.

6. More General Multivariate Rings

Let us consider now general fields $\mathbb{Q}(a_1^{1/n_1},\dots ,a_l^{1/n_l})$, for which the $a_i$ are squarefree and coprime, but for simplicity we will assume that they are independent primes. The results shown in the previous section for multiquadratics cannot be straightforwardly generalized to these fields, as the individual univariate fields $\mathbb{Q}\left(a_i^{1/n_i}\right)$ can easily have common factors in their discriminants (i.e., be non-coprime), in such a way that finding a basis for the multivariate ring of integers is not trivial. We refer the reader to Section 9 for a discussion on the advantages that Order-LWE [51] brings about with respect to RLWE when choosing a basis for the ring of integers.

We explain the followed path that leads to our definition of valid, secure and easily parameterizable multivariate rings. We start by choosing number fields whose ring of integers ${\mathcal{O}}_K$ can be represented as $\mathbb{Z}\left[x\right]/(x^n+ax+b)$, that is, as quotient polynomial rings whose ideal has the form $(x^n+ax+b)$. For this to be a valid ring ${\mathcal{O}}_K$ for K, it has to be irreducible over $\mathbb{Q}$, for which we use Eisensntein’s criterion:

Proposition 2

(Eisenstein’s criterion [54]). The polynomial $p\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$, where $a_i\in \mathbb{Z}$ for all $i=0,\dots ,n$ and $a_n\ne 0$ (which means that the degree of $p\left(x\right)$ is n) is irreducible if some prime number p divides all coefficients $a_0,\dots ,a_{n-1}$, but not the leading coefficient $a_n$ and, moreover, $p^2$ does not divide the constant term $a_0$.

Therefore, we impose the following two conditions on $f\left(x\right)=x^n+ax+b$:

• Both a and b have to be divisible by a prime p and not by $p^2$ (Eisenstein’s criterion).
• If we choose b as a prime, a has to be divisible by b.

Now, we can compute the discriminant for this number field by resorting to ([55], Chapter $2.7$):

Proposition 3

(An example of the calculation of a discriminant [55] ). For the calculation of ${\Delta }_K$ in a number field $K=\mathbb{Q}\left(x\right)$ being a extension of finite degree n of $\mathbb{Q}$ and $f\left(x\right)=x^n+ax+b$ the minimal polynomial of x over $\mathbb{Q}$, we obtain

$${\Delta }_K={(-1)}^{\frac{n(n-1)}{2}}(n^n{b}^{n-1}+{(-1)}^{n-1}{(n-1)}^{n-1}{a}^n).$$

(9)

For $n=2$ (respectively, 3) we rediscover the well-known expressions $a^2-4b$ (respectively, $-27b^2-4a^3$).

Theorem 6

(Theorem $8.11$ from [45] ). For $\mathbb{Z}$-lattices ${\mathcal{L}}^{\prime }\subset \mathcal{L}$ inside K, ${[{\mathcal{L}}^{\prime }:\mathcal{L}]}^2<\infty$ and

$${disc}_{\mathbb{Z}}\left({\mathcal{L}}^{\prime }\right)={[{\mathcal{L}}^{\prime }:\mathcal{L}]}^2·{disc}_{\mathbb{Z}}\left(\mathcal{L}\right).$$

In particular, if ${\mathcal{L}}^{\prime }\subset {\mathcal{O}}_K$ and the integer ${disc}_{\mathbb{Z}}\left({\mathcal{L}}^{\prime }\right)\in \mathbb{Z}-\left\{0\right\}$ is squarefree then $[{\mathcal{O}}_K:{\mathcal{L}}^{\prime }]=1$; i.e., ${\mathcal{L}}^{\prime }={\mathcal{O}}_K$.

If we choose values for a and b such that the polynomial discriminant is squarefree, Theorem 6 guarantees that the ring of integers has a power basis of the form $\{1,\alpha ,{\alpha }^2,\dots \}$, with $\alpha$ a root of $x^n+ax+b$. Consequently, $\mathbb{Z}\left[x\right]/(x^n+ax+b)$ is a valid ring of integers.

By including more “univariate” subrings, $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^n+a_{1}x+b_1,\dots ,x_l^n+a_{l}x+b_l)$ becomes a valid ring of integers when all the discriminants are coprime [49]. Therefore, this is a feasible strategy to define RLWE over a multivariate ring, as the product of univariate rings with polynomial ideals $(x^n+a_{i}x+b_i)$. To define the dual ${\mathcal{O}}_K^{\vee }$ we can make use of Theorem 4 which states that whenever the ring of integers has a power basis, the basis of the dual is the same basis, scaled by $\frac{1}{f^{\prime }\left(\alpha \right)}=\frac{1}{n{\alpha }^{n-1}+a}$, where $\alpha$ is a root of $f\left(x\right)$.

Finding valid parameters for$f\left(x\right)=x^n+ax+b$:

Unfortunately, the two previous conditions (Eisenstein’s criterion from Proposition 2 and Theorem 6) cannot be satisfied at the same time

• To satisfy the Eisenstein’s criterion, b and a have to be divisible by at least a prime p (i.e., $gcd(a,b)=u·p$ for some $u\in \mathbb{Z}$), this introduces a factor $p^{n-1}$ in ${\Delta }_K$ (see Equation (9)), in such a way that ${\Delta }_K$ is not squarefree and not satisfying $[{\mathcal{O}}_K:{\mathcal{L}}^{\prime }]=1$ in Theorem 6.
  We could still work with these multivariate rings provided that their discriminants are coprime, but it seems that there is no straightforward way to determine the “powerful” basis of the ring of integers: starting from Proposition 3, it is known that $\mathbb{Z}\left[\alpha \right]\subseteq {\mathcal{O}}_K\subseteq \frac{1}{{\Delta }_K}\mathbb{Z}\left[\alpha \right]$ where $f\left(\alpha \right)=0$.
• Additionally, Eisenstein’s criterion is a sufficient but not necessary condition for irreducibility of the polynomial functions. Without the imposed restrictions, we could search for squarefree and coprime discriminants, but we would have to verify the irreducibility of the involved functions case-by-case. Nevertheless, this is not impossible to find, as it is known that monogenic fields are not scarce [56]; in fact, for random polynomials f, it has been conjectured that $\mathbb{Z}\left[x\right]/\left(f\right(x\left)\right)$ of degree $\ge 4$ is a ring of integers with probability $\gtrsim 0.307$ [57].

6.1. Transformation Based on Modulus Switching

Let us assume that we have found valid (monogenic) $x_i^n+a_i{x}_i+b_i$ functions defining the ring of integers $\mathbb{Z}\left[x_i\right]/(x_i^n+a_i{x}_i+b_i)$; they do not yet feature the desired $x^n+d$ form.

In order to achieve this, we consider a map from the original RLWE samples to RLWE samples modulo q, that removes the term $ax$ if q divides a. It is worth noting that this transformation is nothing but a modulus switching to q, and if it were possible to break RLWE modulo q, the original secret key could be recovered or at least the indistinguishability assumption could be broken.

The trick relies on all the polynomial functions having the form $f_i\left(x_i\right)=x_i^n+\underset{a_i}{\underbrace{a_i^{\prime }q}}{x}_i+b_i$. Hence, a reduction modulo q converts the polynomial functions into $f_i\left(x_i\right)=x_i^n+b_i$. We show the effect of this transformation on the ring $q{\mathcal{O}}_K^{\vee }$ for the univariate case (it extends to the multivariate case, as dual commutes tensoring):

• ${\mathcal{O}}_K^{\vee }$ is defined as $\frac{1}{f^{\prime }\left(\alpha \right)}{\mathcal{O}}_K$; under the polynomial ring $\mathbb{Z}\left[x\right]/(x^n+a_i^{\prime }qx+b_i)$, this implies that the dual is $\frac{1}{n{x}^{n-1}+a_i^{\prime }q}\mathbb{Z}\left[x\right]/(x^n+a_i^{\prime }qx+b_i)$.
• After reducing modulo q, we obtain $\frac{1}{n{x}^{n-1}}{\mathbb{Z}}_q\left[x\right]/(x^n+b_i)$; considering that x has inverse modulo q, we can multiply numerator and denominator by x to obtain $\frac{x}{n{x}^n}=\frac{x}{-n{b}_i}$.
• The factor $\frac{1}{-n{b}_i}$ can be removed by just a scaling (moving to the ring of integers ${\mathcal{O}}_K$), so we can directly work on ${\mathbb{Z}}_q\left[x\right]/(x^n+b_i)$. This gives a “basis” $\{b_i,x,x^2,\dots ,x^{n-1}\}$ (or a basis $\{\frac{1}{n},\frac{x}{n{b}_i},\frac{x^2}{n{b}_i},\dots ,\frac{x^{n-1}}{n{b}_i}\}$ without scaling).

Decodability of the transformed$x^n+ax+b$:

Elias et al. [56] use an heuristic perturbation method to bound the spectral norm of the canonical embedding with $f\left(x\right)=x^n+ax+b$. As the condition number is stable for most of the random perturbations of the canonical embedding matrix associated to $x^n+1$, they conjecture that many f functions have a bounded spectral norm in terms of a and b; therefore, we can consider that the spectral norm $s_1\left(N_f\right)$ ($N_f$ represents the inverse of the canonical embedding matrix) is likely bounded by $\sqrt{max(a,b)}·det{\left(N_f\right)}^{1/n}$ [58]. Consequently, the same arguments about noise behavior in [37,58] still apply, and in order to guarantee the prevalence of the security reduction (see Proposition 5), the noise wraps around modulo q in some of the polynomial coefficients ($max(a,b)\approx q$). This is due to the large q factor introduced in $f\left(x\right)$, which requires the use of a high error variance, rendering some of the polynomial coefficients modulo q useless. This makes these RLWE samples harder to use for cryptographic applications.

6.2. Valid and Practical Parameterizations for Multivariate Rings

The previous solutions to parameterize multivariate rings with polynomial ideals $(x^n+d)$ are not satisfactory, as (a) the search of valid univariate rings is not easy to handle (due to the impossibility to use Eisenstein’s criterion) and (b) the obtained samples are not practical for cryptographic applications due to their high noise in some polynomial coefficients.

Here we follow a slightly different approach, releasing the condition on equal-degree polynomial functions; that is, we consider multivariate rings as $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^{n_1}+d_1,\dots ,x_l^{n_l}+d_l)$. Again, to simplify the explanation we only use an univariate quotient ring with polynomial ideal $(x^n+d)$, but all the results can be analogously extended to the multivariate case (see Section 5) by requiring coprime discriminants.

First, for $f\left(x\right)=x^n+d$, Equation (9) simplifies to ${\Delta }_K={(-1)}^{\frac{n(n-1)}{2}}{n}^n{d}^{n-1}$.

Let d be a prime number and $n=u^m$ a prime power. Then,

• $f\left(x\right)$ is an irreducible polynomial over $\mathbb{Q}$ by the Eisenstein’s criterion (Propostion 2).
• $f\left(x\right)$ is monogenic for d and n by satisfying the following Proposition 4.

Proposition 4

(Adapted Proposition 3 from [56]). Let n be a power of a prime u. If d is squarefree and $u^2$ does not divide $({(-d)}^{n-1}+1)d$, then the polynomials $x^n+d$ are monogenic.

Proposition 4 shows that $f\left(x\right)$ can be monogenic even when its discriminant is not squarefree. If $f\left(x\right)$ satisfies Proposition 4, we have ${\mathcal{O}}_K=\mathbb{Z}\left[x\right]/(x^n+d)$ and ${\mathcal{O}}_K^{\vee }=\frac{1}{n{x}^{n-1}}\mathbb{Z}\left[x\right]/(x^n+d)$.

In order to extend these results to multivariate rings $\mathbb{Z}[x_1,\dots ,x_l]/(x_1^{n_1}+d_1,\dots ,x_l^{n_l}+d_l)$, we only have to consider functions $\{x_1^{n_1}+d_1,\dots ,x_l^{n_l}+d_l\}$ satisfying Proposition 4 and having coprime discriminants. This basically means that all the $d_i$ and $n_i$ are respectively different primes and power primes.

Analogously to the multiquadratic rings in Section 5, we can directly map the error distribution in the coefficient domain. In particular, for the ring $\frac{1}{n_i{x}^{n_i-1}}\mathbb{Z}\left[x_i\right]/(x_i^{n_i}+d_i)$, the parameter for the error distribution in the $(j-1)$-th coefficient ($1\le j\le n_i$) is given by $\sqrt{n_i}{d}_i^{\frac{n_i-j}{n_i}}r$, where r is the parameter of an independent spherical error distribution in the embedding domain [58]. This extends to multivariate rings by means of the Kronecker product.

Finally, we introduce the definition of multivariate RLWE with the proposed polynomial functions $f_i\left(x_i\right)=d_i+x_i^{n_i}$:

Definition 11

(Multivariate RLWE with polynomial functions as $x_i^{n_i}+d_i$). Given a multivariate polynomial ring $R_q[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=d_j+x_j^{n_j}$ for $j=1,\dots ,l$ where $n={\prod }_j{n}_j$ (where all $n_j$ are prime powers) and an error distribution $\chi [x_1,\dots ,x_l]$ that generates small-norm random multivariate polynomials in $R_q^{\vee }[x_1,\dots ,x_l]$, the multivariate polynomial RLWE relies upon the computational indistinguishability between samples $(a_i,b_i=a_i·s+e_i)$ and $(a_i,u_i)$, where $a_i\leftarrow R_q[x_1,\dots ,x_l]$, $u_i\leftarrow R_q^{\vee }[x_1,\dots ,x_l]$ are chosen uniformly at random from the rings $R_q[x_1,\dots ,x_l]$ and $R_q^{\vee }[x_1,\dots ,x_l]$; $s,e_i\leftarrow \chi [x_1,\dots ,x_l]$ are drawn from the error distribution.

For the ring $R^{\vee }[x_1,\dots ,x_l]$, we define $\chi [x_1,\dots ,x_l]$ as an error distribution generating polynomials belonging to $R^{\vee }[x_1,\dots ,x_l]$ and whose parameter per coefficient satisfies $r{\prod }_{i\in \left[l\right]}\sqrt{n_i}{d}_i^{\frac{n_i-j_i}{n_i}}$, where $1\le j_i\le n_i$ and $1\le i\le l$, and hence represents the parameter for the coefficient associated to the monomial $x_1^{j_1-1}·\dots ·x_l^{j_l-1}$.

Given an adequate parameter setting, the security reduction from Theorem 2 applies to several multivariate versions of the RLWE problem (see Definition 11).

Theorem 7

(Parameter setting—hardness of multivariate RLWE with polynomial functions as $x_i^{n_i}+d_i$). The polynomial-time quantum reduction from Theorem 2 applies to the multivariate RLWE assumption from Definition 11 whenever:

• All $d_i$ are squarefree and all $n_i$ are powers of the primes $u_i$.
• Each $u_i^2$ does not divide $({(-d_i)}^{n_i-1}+1)d_i$.
• All $n_i$ and $d_i$ satisfy $gcd(n_i,n_j)=1$, $gcd(n_i,d_j)=1$ and $gcd(d_i,d_j)=1$ if $i\ne j$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Corollary 2

(Parameter setting—hardness of multivariate RLWE with polynomial functions as $x_i^{n_i}+d_i$, derived from Theorem 7). The polynomial-time quantum reduction from Theorem 2 applies to the multivariate RLWE assumption from Definition 11 whenever:

• All $d_i$ and $n_i$ are, respectively, different odd primes and powers of the odd primes $u_i$.
• All $d_i$ and $u_i$ satisfy $gcd(d_i,u_j)=1$ for all $i,j$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Corollary 3

(Parameter setting—hardness of multivariate RLWE with polynomial functions as $x_i^{n_i}+d_i$, derived from Theorem 7). The polynomial-time quantum reduction from Theorem 2 applies to the multivariate RLWE assumption from Definition 11 whenever:

• All $d_i$ are different primes, and each $n_i$ is a power of $d_i$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Theorem 8

(Parameter setting—hardness of multivariate RLWE with the compositum of rings from Definitions 9 and 11). The polynomial-time quantum reduction from Theorem 2 applies to the multivariate RLWE assumption from Definition 11 whenever:

• For all $f_i\left(x_i\right)=d_i+x_i^{n_i}$ with $n_i=2$:

  -

  The $d_i$ are squarefree integers satisfying $-d_i=1mod4$.

• For all $f_i\left(x_i\right)=d_i+x_i^{n_i}$ with $n_i>2$ a power of a prime $u_i$:

  -

  Each $u_i^2$ does not divide $({(-d_i)}^{n_i-1}+1)d_i$.

• All $d_i$ and all $n_i>2$ satisfy $gcd(n_i,n_j)=1$, $gcd(n_i,d_j)=1$ and $gcd(d_i,d_j)=1$ if $i\ne j$.
• The error distribution satisfies the lower bound $\alpha q\ge 2·\omega \left(1\right)$.

Some examples of valid parameters:

In order to show the feasibility of the proposed parameterization, we exemplify it with some practical use cases for bivariate RLWE; we will consider $n_1=2^{11}=2048$ and $n_2=3^7=2187$, and $d_1=5$, $d_2=7$, for which we prove that they meet the conditions of Proposition 4

• $2^2=4$ does not divide $5^{2047}+1$, or equivalently, $5^{2047}+1\ne 0mod4$. We have $5^{2047}+1mod4=1^{2047}+1=2\ne 0$.
• $3^2=9$ does not divide $7^{3^7-1}+1$, or equivalently, $7^{3^7-1}+1\ne 0mod9$. We have $7^{3^7-1}+1=7^{-1}{7}^{3^7}+1=7^{-1}{7}^{3^{7}mod6}+1=7^2+1=50=5mod9\ne 0$.

Consequently, with this choice of parameters we can work on the number field $K=\mathbb{Q}({(-5)}^{1/2048},{(-7)}^{1/2187})$, with ${\mathcal{O}}_K=\mathbb{Z}[x,y]/(x^{2048}+5,y^{2187}+7)$ and ${\mathcal{O}}_K^{\vee }=\frac{1}{4478976x^{2047}{y}^{2186}}{\mathcal{O}}_K$.

As for the example mentioned in the introduction, with functions $x^{64}+1$ and $y^{27}+5$, we can also verify that

• $x^{64}+1$ is the ${\Phi }_{128}\left(x\right)$ power-of-two cyclomic, hence it is monogenic.
• $y^{27}+5$ is monogenic by Proposition 4, as $3^2=9$ does not divide 5 or $5^{26}+1$.

Additionally, as both discriminants are coprime, the product is directly the corresponding ring of integers.

7. Security of Multivariate RLWE and Example Instantiations

This section includes a discussion on several aspects of the proposed solutions in this work, namely their security, the geometric interpretation of the problem, and the feasibility of the proposed parameterizations. With this purpose, we enumerate the known attacks in the literature and include an example instantiation of a simple bivariate RLWE scheme. We refer to next Sections for a description of the applications enabled by our constructions.

7.1. Resilience against Known Attacks

The formulation proposed in this work involves working with quotient rings whose polynomial ideal is $(x^n+d)$ or, more generally, $(x^n+ax+b)$. Some particular instantiations of these rings have already been studied in the literature and we can find specific attacks to “variants” of the RLWE problem (e.g., PLWE together with non-dual and dual RLWE versions) defined over them.

In general, the known attacks can be divided in two main types [37]:

• Attacks using a reduction modulo an ideal divisor $\mathfrak{q}$ of the modulus $qR$ [56,59,60,61,62,63]. These attacks try to distinguish between the error distribution and the uniform distribution modulo an ideal divisor.
• A reduction to errorless LWE [58] which exploits the relation between RLWE and LWE. Expressing RLWE in its LWE form, the error term of some of the equations can be removed by means of a rounding operation, and linear algebra can be used to search for the secret key.

All these attacks have been generalized and studied in depth by Peikert in [37], where he concludes that all the concrete insecure RLWE instantiations made use of error distributions which were insufficiently well spread relative to the rings, meaning that none of the vulnerable instantiations satisfy the conditions from Theorem 2 to have worst-case hardness. In [37], Peikert also gives sufficient conditions to make RLWE secure against the previous attacks. We summarize the main relevant results for our constructions.

Proposition 5

(Invulnerability condition from [37]). Let $\psi =D_r$ (see Definition 7) be a spherical Gaussian error distribution over $K_{\mathbb{R}}$ for some $r>0$; a sufficient condition for invulnerability to the attacks from [37,56,58,59,60,61,62] is

$$r\ge 2.$$

(10)

The validity of Proposition 5 to resist the previous attacks is shown in the following two theorems: Theorem 9 (for the attack based on reduction modulo an ideal divisor) and Theorem 10 (for the attack based on errorless LWE).

Theorem 9

(Theorem $5.2$ from [37]). Given a Ring-LWE sample $(a,b=s·a+e)\in R_q\times K_{\mathbb{R}}/q{R}^{\vee }$ where $e\leftarrow D_r$ is transformed into n LWE samples $({\mathit{A}}_a,\mathit{b}={\mathit{s}}^T{\mathit{A}}_a+{\mathit{e}}^T)$, where $\mathit{b}\in {(\mathbb{R}/q\mathbb{Z})}^n$ and $\mathit{e}\in {\mathbb{R}}^n$ are respectively the coefficient vectors of $b\in K_{\mathbb{R}}/q{R}^{\vee }$ and $e\in K_{\mathbb{R}}$ (with respect to the chosen basis of $R^{\vee }$), and ${\mathit{A}}_a\in {\mathbb{Z}}_q^{n\times n}$ is the matrix of multiplication by $a\in R_q$ with any element of $R_q^{\vee }$ (with respect to the chosen bases of $R,R^{\vee }$). Then, for any $\mathbb{Z}$-basis $B^{\vee }=\left(b_j^{\vee }\right)$ of $R^{\vee }$ used above, each entry of $\mathit{e}$ is a continuous Gaussian of parameter at least $r\sqrt{n}\ge 2\sqrt{n}$ (which is the required lower bound to apply the worst-case hardness theorems for plain-LWE).

Theorem 10

(Theorem $5.1$ from [37]). Let $\mathfrak{q}\subseteq R$ be any ideal of norm $N\left(\mathfrak{q}\right)\le 2^n$, and let the error parameter $r\ge 2$ satisfy condition (10). Then the reduced error distribution $D_{r}mod\mathfrak{q}{R}^{\vee }$ is within statistical distance $2^{-2n}$ of uniform over $K_{\mathbb{R}}/\mathfrak{q}{R}^{\vee }$.

7.2. Geometric Interpretation and Examples of Multivariate RLWE

In this section, we give a high level overview of how to instantiate a secure multivariate RLWE sample from Definition 11, exemplifying it in the bivariate case (all rings are defined over variables $x,y$, omitted when unambiguous).

This example can also be used as a means to showcase complex numbers packing into slots, obtaining a net improvement on the number of available slots per ciphertext when comparing to the recent results in [39] (see Section 10). For the sake of clarity, we introduce a simple SHE scheme which enables homomorphic additions and multiplications without taking into account some of the more advanced techniques typically considered in the literature.

A Multivariate RLWE Sample

For simplicity, we consider a bivariate RLWE sample $(a,b=a·s+e)\in R_q\times R_q^{\vee }$, where $a\in R_q[x,y]$, $s\in R_q^{\vee }[x,y]$ and $e\leftarrow \chi [x,y]$, with $\chi [x,y]$ generating small-norm random bivariate polynomials in $R^{\vee }[x,y]$. We can use a uniformly random s or follow conventional approaches where s is a small key (see Section 3).

Geometry of R, its dual $R^{\vee }$ and an example for$\{x^2+3,y^2-5\}$:

To easily illustrate the geometry of R and $R^{\vee }$, we use a simple example $R=\mathbb{Z}[x,y]/(x^2+3,y^2-5)$. By means of the canonical embedding, we know that the substitutions $\{x\to \pm \sqrt{-3},y\to \pm \sqrt{5}\}$ yield the four different slots in the embedding domain.

This clearly shows that ${\lambda }_1\left(R\right)\le \sqrt{n}=2$ by the embedding of 1, and we can also obtain the embedding of the elements x, y and $xy$. The term $xy$ can be used to obtain an upper-bound for ${\lambda }_4\left(R\right)$, such that ${\lambda }_4\left(R\right)\le 2\sqrt{15}$.

This is generalizable to any multiquadratic with $l={log}_{2}n$ variables, by considering the embedding of 1 and ${\prod }_{i\in \left[l\right]}{x}_i$, obtaining ${\lambda }_1\left(R\right)\le \sqrt{n}$ and ${\lambda }_n\left(R\right)\le \sqrt{n}{\prod }_{i\in \left[l\right]}\sqrt{d_i}$. As the l-th prime is asymptotically $p_l\sim llogl$, a worst-case for $l={log}_{2}n$ is $d_l^l\sim l^l{(logl)}^l={\left({log}_{2}n\right)}^{{log}_{2}n}{\left({log}_2{log}_{2}n\right)}^{{log}_{2}n}$. Combining the two previous expressions we have that ${\lambda }_n\left(R\right)$ (and hence also the ratio $\frac{{\lambda }_n\left(R\right)}{{\lambda }_1\left(R\right)}$) is polynomially upper-bounded by n.

These bounds are straightforwardly extended to the dual $R^{\vee }$ by taking into account the corresponding “tweak” factor. For the multiquadratic scenario, the dual only suffers a scaling by the square roots of the $d_i$ terms (R is sparser than the dual $R^{\vee }$). However, considering higher degrees in the polynomial functions $x_i^{n_i}+d_i$, the tweak factor can turn the noise in the non-dual version of RLWE into highly non-spherical.

A very detailed analysis of these effects (including also some enlightening visual examples) can be found in [37].

Parameters’ choice:

We show now how to select correct parameters $\{n_x,n_y,d_x,d_y\}$ satisfying the conditions established in Section 5 and Section 6 for valid number fields.

As a brief summary, and focusing on $n_x,n_y>2$, this mainly implies that: (1) the discriminants of $K_x=\mathbb{Q}\left[x\right]/(x^{n_x}+d_x)$ and $K_y=\mathbb{Q}\left[y\right]/(y^{n_y}+d_y)$ are coprime, i.e., $gcd({\Delta }_{K_x},{\Delta }_{K_y})=1$, and (2) $n_x,n_y$ are prime powers satisfying Proposition 4.

This enables the definition of ${\mathcal{O}}_K=R=\mathbb{Z}[x,y]/(x^{n_x}+d_x,y^{n_y}+d_y)$ as the ring of integers. Analogously, the dual is ${\mathcal{O}}_K^{\vee }=\frac{1}{n_x{n}_y{x}^{n_x-1}{y}^{n_y-1}}\mathbb{Z}[x,y]/(x^{n_x}+d_x,y^{n_y}+d_y)$ (see Section 6 for some particular choices).

In this bivariate case, the error distribution $\chi [x,y]$ samples polynomials in ${\mathcal{O}}_K^{\vee }$ whose coefficients are independently sampled from Gaussian distributions with different standard deviations. In particular, $\sigma$ is equal to $r\sqrt{n}{d}_x^{\frac{n_x-j_x}{n_x}}{d}_y^{\frac{n_y-j_y}{n_y}}/\sqrt{2\pi }$ for the coefficient associated to the monomial $x^{j_x-1}{y}^{j_y-1}$ with $1\le j_x\le n_x$ and $1\le j_y\le n_y$.

Working on$q{\mathcal{O}}_K$:

As it is usually done with power-of-two cyclotomics, we can directly transform the dual into the ring of integers by means of a scaling. If we have ${\mathcal{O}}_K^{\vee }=\frac{1}{n_x{n}_y{x}^{n_x-1}{y}^{n_y-1}}\mathbb{Z}[x,y]/(x^{n_x}+d_x,y^{n_y}+d_y)$, we can first multiply the dual by $\frac{xy}{xy}$, to see the simplified relation $\frac{xy}{xy}{\mathcal{O}}_K^{\vee }=\frac{xy}{n{d}_x{d}_y}{\mathcal{O}}_K$.

Finally, analogously to the $x^n+1$ functions, we can scale the $(a,b)$ sample by $n=n_x{n}_y$ and also $d_x{d}_y$. This gives us a sample $(a(x,y),b^{\prime }(x,y)=n{d}_x{d}_{y}xy·b(x,y))\in R_q^2$. Consequently, we can directly work on the ring of integers with $(a,b=as+e)\in R_q^2$ where $a\leftarrow R_q$, $s\leftarrow R_q$ (or also $s\leftarrow \chi [x,y]$) and $e\leftarrow \chi [x,y]$. After the multiplication with the monomial $xy$, the error distribution $\chi [x,y]$ generates independent coefficients from a Gaussian distribution of $\sigma =r\sqrt{n}{d}_x^{\frac{n_x-j_x}{n_x}}{d}_y^{\frac{n_y-j_y}{n_y}}/\sqrt{2\pi }$ for $1<j_x\le n_x$ and $1<j_y\le n_y$, $\sigma =r\sqrt{n}{d}_x^{\frac{2n_x-j_x}{n_x}}{d}_y^{\frac{n_y-j_y}{n_y}}/\sqrt{2\pi }$ for $j_x=1$ and $1<j_y\le n_y$, $\sigma =r\sqrt{n}{d}_x^{\frac{n_x-j_x}{n_x}}{d}_y^{\frac{2n_y-j_y}{n_y}}/\sqrt{2\pi }$ for $1<j_x\le n_x$ and $j_y=1$ while $\sigma =r\sqrt{n}{d}_x^{\frac{2n_x-1}{n_x}}{d}_y^{\frac{2n_y-1}{n_y}}/\sqrt{2\pi }$ for $j_x=j_y=1$.

SHE over Multivariate Rings:

The basic example cryptosystem described in

Table 3. Parameters and primitives of a somewhat homomorphic cryptosystem based on a multivariate version of RLWE (see [8,10]).

Parameters
Let $R_t[x,y]$ be the cleartext ring and $R_q[x,y]$ the ciphertext ring. The noise distribution $\chi [x,y]$ in $R_q[x,y]$ takes its coefficients from a multivariate truncated Gaussian $\mathcal{N}(\mathbf{0},r^2{\mathit{J}}^2)$. q is an integer satisfying $t<q$ and is relatively prime to t. All the previous parameters are chosen in terms of the security parameter $\lambda$ where $n=2^{\lfloor log\lambda \rceil -1}$
Example SHE Cryptographic Primitives
$\mathsf{SH}.\mathsf{KeyGen}$	Process	$s,e\leftarrow \chi [x,y]$, $a_1\leftarrow R_q[x,y]$; $sk=s$ and $pk=(a_0=-(a_{1}s+te),a_1)$
$\mathsf{SH}.\mathsf{Enc}$	Input	$pk=(a_0,a_1)$ and $m\in R_t[x,y]$
	Process	$u,f,g\leftarrow \chi [x,y]$ and the fresh ciphertext is $\mathit{c}=(c_0,c_1)=(a_{0}u+tg+m,a_{1}u+tf)$
$\mathsf{SH}.\mathsf{Dec}$	Input	$sk$ and $\mathit{c}=(c_0,c_1,\cdots ,c_{\gamma -1})$
	Process	$m=\left(\left({\sum }_{i=0}^{\gamma -1}{c}_i{s}^i\right)modq\right)modt$
$\mathsf{SH}.\mathsf{Add}$	Input	$\mathit{c}=(c_0,\cdots ,c_{\beta -1})$ and ${\mathit{c}}^{\prime }=(c_0^{\prime },\cdots ,c_{\gamma -1}^{\prime })$
	Process	${\mathit{c}}_{add}=(c_0+c_0^{\prime },\cdots ,c_{max(\beta ,\gamma )-1}+c_{max(\beta ,\gamma )-1}^{\prime })$
$\mathsf{SH}.\mathsf{Mult}$	Input	$\mathit{c}=(c_0,\cdots ,c_{\beta -1})$ and ${\mathit{c}}^{\prime }=(c_0^{\prime },\cdots ,c_{\gamma -1}^{\prime })$
	Process	Using a symbolic variable v their product ${\mathit{c}}^{\prime \prime }$ can be obtained from the relation $\left({\sum }_{i=0}^{\beta -1}{c}_i{v}^i\right)·\left({\sum }_{i=0}^{\gamma -1}{c}_i^{\prime }{v}^i\right)={\sum }_{i=0}^{\beta +\gamma -2}{c}_i^{\prime \prime }{v}^i$

follows the structure of the SHE version introduced in [64] and implemented in [65]. The main difference relies on the fact that our polynomial elements belong to the multivariate rings $R[x,y]$, $R_t[x,y]$ and $R_q[x,y]$ (see Definition 11), contrarily to the traditional univariate version $\mathbb{Z}\left[x\right]/(1+x^n)$ and its analogous rings modulo t and q. In Table 3 the diagonal of $\mathit{J}$ has the corresponding standard deviations of $\chi$ normalized by r (i.e., $\sigma /r$) for each coefficient of the bivariate polynomials.

In particular, our plaintext ring $R_t$ is basically a bivariate polynomial $R_t[x,y]={\mathbb{Z}}_t[x,y]/(x^{n_x}+d_x,y^{n_y}+d_y)$ which is encoded as a sub-module of $\mathbb{T}=K_{\mathbb{R}}/R^{\vee }$ (see Definition 7). Our example is based on the scheme introduced in [64], but other choices are possible. Regarding the achieved noise bounds, they are analogous to the computations from [64] by taking into account the expansion factor of the involved rings.

The additional variables of the multivariate structure can bring about some significant advantages: more efficient polynomial operations (see Section 8), better space/efficiency tradeoffs when working with automorphisms (see Section 9), and can also be very useful when working with multidimensional structures (see the works [8,10,39] for more details on practical applications). In particular, in [39,40] the authors present a library called MHEAAN, based on multivariate RLWE, which is optimized to perform homomorphic matrix operations.

Correctness and Security:

The condition for correct decryption is that the effective noise ${\left|\right|\left({\sum }_{i=0}^{\gamma -1}{c}_i{s}^i\right)modq\left)\right||}_{\infty }$ remains smaller than $q/2$. Let us consider a simplified version of Theorem 2 from [64] where only the effect of noise is taken into account, and let $max\left\{\sigma \right\}$ be the maximum standard deviation of the polynomials sampled from $\chi [x,y]$. Let M be the maximum coefficient of the evaluated degree-D polynomial; if $M{(tmax\left\{\sigma \right\}{d}_x{d}_{y}n\sqrt{n})}^D$ is smaller than $q/2$, the scheme of Table 3 can evaluate degree-D multivariate polynomials over elements which belong to $R_t[x,y]$. We could also consider a more tight empirical condition for q, as stated in [65].

Regarding the security of this SHE scheme, it relies on the indistiguishability assumption of the polynomial multivariate version of RLWE (with adequately chosen secure parameters $\chi [x,y]$, $\{n_x,d_x,n_y,d_y\}$ and q) featured in Definition 11; breaking this assumption implies, as stated in Theorem 2, the existence of a quantum algorithm which solves short vector problems over ideal lattices. For a practical estimation of the bit security, we can apply the LWE security estimator developed by Albrecht et al. [66,67] to the cryptosystems built on multivariate RLWE and also the estimates included in the standards document [68] for a general random lattice with the same dimension ($n=\prod n_i$). This is plausible, analogously to what it is typically done with ideal lattices, as a secure instantiation of m-RLWE works with full-rank lattices, for which no substantially faster attacks are known than for general lattices.

8. Multiquadratic Rings with Fast Walsh–Hadamard Transforms

Copyright of Section 8 by IEEE: ©2021 IEEE. Reprinted, with permission, from Section 3 and Section 4 of the conference paper: “Multiquadratic Rings and Walsh–Hadamard Transforms for Oblivious Linear Function Evaluation”, 2020 IEEE International Workshop on Information Forensics and Security (WIFS). This section focuses on improving the cost of the underlying polynomial operations for cryptographic primitives based on RLWE, especially polynomial products (convolutions) [43]. We show how the well-known asymptotic cost of $\mathcal{O}(nlogn)$ for cyclotomic rings with polynomials of n coefficients can be improved by a factor of $logn$ in terms of elemental multiplications when working on m-RLWE (or RLWE over a multivariate number field). To this aim, we particularize the multivariate version to degree-2 polynomials and introduce an ($\mathit{\alpha }$-generalized) variant of the Walsh–Hadamard Transform (over finite rings instead of the usual real numbers), featuring a convolution property that relates the coefficient-wise representation with the transformed domain. This transform can be very efficiently computed with FFT algorithms (specifically, with a variant of the Fast Walsh–Hadamard Transform) whose computational cost is only $\mathcal{O}(nlogn)$ additions, hence being much more amenable for a practical implementation. It is worth noting that the effect of the efficiency improvement brought about by our approach goes beyond somewhat homomorphic encryption schemes (including also the NTRU setting [69,70]), also enhancing any cryptographic primitives involving polynomial multiplications, e.g., the candidates of the NIST Post-Quantum challenge [67]. We also exemplify in [43] its use for the efficient implementation of Oblivious Linear Function evaluation.

For this section, we deal with a specific version of m-RLWE where all the used polynomial functions have the same form $f_i\left(x_i\right)=d_i+x_i^2$ (see Definition 9).

The security reduction from Theorem 2 applies to this particular version of the m-RLWE problem. To this aim, parameteres $d_i$ have to be chosen as indicated in the beginning of Section 5. Additionally, Proposition 5 gives a sufficient condition to make the problem secure against the attacks described in Section 7.1.

We introduce next the ($\mathit{\alpha }$-generalized) Hadamard transform, that we apply to reach the aforementioned performance gains on polynomial convolutions.

Faster Polynomial Arithmetic over Multivariate Rings

The Hadamard transform over real numbers is usually applied by means of the recursion

$${\mathit{H}}_i=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}{\mathit{H}}_{i-1}& {\mathit{H}}_{i-1}\\ {\mathit{H}}_{i-1}& -{\mathit{H}}_{i-1}\end{array}\right),$$

(11)

where $i\in \mathbb{N}$ and ${\mathit{H}}_0=1$.

It can be seen that the matrix ${\mathit{H}}_i$ with $i\ge 1$ is equivalent to the Kronecker product of i Discrete Fourier Transform (DFT) matrices of size 2 (${\mathit{H}}_1$ equals the DFT matrix of size 2); that is, it can be seen as a $\underset{itimes}{\underbrace{2\times 2\times \cdots \times 2}}$-DFT transform (defined over i dimensions of length 2 each).

Analogously to the DFT, the Walsh–Hadamard Transform (WHT) of size n possesses a particular fast algorithm called Fast Walsh–Hadamard Transform (FWHT) which can be very efficiently computed with no products and with a cost of $\mathcal{O}(nlogn)$ additions and subtractions (see [71,72]). Hence, when working over rings satisfying a convolution property with the Hadamard transform, it is possible to efficiently compute the multiplication of elements from these rings with a cost of $\mathcal{O}\left(n\right)$ elemental multiplications.

Security reasons prevent us from directly working over rings satisfying this convolution property with the Walsh–Hadamard transform (that is, multivariate quotient rings whose polynomial functions are $f\left(x_i\right)=x_i^2-1$), as they can be easily factored into $(x_i-1)(x_i+1)$ over $\mathbb{Z}$. Therefore, we resort to the type of multivariate rings presented in Definition 9 and apply an ($\mathit{\alpha }$-generalized) variant of the WHT.

$\alpha$-generalized convolutions:

An $\alpha$-generalized convolution corresponds to the ring operation defined over polynomials belonging to ${\mathbb{Z}}_q\left[z\right]/(1-\alpha z^n)$. For example, with $\alpha =-1$ we have a negacyclic convolution. In the literature, this convolution operation is also called negative wrapped convolution. Figure 1 shows the realization of an $\alpha$-generalized convolution between vectors of length N (with $l=0,\dots ,N-1$), by means of a cyclic convolution combined with an element-wise pre/post-processing applied before/after [7,36].

As the cyclic convolution can be efficiently computed by means of standard fast algorithms, this means that an $\alpha$-generalized convolution can be implemented with only a light overhead ($\mathcal{O}\left(n\right)$ scalar products). It is common to include these additional scalar products inside the butterflies of the FFT algorithms to further enhance the efficiency.

$\mathit{\alpha }$-generalized Walsh–Hadamard transform:

We are mainly interested in polynomial functions with the form $x_i^2+d_i$. We can rewrite $1-\alpha x^n$ as $-\alpha \left({(-\alpha )}^{-1}+x^n\right)$. Hence for $x_i^2+d_i$ we have $d_i={(-{\alpha }_i)}^{-1}=-{\alpha }_i^{-1}$. For this particular type of polynomial rings we can define the following direct and inverse transforms:

$${\mathit{W}}_1={\mathit{H}}_1\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_1\right)}^{-1/2}\end{array}\right),\mathrm{and}{\mathit{W}}_1^{-1}=2^{-1}\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_1\right)}^{1/2}\end{array}\right){\mathit{H}}_1,$$

where the square-roots ${\left({\alpha }_i\right)}^{\frac{1}{2}}$ and ${\left({\alpha }_i\right)}^{\frac{-1}{2}}$ have to exist in $R_q$ for all i (see Definition 9). Equivalently, if q is an odd prime, we can make use of the Legendre symbol $\left(\frac{-dmodp}{p}\right)$ to check when the multivariate ring factors into linear terms. To this aim we need that $\left(\frac{-d_{i}modq}{q}\right)=1$ for a prime q and for all i. We also redefine ${\mathit{H}}_1=\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$ without taking into account the normalizing factor $\frac{1}{2}$.

Therefore, now we can extend this definition to multivariate quotient rings with polynomial ideals of the form $(x_i^2+d_i)$: we consider the Kronecker product of the matrices ${\mathit{W}}_1$ and ${\mathit{W}}_1^{-1}$ as ${\mathit{W}}_i={⨂}_{j\in \left[i\right]}{\mathit{W}}_1$ and ${\mathit{W}}_i^{-1}={⨂}_{j\in \left[i\right]}{\mathit{W}}_1^{-1}$, arriving to the following expression:

$${\mathit{W}}_i={\mathit{H}}_i\left(\underset{j\in \left[i\right]}{⨂}\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_j\right)}^{-1/2}\end{array}\right)\right),\mathrm{and}{\mathit{W}}_i^{-1}=2^{-i}\left(\underset{j\in \left[i\right]}{⨂}\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_j\right)}^{1/2}\end{array}\right)\right){\mathit{H}}_i,$$

where the normalizing factors are again left outside ${\mathit{H}}_i$.

Consequently, if we define the vector $\mathit{\alpha }={\left({\alpha }_1,\dots ,{\alpha }_l\right)}^T$, when working over the multivariate ring $R_q[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=d_j+x_j^2$ for $j=1,\dots ,l$ we can use the transforms ${\mathit{W}}_l$ and ${\mathit{W}}_l^{-1}$ analogously to the use of negacyclic NTTs in the univariate RLWE. Both ${\mathit{W}}_l$ and ${\mathit{W}}_l^{-1}$ transforms can be efficiently computed in $\mathcal{O}\left(n\right)$ (where $n=2^l$) elemental multiplications thanks to the FWHT. This enables the computation of the ${\mathit{H}}_l$ matrix multiplications with only $\mathcal{O}(nlogn)$ additions and subtractions and no products, which brings a net improvement with respect to the analogous and wide-spread radix implementation of the NTT.

Implementation of the Fast Walsh–Hadamard Transform (FWHT):

Algorithm 1 shows a pseudocode implementation of the (cyclic) Fast Walsh–Hadamard Transform (FWHT) implementation (see [71,72]), computing the Hadamard transform of a length-n vector $\mathit{a}$. It can be easily seen that this algorithm requires a total of $n{log}_{2}n$ additions (specifically, $\frac{n{log}_{2}n}{2}$ additions and $\frac{n{log}_{2}n}{2}$ subtractions), instead of the $n^2$ additions/subtractions required when directly applying the matrix multiplication.

Algorithm 1  Fast Walsh–Hadamard Transform (${\mathit{H}}_i\mathit{a}$ with $i\ge 1$).

1: procedureFastWalsh–HadamardTransform($\mathit{a}$) 2: Input: 3:     $\mathit{a}$ such that $\mathtt{length}\left(\mathit{a}\right)=n=2^i$ and $i\ge 1$ 4: Algorithm for $\mathtt{FWHT}\left(\mathit{a}\right)$ (computing ${\mathit{H}}_i\mathit{a}$): 5:     $\mathtt{depth}=1$; 6:     for $j=0$ until ${log}_{2}n-1$ do 7:         $\mathtt{scale}=2\ast \mathtt{depth}$; 8:         for $k=0$ until $⌊\frac{\mathtt{length}\left(\mathit{a}\right)-1}{\mathtt{scale}}⌋$ do 9:            for $l=\mathtt{scale}\ast k$ until $\mathtt{scale}\ast k+\mathtt{depth}-1$ do 10:                $\mathtt{ac}=\mathit{a}\left[l\right]$; 11:                $\mathit{a}\left[l\right]=\mathit{a}\left[l\right]+\mathit{a}[l+\mathtt{depth}]$; 12:                $\mathit{a}[l+\mathtt{depth}]=\mathtt{ac}-\mathit{a}[l+\mathtt{depth}]$; 13:         $\mathtt{depth}=2\ast \mathtt{depth}$; 14: Output: 15:     $\mathit{a}\leftarrow {\mathit{H}}_i\mathit{a}$

Finally, the $\mathit{\alpha }$-generalized version of the direct (inverse) FWHT can be defined by adding a right (left) product by a diagonal matrix, so that the total cost for the $\mathit{\alpha }$-generalized FWHT on a length-n vector is n elemental multiplications and $n{log}_{2}n$ additions.

Implementation and evaluation:

Polynomial multiplications are the main bottleneck of lattice cryptography, as they are the most time-consuming basic blocks of any cryptographic algorithm, from encryption/decryption to relinearization and bootstrapping. The replacement of the traditional NTTs by FWHT by transitioning from cryptographic constructions built on univariate RLWE to the proposed multivariate version can bring a considerable improvement in terms of computational efficiency. To showcase the achieved gains, we have implemented Algorithm 1 in C++ and compared it with one of the currently most efficient radix-2 implementations of the NTT [6]; this is the algorithm featured in the NFLlib, one of the fastest lattice-based cryptographic libraries available for homomorphic encryption. NFL also off-loads the complexity of the bit-reversal operation to the INTT, in order to speed up the NTT, and makes use of SSE and AVX2 optimizations to further enhance the obtained performance. Figure 2 shows the comparison of the obtained run times for a wide range of practical values of n (vector size or polynomial degree), when using our FWHT implementations, including an SSE/AVX2 vectorized version. It can be seen that we obtain a reduction to about 45–50% of the time of the NTT (38–43% of the INTT) in the non-vectorized implementation of the FWHT with respect to the fast NTT of NFLlib, while the vectorized one further reduces this figure to 22–24% (19–22% of the INTT). Finally, it is worth noting that the memory consumption of the FWHT is much lower, as it does not need to store the tables of the twiddle factors.

9. Slot Manipulation in Multivariate Rings

In this section we introduce the main improvements that m-RLWE brings to slot manipulation when packing several plaintext inputs into a ciphertext, with applications in relinearization and bootstrapping operations. Packing into slots [73] helps to take advantage of the available space in the plaintext ring, therefore improving cipher expansion. The use of this packing strategy also enables working with homomorphic “slot”-wise additions and multiplications, i.e., Single Instruction, Multiple Data (SIMD) operations with encrypted data.

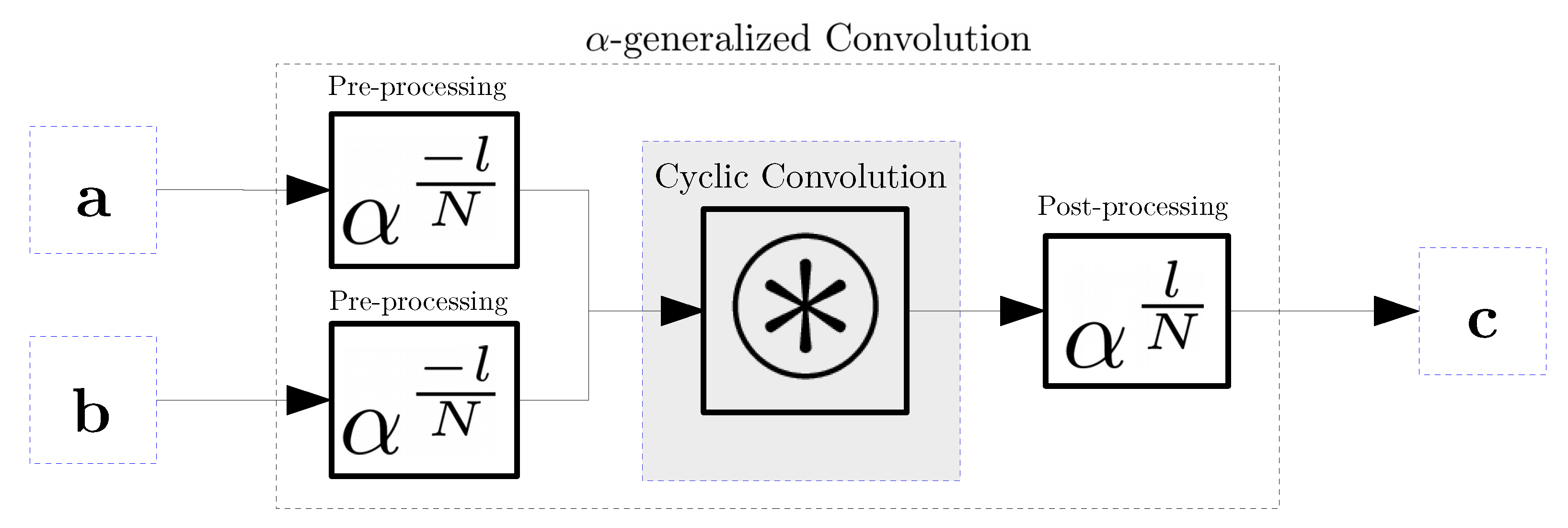
This is usually combined with a mechanism to efficiently move and exchange the plaintext contents across slots, by taking advantage of the properties of the available automorphisms in the used ring. In general, in the ring $R_t={\mathbb{Z}}_t\left[z\right]/\left({\Phi }_m\left(z\right)\right)$, we can define a set of automorphisms $\varphi \left(m\right)$ as different transformations ${\rho }_i:R_t\to R_t$ with $i\in {\mathbb{Z}}_m^{*}$, which apply a change of variable $z\to z^i$ over the elements in $R_t$.

Current lattice-based homomorphic cryptosystems leverage automorphisms to perform linear transformations across plaintext slots. Whereas applying an automorphism is a very efficient operation, it produces a ciphertext encrypted under a different secret key, and consequently, a switching key operation is needed to recover a ciphertext under the original secret key. This switching key process has two main drawbacks [74]: (a) a notable computational overhead and (b) an increase in the memory requirements due to the need of adding additional public information (“switching key/relinearization” matrices, a.k.a. evaluation keys).

In general, there is a tradeoff between these two dimensions: when the number of evaluation keys increases, the involved switching key runtime decreases, and conversely, when the number of keys is reduced, a chain of several switching key operations is needed, hence increasing the runtime. In a recent work [74], Halevi and Shoup explore several strategies to optimize this tradeoff, claiming improvements of even 75 times faster runtimes than those of their previous implementation, together with a reduction of up to a half in the required memory space to store the evaluation keys.

This section focuses on two different aspects: (1) We show how the introduced multivariate rings over the RLWE problem (see Section 5 and Section 6) enable considerable improvements in the efficiency of the homomorphic packing/unpacking into slots, therefore greatly improving essential blocks for homomorphic encryption, such as bootstrapping, and (2) we analyze the structure of the available set of automorphisms on these rings, also showing that our solution can improve on both the runtime and the memory requirements with respect to the state of the art [74].

It is worth highlighting that some of the exemplified solutions in this section are sketched out with negacyclic rings. For completeness, in Section 9.4 we give some insights on how to extend these results to the more general multivariate rings showcased in this manuscript.

9.1. Efficient Slot Packing/Unpacking

The homomorphic packing/unpacking of plaintext values into slots is one of the most important examples of the evaluation of linear transformations on the ciphertexts, bootstrapping being one of the most representative applications [14,15,16]. The way current cryptosystems implement this packing/unpacking is by means of a decomposition of the matrix multiplication into element-wise products between the different diagonals of the matrix and different rotated versions of the ciphertext (hence by adding the result of a set of multiplications between plaintexts and rotated ciphertexts).

The main bottleneck of this process is the number of switching key matrices required to rotate the ciphertexts. Working with n slots, a total of $n-1$ rotations, hence $n-1$ switching key matrices, is required in the worst case. Available strategies to reduce this number of matrices come at the cost of also increasing the runtimes per automorphism/switching key operation.

To the best of our knowledge, the best strategy for homomorphic packing/unpacking is presented in [75] for the HEAAN cryptosystem. Their method, with an input of n slots and parameterized by a radix r, requires $\mathcal{O}\left(r{log}_{r}n\right)$ constant vector multiplications, $\mathcal{O}\left(\sqrt{r}{log}_{r}n\right)$ rotations and a depth of $\mathcal{O}\left({log}_{r}n\right)$.

Thanks to the introduced multiquadratic RLWE with $l={log}_{2}n$ independent variables, we can also break the need of a number of rotations (automorphisms/switching key operations) equal to the number of slots, and we enable homomorphically packing/unpacking operations with a single switching key operation per independent ring variable.

Homomorphic Packing/Unpacking:

Considering a multiquadratic plaintext ring $R_t[x_1,\dots ,x_l]$ (see Definition 11), we arrive to the following packing/unpacking matrices:

$${\mathit{V}}_l=2^{-l}\left(\underset{j\in \left[l\right]}{⨂}\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_j\right)}^{1/2}\end{array}\right)\right){\mathit{H}}_l,\mathrm{and}{\mathit{V}}_l^{-1}={\mathit{H}}_l\left(\underset{j\in \left[l\right]}{⨂}\left(\begin{array}{cc}1& 0\\ 0& {\left({\alpha }_j\right)}^{-1/2}\end{array}\right)\right).$$

These matrices are similar to the ones introduced in Section 8, but now having

$${\mathit{V}}_l=2^{-l}{\mathit{W}}_l^{-1}\mathrm{and} {\mathit{V}}_l^{-1}={\mathit{W}}_l,$$

and being defined over the plaintext ring, so satisfying ${\alpha }_j=-d_{j}modt$ for $j\in \left[l\right]$.

Both packing and unpacking matrices can be decomposed on a matrix of size $2\times 2$ over each independent variable. Additionally, these matrices can be very efficiently computed on a quadratic ring.

Consider, without loss of generality, that we have

$$a(x_1,\dots ,x_l)=a_0(x_1,\dots ,x_{l-1})+x_l{a}_1(x_1,\dots ,x_{l-1})mod{x}_l^2+d_l.$$

By applying now the automorphism $x_l\leftarrow -x_l$, we can efficiently extract both $a_0$ and $a_1$ by computing $a(x_1,\dots ,x_l)+a(x_1,\dots ,-x_l)$, and $a(x_1,\dots ,x_l)-a(x_1,\dots ,-x_l)$.

Once we have extracted $a_0$ and $a_1$, the multiplication with the $2\times 2$ matrix can computed. This process can be recursively applied for each independent variable.

Hence, our proposed method enables homomorphic packing/unpacking on an input of n slots which requires ${log}_{2}n$ rotations and depth ${log}_{2}n$, but now working for BFV-type cryptosytems [76].

Homomorphic Walsh–Hadamard Transform

Consider again a multiquadratic plaintext ring $R_t[x_1,\dots ,x_l]$: by applying the packing method (packed-RLWE) described in [12], we can emulate over a ciphertext composed of multiquadratic rings, a ring homomorphism with a cyclic Walsh–Hadamard ring (i.e., a ring with 1-generalized Walsh–Hadamard transforms, see Section 8).

Then the required matrices for packing and unpacking are respectively:

$${\mathit{V}}_l=2^{-l}{\mathit{H}}_l\mathrm{and} {\mathit{V}}_l^{-1}={\mathit{H}}_l.$$

${\mathit{H}}_l$ evaluation:

It can be seen that the ${\mathit{H}}_l$ matrix can be homomorphically evaluated by means of recursively applying a shift and an automorphism for each independent variable. That is, if we have encrypted a polynomial $a\in R_t[x_1,\dots ,x_i]$, we would do:

$$\tilde{a}(x_1,\dots ,x_l)=\sum _{i\in \left[l\right]}{x}_{i}a(x_1,\dots ,x_i,\dots ,x_l)+a(x_1,\dots ,-x_i,\dots ,x_l).$$

The above operations can be homomorphically evaluated by means of one shift, one automorphism and two additions per independent variable.

9.2. Automorphisms in Multiquadratic Rings and Their Hypercube Structure

We show now how m-RLWE improves on the tradeoffs between space and computational cost when dealing with automorphisms, with respect to the univariate version.

Let $\mathbb{A}\left[z\right]/(1+z^2)$ be a polynomial ring as the one described by Definition 9, and $\alpha$ be an element $\alpha \in \mathbb{A}\left[z\right]/(1+z^2)$; then, we denote by ${\theta }_i^{\left(z\right)}\left(\alpha \right)\in \mathbb{A}\left[z\right]/(1+z^2)$ the transformation over $\alpha$ which applies the change of variable $z\to z^i$ with $i\in {\mathbb{Z}}_4^{*}$. For these particular rings, both transformations are, respectively, the identity $z\to z$ and the negation $z\to -z$. 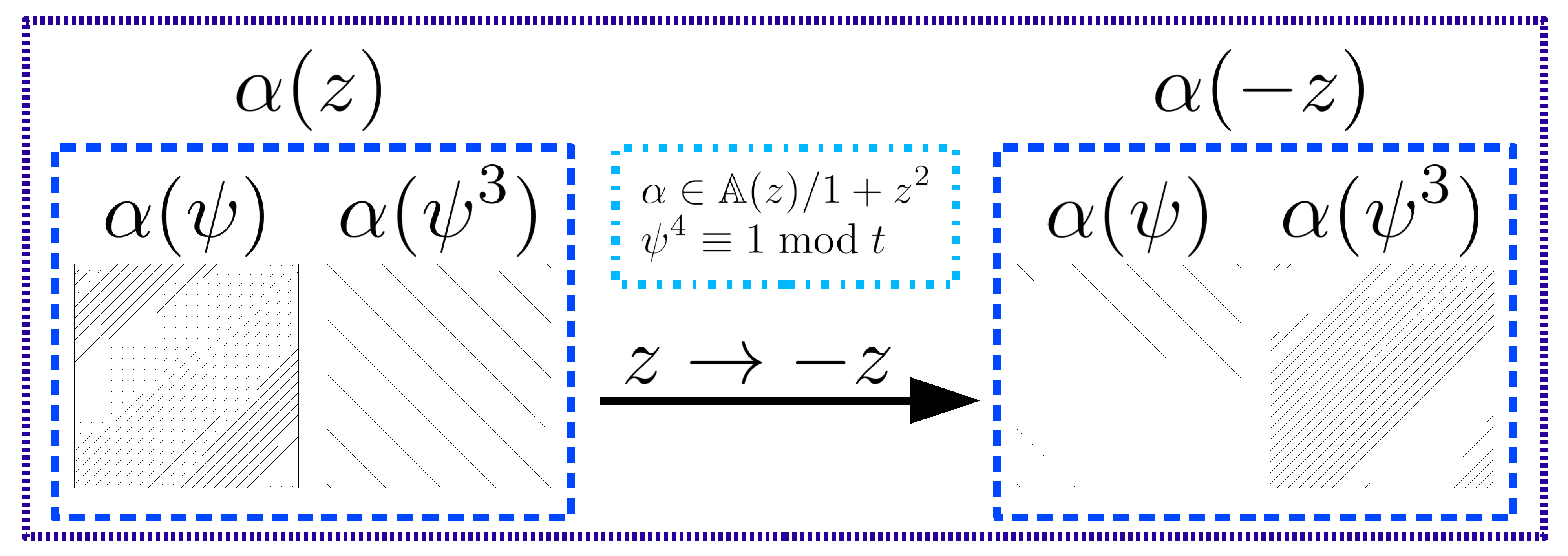Reducing modulo t (the modulo of the plaintext ring), the effect of the latter transformation over the slots would be equivalent to a block shift where each block is composed by one half of the total slots. This shift is graphically illustrated in Figure 3 (also briefly described in

Table 4. Rotation between two blocks of slots (description of Figure 3).

To fix ideas, and without loss of generality, in Figure 3 we represent a plaintext $\alpha$ as an element $\alpha \in \mathbb{A}\left[z\right]/(1+z^2)$, where $\mathbb{A}$ does not depend on z. By reducing modulo t, and by having a 4-th root of unity $\psi$, the polynomial $\alpha \left(z\right)={\alpha }_0+{\alpha }_{1}zmod1+z^2$ can encode a vector with two different block slots $(\underset{{\mathrm{slot}}_0}{\underbrace{\alpha \left(\psi \right)}},\underset{{\mathrm{slot}}_1}{\underbrace{\alpha (-\psi )}})\in {\mathbb{A}}^2$. The concrete structure of these blocks depends on the ring structure of $\mathbb{A}$ modulo t.

Figure 3 showcases the effect of applying the transformation $z\to -z$ under $\alpha \left(z\right)$, i.e., we obtain a new polynomial $\tilde{\alpha }\left(z\right)={\alpha }_0-{\alpha }_{1}zmod1+z^2$. As a result of this automorphism, the polynomial $\tilde{\alpha }\left(z\right)$ now encodes a rotated vector of the original block slots $(\tilde{\alpha }\left(\psi \right),\tilde{\alpha }(-\psi ))=({\mathsf{slot}}_1,{\mathsf{slot}}_0)\in {\mathbb{A}}^2$.

), where $\psi$ is the 4th root of unity modulo t (i.e., ${\psi }^4\equiv 1modt$), and the two blocks of slots encoded respectively in $\alpha \left(\psi \right)$ and $\alpha \left({\psi }^3\right)$ get shifted by applying $z\to -z$. With rings $\mathbb{A}\left[z\right]/(d+z^2)$ we have similar automorphisms $\{z\to z\}$ and $\{z\to -z\}$.

Going back to the notation $R_t[x_1,\dots ,x_l]$ with $f_j\left(x_j\right)=1+x_j^2$ for our ring, we can then apply combinations of these two transformations with the different variables $x_j$ for $j\in \left[l\right]$. Analogously to [74], this gives a multidimensional structure on the automorphisms group considering the composition of transformations

$${\theta }_{i_1,\dots ,i_l}\left(\alpha \right)={\theta }_{i_1}^{\left(x_1\right)}\left({\theta }_{i_2}^{\left(x_2\right)}(\dots {\theta }_{i_l}^{\left(x_l\right)}\left(\alpha \right)\dots )\right)\in R_t[x_1,\dots ,x_l],$$

where $\alpha \in R_t[x_1,\dots ,x_l]$, $t\equiv 1mod4$ and $i_1,\dots ,i_l\in {\mathbb{Z}}_4^{*}$.

This multidimensional structure of the automorphisms group can be seen as an l-tuple with two different values per component (which gives a total of $2^l$ different automorphisms). Hence, similarly to the shift property of a multidimensional DFT [77], this group satisfies both the abelian and sharply transitive properties required to perform any type of permutation [78].

Logarithmic Increase in Space and Computational Cost (Strategy 1):

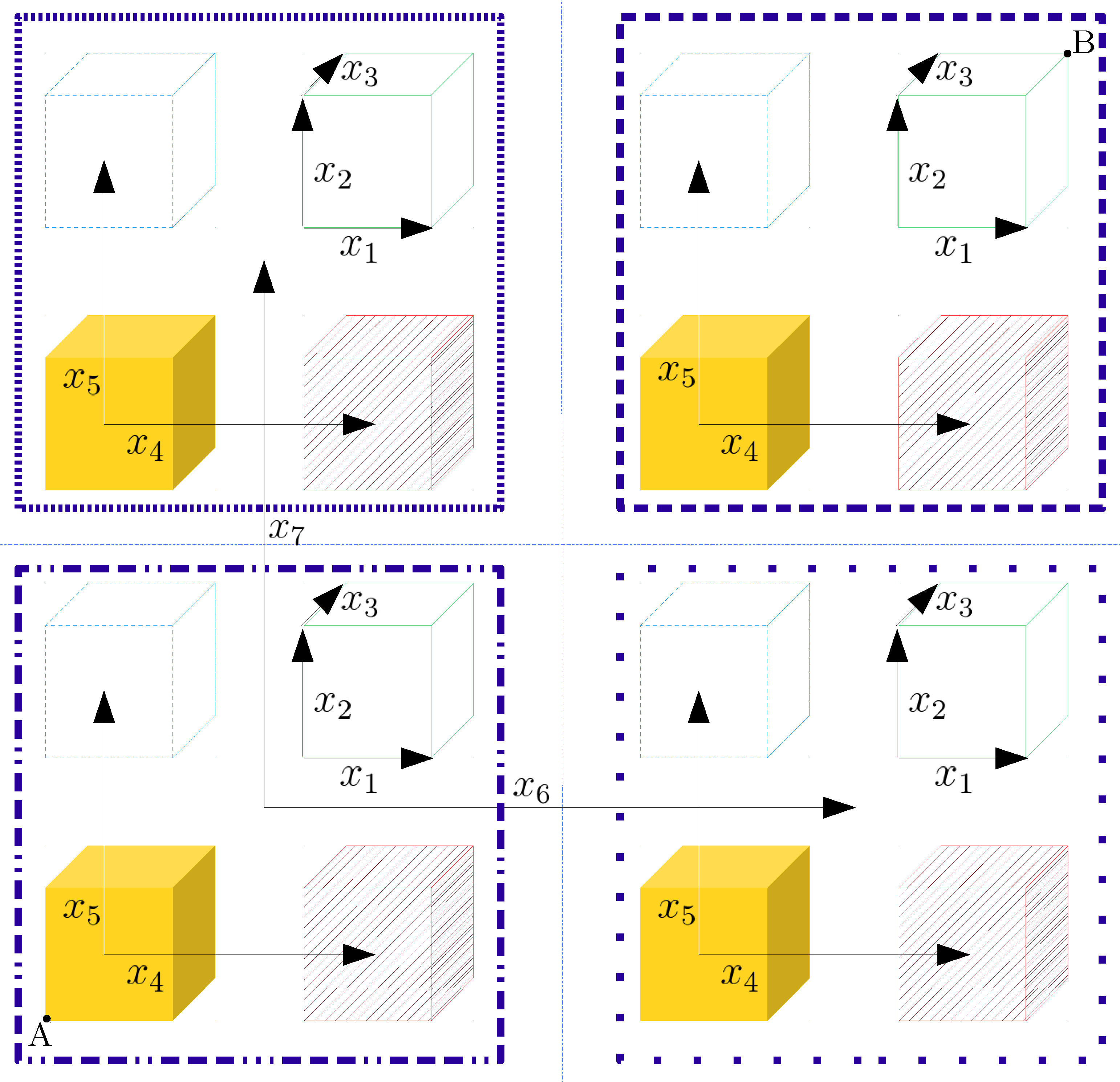
The effect of each of the automorphisms over the slots can be visually represented as a hypercube with as many dimensions as independent variables the rings have, that is, with a total of ${log}_{2}n$ dimensions. As a graphical example, Figure 4 shows the slot structure corresponding to a multivariate ring with seven independent variables; in this case, each different vertex of the hypercube represents one of the $n=128$ available slots, where the allowed transitions between vertices depend on the chosen strategy, as we describe next (see also

Table 5. Hypercube structure of the group of automorphisms (description of Figure 4).

Figure 4 particularizes the block structure of Figure 3 to the case on which $\mathbb{A}={\mathbb{Z}}_t[x_1,\dots ,x_6]/(1+x_1^2,\dots ,1+x_6^2)$. By also considering $z=x_7$, we finally have $\mathbb{B}={\mathbb{Z}}_t[x_1,\dots ,x_7]/(1+x_1^2,\dots ,1+x_7^2)$.

An element $\alpha \in \mathbb{B}$ can encode a vector with 128 slots such as $({\mathsf{slot}}_0,\dots ,{\mathsf{slot}}_{127})\in {\mathbb{Z}}_t^{128}$, where the existing automorphisms correspond to the transformations $x_i\to -x_i$. Figure 4 exemplifies the effect of these rotations by representing the positions of the vector $({\mathrm{slot}}_0,\dots ,{\mathrm{slot}}_{127})$ as the existing vertices in a hypercube of dimension 7. The transformation $x_i\to -x_i$ corresponds to a translation vector between two different vertex locations.

For example, in order to move ${\mathsf{slot}}_{\mathrm{A}}$ (point A) in $\alpha$ to the position of ${\mathsf{slot}}_{\mathrm{B}}$ (point B), all the transformations $x_1\to -x_1$, $x_2\to -x_2$, $x_3\to -x_3$, $x_4\to -x_4$, $x_5\to -x_5$, $x_6\to -x_6$ and $x_7\to -x_7$ must be applied to $\alpha (x_1,\dots ,x_7)$, finally obtaining $\tilde{\alpha }(x_1,\dots ,x_7)=\alpha (-x_1,\dots ,-x_7)$.

).

In case of storing n switching key matrices (corresponding to all the automorphisms), any vertex transition will be allowed through one single switching key operation. However, it is possible to store less switching key matrices (which, combined, represent the whole set of automorphisms), hence increasing the number of subsequent automorphisms/switching key operations for transitioning from one vertex to another.

Due to the specific structure of our multivariate rings, we propose an optimal strategy with ${log}_{2}n$ switching key matrices, each one corresponding to a different transformation $x_i\to -x_i$; with the additional advantage that these transformations are their own inverses. Following this strategy, we can also see the different slots (vertices in Figure 4) as a binary vector of length ${log}_{2}n$, where the available operations are bit-wise XOR operations with vectors

$$\left\{\right(1,0,\dots ,0),(0,1,0,\dots ,0),\dots ,(0,\dots ,0,1\left)\right\}$$

belonging to the standard basis of dimension ${log}_{2}n$. In the example of Figure 4 (with ${log}_{2}n=7$), this method would be equivalent to working with seven independent vectors (of the standard basis) enabling only movements between vertices in the dimension associated to the vector.

It can be seen that with this strategy the farthest slot to a given one is always the slot represented as its ones’ complement, i.e., the opposite vertex. This implies a total of ${log}_{2}n$ automorphisms/switching key operations. Hence, in the worst case we have an increase in the computational cost by a factor of ${log}_{2}n$ when storing ${log}_{2}n$ switching key matrices and working with n slots. This is a considerable reduction in the memory requirements when compared to the approximately $\mathcal{O}\left(D\right)$ and $\mathcal{O}\left(\sqrt{D}\right)$ factors considered by Halevi and Shoup [74] when working with D slots (in one dimension).

As a quick comparison, for the practical values reported in [74], i.e., $n=\varphi \left(m\right)=16,384$, our strategy achieves an increase factor of 14 on the computational cost, which is not considerably higher than their results, but with huge savings in storage for our case: we store only 14 matrices, compared to the 51 matrices and three automorphisms/switching key operations achieved by [74] for a similar value of $\varphi \left(m\right)=15,004$ and one dimension with $D=682$ following a baby-step/giant-step strategy.

Finally, it must be noted that when applying a switching key, noise constraints force the need of decomposing the coefficients of the involved polynomials in some specific base. This is true unless we resort to the strategy of Bajard et al. [79] which takes advantage of the CRT decomposition over the polynomial coefficients. 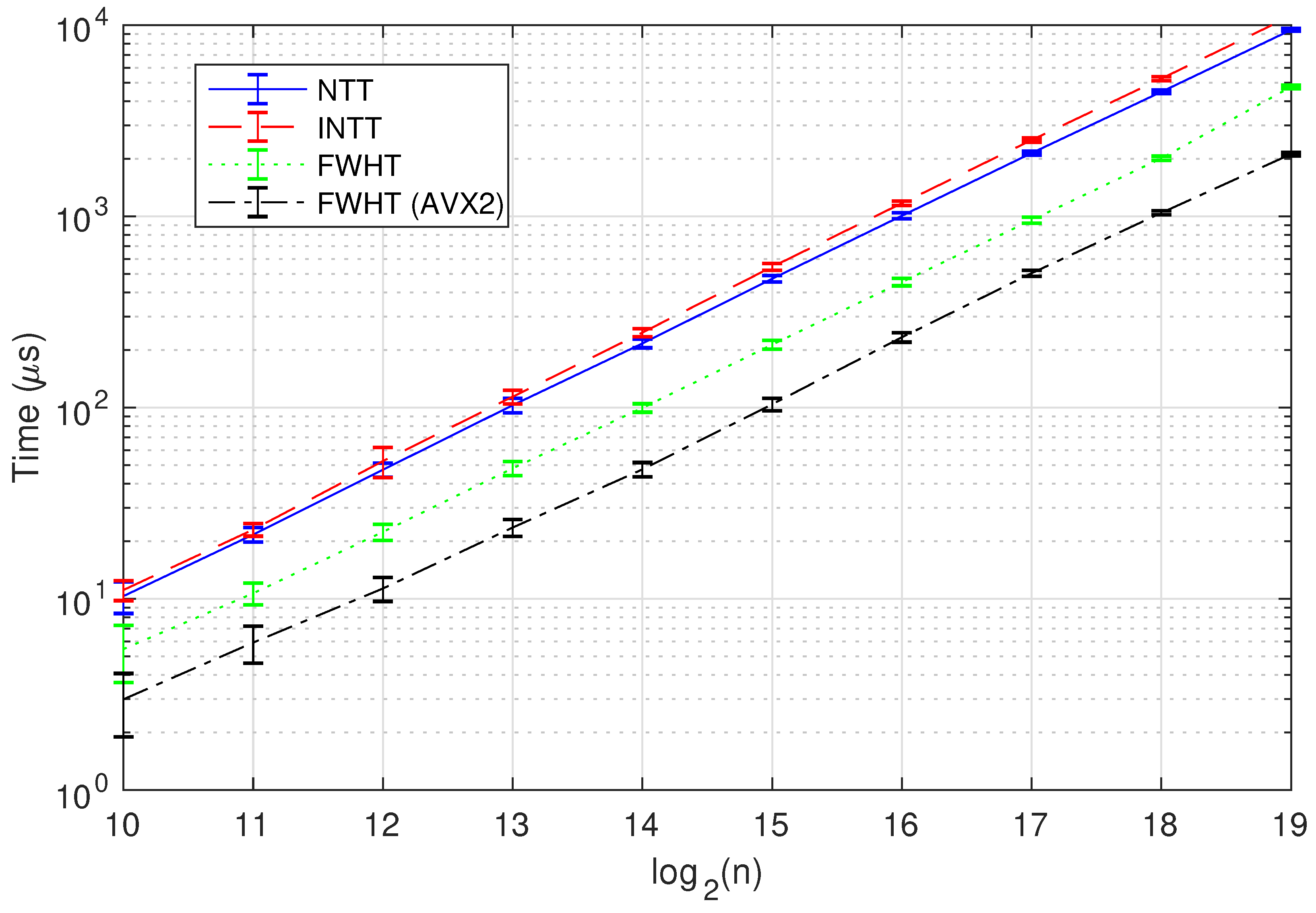However, this strategy cannot be applied always, as it requires a highly composite modulo with primes of an adequate machine size (see [5]). As this base decomposition does not straightforwardly commute with the NTT/INTT (or CRT over the polynomial function) representation, the inverse and direct transforms have to be applied over the polynomials. Our setting in multivariate rings with FWHT enables a reduction on complexity for these transforms by a factor of $\mathcal{O}(logn)$ in terms of elemental products; i.e., this yields a net gain factor of $logn$ in storage while keeping the same order of (multiplicative) computational complexity.

Efficiency/space tradeoffs:

In practical scenarios, the tradeoff between used memory and computational cost might require a different balance with less space efficiency than the ${log}_{2}n$ achieved by the described strategy. Consequently, we also cover two additional strategies which lead to an improvement of the computational cost by a factor of 2.

Strategy 2: Our first approach adds to the previous ${log}_{2}n$ matrices those which are associated to “diagonal” vectors in our hypercube representation of the autormorphisms (see Figure 4); that is, we work with automorphisms $\{x_i\to x_i^{l_i},x_j\to x_j^{l_j}\}$ where $l_i,l_j\in {\mathbb{Z}}_4^{*}$ and $i,j\in \left[{log}_{2}n\right]$, being $i\ne j$. Going back again to the binary representation of the slots, the additional automorphisms could be seen as the result of all pairwise XOR operations of different vectors of the standard basis of length ${log}_{2}n$.

The number of needed switching key matrices is therefore increased to

$$\left(\genfrac{}{}{0pt}{}{1+{log}_{2}n}{2}\right)=\frac{(1+{log}_{2}n){log}_{2}n}{2}.$$

In order to calculate the associated computational cost for this strategy, we resort to induction, working first with the odd natural numbers, and afterwards with the even natural numbers. Let the multivariate ring $R_t[x_1,\dots ,x_l]$ with $f_i\left(x_i\right)=1+x_i^2$ where $i=1,\dots ,l$ and $l={log}_{2}n$, if we consider only the odd values of l we have:

• For $l=1$, any transition can be applied with only one automorphism/relinearization operation.
• Assuming that l variables require k automorphisms/relinearization operations, it can be shown that adding two variables (i.e., $l+2$), $k+1$ automorphisms/relinearization operations are needed. We can graphically see this by resorting to the binary representation: moving between any two slots implies, in the worst case (consider one vector and its ones’ complement), one additional XOR operation.
• Therefore, by induction, odd values of l require $\lceil \frac{l}{2}\rceil$ automorphisms/relinearization operations.

The argument is analogous for even l. First, we consider $l=2$, where with only one automorphism/relinearization operation is enough to move between any of the slots. Next, the same reasoning as before could be applied between l and $l+2$ variables, resulting in a total of $\frac{l}{2}$ automorphisms/relinearization operations for l variables.

Taking into account both results, this strategy yields an increase in the number of automorphisms/switching key operations by a factor of $\lceil \frac{{log}_{2}n}{2}\rceil$. Hence, we can reduce by a half the computational cost compared to our previous strategy, with a quadratic increase in the memory requirements of $\frac{(1+{log}_{2}n){log}_{2}n}{2}$ instead of ${log}_{2}n$. For instance, with $n=16,384$ this would give an increase in cost by a factor of seven and a total of 105 stored matrices.

Strategy 3: The incurred increase in space requirements by Strategy 2 might not be acceptable for certain applications; therefore, our next approach preserves the cost improvement, but achieving a negligible increase in the number of required matrices: $1+{log}_{2}n$ matrices instead of $\mathcal{O}\left({(logn)}^2\right)$.

The idea behind this approach is adding to the switching key matrices for transformations of the form $\{x_i\to -x_i\}$ for $i=1,\dots ,{log}_{2}n$ the following one

$$\{x_1\to -x_1,\dots ,x_{{log}_{2}n}\to -x_{{log}_{2}n}\}.$$

As a graphical explanation, let us consider again the binary representation of the slots: in addition to working with those XOR operations with vectors belonging to the standard basis of length ${log}_{2}n$, now we can also apply the ones’ complement of every “slot” in one operation (e.g., in Figure 4 we could directly move with one automorphism/switching key operation from point A to point B).

Therefore, the worst case automorphism requiring $l=\lceil \frac{{log}_{2}n}{2}\rceil$ matrices with our first strategy can now be computed with just one matrix. Moreover, as we know that $l-\lceil \frac{l}{2}\rceil \le \lceil \frac{l}{2}\rceil$ for any $l\in \mathbb{N}$, then the farthest slot position can be achieved by only $\lceil \frac{l}{2}\rceil =\lceil \frac{{log}_{2}n}{2}\rceil$ automorphisms. Consequently, we can see that with $1+{log}_{2}n$ matrices, we only need a maximum of $\lceil \frac{{log}_{2}n}{2}\rceil$ automorphism/switching key operations. For instance, with $n=16,384$ this would give an increase in cost by a factor of seven and a total of 15 matrices in terms of use of memory.

9.3. Automorphisms in Multivariate Power-of-Two Cyclotomic Rings

It can be useful to expand Definition 9 to also cover more general multivariate rings, which can be leveraged by some applications. Most of these applications consider a general multivariate ring as the R and $R_q$ from Definition 1, where each of the polynomial functions are defined as different power-of-two cyclotomic polynomials $f_i\left(x_i\right)=x_i^{n_i}+1$. Hence, analogously to the procedure we followed with multiquadratics in Section 9.2, we exemplify these results with power-of-two cyclotomics. They can be similarly extended to more general rings of the form $x_i^{n_i}+d_i$. We refer the reader to Section 9.4 for more details.

In this section the discussed efficiency/space tradeoffs achievable with automorphisms on the FWHT-enabled rings will be expanded to these rings (at the cost of lacking the faster FFT algorithms for the negacyclic Hadamard transform).

Tradeoffs in the Size/Efficiency Of Automorphisms

We consider the ring R introduced in Definition 1; particularly, we work with $R_t[x_1,\dots ,x_l]$ where $t\equiv 1mod2n_i$ for $i=1,\dots ,l$. Analogously to our derivation in Section 9.2, when working with an element $\alpha \in R_t[x_1,\dots ,x_l]$, we have the transformations

$${\theta }_{i_1,\dots ,i_l}\left(\alpha \right)={\theta }_{i_1}^{\left(x_1\right)}\left({\theta }_{i_2}^{\left(x_2\right)}(\dots {\theta }_{i_l}^{\left(x_l\right)}\left(\alpha \right)\dots )\right)\in R_t[x_1,\dots ,x_l],$$

now with $i_j\in {\mathbb{Z}}_{2n_j}^{*}$ for all j.

This multidimensional structure can be seen again as an l-tuple, where each component has $n_i$ different values, hence giving a total of $n={\prod }_{i=1}^l{n}_i$ different automorphisms.

Strategy 4: Our main strategy works with $n_i-1$ matrices for each variable $x_i$, where each switching key matrix will correspond to an automorphism $\{x_i\to x_i^{l_i}\}$ for $l_i\in {\mathbb{Z}}_{2n_i}^{*}$ (except $\{x_i\to x_i\}$) and $i=1,\dots ,l$. This strategy yields a total of ${\sum }_{i=1}^l{n}_i-l$ matrices with a computational cost of l automorphism/switching key operations. Let us assume that all the matrices for every “univariate” change of variable have to be stored. However, the number of required matrices per “univariate” change of variable could be further improved [74] (that is, we could work with subsets ${\mathbb{A}}_i\in {\mathbb{Z}}_{2n_i}^{*}$ in such a way that the corresponding automorphisms would be $\{x_i\to x_i^{l_i}\}$ for $l_i\in {\mathbb{A}}_i$ and $i=1,\dots ,l$).

We consider those $n_i=n^{\frac{1}{l}}$ for $i=1,\dots ,l$ (hence being all $n_i$ equal). This gives us several tradeoffs depending on l and n where we have $l(n^{\frac{1}{l}}-1)$ matrices and an increase in the computational cost by a factor of l.

Table 6. Practical space/efficiency tradeoffs of automorphisms for $n=16,384$.

l	2	3	4	5	6	7
# Matrices	256	80	52	36	34	28
# Calls to switching key (worst-case)	2	3	4	5	6	7

shows the number of required matrices and the increase in computational cost for $n=16384$ and several values of l. As $n^{\frac{1}{l}}$ is not always a valid value (that is, a power of two), the choice of $n_i$ can be optimized to achieve the smallest possible number of automorphisms ($\sum n_i$) such that $n=\prod n_i$.

Conversely,

Table 7. Space/efficiency tradeoffs of automorphisms.

Strategy	# Matrices	# Calls to Switching Key (Worst-Case)
Strategy 1 from Section 9.2	${log}_{2}n$	${log}_{2}n$
Strategy 2 from Section 9.2	$\frac{(1+{log}_{2}n){log}_{2}n}{2}$	$\lceil \frac{{log}_{2}n}{2}\rceil$
Strategy 3 from Section 9.2	$1+{log}_{2}n$	$\lceil \frac{{log}_{2}n}{2}\rceil$
Strategy 4 from Section 9.3	$\approx n^{\frac{1}{l}}l-l$	l
Strategy 4 (general) from Section 9.3	${\sum }_{i=1}^l{n}_i-l$	l

summarizes the different tradeoffs we have presented in this section.

9.4. On the Applicability to More General Multivariate Rings

It is worth noting that all the solutions exemplified above (Section 9.2 and Section 9.3) are sketched out with negacyclic rings. In this section, we give some insights on how to extend these results to the more general multivariate rings showcased in this manuscript.

An alternative set of polynomial ideals:

Bernstein et al. [70] propose a different non-cyclotomic ring. The authors argue that with cyclotomic rings it is easy to have non-trivial ring homomorphisms (as the polynomial function usually splits in linear factors to perform FFT algorithms) and a relatively small Galois group. Consequently, the authors propose rings of the form ${\mathbb{Z}}_q\left[x\right]/\left(f_p\left(x\right)\right)$, with an irreducible polynomial function $f_p\left(x\right)=x^p-x-1$ and p prime, where the Galois group is the permutation group $S_p$ with $p!$ elements, and the modulo q is inert in the ring. Hence, ${\mathbb{Z}}_q\left[x\right]/(x^p-x-1)$ is indeed a finite field. See [80] for more details on the properties exhibited by functions of the form $f_n\left(x\right)=x^n-x-1$.

These polynomial functions are also interesting for our purposes, but for very different reasons. Let $K=\mathbb{Q}\left(\alpha \right)$ be a number field with $\alpha$ one of the roots of $x^n-x-1$. We know that [80] polynomial functions $f_n\left(x\right)=x^n-x-1$ with $n\ge 2$ are irreducible, and for $2\le n\le 100$ the discriminant of $f_n\left(x\right)$ is squarefree. According to Theorem 6, this means that K is monogenic and ${\mathcal{O}}_K=\mathbb{Z}\left[x\right]/\left(f_n\left(x\right)\right)$.

Now, from Proposition 3, we have

$${\Delta }_K={(-1)}^{\frac{n(n-1)}{2}}(n^n{(-1)}^{n-1}-{(n-1)}^{n-1}),$$

so it is straightforward to find coprime discriminants for different values of n.

For example, the discriminants of ${\left\{f_i\left(x\right)\right\}}_{i=2,\dots ,7}$ are coprime. Therefore, we can define a multivariate RLWE sample over the ring of integers

$${\mathcal{O}}_K=\mathbb{Z}[x_1,\dots ,x_7]/(f_2\left(x_2\right),\dots ,f_7\left(x_7\right))$$

for a multivariate number field of degree 5040 and 6 dimensions. In general, this gives an easy way to find multivariate number fields with many variables and a small expansion factor.

Operations over these rings are not as efficient as the ones with polynomial ideal $(x^n-d)$, but still acceptable; i.e., in the worst case, multiplications modulo $x^n-x-1$ can be decomposed in multiplications modulo $x^n-x$ and $x^n-1$, hence requiring two parallel efficient “cyclic” convolutions, and afterwards, adding the obtained results.

Automorphisms for more general multivariate rings:

The multivariate rings introduced in Section 6 are, in general, separable but non-Galois field extensions. This implies that the number of available automorphisms is strictly smaller than the degree of the extension (see Corollary 4).

Corollary 4

(Corollary $4.3$ from [81]). If $L/K$ is a finite extension that is either inseparable or not normal then

$$\left|Aut\right(L/K\left)\right|<[L:K],$$

being $[L:K]$ the degree of the field extension.

Fortunately, this is not a problem in practice as we can make use of Theorem 11 to extend the mentioned separable multivariate number fields in Section 6 to a Galois extension, where we have $Gal(L/K)=Aut(L/K)=[L:K]$; hence, automorphisms similar to the case of power-of-two cyclotomics (see Section 9.3) can still be applied.

Theorem 11

(Theorem $4.8$ from [81]). Every finite separable extension of a field can be enlarged to a finite Galois extension of the field. In particular, every finite extension of a field with characteristic 0 can be enlarged to a finite Galois extension.

A toy example for a prime-degree field extension:

Consider the number field $\mathbb{Q}\left(d^{\frac{1}{p}}\right)$ (with $d>1$ and $d\in \mathbb{N}$) isomorphic to the polynomial ring $\mathbb{Q}\left[x\right]/(x^p-d)$ and satisfying the conditions from Section 6 (Proposition 4). We know that the roots of $x^p-d$ are $\{d^{\frac{1}{p}},{\zeta }_p{d}^{\frac{1}{p}},\dots ,{\zeta }_p^{p-1}{d}^{\frac{1}{p}}\}$. These roots are separable, but $\mathbb{Q}\left(d^{\frac{1}{p}}\right)$ is not the corresponding splitting field, and hence $\mathbb{Q}\left(d^{\frac{1}{d}}\right)$ is not a Galois field extension over the rationals $\mathbb{Q}$.

Even so, we know from Theorem 11 that this field can be extended to a Galois field where we have a Galois automorphism group which enables “rotations” of the slots. It suffices to add the root ${\zeta }_p$ by means of a symbolic variable y over the cyclotomic polynomial ${\Phi }_p\left(y\right)={\sum }_{i=0}^{p-1}{y}^i$, i.e., we enlarge the number field (see Theorem 11) to have $\mathbb{Q}(d^{\frac{1}{p}},{\zeta }_p)$ with d and p different primes.

For this extended number field and considering a polynomial representation with $\mathbb{Q}[x,y]/(x^p-d,{\Phi }_p\left(y\right))$ (thanks to the field isomorphism $d^{\frac{1}{p}}\to x,{\zeta }_p\to y$), we have the chain of transformations $\{x\to x{y}^i,y\to y^j\}$ with $i\in {\mathbb{Z}}_p$ and $j\in {\mathbb{Z}}_p^{*}$, which enables homomorphic “rotation” of the slots.

As an example, consider the polynomial $a\left(x\right)={\sum }_{i=0}^{p-1}{a}_i{x}^{i}mod{x}^p-d$. We apply the change of variable $x\to xy$

$$a\left(x\right)=\sum _{i=0}^{p-1}{a}_i{x}^i=\sum _{i=0}^{p-1}{a}_i{x}^i{y}^i=a_{p-1}{y}^{p-1}{x}^{p-1}+\sum _{i=0}^{p-2}{a}_i{y}^i{x}^i.$$

Consider now the following relation given by ${\Phi }_p\left(y\right)$

$$y^{p-1}=-\sum _{i=0}^{p-2}{y}^i.$$

By applying it, we have:

$$\begin{array}{cc}\hfill a_{p-1}{y}^{p-1}{x}^{p-1}+\sum _{i=0}^{p-2}{a}_i{y}^i{x}^i& =-a_{p-1}{x}^{p-1}\sum _{i=0}^{p-2}{y}^i+\sum _{i=0}^{p-2}{a}_i{y}^i{x}^i.\hfill \end{array}$$

It is worth noting that the ring $\mathbb{Z}[x,y]/(x^p-d,{\Phi }_p\left(y\right))$ is not, in general, the ring of integers of the field $\mathbb{Q}(d^{\frac{1}{p}},{\zeta }_p)$, but instead a subring of its ring of integers. This can be easily seen by inspecting the discriminants of $x^p-d$ and ${\Phi }_p\left(y\right)$ which are, respectively, ${(-1)}^{\frac{p(p-1)}{2}}{p}^p{(-d)}^{p-1}$ and $p^{p-2}$. As they are not coprime we cannot assert that the ring of integers of $\mathbb{Q}(d^{\frac{1}{p}},{\zeta }_p)$ is the product of $\mathbb{Z}\left[x\right]/(x^p-d)$ and $\mathbb{Z}\left[y\right]/\left({\Phi }_p\left(y\right)\right)$, but if $x^p-d$ satisfies the conditions established in Proposition 4, $\mathbb{Z}\left[x\right]/(x^p-d)$ is the ring of integers of $\mathbb{Q}\left(d^{\frac{1}{p}}\right)$.

Consequently, when working with rings following Definition 11 in Section 6, if we want to (1) base the security on RLWE over a general number field and also (2) make use of the automorphisms, the reduction from Theorem 2 implies a loss in the lattice dimensionality; in the previous example of $\mathbb{Z}[x,y]/(x^p-d,{\Phi }_p\left(y\right))$, we end up working with a ring of degree $p(p-1)$, but being the original RLWE sample defined over a number field of degree p. Nevertheless, we can avoid this loss by basing the security in a generalization of RLWE called Order-LWE.

A much wider set of ring choices with Order-LWE:

Bolboceanu et al. [51] propose a generalization of RLWE which, instead of considering the ring of integers ${\mathcal{O}}_K$ and its dual ${\mathcal{O}}_K^{\vee }$, relies on the subrings called orders $\mathcal{O}$ and their corresponding duals ${\mathcal{O}}^{\vee }$ to define the underlying ideal lattices.

For a number field K of degree n, an order $\mathcal{O}$ in K is a subring of ${\mathcal{O}}_K$ containing a $\mathbb{Q}$-basis of full-rank n of K such that $\mathcal{O}{\otimes }_{\mathbb{Z}}\mathbb{Q}=K$. The ring of integers is the maximal order of K.

Order-LWE also presents worst-case hardness with respect to short vector problems, but in the invertible-ideal lattices of the considered order [51].

This result enables a relaxation of many of the restrictions imposed for the rings in Section 5 and Section 6, by directly basing their hardness on Order-LWE. The previous example with the field $\mathbb{Q}(d^{\frac{1}{p}},{\zeta }_p)$ and order $\mathbb{Z}(d^{\frac{1}{p}},{\zeta }_p)$ can base its hardness on a lattice of dimension $p(p-1)$ by considering Order-LWE.

The use of the polynomial function ${\Phi }_p\left(y\right)$ seems to contradict our initial requirements regarding the desired form of the polynomial ideal (see Section 1). However, for efficient polynomial products we can substitute ${\Phi }_p\left(y\right)$ by $y^p-1$ by just multiplying both polynomial elements and polynomial function with the term $y-1$.

We plan to extend our results and optimizations to the corresponding relaxations offered by Order-LWE. In this direction, this work provides a wide set of concrete ring instantiations which could be considered to analyze the hardness of Order-LWE.

10. Improving on the Packing Capacity of Complex Numbers

We have addressed packing of integer numbers in Section 9, but complex numbers are more difficult to efficiently pack. Nevertheless, we can also leverage the multivariate structure to represent the complex arithmetic in a much more efficient way than previous recent approaches. Knowing that a total of $n/2$ complex slots can be packed over the ring $\mathbb{Z}\left[z\right]/(1+z^n)$, Cheon et al. [39,82] expand these results to the bivariate case $\mathbb{Z}[x,y]/(1+x^{n_x},1+y^{n_y})$, packing a total of $\frac{n_x}{2}\frac{n_y}{2}=\frac{n}{4}$ complex slots. Generalizing this strategy to l dimensions, packing is restricted to $\frac{n}{2^l}$ complex slots (where $n={\prod }_{i=1}^l{n}_i$) when working over multivariate rings as $\mathbb{Z}[x_1,\dots ,x_l]/(1+x_1^{n_1},\dots 1+x_l^{n_l})$. Consequently, this strategy leaves a huge gap of unused potential slots when transitioning to a multivariate ring. Additionally, while this strategy was introduced for a weak instance of multivariate RLWE (i.e., vulnerable to BCV attack), a similar approach works for rings following Definition 11.

Nevertheless, it is possible to achieve the same number of complex slots as the univariate counterpart (that is, $n/2$ complex slots), effectively substituting the multivariate complex embedding map (as used in [39]) by its univariate version. Let us consider the ring $\mathbb{Z}[x_1,\dots ,x_l]/(d_1+x_1^{n_1},\dots ,d_l+x_l^{n_l})$, and choose one of the l independent variables to work with the canonical embedding map, $x_1$ without loss of generality. If we have a total of $n/2$ complex numbers to pack in one multivariate polynomial plaintext, we organize them as a set of $\frac{n}{n_1}$ complex vectors with length $n_1/2$ ($n_1$ is chosen as a power of two). For each complex vector we use the encoding from [82], defined as the composition of the inverse of the complex embedding map and a discretization. This yields $\frac{n}{n_1}$ polynomials belonging to the ring $\mathbb{A}={\mathbb{Z}}_t\left[x_1\right]/(d_1+x_1^{n_1})$ for an adequately chosen modulo t.

Coming back to the multivariate ring representation, we can consider the new message as a polynomial in the ring ${\mathbb{Z}}_t[x_1,\dots ,x_l]/(d_1+x_1^{n_1},\dots ,d_l+x_l^{n_l})$. Hence, we gather all the polynomials in $\mathbb{A}$ as the different coefficients of the ring $\mathbb{A}[x_2,\dots ,x_l]/(d_2+x_2^{n_2},\dots ,d_l+x_l^{n_l})$, and we define encoding/decoding matrices working over $d_i+x_i^{n_i}$ polynomial functions (i.e., $\alpha$-generalized INTTs/NTTs over t, see Section 8) for $i=2,\dots ,l$, considering the identity matrix ${\mathit{I}}_{n_1}$ of size $n_1\times n_1$ for $x_1$ and the polynomial function $d_1+x_1^{n_1}$. Using the vector representation of the plaintext polynomial, the encoding/decoding is performed by means of one matrix multiplication which can be efficiently realized with FFT-like algorithms.

This method can pack a total of $n/2$ complex slots while preserving the properties for the automorphisms (whenever we enlarge the number field to a Galois extension, see Section 9.4) and also removing the gap of the method used in [39], where the fraction of used slots decreases exponentially with the number of dimensions.

Finally, it is worth looking at the case where the considered multivariate rings are those from Definition 9 in Section 5. In this case, the polynomial ideals have the form $(d_i+x_i^2)$, so the variable $x_1$ can directly represent the imaginary unit, therefore perfectly mapping the complex arithmetic without the need of applying the canonical embedding map over the polynomials in $\mathbb{A}$.

11. Conclusions

This work addresses the main security flaw of the multivariate RLWE problem revealed by Bootland et al. For this purpose, we have defined and parameterized practical and secure instantiations of the multivariate Ring Learning With Errors problem, supported by the extended reduction of the original proof by Lyubashevsky et al. [3,4]. The proposed instantiations are resilient against BCV attack to m-RLWE [25], while still preserving all the efficiency improvements that m-RLWE brings. We have shown how to find practical parameters for the proposed instantiations to make them both secure and usable, therefore enabling improved space-time tradeoffs in many practical applications, comprising the most critical fundamental lattice operations (faster polynomial multiplications through $\mathit{\alpha }$-generalized Walsh–Hadamard Transforms), efficient cryptographic operations such as computation of automorphisms, relinearizations, packing, unpacking and homomorphic slot manipulation, and, consequently, bootstrapping, and optimization of high level applications in encrypted approximate arithmetic, complex processing, and efficient multidimensional signal manipulation.

These contributions, combined, showcase the power and versatility of secure instantiations of the multivariate RLWE problem, and open up new research paths and strategies for realizing efficient (fully) homomorphic encryption.