Time-Varying Comovement of Foreign Exchange Markets: A GLS-Based Time-Varying Model Approach
Abstract
1. Introduction
2. Model
2.1. Exchange Rate Dynamics and Cointegration
2.2. The Vector Error-Correction Model
2.3. The Time-Varying VEC Model
2.4. The Degree of Market Comovement
2.5. Confirming Our Assumption of Constant Cointegrating Vectors
3. Data
4. Empirical Results
4.1. Preliminaries
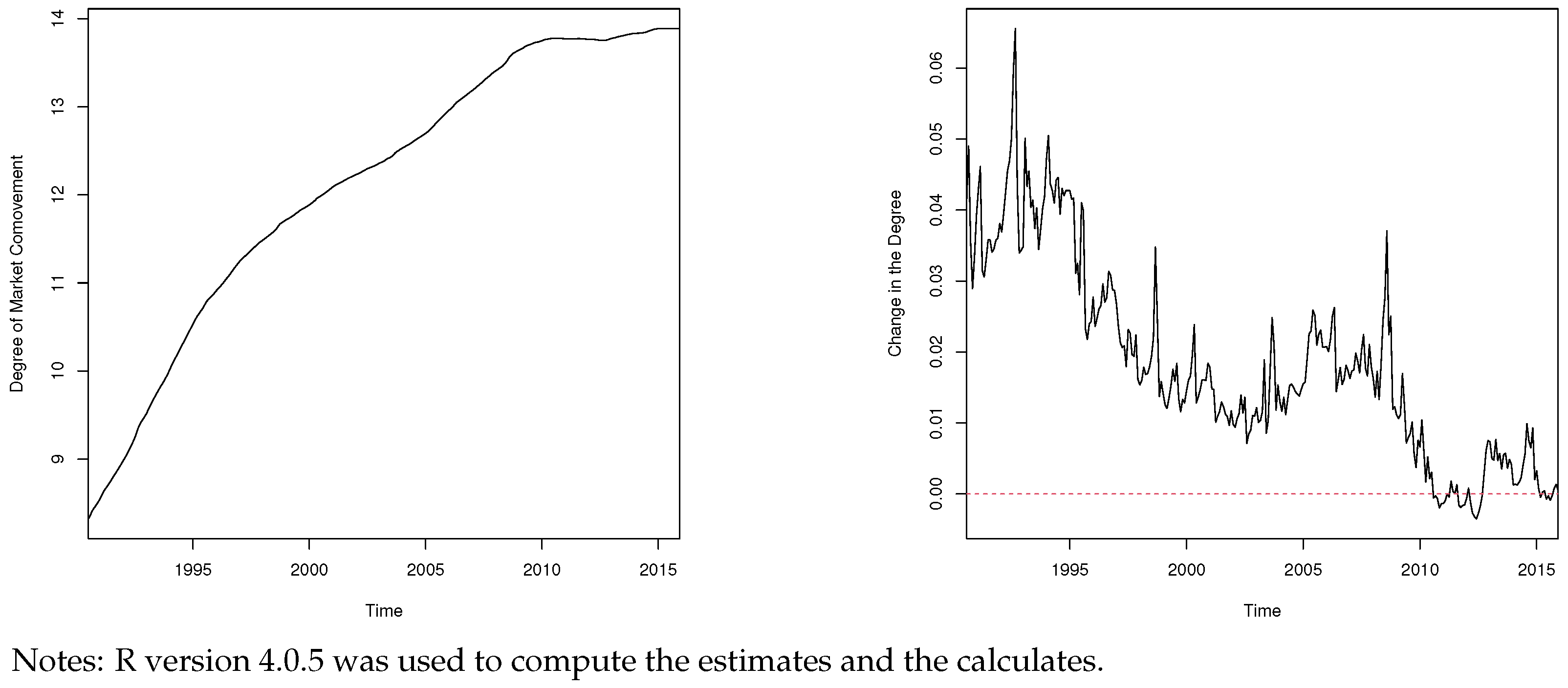
4.2. The Time-Varying Model
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADF | Augmented Dickey-Fuller |
| GLS | Generalized least squares |
| MAIC | modified Akaike information criterion |
| MBIC | Modified Bayesian information criterion |
| MCMC | Markov chain Monte Carlo |
| OLS | Ordinary least squares |
| STAR | Smooth transition autoregressive |
| TV-VEC | time-varying vector error correction |
| VEC | Vector error correction |
Appendix A. Vector Error-Correction Model
Appendix B. Parameter Constancy Test
Appendix C. Time-Varying VEC Model
Appendix D. Degree of Market Comovement
References
- Baillie, R.T.; Bollerslev, T. Common Stochastic Trends in a System of Exchange Rates. J. Financ. 1989, 44, 167–181. [Google Scholar] [CrossRef]
- Diebold, F.X.; Gardeazabal, J.; Yilmaz, K. On Cointegration and Exchange Rate Dynamics. J. Financ. 1994, 49, 727–735. [Google Scholar] [CrossRef]
- Engel, C.; Nelson, C.M.; West, K.D. Exchange Rate Models Are Not As Bad As You Think. NBER Macroecon. Annu. 2007, 22, 381–441. [Google Scholar] [CrossRef]
- Engel, C.; West, K.D. Exchange Rates and Fundamentals. J. Political Econ. 2005, 113, 485–517. [Google Scholar] [CrossRef]
- Ito, M.; Noda, A.; Wada, T. International Stock Market Efficiency: A Non-Bayesian Time-Varying Model Approach. Appl. Econ. 2014, 46, 2744–2754. [Google Scholar] [CrossRef]
- Fama, E.F. Efficient Capital Markets: A Review of Theory and Empirical Work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Kapetanios, G.; Shin, Y.; Snell, A. Testing for a Unit Root in the Nonlinear STAR Framework. J. Econom. 2003, 112, 359–379. [Google Scholar] [CrossRef]
- Clarida, R.H.; Sarno, L.; Taylor, M.P.; Valente, G. The Out-of-Sample Success of Term Structure Models as Exchange Rate Predictors: A Step Beyond. J. Int. Econ. 2003, 60, 61–83. [Google Scholar] [CrossRef]
- Engel, C. A Note of Cointegration and International Capital Market Efficiency. J. Int. Money Financ. 1996, 15, 657–660. [Google Scholar] [CrossRef]
- Hansen, B.E. Testing for Parameter Instability in Linear Models. J. Policy Model. 1992, 14, 517–533. [Google Scholar] [CrossRef]
- Hansen, B.E. Tests for Parameter Instability in Regressions with I (1) Processes. J. Bus. Econ. Stat. 1992, 10, 321–335. [Google Scholar]
- Ito, M.; Noda, A.; Wada, T. An Alternative Estimation Method of a Time-Varying Parameter Model. arXiv 2017, arXiv:1707.06837. [Google Scholar]
- Qu, Z. Searching for Cointegration in a Dynamic System. Econom. J. 2007, 10, 580–604. [Google Scholar] [CrossRef]
- Juselius, K. The Cointegrated VAR Model: Methodology and Applications; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Elliott, G.; Rothenberg, T.J.; Stock, J.H. Efficient Tests for an Autoregressive Unit Root. Econometrica 1996, 64, 813–836. [Google Scholar] [CrossRef]
- Ng, S.; Perron, P. Lag Length Selection and the Construction of Unit Root Tests with Good Size and Power. Econometrica 2001, 69, 1519–1554. [Google Scholar] [CrossRef]
- Johansen, S. Statistical Analysis of Cointegration Vectors. J. Econ. Dyn. Control. 1988, 12, 231–254. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 1991, 59, 1551–1580. [Google Scholar] [CrossRef]
- Newey, W.K.; West, K.D. A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix. Econometrica 1987, 55, 703–708. [Google Scholar] [CrossRef]
- Hansen, H.; Johansen, S. Some Tests for Parameter Constancy in Cointegrated VAR-Models. Econom. J. 1999, 2, 306–333. [Google Scholar] [CrossRef]
- Clark, T.; McCracken, M. Advances in Forecast Evaluation. In Handbook of Economic Forecasting; Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2B. [Google Scholar]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin, Germany, 2005. [Google Scholar]
- Beveridge, S.; Nelson, C.R. A New Approach to Decomposition of Economic Time Series Into Permanent and Transitory Components with Particular Attention to Measurement of the ‘Business Cycle’. J. Monet. Econ. 1981, 7, 151–174. [Google Scholar] [CrossRef]
| Mean | SD | Min | Max | ADF-GLS | Lags | ||||
|---|---|---|---|---|---|---|---|---|---|
| Level | |||||||||
| 1 | 308 | ||||||||
| 1 | |||||||||
| 1 | |||||||||
| 1 | |||||||||
| ** | 1 | ||||||||
| ** | 1 | ||||||||
| First Difference | |||||||||
| *** | 0 | 307 | |||||||
| *** | 0 | ||||||||
| *** | 0 | ||||||||
| *** | 0 | ||||||||
| *** | 0 | ||||||||
| *** | 0 |
| Eigenvalues | Max Eigen | Trace | |
|---|---|---|---|
| None | 0.1352 | 44.45 ** | 100.19 * |
| At most 1 | 0.0826 | 26.39 | 55.74 |
| Difference | |||||||
| Level | |||||||
| Constant | |||||||
| *** | |||||||
| WQ | SQ | |||
|---|---|---|---|---|
| Test Stats | 8.55 *** | 10.81 *** | 8.55 *** | 15.94 *** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ito, M.; Noda, A.; Wada, T. Time-Varying Comovement of Foreign Exchange Markets: A GLS-Based Time-Varying Model Approach. Mathematics 2021, 9, 849. https://doi.org/10.3390/math9080849
Ito M, Noda A, Wada T. Time-Varying Comovement of Foreign Exchange Markets: A GLS-Based Time-Varying Model Approach. Mathematics. 2021; 9(8):849. https://doi.org/10.3390/math9080849
Chicago/Turabian StyleIto, Mikio, Akihiko Noda, and Tatsuma Wada. 2021. "Time-Varying Comovement of Foreign Exchange Markets: A GLS-Based Time-Varying Model Approach" Mathematics 9, no. 8: 849. https://doi.org/10.3390/math9080849
APA StyleIto, M., Noda, A., & Wada, T. (2021). Time-Varying Comovement of Foreign Exchange Markets: A GLS-Based Time-Varying Model Approach. Mathematics, 9(8), 849. https://doi.org/10.3390/math9080849






