Boundary Stabilization of Heat Equation with Multi-Point Heat Source
Abstract
1. Introduction
2. The State Feedback Controller Design by Backstepping
3. Output Feedback Controller Design
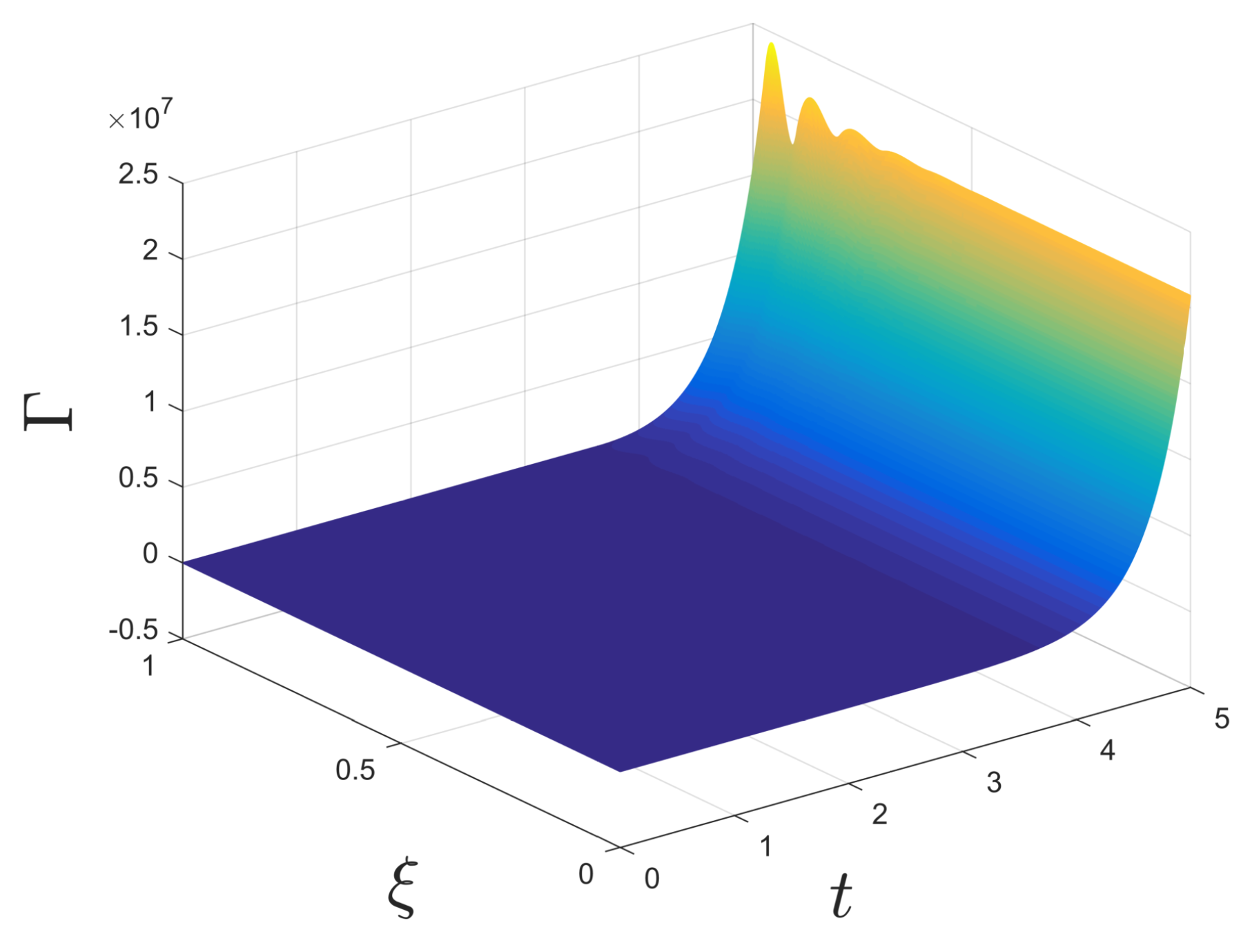
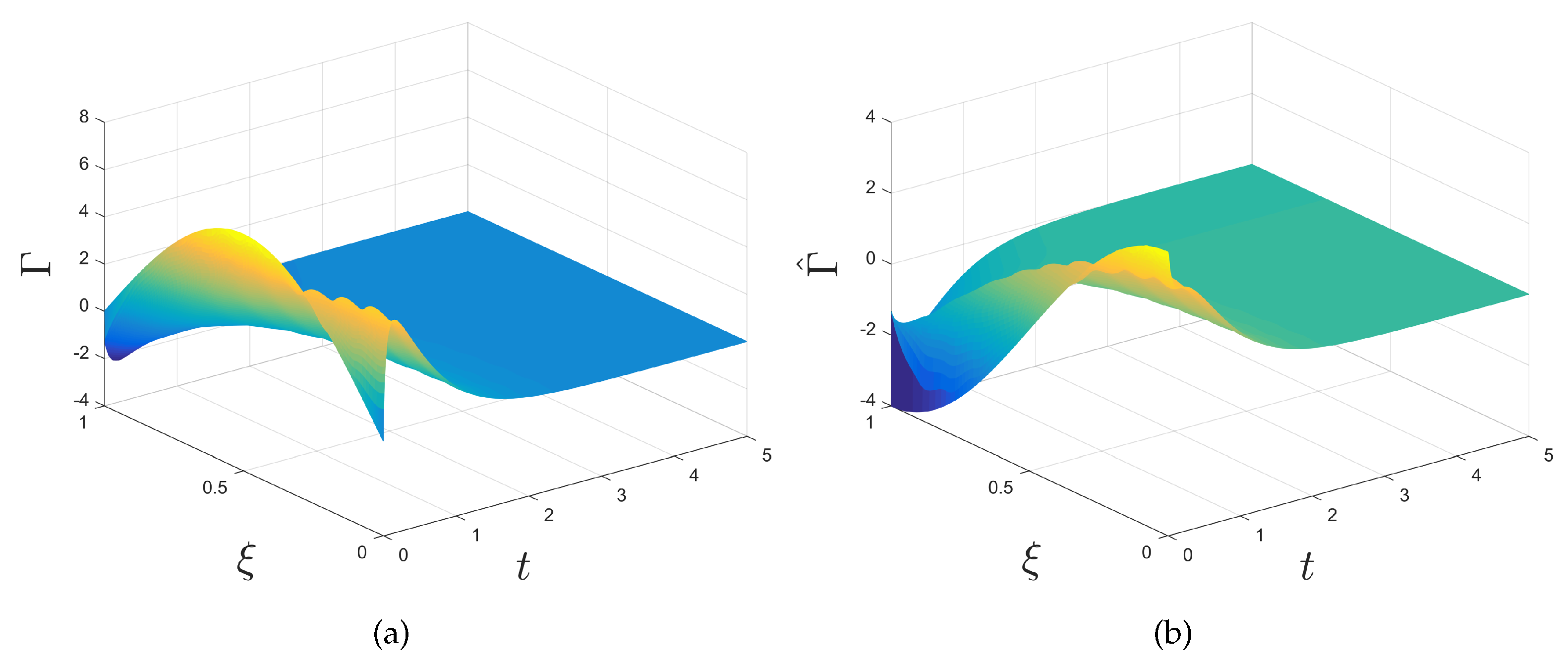
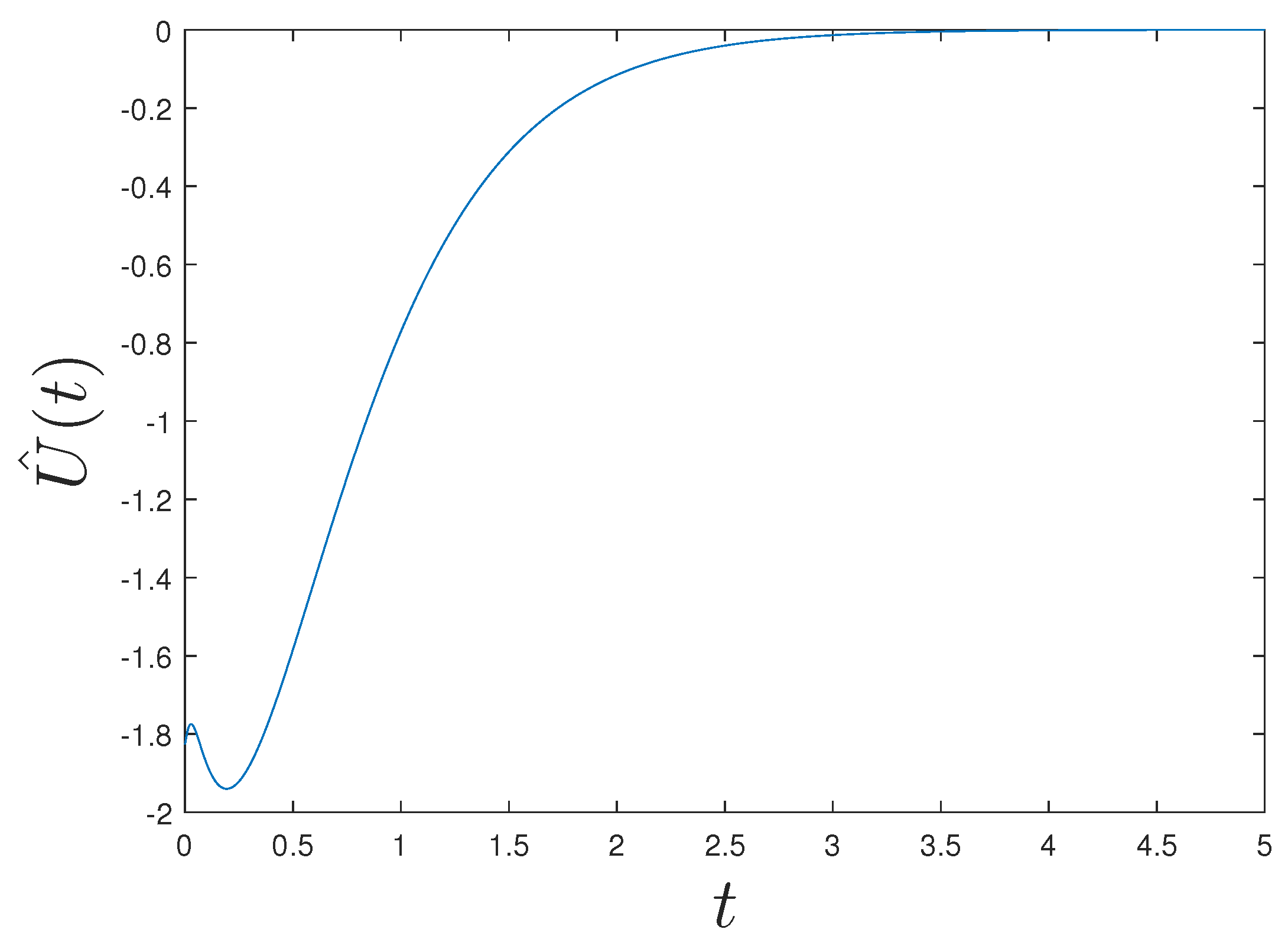
4. Simulation Results
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Masi, A.D.; Ferrari, P.A.; Lebowitz, J.L. Reaction-diffusion equations for interacting particle systems. J. Stat. Phys. 1986, 44, 589–644. [Google Scholar] [CrossRef]
- Price, C.B.; Wambacq, P.; Oosterlinck, A. Applications of reaction-diffusion equations to image processing. In Proceedings of the Third International Conference on Image Processing and its Applications, Warwick, UK, 18–20 July 1989. [Google Scholar]
- Illés, B.; Harsányi, G. Investigating direction characteristics of the heat transfer coefficient in forced convection reflow oven. Exp. Therm. Fluid Sci. 2009, 33, 642–650. [Google Scholar] [CrossRef]
- Pardo, F.; López, P.; Cabello, D.; Balsi, M. Efficient software-hardware 3D heat equation solver with applications on the non-destructive evaluation of minefields. Comput. Geosci. 2009, 35, 2239–2249. [Google Scholar] [CrossRef]
- Gao, Y.; Shao, Q.; Yan, B.Z.; Li, Q.F.; Guo, S.X. Parabolic equation modeling of electromagnetic wave propagation over rough sea surfaces. Sensors 2019, 19, 1252. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.M.; Yuan, R. The spreading property for a prey-predator reaction-diffusion system with fractional diffusion. Frac. Calc. Appl. Anal. 2015, 3, 565–579. [Google Scholar] [CrossRef]
- Guo, W.; Jin, F.F. Adaptive error feedback regulator design for one-dimensional heat equation with unknown harmonic disturbance anticollocated with control. IEEE Trans. Autom. Control 2020, 2, 824–830. [Google Scholar] [CrossRef]
- Jin, F.F.; Guo, B.Z. Performance boundary output tracking for one-dimensional heat equation with boundary unmatched disturbance. Automatica 2018, 96, 1–10. [Google Scholar] [CrossRef]
- Kumar, S.; Cao, J.D.; Li, X.D. A numerical method for time-fractional reaction-diffusion and integro reaction-diffusion equation based on quasi-wavelet. Complexity 2020, 2020, 3291723. [Google Scholar] [CrossRef]
- Ma, T.F.; Yan, B.Q. Positive global solutions of nonlocal boundary value problems for the nonlinear convection reaction-diffusion equations. Bound. Value Probl. 2017, 2017, 9. [Google Scholar] [CrossRef][Green Version]
- Ren, Z.G.; Xu, C.; Zhou, Z.C.; Wu, Z.Z.; Chen, T.H. Boundary stabilization of a class of reaction-advection-diffusion systems via a gradient-based optimization approach. J. Frankl. Inst. 2019, 356, 173–195. [Google Scholar] [CrossRef]
- Liu, W. Boundary feedback stabilization of an unstable heat equation. SIAM J. Control Optim. 2003, 42, 1033–1043. [Google Scholar] [CrossRef]
- Wu, H.N.; Wang, J.W.; Li, H.X. Exponential stabilization for a class of nonlinear parabolic PDE systems via fuzzy control approach. IEEE Trans. Fuzzy Syst. 2012, 20, 318–329. [Google Scholar] [CrossRef]
- Vazquez, R.; Krstic, M. Control of 1-D parabolic PDEs with Volterra nonlinearities, Part I: Design. Automatica 2008, 44, 2778–2790. [Google Scholar] [CrossRef]
- Boškoviā, D.; Balogh, A.; Krstic, M. Backstepping in infinite dimension for a class of parabolic distributed parameter systems. Math. Control Signal Syst. 2003, 16, 44–75. [Google Scholar] [CrossRef]
- Deutsche, J.; Gabrie, J. Fredholm backstepping control of coupled linear parabolic PDEs with input and output delays. IEEE Trans. Autom. Control 2014, 65, 3128–3135. [Google Scholar] [CrossRef]
- Kerschbaum, S.; Deutscher, J. Backstepping control of coupled linear parabolic PDEs with space and time dependent coefficients. IEEE Trans. Autom. Control 2020, 65, 3060–3067. [Google Scholar] [CrossRef]
- Sano, H. Neumann boundary stabilization of one-dimensional linear parabolic systems with input delay. IEEE Trans. Autom. Control 2018, 63, 3105–3111. [Google Scholar] [CrossRef]
- Zhou, Z.C.; Guo, C.L. Stabilization of linear heat equation with a heat source at intermediate point by boundary control. Automatica 2013, 49, 448–456. [Google Scholar] [CrossRef]
- Cerpa, E.; Coron, J.M. Rapid Stabilization for a Korteweg-de Vries equation from the left Dirichlet boundary condition. IEEE Trans. Autom. Control 2013, 58, 1688–1695. [Google Scholar] [CrossRef]
- Si, Y.C.; Xie, C.K.; Zhen, Z.Y.; Zhao, A.L. Local stabilization of coupled nonlinear parabolic equations by boundary control. J. Frankl. Inst. 2018, 355, 5592–5612. [Google Scholar] [CrossRef]
- Yu, X.; Xu, C.; Chu, J. Local exponential stabilization of Fisher’s equation using the backstepping technique. Syst. Control Lett. 2014, 74, 1–7. [Google Scholar] [CrossRef]
- Jadachowski, L.; Meurer, T.; Kugi, A. Backstepping observers for periodic quasi-linear parabolic PDEs. In Proceedings of the Proceedings of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014. [Google Scholar]
- Benabdallah, A. Stabilization of a class of nonlinear uncertain ordinary differential equation by parabolic partial differential equation controller. Int. J. Robust Nonlinear Control 2020, 30, 3023–3038. [Google Scholar] [CrossRef]
- Tang, S.X.; Xie, C.K. Stabilization for a coupled PDE-ODE control system. J. Frankl. Inst. 2011, 348, 2142–2155. [Google Scholar] [CrossRef]
- Tang, S.X.; Xie, C.K.; Zhou, Z.C. Stabilization for a class of delayed coupled PDE-ODE systems with boundary control. In Proceedings of the 2011 Chinese Control and Decision Conference, Mianyang, China, 23–25 May 2011. [Google Scholar]
- Wang, J.; Krstic, M. Output feedback boundary control of a heat PDE sandwiched between two ODEs. IEEE Trans. Autom. Control 2009, 64, 4653–4660. [Google Scholar] [CrossRef]
- Baccoli, A.; Pisanoa, A.; Orlov, Y. Boundary control of coupled reaction-diffusion processes with constant parameters. Automatica 2015, 54, 80–90. [Google Scholar] [CrossRef]
- Dai, J.G.; Ren, B.B. UDE-based robust boundary control for an unstable parabolic PDE with unknown input disturbance. Automatica 2018, 93, 363–368. [Google Scholar] [CrossRef]
- Kang, W.; Guo, B.Z. Stabilization of unstable cascaded heat PDE system subject to boundary disturbance. IET Control Theo. Appl. 2016, 10, 1027–1039. [Google Scholar] [CrossRef]
- Krstic, M.; Smyshlyaev, A. Adaptive boundary control for unstable parabolic PDEs-Part I: Lyapunov design. IEEE Trans. Autom. Control. 2008, 53, 1575–1591. [Google Scholar] [CrossRef]
- Ragusa, M.A. Dirichlet problem associated to divergence form parabolic equations. Commun. Contemp. Math. 2005, 7, 551. [Google Scholar] [CrossRef]
- Smyshlyaev, A.; Krstic, M. Adaptive boundary control for unstable parabolic PDEs-Part II: Estimation-based designs. Automatica 2007, 43, 1543–1556. [Google Scholar] [CrossRef]
- Zhan, H.; Feng, Z. Stability of polytropic filtration equation with variable exponents. Adv. Differ. Equ. 2020, 25, 255–278. [Google Scholar]
- Wang, L.P.; Jin, F.F. Boundary output feedback stabilization of transport equation with non-local term. IMA J. Math. Control Inf. 2020, 37, 752–764. [Google Scholar] [CrossRef]
- Argomedo, F.B.; Krstic, M. Backstepping-forwarding control and observation for hyperbolic PDEs with fredholm integrals. IEEE Trans. Autom. Control 2015, 60, 2145–2160. [Google Scholar] [CrossRef]
- Bernard, P.; Krstic, M. Adaptive output-feedback stabilization of non-local hyperbolic PDEs. Automatica 2014, 50, 2692–2699. [Google Scholar] [CrossRef]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations; Springer: New York, NY, USA, 1983. [Google Scholar]
- Su, L.L.; Guo, W.; Wang, J.M.; Krstic, M. Boundary stabilization of wave equation with velocity recirculation. IEEE Trans. Autom. Control. 2017, 62, 4760–4767. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.-Q.; Jin, F.-F.; Yan, B.-Q. Boundary Stabilization of Heat Equation with Multi-Point Heat Source. Mathematics 2021, 9, 834. https://doi.org/10.3390/math9080834
Hu Q-Q, Jin F-F, Yan B-Q. Boundary Stabilization of Heat Equation with Multi-Point Heat Source. Mathematics. 2021; 9(8):834. https://doi.org/10.3390/math9080834
Chicago/Turabian StyleHu, Qing-Qing, Feng-Fei Jin, and Bao-Qiang Yan. 2021. "Boundary Stabilization of Heat Equation with Multi-Point Heat Source" Mathematics 9, no. 8: 834. https://doi.org/10.3390/math9080834
APA StyleHu, Q.-Q., Jin, F.-F., & Yan, B.-Q. (2021). Boundary Stabilization of Heat Equation with Multi-Point Heat Source. Mathematics, 9(8), 834. https://doi.org/10.3390/math9080834




