An Application of p-Fibonacci Error-Correcting Codes to Cryptography

Abstract

In addition to their usefulness in proving one’s identity electronically, identification protocols based on zero-knowledge proofs allow designing secure cryptographic signature schemes by means of the Fiat–Shamir transform or other similar constructs. This approach has been followed by many cryptographers during the NIST (National Institute of Standards and Technology) standardization process for quantum-resistant signature schemes. NIST candidates include solutions in different settings, such as lattices and multivariate and multiparty computation. While error-correcting codes may also be used, they do not provide very practical parameters, with a few exceptions. In this manuscript, we explored the possibility of using the error-correcting codes proposed by Stakhov in 2006 to design an identification protocol based on zero-knowledge proofs. We showed that this type of code offers a valid alternative in the error-correcting code setting to build such protocols and, consequently, quantum-resistant signature schemes.

1. Introduction

In many situations, it is necessary to electronically prove one’s identity. Typical scenarios include local access to a computer account, remote login to a server over a network, ATM withdrawals, communication permissions through a port, and many others.

The identification protocols (which assure one party of the identity of a second party and also that the second party is participating in the execution of the protocol) allow one entity (the prover) to “prove” its identity to another entity (the verifier) by exchanging some data. Some types of identification protocols avoid the use of digital signatures, public key encryption, block ciphers, sequence numbers, and timestamps, but use asymmetric techniques and are based on interactive proof systems and zero-knowledge proofs. Such protocols allow the prover to be identified by demonstrating knowledge of a secret associated with the prover, without revealing the secret itself to the verifier. This is usually done in three steps, with the prover submitting a commitment, the verifier replying with a challenge, and the prover sending a response to the challenge. An interactive identification scheme involving a commitment-challenge-response sequence can often be converted into a non-interactive signature scheme, by replacing the random challenge of the verifier by the output of a one-way hash applied to the concatenation of the commitment and the message to be signed (the hash essentially plays the role of verifier). This technique has been used to design several quantum-resistant signature schemes based on error-correcting codes [1,2], lattices [3,4], multivariate systems [5], or multiparty computation [6], some of which are recent proposals in the NIST standardization process for quantum secure public key cryptosystems [7].

The topic of this work is identification protocols based on zero-knowledge proofs in the error-correcting code setting. Many proposals of this type have appeared in the literature, but very few can be applied in practice, due to the large size of the parameters of these schemes.

In Section 2, we present an overview of the main identification protocols, and corresponding signature schemes, based on error-correcting codes. In Section 3, we provide a quick review of the theory of p-Fibonacci error-correcting codes, also including some minor original results, and recall the main notions needed to define a zero-knowledge identification protocol. In Section 4, we describe an identification protocol based on p-Fibonacci codes and prove its security in the random oracle model. In Section 5, we compare our solution with similar schemes, and in Section 6, we finally draw the conclusions. In Appendix A, we provide a concrete example of our solution.

2. Related Works

In this section, we provide an overview of the literature regarding identification protocols and corresponding signature schemes, based on error-correcting codes (identification protocols based on other mathematical problems (e.g., [8]) or on symmetric primitives (e.g., [9]) might also exist).

The signature size of a proof of knowledge signature scheme is proportional to the communication cost of the identification protocol. Proof of knowledge signature schemes based on error-correcting codes usually provide very small keys, but large signatures. This comes from the fact that the identification protocol has a non-null cheating probability, i.e., the probability that someone not authorized is still able to authenticate to the verifier. Thus, the protocol must be repeated a certain number of times to reduce this probability close enough to zero.

The first of such schemes is due to Stern. In 1993, he proposed to use the Fiat–Shamir transform for turning a zero-knowledge identification protocol into a signature scheme. Stern’s protocol has a cheating probability of 2/3. Many researchers followed Stern’s approach, trying to improve either the key size or the signature of the scheme, by proposing variations of the underlying identification protocol. In 1997, Veron [2] presented the dual of the three-pass Stern proposal, still with cheating probability 2/3. Veron used a generator matrix G of the code, instead of the parity-check matrix as a public parameter, and used a pair $(x,e)$ as a secret key and a codeword $y=xG+e$ as a public key. This allows sending less data on average during the response step, implying slightly shorter signatures. More than ten years later, in 2010 [10], the authors presented a five-pass identification protocol with a cheating probability of 1/2, using codes over the binary extension field, rather than the binary field, as done by Stern and Veron. Passing from a cheating probability of 2/3 to 1/2 decreased significantly the number of times the identification protocol had to be run, and thus the corresponding signature size. In [11], it was shown how to extend the Fiat–Shamir transform to an n-pass protocol (with n odd). In 2011, Gaborit, Schrek, and Zémor [12] obtained a further significant reduction of both key and signature sizes by presenting the rank metric version of the Stern identification protocol. Switching from the Hamming to rank metric is a common strategy to reduce the parameters size of a code-based cryptosystem, since rank metric decoding has quadratic exponential complexity, while Hamming metric decoding is linear exponential. Again in 2011, Aguilar, Gaborit, and Schrek (AGS) [13], used double circulant codes in the Hamming metric. In this way, they reduced the key size of the Veron scheme; moreover, they presented a five-pass version of it, with the cheating probability approximately equal to 1/2. They also introduced a compression technique that reduced the signature size. Recently, a rank metric version of Veron and CVE (Cayrel-Véron-El Yousfi) was provided, though lacking a security proof [14]. Finally, in [15], the rank metric version of the AGS scheme was presented, currently holding the best signature plus public key size among all signature schemes based on error-correcting codes. A similar construction [16] was also used to build zero-knowledge proofs.

Proof of knowledge signature schemes are also quite common in other post-quantum settings, such as in lattice-based [3,4], multivariate-based [5], or multiparty computation-based [6] signatures.

Our Contribution

In this work, we present the analogue of the three-pass Veron identification protocol [2] using a new type of code, introduced by Stakhov in 2006 [17], which have a simpler set of parameters with respect to the rank metric, but a similar decoding complexity (quadratic in the exponent), thus allowing reaching similar sizes as in the rank metric, but with more simplicity in the selection of the parameters.

In 2006, Stakhov [17] introduced a new technique, based on the so-called Fibonacci p-numbers or p-sequence, further analyzed in [18], to obtain error-correcting codes. A few generalizations of his theory were explored in [17] (Fibonacci $(p,m)$-sequence) [19] (Fibonacci polynomial sequence), and [20] (Fibonacci $M_p$-sequence), but apart from that, the theory behind these codes has not received much attention, probably due to the fact that their error model is very unlikely to be applicable in real life for error correction. The aim of this paper is to show that this type of code deserves to be investigated more deeply, as it could be very useful in cryptographic applications.

3. Preliminaries

In this section, we first introduce the p-Fibonacci error-correcting codes, and then, we provide the fundamental ideas and definitions regarding zero-knowledge identification protocols.

3.1. p-Fibonacci Error Correcting Codes

With ${\mathcal{M}}_r\left(R\right)$, we indicate the set of all square matrices of size $r\times r$ with entries in the ring R. We also indicate with ${\mathbb{N}}_{<2^r}$ the set of integers that are representable with r bits and with ${\mathbb{Q}}_{<2^r}$ the set of rational numbers representable with two integers of r bits each.

The Fibonacci p-numbers, or Fibonacci p-sequence, are defined as the numerical sequence $a_{p,n}$ given by the recursive relation $a_{p,n}=a_{p,n-1}+a_{p,n-p-1}$, with initial values $a_{p,1}=\dots =a_{p,p+1}=1$.

For a given integer $p\ge 1$, the p-Fibonacci matrix $Q_p$ is a $(p+1)\times (p+1)$ matrix of the following form:

$$Q_p=\left[\begin{array}{ccccccc}1& 1& 0& 0& \dots & 0& 0\\ 0& 0& 1& 0& \dots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \dots & 1& 0\\ 0& 0& 0& 0& \dots & 0& 1\\ 1& 0& 0& 0& \dots & 0& 0\end{array}\right].$$

Some of the properties of the $Q_p$ matrix are stated in what follows (see [18]).

Proposition 1.

For any positive integer p and$n=0,\pm 1,\pm 2,\dots :$

• The n-th power of $Q_p$ is given by:

  $$Q_p^n=\left[\begin{array}{ccccc}{a}_{p,n+1}& a_{p,n}& \dots & a_{p,n-p+2}& a_{p,n-p+1}\\ a_{p,n-p+1}& a_{p,n-p}& \dots & a_{p,n-2p+2}& a_{p,n-2p+1}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ a_{p,n-1}& a_{p,n-2}& \dots & a_{p,n-p}& a_{p,n-p-1}\\ a_{p,n}& a_{p,n-1}& \dots & a_{p,n-p+1}& a_{p,n-p}\end{array}\right],$$

  where $a_{p,n}$ is the Fibonacci p-number.
• $Q_p^n·Q_p^m=Q_p^m·Q_p^n=Q_p^{n+m}$,
• $Q_p^n=Q_p^{n-1}+Q_p^{n-p-1}$,
• $det\left(Q_p\right)={(-1)}^p$, and $det\left(Q_p^n\right)={(-1)}^{pn}$.

Notice that since $det\left(Q_p^n\right)\ne 0$, then the matrix $Q_p^n$ is invertible.

Fibonacci $Q_p$ matrices allow defining a method to encode and decode a message M and also detecting and correcting errors that might occur in the transmission of the encoding of M.

The message M must be represented as a $(p+1)\times (p+1)$ matrix over ${\mathbb{N}}_{<2^r}\backslash \left\{0\right\}$, i.e., whose entries are r bit strings representing a positive integer. For this reason, we consider M such that its bit size $\left|M\right|$, which can also be seen as the dimension of the code, is a multiple of ${(p+1)}^2$. Then, the encoding of M is performed with the matrix multiplication $C=M·Q_p^n$ for a certain positive integer n, while the decoding of C, if no error occurred, is done simply by $M=C·{\left(Q_p^n\right)}^{-1}$. Since $det\left(C\right)=det(M·Q_p^n)={(\pm 1)}^{pn}det\left(M\right)$, if this relation does not hold, we can deduce that some errors occurred in the transmission of C, and the received matrix is $R=M·Q_p^n\oplus E$, for some $(p+1)\times (p+1)$ matrix E. Notice that the errors occur by modifying some bits of the transmitted matrix; thus, we have to use the addition ⊕ in the binary field ${\mathbb{F}}_2$, i.e., the XOR operation, when adding the error, rather than the standard addition over the integers. The procedure to correct such errors exploits the fact that the entries $c_{ij}$ of C satisfy a relation of the type:

$$\frac{a_{p,n}}{a_{p,n-k}}\lessgtr \frac{c_{i,j}}{c_{i,j+k}}\lessgtr \frac{a_{p,n+1}}{a_{p,n-k+1}}$$

with $i,j=1,\dots ,p+1$, $k=1,\dots ,p$, $2\le j+k\le p+1$, and $n>p+1$ (see [18] or [21]). In particular, the decoding method described by Stakhov allows correcting up to ${(p+1)}^2-1$ incorrect entries of C, which we refer to as integer errors. As we will show later in this section, the initial analysis of Stakhov did not take into account information theoretic results, as, for example, the Singleton bound. After computing the redundancy of p-Fibonacci codes and applying the Singleton bound [22], we also provide a bound on the maximum number of bit errors that the p-Fibonacci code can correct. Among all possible integer error types, detecting and correcting ${(p+1)}^2-1$ erroneous entries require the highest amount of work. In [19], the authors proved that in this worst case, the error correction can be performed in $\mathcal{O}{2}^{{(p+1)}^2}$ operations. In particular, $2^{{(p+1)}^2}-2$ sub-determinants of R must be computed.

In the following proposition, we provide an upper bound of the redundancy of the code.

Proposition 2.

(p-Fibonacci code redundancy). Let us consider the message space $\mathcal{M}={\{0,1\}}^k$, with $k={(p+1)}^{2}r$ for some integers p and r, so that we can split a message into ${(p+1)}^2$ blocks of an equal bit size. Fix n, then a codeword of a p-Fibonacci code with generator matrix $Q_p^n$ can be represented with $l{(p+1)}^2$ bits, with:

$$l\le r+\lceil {log}_2(p+1)+(n-1){log}_2{\alpha }_1\rceil ,$$

where ${\alpha }_1$ is the root greatest in modulo of $x^{p+1}-x^p-1$.

Proof. 

Let ${\alpha }_1$ be the root greatest in modulo of $x^{p+1}-x^p-1$ and ${\alpha }_2,\dots ,{\alpha }_{p+1}$ the remaining roots. We set $a_{p,-p+1}=\dots =a_{p,0}=0$, so that ${\left(a_{p,n}\right)}_{n\ge -p+1}$ is a linear recurrent sequence with characteristic polynomial $x^{p+1}-x^p-1$. By the Binet formula, we have that:

$$a_{p,i}=A_1{\alpha }_1^{i+p-1}+\dots +A_{p+1}{\alpha }_{p+1}^{i+p-1},$$

for any $i\ge 0$, where $A_1,\dots ,A_{p+1}$ are real numbers depending on the initial conditions of the sequence. Since, $a_{p,-p+1}=\dots =a_{p,0}=0$, and $a_{p,1}=1$, it is straightforward to find that:

$$A_k=\frac{1}{{\prod }_{\begin{array}{c}1\le j\le p+1\\ j\ne k\end{array}}({\alpha }_k-{\alpha }_j)}.$$

Thus,

$$a_{p,i}\approx {\alpha }_1^{i-1}+\dots {\alpha }_{p+1}^{i-1}$$

and $\left|a_{p,i}\right|\le (p+1)\left|{\alpha }_1^{i-1}\right|$. Now, having $M=\left(m_{ij}\right)$ the message, whose entries have bit size r, we consider $C=\left(c_{ij}\right)$ the codeword obtained by $C=M{Q}_p^n$. Since $\left(a_{p,n}\right)$ is an increasing sequence, the entry of C with the maximum length is in the first column. Recalling that all the $m_{ij}$’s have bit size equal to r, the bit size of $c_{ij}$ will be at most $r+\lceil {log}_2(p+1){\alpha }_1^{n-1}\rceil$, i.e.,

$$l\le r+\lceil {log}_2(p+1)+(n-1){log}_2{\alpha }_1\rceil .$$

□

Let us denote with ${\mathsf{w}}_{\mathsf{F}}\left(X\right)$ the number of non-zero entries of the integer matrix X. We refer to this value as the Fibonacci weight of the matrix X.

The following definition allows us to formally define the problem of decoding Fibonacci error-correcting codes.

Definition 1

(Fibonacci Decoding (FD) distribution). For positive integers $r,l,n,p,w_F,\Delta$ with $n>p+1$, $l>r$, the Fibonacci Decoding FD($r,n,p,w_F,\Delta$) distribution chooses $M\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ and $E\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$ with ${\mathsf{w}}_{\mathsf{F}}\left(E\right)=w_F$, and $det\left(M\right)={(\pm 1)}^{pn}\Delta$ and outputs $(Q_p^n,R=M·Q_p^n\oplus E)$.

Problem 1

(Search Fibonacci decoding problem). Given the positive integers $r,l,n,p,w_F,\Delta$ such that $n>p+1$, $l>r$, $(Q_p^n,R)\in {\mathcal{M}}_{p+1}\left(\mathbb{N}\right)\times {\mathcal{M}}_{p+1}\left(\mathbb{N}\right)$ from the FD distribution, the Search Fibonacci Decoding problem SFD($r,n,p,w_F,\Delta$) asks to find $(M,E)\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)\times {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ such that:

1. 

$R=M·Q_p^n+E$,

2. 

${\mathsf{w}}_{\mathsf{F}}\left(E\right)=w_F$,

3. 

$det\left(M\right)={(\pm 1)}^{pn}\Delta$.

Remark 1.

Note that the SFD problem would be easy if we removed the last determinant condition, as one could simply fix a random $E^{\prime }$ with ${\mathsf{w}}_{\mathsf{F}}\left(E^{\prime }\right)=w_F$ and then compute $M=(R\oplus E^{\prime })Q_p^{-n}$. In general, given R and $Q_p^n$, it seems not possible to find two matrices $\tilde{M}$ and $\tilde{E}$ such that the above three conditions are all satisfied. Indeed, this could be done only solving ${(p+1)}^2$ non-linear diophantine equations. Moreover, we can observe that the number of possible matrices $\tilde{M}$ is ${(2^r-1)}^{{p+1}^2}$ and the number of possible matrices $\tilde{E}$ is ${(p+1)}^2·{(2^l-1)}^{{(p+1)}^2-1}$, with $l>r$. Thus, it is very hard to find two matrices $\tilde{M}$ and $\tilde{E}$ by brute force, also for small values of p. Indeed, if we randomly sample a matrix $\tilde{M}$, there is a unique corresponding matrix $\tilde{E}$; thus, the search space for such a matrix $\tilde{E}$ is greater than ${(p+1)}^2·{(2^l-1)}^{{(p+1)}^2-1}$. Moreover, note that not all random matrices in ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ are suitable, since $\tilde{M}$ must satisfy $det\tilde{M}=\pm \Delta$.

The previous problem can be seen as the analogue of the Syndrome Decoding (SD) problem in the Hamming metric or the Rank Syndrome Decoding (RSD) problem in the rank metric. While for the Hamming metric, the SD problem has been proven to be NP-complete [23], the RSD problem has recently been proven difficult with a probabilistic reduction to the Hamming setting in [24]. As we mentioned before, the FD problem is known to be hard in the case of $w_F={(p+1)}^2-1$ errors and becomes easier as $w_F$ decreases.

We can apply a random permutation to the vector components, in order to send a binary vector of a certain Hamming weight to any other vector with the same Hamming weight. These maps are used to hide the error positions from an attacker, so the number of all these maps needs to be large enough so that an attacker cannot explore it in polynomial time. It is possible to define a set of maps with the analogue property in the Fibonacci code case, i.e., maps sending a matrix E with ${\mathsf{w}}_{\mathsf{F}}\left(E\right)=w_F$ to any other matrix of the same Fibonacci weight as follows.

Definition 2.

Given $E\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ and $K_1,K_2\in {\mathcal{M}}_{p+1}\left(\mathbb{Q}\right)$, we define ${\sigma }_{K_1,K_2}\left(E\right):=K_1·E·K_2$. Moreover, let ${\mathcal{L}}_E$ and ${\mathcal{R}}_E$ be the set of matrices $K_1,K_2\in {\mathcal{M}}_{p+1}\left(\mathbb{Q}\right)$ such that:

• $det{\sigma }_{K_1,K_2}\left(E\right)=\pm detE$,
• ${\mathsf{w}}_{\mathsf{F}}\left({\sigma }_{K_1,K_2}\left(E\right)\right)={\mathsf{w}}_{\mathsf{F}}\left(E\right)$,
• ${\sigma }_{K_1,K_2}\left(E\right)\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$.

The previous definition does not provide a methodology to construct the maps ${\mathcal{L}}_E,{\mathcal{R}}_E$. Such a construction turns out to be somehow complex and hard to manipulate in our scenario. We thus define a subset of this map, with a simpler representation, whose cardinality is still large enough to properly hide the secret of our protocol. We can observe that, for all $E\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$, the permutation matrices ${\pi }_1,{\pi }_2$ of dimension $(p+1)\times (p+1)$ belong to ${\mathcal{L}}_E$ and ${\mathcal{R}}_E$. Thus, given a matrix $E\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$, we have a number of possible transformations ${\sigma }_{P_1,P_2}$, which satisfy the three conditions of the above definition, greater than ${((p+1)!)}^2$.

In the rest of the paper, we denote by $S_t$ the set of permutations over the integers $\{1,\dots ,t\}$, so that, with an abuse of notation, ${\sigma }_{P_1,P_2}\left(E\right)$ is defined by to permutations $P_1,P_2\in S_{p+1}$, permuting the rows and the columns of E.

Proposition 3.

1. 

Given $X,Y\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ such that ${\mathsf{w}}_{\mathsf{F}}\left(X\right)={\mathsf{w}}_{\mathsf{F}}\left(Y\right)$ and $detX=\pm detY$, it is possible to find $K_1\in {\mathcal{L}}_Y$ and $K_2\in {\mathcal{R}}_Y$ such that $X={\sigma }_{K_1,K_2}\left(Y\right)$.

2. 

Given $X={\sigma }_{K_1,K_2}\left(Y\right)$, there exist $H_1\in {\mathcal{L}}_X$ and $H_2\in {\mathcal{R}}_X$ such that ${\sigma }_{H_1,H_2}\left(X\right)=Y$.

Proof. 

• It is sufficient to take $K_1$ as the identity matrix and $K_2=Y^{-1}·X$ or $K_1=X·Y^{-1}$ and $K_2$ as the identity matrix.
• It is sufficient to take $H_1=K_1^{-1}$ and $H_2=K_2^{-1}$.

□

3.2. Zero-Knowledge Identification Protocols

For a complete introduction to the subject, we refer to [25], by which the following section was inspired.

An interactive proof system is a randomized (messages are created by means of, ideally fair, coin tosses) communication protocol involving two parties: a prover, denoted by $\mathsf{P}$, and a verifier, denoted by $\mathsf{V}$. The goal of $\mathsf{P}$ is to demonstrate (or prove) to $\mathsf{V}$ that a certain assertion, formulated by $\mathsf{P}$, is true. The role of $\mathsf{V}$ is to either accept or reject the proof (The term “proof” here differs from the traditional mathematical notion of a proof and refers to an interactive game wherein proofs are probabilistic rather than absolute. A proof in this context needs be correct only with bounded probability, although possibly arbitrarily close to one.). In general, it is possible to formulate interactive proofs for identification protocols as proofs of knowledge. In this case, $\mathsf{P}$ can demonstrate the knowledge of a secret s (e.g., a key or a password) by providing correct answers to pre-established queries about s. Note that proving the knowledge of a secret and proving its existence are two different problems.

When an interactive proof possesses the properties of completeness and soundness, it is called a proof of knowledge.

Informally, the property of completeness can be seen as requiring that the protocol behaves as intended, under the assumption that the parties are acting honestly.

Definition 3

(Completeness property). An interactive proof (protocol) is complete if, given an honest prover and an honest verifier, the protocol succeeds with overwhelming probability (i.e., the verifier accepts the prover’s claim).

Usually, with the term “overwhelming”, it is intended that the protocol failure probability is not significant in practice (exponentially small with respect to the input size). For some applications, this term might indicate stricter or more relaxed requirements.

Definition 4

(Soundness property). An interactive proof (protocol) is sound if there exists an expected polynomial time algorithm $\mathcal{A}$ with the following property: if a dishonest prover (impersonating $\mathsf{P}$) can, with non-negligible probability, successfully execute the protocol with $\mathsf{V}$, then $\mathcal{A}$ can be used to extract from this prover knowledge (essentially equivalent to $\mathsf{P}$’s secret), which, with overwhelming probability, allows successful subsequent protocol executions.

The property of soundness serves the purpose of guaranteeing that the protocol is generating an actual proof of knowledge. This is achieved since any impersonation of $\mathsf{P}$ requires the knowledge of $\mathsf{P}$’s secret or of equivalent information (for example, by extracting it from $\mathsf{P}$ in polynomial time by means of $\mathcal{A}$). In other words, soundness assures that no dishonest prover can convince an honest verifier. On the other hand, by itself, soundness does not assure that deriving the secret from $\mathsf{P}$ is hard.

The conventional strategy to prove the soundness property of a protocol is to hypothesize about the existence of a dishonest prover that can run the protocol with a successful outcome and then illustrate how such a capability implies being able to derive the actual secret of $\mathsf{P}$.

While the soundness property is required for an interactive proof of knowledge to be used in cryptography, the crucial aspect of a zero-knowledge protocol is the zero-knowledge property.

In the following, we refer to the the collection of messages resulting from the protocol execution as the transcript.

Definition 5

(Zero-knowledge property). A protocol that is a proof of knowledge has the zero-knowledge property if it is simulatable in the following sense: there exists an expected polynomial time algorithm (simulator) that can produce, upon the input of the assertion(s) to be proven, but without interacting with the real prover, transcripts indistinguishable from those resulting from the interaction with the real prover.

The zero-knowledge property guarantees that from an execution of the protocol between a prover and a (even malicious) verifier, there is no leakage of information about the secret knowledge of the prover, except for the truth of the assertion. The only information that is allowed to be leaked is that that can be computed in polynomial time from the public information alone. As a consequence, assisting the communication does not help in impersonating the prover.

4. Veron Identification Protocol in the Fibonacci Setting

In this section, we describe a variation of the Veron identification protocol [2] using the p-Fibonacci error-correcting codes defined in Section 3.

4.1. Description of the Protocol

We denote by $\lambda$ the security level of the scheme, and with $\mathsf{H}$, we indicate a secure hash function. The key generation algorithm is listed in Figure 1, and we give here a brief example. The Fibonacci identification protocol is listed in Figure 2.

The operation ⊕ used to add $E^{\prime }$ to $M·Q_p^n$ in Step 4 of the key generation is a bit-wise XOR of the corresponding entries of the two matrices. This is done to assure that when adding (over the integers) the artificially constructed error E to $M·Q_p^n$, the entries of the resulting matrix R do not exceed l bits (a Magma implementation of our algorithm is available on GitHub at https://github.com/peacker/p-Fibonacci_identification_protocol, accessed on 5 April 2021).

Commitment Compression

In [13], it was shown how it is possible to reduce the size of commitments of a Stern or Veron-like identification protocol from $3\mathsf{h}$ to $2\mathsf{h}$, where $\mathsf{h}$ is the bit size of the underlying hash function. Furthermore, they showed how the technique can be applied to $\delta$ parallel rounds to reduce the size of commitments from $3\delta \mathsf{h}$ to $(\delta +1)\mathsf{h}$. The idea is that, since the verifier $\mathsf{V}$ is always able to recover two commitments given a certain value of b, then the prover $\mathsf{P}$ can send ${\mathsf{c}}_4=\mathsf{H}({\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3)$ instead of ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$ in the first commitment step and then attach the missing commitment $c^{\prime }$ to the response ${\mathsf{r}}_1,{\mathsf{r}}_2$. At this point, $\mathsf{V}$ only needs to check if the initially received ${\mathsf{c}}_4$ is equal to the hash of the values that it computed concatenated to $c^{\prime }$ in the proper order. In the case of $\delta$ parallel rounds, $\mathsf{P}$ computes $\mathsf{c}=\mathsf{H}({\mathsf{c}}_{1,1}\parallel {\mathsf{c}}_{1,2}\parallel {\mathsf{c}}_{1,3}\parallel \dots \parallel {\mathsf{c}}_{\delta ,1}\parallel {\mathsf{c}}_{\delta ,2}\parallel {\mathsf{c}}_{\delta ,3})$ and sends it to $\mathsf{V}$ as a commitment. Then, $\mathsf{V}$ sends $\delta$ challenges $b_i,i\in \{1,\dots ,\delta \}$ to $\mathsf{P}$, who attaches the proper missing commitment to the response of the corresponding round. Finally, $\mathsf{V}$ checks if $\mathsf{c}$ is equal to the hash of the values that it computed concatenated to the respective $c_i^{\prime }$ in the proper order. Notice that when $b_i=1$, the verifier also needs to check the Fibonacci weight of ${\mathsf{r}}_2$. This compression can be applied to obtain a more compact, though slightly less efficient, signature.

4.2. Zero-Knowledge Properties

In this section, we prove the security of the scheme using standard zero-knowledge proof arguments, meaning that we prove the completeness, soundness, and the zero-knowledge property of the scheme.

The security of the scheme is based on the difficulty of solving the Fibonacci decoding problem, and the security proof exploits the properties of the functions $\gamma$ and $\sigma$.

4.2.1. Completeness

Given the output $(\mathsf{sk},\mathsf{pk})$ of the $\mathsf{KGen}$ function, we can easily see that for all possible $\mathsf{sk}=(M,E)$, then $\mathsf{V}$ always accepts after interacting with $\mathsf{P}$ on common input $\mathsf{pk}$. Indeed, the honest prover, knowing $\mathsf{sk}$, is able to construct the commitments ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$. Moreover, since the verifications match with the given commitments, $\mathsf{V}$ is always able to identify $\mathsf{P}$.

4.2.2. Soundness

Theorem 1.

If a prover ${\mathsf{P}}^{\prime }$ correctly answers all three challenges, then either he/she can find a collision for the hash function or he/she accesses the secret key.

Proof. 

Let us define ${\sigma }_i={\sigma }_{P_{1,i},P_{2,i}},P_{1,i},P_{2,i}\in S_{p+1}$, for some index i. Suppose that, given the three commitments ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$, the prover ${\mathsf{P}}^{\prime }$ is able to answer in the three cases $b=0,1,2$. This means ${\mathsf{P}}^{\prime }$ knows:

• ${\sigma }_0,Z_0$ such that ${\mathsf{c}}_1=\mathsf{H}\left({\sigma }_0\right)$ and ${\mathsf{c}}_2=\mathsf{H}\left({\sigma }_0(Z_0·Q_p^n)\right)$;
• $V_1,W_1,X_1$ such that ${\mathsf{c}}_2=\mathsf{H}\left(V_1\right)$, ${\mathsf{c}}_3=\mathsf{H}(V_1+W_1,X_1)$, $det\left(M\right)=\pm det(V_1+X_1)$, and ${\mathsf{w}}_{\mathsf{F}}\left(W_1\right)={(p+1)}^2-1$;
• ${\sigma }_2,Z_2$ such that ${\mathsf{c}}_1=\mathsf{H}\left({\sigma }_2\right)$ and ${\mathsf{c}}_3=\mathsf{H}({\sigma }_2(Z_2·Q_p^n+R),-{\sigma }_2(Z_2·Q_p^n))$.

Thus, either ${\mathsf{P}}^{\prime }$ has found a collision for the hash function or the preimages of ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$ are equal, meaning that:

• From ${\mathsf{c}}_1$ preimages: ${\sigma }_0={\sigma }_2$,
• From ${\mathsf{c}}_2$ preimages: $V_1={\sigma }_0(Z_0·Q_p^n)$,
• From ${\mathsf{c}}_3$ preimages: $V_1+W_1={\sigma }_2(Z_2·Q_p^n+R)$, and $X_1=-{\sigma }_2(Z_2·Q_p^n)$.

Combining the previous equations, we obtain that: ${\sigma }_0(Z_0·Q_p^n)+W_1={\sigma }_2(Z_2·Q_p^n+R)$. Thanks to the linearity and invertibility of ${\sigma }_0$, we can isolate $R=(Z_0-Z_2)·Q_p^n+{\sigma }_0^{-1}\left(W_1\right)$.

Note that $det(Z_0-Z_2)=\pm det\left({\sigma }_0((Z_0-Z_2)·Q_p^n)\right)=\pm det({\sigma }_0(Z_0·Q_p^n)-{\sigma }_0(Z_2·Q_p^n))=\pm det(V_1+X_1)=\pm det\left(M\right)$.

Since we also have that ${\mathsf{w}}_{\mathsf{F}}\left({\sigma }_0^{-1}\left(W_1\right)\right)={\mathsf{w}}_{\mathsf{F}}\left(W_1\right)={(p+1)}^2-1$, this means that the secret key associated with the public key $\mathsf{pk}=R$ is $(Z_0-Z_2,{\sigma }_0^{-1}\left(W_1\right))$. Thus, ${\mathsf{P}}^{\prime }$ is able to construct the unique secret solution of the Fibonacci decoding problem. □

Since ${\mathsf{P}}^{\prime }$ is never able to answer the three cases, as a corollary, we have that the probability of cheating must be less than or equal to $2/3$. We now prove that it is exactly $2/3$. To properly guess any two challenges among three, a cheater must proceed as follows:

• if $b=0$ or 1:

  −

  pick randomly the values

  $P_1,P_2$ $S_{p+1}$, $Y,Z$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$ such that $det\left(M\right)=\pm det(Y+Z)$, F ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$,

  such that ${\mathsf{w}}_{\mathsf{F}}\left(F\right)={(p+1)}^2-1$.

  −

  Compute ${\mathsf{c}}_1=\mathsf{H}(P_1,P_2),{\mathsf{c}}_2=\mathsf{H}\left({\sigma }_{P_1,P_2}(Z·Q_p^n)\right),{\mathsf{c}}_3=\mathsf{H}({\sigma }_{P_1,P_2}(Z·Q_p^n+F),-$${\sigma }_{P_1,P_2}(Z·Q_p^n))$.

  −

  If $b=0$, reveal $P_1,P_2,Z$.

  If $b=1$, reveal ${\sigma }_{P_1,P_2}(Y·Q_p^n),{\sigma }_{P_1,P_2}(Z·Q_p^n),{\sigma }_{P_1,P_2}\left(F\right)$.

  Verification follows.
• if $b=0$ or 2:

  −

  pick randomly the values

  $P_1,P_2$ $S_{p+1},U$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$, $Z$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$.

  −

  Compute ${\mathsf{c}}_1=\mathsf{H}(P_1,P_2),{\mathsf{c}}_2=\mathsf{H}\left({\sigma }_{P_1,P_2}(Z·Q_p^n)\right),{\mathsf{c}}_3=\mathsf{H}\left({\sigma }_{P_1,P_2}(U·Q_p^n+R)\right)$.

  −

  If $b=0$, reveal $P_1,P_2,Z$.

  If $b=2$, reveal $P_1,P_2,U$.

  Verification follows.
• if $b=1$ or 2:

  −

  pick randomly the values

  $P_1,P_2$ $S_{p+1},U$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ such that $det\left(M\right)=\pm det\left(U\right)$,

  $F$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$, such that ${\mathsf{w}}_{\mathsf{F}}\left(F\right)={(p+1)}^2-1$

  −

  Compute ${\mathsf{c}}_1=\mathsf{H}(P_1,P_2),{\mathsf{c}}_2=\mathsf{H}\left({\sigma }_{P_1,P_2}(U·Q_p^n+R-F)\right),{\mathsf{c}}_3=\mathsf{H}({\sigma }_{P_1,P_2}(U·Q_p^n+R),-{\sigma }_{P_1,P_2}(U·Q_p^n))$.

  −

  If $b=1$, reveal ${\sigma }_{P_1,P_2}(U·Q_p^n-F),{\sigma }_{P_1,P_2}(U·Q_p^n+R-F),{\sigma }_{P_1,P_2}\left(F\right)$.

  If $b=2$, reveal $P_1,P_2,U$.

  Verification follows.

We thus proved that the probability of cheating is exactly $2/3$.

4.2.3. Zero-Knowledge

To prove zero-knowledge, a simulator $\mathsf{Sim}$ of the scheme must be constructed. Let $\mathsf{V}$ be a verifier. It is possible to construct $\mathsf{Sim}$ in such a way that it can answer any of the three challenges, as follows:

• $\mathsf{Sim}$ chooses randomly $P_1,P_2$ $S_{p+1},V,V^{\prime }$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ such that $det(V+V^{\prime })=det\left(M\right)$, and $F$ ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$ such that ${\mathsf{w}}_{\mathsf{F}}\left(F\right)={(p+1)}^2-1$.
  $\mathsf{Sim}$ also chooses $j\in \{0,1,2\}$ corresponding to the challenge it is trying to guess.
  • If $j=0$, $\mathsf{Sim}$ sends ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$ such that:
    ${\mathsf{c}}_1=\mathsf{H}(P_1,P_2),{\mathsf{c}}_2=\mathsf{H}({\sigma }_{P_1,P_2}(V+V^{\prime })·Q_p^n),{\mathsf{c}}_3=\mathsf{H}\left(V\right)$.
  • If $j=1$, $\mathsf{Sim}$ sends ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$ such that:
    ${\mathsf{c}}_1=\mathsf{H}\left(V\right),{\mathsf{c}}_2=\mathsf{H}\left({\sigma }_{P_1,P_2}((V+V^{\prime })·Q_p^n)\right),{\mathsf{c}}_3=\mathsf{H}({\sigma }_{P_1,P_2}(V·Q_p^n+V^{\prime }·Q_p^n+F),-{\sigma }_{P_1,P_2}(V·Q_p^n))$.
  • If $j=2$, $\mathsf{Sim}$ sends ${\mathsf{c}}_1,{\mathsf{c}}_2,{\mathsf{c}}_3$ such that:
    ${\mathsf{c}}_1=\mathsf{H}(P_1,P_2),{\mathsf{c}}_2=\mathsf{H}\left(V\right),{\mathsf{c}}_3=\mathsf{H}\left({\sigma }_{P_1,P_2}(V·Q_p^n+R)\right)$.
• $\mathsf{V}$ chooses $b\in \{0,1,2\}$.
• If $b=0$, $\mathsf{Sim}$ sends $P_1,P_2,V+V^{\prime }$.
  If $b=1$, $\mathsf{Sim}$ sends ${\sigma }_{P_1,P_2}(V^{\prime }·Q_p^n),{\sigma }_{P_1,P_2}((V+V^{\prime })·Q_p^n),{\sigma }_{P_1,P_2}\left(F\right)$.
  If $b=2$, $\mathsf{Sim}$ sends $P_1,P_2,V$.
• If $b=j$, the execution provides a valid transcript ($\mathsf{V}$ verifies correctly), and $\mathsf{Sim}$ saves the execution. Otherwise, $\mathsf{Sim}$ restarts the execution.

$\mathsf{Sim}$ succeeds if it is able to store l transcripts of the execution with $b=j$. This can be achieved by running the execution $3l$ times, since the probability of $b=j$ is $1/3$. The simulated transcript is indistinguishable from the real one, since in the commitment step, only hash values are sent, while in the response step, the following distributions are sent:

• $b=0$: the simulated transcript contains $P_1,P_2,V+V^{\prime }$, while the real one $P_1,P_2,U+M$;
• $b=1$: the simulated transcript contains ${\sigma }_{P_1,P_2}(V·Q_p^n),{\sigma }_{P_1,P_2}((V+V^{\prime })·Q_p^n),{\sigma }_{P_1,P_2}\left(F\right)$, while the real one ${\sigma }_{P_1,P_2}(U·Q_p^n),{\sigma }_{P_1,P_2}((U+M)·Q_p^n),{\sigma }_{P_1,P_2}\left(E\right)$;
• $b=2$: the simulated transcript contains $P_1,P_2,V$, while the real one $P_1,P_2,U$.

The values $V,V^{\prime },P_1,P_2$ are sampled following the uniform distribution, and so do $U+M$ and U in, respectively, steps $b=0$ and $b=2$. In step $b=1$, ${\sigma }_{P_1,P_2}((V+V^{\prime })·Q_p^n)$ follows again the uniform distribution the same way as ${\sigma }_{P_1,P_2}((U+M)·Q_p^n)$, while, because of the property of $P_1,P_2$, ${\sigma }_{P_1,P_2}\left(E\right)$ and ${\sigma }_{P_1,P_2}\left(F\right)$ are taken uniformly from the set of all matrices of weight ${(p+1)}^2-1$.

To conclude, anyone using $\mathsf{Sim}$ can simulate an execution of the scheme without knowledge of the secret key.

This concludes the proof that the scheme is zero-knowledge.

5. Comparisons

The aim of this section it to provide a fair comparison with other three-pass identification protocols based on error-correcting codes. For this comparison, we take into consideration the Veron identification protocol for security level $\lambda =128,96,80$ and its instantiations using a generic linear code and double circulant codes, both in the Hamming and rank metric. We omit the Stern protocol in the comparison as the results would be very similar.

To choose the parameters of our instantiation of the Veron protocol with Fibonacci codes for security level $\lambda =128$, we need to choose an integer p such that ${log}_2\left(2^{{(p+1)}^2}\right)={(p+1)}^2\ge 128$ (this condition implies that the Fibonacci decoding problem is exponentially hard) and such that the space $S_{p+1}^2$ of the permutations $P_1,P_2\in S_{p+1}$ is too large for an adversary to be explored, i.e., $|S_{p+1}^2|{=((p+1)!)}^2\ge 2^{128}$. The smallest such p is 20, for which ${log}_2\left(2^{{(p+1)}^2}\right)=441$ and ${log}_2\left({((p+1)!)}^2\right)\approx 130.94$. Since $n>p+1$, we can choose $n=22$. The smallest meaningful r is two (recall that each entry of the message M has to be positive).

The secret key of the protocol is composed by $M\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ and $E\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$, thus requiring $r{(p+1)}^2+l{(p+1)}^2$ bits.

The public key is the matrix $R\in {\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^l}\right)$, where each entry of the matrix has at most l bits, as shown in Proposition 2, thus requiring $l{(p+1)}^2$ bits. It is easy to verify computationally that for $(p,n)=(20,2)$, then $l=10$. The communication cost of each round of all the variations of the protocol is the same for the commitment and challenge step, i.e., it includes three hashes of length $\mathsf{h}$ for the commitment step and two bits for the challenge step, for a total of $3\mathsf{h}+2$ bits. The response step cost is given by $P_1,P_2$ plus a matrix in ${\mathcal{M}}_{p+1}\left({\mathbb{N}}_{<2^r}\right)$ with probability 2/3 (when $b=0,2$) and three matrices in ${\mathcal{M}}_{p+1}\left({\mathbb{Q}}_{<2^l}\right)$ (where l is the bit size of a single entry of the encoded matrix) with probability 1/3 (when $b=1$). The function $\sigma$ is determined by two permutations of $p+1$ elements, which can be represented with $(p+1){log}_2(p+1)$ bits. Then, the total communication cost sums to $3\mathsf{h}+2+2(p+1){log}_2(p+1)+r{(p+1)}^2$ when $b=0,2$ and to $3\mathsf{h}+2+3l{(p+1)}^2$ when $b=1$.

In

Table 1. Comparison of parameters, keys, and communication bit sizes in various instantiations of the Veron identification protocol. GL, Generic Linear; DC, Double Circulant.

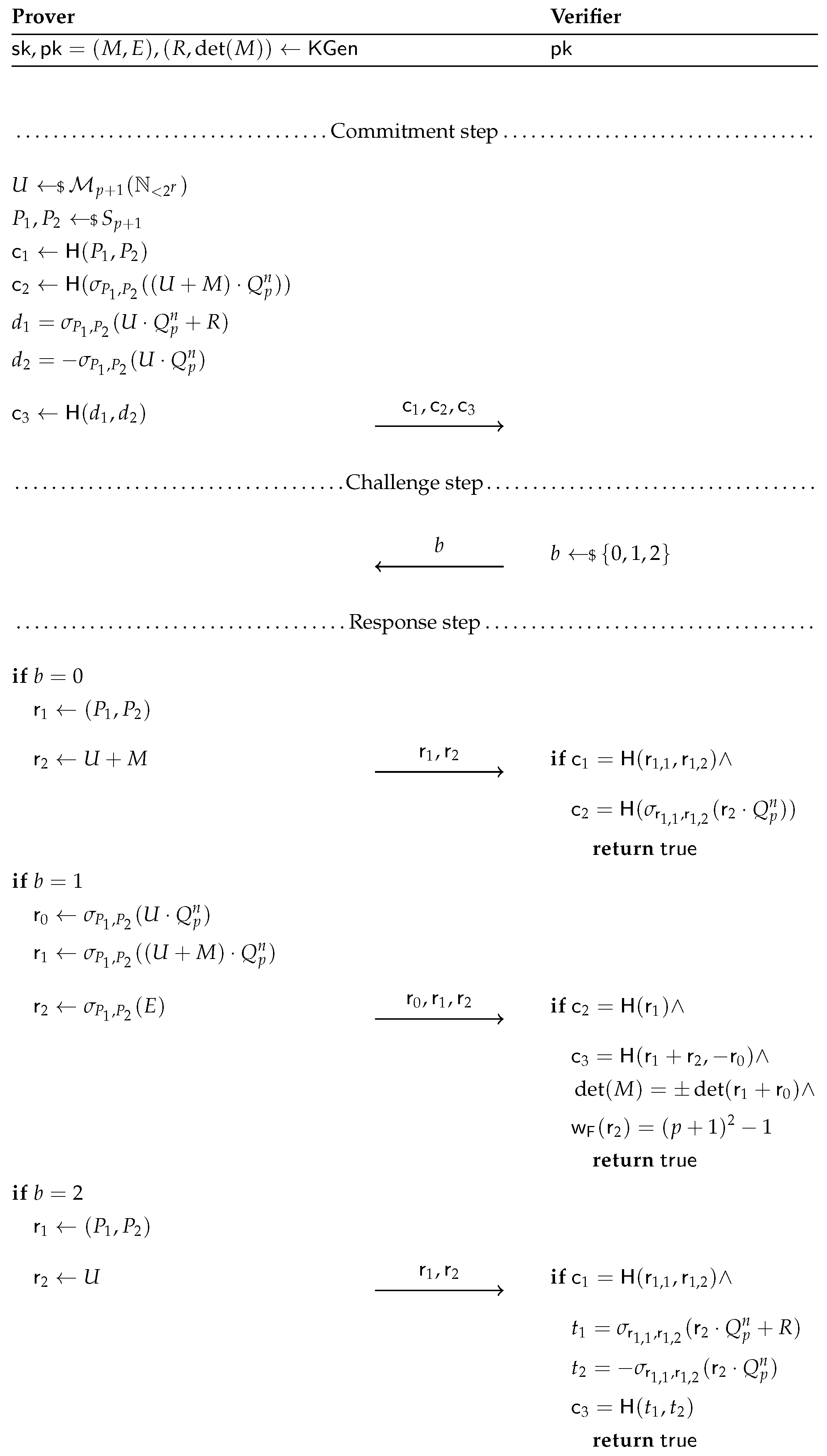
		Hamming		Rank
Code	Fibonacci	GL [2]	DC [13]	GL [14]	DC [15]
Best known attack A	$min(2^{{(p+1)}^2}$ [19], ${((p+1)!)}^2)$	$2^{0.097n}$ [26]		$\begin{array}{cc}\hfill min(& {(n-k)}^3{m}^3{q}^{r\frac{(k+1)m}{n}-m},\hfill \\ & r^3{k}^3{q}^{r⌈\frac{(r+1)(k+1)-(n+1)}{r}⌉})\hfill \end{array}$ [27]
Code parameters	$(r,p,n)$	$(q,n,k,w)$	$(q,n,w)$	$(q,m,n,k,r)$	$(q,m,n,r)$
Public param.size	${log}_{2}r+{log}_{2}p+{log}_{2}n$	$k(n-k)+{log}_r$	$n+{log}_{2}r$	$mk(n-k)+{log}_{2}r$	$mn+{log}_{2}r$
$\left|\mathsf{sk}\right|$	$r{(p+1)}^2+l{(p+1)}^2$	$k+n$	$k+n$	$m(k+n)$	$m(k+n)$
$\left|\mathsf{pk}\right|$	$l{(p+1)}^2$	n	n	$mn$	$mn$
Rsp.step cost $b=0,2$	$2(p+1){log}_2(p+1)+r{(p+1)}^2$	$nlogn+k$	$nlogn+k$	$m^2+n^2+mk$	$m^2+n^2+mk$
Response step cost $b=1$	$3l{(p+1)}^2$	$2n$	$2n$	$2mn$	$2mn$
Concrete parameters for $\lambda \sim 128$
$\lambda ={log}_2\left(A\right)$	130	128	128	124	124
Code parameters	( 2, 20, 22)	( 2, 1320, 660, 140)	( 2, 1320, 140)	( 2, 31, 26, 13, 8)	( 2, 31, 26, 8)
Public param. size	10	435,601	1321	5242	809
$\left|\mathsf{sk}\right|$	5292	1980	1980	1209	1209
$\left|\mathsf{pk}\right|$	4410	1320	1320	806	806
Rsp. step cost $b=0,2$	1066	14,343	14,343	2040	2040
Rsp. step cost $b=1$.	13,230	2640	2640	1612	1612
Concrete parameters for $\lambda \sim 96$
$\lambda ={log}_2\left(A\right)$	96	96	96	95	95
Code parameters	( 2, 16, 18)	( 2, 990, 495, 110)	( 2, 990, 110)	( 2, 29, 22, 11, 7)	( 2, 29, 22, 7)
Public param. size	10	245,026	991	3511	640
$\left|\mathsf{sk}\right|$	3468	1485	1485	957	957
$\left|\mathsf{pk}\right|$	2890	990	990	638	638
Rsp. step cost $b=0,2$	717	10,346	10,346	1644	1644
Rsp. step cost $b=1$.	8670	1980	1980	1276	1276
Concrete parameters for $\lambda \sim 80$
$\lambda ={log}_2\left(A\right)$	80	80	80	78	78
Code parameters	( 2, 14, 16)	( 2, 826, 413, 90)	( 2, 826, 90)	( 2, 23, 22, 11, 6)	( 2, 23, 22, 6)
Public param. size	9	170,570	827	2785	508
$\left|\mathsf{sk}\right|$	2475	1239	1239	759	759
$\left|\mathsf{pk}\right|$	2025	826	826	506	506
Rsp. step cost $b=0,2$	567	8416	8416	1266	1266
Rsp. step cost $b=1$.	6075	1652	1652	1012	1012

, we summarize the comparison with the parameters of the Veron protocol using Fibonacci codes against Generic Linear (GL) codes and Double Circulant (DC) codes both in the Hamming and rank metric. The first set of parameters that we proposed for the Fibonacci code offers a security of $\sim 131$ bit, while the parameters for Hamming and rank metric offer a security of at most 128. To provide a more complete comparison, we also analyzed a set of parameters for the security levels of 96 and 80 bits. For the decoding complexity A, we used the formula provided in [26] for the Hamming metric and in [27] for the rank metric. It is worth noting that in the case of the rank metric, many different algebraic and combinatorial attacks exists (e.g., [27,28,29,30]), depending on the relation among the parameters of the code, which are four (double circulant case) or five (generic linear code case). For this reason, the selection of parameters in the rank metric setting, which is the one providing better sizes, is somehow more involved. As a result of the comparison, we noticed that p-Fibonacci error-correcting codes allow reaching secret and public key sizes that are larger than the corresponding Hamming and rank metric analogues, unless one takes into account the public generator matrix of the code, which is orders of magnitude smaller in the Fibonacci case. The average communication cost is somehow in between the one of the Hamming and the one of rank metric, where a clear advantage is due to the compact communication used for the cases $b=0,2$.

To choose the number of rounds $\delta$, we proceed as follows. The impersonation probability of one single round is $P=2/3$. To reach a security level $\lambda$ with an impersonation probability of P, that is to compute the number of rounds $\delta$, we need to set $\delta ={log}_P(1/2^{\lambda })$. This results in $\delta =137$ for $\lambda =128$.

6. Conclusions and Future Works

We showed that p-Fibonacci error-correcting codes offer a promising solution when used as the underlying difficult problem in three-pass Stern-like protocols, both in terms of parameters, keys, and communication size, as well as in ease of selecting such parameters. On the other hand, the theory behind these codes must be further investigated, in particular the decoding complexity needs to be studied more thoroughly, in order to be able to give a more precise estimation of the parameters. It would also be interesting to understand if there exists some quantum acceleration that allows simplifying the decoding and if a signature scheme derived from our proposed identification protocol can be used as a quantum-resistant signature scheme. Further improvements of the scheme might include the reduction of the the communication cost, either by reducing the cheating probability from 2/3 to 1/2 or by finding a way of reducing the response size in the case of the challenge $b=1$. Finally, it would be interesting to compare our protocol with other instantiations of it using generalizations of the p-Fibonacci sequences, such as those based on Fibonacci polynomials sequences [19] or Fibonacci $M_p$-sequences [20].