1. Introduction
A phylogenetic tree with a given set of leaf labels is a weighted tree whose leaves have labels while their interior nodes do not have labels. In phylogenetics, leaves in a phylogenetic tree represent observable species in the current time and a tree represents an evolutionary relationship between these species in a given set .
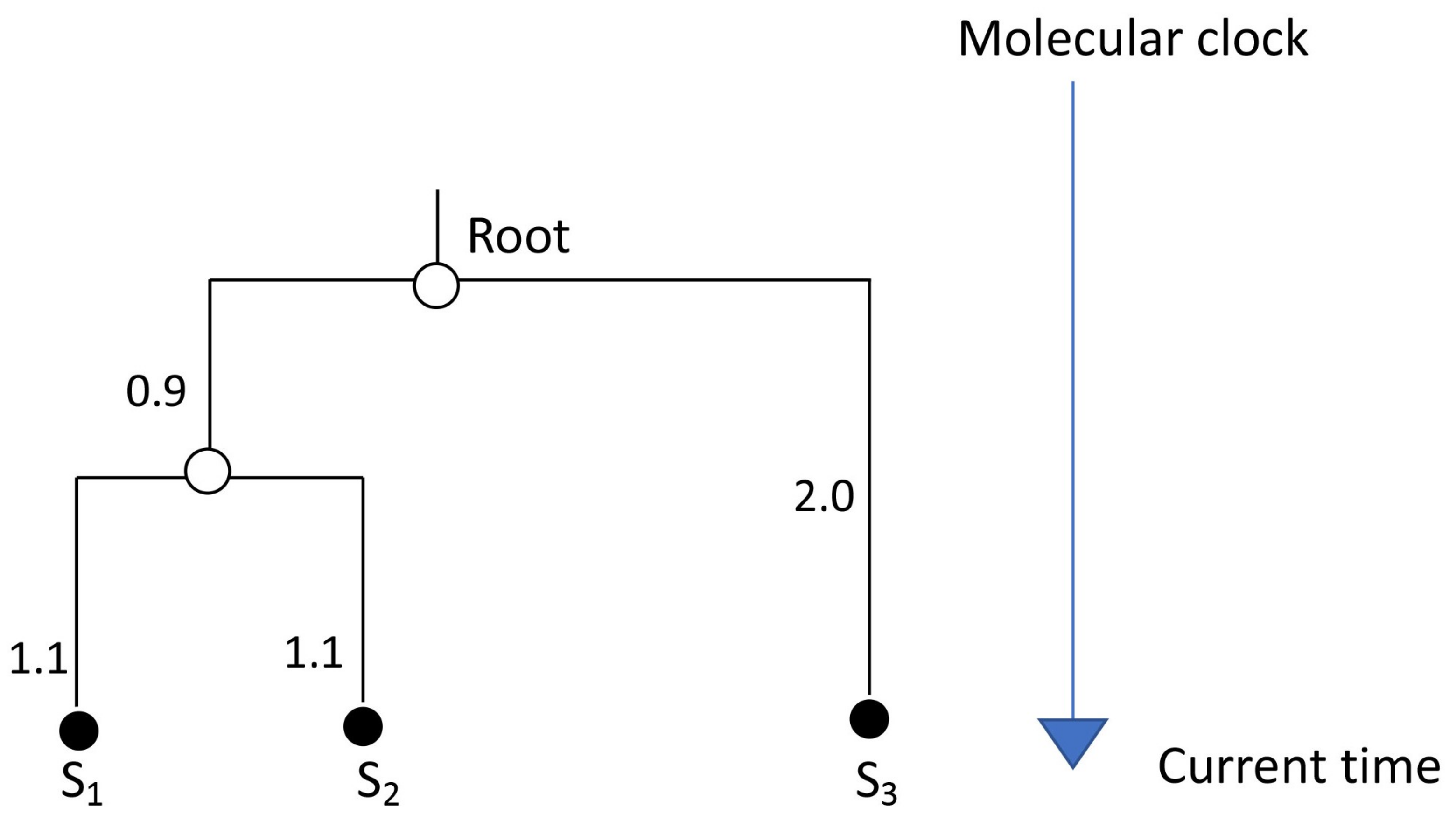
In order to study evolutionary histories of species or genes in terms of molecular clock, leaves in a phylogenetic tree represent a given set of observable species in the current time, internal nodes in the tree represent common ancestors and branch lengths in the tree present evolutionary time in a molecular clock. Since we assume that all species in the tree have the same most common ancestor (the root of a phylogenetic tree), a phylogenetic tree of a given set of species has the property that a distance from its root to each leaf is same for all leaves in the tree. We call such a rooted phylogenetic tree an
equidistant tree. An example of an equidistant tree is shown in
Figure 1. In phylogenetics and phylogenomics, we often use equidistant trees to analyze genome data since multispecies coalescent processes applied to analyze gene trees and species tree in genome data [
1] assume that all gene trees are equidistant trees.
Phylogenomics is a field in which we apply tools from phylogenetics to problems in genomics. More specifically, phylogenomics extracts information from comparative study on entire genomes by constructing phylogenetic trees from each gene. In phylogenomics, researchers are interested in problems like predictions of gene function; evolutionary relationships between genes; and finding lateral gene transfers. For specific examples, genetic drift and gene flow in ancestral populations can cause topological differences between gene trees [
1,
2,
3,
4]. In the statistical point of view, these problems can be seen as finding outliers from a sample of phylogenetics with the same set of leaf labels reconstructed from genes. However, a space of phylogenetics trees (the set of all possible phylogenetic trees with a given set of leaf labels
) is not Euclidean. Thus, we cannot just simply apply statistical methods over a Euclidean space. Therefore, we have to consider a space of phylogenetic trees, which contains all possible phylogenetic trees of the same leaf set.
There are several ways to define a space of phylogenetic trees (also known as a
tree space). These differences come from ways to define a phylogenetic tree and to
vectorize each phylogenetic tree into a vector-representation (see [
5] for details on differences between different tree spaces). In this paper we focus on the space of phylogenetic trees as the set of all equidistant trees with a fixed set of labels for leaves.
In 2009, Speyer and Sturmfels showed a space of phylogenetic trees is a tropical Grassmanian [
6], that is, a tropicalization of a linear space defined by a set of linear equations [
7], which is a linear subspace of the tropical projective torus, with the max-plus algebra. Therefore it is natural to use tropical geometry to develop statistical methods to analyze data points over a space of phylogenetic trees. In this paper, we use the
tropical metric. The tropical metric over a space of phylogenetic tree is well defined and [
8,
9] investigated its properties over the tree space. In 2020, Monod et al. in [
10] introduced
tropical balls over the space of phylogenetic trees with the tropical metric and defined probability measures using tropical balls. In [
10], Monod et al. defined tropical balls with the tropical metric over the tropical projective torus. In this paper we show properties of tropical balls over the tropical projective torus with the tropical metrics as well as the space of phylogenetic trees. Then, we compare tropical balls with balls defined with
norm and
norm.
The
K Nearest Neighbors (KNN) algorithm is an instance-based method which classifies a vector in a high-dimensional vector space into finite categories [
11]. The basic idea of the KNN algorithm is that all data points with the same category should be distributed near to each other. The KNN algorithm, first, considers the ball around the vector which you want to categorize. Next it increases the radius of the ball with a given metric until it contains
K many points from the training set. Then we assign the category to the input vector which is the majority of data points from the training set in the ball. KNN algorithm is well-studied and it is applied to “Big Data” [
12]. For example, [
13] showed that the KNN algorithm is a special case of kernel density estimator.
The KNN algorithm has been applied to classify data points over a lower dimensional manifold (for example, [
14]). However, since a space of phylogenetic trees is not a manifold over a Euclidean space and currently there has not been applied to classify data points over a space of phylogenetic trees. Therefore, in this paper, we consider
tropical KNN, that is, KNN algorithm with the tropical metric defined over the tropical projective torus under the max-plus algebra to KNN and then we applied tropical KNN to classify data points over a space of phylogenetic trees.
The contributions of this paper include that
we show some properties of a tropical ball in the tropical projective torus;
we show some properties of a tropical ball in a space of equidistant trees with a given set of leaves ;
we compare tropical balls with balls defined with norm and norm;
we define a tropical KNN algorithm; and
we applied tropical KNN algorithm to simulated data generated by a multispecies coalescent model.
2. Preliminaries
In this section, we set up some notation and definitions from phylogenetics and tropical geometry. For interested readers, see [
15] for more details.
First we discuss some definitions from phylogenetics. A
dissimilarity map w is a function
such that
If a dissimilarity map w satisfies a triangle inequality then w is called a metric. If there exists a phylogenetic tree T with the leaf labels such that the total branch length from a leaf to a leaf coincides with for all , then we call w a tree metric. In fact if w is a tree metric of a phylogenetic tree T, then T has a unique tree metric w and T is unique for a tree metric w.
Definition 1. If a metric w satisfies the following condition, such thatis achieved twice for every distinct , then we call a metric w an ultrametric.
To vectorize an equidistant tree, we can use an ultrametric w since there is a one-to-one mapping from a set of all possible equidistant trees with a leaf set to the space of all possible ultrametrics:
Theorem 1 ([
10]).
A tree metric w of a phylogenetic tree T with a set of leaf labels is an ultrametric if and only if T is an equidistant tree with a set of leaf labels . Therefore, in this paper, we define a space of equidistant trees with a leaf set as the space of ultrametrics notated as .
Now we shift our attentions to basics from tropical geometry. Throughout this paper we consider the max-plus tropical semiring .
Over this semiring, the tropical arithmetic operations of addition and multiplication are defined as the following:
Any semiring has to have the identity for addition and identity for multiplication. In this semiring, is the identity for addition and 0 is the identity for multiplication.
Let
and let
, where
, be the
tropical projective torus. Note that
. Scalar multiplication and vector addition can be defined as:
where
and
.
Through the paper, we use the tropical metric:
Definition 2. For , the tropical distance
between u and v is defined as: Recall that from Theorem 1 we consider the space of ultrametrics with labels as a space of all equidistant trees with the label set . Let be the space of ultrametrics for equidistant trees with the leaf labels . In fact we can write as the tropicalization of the linear space generated by linear equations over the tropical projective torus where .
Let
be the linear subspace of
defined by the linear equations:
for
. For the linear equations (
2) spanning the linear space
, the max-plus tropicalization
of the linear space
is the tropical linear space with
such that
achieves at least twice for all
. Note that this is exactly the three point condition defined in Definition 1.
Theorem 2 ([
7], [Theorem 2.18]).
is equal to . Therefore, by Theorem 2, is a tropical linear space in where . For example, if , the space of ultrametrics is a union of 15 two-dimensional polyhedral cones over the tropical projective torus .
3. Results
3.1. Properties of Tropical Balls over the Space of Ultrametrics
In this section we investigate the tropical ball in terms of the tropical metric in the space of ultrametrics
. Here we fix the height of the equidistant trees associate with their ultrametrics in
as 1. All proofs for Lemmas and Theorems in this section are in
Section 6. Recall
.
Lemma 1. If is from an ultrametric realizing an equidistant tree of height 1, then there is such that . In addition, We will investigate a tropical ball centered at a point in
with a radius
defined via the tropical metric
. We define a ball
at a point
with a radius
under the tropical metric
as the following:
In the rest of this section, we show some properties on tropical balls in :
Proposition 1. Suppose is the origin, that is, the ultrametric . In terms of equidistant trees, x represents a star tree with its height 1. Then for , Now we show that a tropical ball is convex in terms of the tropical metric. For Lemmas 2 and 3, and Theorem 3, let us consider the tropical projective torus .
Lemma 2. Suppose and . Then Lemma 3. Suppose and . Then Theorem 3. A tropical ball in the tropical projective torus is convex under the tropical metric .
Since is a tropical linear space over the tropical projective torus by Theorem 2 and since is convex, now we have the following theorem by Theorem 3.
Theorem 4. A tropical ball in is convex in terms of the tropical metric .
Until this moment in this section, we consider ultrametrics in . Even with a natural bijection between ultrametrics in and the space of equidistant trees described in Theorem 1, one might want to describe a tropical balls in terms of equidistant trees. In general we can describe a tropical ball in in terms of equidistant trees using the following theorem:
Theorem 5. Let be the set of all equidistant trees with their height and with the leaf set . Also let be a pairwise distance between leaves in an equidistant tree . Suppose . Then let . For an equidistant tree and for , 3.2. Examples in
In this section, we visualize tropical balls in the space of ultrametrics and in order to visualize, we consider
. To visualize tropical balls in
, we map all coordinates in
to the Billera-Holmes-Vogtmann (BHV) treespace [
16] using the one-to-one mapping described in [
17].
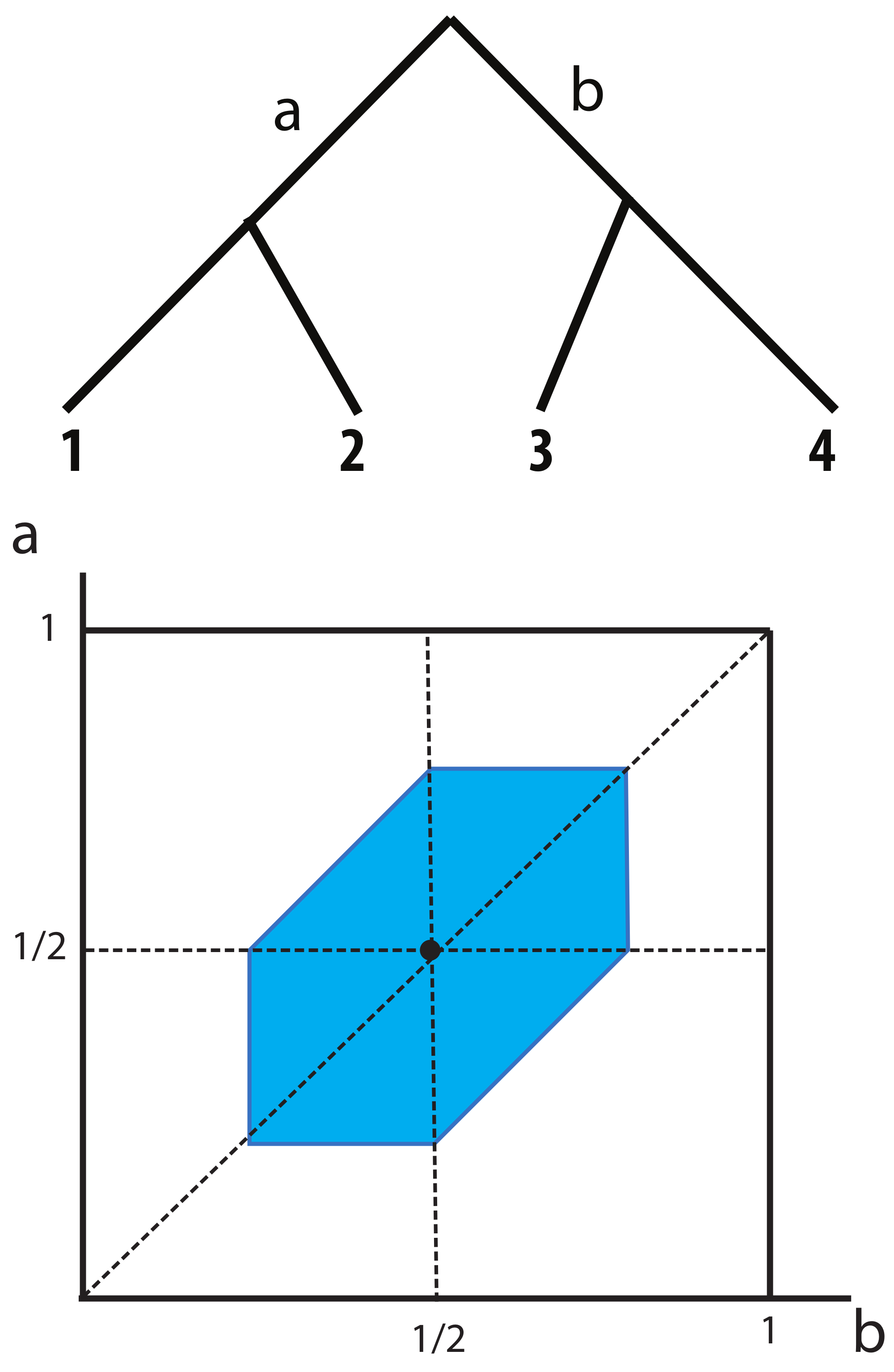
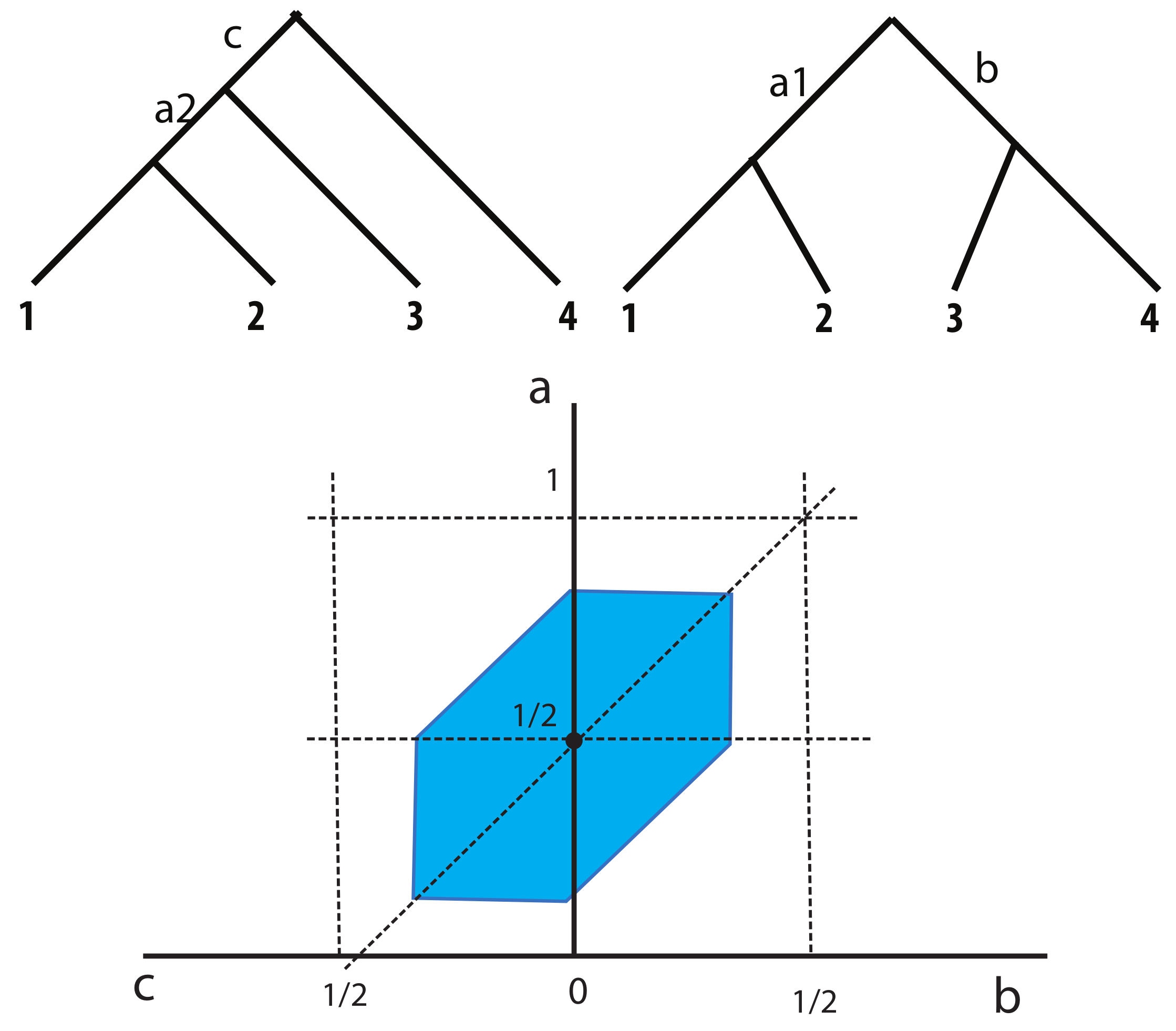
Example 1. First, we consider the tree shown in the left side of Figure 2. This is an example so that the center of a tropical ball and entire tropical ball are inside of an orthant for a tree topology in Figure 2. Here we have the height , so The corresponding ultrametric is The center of this tropical ball in this example is . The corresponding ultrametric is The tropical ball in mapped in the BHV tree space is shown in the right side of Figure 2. Example 2. For the second example, we consider the tree shown in the left side of Figure 3. This is also a tropical ball contained inside of an orthant for the tree topology shown in Figure 3. Here we have the height , so The corresponding ultrametric is The center of this tropical ball in this example is . The corresponding ultrametric is The tropical ball around the ultrametric corresponding the equidistant tree is shown in the right side of Figure 3. Example 3. The third example we consider is given in the left side of Figure 4. This example shows a case that the tropical ball crosses between two orthants for two tree topologies shown in Figure 4. The center tree of the tropical ball in this example is the tree where . This is the tree on the boundary of two orthants in the space of phylogenetic trees in this case. Here we have the height , so The corresponding ultrametrics are The center of the tropical ball in this example is . The corresponding ultrametric is The tropical ball centered around the ultrametric corresponding to the equidistant tree where and is shown in the right side of Figure 4. 3.3. Approximation of a Tropical Ball
In this subsection we discuss how a tropical ball with the radius relates with a ball under the and metrics. Suppose we have . Let be the norm metric and be the norm between x and y.
Suppose we can assume that
for
. Then we have the following proposition:
Proposition 2. We assume that over and . Then we have In this case the tropical ball coincides with the ball defined with the norm. However, if we are working on the space of ultrametrics, we have the constraints that all points have to be ultrametrics and no longer we can assume that and in . Therefore for more general cases, we have the following bounds:
Proposition 3. Suppose we have . Then we have Proof. The second inequality is trivial. Thus we want to prove that
We can define
as
and
□
Using Proposition 3 we have the following theorem:
Theorem 6. Let be a ball around a point with the radius with the metric and let be a ball around a point with the radius with the metric . Then we have Using Theorem 6 we can approximate a tropical KNN algorithm using the classical KNN algorithm with metric. We show some computational experiments using the multi-species coalescent model in the following section.
3.4. Computational Results
By Theorem 6 we can approximate a tropical ball using
metric. Since the KNN algorithm uses the notion of balls to classify each data point in a test set, we can approximate a tropical KNN algorithm using the classical KNN algorithm. In this section we compare the tropical KNN algorithm and the classical KNN algorithm using
with simulated data sets generated under the multi-species coalescent model via the software
Mesquite [
18]. All computations are conducted in Apple Notebook MacBook Pro 2019 with 2.4 GHz 8-Core Intel Core i9 and 64 GB 2667 MHz DDR4. The
R code used for this simulation study can be found at
polytopes.net/tropicalKNN.tar.
First we review the KNN algorithm. The KNN algorithm is a classification model for a data set where the response variable is categorical with finite levels and explanatory variables are all numerical. Suppose we have a data set
where
with
positive integer and
. The outline of the Algorithm 1 is following:
| Algorithm 1: KNN Algorithm. |
| | Input: A data point from a test set, a training set , and a metric d. Positive integer . Output: A class for y. Algorithm: for do Compute end for
|
| | |
| | Order from the smallest to the largest. Suppose be the first k smallest distances.
|
| | |
| | Consider categories of , that is, and assign the class, which is the biggest frequency among , to y.
|
In terms of balls, basically we can think of the KNN algorithm as a method to find a ball around
y, which contains
k many points from the training set. From this view we can think that the KNN algorithm with the tropical metric
can be approximated using the KNN algorithm with the
metric
. For this simulation we implemented the tropical KNN, the KNN algorithm with the tropical metric in
R and we use the KNN algorithm implemented in the “class” package in
R [
19].
For simulated data sets, we use the software
Mesquite, available at
http://mesquiteproject.org [
18], to generate gene trees under the multispecies coalescent model. In this model, we have two parameters, the effective population size
and species depth
. In this simulation study, we set
and varied
For this simulation, we generated species trees under the Yule model and gene trees given the species tree are generated by the multispecies coalescent model via Mesquite.
In computational experiments, we have varied . In addition, we set .
With the knn() function from the “class” package, it took 12.7 s to finish the computations while the tropical metric took several hours since we can speed up the KNN algorithm for the
metric. The results are shown in
Figure 5.
For the weighted tropical KNN, we assigned weight when we compute the majority votes such that
4. Conclusions
In this paper, we discussed a tropical ball over the tropical projective torus and the space of ultrametrics. Then we discussed approximation of tropical balls using the and metrics.
Then we discussed applications of the KNN algorithm and we showed by simulations, using the multi-species coalescent model, that approximation of tropical balls with the metric works well. In addition, we can consider the ensemble model, that is, taking the average of all three methods we used in the simulation study. This will increase the accuracy of the simulation study.
Since the tropical metric considers maximum and minimum of elements in a vector, this metric might be very sensitive to outliers. Therefore, we recommend to conduct analysis on outliers before applying a statistical method with the tropical metric.
5. Discussion
We focused on tropical balls with the tropical metric under the max-plus algebra in this paper. However, we still have many problems to solve. For example, we do not know how to compute a tropical ball over the tropical projective torus and the space of ultrametrics in general even though we can compute some small examples by hand. Explicitly,
Problem 1. Develop an algorithm to compute a tropical ball around a point with the radius , .
Problem 2. Develop an algorithm to compute a tropical ball around a point with the radius , .
In addition, we might want to consider a distribution-based clustering method, such as Density-based spatial clustering of applications with noise (DBSCAN) with the tropical metric for clustering gene trees. Similarly to the results on the KNN, with initial experiments, DBSCAN works fairly well on the data sets generated under the coalescent model shown in
Figure 6.
6. Materials and Methods
In this section, we show proofs for propositions and theorems in
Section 3.
Proof for Lemma 1. Since the root in the equidistant tree has degree of at least two, at least one pairwise distance in u is realized by a path through the root. In addition since the height of an equidistant tree is 1, therefor, the maximum of the pairwise distance from any leaf i to any leaf j is 2. □
Proof for Theorem 5. Let
be an ultrametric associated with the equidistant tree
and let
be an ultrametric associate with the equidistant tree
. Then we have
□
Proof for Lemma 2. Let
. Then we have
□
Proof for Lemma 3. Let
. We have
and
□
Proof for Theorem 3. Let
. Then, we have
and
. We want to show any points in the tropical line segment
between
is in
. Let
. Then there exist
such that
Thus, . □