Time-Decay Estimates for Linearized Two-Phase Navier–Stokes Equations with Surface Tension and Gravity

Abstract

The aim of this paper is to show time-decay estimates of solutions to linearized two-phase Navier-Stokes equations with surface tension and gravity. The original two-phase Navier-Stokes equations describe the two-phase incompressible viscous flow with a sharp interface that is close to the hyperplane $x_N=0$ in the N-dimensional Euclidean space, $N\ge 2$. It is well-known that the Rayleigh–Taylor instability occurs when the upper fluid is heavier than the lower one, while this paper assumes that the lower fluid is heavier than the upper one and proves time-decay estimates of $L_p$-$L_q$ type for the linearized equations. Our approach is based on solution formulas for a resolvent problem associated with the linearized equations.

1. Introduction

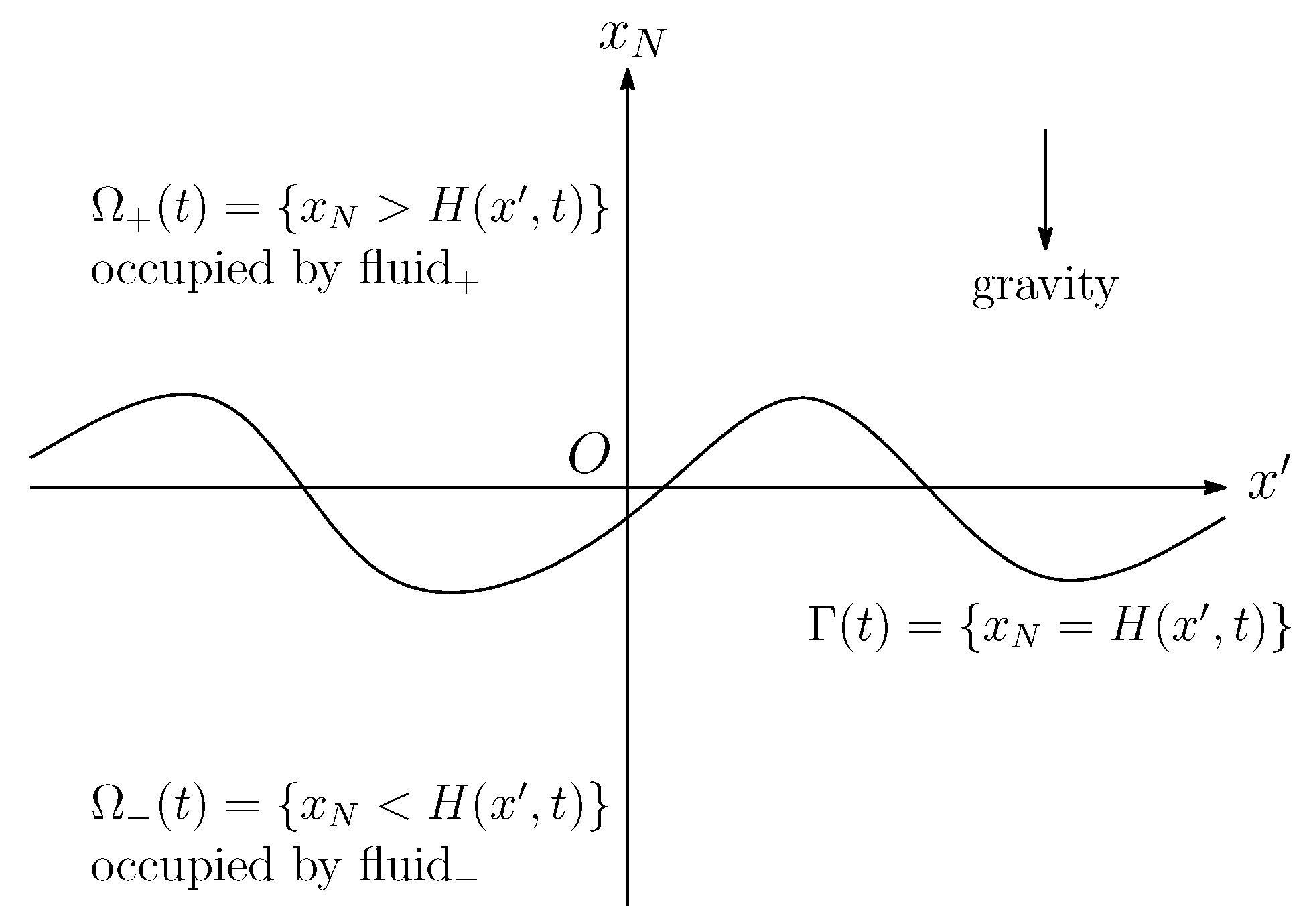
Let us consider the motion of two immiscible, viscous, incompressible capillary fluids, ${\mathrm{fluid}}_{+}$ and ${\mathrm{fluid}}_{-}$, in the N-dimensional Euclidean space ${\mathbf{R}}^N$ for $N\ge 2$. Here the ${\mathrm{fluid}}_{+}$ and ${\mathrm{fluid}}_{-}$ occupy ${\Omega }_{+}\left(t\right)$ and ${\Omega }_{-}\left(t\right)$, respectively, given by

$${\Omega }_{\pm }\left(t\right)=\{(x^{\prime },x_N):x^{\prime }=(x_1,\cdots ,x_{N-1})\in {\mathbf{R}}^{N-1},\pm (x_N-H(x^{\prime },t))>0\}$$

for time $t>0$ and the so-called height function $H=H(x^{\prime },t)$. Here the height function is unknown and needs to be determined as part of the problem. The fluids are thus separated by the interface

$$\Gamma \left(t\right)=\{(x^{\prime },x_N):x^{\prime }=(x_1,\cdots ,x_{N-1})\in {\mathbf{R}}^{N-1},x_N=H(x^{\prime },t)\},$$

see Figure 1 below. We denote the density of ${\mathrm{fluid}}_{\pm }$ by ${\rho }_{\pm }$, while the viscosity coefficient of ${\mathrm{fluid}}_{\pm }$ by ${\mu }_{\pm }$. Suppose that ${\rho }_{\pm }$ and ${\mu }_{\pm }$ are positive constants throughout this paper. The motion of two fluids is governed by the two-phase Navier-Stokes equations where surface tension is included on the interface. In addition, we allow for gravity to act on the fluids. The two-phase Navier-Stokes equations was studied by Prüss and Simonett [1], and they proved that the Rayleigh–Taylor instability occurs in an $L_p$-setting when the upper fluid is heavier than the lower one, i.e., ${\rho }_{+}>{\rho }_{-}$. In the present paper, we assume that the lower fluid is heavier than the upper one, i.e., ${\rho }_{-}>{\rho }_{+}$, and show time-decay estimates of $L_p$-$L_q$ type for some linearized system as the first step in proving global existence results for the two-phase Navier-Stokes equations when ${\rho }_{-}>{\rho }_{+}$.

Figure 1. The domains ${\Omega }_{\pm }\left(t\right)$ and the interface $\Gamma \left(t\right)$

Let us define ${\dot{\mathbf{R}}}^N={\mathbf{R}}_{+}^N\cup {\mathbf{R}}_{-}^N$ for

$${\mathbf{R}}_{\pm }^N=\{(x^{\prime },x_N):x^{\prime }=(x_1,\cdots ,x_{N-1})\in {\mathbf{R}}^{N-1},\pm x_N>0\}.$$

This paper is concerned with the following linearized system of the two-phase Navier-Stokes equations:

$$\left\{\begin{array}{cc}\hfill {\partial }_{t}H-U_N{|}_{x_N=0}& =0\mathrm{on}{\mathbf{R}}^{N-1}\times (0,\infty ),\hfill \\ \hfill \rho {\partial }_t\mathbf{U}-Div(\mu \mathbf{D}\left(\mathbf{U}\right)-P\mathbf{I})& =0\mathrm{in}{\dot{\mathbf{R}}}^N\times (0,\infty ),\hfill \\ \hfill div\mathbf{U}& =0\mathrm{in}{\dot{\mathbf{R}}}^N\times (0,\infty ),\hfill \\ \hfill -⟦(\mu \mathbf{D}\left(\mathbf{U}\right)-P\mathbf{I}){\mathbf{e}}_N⟧+\left(\omega -\sigma {\Delta }^{\prime }\right)H{\mathbf{e}}_N& =0\mathrm{on}{\mathbf{R}}^{N-1}\times (0,\infty ),\hfill \\ \hfill ⟦\mathbf{U}⟧& =0\mathrm{on}{\mathbf{R}}^{N-1}\times (0,\infty ),\hfill \\ \hfill H(x^{\prime },0)=d\left(x^{\prime }\right)(x^{\prime }\in {\mathbf{R}}^{N-1}),& \mathbf{U}(x,0)=\mathbf{f}\left(x\right)(x\in {\dot{\mathbf{R}}}^N),\hfill \end{array}\right.$$

(1)

where $\sigma$ is a positive constant called the surface tension coefficient and one has set for the indicator function ${\mathrm{𝟙}}_A$ of $A\subset {\mathbf{R}}^N$

$$\rho ={\rho }_{+}{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+{\rho }_{-}{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N},\mu ={\mu }_{+}{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+{\mu }_{-}{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N}.$$

Here $\mathbf{U}=\mathbf{U}(x,t)={(U_1(x,t),\cdots ,U_N(x,t))}^{\mathsf{T}}$ and $P=P(x,t)$ respectively denote the velocity field of the fluid and the pressure field of the fluid at position $x\in {\dot{\mathbf{R}}}^N$ and time $t>0$, while $d=d\left(x^{\prime }\right)$ and $\mathbf{f}=\mathbf{f}\left(x\right)={(f_1\left(x\right),\cdots ,f_N\left(x\right))}^{\mathsf{T}}$ are given initial data. Here the superscript ${·}^{\mathsf{T}}$ stands for the transposition. Note that ${\mathbf{e}}_N={(0,\cdots ,0,1)}^{\mathsf{T}}$ and $\mathbf{I}$ is the $N\times N$ identity matrix. Let ${\partial }_j=\partial /\partial x_j$ for $j=1,\cdots ,N$. Then

$$div\mathbf{U}=\sum _{j=1}^N{\partial }_j{U}_j,{\Delta }^{\prime }H=\sum _{j=1}^{N-1}{\partial }_j^{2}H,$$

while $\mathbf{D}\left(\mathbf{U}\right)$ is an $N\times N$ matrix whose $(i,j)$ element is given by ${\partial }_i{U}_j+{\partial }_j{U}_i$. In addition, for matrix-valued functions $\mathbf{M}=\left(M_{ij}\left(x\right)\right)$,

$$Div\mathbf{M}={\left(\sum _{j=1}^N{\partial }_j{M}_{1j},\cdots ,\sum _{j=1}^N{\partial }_j{M}_{Nj}\right)}^{\mathsf{T}}.$$

Let $f=f\left(x\right)$ be a function defined on ${\dot{\mathbf{R}}}^N$. Then $⟦f⟧=⟦f⟧\left(x^{\prime }\right)$ denotes the jump of the quantity f across the interface ${\mathbf{R}}_0^N=\{(x^{\prime },x_N):x^{\prime }\in {\mathbf{R}}^{N-1},x_N=0\}$, that is,

$$⟦f⟧=⟦f⟧\left(x^{\prime }\right)=f(x^{\prime },0+)-f(x^{\prime },0-),$$

where $f(x^{\prime },0\pm )={lim}_{x_N\to 0,\pm x_N>0}f(x^{\prime },x_N)$. Note that $⟦\mathbf{U}⟧=0$ on ${\mathbf{R}}^{N-1}$ implies $U_N{|}_{x_N=0}=U_N(x^{\prime },0+)=U_N(x^{\prime },0-)$. For the acceleration of gravity ${\gamma }_a>0$, the constant $\omega$ is given by

$$\omega =-⟦\rho ⟧{\gamma }_a=({\rho }_{-}-{\rho }_{+}){\gamma }_a,$$

which is positive when ${\rho }_{-}>{\rho }_{+}$.

This paper shows that for some $(d,\mathbf{f})$ the $L_q$-norm of $\mathbf{U}$ satisfies

$${\parallel \mathbf{U}\left(t\right)\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}=O\left(t^{-min\left\{\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)+\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right),\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)\right\}}\right)\mathrm{as}t\to \infty ,$$

(2)

where $1<p<2\le q<\infty$ (cf. Theorem 5 below for details). In [2], the authors considered linearized one-phase Navier-Stokes equations with surface tension and gravity, that is, they considered the case where there are no fluids in ${\mathbf{R}}_{+}^N$. In this case, the velocity $\mathbf{U}$ satisfies

$${\parallel \mathbf{U}\left(t\right)\parallel }_{L_q\left({\mathbf{R}}_{-}^N\right)}=O\left(t^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}\right)\mathrm{as}t\to \infty .$$

(3)

The above difference between the two-phase case and the one-phase case arises from asymptotic expansions of zeros of their boundary symbols, also called Lopatinskii determinant, which are functions of ${\xi }^{\prime }=({\xi }_1,\cdots ,{\xi }_{N-1})\in {\mathbf{R}}^{N-1}$ and the resolvent parameter $\lambda \in \mathbf{C}$. Here ${\xi }^{\prime }$ is the variables on the Fourier transform side. For the two-phase case, the zeros ${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)$ satisfy

$${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)=\pm i{c}_1|{\xi }^{\prime }{|}^{1/2}-c_2(1\pm i)|{\xi }^{\prime }{|}^{5/4}+o\left(\right|{\xi }^{\prime }{|}^{5/4})\mathrm{as}|{\xi }^{\prime }|\to 0,$$

(4)

where $i=\sqrt{-1}$ and $c_1,c_2$ are positive constants; for the one-phase case, the zeros ${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)$ satisfy

$${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)=\pm i{c}_3|{\xi }^{\prime }{|}^{1/2}-c_4|{\xi }^{\prime }{|}^2+o\left(\right|{\xi }^{\prime }{|}^2)\mathrm{as}|{\xi }^{\prime }|\to 0,$$

(5)

where $c_3,c_4$ are positive constants.

To see the relation between the time decay and the asymptotic expansions of ${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)$, we consider the fractional power dissipative equation

$$\left\{\begin{array}{cccc}\hfill {\partial }_{t}u+\nu {(-{\Delta }^{\prime })}^{\theta /2}u& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},t>0,\hfill \\ \hfill {u|}_{t=0}& =u_0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \end{array}\right.$$

(6)

where $\nu$ is a positive constant and ${(-{\Delta }^{\prime })}^{\theta /2}$ is the fractional Laplacian defined by ${(-{\Delta }^{\prime })}^{\theta /2}u={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\right|{\xi }^{\prime }{|}^{\theta }\widehat{u}\left({\xi }^{\prime }\right)]\left(x^{\prime }\right)$, $\theta >0$, with

$$\widehat{u}\left({\xi }^{\prime }\right)={\int }_{{\mathbf{R}}^{N-1}}{e}^{-i{x}^{\prime }·{\xi }^{\prime }}u\left(x^{\prime }\right)d{x}^{\prime },{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[v\right]\left(x^{\prime }\right)=\frac{1}{{\left(2\pi \right)}^{N-1}}{\int }_{{\mathbf{R}}^{N-1}}{e}^{i{x}^{\prime }·{\xi }^{\prime }}v\left({\xi }^{\prime }\right)d{\xi }^{\prime }.$$

Applying the Laplace transform with respect to time t and the Fourier transform $\widehat{·}$ to (6) yields the equation

$$(\lambda +\nu |{\xi }^{\prime }{|}^{\theta })\widehat{u}\left({\xi }^{\prime }\right)={\widehat{u}}_0\left({\xi }^{\prime }\right),$$

and thus the symbol of the operator ${\partial }_t+\nu {(-\Delta )}^{\theta /2}$ has the zero ${\lambda }_{*}\left({\xi }^{\prime }\right)=-\nu {\left|{\xi }^{\prime }\right|}^{\theta }$. This zero gives the time decay of solutions to (6) as follows: the solution u of (6) is given by $u={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{t{\lambda }_{*}\left({\xi }^{\prime }\right)}{\widehat{u}}_0\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right)$, and then Lemma 9 below yields

$${\parallel u\left(t\right)\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}=O\left(t^{-\frac{N-1}{\theta }\left(\frac{1}{p}-\frac{1}{q}\right)}\right)\mathrm{as}t\to \infty .$$

Thus the real term $-c_2{\left|{\xi }^{\prime }\right|}^{5/4}$ in (4), which is the case $\theta =5/4$, yields

$$t^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}$$

in (2); similarly, $-c_4{\left|{\xi }^{\prime }\right|}^2$ in (5), which is the case $\theta =2$, yields

$$t^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}$$

in (3). Note that in (2) and (3) we also have

$$t^{-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)},t^{-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)},$$

which arise from the integration of $\parallel \mathbf{U}(·,x_N){\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}$ with respect to $x_N$, roughly speaking. For more details, see the following sections.

The boundary symbol for (1) can be obtained via solution formulas, which are introduced in Shibata and Shimizu [3] and given in Section 3 below. Then we analyze the asymptotic behavior of zeros of the boundary symbol as mentioned above and combine it with the solution formulas to obtain time-decay estimates of $L_p$-$L_q$ type for solutions of (1) in the present paper. Thus the solution formulas play a crucial role in proving the result of this paper.

At this point, we introduce previous works for the two-phase flow.

Prüss and Simonett [4] considered the boundary symbol of linearized two-phase Navier-Stokes equations with surface tension, but gravity is not taken into account. In this case, they proved the zeros ${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)$ of the boundary symbol satisfy

$${\lambda }_{\pm }\left(\right|{\xi }^{\prime }\left|\right)=\pm i{c}_5|{\xi }^{\prime }{|}^{3/2}-c_6(1\pm i)|{\xi }^{\prime }{|}^{7/4}+o\left(\right|{\xi }^{\prime }{|}^{7/4})\mathrm{as}|{\xi }^{\prime }|\to 0,$$

where $c_5,c_6$ are positive constants.

The local well-posedness for the two-phase Navier-Stokes equations with $\Gamma \left(t\right)$ as above was proved in Prüss and Simonett [5,6]. Note that the local well-posedness holds for any positive constants ${\rho }_{\pm }$, that is, the condition ${\rho }_{-}>{\rho }_{+}$ is not required. Those results were extended to a class of non-Newtonian fluids in [7]. In addition, ref. [8] considered the two-phase inhomogeneous incompressible viscous flow without surface tension when gravity is not taken into account, and proved the local well-posedness in general domains including the above-mentioned ${\Omega }_{\pm }\left(t\right)$. If ${\Omega }_{\pm }\left(t\right)$ are assumed to be layer-like domains, then it is known that the global well-posedness holds when ${\rho }_{-}>{\rho }_{+}$. In fact, it was shown in [9] in a horizontally periodic setting, and also we refer to [10].

Let us recall Shibata and Shimizu [3]. They considered the following two resolvent problems:

$$\left\{\begin{array}{cccc}\hfill \lambda \eta -u_N{|}_{x_N=0}& =d\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill \rho \lambda \mathbf{u}-Div\left(\mu \mathbf{D}\right(\mathbf{u})-\mathfrak{p}\mathbf{I})& =\rho \mathbf{f}\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div\mathbf{u}& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill -⟦(\mu \mathbf{D}\left(\mathbf{u}\right)-\mathfrak{p}\mathbf{I}){\mathbf{e}}_N⟧+(\omega -\sigma {\Delta }^{\prime })\eta {\mathbf{e}}_N& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦\mathbf{u}⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \end{array}\right.$$

(7)

and also

$$\left\{\begin{array}{cccc}\hfill \rho \lambda \mathbf{v}-Div\left(\mu \mathbf{D}\right(\mathbf{v})-\mathfrak{q}\mathbf{I})& =\rho \mathbf{f}\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div\mathbf{v}& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill ⟦(\mu \mathbf{D}\left(\mathbf{v}\right)-\mathfrak{q}\mathbf{I}){\mathbf{e}}_N⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦\mathbf{v}⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1}.\hfill \end{array}\right.$$

(8)

We define the sector

$${\Sigma }_{\epsilon }=\{\lambda \in \mathbf{C}⧵\left\{0\right\}:|arg\lambda |\le \pi -\epsilon \}(0<\epsilon <\pi /2).$$

Let $q\in (1,\infty )$ and $(d,\mathbf{f})\in X_q:=W_q^{2-1/q}\left({\mathbf{R}}^{N-1}\right)\times L_q{\left({\dot{\mathbf{R}}}^N\right)}^N$. In [3], they obtained the following results: there exists a constant ${\lambda }_0\left(\epsilon \right)\ge 1$ such that, for any $\lambda \in {\Sigma }_{\epsilon }$ with $\left|\lambda \right|\ge {\lambda }_0\left(\epsilon \right)$, (7) admits a unique solution $(\eta ,\mathbf{u},\mathfrak{p})\in W_q^{3-1/q}\left({\mathbf{R}}^{N-1}\right)\times H_q^2{\left({\dot{\mathbf{R}}}^N\right)}^N\times {\widehat{H}}_q^1\left({\dot{\mathbf{R}}}^N\right)$, which satisfies

$$\parallel (\lambda \eta ,{\nabla }^{\prime }\eta ){\parallel }_{W_q^{2-1/q}\left({\mathbf{R}}^{N-1}\right)}+\parallel (\lambda \mathbf{u},{\lambda }^{1/2}\nabla \mathbf{u},{\nabla }^2\mathbf{u},\nabla \mathfrak{p}){\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}\le C_{N,q,\epsilon ,{\lambda }_0\left(\epsilon \right)}{\parallel (d,\mathbf{f})\parallel }_{X_q},$$

(9)

where

$$\begin{array}{cccc}\hfill {\nabla }^{\prime }\eta & ={({\partial }_1\eta ,\cdots ,{\partial }_{N-1}\eta )}^{\mathsf{T}},\hfill & \hfill \nabla \mathfrak{p}& ={({\partial }_1\mathfrak{p},\cdots ,{\partial }_{N-1}\mathfrak{p},{\partial }_N\mathfrak{p})}^{\mathsf{T}},\hfill \\ \hfill \nabla \mathbf{u}& =\{{\partial }_j{u}_k:j,k=1,\cdots ,N\},\hfill & \hfill {\nabla }^2\mathbf{u}& =\{{\partial }_j{\partial }_k{u}_l:j,k,l=1,\cdots ,N\};\hfill \end{array}$$

for any $\lambda \in {\Sigma }_{\epsilon }$, (8) admits a unique solution $(\mathbf{v},\mathfrak{q})\in H_q^2{\left({\dot{\mathbf{R}}}^N\right)}^N\times {\widehat{H}}_q^1\left({\dot{\mathbf{R}}}^N\right)$, which satisfies

$$\parallel (\lambda \mathbf{v},{\lambda }^{1/2}\nabla \mathbf{v},{\nabla }^2\mathbf{v},\nabla \mathfrak{q}){\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}\le C_{N,q,\epsilon }{\parallel \mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}.$$

(10)

These results hold for any ${\rho }_{\pm }>0$ and play a key role in proving time-decay estimates of solutions for (1) in the present paper.

This paper is organized as follows. The next section introduces the notation used throughout this paper and states the main result of this paper, that is, time-decay estimates of solutions for (1). More precisely, the result is stated in Theorems 1–5. First, Theorem 1 introduces an evolution operator $T\left(t\right)$ associated with (1), and Theorem 2 gives another evolution operator ${\mathcal{U}}^P\left(t\right)$ and its time-decay estimates. Next, we write $T\left(t\right)(d,\mathbf{f})=\left(\mathcal{H}\right(t\left)\right(d,\mathbf{f}),\mathcal{U}(t\left)\right(d,\mathbf{f}\left)\right)$ and decompose $\mathcal{H}\left(t\right)$, $\mathcal{U}\left(t\right)$ into several terms by using ${\mathcal{U}}^P\left(t\right)$ and cut-off functions on the Fourier transform side, see (21) below. Then Theorem 3 gives time-decay estimates for the low frequency part, while Theorem 4 gives time-decay estimates for the high frequency part. Finally, summing up Theorems 1–4, we have Theorem 5, which gives time-decay estimates of $L_p$-$L_q$ type for the solution $(H,\mathbf{U})=\left(\mathcal{H}\right(t\left)\right(d,\mathbf{f}),\mathcal{U}(t\left)\right(d,\mathbf{f}\left)\right)$ of (1). The proofs of Theorems 1, 2, and 5 are standard or elementary, so that they are omitted in the present paper. Section 3 shows the representation formulas of solutions for (1) by the partial Fourier transform with respect to $x^{\prime }=(x_1,\cdots ,x_{N-1})$ and its inverse transform. Section 4 analyzes the boundary symbol appearing in the representation formulas given in Section 3. Section 5 proves Theorem 3 by using results obtained in Section 3 and Section 4. Section 6 proves Theorem 4 by using results obtained in Section 3 and Section 4.

2. Notation and Main Results

2.1. Notation

First, we introduce function spaces. Let X be a Banach space. Then $X^m$, $m\ge 2$, stands for the m-product space of X, while the norm of $X^m$ is usually denoted by ${\parallel ·\parallel }_X$ instead of ${\parallel ·\parallel }_{X^m}$ for the sake of simplicity. For another Banach space Y, we set ${\parallel u\parallel }_{X\cap Y}={\parallel u\parallel }_X+{\parallel u\parallel }_Y$. Let $\mathbf{N}$ be the set of all natural numbers and ${\mathbf{N}}_0=\mathbf{N}\cup \left\{0\right\}$. Let $p\ge 1$ or $p=\infty$. For an open set $G\subset {\mathbf{R}}^M$, $M\ge 1$, the Lebesgue spaces on G are denoted by $L_p\left(G\right)$ with norm ${\parallel ·\parallel }_{L_p\left(G\right)}$, while the Sobolev spaces on G are denoted by $H_p^n\left(G\right)$, $n\in \mathbf{N}$, with norm ${\parallel ·\parallel }_{H_p^n\left(G\right)}$. Let $H_p^0\left(G\right)=L_p\left(G\right)$. In addition, $C_0^{\infty }\left(G\right)$ is the set of all functions in $C^{\infty }\left(G\right)$ whose supports are compact and contained in G, and $C^{\infty }(I,X)$ is the set of all $C^{\infty }$ functions on an interval $I\subset \mathbf{R}$ with value X. For any multi-index $\alpha =({\alpha }_1,\cdots ,{\alpha }_M)\in {\mathbf{N}}_0^M$,

$${\partial }^{\alpha }u={\partial }_x^{\alpha }u=\frac{{\partial }^{\left|\alpha \right|}u\left(x\right)}{\partial x_1^{{\alpha }_1}\cdots \partial x_M^{{\alpha }_M}}\mathrm{with}\left|\alpha \right|={\alpha }_1+\cdots +{\alpha }_M.$$

Let $q\in (1,\infty )$ and ${\widehat{H}}_q^1\left(G\right)=\{u\in L_{q,\mathrm{loc}}\left(\overline{G}\right):{\partial }^{\alpha }u\in L_q\left(G\right)\mathrm{for}\left|\alpha \right|=1\}$. Let $s\in [0,\infty )⧵\mathbf{N}$ and $\left[s\right]$ be the largest integer less than s. The Sobolev–Slobodeckij spaces on ${\mathbf{R}}^{N-1}$ are defined by

$$\begin{array}{cc}\hfill W_q^s\left({\mathbf{R}}^{N-1}\right)& =\{u\in L_q\left({\mathbf{R}}^{N-1}\right):\parallel u{\parallel }_{W_q^s\left({\mathbf{R}}^{N-1}\right)}<\infty \},\hfill \\ \hfill {\parallel u\parallel }_{W_q^s\left({\mathbf{R}}^{N-1}\right)}& ={\parallel u\parallel }_{H_q^{\left[s\right]}\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & +\sum _{\left|\alpha \right|=\left[s\right]}{\left({\int }_{{\mathbf{R}}^{N-1}}{\int }_{{\mathbf{R}}^{N-1}}\frac{|{\partial }^{\alpha }u\left(x\right)-{\partial }^{\alpha }{u\left(y\right)|}^q}{{|x-y|}^{N+(s-[s\left]\right)q}}dxdy\right)}^{1/q}.\hfill \end{array}$$

Let us define a solenoidal space by

$$J_q\left({\dot{\mathbf{R}}}^N\right)=\{\mathbf{u}\in L_q{\left({\dot{\mathbf{R}}}^N\right)}^N:{(\mathbf{u},\nabla \phi )}_{{\dot{\mathbf{R}}}^N}=0\mathrm{for}\mathrm{any}\phi \in {\widehat{H}}_{q^{\prime }}^1\left({\mathbf{R}}^N\right)\},$$

where $q^{\prime }=q/(q-1)$ and

$${(\mathbf{a},\mathbf{b})}_{{\dot{\mathbf{R}}}^N}={\int }_{{\dot{\mathbf{R}}}^N}\mathbf{a}\left(x\right)·\mathbf{b}\left(x\right)dx=\sum _{j=1}^N{\int }_{{\dot{\mathbf{R}}}^N}{a}_j\left(x\right)b_j\left(x\right)dx.$$

Furthermore, we set

$$\begin{array}{cccc}\hfill X_q& =W_q^{2-1/q}\left({\mathbf{R}}^{N-1}\right)\times L_q{\left({\dot{\mathbf{R}}}^N\right)}^N,\hfill & \hfill J{X}_q& =W_q^{2-1/q}\left({\mathbf{R}}^{N-1}\right)\times J_q\left({\dot{\mathbf{R}}}^N\right),\hfill \\ \hfill Y_q& =L_q\left({\mathbf{R}}^{N-1}\right)\times L_q{\left({\dot{\mathbf{R}}}^N\right)}^N,\hfill & \hfill J{Y}_q& =L_q\left({\mathbf{R}}^{N-1}\right)\times J_q\left({\dot{\mathbf{R}}}^N\right),\hfill \end{array}$$

and also $Y_1=L_1\left({\mathbf{R}}^{N-1}\right)\times L_1{\left({\dot{\mathbf{R}}}^N\right)}^N$.

Next, we define the partial Fourier transform with respect to $x^{\prime }=(x_1,\cdots ,x_{N-1})$ by

$$\widehat{u}({\xi }^{\prime },x_N)={\int }_{{\mathbf{R}}^{N-1}}{e}^{-i{x}^{\prime }·{\xi }^{\prime }}u(x^{\prime },x_N)d{x}^{\prime },$$

where $i=\sqrt{-1}$. Its inverse transform is also defined by

$${\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[v({\xi }^{\prime },x_N)\right]\left(x^{\prime }\right)=\frac{1}{{\left(2\pi \right)}^{N-1}}{\int }_{{\mathbf{R}}^{N-1}}{e}^{i{x}^{\prime }·{\xi }^{\prime }}v({\xi }^{\prime },x_N)d{\xi }^{\prime }.$$

Finally, we introduce some constants and symbols. Let

$${\theta }_j={\mathrm{Tan}}^{-1}\left(\frac{j}{16}\right)\mathrm{for}j=1,2,{\lambda }_1={\lambda }_0\left({\theta }_1\right),$$

(11)

where ${\lambda }_0\left(\epsilon \right)$ is given in (9). In addition, we set

$$\alpha =\frac{\omega }{{\rho }_{+}+{\rho }_{-}}=\frac{({\rho }_{-}-{\rho }_{+}){\gamma }_a}{{\rho }_{+}+{\rho }_{-}},\beta =\frac{\sqrt{{\rho }_{+}{\mu }_{+}}\sqrt{{\rho }_{-}{\mu }_{-}}}{({\rho }_{+}+{\rho }_{-})(\sqrt{{\rho }_{+}{\mu }_{+}}+\sqrt{{\rho }_{-}{\mu }_{-}})}.$$

(12)

The integral path ${\Gamma }_0$ is defined by

$$\begin{array}{cc}\hfill {\Gamma }_0& ={\Gamma }_0^{+}\cup {\Gamma }_0^{-},{\Gamma }_0^{+}=\{\lambda \in \mathbf{C}:\lambda =\frac{2{\lambda }_1}{sin{\theta }_1}+s{e}^{i(\pi -{\theta }_1)},s:0\to \infty \},\hfill \\ \hfill {\Gamma }_0^{-}& =\{\lambda \in \mathbf{C}:\lambda =\frac{2{\lambda }_1}{sin{\theta }_1}+s{e}^{-i(\pi -{\theta }_1)},s:\infty \to 0\}.\hfill \end{array}$$

(13)

2.2. Main Results

We first introduce the existence of solution operator for (1). This immediately follows from the resolvent estimate (9) and the standard theory of operator semigroups.

Theorem 1.

Let $q\in (1,\infty )$ and ${\rho }_{\pm }$ be any positive constants. Let

$$T\left(t\right)(d,\mathbf{f})=\frac{1}{2\pi i}{\int }_{{\Gamma }_0}{e}^{\lambda t}(\eta (x^{\prime },\lambda ),\mathbf{u}(x,\lambda ))d\lambda ,$$

with the solution $(\eta ,\mathbf{u})=(\eta (x^{\prime },\lambda ),\mathbf{u}(x,\lambda ))$ to (7) for $(d,\mathbf{f})\in X_q$. Then the following assertions hold.

(1)

For any $(d,\mathbf{f})\in X_q$, $T\left(t\right)(d,\mathbf{f})\in C^{\infty }((0,\infty ),W_q^{3-1/q}\left({\mathbf{R}}^{N-1}\right)\times H_q^2{\left({\dot{\mathbf{R}}}^N\right)}^N)$.

(2)

${\left\{T\left(t\right)\right\}}_{t\ge 0}$ is an analytic $C_0$-semigroup on $J{X}_q$.

(3)

For any $(d,\mathbf{f})\in J{X}_q$, $(H,\mathbf{U})=T\left(t\right)(d,\mathbf{f})$ is a unique solution to (1) with some pressure $P\in {\widehat{H}}_q^1\left({\dot{\mathbf{R}}}^N\right)$.

Let us define projections $P_1$, $P_2$ by

$$P_1:X_q\ni (a,\mathbf{b})\mapsto a\in W_q^{2-1/q}\left({\mathbf{R}}^{N-1}\right),P_2:X_q\ni (a,\mathbf{b})\mapsto \mathbf{b}\in L_q{\left({\dot{\mathbf{R}}}^N\right)}^N.$$

We set for $(d,\mathbf{f})\in X_q$

$$\begin{array}{cc}\hfill \mathcal{H}\left(t\right)(d,\mathbf{f})& =P_{1}T\left(t\right)(d,\mathbf{f})=\frac{1}{2\pi i}{\int }_{{\Gamma }_0}{e}^{\lambda t}\eta (x^{\prime },\lambda )d\lambda ,\hfill \\ \hfill \mathcal{U}\left(t\right)(d,\mathbf{f})& =P_{2}T\left(t\right)(d,\mathbf{f})=\frac{1}{2\pi i}{\int }_{{\Gamma }_0}{e}^{\lambda t}\mathbf{u}(x,\lambda )d\lambda .\hfill \end{array}$$

(14)

One now decomposes the solution $(\mathbf{u},\mathfrak{p})$ of (7) into a solution of parabolic system and a solution of hyperbolic-parabolic coupled system as follows:

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cccc}\hfill \rho \lambda {\mathbf{u}}^P-Div(\mu \mathbf{D}\left({\mathbf{u}}^P\right)-{\mathfrak{p}}^P\mathbf{I})& =\rho \mathbf{f}\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div{\mathbf{u}}^P& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill ⟦(\mu \mathbf{D}\left({\mathbf{u}}^P\right)-{\mathfrak{p}}^P\mathbf{I}){\mathbf{e}}_N⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦{\mathbf{u}}^P⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \end{array}\right.\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & \left\{\begin{array}{cccc}\hfill \lambda \eta -u_N^H{|}_{x_N=0}& =d+u_N^P{|}_{x_N=0}\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill \rho \lambda {\mathbf{u}}^H-Div(\mu \mathbf{D}\left({\mathbf{u}}^H\right)-{\mathfrak{p}}^H\mathbf{I})& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div{\mathbf{u}}^H& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill -⟦(\mu \mathbf{D}\left({\mathbf{u}}^H\right)-{\mathfrak{p}}^H\mathbf{I}){\mathbf{e}}_N⟧+(\omega -\sigma {\Delta }^{\prime })\eta {\mathbf{e}}_N& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦{\mathbf{u}}^H⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1}.\hfill \end{array}\right.\hfill \end{array}$$

(16)

It then holds that $\mathbf{u}={\mathbf{u}}^P+{\mathbf{u}}^H$ and $\mathfrak{p}={\mathfrak{p}}^P+{\mathfrak{p}}^H$. In addition, we set

$${\mathcal{U}}^P\left(t\right)\mathbf{f}=\frac{1}{2\pi i}{\int }_{{\Gamma }_0}{e}^{\lambda t}{\mathbf{u}}^P(x,\lambda )d\lambda ,{\mathcal{U}}^H\left(t\right)(d,\mathbf{f})=\frac{1}{2\pi i}{\int }_{{\Gamma }_0}{e}^{\lambda t}{\mathbf{u}}^H(x,\lambda )d\lambda ,$$

which implies

$$\mathcal{U}\left(t\right)(d,\mathbf{f})={\mathcal{U}}^P\left(t\right)\mathbf{f}+{\mathcal{U}}^H\left(t\right)(d,\mathbf{f})\mathrm{for}(d,\mathbf{f})\in X_q.$$

(17)

For the parabolic part, we have the following theorem by the resolvent estimate (10) and the standard theory of operator semigroups.

Theorem 2.

Let $r\in (1,\infty )$ and ${\rho }_{\pm }$ be any positive constants. Then the following assertions hold.

(1)

For any $\mathbf{f}\in L_r{\left({\dot{\mathbf{R}}}^N\right)}^N$, ${\mathcal{U}}^P\left(t\right)\mathbf{f}\in C^{\infty }((0,\infty ),H_r^2{\left({\dot{\mathbf{R}}}^N\right)}^N)$.

(2)

${\left\{{\mathcal{U}}^P\left(t\right)\right\}}_{t\ge 0}$ is an analytic $C_0$-semigroup on $J_r\left({\dot{\mathbf{R}}}^N\right)$.

(3)

For any $\mathbf{f}\in J_r\left({\dot{\mathbf{R}}}^N\right)$, $\mathbf{V}={\mathcal{U}}^P\left(t\right)\mathbf{f}$ is a unique solution to

$$\left\{\begin{array}{cc}\hfill \rho {\partial }_t\mathbf{V}-Div(\mu \mathbf{D}\left(\mathbf{V}\right)-Q\mathbf{I})=0,div\mathbf{V}& =0\mathrm{in}{\dot{\mathbf{R}}}^N\times (0,\infty ),\hfill \\ \hfill ⟦(\mu \mathbf{D}\left(\mathbf{V}\right)-Q\mathbf{I}){\mathbf{e}}_N⟧=0,⟦\mathbf{V}⟧& =0\mathrm{on}{\mathbf{R}}^{N-1}\times (0,\infty ),\hfill \\ \hfill {\mathbf{V}|}_{t=0}& =\mathbf{f}\mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \end{array}\right.$$

with some pressure $Q\in {\widehat{H}}_r^1\left({\dot{\mathbf{R}}}^N\right)$.

(4)

Let $j\in {\mathbf{N}}_0$ and $k=0,1,2$. For any $t>0$ and $\mathbf{f}\in J_r\left({\dot{\mathbf{R}}}^N\right)$,

$$\parallel {\partial }_t^j{\nabla }^k{\mathcal{U}}^P{\left(t\right)\mathbf{f}\parallel }_{L_s\left({\dot{\mathbf{R}}}^N\right)}\le C{t}^{-j-\frac{k}{2}-\frac{N}{2}\left(\frac{1}{r}-\frac{1}{s}\right)}{\parallel \mathbf{f}\parallel }_{L_r\left({\dot{\mathbf{R}}}^N\right)},$$

where $r\le s\le \infty$ when $k=0,1$ and $r\le s<\infty$ when $k=2$. Here C is a positive constant independent of t and $\mathbf{f}$.

To complete time-decay estimates for $\mathcal{H}\left(t\right)$ and $\mathcal{U}\left(t\right)$, we further decompose $(\eta ,{\mathbf{u}}^H,{\mathfrak{p}}^H)$ satisfying () as follows: for $z^1=d$ and $z^2=u_N^P{|}_{x_N=0}$, let $({\eta }^k,{\mathbf{u}}^k)$ be the solution to

$$\left\{\begin{array}{cccc}\hfill \lambda {\eta }^k-u_N^k{|}_{x_N=0}& =z^k\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill \rho \lambda {\mathbf{u}}^k-Div(\mu \mathbf{D}\left({\mathbf{u}}^k\right)-{\mathfrak{p}}^k\mathbf{I})& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div{\mathbf{u}}^k& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill -⟦(\mu \mathbf{D}\left({\mathbf{u}}^k\right)-{\mathfrak{p}}^k\mathbf{I}){\mathbf{e}}_N⟧+(\omega -\sigma {\Delta }^{\prime }){\eta }^k{\mathbf{e}}_N& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦{\mathbf{u}}^k⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1}.\hfill \end{array}\right.$$

(18)

It then holds that $\eta ={\eta }^1+{\eta }^2$, ${\mathbf{u}}^H={\mathbf{u}}^1+{\mathbf{u}}^2$, and ${\mathfrak{p}}^H={\mathfrak{p}}^1+{\mathfrak{p}}^2$. Let $\phi =\phi \left({\xi }^{\prime }\right)$ be a function in $C^{\infty }\left({\mathbf{R}}^{N-1}\right)$ and satisfy $0\le \phi \le 1$ with

$$\phi \left({\xi }^{\prime }\right)=\left\{\begin{array}{cccc}\hfill & 1\hfill & \hfill & \left(\right|{\xi }^{\prime }|\le 1),\hfill \\ \hfill & 0\hfill & \hfill & \left(\right|{\xi }^{\prime }|\ge 2).\hfill \end{array}\right.$$

In addition, we set ${\phi }_{A_0}\left({\xi }^{\prime }\right)=\phi ({\xi }^{\prime }/A_0)$ and ${\phi }_{A_{\infty }}\left({\xi }^{\prime }\right)=1-\phi ({\xi }^{\prime }/A_{\infty })$ for positive constants $A_0\in (0,1)$ and $A_{\infty }\ge 2$. Let ${\phi }_{⟨A_0,A_{\infty }⟩}\left({\xi }^{\prime }\right)=1-{\phi }_{A_0}\left({\xi }^{\prime }\right)-{\phi }_{A_{\infty }}\left({\xi }^{\prime }\right)$. Together with these cut-off functions, we define for $Z\in \{A_0,A_{\infty },⟨A_0,A_{\infty }⟩\}$ and for an integral path $\Gamma$

$$\begin{array}{cc}\hfill {\widehat{\mathcal{H}}}_Z^1(t;\Gamma )d& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{\eta }}^1({\xi }^{\prime },\lambda )d\lambda ,\hfill \\ \hfill {\widehat{\mathcal{H}}}_Z^2(t;\Gamma )\mathbf{f}& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{\eta }}^2({\xi }^{\prime },\lambda )d\lambda ,\hfill \\ \hfill {\widehat{\mathcal{U}}}_Z^1(t;\Gamma )d& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{\mathbf{u}}}^1({\xi }^{\prime },x_N,\lambda )d\lambda ,\hfill \\ \hfill {\widehat{\mathcal{U}}}_Z^2(t;\Gamma )\mathbf{f}& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{\mathbf{u}}}^2({\xi }^{\prime },x_N,\lambda )d\lambda .\hfill \end{array}$$

(19)

Furthermore, we set for $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$ and ${\Gamma }_0$ given by (13)

$${\mathcal{S}}_Z^1\left(t\right)d={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_Z^1(t;{\Gamma }_0)d\right]\left(x^{\prime }\right),{\mathcal{S}}_Z^2\left(t\right)\mathbf{f}={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_Z^2(t;{\Gamma }_0)\mathbf{f}\right]\left(x^{\prime }\right).$$

(20)

Noting (17) and ${\phi }_{A_0}+{\phi }_{A_{\infty }}+{\phi }_{⟨A_0,A_{\infty }⟩}=1$, we see the formulas in (14) satisfy

$$\begin{array}{cc}\hfill \mathcal{H}\left(t\right)(d,\mathbf{f})& =\sum _{Z\in \{A_0,A_{\infty },⟨A_0,A_{\infty }⟩\}}\left({\mathcal{H}}_Z^1\left(t\right)d+{\mathcal{H}}_Z^2\left(t\right)\mathbf{f}\right),\hfill \\ \hfill \mathcal{U}\left(t\right)(d,\mathbf{f})& =\sum _{Z\in \{A_0,A_{\infty },⟨A_0,A_{\infty }⟩\}}\left({\mathcal{U}}_Z^1\left(t\right)d+{\mathcal{U}}_Z^2\left(t\right)\mathbf{f}\right)+{\mathcal{U}}^P\left(t\right)\mathbf{f}.\hfill \end{array}$$

(21)

The following two theorems are of central importance in this paper. The first one is time-decay estimates for the low frequency part and proved in Section 5 below.

Theorem 3.

Let $1\le p<2\le q\le \infty$ and suppose that ${\rho }_{-}>{\rho }_{+}>0$. Then there exists a constant $A_0\in (0,1)$ such that the following assertions hold.

(1)

For ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}$ with $|{\xi }^{\prime }|\in (0,A_0)$, let ${\zeta }_{\pm }=\pm i{\alpha }^{1/2}|{\xi }^{\prime }{|}^{1/2}-\sqrt{2}{\alpha }^{1/4}\beta (1\pm i){\left|{\xi }^{\prime }\right|}^{5/4}$ with $\alpha ,\beta$ given in (12) and let

$${\widehat{\Gamma }}_{\mathrm{Res}}^{\pm }=\{\lambda \in \mathbf{C}:\lambda ={\zeta }_{\pm }+|{\xi }^{\prime }{|}^{6/4}{e}^{is},s:0\to 2\pi \}.$$

In addition, for $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$ and $(d,\mathbf{f})\in Y_p$, set

$${\mathcal{S}}_{A_0}^{1\pm }\left(t\right)d={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_{A_0}^1(t;{\widehat{\Gamma }}_{\mathrm{Res}}^{\pm })d\right]\left(x^{\prime }\right),{\mathcal{S}}_{A_0}^{2\pm }\left(t\right)\mathbf{f}={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_{A_0}^2(t;{\widehat{\Gamma }}_{\mathrm{Res}}^{\pm })\mathbf{f}\right]\left(x^{\prime }\right).$$

Then for any $t\ge 1$

$$\begin{array}{cc}\hfill \parallel ({\mathcal{H}}_{A_0}^{1\pm }\left(t\right)d,{\mathcal{H}}_{A_0}^{2\pm }\left(t\right)\mathbf{f}){\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{t}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel (d,\mathbf{f})\parallel }_{Y_p},\hfill \\ \hfill \parallel ({\mathcal{U}}_{A_0}^{1\pm }\left(t\right)d,{\mathcal{U}}_{A_0}^{2\pm }\left(t\right)\mathbf{f}){\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{t}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel (d,\mathbf{f})\parallel }_{Y_p},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

(2)

For $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$ and $(d,\mathbf{f})\in Y_p$, set

$$\begin{array}{cc}\hfill {\tilde{\mathcal{S}}}_{A_0}^1\left(t\right)d& ={\mathcal{S}}_{A_0}^1\left(t\right)d-{\mathcal{S}}_{A_0}^{1+}\left(t\right)d-{\mathcal{S}}_{A_0}^{1-}\left(t\right)d,\hfill \\ \hfill {\tilde{\mathcal{S}}}_{A_0}^2\left(t\right)\mathbf{f}& ={\mathcal{S}}_{A_0}^2\left(t\right)\mathbf{f}-{\mathcal{S}}_{A_0}^{2+}\left(t\right)\mathbf{f}-{\mathcal{S}}_{A_0}^{2-}\left(t\right)\mathbf{f}.\hfill \end{array}$$

Let ${\gamma }_1$ be a constant satisfying

$$0<{\gamma }_1<min\left\{1,2(N-1)\left(\frac{1}{p}-\frac{1}{2}\right)\right\}.$$

Then for any $t\ge 1$

$$\begin{array}{cc}\hfill \parallel ({\tilde{\mathcal{H}}}_{A_0}^1\left(t\right)d,{\tilde{\mathcal{H}}}_{A_0}^2\left(t\right)\mathbf{f}){\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{t}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{4}{\gamma }_1}{\parallel (d,\mathbf{f})\parallel }_{Y_p},\hfill \\ \hfill \parallel ({\tilde{\mathcal{U}}}_{A_0}^1\left(t\right)d,{\tilde{\mathcal{U}}}_{A_0}^2\left(t\right)\mathbf{f}){\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{t}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel (d,\mathbf{f})\parallel }_{Y_p},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

The second one is time-decay estimates for the high frequency part and proved in Section 6 below.

Theorem 4.

Let $q\in (1,\infty )$ and $j\in {\mathbf{N}}_0$. Suppose that ${\rho }_{-}>{\rho }_{+}>0$. Then there exist constants $A_{\infty }\ge 2$ and ${\gamma }_0>0$ such that for any $t\ge 1$ and $(d,\mathbf{f})\in X_q$

$$\begin{array}{cc}\hfill \parallel ({\partial }_t^j{\mathcal{H}}_Z^1\left(t\right)d,{\partial }_t^j{\mathcal{H}}_Z^2\left(t\right)\mathbf{f}){\parallel }_{W_q^{3-1/q}\left({\mathbf{R}}^{N-1}\right)}& \le C{e}^{-{\gamma }_{0}t}{\parallel (d,\mathbf{f})\parallel }_{X_q},\hfill \\ \hfill \parallel ({\partial }_t^j{\mathcal{U}}_Z^1\left(t\right)d,{\partial }_t^j{\mathcal{U}}_Z^2\left(t\right)\mathbf{f}){\parallel }_{H_q^2\left({\dot{\mathbf{R}}}^N\right)}& \le C{e}^{-{\gamma }_{0}t}{\parallel (d,\mathbf{f})\parallel }_{X_q},\hfill \end{array}$$

where $Z\in \{A_{\infty },⟨A_0,A_{\infty }⟩\}$ and C is a positive constant independent of t, d, and $\mathbf{f}$. Here $A_0$ is the positive constant given in Theorem 2.

Recalling (21), we have time-decay estimates of $L_p$-$L_q$ type for the solution $(H,\mathbf{U})=T\left(t\right)(d,\mathbf{f})=\left(\mathcal{H}\right(t\left)\right(d,\mathbf{f}),\mathcal{U}(t\left)\right(d,\mathbf{f}\left)\right)$ of (1) from Theorems 2–4 immediately.

Theorem 5.

Let $1<p<2\le q<\infty$ and suppose that ${\rho }_{-}>{\rho }_{+}>0$. Then for any $t\ge 1$ and $(d,\mathbf{f})\in J{X}_q\cap J{Y}_p$

$$\begin{array}{cc}\hfill {\parallel \mathcal{H}\left(t\right)(d,\mathbf{f})\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{t}^{-min\left\{\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right),\frac{(N-1)}{2}\left(\frac{1}{p}-\frac{1}{q}\right)+\frac{3}{4}{\gamma }_1\right\}}{\parallel (d,\mathbf{f})\parallel }_{X_q\cap Y_p},\hfill \\ \hfill {\parallel \mathcal{U}\left(t\right)(d,\mathbf{f})\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{t}^{-min\left\{\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)+\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right),\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)\right\}}{\parallel (d,\mathbf{f})\parallel }_{X_q\cap Y_p},\hfill \end{array}$$

with a positive constant C independent of t, d, and $\mathbf{f}$, where ${\gamma }_1$ is the positive constant given in Theorem 3.

3. Representation Formulas for Solutions

This section introduces the representation formulas for solutions of (1). In this section, we assume that ${\rho }_{\pm }$ are any positive constants except for Lemma 3 (2) below. Here we collect several symbols appearing in the representation formulas. Let $z_0=min\{{\mu }_{+}/{\rho }_{+},{\mu }_{-}/{\rho }_{-}\}$. For ${\xi }^{\prime }=({\xi }_1,\cdots ,{\xi }_{N-1})\in {\mathbf{R}}^{N-1}$ and $\lambda \in \mathbf{C}⧵(-\infty ,-z_0|{\xi }^{\prime }{|}^2]$, we set

$$A=|{\xi }^{\prime }|,B_{\pm }=\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}\lambda +{\left|{\xi }^{\prime }\right|}^2},$$

(22)

where we have chosen a branch cut along the negative real axis and a branch of the square root so that $\mathfrak{R}\sqrt{z}>0$ for $z\in \mathbf{C}⧵(-\infty ,0]$. In addition,

$$D_{\pm }={\mu }_{\pm }{B}_{\pm }+{\mu }_{\mp }A,E={\mu }_{+}{B}_{+}+{\mu }_{-}{B}_{-},{\mathcal{M}}_{\pm }\left(a\right)=\frac{e^{-Aa}-e^{-B_{\pm }a}}{A-B_{\pm }}(a\ge 0),$$

(23)

and also

$$\begin{array}{cc}\hfill F(A,\lambda )& =-{({\mu }_{+}-{\mu }_{-})}^2{A}^3+\{(3{\mu }_{+}-{\mu }_{-}){\mu }_{+}{B}_{+}+(3{\mu }_{-}-{\mu }_{+}){\mu }_{-}{B}_{-}\}{A}^2\hfill \\ \hfill & +\{{({\mu }_{+}{B}_{+}+{\mu }_{-}{B}_{-})}^2+{\mu }_{+}{\mu }_{-}{(B_{+}+B_{-})}^2\}A\hfill \\ \hfill & +({\mu }_{+}{B}_{+}+{\mu }_{-}{B}_{-})({\mu }_{+}{B}_{+}^2+{\mu }_{-}{B}_{-}^2).\hfill \end{array}$$

(24)

Except for $D_{\pm }$ and E, the above symbols are introduced in (3.3), (3.8), and (3.15) of [3]. Furthermore, the following properties are proved in Lemmas 4.7 and 4.8 of [3].

Lemma 1.

Let $\epsilon \in (0,\pi /2)$ and ${\rho }_{\pm }$ be any positive constants. Then the following assertions hold.

(1)

For any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in {\Sigma }_{\epsilon }\cup \left\{0\right\}$,

$$\begin{array}{cc}\hfill & C_1{\left(\right|\lambda |}^{1/2}+A)\le \mathfrak{R}{B}_{\pm }\le |B_{\pm }|\le C_2{\left(\right|\lambda |}^{1/2}+A),\hfill \\ \hfill & C_1{\left(\right|\lambda |}^{1/2}{+A)}^3\le \left|F(A,\lambda )\right|\le C_2{\left(\right|\lambda |}^{1/2}{+A)}^3,\hfill \end{array}$$

with positive constants $C_1$ and $C_2$ depending on ε, but independent of ${\xi }^{\prime }$ and λ.

(2)

Let $s\in \mathbf{R}$ and ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$. Then for any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in {\Sigma }_{\epsilon }\cup \left\{0\right\}$

$$\begin{array}{cc}\hfill & |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{A}^s|\le C{A}^{s-|{\alpha }^{\prime }|},|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{B}_{\pm }^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^{s-|{\alpha }^{\prime }|},\hfill \\ \hfill & |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{E}^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^{s-|{\alpha }^{\prime }|},\hfill \\ \hfill & |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{(A+B_{\pm })}^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^s{A}^{-|{\alpha }^{\prime }|},\hfill \\ \hfill & |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}F{(A,\lambda )}^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^{3s}{A}^{-|{\alpha }^{\prime }|},\hfill \end{array}$$

where C is a positive constant depending on ε, s, and ${\alpha }^{\prime }$, but independent of ${\xi }^{\prime }$ and λ.

From Lemma 1 and the Bell formula of derivatives of composite functions, we have

Lemma 2.

Let $\epsilon \in (0,\pi /2)$ and ${\rho }_{\pm }$ be any positive constants.

(1)

Let $s\in \mathbf{R}$ and ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$. Then for any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in {\Sigma }_{\epsilon }\cup \left\{0\right\}$

$$\begin{array}{c}\hfill |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{D}_{\pm }^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^s{A}^{-|{\alpha }^{\prime }|},|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{(D_{+}+D_{-})}^s{|\le C(\left|\lambda \right|}^{1/2}{+A)}^s{A}^{-|{\alpha }^{\prime }|},\end{array}$$

where C is a positive constant depending on ε, s, and ${\alpha }^{\prime }$, but independent of ${\xi }^{\prime }$ and λ.

(2)

Let $\theta ,\nu ,\tau >0$ and ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$. Then there exists a positive constant $C_{{\alpha }^{\prime },\theta }$, independent of ν and τ, such that for any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$

$$|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{e}^{-\nu \tau A^{\theta }}|\le C_{{\alpha }^{\prime },\theta }{A}^{-|{\alpha }^{\prime }|}{e}^{-\left(\nu \tau A^{\theta }\right)/2}.$$

3.1. A Representation Formula for the Parabolic Part

In this subsection, we introduce a representation formula for solutions of (15). Note that (15) admits a unique solution $({\mathbf{u}}^P,{\mathfrak{p}}^P)$ for $\lambda \in {\Sigma }_{\epsilon }$ and $\mathbf{f}\in L_q{\left({\dot{\mathbf{R}}}^N\right)}^N$, $\epsilon \in (0,\pi /2)$ and $q\in (1,\infty )$, as discussed in Section 1. Since $C_0^{\infty }\left({\dot{\mathbf{R}}}^N\right)$ is dense in $L_p\left({\dot{\mathbf{R}}}^N\right)$ for $1\le p<\infty$, it suffices to consider $\mathbf{f}\in C_0^{\infty }{\left({\dot{\mathbf{R}}}^N\right)}^N$ in what follows. Our aim is to prove

Proposition 1.

Let $\epsilon \in (0,\pi /2)$ and ${\rho }_{\pm }$ be any positive constants. Suppose that $({\mathbf{u}}^P,{\mathfrak{p}}^P)$ is a solution to (15) for some $\lambda \in {\Sigma }_{\epsilon }$ and $\mathbf{f}={(f_1,\cdots ,f_N)}^{\mathsf{T}}\in C_0^{\infty }{\left({\dot{\mathbf{R}}}^N\right)}^N$. Then there holds

$$\begin{array}{cc}\hfill & {\widehat{u}}_N^P({\xi }^{\prime },x_N,\lambda ){|}_{x_N=0}\hfill \\ \hfill & =\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A(A+B_{\mathfrak{b}})F(A,\lambda )}{\mathcal{M}}_{\mathfrak{b}}\left(y_N\right){\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N\hfill \\ \hfill & +\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(A+B_{\mathfrak{b}})F(A,\lambda )}{e}^{-B_{\mathfrak{b}}{y}_N}{\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N.\hfill \end{array}$$

Here ${\widehat{u}}_N^P({\xi }^{\prime },x_N,\lambda )$ stands for the partial Fourier transform of the Nth component of ${\mathbf{u}}^P$ and

$$\begin{array}{cc}\hfill {\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )& =\sum _{\begin{array}{c}|{\alpha }^{\prime }|+k+l+m=5\\ |{\alpha }^{\prime }|+k\ge 2\end{array}}{C}_{j,{\alpha }^{\prime },k,l,m}^{\mathfrak{a},\mathfrak{b}}{\left({\xi }^{\prime }\right)}^{{\alpha }^{\prime }}{A}^k{B}_{+}^l{B}_{-}^m,\hfill \\ \hfill {\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )& =\sum _{\begin{array}{c}|{\alpha }^{\prime }|+k+l+m=5\\ |{\alpha }^{\prime }|+k\ge 2\end{array}}{\tilde{C}}_{j,{\alpha }^{\prime },k,l,m}^{\mathfrak{a},\mathfrak{b}}{\left({\xi }^{\prime }\right)}^{{\alpha }^{\prime }}{A}^k{B}_{+}^l{B}_{-}^m,\hfill \end{array}$$

with constants $C_{j,{\alpha }^{\prime },k,l,m}^{\mathfrak{a},\mathfrak{b}}$ and ${\tilde{C}}_{j,{\alpha }^{\prime },k,l,m}^{\mathfrak{a},\mathfrak{b}}$ independent of ${\xi }^{\prime }$ and λ.

Proof. 

Let $j=1,\cdots ,N-1$ and $J=1,\cdots ,N$ in this proof. Although we follow calculations in Section 3 of [3], we will achieve a set of equations simpler than (3.6) of [3] in what follows, see (45) below.

Step 1. We compute ${\widehat{w}}_N({\xi }^{\prime },0-,\lambda )$ for the following resolvent problem:

$$\left\{\begin{array}{cccc}\hfill \rho \lambda \mathbf{w}-Div\left(\mu \mathbf{D}\right(\mathbf{w})-\mathfrak{r}\mathbf{I})& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div\mathbf{w}& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill ⟦(\mu \mathbf{D}\left(\mathbf{w}\right)-\mathfrak{r}\mathbf{I}){\mathbf{e}}_N⟧& =\mathbf{g}\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦\mathbf{w}⟧& =\mathbf{h}\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \end{array}\right.$$

(25)

where $\mathbf{g}={(g_1,\cdots ,g_N)}^{\mathsf{T}}$ and $\mathbf{h}={(h_1,\cdots ,h_N)}^{\mathsf{T}}$ are suitable functions on ${\mathbf{R}}^{N-1}$ specified in Step 2 below. The restriction of $\mathbf{w}$ and $\mathfrak{r}$ to ${\mathbf{R}}_{\pm }^N$ are denoted by ${\mathbf{w}}_{\pm }$ and ${\mathfrak{r}}_{\pm }$, respectively. Let us write the Jth component of ${\mathbf{w}}_{\pm }$ by $w_{J\pm }$ and observe $Div\left(\mu \mathbf{D}\left({\mathbf{w}}_{\pm }\right)\right)={\mu }_{\pm }\Delta {\mathbf{w}}_{\pm }$ by $div{\mathbf{w}}_{\pm }=0$ in ${\mathbf{R}}_{\pm }^N$. Then (25) can be written as

$$\left\{\begin{array}{cccc}\hfill {\rho }_{\pm }\lambda w_{J\pm }-{\mu }_{\pm }\Delta w_{J\pm }+{\partial }_J{\mathfrak{r}}_{\pm }& =0\hfill & \hfill & \mathrm{in}{\mathbf{R}}_{\pm }^N,\hfill \\ \hfill \sum _{j=1}^{N-1}{\partial }_j{w}_{j\pm }+{\partial }_N{w}_{N\pm }& =0\hfill & \hfill & \mathrm{in}{\mathbf{R}}_{\pm }^N,\hfill \\ \hfill {\mu }_{+}({\partial }_N{w}_{j+}+{\partial }_j{w}_{N+}){{|}_{x_N=0}-{\mu }_{-}({\partial }_N{w}_{j-}+{\partial }_j{w}_{N-})|}_{x_N=0}& =g_j\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill (2{\mu }_{+}{\partial }_N{w}_{N+}-{\mathfrak{r}}_{+}){{|}_{x_N=0}-(2{\mu }_{-}{\partial }_N{w}_{N-}-{\mathfrak{r}}_{-})|}_{x_N=0}& =g_N\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill w_{J+}{{|}_{x_N=0}-w_{J-}|}_{x_N=0}& =h_J\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1}.\hfill \end{array}\right.$$

Let ${\widehat{w}}_{J\pm }\left(x_N\right)={\widehat{w}}_{J\pm }({\xi }^{\prime },x_N,\lambda )$ and ${\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)={\widehat{\mathfrak{r}}}_{\pm }({\xi }^{\prime },x_N,\lambda )$. Applying the partial Fourier transform to the last system yields

$$\begin{array}{cc}\hfill {\rho }_{\pm }\lambda {\widehat{w}}_{j\pm }\left(x_N\right)-{\mu }_{\pm }({\partial }_N^2-|{\xi }^{\prime }{|}^2){\widehat{w}}_{j\pm }\left(x_N\right)+i{\xi }_j{\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)& =0,\pm x_N>0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill {\rho }_{\pm }\lambda {\widehat{w}}_{N\pm }\left(x_N\right)-{\mu }_{\pm }({\partial }_N^2-|{\xi }^{\prime }{|}^2){\widehat{w}}_{N\pm }\left(x_N\right)+{\partial }_N{\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)& =0,\pm x_N>0,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill \sum _{j=1}^{N-1}i{\xi }_j{\widehat{w}}_{j\pm }\left(x_N\right)+{\partial }_N{\widehat{w}}_{N\pm }\left(x_N\right)& =0,\pm x_N>0,\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {\mu }_{+}({\partial }_N{\widehat{w}}_{j+}\left(0\right)+i{\xi }_j{\widehat{w}}_{N+}\left(0\right))-{\mu }_{-}({\partial }_N{\widehat{w}}_{j-}\left(0\right)+i{\xi }_j{\widehat{w}}_{N-}\left(0\right))& ={\widehat{g}}_j,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill (2{\mu }_{+}{\partial }_N{\widehat{w}}_{N+}\left(0\right)-{\widehat{\mathfrak{r}}}_{+}\left(0\right))-(2{\mu }_{-}{\partial }_N{\widehat{w}}_{N-}\left(0\right)-{\widehat{\mathfrak{r}}}_{-}\left(0\right))& ={\widehat{g}}_N,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\widehat{w}}_{J+}\left(0\right)-{\widehat{w}}_{J-}\left(0\right)& ={\widehat{h}}_J,\hfill \end{array}$$

(31)

where ${\widehat{g}}_J={\widehat{g}}_J\left({\xi }^{\prime }\right)$ and ${\widehat{h}}_J={\widehat{h}}_J\left({\xi }^{\prime }\right)$. Note that (26) and (27) are respectively equivalent to

$$\begin{array}{cc}\hfill -{\mu }_{\pm }({\partial }_N^2-B_{\pm }^2){\widehat{w}}_{j\pm }\left(x_N\right)+i{\xi }_j{\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)& =0,\pm x_N>0,\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill -{\mu }_{\pm }({\partial }_N^2-B_{\pm }^2){\widehat{w}}_{N\pm }\left(x_N\right)+{\partial }_N{\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)& =0,\pm x_N>0.\hfill \end{array}$$

(33)

From now on, we look for ${\widehat{w}}_{J\pm }\left(x_N\right)$ and ${\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)$ of the forms: for $\pm x_N>0$,

$${\widehat{w}}_{J\pm }\left(x_N\right)={\alpha }_{J\pm }(e^{\mp A{x}_N}-e^{\mp B_{\pm }{x}_N})+{\beta }_{J\pm }{e}^{\mp B_{\pm }{x}_N},{\widehat{\mathfrak{r}}}_{\pm }\left(x_N\right)={\gamma }_{\pm }{e}^{\mp A{x}_N}.$$

(34)

Inserting these formulas into (32), (33) and (28)–(31) furnishes

$$\begin{array}{cc}\hfill -{\mu }_{\pm }{\alpha }_{j\pm }(A^2-B_{\pm }^2)+i{\xi }_j{\gamma }_{\pm }=0,-{\mu }_{\pm }{\alpha }_{N\pm }(A^2-B_{\pm }^2)\mp A{\gamma }_{\pm }& =0,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill i{\xi }^{\prime }·{\alpha }_{\pm }^{\prime }\mp A{\alpha }_{N\pm }=0,-i{\xi }^{\prime }·{\alpha }_{\pm }^{\prime }+i{\xi }^{\prime }·{\beta }_{\pm }^{\prime }\pm B_{\pm }{\alpha }_{N\pm }\mp B_{\pm }{\beta }_{N\pm }& =0,\hfill \\ \hfill {\mu }_{+}\{{\alpha }_{j+}(-A+B_{+})-{\beta }_{j+}{B}_{+}+i{\xi }_j{\beta }_{N+}\}& \hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill -{\mu }_{-}\{{\alpha }_{j-}(A-B_{-})+{\beta }_{j-}{B}_{-}+i{\xi }_j{\beta }_{N-}\}& ={\widehat{g}}_j,\hfill \\ \hfill {\mu }_{+}\{{\alpha }_{N+}(-A+B_{+})-{\beta }_{N+}{B}_{+}\}-{\gamma }_{+}]& \hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill -[2{\mu }_{-}\{{\alpha }_{N-}(A-B_{-})+{\beta }_{N-}{B}_{-}\}-{\gamma }_{-}]& ={\widehat{g}}_N,\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill {\beta }_{J+}-{\beta }_{J-}& ={\widehat{h}}_J,\hfill \end{array}$$

(39)

where $i{\xi }^{\prime }·{\alpha }_{\pm }^{\prime }={\sum }_{j=1}^{N-1}i{\xi }_j{\alpha }_{j\pm }$ and $i{\xi }^{\prime }·{\beta }^{\prime }={\sum }_{j=1}^{N-1}i{\xi }_j{\beta }_{j\pm }$.

Let us solve the Equations (35)–(39). By (36), we have

$${\alpha }_{N\pm }=\pm \frac{(i{\xi }^{\prime }·{\beta }_{\pm }^{\prime }\mp B_{\pm }{\beta }_{N\pm })}{A-B_{\pm }},i{\xi }^{\prime }·{\alpha }_{\pm }^{\prime }=\frac{A(i{\xi }^{\prime }·{\beta }_{\pm }^{\prime }\mp B_{\pm }{\beta }_{N\pm })}{A-B_{\pm }}.$$

(40)

By the first Equation of (40) and the second Equation of (35),

$${\gamma }_{\pm }=-\frac{{\mu }_{\pm }(A+B_{\pm })}{A}(i{\xi }^{\prime }·{\beta }_{\pm }^{\prime }\mp B_{\pm }{\beta }_{N\pm }).$$

(41)

Multiplying (37) by $i{\xi }_j$ and summing the resultant formulas yield

$$\begin{array}{c}{\mu }_{+}\{i{\xi }^{\prime }·{\alpha }_{+}^{\prime }(-A+B_{+})-i{\xi }^{\prime }·{\beta }_{+}^{\prime }{B}_{+}-A^2{\beta }_{N+}\}\hfill \\ \hfill -{\mu }_{-}\{i{\xi }^{\prime }·{\alpha }_{-}^{\prime }(A-B_{-})+i{\xi }^{\prime }·{\beta }_{-}^{\prime }{B}_{-}-A^2{\beta }_{N-}\}=i{\xi }^{\prime }·{\widehat{g}}^{\prime },\end{array}$$

where $i{\xi }^{\prime }·{\widehat{g}}^{\prime }={\sum }_{j=1}^{N-1}i{\xi }_j{\widehat{g}}_j$. Combining this equation with the second one of (40) furnishes

$$\begin{array}{c}{\mu }_{+}\{-(A+B_{+})i{\xi }^{\prime }·{\beta }_{+}^{\prime }+A(B_{+}-A){\beta }_{N+}\}\hfill \\ \hfill -{\mu }_{-}\{(A+B_{-})i{\xi }^{\prime }·{\beta }_{-}^{\prime }+A(B_{-}-A){\beta }_{N-}\}=i{\xi }^{\prime }·{\widehat{g}}^{\prime }.\end{array}$$

(42)

In addition, by (38) and (41) together with the first Equation of (40),

$$\begin{array}{c}{\mu }_{+}\{(-A+B_{+})i{\xi }^{\prime }·{\beta }_{+}^{\prime }-B_{+}(A+B_{+}){\beta }_{N+}\}\hfill \\ \hfill -{\mu }_{-}\{(-A+B_{-})i{\xi }^{\prime }·{\beta }_{-}^{\prime }+B_{-}(B_{-}+A){\beta }_{N-}\}=A{\widehat{g}}_N.\end{array}$$

(43)

Since it follows from (39) that $i{\xi }^{\prime }·{\beta }_{+}^{\prime }=i{\xi }^{\prime }·{\beta }_{-}^{\prime }+i{\xi }^{\prime }·{\widehat{h}}^{\prime }$ and ${\beta }_{N+}={\beta }_{N-}+{\widehat{h}}_N$, it holds by (42) and (43) that

$$\begin{array}{cc}\hfill & \{{\mu }_{+}(A+B_{+})+{\mu }_{-}(A+B_{-})\}i{\xi }^{\prime }·{\beta }_{-}^{\prime }-\{{\mu }_{+}A(B_{+}-A)-{\mu }_{-}A(B_{-}-A)\}{\beta }_{N-}\hfill \\ \hfill & =-i{\xi }^{\prime }·{\widehat{g}}^{\prime }-{\mu }_{+}(A+B_{+})i{\xi }^{\prime }·{\widehat{h}}^{\prime }+{\mu }_{+}A(B_{+}-A){\widehat{h}}_N=:G(\mathbf{g},\mathbf{h}),\hfill \\ \hfill & -\{{\mu }_{+}(-A+B_{+})-{\mu }_{-}(-A+B_{-})\}i{\xi }^{\prime }·{\beta }_{-}^{\prime }\hfill \\ \hfill & +\{{\mu }_{+}{B}_{+}(A+B_{+})+{\mu }_{-}{B}_{-}(B_{-}+A)\}{\beta }_{N-}\hfill \\ \hfill & =-A{\widehat{g}}_N+{\mu }_{+}(-A+B_{+})i{\xi }^{\prime }·{\widehat{h}}^{\prime }-{\mu }_{+}{B}_{+}(A+B_{+}){\widehat{h}}_N=:H(\mathbf{g},\mathbf{h}).\hfill \end{array}$$

(44)

We have thus achieved

$$\mathbf{L}\left(\begin{array}{c}i{\xi }^{\prime }·{\beta }_{-}^{\prime }\\ {\beta }_{N-}\end{array}\right)=\left(\begin{array}{c}G(\mathbf{g},\mathbf{h})\\ H(\mathbf{g},\mathbf{h})\end{array}\right),$$

(45)

where

$$\mathbf{L}=\left(\begin{array}{cc}{\mu }_{+}(A+B_{+})+{\mu }_{-}(A+B_{-})& -{\mu }_{+}A(B_{+}-A)+{\mu }_{-}A(B_{-}-A)\\ -{\mu }_{+}(-A+B_{+})+{\mu }_{-}(-A+B_{-})& {\mu }_{+}{B}_{+}(A+B_{+})+{\mu }_{-}{B}_{-}(B_{-}+A)\end{array}\right).$$

Then the inverse matrix ${\mathbf{L}}^{-1}$ of $\mathbf{L}$ is given by

$${\mathbf{L}}^{-1}=\frac{1}{F(A,\lambda )}\left(\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right),$$

where $F(A,\lambda )$ is defined in (24) and

$$\begin{array}{cc}{L}_{11}\hfill & ={\mu }_{+}{B}_{+}(A+B_{+})+{\mu }_{-}{B}_{-}(B_{-}+A),\hfill \\ L_{12}\hfill & ={\mu }_{+}A(B_{+}-A)-{\mu }_{-}A(B_{-}-A),\hfill \\ L_{21}\hfill & ={\mu }_{+}(-A+B_{+})-{\mu }_{-}(-A+B_{-}),\hfill \\ L_{22}\hfill & ={\mu }_{+}(A+B_{+})+{\mu }_{-}(A+B_{-}).\hfill \end{array}$$

(46)

Solving (45), we have

$$i{\xi }^{\prime }·{\beta }_{-}^{\prime }=\frac{L_{11}G(\mathbf{g},\mathbf{h})+L_{12}H(\mathbf{g},\mathbf{h})}{F(A,\lambda )},{\beta }_{N-}=\frac{L_{21}G(\mathbf{g},\mathbf{h})+L_{22}H(\mathbf{g},\mathbf{h})}{F(A,\lambda )}.$$

(47)

Since ${\widehat{w}}_N({\xi }^{\prime },0-,\lambda )={\widehat{w}}_{N-}({\xi }^{\prime },0,\lambda )={\beta }_{N-}$, there holds

$${\widehat{w}}_N({\xi }^{\prime },0-,\lambda )=\frac{L_{21}G(\mathbf{g},\mathbf{h})+L_{22}H(\mathbf{g},\mathbf{h})}{F(A,\lambda )}.$$

(48)

Step 2. We compute the formula of ${\widehat{u}}_N^P({\xi }^{\prime },0,\lambda )$. Let

$$({\psi }_{\pm },{\varphi }_{\pm })=({\psi }_{1\pm },\cdots ,{\psi }_{N\pm },{\varphi }_{\pm })$$

be the solutions to the following whole space problems without interface:

$$\left\{\begin{array}{c}\hfill {\rho }_{+}\lambda {\psi }_{+}-Div({\mu }_{+}\mathbf{D}\left({\psi }_{+}\right)-{\varphi }_{+}\mathbf{I})=\mathbf{F},div{\psi }_{+}=0\mathrm{in}{\mathbf{R}}^N,\\ \hfill {\rho }_{-}\lambda {\psi }_{-}-Div({\mu }_{-}\mathbf{D}\left({\psi }_{-}\right)-{\varphi }_{-}\mathbf{I})=\mathbf{F},div{\psi }_{-}=0\mathrm{in}{\mathbf{R}}^N,\end{array}\right.$$

(49)

where $\mathbf{F}=\rho \mathbf{f}$. Set $\psi ={\psi }_{+}{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+{\psi }_{-}{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N}$ and $\varphi ={\varphi }_{+}{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+{\varphi }_{-}{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N}$, and then $(\psi ,\varphi )$ satisfies

$$\rho \lambda -Div\left(\mu \mathbf{D}\right(\psi )-\varphi \mathbf{I})=\rho \mathbf{f},div\psi =0\mathrm{in}{\dot{\mathbf{R}}}^N.$$

In addition, $⟦\varphi ⟧=0$ as discussed in the Appendix A below. Thus $({\mathbf{u}}^P,{\mathfrak{p}}^P)$ are given by ${\mathbf{u}}^P=\psi +\mathbf{v}$ and ${\mathfrak{p}}^P=\varphi +\mathfrak{q}$ for the solution $(\mathbf{v},\mathfrak{q})$ to

$$\left\{\begin{array}{cccc}\hfill \rho \lambda \mathbf{v}-Div\left(\mu \mathbf{D}\right(\mathbf{v})-\mathfrak{q}\mathbf{I})& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div\mathbf{v}& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill ⟦(\mu \mathbf{D}\left(\mathbf{v}\right)-\mathfrak{q}\mathbf{I}){\mathbf{e}}_N⟧& =-⟦\mu \mathbf{D}\left(\psi \right){\mathbf{e}}_N⟧\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦\mathbf{v}⟧& =-⟦\psi ⟧\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1}.\hfill \end{array}\right.$$

We now see that by (48) with $\mathbf{g}=-⟦\mu \mathbf{D}\left(\psi \right){\mathbf{e}}_N⟧$ and $\mathbf{h}=-⟦\psi ⟧$

$$\begin{array}{cc}\hfill {\widehat{v}}_N({\xi }^{\prime },0-,\lambda )& =\frac{L_{21}}{F(A,\lambda )}\{{\mu }_{+}(i{\xi }^{\prime }·{\partial }_N{\widehat{\psi }}_{+}^{\prime }({\xi }^{\prime },0,\lambda )-A^2{\widehat{\psi }}_{N+}({\xi }^{\prime },0,\lambda ))\hfill \\ \hfill & -{\mu }_{-}(i{\xi }^{\prime }·{\partial }_N{\widehat{\psi }}_{-}^{\prime }({\xi }^{\prime },0,\lambda )-A^2{\widehat{\psi }}_{N-}({\xi }^{\prime },0,\lambda ))\hfill \\ \hfill & +{\mu }_{+}(A+B_{+})i{\xi }^{\prime }·({\widehat{\psi }}_{+}^{\prime }({\xi }^{\prime },0,\lambda )-{\widehat{\psi }}_{-}^{\prime }({\xi }^{\prime },0,\lambda ))\hfill \\ \hfill & -{\mu }_{+}A(B_{+}-A)({\widehat{\psi }}_{N+}({\xi }^{\prime },0,\lambda )-{\widehat{\psi }}_{N-}({\xi }^{\prime },0,\lambda ))\}\hfill \\ \hfill & +\frac{L_{22}}{F(A,\lambda )}\{A(2{\mu }_{+}{\partial }_N{\widehat{\psi }}_{N+}-2{\mu }_{-}{\partial }_N{\widehat{\psi }}_{N-})\hfill \\ \hfill & -{\mu }_{+}(-A+B_{+})i{\xi }^{\prime }·({\widehat{\psi }}_{+}^{\prime }({\xi }^{\prime },0,\lambda )-{\widehat{\psi }}_{-}^{\prime }({\xi }^{\prime },0,\lambda ))\hfill \\ \hfill & +{\mu }_{+}{B}_{+}(A+B_{+})({\widehat{\psi }}_{N+}({\xi }^{\prime },0,\lambda )-{\widehat{\psi }}_{N-}({\xi }^{\prime },0,\lambda ))\}.\hfill \end{array}$$

Since ${\widehat{u}}_N^P({\xi }^{\prime },0,\lambda )={\widehat{u}}_N^P({\xi }^{\prime },0-,\lambda )$ by $⟦{\mathbf{u}}^P⟧=0$, there holds

$${\widehat{u}}_N^P({\xi }^{\prime },0,\lambda )={\widehat{\psi }}_{N-}({\xi }^{\prime },0,\lambda )+{\widehat{v}}_N({\xi }^{\prime },0-,\lambda ).$$

Combing this property with the above formula of ${\widehat{v}}_N({\xi }^{\prime },0-,\lambda )$ and (A1) in the Appendix A below yields the desired formula of ${\widehat{u}}_N^P({\xi }^{\prime },0,\lambda )$. This completes the proof of Proposition 1. □

3.2. Solution Formulas for the Hyperbolic-Parabolic Part

In this subsection, we introduce solution formulas of $({\eta }^k,{\mathbf{u}}^k,{\mathfrak{p}}^k)$, $k=1,2$, for (18). System (18) can be written as

$$\left\{\begin{array}{cccc}\hfill \rho \lambda {\mathbf{u}}^k-Div(\mu \mathbf{D}\left({\mathbf{u}}^k\right)-{\mathfrak{p}}^k\mathbf{I})& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill div{\mathbf{u}}^k& =0\hfill & \hfill & \mathrm{in}{\dot{\mathbf{R}}}^N,\hfill \\ \hfill ⟦(\mu \mathbf{D}\left({\mathbf{u}}^k\right)-{\mathfrak{p}}^k\mathbf{I}){\mathbf{e}}_N⟧& =(\omega -\sigma {\Delta }^{\prime }){\eta }^k{\mathbf{e}}_N\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \\ \hfill ⟦{\mathbf{u}}^k⟧& =0\hfill & \hfill & \mathrm{on}{\mathbf{R}}^{N-1},\hfill \end{array}\right.$$

coupled with

$$\lambda {\eta }^k-u_N^k{|}_{x_N=0}=z^k\mathrm{on}{\mathbf{R}}^{N-1}.$$

(50)

In what follows, we apply the argumentation in Step 1 for the proof of Proposition 1 in the previous subsection. To this end, we set $\mathbf{g}={(0,\cdots ,0,(\omega -\sigma {\Delta }^{\prime }){\eta }^k)}^{\mathsf{T}}$ and $\mathbf{h}=0$ in (25). Then $G(\mathbf{g},\mathbf{h})$ and $H(\mathbf{g},\mathbf{h})$ in (44) are given by

$$G(\mathbf{g},\mathbf{h})=0,H(\mathbf{g},\mathbf{h})=-A(\omega +\sigma A^2){\widehat{\eta }}^k.$$

(51)

Since $\mathbf{h}=0$, we have by ()

$${\beta }_{J+}={\beta }_{J-}(J=1,\cdots ,N).$$

(52)

Combining this relation with (47) and (51) furnishes

$${\beta }_{N+}={\beta }_{N-}=-\frac{L_{22}}{F(A,\lambda )}A(\omega +\sigma A^2){\widehat{\eta }}^k,$$

(53)

and thus (34) gives

$${\widehat{u}}_N^k\left(0\right)=-\frac{L_{22}}{F(A,\lambda )}A(\omega +\sigma A^2){\widehat{\eta }}^k.$$

Inserting this formula into (50) yields

$$\lambda {\widehat{\eta }}^k+\frac{L_{22}}{F(A,\lambda )}A(\omega +\sigma A^2){\widehat{\eta }}^k={\widehat{z}}^k.$$

Solving this equation, we obtain

$${\widehat{\eta }}^k=\frac{F(A,\lambda )}{L(A,\lambda )}{\widehat{z}}^k,L(A,\lambda )=\lambda F(A,\lambda )+A(\omega +\sigma A^2)(D_{+}+D_{-}),$$

(54)

where we have used $L_{22}=D_{+}+D_{-}$ with $D_{\pm }={\mu }_{\pm }{B}_{\pm }+{\mu }_{\mp }A$ given in (23). At this point, we note the following lemma.

Lemma 3.

(1)

Let $\epsilon \in (0,\pi /2)$ and ${\rho }_{\pm }$ be any positive constants. Then there exists a constant ${\delta }_0\ge 1$ such that for any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in {\Sigma }_{\epsilon }$ with $\left|\lambda \right|\ge {\delta }_0$

$$\begin{array}{cc}\hfill \left|L\right(A,\lambda \left)\right|& \ge C_{\epsilon }{\left(\right|\lambda |}^{1/2}+{A\left)\right\{\left|\lambda \right|\left(\right|\lambda |}^{1/2}+A{)}^2+\sigma A^3\},\hfill \\ \hfill |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}L{(A,\lambda )}^{-1}|& \le C_{{\alpha }^{\prime },\epsilon }{\left[\right(\left|\lambda \right|}^{1/2}+{A\left)\right\{\left|\lambda \right|\left(\right|\lambda |}^{1/2}{+A)}^2+\sigma A^3{\left\}\right]}^{-1}{A}^{-|{\alpha }^{\prime }|},\hfill \end{array}$$

where ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$ and $C_{\epsilon }$, $C_{{\alpha }^{\prime },\epsilon }$ are positive constants independent of ${\xi }^{\prime }$ and λ.

(2)

Suppose that ${\rho }_{-}>{\rho }_{+}>0$. Let ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in \mathbf{C}$ with $\mathfrak{R}\lambda \ge 0$. Then $L(A,\lambda )\ne 0$.

Proof. 

(1) See Lemma 6.1 of [3].

(2) The proof is similar to Lemma 3.2 of [2], so that the detailed proof may be omitted. □

We continue to calculate the solution formulas for (18). By (53) and (54)

$${\beta }_{N+}={\beta }_{N-}=-\frac{L_{22}}{L(A,\lambda )}A(\omega +\sigma A^2){\widehat{z}}^k,$$

(55)

while by (47), (51) and (52)

$$i{\xi }^{\prime }·{\beta }_{+}^{\prime }=i{\xi }^{\prime }·{\beta }_{-}^{\prime }=-\frac{L_{12}}{L(A,\lambda )}A(\omega +\sigma A^2){\widehat{z}}^k.$$

(56)

It thus holds by (55) and (56) that

$$i{\xi }^{\prime }·{\beta }_{\pm }^{\prime }\mp B_{\pm }{\beta }_{N\pm }=-\frac{A(\omega +\sigma A^2)}{L(A,\lambda )}\left(L_{12}\mp B_{\pm }{L}_{22}\right){\widehat{z}}^k,$$

which, combined with (40) and (41), furnishes

$$\begin{array}{cc}\hfill & {\alpha }_{N\pm }=\mp \frac{1}{A-B_{\pm }}·\frac{A(\omega +\sigma A^2)}{L(A,\lambda )}\left(L_{12}\mp B_{\pm }{L}_{22}\right){\widehat{z}}^k,\hfill \\ \hfill & {\gamma }_{\pm }=\frac{{\mu }_{\pm }(A+B_{\pm })}{A}·\frac{A(\omega +\sigma A^2)}{L(A,\lambda )}\left(L_{12}\mp B_{\pm }{L}_{22}\right){\widehat{z}}^k.\hfill \end{array}$$

(57)

By the first Equation of (35) and the above formula of ${\gamma }_{\pm }$, we have

$${\alpha }_{j\pm }=\frac{i{\xi }_j}{(A-B_{\pm })A}·\frac{A(\omega +\sigma A^2)}{L(A,\lambda )}\left(L_{12}\mp B_{\pm }{L}_{22}\right){\widehat{z}}^k(j=1,\cdots ,N-1).$$

(58)

Noting $g_j=0$ for $j=1,\cdots ,N-1$, we have by (37), (52), (55) and (58)

$$\begin{array}{cc}\hfill & {\beta }_{j+}={\beta }_{j-}=\hfill \\ \hfill & -\frac{i{\xi }_j(\omega +\sigma A^2)}{EL(A,\lambda )}\left[({\mu }_{+}+{\mu }_{-})L_{12}+\left\{{\mu }_{+}(A-B_{+})-{\mu }_{-}(A-B_{-})\right\}{L}_{22}\right]{\widehat{z}}^k,\hfill \end{array}$$

(59)

together with $E={\mu }_{+}{B}_{+}+{\mu }_{-}{B}_{-}$ given in (23).

Let us define for $j=1,\cdots ,N-1$

$$\begin{array}{cc}\hfill {\mathcal{I}}_{j\pm }({\xi }^{\prime },\lambda )& =i{\xi }_j(\omega +\sigma A^2)(L_{12}\mp B_{\pm }{L}_{22}),\hfill \\ \hfill {\mathcal{I}}_{N\pm }({\xi }^{\prime },\lambda )& =\mp A(\omega +\sigma A^2)(L_{12}\mp B_{\pm }{L}_{22}),\hfill \\ \hfill {\mathcal{J}}_j({\xi }^{\prime },\lambda )& =-i{\xi }_j(\omega +\sigma A^2)\left[({\mu }_{+}+{\mu }_{-})L_{12}+\left\{{\mu }_{+}(A-B_{+})-{\mu }_{-}(A-B_{-})\right\}{L}_{22}\right],\hfill \\ \hfill {\mathcal{J}}_N({\xi }^{\prime },\lambda )& =-E{L}_{22}A(\omega +\sigma A^2),\hfill \end{array}$$

(60)

where $L_{11}$, $L_{12}$, $L_{21}$, and $L_{22}$ are given in (46). Recall ${\mathcal{M}}_{\pm }\left(a\right)$ in (23). Then, in view of (34), we have achieved by (55), (57)–(59)

$${\widehat{u}}_{m\pm }^k\left(x_N\right)=\frac{{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{L(A,\lambda )}{\mathcal{M}}_{\pm }(\pm x_N){\widehat{z}}^k+\frac{{\mathcal{J}}_m({\xi }^{\prime },\lambda )}{EL(A,\lambda )}{e}^{\mp B_{\pm }{x}_N}{\widehat{z}}^k$$

(61)

for $\pm x_N>0$ and $m=1,\cdots ,N$, with the pressure ${\widehat{\mathfrak{p}}}_{\pm }^k\left(x_N\right)={\gamma }_{\pm }{e}^{\mp x_N}$$(\pm x_N>0)$. For the above ${\widehat{\eta }}^k$, ${\widehat{u}}_{m\pm }^k\left(x_N\right)$, and ${\widehat{\mathfrak{p}}}_{\pm }^k\left(x_N\right)$, we define

$$\begin{array}{cc}\hfill & {\eta }^k={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\eta }}^k({\xi }^{\prime },\lambda )\right]\left(x^{\prime }\right),u_{m\pm }^k={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{u}}_{m\pm }^k({\xi }^{\prime },x_N,\lambda )\right]\left(x^{\prime }\right),\hfill \\ \hfill & {\mathfrak{p}}_{\pm }^k={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathfrak{p}}}_{\pm }^k({\xi }^{\prime },x_N,\lambda )\right]\left(x^{\prime }\right).\hfill \end{array}$$

Then setting

$$u_m^k=u_{m+}^k{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+u_{m-}^k{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N}\mathrm{and}{\mathfrak{p}}^k={\mathfrak{p}}_{+}^k{\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+{\mathfrak{p}}_{-}^k{\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N},$$

we observe that ${\eta }^k$, ${\mathbf{u}}^k={(u_1^k,\cdots ,u_N^k)}^{\mathsf{T}}$, and ${\mathfrak{p}}^k$ become a solution to (18). This completes the calculation of solution formulas for (18).

3.3. Representation Formulas for (1)

In this subsection, we give the representation formulas of solutions for (1). To this end, we first consider ${\mathcal{H}}_Z^1\left(t\right)d$, ${\mathcal{H}}_Z^2\left(t\right)\mathbf{f}$, ${\mathcal{U}}_Z^1\left(t\right)d$, and ${\mathcal{U}}_Z^2\left(t\right)\mathbf{f}$ given in (20). Together with Proposition 1, inserting ${\widehat{\eta }}^1$ and ${\widehat{\eta }}^2$ of (54) into ${\widehat{\mathcal{H}}}_Z^1(t;\Gamma )d$ and ${\widehat{\mathcal{H}}}_Z^2(t;\Gamma )\mathbf{f}$ in (19), respectively, yields

$$\begin{array}{cc}\hfill & {\widehat{\mathcal{H}}}_Z^1(t;\Gamma )d=\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{F(A,\lambda )}{L(A,\lambda )}d\lambda \widehat{d}\left({\xi }^{\prime }\right),\hfill \\ \hfill & {\widehat{\mathcal{H}}}_Z^2(t;\Gamma )\mathbf{f}\hfill \\ \hfill & =\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)}{A(B_{\mathfrak{b}}+A)L(A,\lambda )}d\lambda \right){\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N\hfill \\ \hfill & +\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )e^{-B_{\mathfrak{b}}{y}_N}}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)L(A,\lambda )}d\lambda \right){\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N.\hfill \end{array}$$

Let us define for $\pm x_N>0$ and $m=1,\cdots ,N$

$$\begin{array}{cc}\hfill {\widehat{\mathcal{U}}}_{Z,m\pm }^1(t;\Gamma )d& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{u}}_{m\pm }^1({\xi }^{\prime },x_N,\lambda )d\lambda ,\hfill \\ \hfill {\widehat{\mathcal{U}}}_{Z,m\pm }^2(t;\Gamma )\mathbf{f}& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}{\widehat{u}}_{m\pm }^2({\xi }^{\prime },x_N,\lambda )d\lambda .\hfill \end{array}$$

Together with Proposition 1, inserting ${\widehat{u}}_{m\pm }^1$ and ${\widehat{u}}_{m\pm }^2$ of (61) into ${\widehat{\mathcal{U}}}_{Z,m\pm }^1(t;\Gamma )d$ and ${\widehat{\mathcal{U}}}_{Z,m\pm }^2(t;\Gamma )\mathbf{f}$, respectively, yields the following formulas: for $\pm x_N>0$ and $m=1,\cdots ,N$

$$\begin{array}{cc}\hfill {\widehat{\mathcal{U}}}_{Z,m\pm }^1(t;\Gamma )d& =\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{L(A,\lambda )}{\mathcal{M}}_{\pm }(\pm x_N)d\lambda \widehat{d}\left({\xi }^{\prime }\right)\hfill \\ \hfill & +\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\mathcal{J}}_m({\xi }^{\prime },\lambda )}{EL(A,\lambda )}{e}^{\mp B_{\pm }{x}_N}d\lambda \widehat{d}\left({\xi }^{\prime }\right),\hfill \end{array}$$

and furthermore,

$$\begin{array}{cc}\hfill & {\widehat{\mathcal{U}}}_{Z,m\pm }^2(t;\Gamma )\mathbf{f}\hfill \\ \hfill & =\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda ){\mathcal{M}}_{\pm }(\pm x_N){\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)}{A(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}d\lambda \right)\hfill \\ \hfill & \times {\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N\hfill \\ \hfill & +\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda ){\mathcal{M}}_{\pm }(\pm x_N)e^{-B_{\mathfrak{b}}{y}_N}}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}d\lambda \right)\hfill \\ \hfill & \times {\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N\hfill \\ \hfill & +\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )e^{\mp B_{\pm }{x}_N}{\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)}{A(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}d\lambda \right)\hfill \\ \hfill & \times {\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N\hfill \\ \hfill & +\sum _{\mathfrak{a},\mathfrak{b}\in \{+,-\}}\sum _{j=1}^N{\int }_0^{\infty }\left(\frac{{\phi }_Z\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\Gamma }{e}^{\lambda t}\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )e^{\mp B_{\pm }{x}_N}{e}^{-B_{\mathfrak{b}}{y}_N}}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}d\lambda \right)\hfill \\ \hfill & \times {\widehat{f}}_j({\xi }^{\prime },\mathfrak{a}{y}_N)d{y}_N.\hfill \end{array}$$

One defines

$$\begin{array}{cc}\hfill {\widehat{\mathcal{U}}}_{Z,m}^1(t;\Gamma )d& =\left({\widehat{\mathcal{U}}}_{Z,m+}^1(t;\Gamma )d\right){\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+\left({\widehat{\mathcal{U}}}_{Z,m-}^1(t;\Gamma )d\right){\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N},\hfill \\ \hfill {\widehat{\mathcal{U}}}_{Z,m}^2(t;\Gamma )\mathbf{f}& =\left({\widehat{\mathcal{U}}}_{Z,m+}^2(t;\Gamma )\mathbf{f}\right){\mathrm{𝟙}}_{{\mathbf{R}}_{+}^N}+\left({\widehat{\mathcal{U}}}_{Z,m-}^2(t;\Gamma )\mathbf{f}\right){\mathrm{𝟙}}_{{\mathbf{R}}_{-}^N},\hfill \end{array}$$

and then there holds the following relation between these formulas and ${\widehat{\mathcal{U}}}_Z^1(t;\Gamma )d$, ${\widehat{\mathcal{U}}}_Z^2(t;\Gamma )\mathbf{f}$ given in (19):

$$\begin{array}{cc}\hfill {\widehat{\mathcal{U}}}_Z^1(t;\Gamma )d& ={({\widehat{\mathcal{U}}}_{Z,1}^1(t;\Gamma )d,\cdots ,{\widehat{\mathcal{U}}}_{Z,N}^1(t;\Gamma )d)}^{\mathsf{T}},\hfill \\ \hfill {\widehat{\mathcal{U}}}_Z^2(t;\Gamma )\mathbf{f}& ={({\widehat{\mathcal{U}}}_{Z,1}^2(t;\Gamma )\mathbf{f},\cdots ,{\widehat{\mathcal{U}}}_{Z,N}^2(t;\Gamma )\mathbf{f})}^{\mathsf{T}}.\hfill \end{array}$$

Summing up the above argumentation, we have obtained the representation formulas of ${\mathcal{H}}_Z^1\left(t\right)d$, ${\mathcal{H}}_Z^2\left(t\right)\mathbf{f}$, ${\mathcal{U}}_Z^1\left(t\right)d$, and ${\mathcal{U}}_Z^2\left(t\right)\mathbf{f}$ given in (20) from the formulas of ${\widehat{\mathcal{H}}}_Z^1(t;\Gamma )d$, ${\widehat{\mathcal{H}}}_Z^2(t;\Gamma )\mathbf{f}$, ${\widehat{\mathcal{U}}}_Z^1(t;\Gamma )d$, and ${\widehat{\mathcal{U}}}_Z^2(t;\Gamma )\mathbf{f}$ as above. Furthermore, those representation formulas of ${\mathcal{H}}_Z^1\left(t\right)d$, ${\mathcal{H}}_Z^2\left(t\right)\mathbf{f}$, ${\mathcal{U}}_Z^1\left(t\right)d$, and ${\mathcal{U}}_Z^2\left(t\right)\mathbf{f}$ give the representation formulas of solutions for (1) by the relation (21).

Finally, we introduce another useful formula of $L(A,\lambda )$.

Lemma 4.

Let $L(A,\lambda )$ be given in (54) and set

$${\mathcal{L}}_A\left(\lambda \right)={\lambda }^2+\frac{4A{D}_{+}{D}_{-}}{({\rho }_{+}+{\rho }_{-})(D_{+}+D_{-})}\lambda +\alpha A+\frac{\sigma A^3}{{\rho }_{+}+{\rho }_{-}},$$

where $D_{\pm }$ and α are defined in (23) and (12), respectively. Then

$$L(A,\lambda )=({\rho }_{+}+{\rho }_{-})(D_{+}+D_{-}){\mathcal{L}}_A\left(\lambda \right).$$

Proof. 

The desired relation follows from an elementary calculation, so that the detailed proof may be omitted. □

4. Analysis of Boundary Symbol

We assume ${\rho }_{-}>{\rho }_{+}>0$ throughout this section and analyze mainly the boundary symbol ${\mathcal{L}}_A\left(\lambda \right)$ introduced in the last part of the previous section. Note that $\alpha$ in (12) is positive by the assumption ${\rho }_{-}>{\rho }_{+}>0$ and that the symbols, defined in the previous section, such as

$$A=|{\xi }^{\prime }|,B_{\pm }=\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}+A^2},D_{\pm }={\mu }_{\pm }{B}_{\pm }+{\mu }_{\mp }A$$

are used in this section.

4.1. Analysis of Low Frequency Part

Recalling ${\theta }_2,{\lambda }_1$ given in (11) and $z_0=min\{{\mu }_{+}/{\rho }_{+},{\mu }_{-}/{\rho }_{-}\}$, we define for $A=|{\xi }^{\prime }|$

$$z_1^{\pm }=-\frac{z_0}{2}{A}^2\pm i\frac{z_0}{4}{A}^2,z_2^{\pm }={\lambda }_1{e}^{\pm i(\pi -{\theta }_2)},$$

(62)

and also

$$\begin{array}{cc}\hfill {\widehat{\Gamma }}_1^{\pm }& =\{\lambda \in \mathbf{C}:\lambda =-\frac{z_0}{2}{A}^2+\frac{z_0}{4}{A}^2{e}^{\pm is},0\le s\le \frac{\pi }{2}\},\hfill \\ \hfill {\widehat{\Gamma }}_2^{\pm }& =\{\lambda \in \mathbf{C}:\lambda =z_1^{\pm }(1-s)+z_2^{\pm }s,0\le s\le 1\},\hfill \\ \hfill {\widehat{\Gamma }}_3& =\{\lambda \in \mathbf{C}:\lambda ={\lambda }_1{e}^{is},-(\pi -{\theta }_2)\le s\le \pi -{\theta }_2\}.\hfill \end{array}$$

(63)

In addition, we set

$${\mathcal{F}}_A\left(\lambda \right)=(\lambda -{\zeta }_{+})(\lambda -{\zeta }_{-}),{\mathcal{G}}_A\left(\lambda \right)={\mathcal{L}}_A\left(\lambda \right)-{\mathcal{F}}_A\left(\lambda \right),$$

where ${\zeta }_{\pm }$ and ${\mathcal{L}}_A\left(A\right)$ are given in Theorem 3 and Lemma 4, respectively. Then

$$\begin{array}{cc}\hfill {\mathcal{G}}_A\left(\lambda \right)& =\frac{4A{D}_{+}{D}_{-}}{({\rho }_{+}+{\rho }_{-})(D_{+}+D_{-})}\lambda +\frac{\sigma A^3}{{\rho }_{+}+{\rho }_{-}}\hfill \\ \hfill & -2\sqrt{2}{\alpha }^{1/4}\beta A^{5/4}\lambda +2\sqrt{2}{\alpha }^{3/4}\beta A^{7/4}-4{\alpha }^{1/2}{\beta }^2{A}^{10/4}\hfill \end{array}$$

(64)

for $\alpha$, $\beta$ given in (12), and the following lemma holds.

Lemma 5.

There exists a constant $A_1\in (0,1)$ such that $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_1)$ and $\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}\cup {\widehat{\Gamma }}_2^{+}\cup {\widehat{\Gamma }}_2^{-}\cup {\widehat{\Gamma }}_3$.

Proof. Case 1: 

$\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}$. Let $\lambda =-(z_0/2)A^2+(z_0/4)A^2{e}^{is}$$(-\pi /2\le s\le \pi /2)$. It is clear that

$$|{\mathcal{F}}_A\left(\lambda \right)|\ge CA\mathrm{for}A\in (0,A_1),$$

with a sufficiently small $A_1$ and a positive constant C independent of A and $\lambda$.

Next, we estimate $|{\mathcal{G}}_A\left(\lambda \right)|$ from above. Since

$$\begin{array}{c}\hfill D_{\pm }=A\left({\mu }_{\pm }\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}\left(-\frac{z_0}{2}+\frac{z_0}{4}{e}^{is}\right)+1}+{\mu }_{\mp }\right),\\ \hfill \mathfrak{R}\left(\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}\left(-\frac{z_0}{2}+\frac{z_0}{4}{e}^{is}\right)+1}\right)>0,\end{array}$$

there holds

$$\left|\frac{D_{+}{D}_{-}}{D_{+}+D_{-}}\right|\le \frac{|D_{+}\left|\right|D_{-}|}{\left(\mathfrak{R}{D}_{+}\right)+\left(\mathfrak{R}{D}_{-}\right)}\le CA\mathrm{for}A>0.$$

One thus sees that

$$|{\mathcal{G}}_A\left(\lambda \right)|\le C{A}^{7/4}\mathrm{for}A\in (0,1),$$

which implies $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_1)$ when $A_1$ is sufficiently small.

Case 2: $\lambda \in {\widehat{\Gamma }}_2^{+}\cup {\widehat{\Gamma }}_2^{-}$. We consider $\lambda \in {\widehat{\Gamma }}_2^{+}$ only. Let $\lambda =z_1^{+}(1-s)+z_2^{+}s$$(0\le s\le 1)$. We write $\lambda =-a+bi$$(a,b\ge 0)$, that is,

$$a=\frac{z_0}{2}{A}^2(1-s)+{\lambda }_1(cos{\theta }_2)s,b=\frac{z_0}{4}{A}^2(1-s)+{\lambda }_1(sin{\theta }_2)s.$$

We then observe that

$$\begin{array}{cc}\hfill |\lambda -{\zeta }_{\pm }{|}^2& ={(-a+\sqrt{2}{\alpha }^{1/4}\beta A^{5/4})}^2+{(b\mp {\alpha }^{1/2}{A}^{1/2}\pm \sqrt{2}{\alpha }^{1/4}\beta A^{5/4})}^2\hfill \\ \hfill & =a^2+b^2+\alpha A\mp 2{\alpha }^{1/2}{A}^{1/2}b+O\left(A^{5/4}\right)\mathrm{as}A\to 0.\hfill \end{array}$$

(65)

From this, we immediately see that there exists a constant $A_1\in (0,1)$ such that

$$|\lambda -{\zeta }_{-}|\ge C(\left|\lambda \right|+A^{1/2})\mathrm{for}A\in (0,A_1).$$

Since $2{\alpha }^{1/2}{A}^{1/2}b\le \epsilon \alpha A+b^2/\epsilon$$(\epsilon >0)$, choosing $\epsilon =2/3$ furnishes

$$a^2+b^2+\alpha A-2{\alpha }^{1/2}{A}^{1/2}b\ge a^2-\frac{1}{2}{b}^2+\frac{1}{3}\alpha A.$$

(66)

In addition,

$$b=\frac{z_0}{4}{A}^2(1-s)+tan{\theta }_2·{\lambda }_1(cos{\theta }_2)s=\frac{1}{2}\left\{\frac{z_0}{2}{A}^2(1-s)+\frac{1}{4}{\lambda }_1(cos{\theta }_2)s\right\}\le \frac{1}{2}a,$$

which implies

$$a^2-\frac{1}{2}{b}^2=\frac{1}{4}(a^2+b^2)+\frac{3}{4}(a^2-b^2)\ge \frac{1}{4}(a^2+b^2).$$

It thus holds by (65) and (66) that $|\lambda -{\zeta }_{+}|\ge C(\left|\lambda \right|+A^{1/2})$ when A is small enough, and therefore

$$|{\mathcal{F}}_A\left(\lambda \right)|\ge C(\left|\lambda \right|+A^{1/2}{)}^2\mathrm{for}A\in (0,A_1).$$

(67)

In particular,

$$|{\mathcal{F}}_A\left(\lambda \right)|\ge C{A}^{1/2}\left(\right|\lambda |+A^{1/2})\mathrm{for}A\in (0,A_1).$$

(68)

Next, we estimate $|{\mathcal{G}}_A\left(\lambda \right)|$ from above. By Lemma 2 and (64), we have for $A\in (0,1)$

$$\begin{array}{cc}\hfill |{\mathcal{G}}_A\left(\lambda \right)|& \le C\left({A\left|\lambda \right|\left(\right|\lambda |}^{1/2}+A)+A^{5/4}\left|\lambda \right|+A^{7/4}\right)\hfill \\ \hfill & =C{A}^{3/4}\left(A^{1/4}{\left|\lambda \right|\left(\right|\lambda |}^{1/2}+A)+A^{1/2}\left|\lambda \right|+A\right).\hfill \end{array}$$

(69)

Since $\left|\lambda \right|\le {\lambda }_1$, one sees for $A\in (0,1)$ that

$$A^{1/4}{\left|\lambda \right|\left(\right|\lambda |}^{1/2}{+A)\le |\lambda \left|\right(\left|\lambda \right|}^{1/2}+A^{1/2})\le {\lambda }_1^{1/2}\left(\right|\lambda |+{\lambda }_1^{1/2}A)\le C(\left|\lambda \right|+A^{1/2})$$

and that $A^{1/2}\left|\lambda \right|+A\le \left|\lambda \right|+A^{1/2}$. Combining these inequalities with (69) furnishes

$$|{\mathcal{G}}_A\left(\lambda \right)|\le C{A}^{3/4}\left(\right|\lambda |+A^{1/2})\mathrm{for}A\in (0,1),$$

which implies $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_1)$ when $A_1$ is sufficiently small.

Case 3: $\lambda \in {\widehat{\Gamma }}_3$. Let $\lambda ={\lambda }_1{e}^{is}$$(-(\pi -{\theta }_2)\le s\le \pi -{\theta }_2)$. Then

$$|{\mathcal{F}}_A\left(\lambda \right)|\ge C\mathrm{for}A\in (0,A_1),$$

with a sufficiently small $A_1$ and a positive constant C independent of A and $\lambda$. Since (69) is also valid for $\lambda \in {\widehat{\Gamma }}_3$ when $A\in (0,1)$, there holds

$$|{\mathcal{G}}_A\left(\lambda \right)|\le C{A}^{3/4}\mathrm{for}A\in (0,1).$$

It therefore holds that $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_1)$ when $A_1$ is sufficiently small. This completes the proof of Lemma 5. □

By Lemma 5 and Rouché’s theorem, we immediately have

Proposition 2.

Let $A_1$ be the positive constant given in Lemma 5 and $A\in (0,A_1)$. Let K be the region enclosed by ${\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}\cup {\widehat{\Gamma }}_2^{+}\cup {\widehat{\Gamma }}_2^{-}\cup {\widehat{\Gamma }}_3$. Then ${\mathcal{L}}_A\left(\lambda \right)$ has two zeros in K.

Recalling ${\widehat{\Gamma }}_{\mathrm{res}}^{\pm }$ given in Theorem 3, we prove

Lemma 6.

There exists a constant $A_2\in (0,1)$ such that $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_2)$ and $\lambda \in {\widehat{\Gamma }}_{\mathrm{Res}}^{+}\cup {\widehat{\Gamma }}_{\mathrm{Res}}^{-}$.

Proof. 

We consider $\lambda \in {\widehat{\Gamma }}_{\mathrm{Res}}^{+}$ only. Let $\lambda ={\zeta }_{+}+A^{6/4}{e}^{is}$$(0\le s\le 2\pi )$. It is clear that

$$|{\mathcal{F}}_A\left(\lambda \right)|\ge C{A}^{8/4}\mathrm{for}A\in (0,A_2),$$

with a sufficiently small $A_2$ and a positive constant C independent of A and $\lambda$.

Next, we estimate $|{\mathcal{G}}_A\left(\lambda \right)|$ from above. It holds that

$$B_{\pm }=\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}}{e}^{i(\pi /4)}{\alpha }^{1/4}{A}^{1/4}(1+O\left(A^{3/4}\right))\mathrm{as}A\to 0,$$

which implies

$$D_{\pm }=\sqrt{{\rho }_{\pm }{\mu }_{\pm }}{e}^{i(\pi /4)}{\alpha }^{1/4}{A}^{1/4}+O\left(A\right)\mathrm{as}A\to 0.$$

Therefore,

$$\frac{D_{+}{D}_{-}}{D_{+}+D_{-}}=\frac{\sqrt{{\rho }_{+}{\mu }_{+}}\sqrt{{\rho }_{-}{\mu }_{-}}}{\sqrt{{\rho }_{+}{\mu }_{+}}+\sqrt{{\rho }_{-}{\mu }_{-}}}{e}^{i(\pi /4)}{\alpha }^{1/4}{A}^{1/4}+O\left(A\right)\mathrm{as}A\to 0.$$

From this, recalling the definition of $\beta$ given in (12), we have

$$\frac{4A{D}_{+}{D}_{-}}{({\rho }_{+}+{\rho }_{-})(D_{+}+D_{-})}\lambda =(-1+i)·2\sqrt{2}{\alpha }^{3/4}\beta A^{7/4}+O\left(A^{10/4}\right)\mathrm{as}A\to 0.$$

In addition,

$$-2\sqrt{2}{\alpha }^{1/4}\beta A^{5/4}\lambda =-i·2\sqrt{2}{\alpha }^{3/4}\beta A^{7/4}+O\left(A^{10/4}\right)\mathrm{as}A\to 0.$$

Combining these two formulas with (64) shows that

$$\begin{array}{c}\hfill {\mathcal{G}}_A\left(\lambda \right)=O\left(A^{10/4}\right)\mathrm{as}A\to 0,\end{array}$$

which implies $|{\mathcal{F}}_A\left(\lambda \right)|>|{\mathcal{G}}_A\left(\lambda \right)|$ for $A\in (0,A_2)$ when $A_2$ is sufficiently small. This completes the proof of Lemma 6. □

We now obtain

Proposition 3.

Let $A_1$ and $A_2$ be the positive constants given in Lemmas 5 and 6, respectively. Then there exists a constant $A_3\in (0,min\{A_1,A_2\})$ such that the following assertions hold.

(1)

Let $A\in (0,A_3)$ and K be the region given in Proposition 2. Then

$$\begin{array}{cc}\hfill & {\widehat{\Gamma }}_{\mathrm{Res}}^{+}\subset K\cap \{\lambda \in \mathbf{C}⧵\left\{0\right\}:\frac{\pi }{2}<arg\lambda <\frac{3}{4}\pi \},\hfill \\ \hfill & {\widehat{\Gamma }}_{\mathrm{Res}}^{-}\subset K\cap \{\lambda \in \mathbf{C}⧵\left\{0\right\}:-\frac{3}{4}\pi <arg\lambda <-\frac{\pi }{2}\}.\hfill \end{array}$$

(2)

Let $A\in (0,A_3)$ and $K_{\pm }$ be the regions enclosed by ${\widehat{\Gamma }}_{\mathrm{Res}}^{\pm }$, respectively. Then ${\mathcal{L}}_A\left(\lambda \right)$ has a simple zero denoted by ${\lambda }_{+}$ in $K_{+}$ and another simple zero denoted by ${\lambda }_{-}$ in $K_{-}$.

(3)

Let ${\mathcal{L}}_A^{\prime }\left(\lambda \right)$ be the derivative of ${\mathcal{L}}_A\left(\lambda \right)$ with respect to λ. Then the inequalities

$$|{\mathcal{L}}_A^{\prime }\left({\lambda }_{+}\right)|\ge C{A}^{1/2},\left|{\mathcal{L}}_A^{\prime }\left({\lambda }_{-}\right)\right|\ge C{A}^{1/2}$$

hold for $A\in (0,A_3)$ and a positive constant C independent of A.

Remark 1.

The zeros ${\lambda }_{\pm }$ of ${\mathcal{L}}_A\left(\lambda \right)$ satisfy

$${\lambda }_{\pm }={\zeta }_{\pm }+O\left(A^{6/4}\right)=\pm i{\alpha }^{1/2}{A}^{1/2}-\sqrt{2}{\alpha }^{1/4}\beta (1\pm i)A^{5/4}+O\left(A^{6/4}\right)\mathrm{as}A\to 0.$$

When gravity is not taken into account, i.e., $\alpha =0$, the asymptotics of the zeros of ${\mathcal{L}}_A\left(\lambda \right)$ are obtained in [4] as seen in Section 1.

Proof of Proposition 3.

(1) The desired properties can be proved by an elementary calculation, so that the detailed proof may be omitted.

(2) The result follows from Lemma 6 and Rouché’s theorem immediately.

(3) Since ${\mathcal{L}}_A^{\prime }\left({\lambda }_{\pm }\right)={\mathcal{F}}_A^{\prime }\left({\lambda }_{\pm }\right)+{\mathcal{G}}_A^{\prime }\left({\lambda }_{\pm }\right)$, one has the desired inequalities immediately by direct calculations together with (64). This completes the proof of Proposition 3. □

4.2. Analysis of High Frequency Part

Let us define

$$\Lambda (a,b)=\{\lambda \in \mathbf{C}:\lambda =x+yi,-a\le x\le 0,-b\le y\le b\}(a,b\ge 0).$$

(70)

Then we have

Proposition 4.

Let $a,b>0$. Then there exists a sufficiently large positive number $A_{\mathrm{high}}=A_{\mathrm{high}}(a,b)$ such that the following assertions hold.

(1)

For any $A\ge A_{\mathrm{high}}$ and $\lambda \in \Lambda (a,b)$,

$$C_{1}A\le \mathfrak{R}{B}_{\pm }\le \left|B_{\pm }\right|\le C_{2}A,$$

where $C_1$ and $C_2$ are positive constants independent of A and λ.

(2)

For any $A\ge A_{\mathrm{high}}$ and $\lambda \in \Lambda (a,b)$,

$$\left|F(A,\lambda )\right|\ge C{A}^3,\left|L(A,\lambda )\right|\ge C\sigma A^4,$$

with a positive constant C independent of A, λ, and σ, where $F(A,\lambda )$ and $L(A,\lambda )$ are given in (24) and (54), respectively.

Proof. 

(1) See Lemma 5.3 of [2].

(2) First, we estimate $\left|F\right(A,\lambda \left)\right|$ from below. Since

$$B_{\pm }=A+O\left(\frac{1}{A}\right)\mathrm{as}A\to \infty ,$$

(71)

it holds that

$$F(A,\lambda )=4{({\mu }_{+}+{\mu }_{-})}^2{A}^3+O\left(A\right)\mathrm{as}A\to \infty .$$

This implies the desired inequality for $\left|F\right(A,\lambda \left)\right|$.

Next, we estimate $\left|L\right(A,\lambda \left)\right|$ from below. Recall the formula of ${\mathcal{L}}_A\left(\lambda \right)$ in Lemma 4. The asymptotics (71) gives

$$D_{\pm }=({\mu }_{+}+{\mu }_{-})A+O\left(\frac{1}{A}\right)\mathrm{as}A\to \infty ,$$

which implies

$${\mathcal{L}}_A\left(\lambda \right)=\frac{\sigma A^3}{{\rho }_{+}+{\rho }_{-}}+O\left(A^2\right)\mathrm{as}A\to \infty .$$

Thus, from the formula of $L(A,\lambda )$ in Lemma 4, we see that

$$L(A,\lambda )=2({\mu }_{+}+{\mu }_{-})\sigma A^4+O\left(A^3\right)\mathrm{as}A\to \infty .$$

This yields the desired inequality of $\left|L\right(A,\lambda \left)\right|$ immediately, which completes the proof of Proposition 4. □

Next, we consider $A\in [M_1,M_2]$ for $M_2>M_1>0$.

Proposition 5.

Let $b>0$ and $M_2>M_1>0$. Then there exists a sufficiently small positive number $a_0$ such that the following assertions hold.

(1)

For any $A\in [M_1,M_2]$ and $\lambda \in \Lambda (a_0,b)$,

$$C_1\le \mathfrak{R}{B}_{\pm }\le \left|B_{\pm }\right|\le C_2,$$

where $C_1$ and $C_2$ are positive constants independent of A and λ.

(2)

For any $A\in [M_1,M_2]$ and $\lambda \in \Lambda (a_0,b)$,

$$\left|F\right(A,\lambda \left)\right|\ge C,\left|L\right(A,\lambda \left)\right|\ge C,$$

with a positive constant C independent of A and λ, where $F(A,\lambda )$ and $L(A,\lambda )$ are given in (24) and (54), respectively.

Proof. 

(1) The desired inequalities can be proved by an elementary calculation, so that the detailed proof may be omitted.

(2) By Lemma 1, we see that $F(A,\lambda )\ne 0$ for $A>0$ and $\mathfrak{R}\lambda \ge 0$. Then the continuity of $F(A,\lambda )$ and the compactness of $[M_1,M_2]\times \Lambda (0,b)$ implies there exists an $m:=min\left\{\right|F(A,\lambda )|:A\in [M_1,M_2],\lambda \in \Lambda (0,b)\}>0$. Choosing a sufficiently small $a_1\in (0,1)$, we see that $F(A,\lambda )$ is uniformly continuous on $[M_1,M_2]\times \Lambda (a_1,b)$. Thus there exists an $a_0\in (0,a_1]$ such that

$$\left|F(A,\lambda )\right|\ge \frac{m}{2}\mathrm{for}(A,\lambda )\in [M_1,M_2]\times \Lambda (a_0,b),$$

which implies the desired inequality of $\left|F\right(A,\lambda \left)\right|$ holds. Analogously, the inequality for $\left|L\right(A,\lambda \left)\right|$ follows from Lemma 3 (2). This completes the proof of Proposition 5. □

5. Time-Decay Estimates for Low Frequency Part

This section proves Theorem 3. Suppose ${\rho }_{-}>{\rho }_{+}>0$ throughout this section.

Let us denote the points of intersection between $\lambda =s{e}^{\pm i(3\pi /4)}$$(s\ge 0)$ and ${\Gamma }_0^{\pm }$ given in (13) by $z_3^{\pm }$. Then we define

$$\begin{array}{cc}\hfill {\widehat{\Gamma }}_4^{\pm }& =\{\lambda \in \mathbf{C}:\lambda =z_1^{\pm }(1-s)+z_3^{\pm }s,0\le s\le 1\},\hfill \\ \hfill {\widehat{\Gamma }}_5^{\pm }& =\{\lambda \in \mathbf{C}:\lambda =z_3^{\pm }+s{e}^{\pm i(\pi -{\theta }_1)},s\ge 0\},\hfill \end{array}$$

where $z_1^{\pm }$ are given in (62). Let $A_3$ be the positive constant given in Proposition 3 and let $A_0\in (0,A_3)$. Recalling (20) and the representation formulas in Section 3.3, we have, by Cauchy’s integral theorem and Propositions 2 and 3,

$$\begin{array}{cc}\hfill {\mathcal{S}}_{A_0}^1\left(t\right)d& =\sum _{\mathfrak{a}\in \{+,-\}}\sum _{j\in \{\mathrm{Res},1,4,5\}}{\mathcal{S}}_{A_0}^1(t;{\Gamma }_j^{\mathfrak{a}})d,{\mathcal{S}}_{A_0}^1(t;{\Gamma }_j^{\mathfrak{a}})d:={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_{A_0}^1(t;{\widehat{\Gamma }}_j^{\mathfrak{a}})d\right]\left(x^{\prime }\right),\hfill \\ \hfill {\mathcal{S}}_{A_0}^2\left(t\right)\mathbf{f}& =\sum _{\mathfrak{a}\in \{+,-\}}\sum _{j\in \{\mathrm{Res},1,4,5\}}{\mathcal{S}}_{A_0}^2(t;{\Gamma }_j^{\mathfrak{a}})\mathbf{f},{\mathcal{S}}_{A_0}^2(t;{\Gamma }_j^{\mathfrak{a}})\mathbf{f}:={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_{A_0}^2(t;{\widehat{\Gamma }}_j^{\mathfrak{a}})\mathbf{f}\right]\left(x^{\prime }\right),\hfill \end{array}$$

(72)

where $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$. Here we have used ${\widehat{\Gamma }}_{\mathrm{Res}}^{\pm }$ and ${\widehat{\Gamma }}_1^{\pm }$ given in Theorem 3 and (63), respectively, and the symbols ${\widehat{\mathcal{S}}}_{A_0}^1(t;{\widehat{\Gamma }}_j^{\mathfrak{a}})d$ and ${\widehat{\mathcal{S}}}_{A_0}^2(t;{\widehat{\Gamma }}_j^{\mathfrak{a}})\mathbf{f}$ introduced in Section 3.3. Throughout this section, we use symbols, given in Section 3, such as (22)–(24), (54), (60), ${\mathcal{L}}_A\left(\lambda \right)$ in Lemma 4, and ${\Phi }_j^{\mathfrak{a},\mathfrak{b}}$, ${\Psi }_j^{\mathfrak{a},\mathfrak{b}}$ in Proposition 1.

At this point, we introduce several lemmas used in the following argumentation. From Lemmas 4.3 and 4.4 of [2], we have the following two lemmas.

Lemma 7.

Let $c_1,c_2,d\ge 0$ and ${\nu }_1,{\nu }_2>0$. Then there exists a positive constant C such that for any $\tau \ge 0$, $a\ge 0$, and $Z\ge 0$

$$e^{-c_1\left(Z^{{\nu }_1}\right)\tau }{Z}^d{e}^{-c_2\left(Z^{{\nu }_2}\right)a}\le C{({\tau }^{d/{\nu }_1}+a^{d/{\nu }_2})}^{-1}.$$

Lemma 8.

Let $1\le p,q\le \infty$ and r be the dual exponent of p. Suppose that $a>0$, $b_1>0$, and $b_2>0$.

(1)

For $f\in L_p(0,\infty )$, $x_N>0$, and $\tau >0$, set

$$I(x_N,\tau )={\int }_0^{\infty }\frac{f\left(y_N\right)}{{\tau }^a+{\left(x_N\right)}^{b_1}+{\left(y_N\right)}^{b_2}}d{y}_N.$$

Then there exists a positive constant C, independent of f, such that for any $\tau >0$

$${\parallel I(·,\tau )\parallel }_{L_q(0,\infty )}\le C{\tau }^{-a\left(1-\frac{1}{b_{1}q}-\frac{1}{b_{2}r}\right)}{\parallel f\parallel }_{L_p(0,\infty )},$$

provided that $b_{1}q>1$ and $b_{2}r(1-1/\left(b_{1}q\right))>1$.

(2)

For $f\in L_p(0,\infty )$ and $\tau >0$, set

$$J\left(\tau \right)={\int }_0^{\infty }\frac{f\left(y_N\right)}{{\tau }^a+{\left(y_N\right)}^{b_2}}d{y}_N.$$

Then there exists a positive constant C, independent of f, such that for any $\tau >0$

$$\left|J\left(\tau \right)\right|\le C{\tau }^{-a\left(1-\frac{1}{b_{2}r}\right)}{\parallel f\parallel }_{L_p(0,\infty )},$$

provided that $b_{2}r>1$.

Next, we introduce time-decay estimates arising in the study of an evolution equation with the fractional Laplacian.

Lemma 9.

Let $\theta >0$ and $\nu >0$. Then the following assertions hold.

(1)

Let $1\le p\le q\le \infty$. Then for any $\tau >0$ and $\phi \in L_p\left({\mathbf{R}}^{N-1}\right)$

$$\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}[e^{-\nu \tau |{\xi }^{\prime }{|}^{\theta }}\widehat{\phi }\left({\xi }^{\prime }\right)]{\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\le C{\tau }^{-\frac{N-1}{\theta }\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \phi \parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},$$

with a positive constant C independent of τ and φ.

(2)

Let $1\le p\le 2$. Then for any $\tau >0$ and $\phi \in L_p\left({\mathbf{R}}^{N-1}\right)$

$$\parallel e^{-\nu \tau |{\xi }^{\prime }{|}^{\theta }}\widehat{\phi }{\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}\le C{\tau }^{-\frac{N-1}{\theta }\left(\frac{1}{p}-\frac{1}{2}\right)}{\parallel \phi \parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},$$

with a positive constant C independent of τ and φ.

Proof. 

(1) See e.g., Lemma 3.1 of [11], Lemma 2.5 of [12].

(2) The desired estimate follows from (1) and Parseval’s identity immediately. This completes the proof of Lemma 9. □

Let $L_p({\mathbf{R}}^n,X)$ be the X-valued Lebesgue spaces on ${\mathbf{R}}^n$, $n\in \mathbf{N}$, for $1\le p\le \infty$. The following lemma is proved in Theorem 2.3 of [13].

Lemma 10.

Let X be a Banach space and ${\parallel ·\parallel }_X$ its norm. Suppose that L and n be a non-negative integer and positive integer, respectively. Let $0<\sigma \le 1$ and $s=L+\sigma -n$. Let $f\left(\xi \right)$ be a $C^{\infty }$-function on ${\mathbf{R}}^n⧵\left\{0\right\}$ with value X and satisfy the following two conditions:

(1)

${\partial }_{\xi }^{\gamma }f\in L_1({\mathbf{R}}^n,X)$ for any multi-index $\gamma \in {\mathbf{N}}_0^n$ with $\left|\gamma \right|\le L$.

(2)

For any multi-index $\gamma \in {\mathbf{N}}_0^n$, there exists a positive constant $M_{\gamma }$ such that

$$\parallel {\partial }_{\xi }^{\gamma }{f\left(\xi \right)\parallel }_X\le M_{\gamma }{\left|\xi \right|}^{s-\left|\delta \right|}(\xi \in {\mathbf{R}}^n⧵\left\{0\right\}).$$

Then there exists a positive constant $C_{n,s}$ such that

$$\parallel {\mathcal{F}}_{\xi }^{-1}{\left[f\right]\left(x\right)\parallel }_X\le C_{n,s}\left(\underset{\left|\gamma \right|\le L+2}{max}{M}_{\gamma }\right){\left|x\right|}^{-(n+s)}(x\in {\mathbf{R}}^n⧵\left\{0\right\}),$$

where ${\mathcal{F}}_{\xi }^{-1}\left[f\right]\left(x\right)={\left(2\pi \right)}^{-n}{\int }_{{\mathbf{R}}^n}{e}^{ix·\xi }f\left(\xi \right)d\xi$.

5.1. Analysis for ${\Gamma }_{\mathrm{Res}}^{\pm }$.

In this subsection, we prove

Theorem 6.

Let $1\le p<2\le q\le \infty$ and $⟨t⟩=t+1$. Then there exists a constant $A_0\in (0,A_3)$ such that for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel {\mathcal{H}}_{A_0}^1(t;{\Gamma }_{\mathrm{Res}}^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{H}}_{A_0}^2(t;{\Gamma }_{\mathrm{Res}}^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{p}-\frac{1}{2}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^1(t;{\Gamma }_{\mathrm{Res}}^{\pm }){d\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^2(t;{\Gamma }_{\mathrm{Res}}^{\pm }){\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{4N}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \end{array}$$

where C is a positive constant independent of t, d, and $\mathbf{f}$.

Recalling $A=|{\xi }^{\prime }|$ and ${\lambda }_{\pm }$ given in Proposition 3, we define

$${\mathcal{B}}_{\pm }=\sqrt{\frac{{\rho }_{\pm }}{{\mu }_{\pm }}{\lambda }_{\pm }+A^2},{\mathcal{D}}_{\pm }={\mu }_{\pm }{\mathcal{B}}_{\pm }+{\mu }_{\mp }A,\mathcal{E}={\mu }_{+}{\mathcal{B}}_{+}+{\mu }_{-}{\mathcal{B}}_{-}.$$

Then we immediately obtain.

Lemma 11.

There exists a constant $A_4\in (0,A_3)$ such that for any $A\in (0,A_4)$

$$C_1{A}^{1/4}\le \mathfrak{R}{\mathcal{B}}_{\pm }\le |{\mathcal{B}}_{\pm }|\le C_2{A}^{1/4},C_1{A}^{3/4}\le \left|F(A,{\lambda }_{\pm })\right|\le C_2{A}^{3/4},$$

with positive constants $C_1$ and $C_2$ independent of ${\xi }^{\prime }$, and also

$$\begin{array}{cccc}\hfill |{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{2+(3/4)},\hfill & \hfill |{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{2+(3/4)},\hfill \\ \hfill |{\mathcal{I}}_{m\pm }({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{1+(2/4)},\hfill & \hfill |{\mathcal{J}}_m({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{1+(2/4)},\hfill \end{array}$$

with a positive constant C independent of ${\xi }^{\prime }$, where $\mathfrak{a},\mathfrak{b}\in \{+,-\}$ and $j,m=1,\cdots ,N$.

Let $A\in (0,A_4)$. Then, by Lemma 11, we have the following estimates for the symbols of the representation formulas given in Section 3.3: for the height function,

$$\begin{array}{cc}\hfill \left|\frac{F(A,{\lambda }_{\pm })}{{\mathcal{D}}_{+}+{\mathcal{D}}_{-}}\right|\le C{A}^{1/2},\left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm })}{A({\mathcal{B}}_{\mathfrak{b}}+A)({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le C{A}^{5/4},\hfill \\ \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm })}{A{\mathcal{B}}_{\mathfrak{b}}({\mathcal{B}}_{\mathfrak{b}}+A)({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le CA;\hfill \end{array}$$

(73)

for the fluid velocity,

$$\begin{array}{cc}\hfill \left|\frac{{\mathcal{I}}_{m\pm }({\xi }^{\prime },{\lambda }_{\pm })}{{\mathcal{D}}_{+}+{\mathcal{D}}_{-}}\right|\le C{A}^{5/4},\left|\frac{{\mathcal{J}}_m({\xi }^{\prime },{\lambda }_{\pm })}{\mathcal{E}({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le CA,\hfill \\ \hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm }){\mathcal{I}}_{m\pm }({\xi }^{\prime },{\lambda }_{\pm })}{A({\mathcal{B}}_{\mathfrak{b}}+A)F(A,{\lambda }_{\pm })({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le C{A}^2,\hfill \\ \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm }){\mathcal{I}}_{m\pm }({\xi }^{\prime },{\lambda }_{\pm })}{A{\mathcal{B}}_{\mathfrak{b}}({\mathcal{B}}_{\mathfrak{b}}+A)F(A,{\lambda }_{\pm })({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le C{A}^{7/4},\hfill \\ \hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm }){\mathcal{J}}_m({\xi }^{\prime },{\lambda }_{\pm })}{A({\mathcal{B}}_{\mathfrak{b}}+A)F(A,{\lambda }_{\pm })\mathcal{E}({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le C{A}^{7/4},\hfill \\ \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },{\lambda }_{\pm }){\mathcal{J}}_m({\xi }^{\prime },{\lambda }_{\pm })}{A{\mathcal{B}}_{\mathfrak{b}}({\mathcal{B}}_{\mathfrak{b}}+A)F(A,{\lambda }_{\pm })\mathcal{E}({\mathcal{D}}_{+}+{\mathcal{D}}_{-})}\right|& \le C{A}^{6/4}.\hfill \end{array}$$

(74)

To prove Theorem 6, we introduce some technical lemma. Let us define the following operators:

$$\begin{array}{cc}\hfill & \left[K_{A_0}(t;\Gamma )d\right]\left(x\right)={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}k({\xi }^{\prime },\lambda )d\lambda \widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right),\hfill \\ \hfill & \left[K_{A_0,\mathcal{M}}^{\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{k}_{\mathcal{M}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N,\hfill \\ \hfill & \left[K_{A_0,B}^{\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{k}_B({\xi }^{\prime },\lambda )e^{-B_{\mathfrak{b}}{y}_N}d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N,\hfill \end{array}$$

(75)

and also for $\pm x_N>0$

$$\begin{array}{cc}\hfill & \left[L_{A_0,\mathcal{M}}^{\pm }(t;\Gamma )d\right]\left(x\right)={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_{\mathcal{M}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{\pm }(\pm x_N)d\lambda \widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right),\hfill \\ \hfill & \left[L_{A_0,B}^{\pm }(t;\Gamma )d\right]\left(x\right)={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_B({\xi }^{\prime },\lambda )e^{\mp B_{\pm }{y}_N}d\lambda \widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right),\hfill \\ \hfill & \left[L_{A_0,\mathcal{M}\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_{\mathcal{M}\mathcal{M}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{\pm }(\pm x_N){\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N,\hfill \\ \hfill & \left[L_{A_0,\mathcal{M}B}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_{\mathcal{M}B}({\xi }^{\prime },\lambda ){\mathcal{M}}_{\pm }(\pm x_N)e^{-B_{\mathfrak{b}}{y}_N}d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N,\hfill \\ \hfill & \left[L_{A_0,B\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_{B\mathcal{M}}({\xi }^{\prime },\lambda )e^{\mp B_{\pm }{x}_N}{\mathcal{M}}_{\mathfrak{b}}\left(y_N\right)d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N,\hfill \\ \hfill & \left[L_{A_0,BB}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma )\mathbf{f}\right]\left(x\right)\hfill \\ \hfill & ={\int }_0^{\infty }{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_{\widehat{\Gamma }}{e}^{\lambda t}{l}_{BB}({\xi }^{\prime },\lambda )e^{\mp B_{\pm }{x}_N}{e}^{-B_{\mathfrak{b}}{y}_N}d\lambda \widehat{\mathbf{f}}({\xi }^{\prime },\mathfrak{a}{y}_N)\right]\left(x^{\prime }\right)d{y}_N.\hfill \end{array}$$

(76)

Here it is assumed that the symbols

$$\begin{array}{cc}\hfill & k({\xi }^{\prime },\lambda ),k_{\mathcal{M}}({\xi }^{\prime },\lambda ),k_B({\xi }^{\prime },\lambda ),l_{\mathcal{M}}({\xi }^{\prime },\lambda ),l_B({\xi }^{\prime },\lambda ),\hfill \\ \hfill & l_{\mathcal{M}\mathcal{M}}({\xi }^{\prime },\lambda ),l_{\mathcal{M}B}({\xi }^{\prime },\lambda ),l_{B\mathcal{M}}({\xi }^{\prime },\lambda ),l_{BB}({\xi }^{\prime },\lambda )\hfill \end{array}$$

are infinitely many times differentiable with respect to ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and holomorphic with respect to $\lambda \in \mathbf{C}⧵(-\infty ,-z_0|{\xi }^{\prime }{|}^2]$ for $z_0=min\{{\mu }_{+}/{\rho }_{+},{\mu }_{-}/{\rho }_{-}\}$. Then we have

Lemma 12.

Let $1\le p<2\le q\le \infty$, $⟨t⟩=t+1$, and $\mathfrak{a},\mathfrak{b}\in \{+,-\}$. Suppose that

$$Z({\xi }^{\prime },\lambda )=\frac{\tilde{Z}({\xi }^{\prime },\lambda )}{{\mathcal{L}}_A\left(\lambda \right)}\mathrm{for}Z\in \{k,k_{\mathcal{M}},k_B,l_{\mathcal{M}},l_B,l_{\mathcal{M}\mathcal{M}},l_{\mathcal{M}B},l_{B\mathcal{M}},l_{BB}\}$$

and that there exists a constant $A_5\in (0,A_3)$ such that for any $A\in (0,A_5)$

$$\begin{array}{cccccc}\hfill |\tilde{k}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{1/2},\hfill & \hfill |{\tilde{k}}_{\mathcal{M}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{5/4},\hfill & \hfill |{\tilde{k}}_B({\xi }^{\prime },{\lambda }_{\pm })|& \le CA,\hfill \\ \hfill |l_{\mathcal{M}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{5/4},\hfill & \hfill |{\tilde{l}}_B({\xi }^{\prime },{\lambda }_{\pm })|& \le CA,\hfill & \hfill |{\tilde{l}}_{\mathcal{M}\mathcal{M}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^2,\hfill \\ \hfill |l_{\mathcal{M}B}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{7/4},\hfill & \hfill |{\tilde{l}}_{B\mathcal{M}}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{7/4},\hfill & \hfill |{\tilde{l}}_{BB}({\xi }^{\prime },{\lambda }_{\pm })|& \le C{A}^{6/4},\hfill \end{array}$$

with some positive constant C independent of ${\xi }^{\prime }$. Then there exists a constant $A_0\in (0,A_5)$ such that the following assertions hold.

(1)

For any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel K_{A_0,\mathcal{M}}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_{\mathrm{Res}}^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{p}-\frac{1}{2}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel K_{A_0,B}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_{\mathrm{Res}}^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{p}-\frac{1}{2}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

(2)

Let $\Gamma ={\Gamma }_{\mathrm{Res}}^{+}$ or $\Gamma ={\Gamma }_{\mathrm{Res}}^{-}$. Then for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel L_{A_0,\mathcal{M}}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,B}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4N}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}B}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4N}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,B\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4N}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,BB}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{4N}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

Proof. 

We here consider

$$K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+}),K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_{\mathrm{Res}}^{+}),L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_{\mathrm{Res}}^{+}),L_{A_0,\mathcal{M}\mathcal{M}}^{+,+,+}(t;{\Gamma }_{\mathrm{Res}}^{+}),$$

only. The other cases can be proved analogously (cf. also Section 4.1 of [2]).

Case 1: $K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+})$. By the residue theorem, we have

$$\left[K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+})d\right]\left(x^{\prime }\right)={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\phi }_{A_0}\left({\xi }^{\prime }\right)e^{{\lambda }_{+}t}\frac{\tilde{k}({\xi }^{\prime },{\lambda }_{+})}{{\mathcal{L}}_A^{\prime }\left({\lambda }_{+}\right)}d\lambda \widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right).$$

Recalling $\mathfrak{R}{\zeta }_{\pm }=-\sqrt{2}{\alpha }^{1/4}\beta A^{5/4}$, we write this formula as

$$\left[K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+})d\right]\left(x^{\prime }\right)={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\phi }_{A_0}\left({\xi }^{\prime }\right)e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{e}^{-\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{e}^{{\lambda }_{+}t}\frac{\tilde{k}({\xi }^{\prime },{\lambda }_{+})}{{\mathcal{L}}_A^{\prime }\left({\lambda }_{+}\right)}\widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right).$$

Combining this formula with Lemma 9 yields

$$\begin{array}{cc}\hfill & \parallel K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+}){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\phi }_{A_0}\left({\xi }^{\prime }\right)e^{-\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{e}^{{\lambda }_{+}t}\frac{\tilde{k}({\xi }^{\prime },{\lambda }_{+})}{{\mathcal{L}}_A^{\prime }\left({\lambda }_{+}\right)}\widehat{d}\right]{\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}=:I_1\left(t\right).\hfill \end{array}$$

We choose a sufficiently small $A_0$ so that

$$|e^{-\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{e}^{{\lambda }_{+}t}|\le C{e}^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}\mathrm{on}supp{\phi }_{A_0},$$

and thus we have by Parseval’s identity, Proposition 3, and the assumption for $\tilde{k}({\xi }^{\prime },{\lambda }_{+})$

$$I_1\left(t\right)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}\widehat{d}\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}.$$

(77)

Since $0\le {\phi }_{A_0}\le 1$, this implies

$$I_1\left(t\right)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel e^{(\mathfrak{R}{\zeta }_{+}/3)⟨t⟩}\widehat{d}\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}.$$

Applying Lemma 9 to the right-hand side of the last inequality furnishes the desired estimate for $K_{A_0}(t;{\Gamma }_{\mathrm{Res}}^{+})$. This completes the proof of Case 1.

Case 2: $K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_{\mathrm{Res}}^{+})$. In the same way as we have obtained (77), we obtain

$$\begin{array}{cc}\hfill & \parallel K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_{\mathrm{Res}}^{+}){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^{\infty }{\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{3/4}{\mathcal{M}}_{+}\left(y_N\right)\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N\hfill \\ \hfill & =:I_2\left(t\right).\hfill \end{array}$$

We choose a sufficiently small $A_0$ so that

$$|{\mathcal{M}}_{+}\left(y_N\right)|\le C{A}^{-1/4}{e}^{-cA{y}_N}\mathrm{on}supp{\phi }_{A_0}$$

(78)

for positive constant C and c. Then

$$I_2\left(t\right)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^{\infty }{\parallel e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{1/2}{e}^{-cA{y}_N}\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N,$$

which, combined with Lemmas 7 and 9, implies

$$I_2\left(t\right)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\int }_0^{\infty }\frac{\parallel \mathbf{f}({\xi }^{\prime },y_N){\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)}}{{⟨t⟩}^{2/5}+y_N^{1/2}}d{y}_N.$$

Since $1\le p<2$, applying Lemma 8 to the right-hand side of the last inequality shows that the desired estimate for $K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_{\mathrm{Res}}^{+})$ holds. This completes the proof of Case 2.

Case 3: $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_{\mathrm{Res}}^{+})$. In the same way as we have obtained (77), we obtain

$$\begin{array}{cc}\hfill & \parallel L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_{\mathrm{Res}}^{+}){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{3/4}{\mathcal{M}}_{+}\left(x_N\right)\widehat{d}\left({\xi }^{\prime }\right)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}=:I_3(x_N,t).\hfill \end{array}$$

By (78), we see that

$$I_3(x_N,t)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\parallel e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{1/2}{e}^{-cA{x}_N}\widehat{d}\left({\xi }^{\prime }\right)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}.$$

(79)

When $q=2$, it follows from (79) that

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{I}_3{(x_N,t)}^{2}d{x}_N& \le C{\int }_0^{\infty }{\parallel e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{1/2}{e}^{-cA{x}_N}\widehat{d}\left({\xi }^{\prime }\right)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}^{2}d{x}_N\hfill \\ \hfill & \le C\parallel e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}\widehat{d}\left({\xi }^{\prime }\right){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}^2.\hfill \end{array}$$

Combining this with Lemma 9 yields the desired estimate of $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_{\mathrm{Res}}^{+})$ for $q=2$. When $q>2$, it follows from (79) and Lemmas 7 and 9 that

$$\begin{array}{c}\hfill I(x_N,t)\le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}\frac{{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)}}{{⟨t⟩}^{2/5}+x_N^{1/2}}.\end{array}$$

In this inequality, taking $L_q$-norm of both sides with respect to $x_N\in (0,\infty )$ furnishes the desired estimate of $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_{\mathrm{Res}}^{+})$ for $q>2$. This completes the proof of Case 3.

Case 4: $L_{A_0,\mathcal{M}\mathcal{M}}^{+,+,+}(t;{\Gamma }_{\mathrm{Res}}^{+})$. In the same way as we have obtained (77), we obtain

$$\begin{array}{cc}\hfill & \parallel L_{A_0,\mathcal{M}\mathcal{M}}^{+,+,+}(t;{\Gamma }_{\mathrm{Res}}^{+}){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^{\infty }{\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}{A}^{\frac{6}{4}}{\mathcal{M}}_{+}\left(x_N\right){\mathcal{M}}_{+}\left(y_N\right)\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N\hfill \\ \hfill & =:I_4(x_N,t).\hfill \end{array}$$

Combining this with (78) and Lemmas 7 and 9 yields

$$\begin{array}{cc}\hfill & I_4(x_N,t)\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4}{5}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^{\infty }{\parallel e^{\frac{\mathfrak{R}{\zeta }_{+}}{3}⟨t⟩}A{e}^{-cA(x_N+y_N)}\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{4(N-1)}{5}\left(\frac{1}{p}-\frac{1}{q}\right)}{\int }_0^{\infty }\frac{\parallel \mathbf{f}({\xi }^{\prime },y_N){\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)}}{{⟨t⟩}^{4/5}+x_N+y_N}d{y}_N.\hfill \end{array}$$

Lemma 8 thus yields the desired estimate for $L_{A_0,\mathcal{M}\mathcal{M}}^{+,+,+}(t;{\Gamma }_{\mathrm{Res}}^{+})$. This completes the proof of Lemma 12. □

Combining Lemma 12 with (73) and (74) yields Theorem 6 immediately. This completes the proof of Theorem 6.

5.2. Analysis for ${\Gamma }_1^{\pm }$.

In this subsection, we prove

Theorem 7.

Let $1\le p\le 2\le q\le \infty$ and $⟨t⟩=t+1$. Then there exists a constant $A_0\in (0,A_3)$ such that for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel {\mathcal{H}}_{A_0}^1(t;{\Gamma }_1^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{2}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{H}}_{A_0}^2(t;{\Gamma }_1^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^1(t;{\Gamma }_1^{\pm }){d\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^2(t;{\Gamma }_1^{\pm }){\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \end{array}$$

where C is a positive constant independent of t, d, and $\mathbf{f}$.

To prove Theorem 7, we start with the following lemma.

Lemma 13.

There exists a constant $A_6\in (0,A_3)$ such that for any $A\in (0,A_6)$ and $\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}$

$$C_{1}A\le \mathfrak{R}{B}_{\pm }\le |B_{\pm }|\le C_{2}A,C_1{A}^3\le \left|F(A,\lambda )\right|\le C_2{A}^3,$$

with positive constants $C_1$ and $C_2$ independent of ${\xi }^{\prime }$ and λ, and also

$$\begin{array}{cccc}\hfill |{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )|& \le C{A}^5,\hfill & \hfill |{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )|& \le C{A}^5,\hfill \\ \hfill |{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )|& \le C{A}^3,\hfill & \hfill |{\mathcal{J}}_m({\xi }^{\prime },\lambda )|& \le C{A}^3,\hfill \end{array}$$

with a positive constant C independent of ${\xi }^{\prime }$ and λ, where $\mathfrak{a},\mathfrak{b}\in \{+,-\}$ and $j,m=1,\cdots ,N$.

Proof. 

See Lemma 4.9 of [2] for $B_{\pm }$. Then the desired estimates for ${\Phi }_j^{\mathfrak{a},\mathfrak{b}}$, ${\Psi }_j^{\mathfrak{a},\mathfrak{b}}$, ${\mathcal{I}}_{m\pm }$, and ${\mathcal{J}}_m$ follow from the estimates of $B_{\pm }$ immediately.

We now estimate $\left|F\right(A,\lambda \left)\right|$. Let $\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}$. It is clear that $\left|F(A,\lambda )\right|\le C{A}^3$ by $|B_{\pm }|\le CA$. In what follows, we prove $\left|F\right(A,\lambda \left)\right|$ from below. Since $\lambda =-(z_0/2)A^2+(z_0/4)A^2{e}^{is}$ for $s\in [-\pi /2,\pi /2]$, there holds

$$F(A,\lambda )=A^{3}F(1,\zeta ),\zeta =-\frac{z_0}{2}+\frac{z_0}{4}{e}^{is}.$$

(80)

It suffices to show that

$$\left|F\right(1,\zeta \left)\right|\ne 0\mathrm{for}s\in [-\pi /2,\pi /2].$$

(81)

Let $s\ne 0$. Then $\zeta \in {\Sigma }_{\epsilon }$ for some $\epsilon =\epsilon \left(s\right)$. Therefore $\left|F\right(1,\zeta \left)\right|\ne 0$, since $\left|F(1,\zeta )\right|\ge C_{\epsilon }$ for some positive constant $C_{\epsilon }$ by Lemma 1.

Next, we consider $s=0$. In this case, $\zeta =-z_0/4$ and set $b_{\pm }=\sqrt{({\rho }_{\pm }/{\mu }_{\pm })\zeta +1}\in \mathbf{R}$. Then

$$\frac{\sqrt{3}}{2}\le b_{\pm }<1,$$

(82)

and $F(1,\zeta )\in \mathbf{R}$ can be written as

$$\begin{array}{cc}\hfill F(1,\zeta )& =-{({\mu }_{+}-{\mu }_{-})}^2+(3{\mu }_{+}-{\mu }_{-}){\mu }_{+}{b}_{+}+(3{\mu }_{-}-{\mu }_{+}){\mu }_{-}{b}_{-}\hfill \\ \hfill & +{({\mu }_{+}{b}_{+}+{\mu }_{-}{b}_{-})}^2+{\mu }_{+}{\mu }_{-}{(b_{+}+b_{-})}^2+({\mu }_{+}{b}_{+}+{\mu }_{-}{b}_{-})({\mu }_{+}{b}_{+}^2+{\mu }_{-}{b}_{-}^2).\hfill \end{array}$$

Since it follows from (82) that

$$\begin{array}{cc}\hfill & -{({\mu }_{+}-{\mu }_{-})}^2+(3{\mu }_{+}-{\mu }_{-}){\mu }_{+}{b}_{+}+(3{\mu }_{-}-{\mu }_{+}){\mu }_{-}{b}_{-}\hfill \\ \hfill & =-({\mu }_{+}^2+{\mu }_{-}^2)+2{\mu }_{+}{\mu }_{-}+3{\mu }_{+}^2{b}_{+}+3{\mu }_{-}^2{b}_{-}-{\mu }_{+}{\mu }_{-}(b_{+}+b_{-})\hfill \\ \hfill & \ge -({\mu }_{+}^2+{\mu }_{-}^2)+2{\mu }_{+}{\mu }_{-}+\frac{3\sqrt{3}}{2}({\mu }_{+}^2+{\mu }_{-}^2)-2{\mu }_{+}{\mu }_{-}>0,\hfill \end{array}$$

we have $F(1,\zeta )>0$ for $s=0$. Thus (81) holds, which implies $\left|F\right(1,\zeta \left)\right|\ge C$ for any $s\in [-\pi /2,\pi /2]$ and a positive constant C independent of s. Therefore $\left|F(A,\lambda )\right|\ge C{A}^3$ by (80), which completes the proof of Lemma 13. □

Note that $|{\mathcal{L}}_A\left(\lambda \right)|\ge CA$ for $\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}$ when A is small enough as seen in Case 1 of the proof of Lemma 5, and thus it follows from Lemma 13 that $\left|L(A,\lambda )\right|\ge C{A}^2$. By this inequality and Lemma 13, we have the following estimates for the symbols of the representation formulas given in Section 3.3: for the height function,

$$\left|\frac{F(A,\lambda )}{L(A,\lambda )}\right|\le CA,\left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)L(A,\lambda )}\right|\le CA,\left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)L(A,\lambda )}\right|\le C;$$

(83)

for the fluid velocity

$$\begin{array}{cccc}\hfill \left|\frac{{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{L(A,\lambda )}\right|& \le CA,\hfill & \hfill \left|\frac{{\mathcal{J}}_m({\xi }^{\prime },\lambda )}{EL(A,\lambda )}\right|& \le C,\hfill \\ \hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}\right|& \le CA,\hfill & \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}\right|& \le C,\hfill \\ \hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}\right|& \le C,\hfill & \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}\right|& \le \frac{C}{A}.\hfill \end{array}$$

(84)

Now, recalling the operators difined in (75) and (76), we introduce the following lemma (cf. [2] (Lemma 4.10) for details).

Lemma 14.

Let $1\le p\le 2\le q\le \infty$, $⟨t⟩=t+1$, and $\mathfrak{a},\mathfrak{b}\in \{+,-\}$. Suppose that there exists a constant $A_7\in (0,A_3)$ such that for any $A\in (0,A_7)$ and $\lambda \in {\widehat{\Gamma }}_1^{+}\cup {\widehat{\Gamma }}_1^{-}$

$$\begin{array}{cccccc}\hfill \left|k\right({\xi }^{\prime },\lambda \left)\right|& \le CA,\hfill & \hfill |k_{\mathcal{M}}({\xi }^{\prime },\lambda )|& \le CA,\hfill & \hfill |k_B({\xi }^{\prime },\lambda )|& \le C,\hfill \\ \hfill |l_{\mathcal{M}}({\xi }^{\prime },\lambda )|& \le CA,\hfill & \hfill |l_B({\xi }^{\prime },\lambda )|& \le C,\hfill & \hfill |l_{\mathcal{M}\mathcal{M}}({\xi }^{\prime },\lambda )|& \le CA,\hfill \\ \hfill |l_{\mathcal{M}B}({\xi }^{\prime },\lambda )|& \le C,\hfill & \hfill |l_{B\mathcal{M}}({\xi }^{\prime },\lambda )|& \le C,\hfill & \hfill |l_{BB}({\xi }^{\prime },\lambda )|& \le C{A}^{-1},\hfill \end{array}$$

with some positive constant C independent of ${\xi }^{\prime }$ and λ. Then there exists a constant $A_0\in (0,A_7)$ such that the following assertions hold.

(1)

For any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel K_{A_0}(t;{\Gamma }_1^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{2}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel K_{A_0,\mathcal{M}}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_1^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel K_{A_0,B}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_1^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

(2)

Let $\Gamma ={\Gamma }_1^{+}$ or $\Gamma ={\Gamma }_1^{-}$. Then for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel L_{A_0,\mathcal{M}}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,B}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}B}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,B\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,BB}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

Combining Lemma 14 with (83) and (84) proves Theorem 7 immediately. This completes the proof of Theorem 7.

5.3. Analysis for ${\Gamma }_4^{\pm }$.

In this subsection, we prove

Theorem 8.

Let $1\le p<2\le q\le \infty$ and $⟨t⟩=t+1$ Then there exists a constant $A_0\in (0,A_3)$ such that for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel {\mathcal{H}}_{A_0}^1(t;{\Gamma }_4^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{4}{\gamma }_1}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{H}}_{A_0}^2(t;{\Gamma }_4^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}{\gamma }_2}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^1(t;{\Gamma }_4^{\pm }){d\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}{\gamma }_3}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^2(t;{\Gamma }_4^{\pm }){\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \end{array}$$

where C is a positive constant independent of t, d, and $\mathbf{f}$. Here

$$\begin{array}{cc}\hfill & 0<{\gamma }_1<min\left\{1,2(N-1)\left(\frac{1}{p}-\frac{1}{2}\right)\right\},0<{\gamma }_2<min\left\{1,2N\left(\frac{1}{p}-\frac{1}{2}\right)\right\},\hfill \\ \hfill & 0<{\gamma }_3<min\left\{1,2\left((N-1)\left(\frac{1}{p}-\frac{1}{2}\right)+\frac{1}{2}-\frac{1}{q}\right)\right\}.\hfill \end{array}$$

Note that ${\widehat{\Gamma }}_4^{+}\cup {\widehat{\Gamma }}_4^{-}\subset {\Sigma }_{{\theta }_2}$ for ${\theta }_2$ given in (11). By Lemma 1, we have for any ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$ and $\lambda \in {\widehat{\Gamma }}_{+}^4\cup {\widehat{\Gamma }}_{-}^4$

$$\begin{array}{cccc}\hfill |{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )|& \le C{A}^2{\left(\right|\lambda |}^{1/2}{+A)}^3,\hfill & \hfill |{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )|& \le C{A}^2{\left(\right|\lambda |}^{1/2}{+A)}^3,\hfill \\ \hfill |{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )|& \le {CA\left(\right|\lambda |}^{1/2}{+A)}^2,\hfill & \hfill |{\mathcal{J}}_m({\xi }^{\prime },\lambda )|& \le {CA\left(\right|\lambda |}^{1/2}{+A)}^2,\hfill \end{array}$$

(85)

where $\mathfrak{a},\mathfrak{b}\in \{+,-\}$ and $j,m=1,\cdots ,N$. In addition, similarly to (67), there holds

$$|{\mathcal{L}}_A\left(\lambda \right)|\ge C(\left|\lambda \right|+A^{1/2}{)}^2$$

for a sufficiently small A and $\lambda \in {\widehat{\Gamma }}_{+}^4\cup {\widehat{\Gamma }}_{-}^4$, which, combined with $\left|\lambda \right|+A^{1/2}\ge {(1/2)\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2$ and Lemmas 2 and 4, furnishes

$$\left|L(A,\lambda )\right|=({\rho }_{+}+{\rho }_{-})|D_{+}+D_{-}\left|\right|{\mathcal{L}}_A\left(\lambda \right){|\ge C(\left|\lambda \right|}^{1/2}+{A\left)\right(\left|\lambda \right|}^{1/2}+A^{1/4}{)}^4.$$

By this inequality together with (85) and Lemma 1, we have the following estimates for the symbols of the representation formulas given in Section 3.3: for the height function

$$\begin{array}{cc}\hfill & \left|\frac{F(A,\lambda )}{L(A,\lambda )}\right|\le \frac{C}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2},\left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)L(A,\lambda )}\right|\le \frac{CA\left(\right|\lambda {|}^{1/2}+A)}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\hfill \\ \hfill & \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)L(A,\lambda )}\right|\le \frac{CA}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4};\hfill \end{array}$$

(86)

for the fluid velocity

$$\left|\frac{{\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{L(A,\lambda )}\right|\le \frac{CA\left(\right|\lambda {|}^{1/2}+A)}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\left|\frac{{\mathcal{J}}_m({\xi }^{\prime },\lambda )}{EL(A,\lambda )}\right|\le \frac{CA}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},$$

(87)

and also

$$\begin{array}{cc}\hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}\right|& \le CA,\hfill \\ \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{I}}_{m\pm }({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )L(A,\lambda )}\right|& \le \frac{CA}{{\left|\lambda \right|}^{1/2}+A},\hfill \\ \hfill \left|\frac{{\Phi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )}{A(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}\right|& \le \frac{CA}{{\left|\lambda \right|}^{1/2}+A},\hfill \\ \hfill \left|\frac{{\Psi }_j^{\mathfrak{a},\mathfrak{b}}({\xi }^{\prime },\lambda ){\mathcal{J}}_m({\xi }^{\prime },\lambda )}{A{B}_{\mathfrak{b}}(B_{\mathfrak{b}}+A)F(A,\lambda )EL(A,\lambda )}\right|& \le \frac{CA}{{\left(\right|\lambda |}^{1/2}{+A)}^2}.\hfill \end{array}$$

(88)

We now prove

Lemma 15.

Let $1\le p<2\le q\le \infty$, $⟨t⟩=t+1$, and $\mathfrak{a},\mathfrak{b}\in \{+,-\}$. Suppose that there exists a constant $A_8\in (0,A_3)$ such that for any $A\in (0,A_8)$ and $\lambda \in {\widehat{\Gamma }}_4^{+}\cup {\widehat{\Gamma }}_4^{-}$

$$\begin{array}{cccc}& |k({\xi }^{\prime },\lambda )|\le \frac{C}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2},\hfill & & |k_{\mathcal{M}}({\xi }^{\prime },\lambda )|\le \frac{CA\left(\right|\lambda {|}^{1/2}+A)}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\hfill \\ & |k_B({\xi }^{\prime },\lambda )|\le \frac{CA}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\hfill & & |l_{\mathcal{M}}({\xi }^{\prime },\lambda )|\le \frac{CA\left(\right|\lambda {|}^{1/2}+A)}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\hfill \\ & |l_B({\xi }^{\prime },\lambda )|\le \frac{CA}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^4},\hfill & & |l_{\mathcal{M}\mathcal{M}}({\xi }^{\prime },\lambda )|\le CA,\hfill \\ & |l_{\mathcal{M}B}({\xi }^{\prime },\lambda )|\le \frac{CA}{{\left|\lambda \right|}^{1/2}+A},\hfill & & |l_{B\mathcal{M}}({\xi }^{\prime },\lambda )|\le \frac{CA}{{\left|\lambda \right|}^{1/2}+A},\hfill \\ & |l_{BB}({\xi }^{\prime },\lambda )|\le \frac{CA}{{\left(\right|\lambda |}^{1/2}{+A)}^2},\hfill \end{array}$$

with some positive constant of ${\xi }^{\prime }$ and λ. Then there exists a constant $A_0\in (0,A_8)$ such that the following assertions hold.

(1) 

For any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel K_{A_0}(t;{\Gamma }_4^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{4}{\gamma }_1}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel K_{A_0,\mathcal{M}}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_4^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}{\gamma }_2}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel K_{A_0,B}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_4^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{4}}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

(2) 

Let $\Gamma ={\Gamma }_4^{+}$ or $\Gamma ={\Gamma }_4^{-}$. Then for any $t>0$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel L_{A_0,\mathcal{M}}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}{\gamma }_3}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,B}^{\pm }{(t;\Gamma )d\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{4}}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,\mathcal{M}B}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,B\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \\ \hfill \parallel L_{A_0,BB}^{\pm ,\mathfrak{a},\mathfrak{b}}{(t;\Gamma )\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}_{\pm }^N\right)}& \le C{⟨t⟩}^{-\frac{N}{2}\left(\frac{1}{p}-\frac{1}{q}\right)}{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{\mathfrak{a}}^N\right)},\hfill \end{array}$$

with some positive constant C independent of t, d, and $\mathbf{f}$.

Proof. 

We here consider $K_{A_0}(t;{\Gamma }_4^{+})$, $K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_4^{+})$, and $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_4^{+})$ only. The desired estimates for

$$L_{A_0,B}^{\pm }(t;\Gamma ),L_{A_0,\mathcal{M}\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma ),L_{A_0,\mathcal{M}B}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma ),L_{A_0,B\mathcal{M}}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma ),L_{A_0,BB}^{\pm ,\mathfrak{a},\mathfrak{b}}(t;\Gamma )$$

are proved in Lemma 4.13 of [2], and $K_{A_0,B}^{\mathfrak{a},\mathfrak{b}}(t;{\Gamma }_4^{\pm })$ can be proved similarly to the case of $L_{A_0,B}^{\pm }(t;\Gamma )$.

Case 1: $K_{A_0}(t;{\Gamma }_4^{+})$. Since $\lambda =z_1^{+}(1-s)+z_3^{+}s$ for $0\le s\le 1$, there holds

$$\begin{array}{cc}\hfill & \left[K_{A_0}(t,{\Gamma }_4^{+})d\right]\left(x^{\prime }\right)\hfill \\ \hfill & ={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}·e^{z_0{A}^2⟨t⟩/8}\frac{{\phi }_{A_0}\left({\xi }^{\prime }\right)}{2\pi i}{\int }_0^1{e}^{\lambda t}k({\xi }^{\prime },\lambda )(z_3^{+}-z_1^{+})ds\widehat{d}\left({\xi }^{\prime }\right)\right]\left(x^{\prime }\right).\hfill \end{array}$$

It thus holds that by Lemma 9, Parseval’s identity, and the assumption for $k({\xi }^{\prime },\lambda )$

$$\begin{array}{cc}\hfill & \parallel K_{A_0}(t,{\Gamma }_4^{+}){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^1\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)\frac{e^{z_0{A}^2⟨t⟩/8}{e}^{\left(\mathfrak{R}\lambda \right)t}}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2}\widehat{d}\left({\xi }^{\prime }\right){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}ds=:I_1\left(t\right).\hfill \end{array}$$

We choose a sufficiently small $A_0\in (0,1)$ so that

$$e^{z_0{A}^2⟨t⟩/8}{e}^{\left(\mathfrak{R}\lambda \right)t}\le C{e}^{-z_0{A}^2⟨t⟩/8}{e}^{-cs⟨t⟩}\mathrm{on}supp{\phi }_{A_0}$$

for positive constants C and c. Then

$$I_1\left(t\right)\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^1{e}^{-cs⟨t⟩}\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)\frac{e^{-z_0{A}^2⟨t⟩/8}}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2}\widehat{d}\left({\xi }^{\prime }\right){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}ds.$$

(89)

Let $0<\delta <2$. Since

$${\left|\lambda \right|}^{1/2}\ge C(A\sqrt{1-s}+\sqrt{s})\mathrm{for}s\in [0,1],$$

we see that

$${\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2\ge {\left(\right|\lambda |}^{1/2}{)}^{2-\delta }{A}^{\delta /4}\ge C{\left(\sqrt{s}\right)}^{2-\delta }{A}^{\delta /4}.$$

(90)

Combining this inequality with (89) furnishes

$$\begin{array}{cc}\hfill I_1\left(t\right)& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^1\frac{e^{-cs⟨t⟩}}{{\sqrt{s}}^{2-\delta }}ds·\parallel e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\widehat{d}\left({\xi }^{\prime }\right){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}\parallel e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\widehat{d}\left({\xi }^{\prime }\right){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)},\hfill \end{array}$$

which, combined with Parseval’s identity and Young’s inequality, yields

$$\begin{array}{cc}\hfill I_1\left(t\right)& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\widehat{d}\left({\xi }^{\prime }\right)\right]{\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right]{\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \end{array}$$

where $1+(1/2)=(1/p)+(1/r)$.

From now on, we estimate $J_1\left(t\right):={\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right]\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}$ by Lemma 10. By the Leibniz rule and Lemmas 1 and 2, we have for any multi-index ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$ and ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$

$$|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}\left(e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right)|\le C_{{\alpha }^{\prime }}{A}^{-(\delta /4)-|{\alpha }^{\prime }|}{e}^{-z_0{A}^2⟨t⟩/16},$$

where $C_{{\alpha }^{\prime }}$ is a positive constant independent of ${\xi }^{\prime }$ and t. Lemma 10 with $\sigma =1-(\delta /4)$, $L=N-2$, and $n=N-1$ then furnishes

$$|{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right]\left(x^{\prime }\right)|\le C|x^{\prime }{|}^{-(N-1-(\delta /4\left)\right)}(x^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}).$$

By direct calculations, we also have

$$|{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right]\left(x^{\prime }\right)|\le C{\int }_{{\mathbf{R}}^{N-1}}{e}^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}d{\xi }^{\prime }\le C{⟨t⟩}^{-(N-1-(\delta /4\left)\right)/2},$$

and thus we obtain from these two inequalities

$$|{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{-\delta /4}\right]\left(x^{\prime }\right)|\le \frac{C}{{⟨t⟩}^{(N-1-(\delta /4\left)\right)/2}+{\left|x^{\prime }\right|}^{N-1-(\delta /4)}}.$$

Let us choose the above $\delta$ so that

$$0<\delta <min\left\{2,4(N-1)\left(\frac{1}{p}-\frac{1}{2}\right)\right\}.$$

Then we have

$$J_1\left(t\right)\le C{⟨t⟩}^{-\frac{1}{2}(N-1-\frac{\delta }{4})+\frac{N-1}{2r}}=C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)+\frac{\delta }{8}}.$$

Hence

$$I_1\left(t\right)\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{3}{8}\delta }{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},$$

which implies the desired estimate for $K_{A_0}(t;{\Gamma }_4^{+})$ holds.

Case 2: $K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_4^{+})$. In the same way as we have obtained (89), we obtain

$$\begin{array}{cc}\hfill & \parallel K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_4^{+}){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}\hfill \\ \hfill & \times {\int }_0^{\infty }{\int }_0^1{e}^{-cs⟨t⟩}\parallel {\phi }_{A_0}\left({\xi }^{\prime }\right)e^{-z_0{A}^2⟨t⟩/8}{k}_{\mathcal{M}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{+}\left(y_N\right)\widehat{\mathbf{f}}({\xi }^{\prime },y_N){\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}dsd{y}_N\hfill \\ \hfill & =:I_2\left(t\right).\hfill \end{array}$$

Since it holds by Lemma 1 that $C_1{\left(\right|\lambda |}^{1/2}+A)\le |B_{+}+A|\le C_2{\left|\lambda \right|}^{1/2}$ for $A\in (0,1)$ and $\lambda \in {\widehat{\Gamma }}_4^{+}$, we see that

$$\left|\frac{1}{B_{+}-A}\right|=\left|\frac{B_{+}+A}{B_{+}^2-A^2}\right|\le \frac{C}{{\left|\lambda \right|}^{1/2}}\le \frac{\tilde{C}}{{\left|\lambda \right|}^{1/2}+A}.$$

Therefore for $A\in (0,1)$ and $\lambda \in {\widehat{\Gamma }}_4^{+}$

$$|{\mathcal{M}}_{+}\left(y_N\right)|\le \frac{C{e}^{-cA{y}_N}}{{\left|\lambda \right|}^{1/2}+A},$$

with positive constants C and c, which, combined with the assumption for $k_{\mathcal{M}}({\xi }^{\prime },\lambda )$ and (90), furnishes

$$|k_{\mathcal{M}}({\xi }^{\prime },\lambda ){\mathcal{M}}_{+}\left(y_N\right)|\le C\frac{A^{1/2}{e}^{-cA{y}_N}}{{\left(\right|\lambda |}^{1/2}+A^{1/4}{)}^2}\le C\frac{A^{1/2}{e}^{-cA{y}_N}}{{\left(\sqrt{s}\right)}^{2-\delta }{A}^{\delta /4}}(0<\delta <2).$$

One now sees that

$$\begin{array}{cc}\hfill I_2\left(t\right)& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)}{\int }_0^1\frac{e^{-cs⟨t⟩}}{{\left(\sqrt{s}\right)}^{2-\delta }}ds\hfill \\ \hfill & \times {\int }_0^{\infty }{\parallel e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}{\int }_0^{\infty }{\parallel e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\widehat{\mathbf{f}}({\xi }^{\prime },y_N)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}d{y}_N,\hfill \end{array}$$

(91)

and thus for $1+(1/2)=(1/p)+(1/r)$

$$\begin{array}{cc}\hfill I_2\left(t\right)& \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}\hfill \\ \hfill & \times {\int }_0^{\infty }\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]{\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}{\parallel \mathbf{f}(·,y_N)\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)}d{y}_N\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}{J}_2\left(t\right){\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{+}^N\right)},\hfill \end{array}$$

where for $p^{\prime }=p/(p-1)$

$$\begin{array}{cc}\hfill & J_2\left(t\right)=\hfill \\ \hfill & \left\{\begin{array}{cccc}\hfill & {\left({\int }_0^{\infty }{\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}^{p^{\prime }}d{y}_N\right)}^{1/p^{\prime }}\hfill & \hfill & (1<p<2),\hfill \\ \hfill & \underset{y_N>0}{sup}{\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}\hfill & \hfill & (p=1).\hfill \end{array}\right.\hfill \end{array}$$

By the Leibniz rule and Lemmas 1 and 2, we have for any multi-index ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$ and ${\xi }^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}$

$$|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}\left(e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right)|\le C_{{\alpha }^{\prime }}{A}^{1/2-\delta /4-|{\alpha }^{\prime }|}{e}^{-z_0{A}^2⟨t⟩/16},$$

where $C_{{\alpha }^{\prime }}$ is a positive constant independent of ${\xi }^{\prime }$ and t. Lemma 10 with $\sigma =1/2-\delta /4$, $L=N-1$, and $n=N-1$ then furnishes

$$|{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\left(x^{\prime }\right)|\le C|x^{\prime }{|}^{-(N-1+\sigma )}(x^{\prime }\in {\mathbf{R}}^{N-1}⧵\left\{0\right\}).$$

By direct calculations, we also have

$$\begin{array}{cc}\hfill & |{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\left(x^{\prime }\right)|\hfill \\ \hfill & \le C{\int }_{{\mathbf{R}}^{N-1}}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}d{\xi }^{\prime }\le C{y}_N^{-(N-1+\sigma )}(y_N>0),\hfill \\ \hfill & |{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\left(x^{\prime }\right)|\hfill \\ \hfill & \le C{\int }_{{\mathbf{R}}^{N-1}}{e}^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}d{\xi }^{\prime }\le C{⟨t⟩}^{-\frac{1}{2}(N-1+\sigma )}(t>0).\hfill \end{array}$$

Combining these three inequalities yields

$$|{\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]\left(x^{\prime }\right)|\le \frac{C}{|x^{\prime }{|}^{N-1+\sigma }+y_N^{N-1+\sigma }+{⟨t⟩}^{(N-1+\sigma )/2}},$$

which implies for any $\delta \in (0,2)$

$$\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{y}_N}\right]{\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}\le C{(y_N+{⟨t⟩}^{1/2})}^{-(N-1)\left(\frac{1}{p}-\frac{1}{2}\right)-\left(\frac{1}{2}-\frac{\delta }{4}\right)}.$$

Let us choose the above $\delta$ so that

$$0<\delta <min\left\{2,4N\left(\frac{1}{p}-\frac{1}{2}\right)\right\}.$$

Then we have

$$J_2\left(t\right)\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)+\frac{\delta }{8}}.$$

Hence

$$I_2\left(t\right)\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{p}-\frac{1}{2}\right)-\frac{3}{8}\delta }{\parallel \mathbf{f}\parallel }_{L_p\left({\mathbf{R}}_{+}^N\right)},$$

which implies the desired estimate for $K_{A_0,\mathcal{M}}^{+,+}(t;{\Gamma }_4^{+})$ holds.

Case 3: $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_4^{+})$. In the same way as we have obtained (91), we obtain for $\delta \in (0,2)$

$$\begin{array}{cc}\hfill & \parallel \left[L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_4^{+})d\right](·,x_N){\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}{\parallel e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{x}_N}\widehat{d}\left({\xi }^{\prime }\right)\parallel }_{L_2\left({\mathbf{R}}^{N-1}\right)}=:I_3(x_N,t).\hfill \end{array}$$

By Parseval’s identity and Young’s inequality,

$$\begin{array}{cc}\hfill & I_3(x_N,t)\hfill \\ \hfill & \le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{\delta }{2}}\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{x}_N}\right]{\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \end{array}$$

where $1+(1/2)=(1/p)+(1/r)$. Similarly to $J_2\left(t\right)$ in Case 2, we observe for any $\delta \in (0,2)$ that

$$\parallel {\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[e^{-z_0{A}^2⟨t⟩/8}{A}^{1/2-\delta /4}{e}^{-cA{x}_N}\right]{\parallel }_{L_r\left({\mathbf{R}}^{N-1}\right)}\le C{(x_N+{⟨t⟩}^{1/2})}^{-(N-1)\left(\frac{1}{p}-\frac{1}{2}\right)-\left(\frac{1}{2}-\frac{\delta }{4}\right)}.$$

Thus, by choosing

$$0<\delta <min\left\{2,4\left((N-1)\left(\frac{1}{p}-\frac{1}{2}\right)+\frac{1}{2}-\frac{1}{q}\right)\right\},$$

we have

$${\left({\int }_0^{\infty }{I}_3{(x_N,t)}^{q}d{x}_N\right)}^{1/q}\le C{⟨t⟩}^{-\frac{N-1}{2}\left(\frac{1}{p}-\frac{1}{q}\right)-\frac{1}{2}\left(\frac{1}{2}-\frac{1}{q}\right)-\frac{3}{8}\delta }{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)}.$$

This inequality furnishes the desired estimate for $L_{A_0,\mathcal{M}}^{+}(t;{\Gamma }_4^{+})$, which completes the proof of Lemma 15. □

Combining Lemma 15 with (86)–(88) yields Theorem 8 immediately. This completes the proof of Theorem 8.

5.4. Analysis for ${\Gamma }_5^{\pm }$.

Similarly to Subsection 4.4 of [2], we can prove by Lemmas 1 and 3 the following theorem.

Theorem 9.

Let $1\le p\le 2\le q\le \infty$. Then there exist constants $A_0\in (0,A_3)$ and $c_0>0$ such that for any $t\ge 1$ and $(d,\mathbf{f})\in Y_p$

$$\begin{array}{cc}\hfill \parallel {\mathcal{H}}_{A_0}^1(t;{\Gamma }_5^{\pm }){d\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{e}^{-c_{0}t}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{H}}_{A_0}^2(t;{\Gamma }_5^{\pm }){\mathbf{f}\parallel }_{L_q\left({\mathbf{R}}^{N-1}\right)}& \le C{e}^{-c_{0}t}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^1(t;{\Gamma }_5^{\pm }){d\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{e}^{-c_{0}t}{\parallel d\parallel }_{L_p\left({\mathbf{R}}^{N-1}\right)},\hfill \\ \hfill \parallel {\mathcal{U}}_{A_0}^2(t;{\Gamma }_5^{\pm }){\mathbf{f}\parallel }_{L_q\left({\dot{\mathbf{R}}}^N\right)}& \le C{e}^{-c_{0}t}{\parallel \mathbf{f}\parallel }_{L_p\left({\dot{\mathbf{R}}}^N\right)},\hfill \end{array}$$

where C is a positive constant independent of t, d, and $\mathbf{f}$.

5.5. Proof of Theorem 3.

Recalling (72), we observe for $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$ that the operators in Theorem 3 are given by

$$\begin{array}{cccc}\hfill {\mathcal{S}}_{A_0}^{1\pm }\left(t\right)d& ={\mathcal{S}}_{A_0}^1(t;{\Gamma }_{\mathrm{res}}^{\pm })d,\hfill & \hfill {\mathcal{S}}_{A_0}^{2\pm }\left(t\right)\mathbf{f}& ={\mathcal{S}}_{A_0}^2(t;{\Gamma }_{\mathrm{res}}^{\pm })\mathbf{f},\hfill \\ \hfill {\tilde{\mathcal{S}}}_{A_0}^1\left(t\right)d& =\sum _{\mathfrak{a}\in \{+,-\}}\sum _{j\in \{1,4,5\}}{\mathcal{S}}_{A_0}^1(t;{\Gamma }_j^{\mathfrak{a}})d,\hfill & \hfill {\tilde{\mathcal{S}}}_{A_0}^2\left(t\right)\mathbf{f}& =\sum _{\mathfrak{a}\in \{+,-\}}\sum _{j\in \{1,4,5\}}{\mathcal{S}}_{A_0}^2(t;{\Gamma }_j^{\mathfrak{a}})\mathbf{f}.\hfill \end{array}$$

Theorems 6–9 then yields Theorem 3 immediately. This completes the proof of Theorem 3.

6. Time-Decay Estimates for High Frequency Part

This section proves Theorem 4. Suppose ${\rho }_{-}>{\rho }_{+}>0$ throughout this section.

Let us denote the points of intersection between $\lambda =-1+is$$(s\in \mathbf{R})$ and ${\Gamma }_0^{\pm }$ given in (13) by $z_4^{\pm }$, and let $A_0$ be the positive constant given in Theorem 3. We define $A_{\infty }=A_{\mathrm{high}}(1,\Im z_4^{+})$ for the positive constant $A_{\mathrm{high}}$ given in Proposition 4. In addition, we set $M_1=A_0/2$ and $M_2=3A_{\infty }$ in Proposition 5. Then we have $a_0\in (0,1)$ from Proposition 5 and denote the points of intersection between $\lambda =-a_0+is$$(s\in \mathbf{R})$ and ${\Gamma }_0^{\pm }$ by $z_5^{\pm }$. Note that $\Im z_5^{-}=-\Im z_5^{+}$.

Now we define integral paths ${\widehat{\Gamma }}_6$ and ${\widehat{\Gamma }}_7$ as follows:

$$\begin{array}{cc}\hfill {\widehat{\Gamma }}_6& =\{\lambda \in \mathbf{C}:\lambda =-a_0+si,-\Im z_5^{+}\le s\le \Im z_5^{+}\},\hfill \\ \hfill {\widehat{\Gamma }}_7& =\{\lambda \in \mathbf{C}:\lambda =-a_0+i\Im z_5^{+}+s{e}^{i(\pi -{\theta }_1)},s\ge 0\}\hfill \\ \hfill & \cup \{\lambda \in \mathbf{C}:\lambda =-a_0-i\Im z_5^{+}+s{e}^{-i(\pi -{\theta }_1)},s\ge 0\},\hfill \end{array}$$

where ${\theta }_1$ is given in (11). Recalling the symbols (22)–(24) and (54), we have from Propositions 4 and 5 the following lemma.

Lemma 16.

(1)

$\mathfrak{R}{B}_{\pm }>0$, $F(A,\lambda )\ne 0$, and $L(A,\lambda )\ne 0$ for $A\ge A_0/2$ and $\lambda \in \Lambda (a_0,\Im z_5^{+})$, where $\Lambda (a_0,\Im z_5^{+})$ is defined by (70) with $a=a_0$ and $b=\Im z_5^{+}$.

(2)

Let $s\in \mathbf{R}$ and ${\alpha }^{\prime }\in {\mathbf{N}}_0^{N-1}$. Then for any $\lambda \in {\widehat{\Gamma }}_6$ it holds that on $supp{\phi }_{A_{\infty }}\cup supp{\phi }_{⟨A_0,A_{\infty }⟩}$

$$\begin{array}{cc}\hfill & |{\partial }_{\xi }^{\prime }{B}_{\pm }^s|\le C{A}^{s-|{\alpha }^{\prime }|},|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{E}^s|\le C{A}^{s-|{\alpha }^{\prime }|},\left|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}{(A+B_{\pm })}^s\right|\le C{A}^{s-|{\alpha }^{\prime }|},\hfill \\ \hfill & |{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}F{(A,\lambda )}^s|\le C{A}^{3s-|{\alpha }^{\prime }|},\left|{\partial }_{{\xi }^{\prime }}^{{\alpha }^{\prime }}L{(A,\lambda )}^{-1}\right|\le C{A}^{-4-|{\alpha }^{\prime }|}.\hfill \end{array}$$

Let $\mathcal{S}\in \{\mathcal{H},\mathcal{U}\}$ and $Z\in \{A_{\infty },⟨A_0,A_{\infty }⟩\}$. Recalling (20) and the representation formulas in Section 3.3, we have, by Cauchy’s integral theorem and Lemma 16 (1)

$$\begin{array}{cccc}\hfill {\mathcal{S}}_Z^1\left(t\right)d& =\sum _{j=6}^7{\mathcal{S}}_Z^1(t;{\Gamma }_j)d,\hfill & \hfill {\mathcal{S}}_Z^1(t;{\Gamma }_j)d& :={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_Z^1(t;{\widehat{\Gamma }}_j)d\right]\left(x^{\prime }\right),\hfill \\ \hfill {\mathcal{S}}_Z^2\left(t\right)\mathbf{f}& =\sum _{j=6}^7{\mathcal{S}}_Z^2(t;{\Gamma }_j)\mathbf{f},\hfill & \hfill {\mathcal{S}}_Z^2(t;{\Gamma }_j)\mathbf{f}& :={\mathcal{F}}_{{\xi }^{\prime }}^{-1}\left[{\widehat{\mathcal{S}}}_Z^2(t;{\widehat{\Gamma }}_j)\mathbf{f}\right]\left(x^{\prime }\right).\hfill \end{array}$$

(92)

Similarly to Section 5 of [2], we can prove the following theorem from Lemmas 1, 3, and 16 by choosing larger $A_{\infty }$ if necessary.

Theorem 10.

Let $q\in (1,\infty )$ and $Z\in \{A_{\infty },⟨A_0,A_{\infty }⟩\}$. Let $j=6,7$ and $k\in {\mathbf{N}}_0$. Then for any $t\ge 1$ and $(d,\mathbf{f})\in X_q$

$$\begin{array}{cc}\hfill \parallel ({\partial }_t^k{\mathcal{H}}_Z^1(t;{\Gamma }_j)d,{\partial }_t^k{\mathcal{H}}_Z^2(t;{\Gamma }_j)\mathbf{f}){\parallel }_{W_q^{3-1/q}\left({\mathbf{R}}^{N-1}\right)}& \le C{e}^{-ct}{\parallel (d,\mathbf{f})\parallel }_{X_q},\hfill \\ \hfill \parallel ({\partial }_t^k{\mathcal{U}}_Z^1(t;{\Gamma }_j)d,{\partial }_t^k{\mathcal{U}}_Z^2(t;{\Gamma }_j)\mathbf{f}){\parallel }_{H_q^2\left({\dot{\mathbf{R}}}^N\right)}& \le C{e}^{-ct}{\parallel (d,\mathbf{f})\parallel }_{X_q},\hfill \end{array}$$

where C and c are positive constants independent of t, d, and $\mathbf{f}$.

Theorem 10 with (92) yields Theorem 4 immediately. This completes the proof of Theorem 4.