Feature Selection in a Credit Scoring Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Credit Risk Management
2.2. Machine Learning and Credit Scoring: A Review of Literature
3. Methods and Materials
3.1. Classification Algorithms
3.1.1. Logistic Regression
3.1.2. Support Vector Machines
3.1.3. K-Nearest Neighbors
3.1.4. Random Forest
3.2. Curse of Dimensionality
3.2.1. Wrapper Methods
- (1)
- Forward stepwise selection
- (2)
- Backward stepwise selection
3.2.2. Filter Methods
- (1)
- Chi-squared test
- (2)
- Correlation coefficient
3.2.3. Embedded Methods
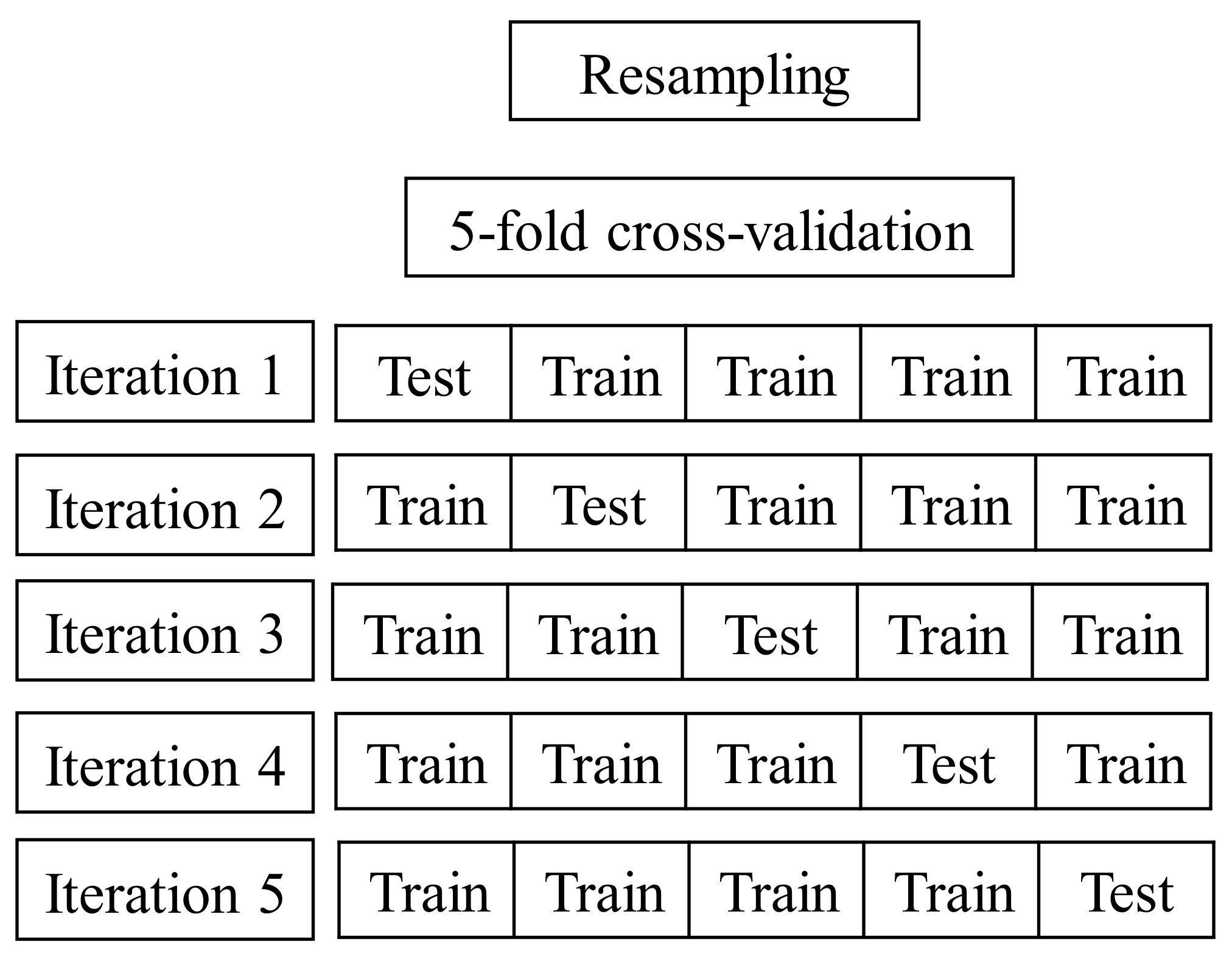
3.3. Resampling
4. Empirical Analysis
4.1. Sample Data and Variables
4.2. The Determination of Model Parameters for the KNN-Algorithm
4.3. Empirical Results and Discussion
4.3.1. Comparison of Findings with Existing Literature—Managerial Implications
4.3.2. Revisiting Credit Scoring Models: From Altman Z-Score to Machine Learning with Feature Selection Methods
4.3.3. Limitations and Future Research
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jacobson, T.; Roszbach, K. Bank lending policy, credit scoring and value-at-risk. J. Bank. Financ. 2003, 27, 615–633. [Google Scholar] [CrossRef]
- Saunders, A.; Cornett, M.M. Financial Institutions Management: A Risk Management Approach; McGraw-Hill Education: New York, NY, USA, 2017; pp. 1–912. [Google Scholar]
- Ong, C.-S.; Huang, J.-J.; Tzeng, G.-H. Building credit scoring models using genetic programming. Expert Syst. Appl. 2005, 29, 41–47. [Google Scholar] [CrossRef]
- Hand, D.J.; Henley, W.E. Statistical Classification Methods in Consumer Credit Scoring: A Review. J. R. Stat. Soc. Ser. A Stat. Soc. 1997, 160, 523–541. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2010; pp. 1–579. [Google Scholar]
- Abellán, J.; Castellano, J.G. A comparative study on base classifiers in ensemble methods for credit scoring. Expert Syst. Appl. 2017, 73, 1–10. [Google Scholar] [CrossRef]
- Lessmann, S.; Baesens, B.; Seow, H.-V.; Thomas, L.C. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. Eur. J. Oper. Res. 2015, 247, 124–136. [Google Scholar] [CrossRef]
- Baesens, B.; Van Gestel, T.; Viaene, S.; Stepanova, M.; Suykens, J.; Vanthienen, J. Benchmarking state-of-the-art classification algorithms for credit scoring. J. Oper. Res. Soc. 2003, 54, 627–635. [Google Scholar] [CrossRef]
- Garcia, V.; Marqués, A.I.; Sánchez, J.S.; Garreta, J.S.S. Non-parametric Statistical Analysis of Machine Learning Methods for Credit Scoring. Adv. Intell. Syst. Comput. 2012, 171, 263–272. [Google Scholar] [CrossRef]
- Hung, C.; Chen, J.-H. A selective ensemble based on expected probabilities for bankruptcy prediction. Expert Syst. Appl. 2009, 36, 5297–5303. [Google Scholar] [CrossRef]
- Dastile, X.; Celik, T.; Potsane, M. Statistical and machine learning models in credit scoring: A systematic literature survey. Appl. Soft Comput. 2020, 91, 106263. [Google Scholar] [CrossRef]
- Liu, Y.; Schumann, M. Data mining feature selection for credit scoring models. J. Oper. Res. Soc. 2005, 56, 1099–1108. [Google Scholar] [CrossRef]
- Tripathi, D.; Edla, D.R.; Cheruku, R.; Kuppili, V. A novel hybrid credit scoring model based on ensemble feature selection and multilayer ensemble classification. Comput. Intell. 2019, 35, 371–394. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, D.; Zhang, S.; Ablanedo-Rosas, J.H.; Wu, X.; Lou, Y. A novel multi-stage ensemble model with enhanced outlier adaptation for credit scoring. Expert Syst. Appl. 2021, 165, 113872. [Google Scholar] [CrossRef]
- Wang, T.; Qin, Z.; Zhang, S.; Zhang, C. Cost-sensitive classification with inadequate labeled data. Inf. Syst. 2012, 37, 508–516. [Google Scholar] [CrossRef]
- Kraus, A. Recent Methods from Statistics and Machine Learning for Credit Scoring. Ph.D. Thesis, Fakultät für Math-Ematik, Informatik und Statistik, Ludwig-Maximilians-Universit at Munchen, München, Germany, 2014. [Google Scholar]
- Munkhdalai, L.; Munkhdalai, T.; Namsrai, O.-E.; Lee, J.Y.; Ryu, K.H. An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments. Sustainability 2019, 11, 699. [Google Scholar] [CrossRef]
- Teles, G.; Rodrigues, J.J.P.C.; Saleem, K.; Kozlov, S.; Rabêlo, R.A.L. Machine learning and decision support system on credit scoring. Neural Comput. Appl. 2020, 32, 9809–9826. [Google Scholar] [CrossRef]
- Akkoç, S. An empirical comparison of conventional techniques, neural networks and the three stage hybrid Adaptive Neuro Fuzzy Inference System (ANFIS) model for credit scoring analysis: The case of Turkish credit card data. Eur. J. Oper. Res. 2012, 222, 168–178. [Google Scholar] [CrossRef]
- Lee, T.H.; Sung-Chang, J. Forecasting creditworthiness: Logistic vs. artificial neural network. J. Bus. Fore-Cast. Methods Syst. 2000, 18, 28–30. [Google Scholar]
- Nie, G.; Rowe, W.; Zhang, L.; Tian, Y.; Shi, Y. Credit card churn forecasting by logistic regression and decision tree. Expert Syst. Appl. 2011, 38, 15273–15285. [Google Scholar] [CrossRef]
- Srinivasan, V.; Kim, Y.H. Credit Granting: A Comparative Analysis of Classification Procedures. J. Financ. 1987, 42, 665–681. [Google Scholar] [CrossRef]
- Shin, K.-S.; Lee, T.S.; Kim, H.-J. An application of support vector machines in bankruptcy prediction model. Expert Syst. Appl. 2005, 28, 127–135. [Google Scholar] [CrossRef]
- Bellotti, T.; Crook, J. Support vector machines for credit scoring and discovery of significant features. Expert Syst. Appl. 2009, 36, 3302–3308. [Google Scholar] [CrossRef]
- Danenas, P.; Garsva, G.; Gudas, S. Credit Risk Evaluation Model Development Using Support Vector Based Classifiers. Procedia Comput. Sci. 2011, 4, 1699–1707. [Google Scholar] [CrossRef]
- Kim, H.S.; Sohn, S.Y. Support vector machines for default prediction of SMEs based on technology credit. Eur. J. Oper. Res. 2010, 201, 838–846. [Google Scholar] [CrossRef]
- Martens, D.; Baesens, B.; Van Gestel, T.; Vanthienen, J. Comprehensible credit scoring models using rule extraction from support vector machines. Eur. J. Oper. Res. 2007, 183, 1466–1476. [Google Scholar] [CrossRef]
- Camastra, F. A SVM-based cursive character recognizer. Pattern Recognit. 2007, 40, 3721–3727. [Google Scholar] [CrossRef]
- Lu, C.; Van Gestel, T.; Suykens, J.; Van Huffel, S.; Vergote, I.; Timmerman, D. Preoperative prediction of malignancy of ovarian tumors using least squares support vector machines. Artif. Intell. Med. 2003, 28, 281–306. [Google Scholar] [CrossRef]
- Akay, M.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
- Tay, F.E.; Cao, L. Application of support vector machines in financial time series forecasting. Omega 2001, 29, 309–317. [Google Scholar] [CrossRef]
- Kim, K.-J. Financial time series forecasting using support vector machines. Neurocomputing 2003, 55, 307–319. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Wang, G.; Hao, J.; Ma, J.; Jiang, H. A comparative assessment of ensemble learning for credit scoring. Expert Syst. Appl. 2011, 38, 223–230. [Google Scholar] [CrossRef]
- Zhang, S. Nearest neighbor selection for iteratively kNN imputation. J. Syst. Softw. 2012, 85, 2541–2552. [Google Scholar] [CrossRef]
- Zhu, X.; Li, X.; Zhang, S. Block-Row Sparse Multiview Multilabel Learning for Image Classification. IEEE Trans. Cybern. 2016, 46, 450–461. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A Nearest Neighbor Bootstrap for Resampling Hydrologic Time Series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, S.; Jin, Z.; Zhang, Z.; Xu, Z. Missing Value Estimation for Mixed-Attribute Data Sets. IEEE Trans. Knowl. Data Eng. 2011, 23, 110–121. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R; Springer: Berlin/Heidelberg, Germany, 2013; pp. 995–1039. [Google Scholar]
- Frydman, H.; Altman, E.I.; Kao, D.-L. Introducing Recursive Partitioning for Financial Classification: The Case of Financial Distress. J. Financ. 1985, 40, 269–291. [Google Scholar] [CrossRef]
- Zhang, D.; Zhou, X.; Leung, S.C.; Zheng, J. Vertical bagging decision trees model for credit scoring. Expert Syst. Appl. 2010, 37, 7838–7843. [Google Scholar] [CrossRef]
- Zibanezhad, E.; Foroghi, D.; Monadjemi, A. Applying decision tree to predict bankruptcy. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering, CSAE, Shanghai, China, 10–12 June 2011; pp. 165–169. [Google Scholar] [CrossRef]
- Laborda, R.; Laborda, J. Can tree-structured classifiers add value to the investor? Financ. Res. Lett. 2017, 22, 211–226. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Jarman, K.H. Beyond Basic Statistics: Tips, Tricks, and Techniques Every Data Analyst Should Know. In Beyond Basic Statistics: Tips, Tricks, and Techniques Every Data Analyst Should Know, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–190. [Google Scholar] [CrossRef]
- Famili, A.; Shen, W.-M.; Weber, R.; Simoudis, E. Data Preprocessing and Intelligent Data Analysis. Intell. Data Anal. 1997, 1, 3–23. [Google Scholar] [CrossRef]
- Bermingham, M.L.; Pongwong, R.; Spiliopoulou, A.; Hayward, C.; Rudan, I.; Campbell, H.; Wright, A.F.; Wilson, J.F.; Agakov, F.; Navarro, P.; et al. Application of high-dimensional feature selection: Evaluation for genomic prediction in man. Sci. Rep. 2015, 5, 10312. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R.; Ishwaran, H.; Knight, K.; Loubes, J.M.; Massart, P.; Madigan, D.; Ridgeway, G.; et al. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Smith, G. Step away from stepwise. J. Big Data 2018, 5, 32. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modelling; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–600. [Google Scholar]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Belsley, D.A. A Guide to using the collinearity diagnostics. Comput. Sci. Econ. Manag. 1991, 4, 33–50. [Google Scholar] [CrossRef]
- Goldstein, M.; Chatterjee, S.; Price, B. Regression Analysis by Example. J. R. Stat. Soc. Ser. A Stat. Soc. 1979, 142, 512. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Yeh, I.-C.; Lien, C.-H. The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients. Expert Syst. Appl. 2009, 36, 2473–2480. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Abbadi, M.A.; Altarawneh, G.A.; Alhasanat, A.A. Optimal K parameter for KNN Classifier with square root. Int. J. Comput. Sci. Inf. Secur. 2014, 12, 33–39. [Google Scholar]
- Ben-David, A.; Frank, E. Accuracy of machine learning models versus “hand crafted” expert systems—A credit scoring case study. Expert Syst. Appl. 2009, 36, 5264–5271. [Google Scholar] [CrossRef]
- Gambacorta, L.; Huang, Y.; Qiu, H.; Wang, J. How do Machine Learning and Non-Traditional Data Affect Credit Scoring? New Evidence from a Chinese Fintech Firm. BIS Working Papers 834. Available online: https://www.bis.org/publ/work834.pdf (accessed on 30 November 2020).
- Altman, E.I. Financial Ratios, Discriminant Analysis and the Prediction of Corporate Bankruptcy. J. Financ. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- Mahmoudi, N.; Duman, E. Detecting credit card fraud by Modified Fisher Discriminant Analysis. Expert Syst. Appl. 2015, 42, 2510–2516. [Google Scholar] [CrossRef]
- McLeay, S.; Omar, A. The Sensitivity of Prediction Models to the Non-Normality of Bounded and Unbounded Financial Ratios. Br. Account. Rev. 2000, 32, 213–230. [Google Scholar] [CrossRef]
- Shumway, T. Forecasting Bankruptcy More Accurately: A Simple Hazard Model. J. Bus. 2001, 74, 101–124. [Google Scholar] [CrossRef]
- Chava, S.; Jarrow, R.A. Bankruptcy Prediction with Industry Effects. Rev. Financ. 2004, 8, 537–569. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Hilscher, J.; Szilagyi, J. In Search of Distress Risk. J. Financ. 2008, 63, 2899–2939. [Google Scholar] [CrossRef]
- De Menezes, F.S.; Liska, G.R.; Cirillo, M.A.; Vivanco, M.J. Data classification with binary response through the Boosting algorithm and logistic regression. Expert Syst. Appl. 2017, 69, 62–73. [Google Scholar] [CrossRef]
- Kruppa, J.; Schwarz, A.; Arminger, G.; Ziegler, A. Consumer credit risk: Individual probability estimates using machine learning. Expert Syst. Appl. 2013, 40, 5125–5131. [Google Scholar] [CrossRef]
- Pal, R.; Kupka, K.; Aneja, A.P.; Militky, J. Business health characterization: A hybrid regression and support vector machine analysis. Expert Syst. Appl. 2016, 49, 48–59. [Google Scholar] [CrossRef]
- Duéñez-Guzmán, E.A.; Vose, M.D. No Free Lunch and Benchmarks. Evol. Comput. 2013, 21, 293–312. [Google Scholar] [CrossRef]



| Evaluation Criteria | ||||
|---|---|---|---|---|
| Threshold Metrics | Statistical Hypothesis Testing | Area under the Curve | ||
| Classifier | Logistic regression | [7,12,15] | [9] | [7,16,17] |
| Decision tree | [12,15,18] | [9,18] | ||
| Support vector machine (SVM) | [7,8,15] | [8,9] | [7,8,17] | |
| Artificial neural networks (ANN) | [7,8,12,15] | [8,9] | [7,8] | |
| Bayesian model | [7] | [9] | [7] | |
| CART | [7] | [7,16] | ||
| Extreme learning machine (ELM) | [7] | [7] | ||
| K-nearest neighbor (KNN) | [7,12] | [9] | [7] | |
| Rule induction algorithms | [9] | |||
| Discriminant analysis | [7] | [7] | ||
| Voted perceptron (VP) | [7] | [7] | ||
| Naïve Bayes (NB) | [7] | [7] | ||
| J4.8 | [7] | [7] | ||
| Fuzzy logic | [18] | [18] | ||
| Ensemble classifier | [6,7,13,14,15] | [9,10,14] | [6,7,14,16,17] | |
| Variables | Description | Values |
|---|---|---|
| ID | ID of each client | |
| LIMIT_BAL | Amount of the credit that each client has | |
| SEX | Gender | 1 = male, 2 = female |
| EDUCATION | Education | 1 = graduate school, 2 = university, 3 = high school, 4 = others |
| MARRIAGE | Marital status | 1 = married, 2 = single, 3 = others |
| AGE | Age | |
| PAY_1 | Repayment status in September, 2005 | −1 = if paid in time, 1 = if delayed for one month, …, 9 = if delayed for nine months or more. |
| PAY_2 | Repayment status in August, 2005 | Same |
| PAY_3 | Repayment status in July, 2005 | Same |
| PAY_4 | Repayment status in June, 2005 | Same |
| PAY_5 | Repayment status in May, 2005 | Same |
| PAY_6 | Repayment status in April, 2005 | Same |
| BILL_AMT1 | Amount of bill in September 2005 | |
| BILL_AMT2 | Amount of bill in August, 2005 | |
| BILL_AMT3 | Amount of bill in July, 2005 | |
| BILL_AMT4 | Amount of bill in June, 2005 | |
| BILL_AMT5 | Amount of bill in May, 2005 | |
| BILL_AMT6 | Amount of bill in April, 2005 | |
| PAY_AMT1 | Amount paid in September, 2005 | |
| PAY_AMT2 | Amount paid in August, 2005 | |
| PAY_AMT3 | Amount paid in July, 2005 | |
| PAY_AMT4 | Amount paid in June, 2005 | |
| PAY_AMT5 | Amount paid in May, 2005 | |
| PAY_AMT6 | Amount paid in April, 2005 | |
| DEFAULT | Default status | 1 = yes, 0 = no |
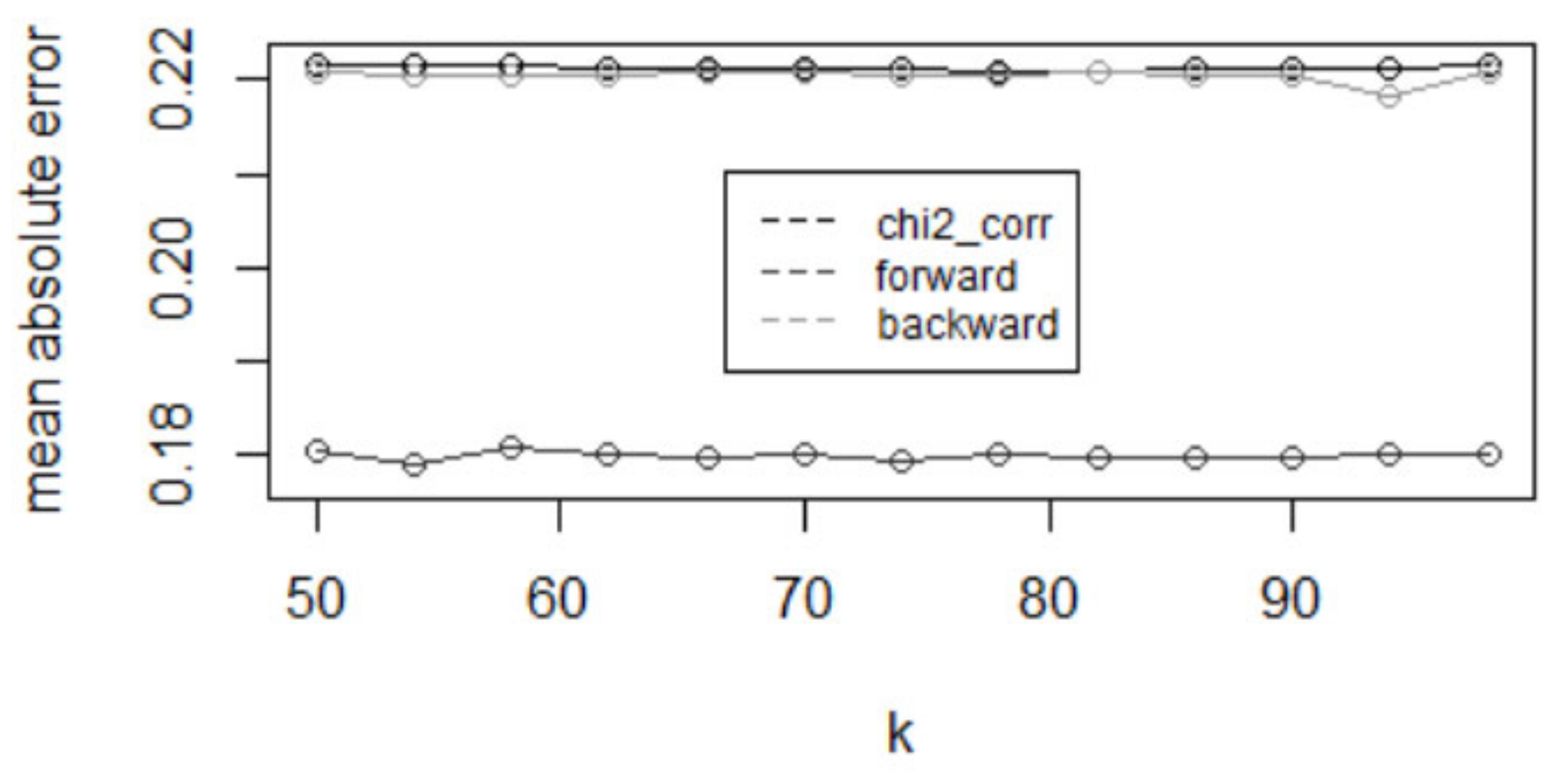
| Models | No. of Features | Mean Absolute Error (%) |
|---|---|---|
| Logistic regression | 24 | 22.120 |
| KNN (K = 73) | 24 | 22.057 |
| SVM | 24 | 22.120 |
| Random forests | 24 | 25.267 |
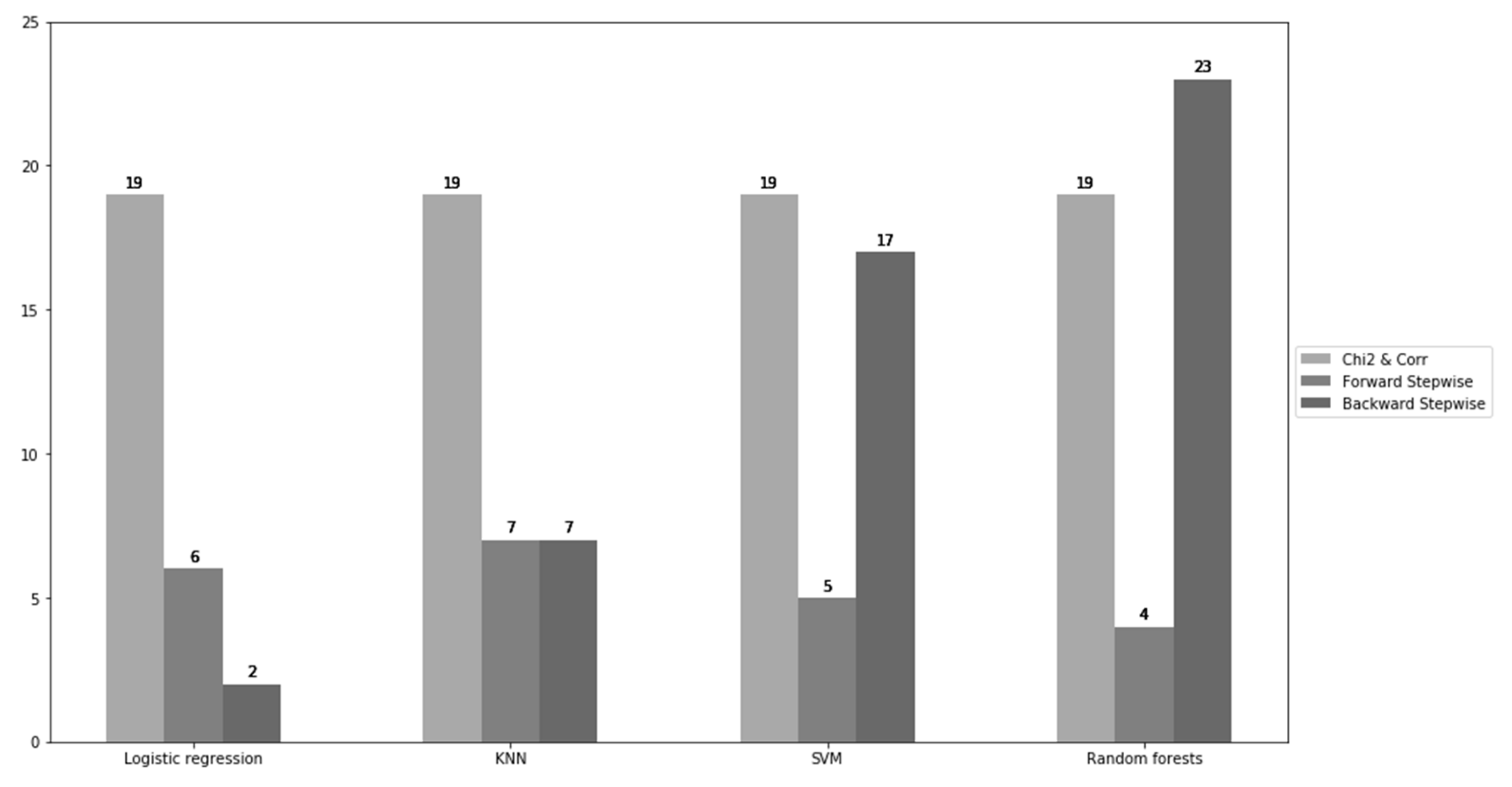
| Models/Feature Selection | Chi2 and Corr |
|---|---|
| Logistic regression | (‘SEX’, ‘MARRIAGE’, ‘EDUCATION’, ‘LIMIT_BAL’, ‘PAY_1’, ‘PAY_2’, ‘PAY_3’, ‘PAY_4’, ‘PAY_5’, ‘PAY_6’, ‘BILL_AMT1’, ‘BILL_AMT3’, ‘PAY_AMT1’, ‘PAY_AMT2’, ‘PAY_AMT3’, ‘PAY_AMT4’, ‘PAY_AMT5’, ‘PAY_AMT6’) |
| KNN | Same |
| SVM | Same |
| Random forests | Same |
| Models/Feature Selection | Forward Stepwise Selection |
|---|---|
| Logistic regression | (‘SEX’, ‘EDUCATION’, ‘AGE’, ‘PAY_1’, ‘PAY_5’, ‘PAY_6’) |
| KNN | (‘SEX’, ‘EDUCATION’, ‘MARRIAGE’, ‘PAY_1’, ‘PAY_3’, ‘PAY_5’, ‘PAY_6’) |
| SVM | (‘EDUCATION’, ‘PAY_1’, ‘PAY_4’, ‘PAY_5’, ‘PAY_6’) |
| Random forests | (‘EDUCATION’, ‘MARRIAGE’, ‘PAY_1’, ‘PAY_2’) |
| Models/Feature Selection | Backward Stepwise Selection |
|---|---|
| Logistic regression | (‘SEX’, ‘PAY_1’) |
| KNN | (‘BILL_AMT3’, ‘BILL_AMT6’, ‘PAY_AMT1’, ‘PAY_AMT2’, ‘PAY_AMT3’, ‘PAY_AMT4’, ‘PAY_AMT5’) |
| SVM | (‘SEX’, ‘EDUCATION’, ‘MARRIAGE’, ‘AGE’, ‘PAY_1’, ‘PAY_2’, ‘PAY_3’, ‘PAY_4’, ‘PAY_5’, ‘PAY_6’, ‘BILL_AMT1’, ‘BILL_AMT2’, ‘BILL_AMT3’, ‘BILL_AMT4’, ‘BILL_AMT6’, ‘PAY_AMT1’) |
| Random forests | (‘LIMIT_BAL’, ‘SEX’, ‘EDUCATION’, ‘MARRIAGE’, ‘AGE’, ‘PAY_1’, ‘PAY_2’, ‘PAY_3’, ‘PAY_5’, ‘PAY_6’, ‘BILL_AMT1’, ‘BILL_AMT2’, ‘BILL_AMT3’, ‘BILL_AMT4’, ‘BILL_AMT5’, ‘BILL_AMT6’, ‘PAY_AMT1’, ‘PAY_AMT2’, ‘PAY_AMT3’, ‘PAY_AMT4’, ‘PAY_AMT5’, ‘PAY_AMT6’) |
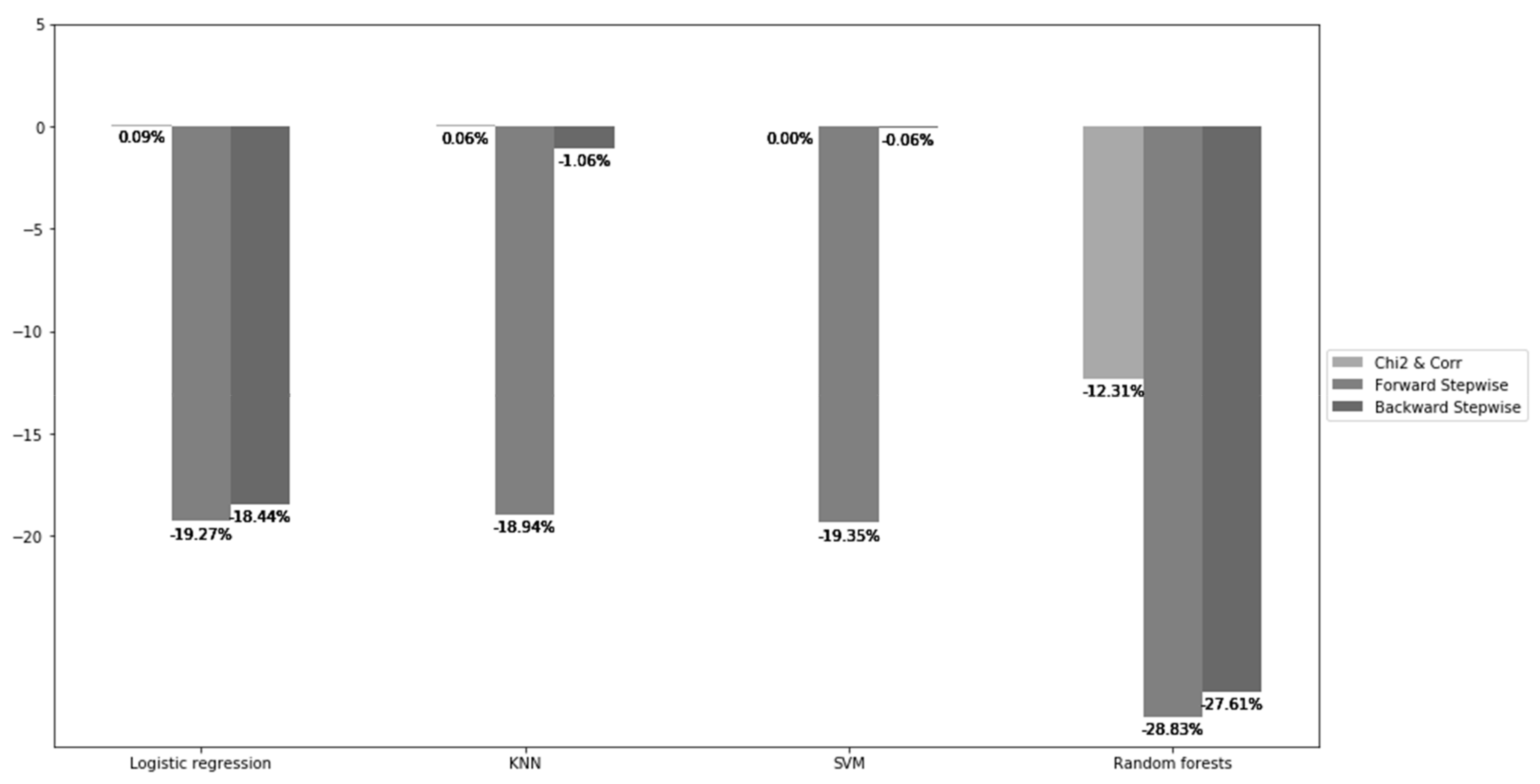
| Models/Feature Selection | Chi2 and Corr | Forward Stepwise | Backward Stepwise |
|---|---|---|---|
| Logistic regression | (1) −5 (2) +0.0904% | (1) −18 (2) −19.2736% | (1) −22 (2) −18.4449% |
| KNN | (1) −5 (2) 0.0603% | (1) −17 (2) −18.9362% | (1) −17 (2) −1.0577% |
| SVM | (1) −5 (2) 0% | (1) −19 (2) −19.3491% | (1) −7 (2) −0.0601% |
| Random forests | (1) −5 (2) −12.3084% | (1) −20 (2) −28.8259% | (1) −1 (2) −27.6121% |
| Models | Advantages | Disadvantages |
|---|---|---|
| Multivariate Discriminant Analysis | (1) First model to predict bankruptcy (2) Simplicity: easy to interpret | (1) Required normally distributed variables (2) Sensitivity to outliers (3) It does not include nonlinearities (4) It does not offer a non-parametric approach |
| Logistic Regression | (1) Assumptions are less restrictive (2) It produces a [0, 1] interval result that can be interpreted as a probability of a given observation being a member of a specific group (3) Good interpretability and simple explanation | (1) Assumes a logistic regression: it is limited to additive form of the model (2) Assumes linearity in the covariances (3) It does not include nonlinearities (4) It does not offer a non-parametric approach |
| Machine Learning without Features Selection | (1) Credit risk analysis is similar to pattern recognition problems (2) It improves traditional models based on a simple multivariate statistical technique (3) It includes nonlinearities (4) It offers non-parametric approaches | (1) Sometimes complex models harder to interpret (2) High variance and overfitting in the curse of dimensionality (3) Excessive variety of possible models and combined techniques |
| Machine Learning with Features Selection | (1) Credit risk analysis is similar to pattern recognition problems (2) It improves traditional models based on a simple multivariate statistical technique (3) It includes nonlinearities (4) It offers non-parametric approaches (5) Simpler models easy to interpret (6) No overfitting | (1) Excessive variety of possible models and combined techniques |
| Benefits | Future Lines of Research |
|---|---|
| (1) Main concern is the practical use of models (2) Designed research is clear (3) Different classification algorithms are used (4) Performance measures used, model simplicity (number of selected features), and model accuracy (MAE) avoid false-positive findings, over-selection of features and model overfitting (5) Either the attributes selected or the number of them is indicated | (1) Combined techniques (2) Include change and/or growth variables. (3) Comparison with other performance measures (4) Classify borrowers in more than two variables (5) Other real data set for other countries would be needed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laborda, J.; Ryoo, S. Feature Selection in a Credit Scoring Model. Mathematics 2021, 9, 746. https://doi.org/10.3390/math9070746
Laborda J, Ryoo S. Feature Selection in a Credit Scoring Model. Mathematics. 2021; 9(7):746. https://doi.org/10.3390/math9070746
Chicago/Turabian StyleLaborda, Juan, and Seyong Ryoo. 2021. "Feature Selection in a Credit Scoring Model" Mathematics 9, no. 7: 746. https://doi.org/10.3390/math9070746
APA StyleLaborda, J., & Ryoo, S. (2021). Feature Selection in a Credit Scoring Model. Mathematics, 9(7), 746. https://doi.org/10.3390/math9070746







