Classroom Methodologies for Teaching and Learning Ordinary Differential Equations: A Systemic Literature Review and Bibliometric Analysis
Abstract
1. Introduction
- 1.
- We propose a classification for the research in teaching and learning ordinary differential equations according to the didactic methodologies: traditional teaching and learning methodology, graphical and numerical approaches to the teaching, active learning methods, mathematical modeling-based methodology, information and communication technology-based methodologies, and project-based learning.
- 2.
- We introduce five groups given a categorization of the mathematical topics addressed in the papers: basic concepts of ordinary differential equation, biomathematical models, scalar-based models, systems-based on physic models, and other concepts.
- 3.
- We found that results about effectiveness of innovation were reported only in a few articles.
2. Research Methodology
- Step 1. Framing questions for a review.
- Step 2. Identifying relevant work.
- Step 3. Assessing the quality of studies.
- Step 4. Summarizing the evidence.
- Step 5. Interpreting the findings.
3. Framing Questions for a Review (Step 1)
- Question 1: What are the studies developed for teaching and learning of ordinary differential equations with a reported classroom experiences? What types of didactic methodologies have been used in those studies?
- Question 2: What topics of ordinary differential equations have been explored in the previous studies?
- Question 3: What are the results for the effectiveness of traditional and new didactic methodologies to teach and learning ordinary differential equations, as reported in previous studies?
4. Identifying Relevant Work (Step 2)
- (a)
- We have selected the following databases:
- -
- Web of Science (https://clarivate.com/products/web-of-science accessed on 8 August 2020),
- -
- Scopus (https://www.elsevier.com/solutions/scopus accessed on 8 August 2020),
- -
- Qualis (http://qualis.capes.gov.br accessed on 8 August 2020)
- -
- Zbmath (https://zbmath.org accessed on 8 August 2020), and
- -
- Scielo (https://scielo.org accessed on 8 August 2020).
- (b)
- In the case of Web of Science and Scopus, we have derived two major keywords to answer Questions 1–3 and we have replaced them in the search engine of databases by some synonyms and some alternative terms, as specified below:
- Ordinary differential equations. Differential equation; solution to differential equations; graphical interpretation; graphical solution; qualitative solutions; numerical solutions; analytic solutions; first order equations; higher order equations; Laplace transform; power series method; variable separable equation; reducible to variable separable equation; homogeneous equation; reducible to homogeneous equation; exact equation; reducible to exact equation; Bernoulli equation; linear equation; Ricatti equation; phase plane; isoclines; slope fields; equilibrium; stability of solutions; initial value problems; boundary value problems; scalar equations; systems of equations; linear; nonlinear.
- Didactic methodologies. Teaching methodologies; students’ understanding and difficulties; interpretation of solutions; registers of representations; mathematical modeling; mathematical models; problem-based learning; problem solving; error analysis; mathematics teaching practices; real world situation; computational resources; mathematical application; classroom discourse; didactic of differential equations; critical discourse analysis.
More specifically the strings are given in Appendix A. First we searched the list of selected words in all fields of the search engine of databases, i.e., in titles, article keywords, abstracts, author, topic, and full paper text.The search on Web of Science was restricted to all journals indexed to “Science Citation Index Expanded (SCI-Expanded)”, “Social Sciences Citation Index (SSCI)”, “Arts & Humanities Citation Index (A&HCI)”, and “Emerging Sources Citation Index (ESCI)”. We get a total of 342,179 publications. Then, we refined the results using the “Document Types” option by “article” and the option “Web of Science Categories” by “Social Sciences Mathematical Methods or Education Educational Research or Education Scientific Disciplines” generating a list of 3366 articles.In Scopus, when restricting the search to Document Type “article”, a total of 23,967 publications were found. Then, we refined the option “subject area” by selecting “psychology or “social sciences”, getting a list of 4276 articles. - (c)
- In the case of Qualis, zbMATH, and Scielo. we selected the journals associated to Mathematics Education as specified below. In the database Qualis, we find that a total of 1434 journals are associated to quadrennium 2013–2016 and are classified as A1, A2, B1, B2, B3, B4, B5, and C in the evaluation area Teaching (ensino). Then, we selected a list of 58 journals associated with Mathematics Education, see Table 1. For zbMATH database, we used the list of journals suggested by Godino [46], where the author present a list of journals from zbMATH classified in two sections labeled as “Serie A” and “Serie B” journals. Moreover, in each category there are three groups or types of journals called A, B, and C, the total of journals of each serie and the corresponding types are summarized in Table 1. Now, from Scielo database we have selected a total of 17 journals associated with the scope in Mathematics Education. Thus, combining the three list of journals and deleting the duplicated ones, we get a list of 132 journals, see Table A1 in Appendix B.
- (d)
- We examined the titles, abstract, and full paper text in the list of papers from Web of Science and Scopus generated in step (b). Then, we retained the paper if it was related to the teaching and learning of ordinary differential equations. After a careful examination, we have identified 104 and 55 articles from Web of Science and Scopus, respectively. Moreover, in the case of the selected journals of step (c), we have applied two types of searches: (i) we consulted the index of each volume of the journal from the years specified on the column labeled as “Years Consulted” in Table A1 and (ii) we have searched for key words in the search engines of each journal. As a result, a total of 313 articles were considered to be analyzed.
- (e)
- Combining the three list of articles and deleting the duplicated ones, we get a list of 405 articles. Then, in order to focus our analysis on classroom methodologies, we classified the 405 articles in three types: notes, curriculum, and research in classroom. We consider that an article is a note or a classroom note, when there is a proposal for teaching some concepts related to differential equations, but there is not a specific didactic methodology or at least, it was never implemented in the classroom. In the class curriculum, we consider all works where the aim of the paper was the curriculum innovation proposal and there is not an specific application in the classroom. Meanwhile, we assume that a paper is of the type research in classroom, when there is a proposal to teach some topic of ordinary differential equations, there is an explicit didactic methodology, and also includes the implementation in the classroom with a well detailed report of the experience. Thus, by a revision of all 405 papers, we deduce that there were a total of 262, 23 and 120 articles belonging to types classroom notes, curriculum, and research in classroom, respectively. In Figure 2, we present a classification by year and by decade from 1970 to 2020. An isolated case, which is not presented in Figure 2, is the classroom note [47] published in 1913.
- Argentina, Azerbaijan, Bahrain, Brunei, Canada, Chile, China, Colombia, Costa Rica, Cuba, Czechia, Ethiopia, France, Ghana, Grece, Holland, Hungary, Iceland, Iran, Iraq, Italy, Kenya, Lebanon, Libya, Lithuania, Malaysia, Netherlands, New Zeland, Nigeria, Norway, Perú, Poland, Portugal, Romania, Russia, Saudia Arabia, Serbia, Singapore, Slovakia, Slovenia, South Africa, South Korea, Spalj, Sweden, Switzerland, Taiwan, Ukraine, United Arab Emirates, and Uruguay.
- Argentina, Azerbaijan, Bahrain, Brunei, Canada, China, Colombia Cuba, Denmark, Ethiopia, France, Ghana, Grece, Holland, Hungary, Iceland Iran, Italy, Kenya, Libya, Lithuania, Malaysia, Netherlands, New Zeland, Nigeria, Norway, Peru, Poland, Portugal, Russia, Saudia Arabia, Serbia, Singapore, Slovakia, South Africa, South Korea Spalj, Switzerland, United Arab Emirates, and Uruguay.
5. Assessing the Quality of Studies (Step 3)
- (i)
- Total number of publications by geographic location. In Section 4, we present initial information regarding the location of origin, which is declared in the affiliation of authors. The top three regions are USA, Brazil, and México with percentages of coincidences of 25%, 8%, and 5%, respectively; see Figure 3d.
- (ii)
- Total number of publications by year. In Figure 2, we present six histograms considering all the articles (notes, curriculum, and research in classroom) decade by decade from 1970 to 2020. In Figure 2f, we can see an increase in the number of publications along the years. The first publications are from 1970s, one related to research in classroom and one related to curriculum, see Figure 2a. Regarding research in classroom, the first article retained is from 1975 and is unique in the 1970s. The 2010s have the largest number of publications with a record count of 76 papers, where 2016 and 2017 were the years with more publications with 10 records each year, see Figure 2f,e, respectively. The graphs also show how the research related to curriculum has evolved slowly.
- (iii)
- The most prolific journals. There are 46 journals associated to the retained list of papers. Table 2 shows the 13 journals which are in the top four positions according to the number of published articles. The first three journals show a similarity in the declared scope, all of them are focused on teaching and learning mathematics. These journals publish research regarding learning and teaching mathematics for different scholar levels and particularly for undergraduate mathematics. These coincidences in the journals’ aims are probably the reason which they have the most publications in the area of differential equations, which is traditionally a topic of undergraduate mathematics. Additionally, we found 33 journals with less than 3 publications each one, which are distributed as follows: 9 and 24 journals with 2 and 1 articles, respectively.
- (iv)
- Ranking of journals by the H index. In Table 3 we show the top 11 retained journals according to the H index of SCImago Journal & Country Rank (https://www.scimagojr.com/ accessed on 1 September 2020), where the indicator SJR 2019 is also included, quartil, and subject area of those journals.
- (v)
- The most prolific authors.Table 4 shows the most prolific authors in the retained list of research in classroom articles. The top author in the field is Chris Rasmussen with 12 articles (9.52%). Moreover, we observe that there are four authors from the USA which is naturally related with the higher impact of the research developed in the field by institutions from the USA, see Figure 3d.
- (vi)
- The impact of articles. In Table 5, we show the top 10 articles, where the ranking is established by the number of citations reported in google scholar in September 2020. We observe that the research line introduced by Rasmussen and collaborators in the 2000s decade is one of the most prolific, since 8 of the top 10 articles are authored or coauthored by Chris Rasmussen.
6. Summarizing the Evidence (Step 4)
7. Interpreting the Findings (Step 5)
7.1. Question 1: What Are the Studies Developed for Teaching and Learning of Ordinary Differential Equations with a Reported Classroom Experiences? What Types of Didactic Methodologies Have Been Used in Those Studies?
- -
- the traditional teaching and learning methodology,
- -
- graphical or qualitative and numerical approach of teaching,
- -
- active learning methods,
- -
- The mathematical modeling-based methodology,
- -
- information and communication technology-based methodologies,
- -
- project-based learning, and
- -
- other methodologies,
7.1.1. The Traditional Teaching and Learning Methodology
7.1.2. Qualitative and Numerical Approach to Teaching Differential Equations
7.1.3. Active Learning Methods
- (a)
- Inquiry-based learning. The “inquiry-based learning” is one kind of active learning methodology with several implementations in math classroom and its particular form of implementation is the “inquiry-based instruction” [71]. The methodology of inquiry-oriented instruction consists of four main steps: the generation of ways for reasoning of students, the analysis of student contributions, the development of a shared understanding, and the connection of finding in the development of research tasks to standard mathematical language and notation. Thus, the inquiry-oriented instruction generates classroom environments where the students practice an authentic research mathematical activity meanwhile they discover mathematical concepts, answering to purposefully designed tasks.The inquiry-based instruction for ordinary differential equations is researched in the following articles [15,16,71,79,81,87,89,106,107,108,109,110,124,125]. In [71], the author reports the findings about the students’ work with concepts related to slope fields, horizontal and vertical translation of solutions, systems modeling species interaction, and graphical solution of scalar autonomous differential equations. The author concludes that several advantages are generated by the inquiry oriented environment. Particularly he pointed out the following results: the students showed a notable cognitive gain in understanding and thinking; through the intervention of the instructor guiding the discussion the students reinvented knowledge; and they expressed their satisfaction with the inquiry instruction environment. In [79], the authors focus on the teaching of slope direction fields and the conception of solutions. Through a quantitative analysis, they showed that the students were able to successfully identify direction fields when the ordinary differential equation was given in analytical form, matching the appropriate direction field and the solution curve. They also found that students improved their understanding of the concept of solution for an ordinary differential equation as a result of the inquiry oriented intervention. The authors claim that the training had a long-lasting impact. In [81], discourse analysis is used to study the students mathematical narratives when learning the basic concepts of ordinary differential equations in a inquiry-oriented classroom environment, particularly the student’s positions and beliefs related to learning mathematics. The articles [15,16,87,89,106,107,108,109,110,125] are part of the line of research introduced by Chris Rasmussen and collaborators. These papers are mainly focused on studying the retention of mathematical knowledge, students reasoning with mathematical ideas, and conceptual understanding, in the context of learning differential equations. From these studies, the inquiry-oriented methodology stands out for its potential to facilitate the development of mathematical reasoning ability and fostering meaningful learning. With a different perspective, in the article [124], the authors discuss the knowledge and capacity of the instructor to manage whole-class discussions concluding that the teacher’s knowledge is a valuable component to be considered in the curricular reforms or in the classroom reforms under the inquiry-oriented perspective.
- (b)
- Problem-based learning. The problem-based learning is an innovation of the pedagogical teaching and learning process which is learning student centered, promoting significant learning, and developing important skills and abilities which will be useful in the student’s professional careers. The principle of problem-based learning is the use of problems as a starting point for the acquisition and integration of new knowledge [142]. The methodology is developed through students work in small groups where they participate in a cooperative learning experience with the aim to solve a problem proposed by the instructor, meanwhile they get a self-learning process. The self-learning process takes several steps like: read and analyze the problem, a focus group, make a list with the known and unknown facts about the problem, make a list of tasks to do, give a formal definition of the problem, get new information, and give a solution to the problem. From our list, 3 articles [55,73,93] are focused on the teaching and learning of ordinary differential equations under the problem-based learning methodology.
- (c)
- Other active learning methodologies. Here we included other works related with research on active learning [3,6,7,23,30,50,51,64,66,67,84,85,86,96,111,112,113,114,121,132,133]. In [3,23,30,51,121], the authors apply the problem solving methodology. In [50], the authors develop a methodology based on the analysis of errors. In [6], the authors use the actions-processes-objects-schemas (APOS) theory. In [7], a competences-based methodology is used. In [64], a knowledge-guided based on discursive strategies is implemented. In [66], a guided small-group tasks perspective is applied. In [67], a methodology based on inquiry approach to learning in the context of community of practice theory is used. In [84], the authors compare the students performance when using three different methods for visualizing differential equations and their solutions, they also introduce a new method of visualization called Dynamic Method. In [85], a problem-centered methodology is used. In [86], the author presents a characterization of dynamic reasoning to improve student understanding in time related areas of mathematics. In [96], a discovery-based approached is applied for constructing the solutions of first and second-order linear ordinary differential equations and in [132] a learning methodology supported in embodied cognition and conceptual metaphors are discussed. Now, in the articles [111,112,113,114], innovative active learning methodologies are introduced in order to teach advanced topics of ordinary differential equations. For instance, in [111], the called framework of layers concepts–conditions–connectives–conclusions is presented, which was used to teach the interpretation and usage of existence and uniqueness theorems for ordinary differential equations.
7.1.4. The Mathematical Modeling Based Methodology
- (a)
- Development of skills for mathematical modeling. We find some articles where the aim was to study the development of mathematical modeling abilities in order to solve real problem models by employing mathematical theory knowledge related to ordinary differential equations [8,17,20,54,63,65,68,88,91,100]. The papers [20,63] are focused on the teaching and learning of mathematical models, particularly in the construction and application of mathematical models through mathematical activities. In [20], the authors present two activities, one of them is based on mathematical models already known in the literature of ordinary differential equations and, the other one is based on the treatment of quantitative information for a new situation, concluding that different approaches to mathematical modeling lead to different actions of the students. In [8], the author introduces the methodological tool “Modeling Transition Diagrams” for capturing and representing the individual modeling process which uses this tool to examine the mathematical thinking while the students participate in modeling activities. The authors of article [65] are interested in the experience of implementing a mathematical modeling course, they report that the students adopt different approaches to learn mathematical models and conclude that after the experience, the students appreciate mathematical models, and suggest the usage of mathematical modeling to engage students into higher level learning approaches. The authors of [68,88] report the results of an innovative approach for teaching mathematical modeling with emphases in topics of environment, ecology, and epidemiology. Particularly, in [88] the students were involved in the solution of real-life problems adjusted to their region, by using the mathematical modeling tools were encouraged to pay attention to environmental issues like survival and sustainability. The paper [91] is focused on how to use ordinary differential equations as a pedagogical strategy to introduce students to the concepts of mathematical modeling. The author of [100] presents an application of mathematical modeling as a contextualized activity in several topics of an integral calculus with a small introduction to some topics of ordinary differential equations. In [17], the author studies the transposition of the mathematical modeling process used by the experts into the learning and teaching of mathematical modeling for undergraduate students.
- (b)
- Modeling as pedagogical strategy to teach concepts of ordinary differential equations. In these papers, the authors are focused on several topics of ordinary differential equations which are taught by using mathematical modeling. In a broad sense, the authors deduce several advantages in the teaching and learning process and also present some conclusions that promise a continuous development of mathematical modeling as a pedagogical methodology for the following years. Among the advantages pointed out by the authors, we highlight that mathematical modeling is a pedagogical methodology that promotes meaningful learning and, it is a significant and concrete alternative to the questioned traditional teaching. In this group of papers, we have include the following articles [9,54,94,127,134]. In [54] is presented a research about how mathematical modeling as teaching and learning methodology can provide meaningful learning for the students. In [9], the author develops a comparative study of two instructional approaches used in the teaching of ordinary differential equations for engineering students. In one classroom, decontextualized techniques are emphasized, while in the other one, the teaching is based on modeling principles. She concludes that mathematical modeling practice as an instructional approach is a technique that can be used to circumvent several cognitive obstacles identified in the learning of differential equations. The authors of [94] develop a preliminary study of the application of mathematical modeling as a pedagogical tool for teaching several concepts of applied mathematics, particularly the geometric solutions of scalar and systems of ordinary differential equations. In [127], the author is interested in the students’ understanding when learn ordinary differential equations under the mathematical modeling perspective. She develops an analysis using the APOS theory and mainly concludes that the modeling stimulates discussion, reflection, and the construction of new processes, objects, and schemes. Based on the didactic engineering perspective, the authors of [134] present the results of experimenting mathematical modeling process as didactic methodology for teaching ordinary differential equations.
- (c)
- Language games, representations, and relations of mathematics with other sciences. There are some papers paying attention to some aspects like the different language games developed by the students involved in modeling activities [48], the usage of registers of representation for making relationships between the context and elements in ordinary differential equations [13], and the role of mathematical modeling to establish a relation between mathematics and other sciences [4,5,98].
- (d)
- Modeling activities using ordinary differential equations to teach other concepts. Other articles are focused on the study of mathematical models based on ordinary differential equations for teaching concepts of other areas of mathematics or even other disciplines. More precisely, in [22] a study where the students were involved in the learning of concepts like drug administration by using simulations of the mathematical was developed. This experience was supported on modeling drug administration regimes for asthma through systems of coupled differential equations. In [115], the authors are focused in the teaching of concepts from cardiovascular physiology by using an analogous mathematical model to electronic circuits. In [116], some concepts of mechanics are introduced to the students through modeling fighter pilot ejection. In [118,119], the authors study how students understand units and rate of change when working with ordinary differential equations. In [30], some concepts of physical dynamic systems like the stability using mathematical models based on ordinary differential equation systems are studied; and in [128] the authors study some concepts of fluid dynamics using models based on the Bernoulli equation.
7.1.5. Information and Communication Technology-Based Methodologies
- (a)
- Computer algebra system. The concept of computer algebra system is widely used to refer a type of software package that is used in learning some concepts by the manipulation of some appropriate mathematical formulae, and it is used in those cases where the algebraic, graphic, or algorithmic manipulations are tedious tasks with a low level of learning [149]. There are several papers focused in the usage of technological tools to find the analytic, numeric, or graphical solution of differential equations or even to analyze the qualitative behavior. Specifically, the articles [3,4,10,11,12,13,19,28,29,32,49,73,74,94,95,99,100,101,103,120,123] are related to the computer algebra system approach. In [28], the use of the software “Scientific Notebook” is studied to obtain the analytic and graphical solution of ordinary differential equations. The authors of [49] are focused on researching the teaching of differential equations through mathematical modeling in a computer enriched environment. In [29], it is reported a study where the students were encouraged to develop simulations of freefall problem by using a spreadsheet based on mathematical models. The authors study if the activities contribute to the mathematical, physical, and technological knowledge of students. The paper [3] discusses the cognitive process developed by students when participating in a teaching module for ordinary differential equations, which is based on problem solving and the usage of the VoyageTM200 calculator. The authors of [4,11] are interested in analyzing the different representations developed by students when learned ordinary differential equations using a computer algebra system as mediator. Indeed, in [4] some results about the application of spreadsheets and the HPGSolver software for visualizing and interpreting the properties of a given phenomenon arising in population dynamics are reported, and [11] contributes to study the connections between symbolic and graphical representations. The authors of [10,94] use the software Modellus to teach some properties of a Lotka–Volterra type system by using numerical simulations. In the research developed in [12,13], it is reported how the students were able to use several digital tools such as Excel, Derive, Wolfram-Alpha, Geogebra, to explore ordinary differential equations and their solutions. Particularly in [12], the students used an Applet to visualize and interpret the behavior of solutions of ordinary differential equations, some students’ difficulties were found in this work; and in [13] the students were encouraged to use different digital tools as mentioned before and a computer package “GeomED” particularly designed to visualize and analyze the direction fields. In the research reported in [73] the software called STELLA was used to simulate the physical cascade system. In [74], the authors are focused on teaching mathematical models building for some given physical situations and in the numerical validation using technology. In [95], the authors use Maple to assist students in understanding the construction of analytic solution into the classroom. The authors of [99] present the experience of a project for teaching mathematics at the Massachusetts Institute of Technology and particularly present the result of a developed software called “mathlets” which was used for teaching concepts of dynamical systems. The author of [32,100,101] presents an experience of teaching several topics of calculus and ordinary differential equations using an integrated learning environment enriched with projects, mathematical modeling, and information and communication technology. In the article [103], some innovative ways to use free network computing laboratory called NCLab to the teaching of differential equations and applications are presented. In [120], the authors research how Maple helps the students in algebraic skills and construction of graphs, meanwhile the students learn some concepts related with the Laplace transform. The authors of [123] investigate the usage of Web-based simulations to learn ordinary differential equations. In [19], the authors studied the development of several mathematical thinking processes when the students learn ordinary differential equations using the software Maxima.
- (b)
- Simulation-based learning for teaching applications of ordinary differential equations. There are some articles where the simulation-based learning or computer-assisted learning methodologies are used to teach the applications of ordinary differential equations to several areas like physics, biology, chemistry, or related areas. In those papers, the emphasis of teaching is given on concepts which are not included in a traditional course of differential equations. The numerical simulations are typically used to develop the understanding in the students by providing a visual animation and also for develop the intuition with respect to the change of some parameters, for instance, the initial conditions or the coefficients in an specific ordinary differential equations. The papers of this type are [18,27,60,75,92,102,115,122]. In [27], the authors review the traditional engineering textbooks and propose the computer simulations to teach the systems of ordinary differential equations arising in polymer molecular reaction dynamics. The authors of [60] are focused on the teaching several concepts of electric circuits theory by using some concepts of mathematical modeling, the Laplace transform, numerical simulations with MATLAB, and experiments. In [75], the aim was teaching some concepts of hydrostatic and atmospheric theories by using some mathematical models based on ordinary and partial differential equations and their simulation using spreadsheets. The authors of [92] are focused on helping to understand the applications of eigenvalue problems and develop a software using Visual BASIC for a simulation of solutions for the ordinary differential equations system modeling the problem of the two-mass two-spring physical system. The software simulates the vibration of the physical system, allowing the introduction by the user of some parameters such as the body masses and spring constants, solves the mathematical model, and shows on the screen the numerical and graphical results. In [102], it is reported the application of spreadsheet simulations to teach some topics of differential equations arising in a course of chemistry for undergraduate students. In [115], the authors propose the computer-based simulations to teach physiological processes like capacitance and resistance, and also suggest the introduction of those kind of teaching in undergraduate cardiovascular physiology courses. The authors of [18] study the simulation of electric circuits by using the construction of a physical laboratory model and a graphical calculator. In [122], the authors use Phyton to develop a software called REAJA, which is used for teaching some concepts in the undergraduate course of Chemical Processes.
- (c)
- Flipped classroom. The pedagogical methodology called “flipped classroom” or “inverted classroom” has been widely used in the last decades to replace traditional lectures given in the classroom by an active learning. The main feature of this methodology is that the responsibility for learning the rest is on the learners, through the design of meaningful activities students have opportunities to control their own processes of leaning before the class. In principle, the activities may or may not be technology-based. However, the advances of information and communication technologies in the last years have increased individual instruction computer-based. The traditional lectures given in the classroom are temporally displaced by videos or similar resources which are previously available for students in a server, then the activities inside the classroom are developed on interactive groups of learning. Particularly, in [33,34] the authors apply the flipped classroom to study the teaching of topics related to ordinary differential equations. In [33], the authors study the effectiveness of flipped classroom to develop skills related to the application of MATLAB/Simulink in the solution of ordinary differential equation mathematical models arising in a chemical course. Meanwhile, in [34], the authors combine the flipped classroom methodology with the cycle of mathematical model in order to study the introductory concepts of ordinary differential equations. In both works, supported on strong evidence, the authors conclude that the flipped classroom improves the active learning achievement of students.
7.1.6. Project-Based Learning
7.1.7. Other Methodologies
7.2. Question 2: What Topics of Ordinary Differential Equations Have Been Explored in the Previous Studies?
- (a)
- Basic concepts of ordinary differential equation. We refer to as basic concepts the definition of ordinary differential equation and their solutions. For instance, in [72], the author analyzed the answer of students to the question “What comes to your mind when you are asked to solve an ODE?” in two instants of a course, at the beginning and after the intervention. He found that firstly all students think about concepts related to the analytic solution and in the second two-thirds of students consider a change of their answers including some concepts related with the qualitative approach. A similar study was conducted in [69], where the answers of students to the following exam question were analyzed:
- In your own words, define a differential equation. Explain what constitutes a solution to a differential equation. How can you represent geometrically a differential equation? Can the geometric representation of the differential equation help in sketching approximate solutions? In your opinion, how would you solve a differential equation?” [69] (p. 654)
In the same study, the results of a semi-structured interview to the students who were asked six questions related with the definition of ordinary differential equation, the solution concept, the concept of geometric solution, and feeling of learning differential equations were also presented. In relation to the student construction of the concept solution a framework of four facets (context-entity-process-object) is introduced to analyze that type of constructions developed, see also [114]. The teaching of the concept of equilibrium solution in the case of scalar equations was investigated in [87]. More recently in [79], the authors research on the students conceptions about the solution of ordinary differential equations. Moreover, there are some works focused in the basic concepts related with graphical and numerical solution of an ordinary differential equation. In the case of graphical solution, researchers explore new ways for the students to interpret and give meaning to the information represented by a slope field. The initial value problem or Cauchy problem, autonomous differential equations, and the asymptotic behavior of solutions are also widely studied [12,71,84]. Regarding the numerical solution, the students have been introduced to learn the concepts of stability of the solution with respect to the initial condition and the coefficients of the equation by empirical examples [29]. - (b)
- Biomathematical models. There are several works that introduce some models arising in biomathematics which are based on differential equations. It is possible to find different types of population growth models, for example models from epidemics transmission. In those papers, the authors also pay attention to the introduction of qualitative analysis of solutions.In the case of scalar models we have the articles [4,12,13,20,31,49,63,91,98,124], where the authors introduce the Malthus or Gompertz models and the Verhulst type models. Firstly, related with Malthus or Gompertz models, in [31] is presented research where the students are introduced in the study of population models according to:contextualized to the case of representing the density of carcinogenic cells of a tumor at the time t, with the measured initial density and r is a positive constant. A similar topic of ordinary differential equations is also developed by [63,91,98,124]; particularly in [98] the authors study a model for disinfection and modify the assumption on r by considering that r is a negative constant. Now, concerning with Verhulst type models, in [20] the authors use the mathematical modeling to teach the population models of the formwhere is the number of individuals at time t living in a given bounded region; r and K are positive constants used for the increasing rate and the caring capacity, respectively; is the predation function; and is the initial population. The attention in [20] is reduced to predation function satisfying the properties when and when with a positive number, for instance considering with a positive constant. We notice that when the model (3)–(4) is reduced to the Verhulst or logistic equation, which is also treated by [49]. A similar model is taught by [4,12,13] where and , respectively.On the other hand, in the case of systems of differential equations, we have the Lotka–Volterra model in competence of species and epidemiology, which are treated by [10,71,86,88,94,97,101,109,134]. In [10], the authors use mathematical modeling for describing the transmission of Malaria to the humans by the female mosquitoes of the genus Anopheles, given by the following systemwhere is the number of infected humans in time t; is the number of (female) mosquitoes infected at time t; N is the total population of humans; M is the total population of mosquitoes; and and are positive constants. The system (5)–(8) is a particular example of the wide class of the models well known as Lotka–Volterra like systems and is used to model competence of species, which are also treated by [71,86,88,94,97,101,109,134].Other common topics covered by the articles in teaching biomathematical modeling are related to some advances in model design and mathematical analysis. In the case of mathematical modeling, the core of teaching is focused on the simplification of some biological phenomenon using mathematical concepts recognized by the group of students involved in the experience. Related with the mathematical analysis, the works draw attention to understanding the meaning of the equations in the biology context and to the characteristics of the behavior of the solutions. For instance, in [10] the students belong to a course in an undergraduate program in Biology. The students had a previous knowledge about the disease of malaria caused by a parasite of the genus Plasmodium from a female mosquitoes of the genus Anopheles and they also mastered some concepts of calculus. The research reports, that firstly the aim of the modeling design was to increase the relations that the students could build between calculus concepts and Biology elements. In addition, the most important simplifications associated to Biology were stated as follows: the period of incubation is discarded; the human natality and mortality are ignored; the progressive acquisition of immunity in humans is ignored; and infected mosquitoes will prevail infected until death. Then, precisely stating the variables and parameters and, considering the behavior of populations interactions students formulated the model given by (5)–(8). The main two dependent variables at time t are the infected humans and the infected (female) mosquitoes populations given by and , respectively. Two parameters to be considered are total population of humans and mosquitoes given by N and M, respectively. To deduce the equation (5), describing the change over time of population for infected humans by interaction with mosquitoes, it is assumed that and infected mosquito bites a health human with a certain probably and the sick persons are recovered. The factors and represent the health human and the number of bites given by a mosquito per unit of time with a probability of health humans to be infected equal to p, respectively. Meanwhile, the recovered of infected humans is described by the term with g a parameter for the recovery rate. Similar arguments are used to deduce the Equation (6), mainly the term is the change of infected mosquitoes when a non-infected mosquito bites into an infected human in a unit of time with a probability to be infected equal to c, and the term is the infected mosquitoes that die at mortality rate . Second, concerning the mathematical analysis of (5)–(8), the authors observe that the system is non-linear and prevents the students from achieving analytical solutions and allows them access to the solutions using the software Modellus. The students worked with Modellus were guided by a set of activities that strengthen the concepts of calculus like functions, tangent line, derivative, and maxima and minima.
- (c)
- Scalar-based models. We have some work using mathematical models based on scalar differential equations to teach some concepts of differential equations.For mathematical models based on first order scalar equations, we have four groups of articles. Firstly, we have the increasing (or decreasing) mathematical models based on an ordinary differential equation of the formwhere k is a positive (or negative) constant, t is the time, and is the measurement of some physical quantity such that the initial time is . In [51], the authors propose five activities in the context of problem solving and guided discovery methodologies, where particularly the four labeled activities are contextualized to radioactive decay modeled by (9) with the quantity of radium in a body which is decreasing in time. The radioactive decay in the context of mathematical modeling is also considered by the authors of [39] where is the number of radioactive atoms. A close problem is the model for uranium decay explored in [3], which is described as a variation of (9), with the amount of mercury in a given reservoir at any instant of time t. Related with the increasing behavior we have the works Malthus or Gompertz type described in the Biomathematical models, see the works for (1)–(2). Moreover, in [76] the authors use a difference equation of the formarising in kinetic reactions and introduce the teach of convergence of discrete models to continuous models of the form (10) or to teach the relation of difference and differential equations. A second group of works are [3,8,17,29,39,48,51,85,100,116,117,131,132], where the authors use mathematical models based on first order differential equations. Here we distinguish four types of mathematical models. Firstly, we have the well known “freefall mathematical model”, which is given by a differential equation of the typewith m denoting the mass of a body, g is the acceleration due to gravity, b is a constant associated to air resistance, is the initial velocity of the body, t is the time, and the unknown v is the velocity of the body. In [29], the author uses numerical methods to simulate the solution of (10) in the case of vacuum () and with air resistance (). Ref. [8] is focused on the research of mathematical thinking process when the students analyze and solve a freefall problem, and in [131] the authors are focused on the analytic solution of (10) by the variable separation method. Third, the model for describing “Newton’s law of cooling” given by a differential equation of the formwhere h is a positive constant called the convective cooling coefficient, represents the environment temperature of cooling medium, M is the mass of the body, C is the specific heat, and is the unknown temperature of the body in a time t with known initial condition . The model of type (11) is treated in [39,85,91,100]. The fourth type of mathematical model is based on “Kirchoff and Ohm laws” given bywith as the constant for the resistance of the capacitor, the unknown is the voltage in the capacitor, and E is the voltage of the capacitor at ; this equation is studied in [17,18].On the other hand, a second group of scalar models of second order are presented in [5,99], where the authors use mathematical models arising in electric circuits and vibration problems, respectively. Indeed, in [5] the authors consider the modelwhere the I is the current intensity crossing the circuit and in [99] the authors use an interactive software for explore the equationwhere and are constants and x is the displacement of the mass from equilibrium in a spring-mass system. In the case of [5], the authors study physical concepts such as the inductance and resistance and in [99] the authors study some concepts of Mechanical Vibration Theory like amplitude and phase.
- (d)
- Systems based on mechanical theory. The works [92,117] consider second order systems arising in Mechanical Vibration Theory. To be more precise, in [92] the authors consider a system modeling a two-mass two-spring vibration system of the following typewhere are the masses of two bodies connected by two springs with constants and and fixed at the top and and are the displacement from the equilibrium of the bodies. Moreover, in [92] several concepts like amplitude, modes of vibration, period, and frequency are taught.
- (e)
7.3. Question 3: What Are the Results for the Effectiveness of Traditional and New Didactic Methodologies to Teach and Learning Ordinary Differential Equations, as Reported in Previous Studies?
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. String Search Used in Web of Science and Scopus
- ALL FIELDS: (“differential equation*” or “solution* to differential equation*” or “graphical interpretation” or “graphical solution*” or “qualitative solution*” or “numerical solution*” or “analytic solution*” or “first order equation*” or “higher order equation*”) OR ALL FIELDS: (“Laplace transform” or “power series method” or “variable separable equation*” or “reducible to variable separable equation*” or “homogeneous equation*” or “reducible to homogeneous equation*” or “exact equation*” or “reducible to exact equation*” or “Bernoulli equation*”) OR ALL FIELDS: (“linear equation*” or “Ricatti equation*” or “phase plane” or “isocline*” or “slope field*” or “equilibrium” or “stability of solution*” or “initial value problem*” or “boundary value problem*” or “scalar equation*” or “systems of equations” or “ linear” or “nonlinear”) AND ALL FIELDS: (“teaching methodologies” or “students’ understanding and difficulties” or “interpretation of solutions” or “registers of representations” or “mathematical modeling” or “mathematical models” or “problem-based learning” or “problem solving”) OR ALL FIELDS: (“error analysis” or “mathematics teaching practices” or “real world situation” or “computational resources” or “mathematical application” or “classroom discourse” or “didactic of differential equations” or “critical discourse analysis”).
- (TITLE-ABS-KEY (“differential equation” OR “solution* to differential equation*” OR “graphical interpretation” OR “graphical solution*” OR “qualitative solution*” OR “numerical solution*” OR “analytic solution*” OR “first order equation*”) OR ALL (“higher order equation*” OR “Laplace transform” OR “power series method” OR “variable separable equation*” OR “reducible to variable separable equation*” OR “homogeneous equation*” OR “reducible to homogeneous equation*” OR “exact equation*”) OR TITLE-ABS-KEY (“Bernoulli equation*” OR “linear equation*” OR “Ricatti equation*” OR “phase plane” OR “isocline*” OR “slope field*” OR “equilibrium” OR “stability of solution*” OR “initial value problem*”) OR TITLE-ABS-KEY (“boundary value problem*” OR “scalar equation*” OR “systems of equations” OR “ linear” OR “nonlinear”) AND TITLE-ABS-KEY (“teaching methodologies” OR “students’ understanding and difficulties” OR “interpretation of solutions”) OR TITLE-ABS-KEY (“registers of representations” OR “mathematical modeling” OR “mathematical models” OR “problem based learning” OR “problem solving” OR “error analysis” OR “mathematics teaching”))
Appendix B. List of Journals from Qualis, zbMATH, Scielo, WOS, and Scopus Datbases
| Journal Title | ISSN | Qualis Class | zbMATH Class | Scielo | Years Consulted | |
|---|---|---|---|---|---|---|
| 1 | Academia journal of educational research | 2315-7704 | B3 | 2013-2020 | ||
| 2 | Acta scientiae | 2178-7727 | A2 | 1999–2019 | ||
| 3 | Actualidades investigativas en educación | 1409-4703 | SC | 2011–2020 | ||
| 4 | American mathematical monthly | 0002-9890 | BA | 1894–2020 | ||
| 5 | Applied measurement in education | 0895-7347 | BA | 1988–2020 | ||
| 6 | Australian journal of education | 0004-9441 | BC | 1957–2019 | ||
| 7 | BOLEMA: Boletim de educação matemática | 1980-4415 | A1 | AA | SC | 1985–2019 |
| 8 | Boletim cearense de educação e história da matemática | 2357-8661 | B3 | 2014–2019 | ||
| 9 | Boletim online de educação matemática | 2357-724X | B1 | 2013–2019 | ||
| 10 | Boletín das ciencias | 0214-7807 | B3 | 1988–2019 | ||
| 11 | British educational research journal | 6469-3118 | BA | 1975–2019 | ||
| 12 | British journal of educational psychology | 2044-8279 | BA | 1931–2020 | ||
| 13 | British journal of educational technology | 1467-8535 | BA | 1970–2019 | ||
| 14 | Child development | 1467-8624 | BA | 1990–2020 | ||
| 15 | Ciência & educação | 1980-850X | A1 | SC | 1988–2019 | |
| 16 | Ciencia, docencia y tecnología | 1851-1716 | SC | 2000–2019 | ||
| 17 | Cognition | 0010-0277 | BB | 1972–2020 | ||
| 18 | Cognition and instruction | 0737-0008 | BA | 1984–2020 | ||
| 19 | Comparative education | 0305-0068 | BA | 1964–2020 | ||
| 20 | comparative education review | 0010-4086 | BA | 1957–2020 | ||
| 21 | Cpu-e. revista de investigación educativa | 1870-5308 | SC | 2005–2020 | ||
| 22 | Cuadernos de investigación educativa | 1510-2432 | SC | 1997–2019 | ||
| 23 | Economics of education review | 0272-7757 | BA | 1981–2020 | ||
| 24 | Educação e matemática: revista da associação de professores de matemática | 0871-7222 | B1 | 1987–2019 | ||
| 25 | Educação matemática em foco | 1981-6979 | B3 | 2017–2019 | ||
| 26 | Educação matemática em revista | 2317-904X | A2 | 1983–2019 | ||
| 27 | Educaçao matematica pesquisa | 1516-5388 | A2 | AB | 1999–2019 | |
| 28 | Educación | 1019-9403 | SC | 1992–2020 | ||
| 29 | Educación matemática | 1665-5826 | AC | SC | 1989–2019 | |
| 30 | Educación y educadores | 0123-1294 | SC | 1997–2019 | ||
| 31 | Educar em revista | 1984-0411 | A1 | 1977–2019 | ||
| 32 | Educational measurement: issues and practice | 1742-3992 | BB | 1982–2020 | ||
| 33 | Educational research | 0013-1881 | BA | 1958–2020 | ||
| 34 | Educational studies in mathematics | 0013-1954 | A1 | AB | 1968–2020 | |
| 35 | Educational technology research and development | 1556-6501 | BB | 1953–2019 | ||
| 36 | Educational technology: the magazine for managers of change in education | 0013-1962 | BC | 1960–2017 | ||
| 37 | Elementary school journal | 0013-5984 | BA | 1914–2019 | ||
| 38 | Em teia-revista de educação matemática e tecnológica iberoamericana | 2177-9309 | B1 | 2010–2019 | ||
| 39 | Enseignement mathematique, l’ | 0013-8584 | BC | 2009–2019 | ||
| 40 | Enseñanza de las ciencias | 0212-4521 | A1 | BA | 1983–2019 | |
| 41 | Ensino da matemática em debate | 2358-4122 | B4 | 2010–2019 | ||
| 42 | Epsilon | 2340-714X | AC | 1984–2019 | ||
| 43 | Estudios-centro de estudios avanzados. universidad nacional de córdoba | 1852-1568 | SC | 1993–2019 | ||
| 44 | Focus on learning problems in mathematics and science teaching | 0272-8893 | BC | 1988–1991 | ||
| 45 | For the learning of mathematics | 0228-0671 | A1 | AB | 1980–2017 | |
| 46 | Formação docente | 2176-4360 | B1 | 2009–2019 | ||
| 47 | Hiroshima journal of mathematics education | 0919-1720 | AB | 1993–2020 | ||
| 48 | IEEE revista iberoamericana de tecnologias del aprendizaje | 2255-5706 | B3 | 2006–2012 | ||
| 49 | Insegnamento della matematica e delle scienze integrate, l’ | 1123-7570 | BC | 1970–2020 | ||
| 50 | Integración y conocimiento | 2347-0658 | C | 2012–2020 | ||
| 51 | Interciencia | 0378-1844 | A1 | 2009–2020 | ||
| 52 | International electronic journal of mathematics education | 2468-4945 | C | 2006–2020 | ||
| 53 | International journal of engineering education | 0949-149X | A1 | 1991–2020 | ||
| 54 | International journal of engineering research and applications | 2248-9622 | C | 2011–2020 | ||
| 55 | International journal of mathematical education in science and technology | 0020-739X | A1 | BB | 1970–2020 | |
| 56 | International journal of science and mathematical education | 1571-0068 | A1 | 1970–2019 | ||
| 57 | International statistical review | 1751-5823 | BA | 1990–2020 | ||
| 58 | Jornal internacional de estudos em educação matemática | 2176-5634 | A2 | 2009–2020 | ||
| 59 | Journal for research in mathematics education | 0021-8251 | AA | 1970–2020 | ||
| 60 | Journal für mathematik-didaktik | 0173-5322 | AC | 1980–2020 | ||
| 61 | Journal of computers in mathematics and science teaching | 0731-9258 | BC | 1981–2020 | ||
| 62 | Journal of educational psychology | 0022-0663 | BA | 2002–2020 | ||
| 63 | Journal of educational research | 0022-0671 | BA | 1920–2020 | ||
| 64 | Journal of mathematics teacher education | 1386-4416 | AB | 1998–2020 | ||
| 65 | Journal of recreational mathematics | 0022-412X | BC | 1968–2014 | ||
| 66 | Journal of research in science teaching | 1098-2736 | BA | 1960–2020 | ||
| 67 | Journal of statistics education | 1069-1898 | AC | 1993–2015 | ||
| 68 | Journal of the learning sciences | 1050-8409 | BA | 1991–2020 | ||
| 69 | Journal of urban mathematics education | 2151-2612 | B1 | 2008–2019 | ||
| 70 | Learning and instruction | 0959-4752 | BA | 1991–2020 | ||
| 71 | Matemática e estatística em foco | 2318-0552 | B5 | 2013–2019 | ||
| 72 | Matematica e la sua didactica, la | 1120-9968 | AC | 2016–2020 | ||
| 73 | Mathematical journal of interdisciplinary sciences | 2278-9561 | B5 | 2012–2020 | ||
| 74 | Mathematics education research journal | 0021-8251 | AB | 1989–2020 | ||
| 75 | Mathematics in school | 0305-7259 | AC | 1971–2014 | ||
| 76 | Mathematics teacher | 0025-5769 | AC | 1990–2020 | ||
| 77 | Mathematics teaching | 0025-5785 | AC | 1871–2020 | ||
| 78 | Mathematics teaching in the middle school | 1072-0839 | AC | 1994–2019 | ||
| 79 | Mathematical thinking and learning | 1098-6065 | AB | 1999–2020 | ||
| 80 | Mediterranean journal for research in mathematics education | 1450-1104 | AB | 2002–2020 | ||
| 81 | Numeros | 0212-3096 | AC | 1981–2020 | ||
| 82 | Paradígma | 1011-2251 | A2 | SC | 1997–2019 | |
| 83 | Perspectivas da educação matemática | 2359-2842 | B1 | 2008–2019 | ||
| 84 | Petit X | 0759-9188 | AC | 1986–2007 | ||
| 85 | Phi delta kappan | 0031-7217 | BA | 2000–2020 | ||
| 86 | Plot: mathematiques et enseignement | 0397-7471 | AC | 1987–2017 | ||
| 87 | PNA: revista de investigación en didáctica de la matemática | 1887-3987 | A2 | 2006–2020 | ||
| 88 | Professor de matemática online | 2319-023X | B4 | 2013–2019 | ||
| 89 | Psychology in the schools | 1520-6807 | BA | 1964–2020 | ||
| 90 | Quadrante | 2183-2838 | AB | 1992–2020 | ||
| 91 | Recherches en didactique des mathematiques | 0246-9367 | AB | 2000–2019 | ||
| 92 | Redimat- revista de investigación en didáctica de las matemáticas | 2014-3621 | A2 | 2012–2020 | ||
| 93 | REEC. revista electrónica de enseñanza de las ciencias | 1579-1513 | A2 | 2002–2019 | ||
| 94 | Remat: revista eletrônica da matemática | 2447-2689 | B3 | 2015–2020 | ||
| 95 | Rematec. revista de matemática, ensino e cultura (ufrn) | 1980-3141 | B2 | 2006–2019 | ||
| 96 | Rencimat | 2179-426X | A2 | 2010–2019 | ||
| 98 | Revemat: revista eletrônica de educação matemática | 1981-1322 | A2 | 2006–2020 | ||
| 99 | Revista de ciência & tecnologia (unig) | 1519-8022 | B5 | 1995–2019 | ||
| 100 | Revista de ciências da educação | 2317-6091 | B1 | 2012–2020 | ||
| 101 | Revista de educação, ciências e matemática | 2238-2380 | A2 | 2011–2019 | ||
| 102 | Revista de produção discente em educação matemática | 2238-8044 | B3 | 2012–2019 | ||
| 103 | Revista digital de investigación en docencia universitaria | 2223-2516 | SC | 2005–2019 | ||
| 104 | Revista docência do ensino superior | 2237-5864 | B1 | 2011–2020 | ||
| 105 | Revista electrónica de investigación educativa | 1607-4041 | A1 | 1999–2020 | ||
| 106 | Revista electronica de investigacion en educacion en ciencias | 1850-6666 | A2 | SC | 2006–2019 | |
| 107 | Revista eureka sobre enseñanza y divulgación de las ciencias | 1697-011X | A1 | 2004–2020 | ||
| 108 | Revista iberoamericana de educación superior | 2007-2872 | SC | 2010–2020 | ||
| 109 | Revista internacional de aprendizaje en ciencia, matemáticas y tecnología | 2386-8791 | B3 | 2014–2019 | ||
| 110 | Revista latinoamericana de investigación en matemática educativa | 2007-6819 | A2 | AA | SC | 1997–2020 |
| 111 | Revista mexicana de investigación educativa | 1405-6666 | SC | 1996–2020 | ||
| 112 | School effectiveness and school improvement | 0924-3453 | BA | 1990–2020 | ||
| 113 | School psychology quarterly | 2578-4218 | BA | 1986–2020 | ||
| 114 | School science and mathematics | 1949-8594 | BC | 1901–2020 | ||
| 115 | Science education | 1098-237X | BA | 2001–2020 | ||
| 116 | Science journal of education | 2329-0897 | B4 | 2013–2020 | ||
| 117 | Sociology of education | 0038-0407 | BA | 2004–2020 | ||
| 118 | Statistics education research journal | 1570-1824 | AB | 2002–2020 | ||
| 119 | Suma | 1130-488X | AC | 1988–2019 | ||
| 120 | Teaching and teacher education | 0742-051X | BA | 1985–2020 | ||
| 121 | Teaching children mathematics | 1073-5836 | AC | 1954–2019 | ||
| 122 | Teaching mathematics and its applications | 0268-3679 | A1 | 1982–2020 | ||
| 123 | Thai journal of mathematics | 1686-0209 | B4 | 2003–2020 | ||
| 124 | The college mathematics journal | 0746-8342 | BC | 1984–2020 | ||
| 125 | The electronic journal of mathematics & technology | 1933-2823 | B1 | 2007–2020 | ||
| 126 | The journal of mathematical behavior | 0732-3123 | A1 | AB | 1994–2020 | |
| 127 | Uniciencia | 1011-0275 | SC | 1984–2020 | ||
| 128 | Unión revista iberoamericana de educación matemática | 1815-0640 | AC | 2005–2019 | ||
| 129 | Uno. revista de didactica de las matematicas | 1133-9853 | AC | 1994–2019 | ||
| 130 | Young children | 0044-0728 | BA | 1964–2001 | ||
| 131 | Zentralblatt fur didactic der mathematik | 1863-9690 | A1 | AB | 1997–2021 | |
| 132 | Zetetiké | 2176-1744 | AB | 1993–2020 |
| Journal Title | ISSN | Journal Title | ISSN |
|---|---|---|---|
| Advances in physiology education | 1043-4046 | International journal of research in undergraduate mathematics education | 2198-9745 |
| American journal of physics | 0002-9505 | Journal of chemical education | 0021-9584 |
| Biochemistry and molecular biology education | 1470-8175 | Journal of professional issues in engineering education and practice | 1052-3928 |
| CBE-Life sciences education | 1931-7913 | Journal of science education and technology | 1059-0145 |
| Computer applications in engineering education | 1061-3773 | Mathematics teaching-research journal online | 2573-4377 |
| Computers & education | 0360-1315 | Physical review-physics education research | 2469-9896 |
| Education for chemical engineers | 1749-7728 | PRIMUS: problems, resources, and issues in mathematics undergraduate studies | 1051-1970 |
| Eurasia journal of mathematics science and technology education | 1305-8215 | Research in mathematics education | 1479-4802 |
| European journal of engineering education | 0304-3797 | Research in science & technological education | 0263-5143 |
| European journal of physics | 0143-0807 | Resonance-journal of science education | 0971-8044 |
| Global journal of engineering education | 1328-3154 | Revista brasileira de ensino de fisica | 1806-1117 |
| IEEE transactions on education | 0018-9359 | Revista cientifica | 0124-2253 |
| Information technologies and learning tools | 2076-8184 | Revista conrado | 1990-8644 |
| Interdisciplinary science reviews | 0308-0188 | Revista electronica de humanidades educacion y comunicacion social | 1856-9331 |
| International journal for technology in mathematics education | 1744-2710 | Revista publicando | 1390-9304 |
| international journal of education and information technologies | 2074-1316 | Teaching of mathematics | 1451-4966 |
| International journal of electrical engineering education | 0020-7209 | The American mathematical monthly | 0002-9890 |
| International journal of engineering pedagogy | 2192-4880 | The physics teacher | 0031-921X |
| International journal of mechanical engineering education | 0306-4190 | The Turkish online journal of educational technology | 2146-7242 |
| International journal of psychosocial rehabilitation | 1475-7192 |
References
- Arslan, S. Do students really understand what an ordinary differential equation is? Int. J. Math. Educ. Sci. Technol. 2010, 41, 873–888. [Google Scholar] [CrossRef]
- Arslan, S. Traditional instruction of differential equations and conceptual learning. Teach. Math. Its Appl. 2010, 29, 94–107. [Google Scholar] [CrossRef]
- Camacho, M.; Perdomo, J.; Santos, M. Newblock Conceptual and cognitive processes in the introduction of ordinary differential equations through problem solving. Ensen. Las Cienc. Rev. De Investig. Exp. Didácticas 2012, 30, 9–32. [Google Scholar]
- Camacho-Machín, M.; Guerrero-Ortiz, C. Identifying and exploring relationships between contextual situations and ordinary differential equations. Int. J. Math. Educ. Sci. Technol. 2015, 46, 177–195. [Google Scholar] [CrossRef]
- Chaachoua, H.; Saglam, A. Modelling by differential equations. Teach. Math. Its Appl. 2006, 25, 15–22. [Google Scholar] [CrossRef]
- Cordero, F.; Miranda, E. El entendimiento de la transformada de laplace: Una epistemología como base de una descomposición genética. Rev. Latinoam. De Investig. Matemática Educ. 2002, 5, 133–168. [Google Scholar]
- Curia, L.; Pérez, M.; Lavalle, A. Evaluation of the contents of differential equations through mathematical competences. Rev. ElectrÓnica Humanidades Educación Comun. Soc. 2018, 26, 9–27. [Google Scholar]
- Czocher, J.A. Introducing modeling transition diagrams as a tool to connect mathematical modeling to mathematical thinking. Math. Think. Learn. 2016, 18, 77–106. [Google Scholar] [CrossRef]
- Czocher, J.A. How can emphasizing mathematical modeling principles benefit students in a traditionally taught differential equations course? J. Math. Behav. 2017, 45, 78–94. [Google Scholar] [CrossRef]
- da Silva, D.; Borba, M.C. The role of software modellus in a teaching approach based on model analysis. ZDM Math. Educ. 2014, 46, 575–587. [Google Scholar]
- Dana-Picard, T.; Kidron, I. Exploring the phase space of a system of differential equations: Different mathematical registers. Int. J. Sci. Math. Educ. 2008, 6, 695–717. [Google Scholar] [CrossRef]
- Guerrero-Ortiz, C.; Camacho-Machín, M.; Mejía-Velasco, H.R. Difficulties experienced by students in the interpretation of the solutions of ordinary differential equations that models a problem. Ensen. Las Cienc. Rev. Investig. Exp. Didácticas 2010, 28, 341–352. [Google Scholar] [CrossRef]
- Guerrero-Ortiz, C.; Mejía-Velasco, H.R.; Camacho-Machín, M. Representations of a mathematical model as a means of analysing growth phenomena. J. Math. Behav. 2016, 42, 109–126. [Google Scholar] [CrossRef]
- Rasmussen, C.; Keene, K. Knowing solutions to differential equations with rate of change as a function: Waypoints in the journey. J. Math. Behav. 2019, 56, 100695. [Google Scholar] [CrossRef]
- Rasmussen, C.L. New directions in differential equations: A framework for interpreting students’ understandings and difficulties. J. Math. Behav. 2001, 20, 55–87. [Google Scholar] [CrossRef]
- Rasmussen, C.L.; King, K.D. Locating starting points in differential equations: A realistic mathematics education approach. Int. J. Math. Educ. Sci. Technol. 2000, 31, 161–172. [Google Scholar] [CrossRef]
- Rodríguez, R. Teaching and learning modelling: The case of differential equations. Rev. Latinoam. Investig. Matemática Educ. 2010, 13, 191–210. [Google Scholar]
- Rodríguez-Gallegos, R.; Quiroz-Rivera, S. The role of technology in the process of mathematical modeling for teaching differential equations. Rev. Latinoam. Investig. Matemática Educ. 2016, 19, 99–124. [Google Scholar]
- Zeynivandnezhad, F.; Bates, R. Explicating mathematical thinking in differential equations using a computer algebra system. Int. J. Math. Educ. Sci. Technol. 2017, 49, 680–704. [Google Scholar] [CrossRef]
- Almeida, L.M.; Kato, L.A. Different approaches to mathematical modelling: Deduction of models and studens’ actions. Int. Electron. J. Math. Educ. 2014, 9, 3–11. [Google Scholar]
- Alves de Oliveira, E.; Camargo, S.B. Ensino e aprendizagem de equações diferenciais: Um levantamento preliminar da produção científica. Teia Rev. Educ. Matemática e Tecnológica Iberoam. 2013, 4, 1–24. [Google Scholar]
- András, S.; Szilágyi, J. Modelling drug administration regimes for asthma: A romanian experience. Teach. Math. Its Appl. 2010, 29, 1–13. [Google Scholar] [CrossRef]
- Blass, L.; Huguenim, A.F.; Irala, V.B.; da Silva, V. O estudo de equações diferenciais através da aplicação do perfil logarítmico do vento. Teia Rev. Educ. Matemática Tecnológica Iberoam. 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Dreyer, T.P. Modelling with Ordinary Differential Equations; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; Classics in Applied Mathematics, 46; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2005. [Google Scholar]
- Segel, L.A.; Edelstein-Keshet, L. A Primer on Mathematical Models in Biology; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2013. [Google Scholar]
- Al-Moameri, H.H.; Jaf, L.A.; Suppes, G.J. Simulation approach to learning polymer science. J. Chem. Educ. 2018, 95, 1554–1561. [Google Scholar] [CrossRef]
- Anderson, M.; Bloom, L.; Mueller, U.; Pedler, P. Enhancing the teaching of engineering differential equations with scientificnotebook. Int. J. Eng. Educ. 2000, 16, 73–79. [Google Scholar]
- Benacka, J. Numerical modelling with spreadsheets as a means to promote stem to high school students. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 947–964. [Google Scholar] [CrossRef]
- Vajravelu, K. Innovative strategies for learning and teaching of large differential equations classes. Int. Electron. J. Math. Educ. 2018, 13, 91–95. [Google Scholar] [CrossRef][Green Version]
- Beier, J.C.; Gevertz, J.L.; Howard, K.E. Building context with tumor growth modeling projects in differential equations. PRIMUS Probl. Resour. Issues Math. Undergrad. Stud. 2015, 25, 297–325. [Google Scholar] [CrossRef]
- Molina, J.A. Experience in the incorporation of ict in teaching differential equations applied. Rev. Iberoam. Educ. 2015, 69, 79–96. [Google Scholar]
- Li, X.; Huang, Z. An inverted classroom approach to educate matlab in chemical process control. Educ. Chem. Eng. 2017, 19, 1–12. [Google Scholar] [CrossRef]
- Yong, D.; Levy, R.; Lape, N. Why no difference? a controlled flipped classroom study for an introductory differential equations course. PRIMUS Probl. Resour. Issues Math. Stud. 2015, 25, 907–921. [Google Scholar] [CrossRef]
- Sierpinska, A. Some Reflections on the Phenomenon of French didactique. J. Für-Math. Didakt. 1995, 16, 163–192. [Google Scholar] [CrossRef]
- Durán, P.A.; Marshall, J.A. Mathematics for biological sciences undergraduates: A needs assessment. Int. J. Math. Educ. Sci. Technol. 2019, 50, 807–824. [Google Scholar] [CrossRef]
- Bibi, A.; Syed, S.; Abedalaziz, N.; Ahmad, M. Teaching and Learning of Differential Equation: A Critical Review to Explore Potential Area for Reform Movement. Int. J. Innov. Multidiscip. Field 2017, 3, 225–235. [Google Scholar]
- Khan, K.S.; Kunz, R.; Kleijnen, J.; Antes, G. Five steps to conducting a systematic review. J. R. Soc. Med. 2003, 96, 118–121. [Google Scholar] [CrossRef] [PubMed]
- Dullius, M.M.; Araujo, I.S.; Veit, E.A. Teaching and learning of differential equations with graphical, numerical and analytical approach: An experience in engineering courses. BOLEMA Bol. Educ. Matemática 2011, 24, 17–42. [Google Scholar]
- Dullius, M.M. Enseñanza y Aprendizaje en Ecuaciones Diferenciales con Abordaje Gráfico, Numérico y Analítico. Ph.D. Thesis, Universidad de Burgos, Burgos, Spain, 2009. [Google Scholar]
- Valenzuela, J.R.; Flores, M. Fundamentos de Investigación Educativa (Tres Volúmenes) (eBook); Editorial Digital Tecnológico de Monterrey: Monterrey, México, 2012. [Google Scholar]
- Murphy, C.M. Writing an effective review article. J. Med. Toxicol. 2012, 8, 89–90. [Google Scholar] [CrossRef] [PubMed]
- Narin, F.; Hamilton, K.S. Bibliometric performance measures. Scientometrics 1996, 36, 293–310. [Google Scholar] [CrossRef]
- Ferrari, R. Writing narrative style literature reviews. Med. Writ. 2015, 24, 230–235. [Google Scholar] [CrossRef]
- Benitti, F.B.V. Exploring the educational potential of robotics in schools: A systematic review. Comput. Educ. 2012, 58, 978–988. [Google Scholar] [CrossRef]
- Godino, J. Perspective of the Didactics of Mathematics as a Technoscientific Discipline. Available online: http://www.ugr.es/local/jgodino (accessed on 1 July 2020). (In Spanish).
- Running, T. A Graphical Solution of the Differential Equation of the First Order. Am. Math. Mon. 1913, 20, 279–281. [Google Scholar] [CrossRef]
- Alvim, B.N.P.; de Almeida, L.M.W. Linguistic appropriation and meaning in mathematical modeling activities. BOLEMA Bol. Educ. Matemática 2019, 33, 1195–1214. [Google Scholar]
- Andresen, M. Modeling with the software ’derive’ to support a constructivist approach to teaching. Int. Electron. J. Math. Educ. 2007, 2, 1–15. [Google Scholar]
- Barbarán, J.J.; Fernéz, J.A. The analysis of errors in the solution of ordinary differential equations. a methodology to develop mathematical competence. Ensenanza Las Cienc. Rev. De Investig. Exp. Didácticas 2014, 32, 173–186. [Google Scholar]
- Barros, A.A.; Laudares, J.B.; de Miranda, D.F. A resolução de problemas em ciências com equações diferenciais ordinárias de 1a e 2a ordem usando análise gráfica. Educ. Matemática Pesqui. 2014, 16, 323–348. [Google Scholar]
- Blomhøj, M.; Kjeldsen, T.H. Project organised science studies at university level: Exemplarity and interdisciplinarity. ZDM Math. Educ. 2009, 41, 183–198. [Google Scholar] [CrossRef]
- Blomhøj, M.; Kjeldsen, T.H. Teaching mathematical modelling through project work. ZDM Math. Educ. 2006, 38, 163–177. [Google Scholar] [CrossRef]
- Borssoi, A.H.; de Almeida, L.M.W. Modelagem matemática e aprendizagem significativa: Uma proposta para o estudo de equações diferencias ordinárias. Educ. Matemática Pesqui. 2004, 6, 91–121. [Google Scholar]
- Brito, L.; Farias, P.H.; Cardoso, J.V.; Ribeiro, R. Teaching of ordinary differential equations using the assumptions of the pbl method. Int. J. Eng. Pedagog. 2020, 10, 7–20. [Google Scholar]
- Bukova-Güzel, E. An examination of pre-service mathematics teachers’ approaches to construct and solve mathematical modelling problems. Teach. Math. Its Appl. 2011, 30, 19–36. [Google Scholar] [CrossRef]
- Camunga, A.; Batard, L.F. Developing skills for selecting the most appropriate method for the solution of superior order ordinary differential equations. Rev. Conrado 2017, 13, 82–88. [Google Scholar]
- Canu, M.; de Hosson, C.; Duque, M. Students’ understanding of equilibrium and stability: The case of dynamic systems. Int. J. Sci. Math. Educ. 2016, 14, 101–123. [Google Scholar] [CrossRef][Green Version]
- Carr, M.; Prendergast, M.; Breen, C.; Faulkner, F. How well do engineering students retain core mathematical knowledge after a series of high threshold online mathematics tests? Teach. Math. Its Appl. 2017, 36, 136–150. [Google Scholar] [CrossRef]
- Carstensen, A.-K.; Bernhard, J. Student learning in an electric circuit theory course: Critical aspects and task design. Eur. J. Eng. Educ. 2009, 34, 393–408. [Google Scholar] [CrossRef]
- Darlington, E. What benefits could extension papers and admissions tests have for university mathematics applicants? Teach. Math. Its Appl. 2015, 34, 179–193. [Google Scholar] [CrossRef]
- Darlington, E.; Bowyer, J. Engineering undergraduates’ views of a-level mathematics and further mathematics as preparation for their degree. Teach. Math. Its Appl. 2016, 36, 200–216. [Google Scholar] [CrossRef][Green Version]
- de Almeida, L.M.W. Considerations on the use of mathematics in modeling activities. ZDM Math. Educ. 2018, 50, 19–30. [Google Scholar] [CrossRef]
- Dehesa de Gyves, N. Discursos en los registros algebraico y geométrico de las ecuaciones diferenciales ordinarias. Educ. Matemática 2006, 18, 123–148. [Google Scholar]
- Flegg, J.A.; Mallet, D.G.; Lupton, M. Students’ approaches to learning a new mathematical model. Teach. Math. Its Appl. 2013, 32, 28–37. [Google Scholar] [CrossRef]
- Gijsbers, D.; de Putter-Smits, L.; Pepin, B. Changing students’ beliefs about the relevance of mathematics in an advanced secondary mathematics class. Int. J. Math. Educ. Sci. Technol. 2020, 51, 87–102. [Google Scholar] [CrossRef]
- Goodchild, S.; Apkarian, N.; Rasmussen, C.; Katz, B. Critical stance within a community of inquiry in an advanced mathematics course for pre-service teachers. J. Math. Teach. Educ. 2020. [Google Scholar] [CrossRef]
- Gruenwald, N.; Sauerbier, G.; Narayanan, A.; Klymchuk, S.; Zverkova, T. Applications in unusual contexts in engineering mathematics: Students’ attitudes. Math. Teach. Res. J. Online 2010, 4, 53–67. [Google Scholar]
- Habre, S. Investigating students’ approval of a geometrical approach to differential equations and their solutions. Int. J. Math. Educ. Sci. Technol. 2003, 34, 651–662. [Google Scholar] [CrossRef]
- Habre, S. Improving understanding in ordinary differential equations through writing in a dynamical environment. Teach. Math. Its Appl. 2012, 31, 153–166. [Google Scholar] [CrossRef]
- Habre, S. Inquiry-oriented differential equations: A guided journey of learning. Teach. Math. Its Appl. 2019, 39, 201–212. [Google Scholar] [CrossRef]
- Habre, S. Exploring students’ strategies to solve ordinary differential equations in a reformed setting. J. Math. Behav. 2000, 18, 455–472. [Google Scholar] [CrossRef]
- Hansen, D.; Cavers, W.; George, G.H. Use of a physical linear cascade to teach systems modelling. Int. J. Eng. Educ. 2003, 19, 682–695. [Google Scholar]
- Heck, A. Bringing reality into the classroom. Teach. Math. Its Appl. 2009, 28, 164–179. [Google Scholar] [CrossRef]
- Herman, R. Spreadsheet physics: Examples in meteorology and planetary science. Am. J. Phys. 2009, 77, 1124–1129. [Google Scholar] [CrossRef]
- Hernández, L. Solving simple kinetics without integrals. J. Chem. Educ. 2016, 93, 669–675. [Google Scholar] [CrossRef]
- Holmberg, M.; Bernhard, J. University teachers’ perspectives on the role of the laplace transform in engineering education. Eur. J. Eng. Educ. 2017, 42, 413–428. [Google Scholar] [CrossRef]
- Humble, S. Rolling and spinning coin: A level gyroscopic processional motion. Teach. Math. Its Appl. 2001, 20, 18–24. [Google Scholar] [CrossRef]
- Hyland, D.; Van Kampen, P.; Nolan, B.C. Introducing direction fields to students learning ordinary differential equations (odes) through guided inquiry. Int. J. Math. Educ. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Hyland, D.; van Kampen, P.; Nolan, B.C. Outcomes of a service teaching module on odes for physics students. Int. J. Math. Educ. Sci. Technol. 2018, 49, 743–758. [Google Scholar] [CrossRef]
- Ju, M.-K.; Kwon, O.N. Ways of talking and ways of positioning: Students’ beliefs in an inquiry-oriented differential equations class. J. Math. Behav. 2007, 26, 267–280. [Google Scholar] [CrossRef]
- Kamps, H.J.L.; Van Lint, J.H. A comparison of a classical calculus test with a similar multiple choice test. Educ. Stud. Math. 1975, 6, 259–271. [Google Scholar] [CrossRef][Green Version]
- Karakok, G. Making connections among representations of eigenvector: What sort of a beast is it? ZDM Math. Educ. 2019, 51, 1141–1152. [Google Scholar] [CrossRef]
- KarimiFardinpour, Y.; Gooya, Z. Comparing three methods of geometrical approach in visualizing differential equations. Int. J. Res. Undergrad. Math. 2018, 4, 286–304. [Google Scholar] [CrossRef]
- Kaw, A.K.; Yalcin, A. Problem-centered approach in a numerical methods course. J. Prof. Issues Eng. Pract. 2008, 134, 359–364. [Google Scholar] [CrossRef]
- Keene, K.A. A characterization of dynamic reasoning: Reasoning with time as parameter. J. Math. Behav. 2007, 26, 230–246. [Google Scholar] [CrossRef]
- Keene, K.A.; Rasmussen, C.; Stephan, M. Gestures and a chain of signification: The case of equilibrium solutions. Math. Educ. Res. J. 2012, 24, 347–369. [Google Scholar] [CrossRef]
- Klymchuk, S.; Zverkova, T.; Gruenwald, N.; Sauerbier, G. Increasing engineering students’ awareness to environment through innovative teaching of mathematical modelling. Teach. Math. Its Appl. 2008, 27, 123–130. [Google Scholar] [CrossRef]
- Kwon, O.N.; Rasmussen, C.; Allen, K. Students’ retention of mathematical knowledge and skills in differential equations. Sch. Sci. Math. 2005, 105, 227–239. [Google Scholar] [CrossRef]
- Latulippe, C.; Latulippe, J. Student perceptions of writing projects in a university differential-equations course. Int. J. Math. Educ. Sci. Technol. 2013, 45, 1–11. [Google Scholar] [CrossRef]
- Laudares, B.J.; de Miranda, D.F. Investigando a iniciação à modelagem matemática nas ciências com equações diferenciais. Educ. Matemática Pesqui. 2007, 9, 103–120. [Google Scholar]
- Lee, W.-P.; Lu, M.-S. A digital simulation of the vibration of a two-mass two-spring system. Comput. Appl. Eng. Educ. 2010, 18, 563–573. [Google Scholar] [CrossRef]
- Lewis, M.; Powell, J.A. Modeling zombie outbreaks: A problem-based approach to improving mathematics one brain at a time. PRIMUS Probl. Resour. Issues Math. Stud. 2016, 26, 705–726. [Google Scholar] [CrossRef]
- Liberatti, S.; da Silva, D. Mathematical modeling and analysis of mathematical models in mathematics education. Acta Sci. 2012, 14, 260–275. [Google Scholar]
- Maat, S.M.; Zakaria, E. Exploring students’ understanding of ordinary differential equations using computer algebraic system (cas). Turk. Online J. Educ. Technol. 2011, 10, 123–128. [Google Scholar]
- Mallet, D.G.; McCue, S.W. Constructive development of the solutions of linear equations in introductory ordinary differential equations. Int. J. Math. Educ. Sci. Technol. 2009, 40, 587–595. [Google Scholar] [CrossRef]
- Marrongelle, K. The function of graphs and gestures in algorithmatization. J. Math. Behav. 2007, 26, 211–229. [Google Scholar] [CrossRef]
- Melendez, B.; Bowman, S.; Erickson, K.; Swim, E. An integrative learning experience within a mathematics curriculum. Teach. Math. Its Appl. 2009, 28, 131–144. [Google Scholar] [CrossRef]
- Miller, H.R.; Upton, D.S. Computer manipulatives in an ordinary differential equations course: Development, implementation, and assessment. J. Sci. Educ. Technol. 2008, 17, 124–137. [Google Scholar] [CrossRef][Green Version]
- Molina-Mora, J.A. Mathematical modeling as a didactic strategy for calculus teaching. Uniciencia 2017, 31, 19–36. [Google Scholar] [CrossRef][Green Version]
- Molina-Mora, J.-A. ICT-projects-modeling based experience for teaching of systems of differential equations. Uniciencia 2015, 29, 46–61. [Google Scholar]
- Nachtigalova, I.; Finkeova, J.; Krbcova, Z.; Souskova, H. A spreadsheet-based tool for education of chemical process simulation and control fundamentals. Comput. Appl. Eng. Educ. 2020, 28, 923–937. [Google Scholar] [CrossRef]
- Padmanabhan, S.; Solin, P. Enhancing student learning of differential equations through technology. Int. J. Technol. Math. Educ. 2017, 24, 207–216. [Google Scholar]
- Pino-Fan, L.R.; Font, V.; Gordillo, W.; Larios, V.; Breda, A. Analysis of the meanings of the antiderivative used by students of the first engineering courses. Int. J. Sci. Math. Educ. 2018, 16, 1091–1113. [Google Scholar] [CrossRef]
- Quinn, D.; Aarão, J. Blended learning in first year engineering mathematics. ZDM Math. Educ. 2020, 52, 927–941. [Google Scholar] [CrossRef]
- Rasmussen, C.; Stephan, M.; Allen, K. Classroom mathematical practices and gesturing. J. Math. Behav. 2004, 23, 301–323. [Google Scholar] [CrossRef]
- Rasmussen, C.; Zandieh, M.; King, K.; Tepo, A. Advancing mathematical activity: A practice-oriented view of advanced mathematical thinking. Math. Think. Learn. 2005, 7, 51–73. [Google Scholar] [CrossRef]
- Rasmussen, C.; Marrongelle, K. Pedagogical content tools: Integrating student reasoning and mathematics in instruction. J. Res. Math. Educ. 2006, 37, 388–420. [Google Scholar]
- Rasmussen, C.; Blumenfeld, H. Reinventing solutions to systems of linear differential equations: A case of emergent models involving analytic expressions. J. Math. Behav. 2007, 26, 195–210. [Google Scholar] [CrossRef]
- Rasmussen, C.; Kwon, O.N. An inquiry-oriented approach to undergraduate mathematics. J. Math. Behav. 2007, 26, 189–194. [Google Scholar] [CrossRef]
- Raychaudhuri, D. A layer framework to investigate student understanding and application of the existence and uniqueness theorems of differential equations. Int. J. Math. Educ. Sci. Technol. 2007, 38, 367–381. [Google Scholar] [CrossRef]
- Raychaudhuri, D. Dynamics of a definition: A framework to analyse student construction of the concept of solution to a differential equation. Int. J. Math. Educ. Sci. Technol. 2008, 39, 161–177. [Google Scholar] [CrossRef]
- Raychaudhuri, D. Adaptation and extension of the framework of reducing abstraction in the case of differential equations. Int. J. Math. Educ. Sci. Technol. 2013, 45, 35–57. [Google Scholar] [CrossRef]
- Raychaudhuri, D. A framework to categorize students as learners based on their cognitive practices while learning differential equations and related concepts. Int. J. Math. Educ. Sci. Technol. 2013, 44, 139–1256. [Google Scholar] [CrossRef]
- Ribaric, S.; Kordas, M. Teaching cardiovascular physiology with equivalent electronic circuits in a practically oriented teaching module. Adv. Physiol. Educ. 2011, 35, 149–160. [Google Scholar] [CrossRef]
- Robinson, G.; Jovanoski, Z. Fighter pilot ejection study as an educational tool. Teach. Math. Its Appl. 2010, 29, 176–192. [Google Scholar] [CrossRef]
- Rooch, A.; Junker, P.; Härterich, J.; Hackl, K. Linking mathematics with engineering applications at an early stage - implementation, experimental set-up and evaluation of a pilot project. Eur. J. Eng. Educ. 2016, 41, 172–191. [Google Scholar] [CrossRef]
- Rowland, D.R. Student difficulties with units in differential equations in modelling contexts. Int. J. Math. Educ. Sci. Technol. 2006, 37, 553–558. [Google Scholar] [CrossRef]
- Rowland, D.R.; Jovanoski, Z. Student interpretations of the terms in first-order ordinary differential equations in modelling contexts. Int. J. Math. Educ. Sci. Technol. 2004, 35, 503–516. [Google Scholar] [CrossRef]
- Ruiz, L.; Gallardo, P.C.; Del Rivero, S. Deficient prerequisites with mathematical software in new concepts: Laplace transform. Rev. Mex. Investig. Educ. 2016, 21, 349–383. [Google Scholar]
- Sabag, N. The effect of integrating lab experiments in electronic circuits into mathematic studies—A case study. Res. Sci. Technol. Educ. 2017, 35, 427–444. [Google Scholar] [CrossRef]
- Sawaki, R.V.; Tannous, K.; Filho, J.B.F. Development of an educational tool aimed at designing ideal chemical reactors. Comput. Appl. Eng. Educ. 2020, 28, 459–476. [Google Scholar] [CrossRef]
- Slavit, D.; LoFaro, T.; Cooper, K. Understandings of solutions to differential equations through contexts, web-based simulations, and student discussion. Sch. Sci. Math. 2002, 102, 380–390. [Google Scholar] [CrossRef]
- Speer, N.M.; Wagner, J.F. Knowledge needed by a teacher to provide analytic scaffolding during undergraduate mathematics classroom discussions. J. Res. Math. Educ. 2009, 40, 530–562. [Google Scholar] [CrossRef]
- Stephan, M.; Rasmussen, C. Classroom mathematical practices in differential equations. J. Math. Behav. 2002, 21, 459–490. [Google Scholar] [CrossRef]
- Tisdell, C.C. On mnemonic instruction and the shields acronym in the pedagogy of first-order differential equations. Teach. Math. Its Appl. 2019, 38, 74–84. [Google Scholar] [CrossRef]
- Trigueros, M. Vínculo entre la modelación y el uso de representaciones en la comprensión de los conceptos de ecuación diferencial de primer orden y de solución. Educ. Matemática 2014, 25, 207–226. [Google Scholar]
- Vega-Calderon, F.; Gallegos-Cazares, L.; Flores-Camachoc, F. Conceptual difficulties in understanding the bernoulli’s equation. Rev. Eureka Sobre Ensenanza Divulg. Las Ciencias 2017, 14, 339–352. [Google Scholar]
- Villar, M.T.; Llinares, S. Análisis de errores en la conceptualizacion y simbolizacion de ecuaciones diferenciales en alumnos de química. Educ. Matemática 1996, 8, 90–101. [Google Scholar]
- Vinner, S. A different test and different result analysis— An example from a calculus exam. J. Für-Math. Didakt. 1994, 15, 311–326. [Google Scholar] [CrossRef]
- Wittmann, M.C.; Black, K.E. Mathematical actions as procedural resources: An example from the separation of variables. Phys. Rev. Spec. Top. Phys. Educ. Res. 2015, 11, 1–13. [Google Scholar] [CrossRef]
- Wittmann, M.C.; Flood, V.J.; Black, K.E. Algebraic manipulation as motion within a landscape. Educ. Stud. Math. 2013, 82, 169–181. [Google Scholar] [CrossRef]
- Yackel, E.; Rasmussen, C.; King, K. Social and sociomathematical norms in an—Advanced undergraduate mathematics course. J. Math. Behav. 2000, 19, 275–287. [Google Scholar] [CrossRef]
- Zang, C.M.; Fernández, G.A.; León, M.N. Reflexiones sobre la implementación de problemas de modelado para la construcción y resignificación de objetos matemáticos vinculados a las ecuaciones diferenciales. UNION Rev. Iberoam. Educ. Matemática 2015, 42, 150–165. [Google Scholar]
- Zhu, N. Embedding active learning and design-based projects in a noise and vibration course for the undergraduate mechanical engineering program. Int. J. Mech. Eng. Educ. 2020. [Google Scholar] [CrossRef]
- Czocher, J.A.; Tague, J.; Baker, G. Where does the calculus go? An investigation of how calculus ideas are used in later coursework. Int. J. Math. Sci. Technol. 2013, 44, 673–684. [Google Scholar] [CrossRef]
- Artigue, M.; Gautheron, V. Systemes Differentiels: Etude Graphique; Cedic: Paris, France, 1983. [Google Scholar]
- Artigue, M. Une recherche d’ ingenierie didactique sur l’enseignement des equations differentielles en primer cycle universitarie. Irem Univ. Paris 1989, 107, 284–309. [Google Scholar]
- Hernandez, A. Obstáculos en la Articulacion de los Marcos Numérico, Gráfico y Algebraíco en Relación con las Ecuaciones Diferenciales. Ph.D. Thesis, Cinvestav, Mexico City, Mexico, 1995. [Google Scholar]
- Blanchard, P. Teaching differential equations with a dynamical systems viewpoint. Coll. Math. J. 1994, 25, 385–393. [Google Scholar] [CrossRef]
- CMBS. 2016. Available online: http://www.cbmsweb.org/archive/Statements/Active_Learning_Statement.pdf (accessed on 1 September 2020).
- Barrows, H.S. A Taxonomy of problem-based learning methods. Med. Educ. 1986, 20, 481–486. [Google Scholar] [CrossRef]
- Leung, F.; Stillman, G.; Kaiser, G.; Won, K. (Eds.) Mathematical modelling education in east and west. In International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2021. [Google Scholar]
- Stillman, G.; Blum, W.; Kaiser, G. (Eds.) Mathematical Modelling and Applications. In ICTMA 17, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer: Dordrecht, The Netherlands, 2017. [Google Scholar]
- Galbraigth, P. Models of Modelling: Genres, Purposes or Perspectives. J. Math. Model. Appl. 2012, 1, 3–16. [Google Scholar]
- Borromeo, R. Theoretical and empirical differentiations of phases in the modelling process. ZDM Math. Educ. 2006, 38, 86–95. [Google Scholar]
- Zbiek, R.M.; Conner, A. Beyond motivation: Exploring mathematical modeling as a context for deepening students’ understandings of curricular mathematics. Educ. Stud. Math. 2006, 63, 89–112. [Google Scholar] [CrossRef]
- Hoyles, C. Transforming the mathematical practices of learners and teachers through digital technology. Res. Math. Educ. 2018, 20, 209–228. [Google Scholar] [CrossRef]
- Artigue, M. Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. Int. J. Comput. Math. Learn. 2002, 7, 245–274. [Google Scholar] [CrossRef]
- Cohen, M.S.; Gaughan, E.D.; Knoebel, A.; Kurtz, D.S.; Penegelley, D.J. Student Research Projects in Calculus; Mathematical Association of America: Washington, DC, USA, 1991. [Google Scholar]
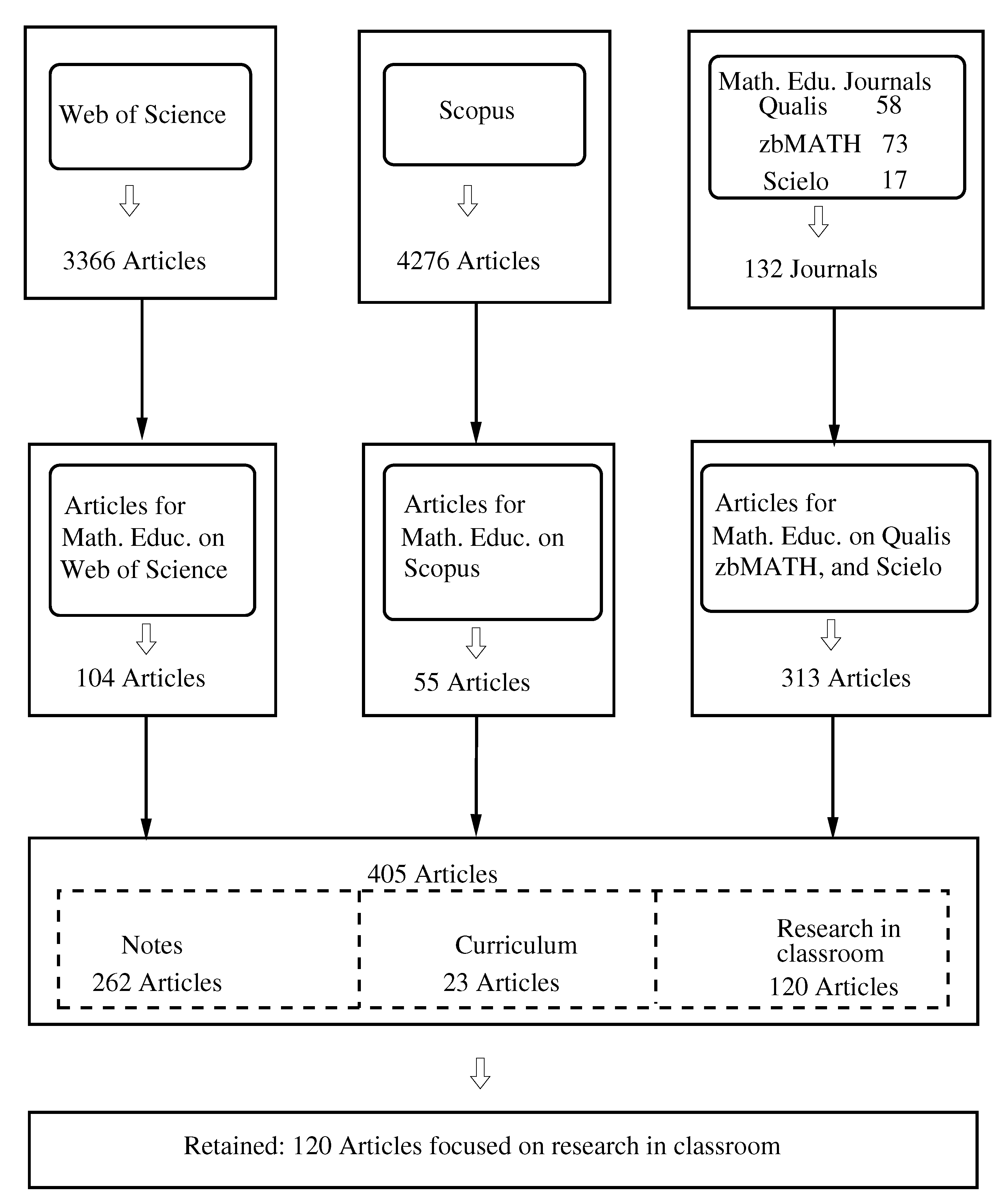

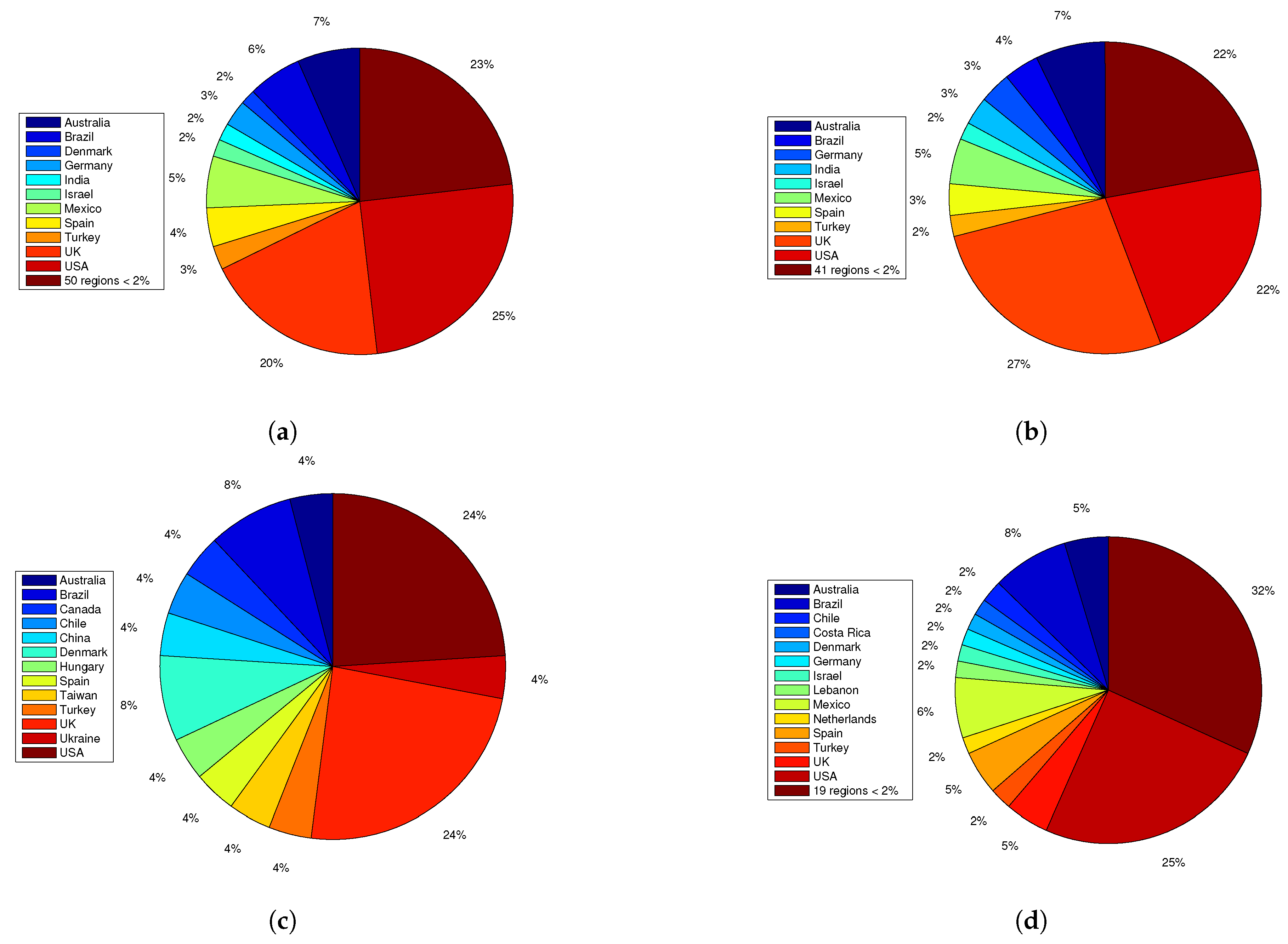

| Classification Qualis | A1 | A2 | B1 | B2 | B3 | B4 | B5 | C | Total |
|---|---|---|---|---|---|---|---|---|---|
| J. of Math./Prob. | 120 | 145 | 260 | 229 | 170 | 135 | 179 | 196 | 1434 |
| J. Math. Educ. | 15 | 15 | 9 | 1 | 8 | 4 | 3 | 3 | 58 |
| Classification for zbMATH [46] | A | B | C | Total | |||||
| Serie A: Didact. of Math. | 3 | 14 | 16 | 33 | |||||
| Serie B: Related Areas | 27 | 4 | 9 | 40 |
| Rank | Journal | Record Count | % of 120 |
|---|---|---|---|
| 1 | Teaching mathematics and its applications | 16 | 13.33% |
| International journal of mathematical education in science and technology | 16 | 13.33% | |
| 2 | The journal of mathematical behavior | 13 | 10.83% |
| 3 | ZDM–Mathematics Education | 6 | 5.00% |
| 4 | Computer applications in engineering education | 3 | 2.50% |
| Educação matemática pesquisa | 3 | 2.50% | |
| Educación matemática | 3 | 2.50% | |
| Enseñanza de las ciencias: revista de investigación y experiencias didácticas | 3 | 2.50% | |
| European journal of engineering education | 3 | 2.50% | |
| International electronic journal of mathematics education | 3 | 2.50% | |
| International journal of science and mathematics education | 3 | 2.50% | |
| PRIMUS: problems, resources, and issues in mathematics undergraduate studies | 3 | 2.50% | |
| Revista latinoamericana de investigación en matemática educativa | 3 | 2.50% |
| Rank | Journal | H Index | SJR 2019 | Quartil | Subject Area and Category |
|---|---|---|---|---|---|
| 1 | American journal of physics | 88 | 0.51 | Q2 | Physics and astronomy (miscellaneous) |
| 2 | Journal of chemical education | 77 | 0.47 | Q2 | Physics and astronomy (miscellaneous) |
| 3 | Journal for research in mathematics education | 74 | 2.92 | Q1 | Education |
| 4 | Educational studies in mathematics | 60 | 1.57 | Q1 | Education |
| 5 | Journal of science education and technology | 56 | 1.17 | Q1 | Education |
| 6 | Advances in physiology education | 55 | 0.52 | Q2 | Education |
| 7 | International journal of engineering education | 47 | 0.45 | Q1 | Engineering (miscellaneous) |
| 8 | European journal of engineering education, | 41 | 0.7 | Q1 | Engineering (miscellaneous) |
| Physical review special topics-physics education research | 41 | – | – | – | |
| 9 | Journal of professional issues in engineering education and practice | 37 | 0.45 | Q2 | Civil and structural engineering |
| 10 | ZDM–Mathematics Education | 36 | 1.08 | Q1 | Education |
| 11 | International journal of science and mathematics education | 35 | 0.9 | Q1 | Education |
| Journal of mathematics teacher education | 35 | 1.96 | Q1 | Education |
| Author | Institution | Number of Articles |
|---|---|---|
| Chris Rasmussen | San Diego State University, USA | 13 |
| Matías Camacho-Machín | University of La Laguna, Spain | 4 |
| Samer Habre | Lebanese American University, Lebanon | 4 |
| Debasree Raychaudhuri | California State University, USA | 4 |
| Lourdes Maria Werle de Almeida | State University of Londrina, Brazil | 3 |
| Carolina Guerrero-Ortiz | Potificia Universidad Católica de Valparaiso, Chile | 3 |
| Karen Allen Keene | North Carolina State University, USA | 3 |
| Karen King | Michigan State University, USA | 3 |
| Oh Nam Kwon | Seoul National University, South Korea | 3 |
| José Arturo Molina-Mora | Universidad de Costa Rica, Costa Rica | 3 |
| Article Title and Reference | Number of Cites |
|---|---|
| New directions in differential equations: a framework for interpreting students’ understandings and difficulties [15]. | 196 |
| Advancing mathematical activity: a practice-oriented view of advanced mathematical thinking [15]. | 187 |
| An inquiry-oriented approach to undergraduate mathematics [109]. | 186 |
| Classroom mathematical practices in differential equations [125]. | 184 |
| Teaching mathematical modeling through project work [53]. | 174 |
| Knowledge needed by a teacher to provide analytic scaffolding during undergraduate mathematics classroom discussions [124]. | 171 |
| Social and sociomathematical norms in an advanced undergraduate mathematics course [133]. | 160 |
| Students’ retention of mathematical knowledge and skills in differential equations [89]. | 136 |
| Locating starting points in differential equations: a realistic mathematics education approach [16]. | 135 |
| Classroom mathematical practices and gesturing [106]. | 106 |
| Ref. | Didactic Methodology | Topics Taught or Evaluated |
|---|---|---|
| [1] | Traditional methodology | Scalar: first order, second order, orthogonal curves, existence and uniqueness theorem |
| [2] | Traditional methodology | Scalar: first order, second order, orthogonal curves, existence, and uniqueness theorem |
| [3] | Geometric and qualitative solutions, Active learning, Information and communication technology | Scalar: first order, applications to exponential decay problems |
| [4] | Geometric and qualitative solutions, Mathematical modeling, Information and communication technology | Scalar: Malthus model, logistic generalized |
| [5] | Mathematical modeling | Scalar: second order and applications to electronic circuits |
| [6] | Active learning | Scalar and systems: Laplace Transform |
| [7] | Active learning | |
| [8] | Mathematical modeling | Scalar: first order, applications to mixing problems, freefall problems |
| [9] | Mathematical modeling | Scalar: first order, applications to mixing problems, second order |
| [10] | Information and communication technology | Systems: Lotka–Volterra model |
| [11] | Information and communication technology | Systems: plane phase, linear system, qualitative behavior |
| [12] | Information and communication technology | Scalar: first order, slope fields, asymptotic behavior |
| [13] | Mathematical modeling, Information and communication technology | Scalar: first order, logistic generalized |
| [14] | Geometric and qualitative solutions, Active learning | Scalar: rate of change |
| [15] | Active learning | Scalar and systems: several topics |
| [16] | Active learning | Scalar and systems: several topics |
| [17] | Mathematical modeling | Scalar: first order, applications to electronic circuits |
| [18] | Information and communication technology | Scalar: first order, applications to electronic circuits |
| [19] | Information and communication technology | Scalar: first order, second order, graphical solution, Laplace transform |
| [20] | Mathematical modeling | Scalar: Malthus model, Verhulst model, equilibrium analysis. |
| [21] | Others | |
| [22] | Geometric and qualitative solutions Mathematical modeling | Systems: applications for asthma |
| [23] | Active learning | Scalar: first order |
| [27] | Information and communication technology | Systems: applications for Chemical reactions |
| [28] | Information and communication technology | Scalar: first order, second order, graphical solution, Laplace transform |
| [29] | Information and communication technology | Scalar: first order, freefall problems |
| [30] | Project-based learning | |
| [31] | Projects-based learning | Scalar: first order, applications to tumor growth, Gompertz model, graphical solutions, bifurcation |
| [32] | Information and communication technology | Scalar and systems: several topics |
| [33] | Information and communication technology | Scalar and systems: first order, Laplace transform, application to chemical reaction and control |
| [34] | Information and communication technology | Scalar and systems: several topics |
| [39] | Traditional methodology, Geometric and qualitative solutions | Scalar: first order, applications to exponential decay problems |
| [48] | Mathematical modeling | Scalar: Newton’s law of cooling and laws for velocity, acceleration and volume |
| [49] | Information and communication technology | Scalar: Verhulst model, generalized logistic. |
| [50] | Active learning | Scalar: first order, linear, Bernoulli |
| [51] | Active learning | Scalar: first order, applications to exponential decay problems |
| [52] | Projects-based learning | |
| [53] | Projects-based learning | Scalar and systems: populations model, linear system |
| [54] | Mathematical modeling | Scalar: first order, applications to mixing problems |
| [55] | Active learning | |
| [56] | Geometric and qualitative solutions | Scalar: first order |
| [57] | Traditional methodology | Scalar: linear higher order |
| [58] | Mathematical modeling | Systems: equilibrium |
| [59] | Traditional methodology | Scalar: first order |
| [60] | Information and communication technology | Scalar: applications to electronic circuits |
| [61] | Others | Scalar: First order |
| [62] | Others | |
| [63] | Mathematical modeling | Scalar: Malthus model |
| [64] | Traditional methodology, Geometric and qualitative solutions | Scalar: first order, second order, graphical solution, slopy fields |
| [65] | Mathematical modeling | |
| [66] | Active learning | Scalar: first order, second order, several applications (biomedical, scientific, and social-economic contexts) |
| [67] | Active learning | Scalar: First order, Verhulst equation |
| [68] | Mathematical modeling | Scalar and systems: linear, exponential, logistic, and ecology applications |
| [69] | Geometric and qualitative solutions | Scalar: first order |
| [70] | Geometric and qualitative solutions | Scalar: first order |
| [71] | Geometric and qualitative solutions, Active learning | Scalar and systems: first order, autonomous differential equations, slope fields, Lotka–Volterra models |
| [72] | Geometric and qualitative solutions | Scalar and systems: graphical solutions |
| [73] | Active learning, Information and communication technology | Scalar: first order, applications to mixing problems |
| [74] | Information and communication technology | Systems: first order, validation with real data |
| [75] | Information and communication technology | Scalar: first order |
| [76] | Traditional methodology | Scalar: first order, applications to kinetics |
| [77] | Others | Scalar: Laplace transform |
| [78] | Mathematical modeling | Systems: first order |
| [79] | Active learning | Scalar: first order, second order, slope fields, several applications |
| [80] | Traditional methodology | Scalar: first order |
| [81] | Active learning | |
| [82] | Traditional methodology | Scalar: first order, higher order |
| [83] | Others | |
| [84] | Geometric and qualitative solutions, Active learning | Scalar: first order, autonomous differential equations, slope fields |
| [85] | Active learning | Scalar: first order, Newton’s law of cooling |
| [86] | Active learning | Systems: first order, linear, slope fields, Lotka–Volterra models |
| [87] | Active learning | Scalar: first order, autonomous differential equations, slope fields |
| [88] | Mathematical modeling | Systems: Lotka–Volterra model, phase plane, equilibrium solutions, phase trajectories |
| [89] | Active learning | Scalar and systems: first order, second order, slope field, linear system |
| [90] | Projects-based learning | |
| [91] | Mathematical modeling | Scalar: first, order, Malthus model, Newton’s law of cooling |
| [92] | Information and communication technology | Systems: second order, applications to vibration of a two-mass two-spring problems |
| [93] | Active learning | Scalar: first order, zombies models |
| [94] | Mathematical modeling, Information and communication technology | Scalar and systems: first order, freefall problems, generalized Lotka–Volterra |
| [95] | Active learning, Information and communication technology | Scalar: second order |
| [96] | Active learning | Scalar: first order, second order |
| [97] | Geometric and qualitative solutions | Scalar and systems: first order, Lotka–Volterra model, Euler methods |
| [98] | Mathematical modeling | Scalar: first, order, Malthus model, AIDS models |
| [99] | Information and communication technology | Scalar and systems: amplitude and phase in second order equations, linear phase portraits in linear system, Fourier coefficients, vibrations applications |
| [100] | Mathematical modeling, Information and communication technology | Laplace Transform, Newton’s law of cooling |
| [101] | Information and communication technology, Projects-based learning | Systems: Lotka–Volterra model, pancreatitis model |
| [102] | Information and communication technology | Scalar: first order, applications to energy balance, chemical process and control fundamentals |
| [103] | Information and communication technology | Systems: applications to epidemics |
| [104] | Others | Scalar: first order |
| [105] | Others | Scalar: firs order |
| [106] | Active learning | |
| [107] | Active learning | Scalar and systems: Verhulst equation, bifurcation |
| [108] | Active learning | |
| [109] | Active learning | Scalar and systems: first order, slope fields, second order with spring-mass applications, linear systems, straight-line solutions, Lotka–Volterra models |
| [110] | Geometric and qualitative solutions, Active learning | |
| [111] | Active learning | Scalar: existence and uniqueness theorem of first order |
| [112] | Active learning | Scalar: concept of solution of first order equation |
| [113] | Active learning | Scalar: first order |
| [114] | Active learning | Scalar and systems: several topics |
| [115] | Mathematical modeling, Information and communication technology | Systems: applications to electronic circuits |
| [116] | Mathematical modeling | Scalar: second order, applications of Newton’s second law |
| [117] | Others | Scalar and systems: second order, applications of Newton’s second law |
| [119] | Mathematical modeling | Scalar: first order |
| [118] | Mathematical modeling | Scalar: first order |
| [120] | Information and communication technology | Scalar: first order, Laplace transform |
| [121] | Active learning | Scalar: first order, applications to electronic circuits |
| [122] | Information and communication technology | Scalar: first order, applications to molar and energy balances |
| [123] | Traditional methodology, Information and communication technology | Scalar: definition of differential equations, graphical solution, applications. |
| [124] | Active learning | Scalar: first order, Malthus model |
| [125] | Active learning | Scalar: first order |
| [126] | Traditional methodology | Scalar: first order |
| [127] | Mathematical modeling | Scalar: first order |
| [128] | Mathematical modeling | Scalar: first order, Bernoulli’s equation |
| [129] | Traditional methodology | Several topics |
| [130] | Mathematical modeling | Scalar: first order, population mathematical model |
| [131] | Traditional methodology | Scalar: first order, freefall problems |
| [132] | Active learning | Scalar: first order |
| [133] | Active learning | Scalar: first order |
| [134] | Mathematical modeling | Scalar and systems: first order, applications to exponential decay problems, Lotka–Volterra model |
| [135] | Projects-based learning | Several topics of noise and vibrations concepts |
| Class | Properties of Functions f, M or N |
|---|---|
| Separable | with h and g real functions |
| Homogeneous | for all and |
| Exact | |
| Linear | with p and q real functions |
| Bernoulli | with real functions and |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lozada, E.; Guerrero-Ortiz, C.; Coronel, A.; Medina, R. Classroom Methodologies for Teaching and Learning Ordinary Differential Equations: A Systemic Literature Review and Bibliometric Analysis. Mathematics 2021, 9, 745. https://doi.org/10.3390/math9070745
Lozada E, Guerrero-Ortiz C, Coronel A, Medina R. Classroom Methodologies for Teaching and Learning Ordinary Differential Equations: A Systemic Literature Review and Bibliometric Analysis. Mathematics. 2021; 9(7):745. https://doi.org/10.3390/math9070745
Chicago/Turabian StyleLozada, Esperanza, Carolina Guerrero-Ortiz, Aníbal Coronel, and Rigoberto Medina. 2021. "Classroom Methodologies for Teaching and Learning Ordinary Differential Equations: A Systemic Literature Review and Bibliometric Analysis" Mathematics 9, no. 7: 745. https://doi.org/10.3390/math9070745
APA StyleLozada, E., Guerrero-Ortiz, C., Coronel, A., & Medina, R. (2021). Classroom Methodologies for Teaching and Learning Ordinary Differential Equations: A Systemic Literature Review and Bibliometric Analysis. Mathematics, 9(7), 745. https://doi.org/10.3390/math9070745








