Robust Fractional-Order Control Using a Decoupled Pitch and Roll Actuation Strategy for the I-Support Soft Robot
Abstract
1. Introduction
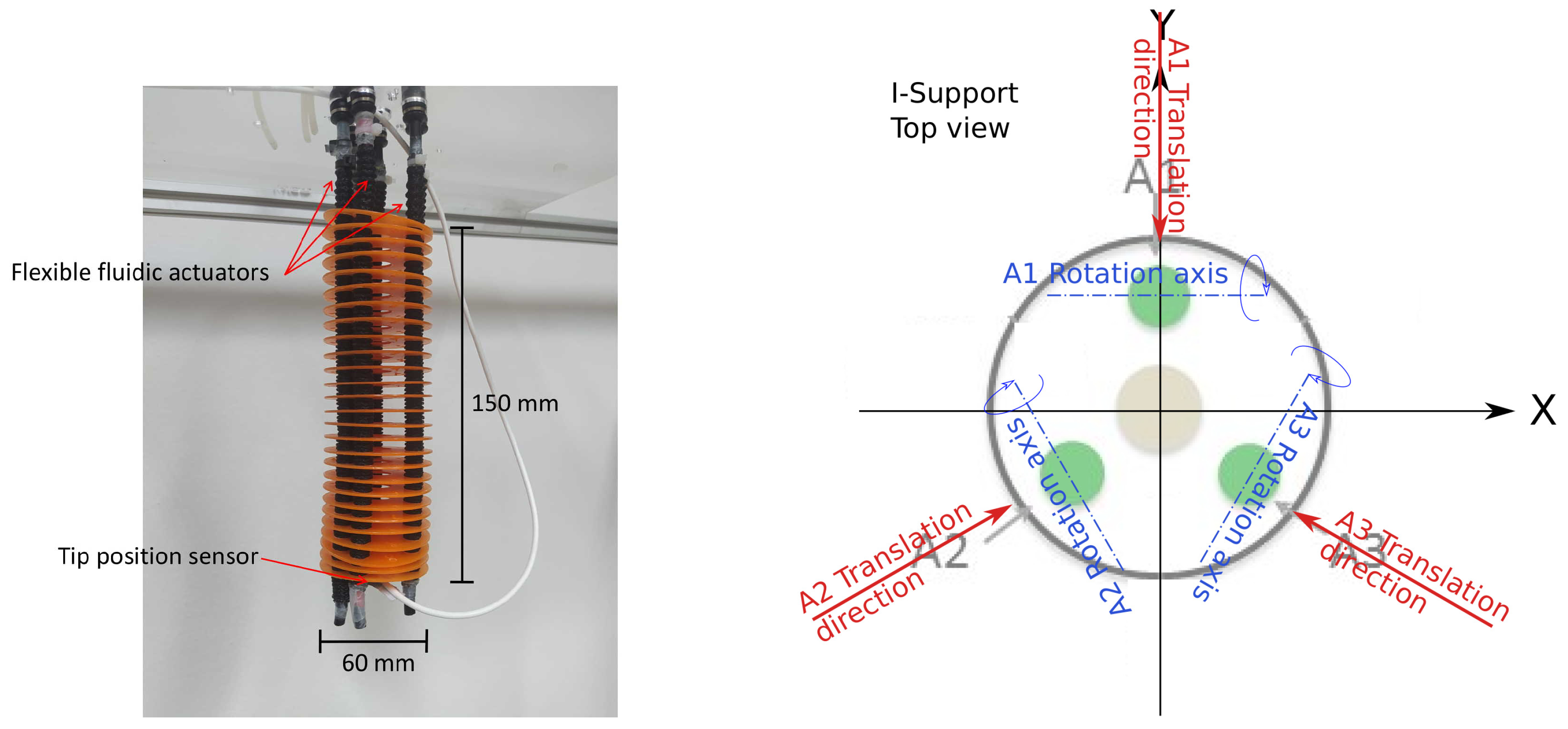
2. Materials and Methods
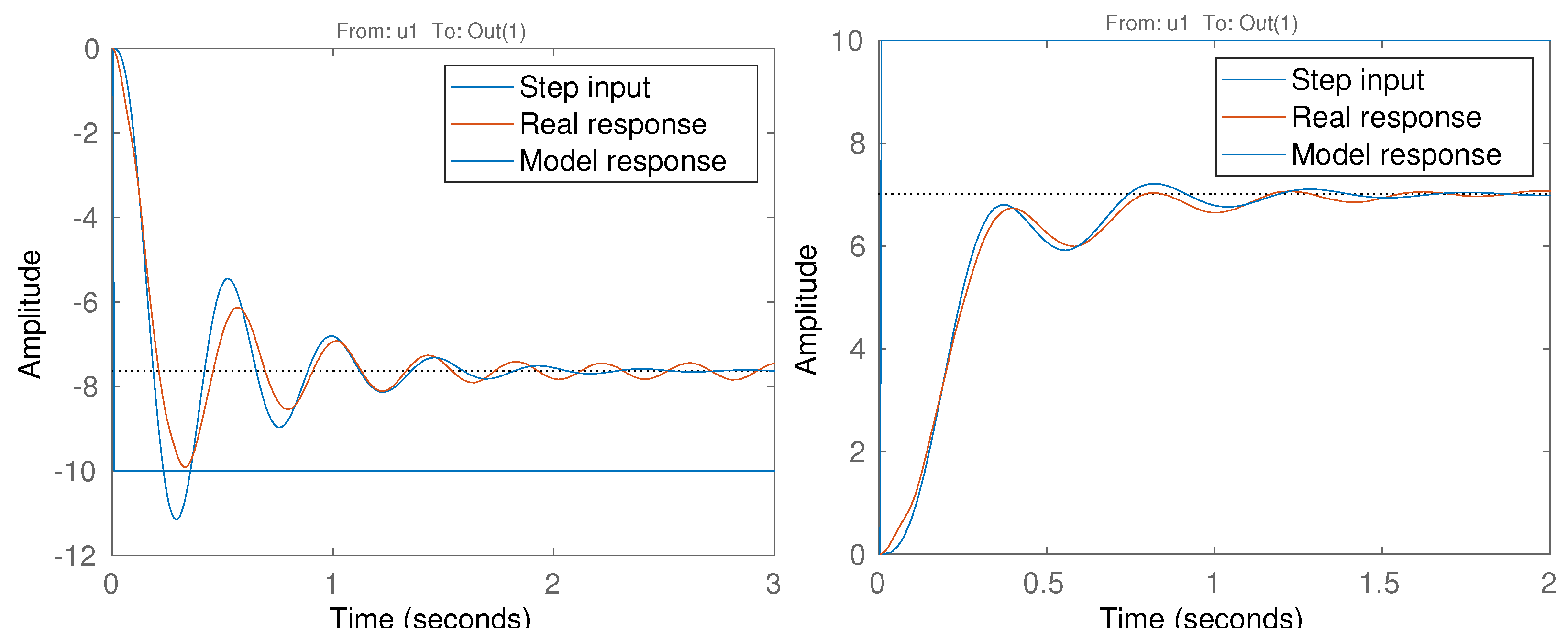
2.1. Plant Model
2.2. Control Strategy
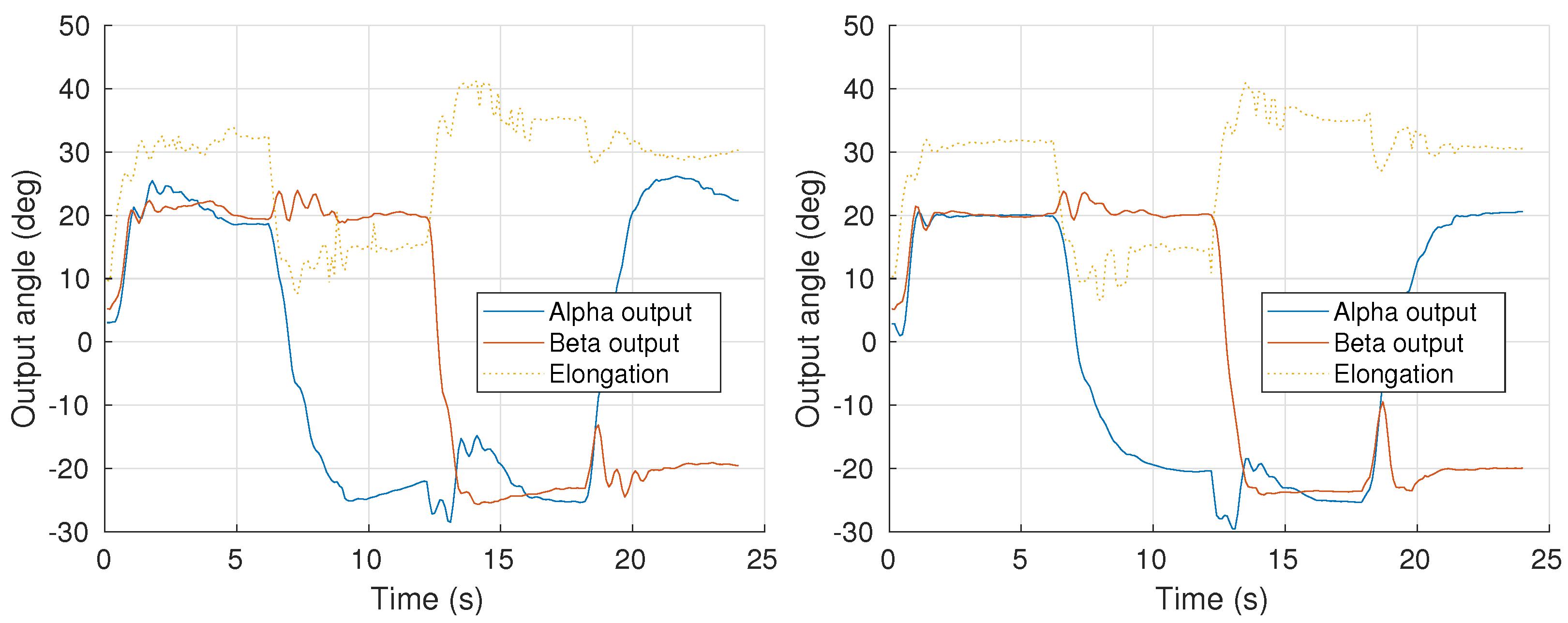
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PID | Proportional integral derivative |
| FOPID | Fractional order proportional integral derivative |
| FOPI | Fractional order proportional integral |
References
- Kim, S.; Laschi, C.; Trimmer, B. Soft robotics: A bioinspired evolution in robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef]
- Laschi, C.; Cianchetti, M.; Mazzolai, B.; Margheri, L.; Follador, M.; Dario, P. Soft Robot Arm Inspired by the Octopus. Adv. Robot. 2012, 26, 709–727. [Google Scholar] [CrossRef]
- George Thuruthel, T.; Ansari, Y.; Falotico, E.; Laschi, C. Control strategies for soft robotic manipulators: A survey. Soft Robot. 2018, 5, 149–163. [Google Scholar] [CrossRef] [PubMed]
- Renda, F.; Giorelli, M.; Calisti, M.; Cianchetti, M.; Laschi, C. Dynamic model of a multibending soft robot arm driven by cables. IEEE Trans. Robot. 2014, 30, 1109–1122. [Google Scholar] [CrossRef]
- Jones, B.A.; Walker, I.D. Kinematics for multisection continuum robots. IEEE Trans. Robot. 2006, 22, 43–55. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Falotico, E.; Renda, F.; Laschi, C. Model-based reinforcement learning for closed-loop dynamic control of soft robotic manipulators. IEEE Trans. Robot. 2018, 35, 124–134. [Google Scholar] [CrossRef]
- Ansari, Y.; Falotico, E.; Mollard, Y.; Busch, B.; Cianchetti, M.; Laschi, C. A Multiagent Reinforcement Learning approach for inverse kinematics of high dimensional manipulators with precision positioning. In Proceedings of the IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics, Singapore, 26–29 June 2016; pp. 457–463. [Google Scholar]
- Thuruthel, T.G.; Falotico, E.; Manti, M.; Laschi, C. Stable Open Loop Control of Soft Robotic Manipulators. IEEE Robot. Autom. Lett. 2018, 3, 1292–1298. [Google Scholar] [CrossRef]
- Piqué, F.; Kalidindi, H.T.; Menciassi, A.; Laschi, C.; Falotico, E. A Learning-based Approach for Adaptive Closed-loop Control of a Soft Robotic Arm. In Proceedings of the I-RIM 3D Conference, online, 10–12 December 2020. [Google Scholar]
- Della Santina, C.; Bianchi, M.; Grioli, G.; Angelini, F.; Catalano, M.; Garabini, M.; Bicchi, A. Controlling Soft Robots: Balancing Feedback and Feedforward Elements. IEEE Robot. Autom. Mag. 2017, 24, 75–83. [Google Scholar] [CrossRef]
- Yip, M.C.; Camarillo, D.B. Model-Less Feedback Control of Continuum Manipulators in Constrained Environments. IEEE Trans. Robot. 2014, 30, 880–889. [Google Scholar] [CrossRef]
- Kapadia, A.; Walker, I.D. Task-space control of extensible continuum manipulators. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1087–1092. [Google Scholar] [CrossRef]
- Deutschmann, B.; Ott, C.; Monje, C.A.; Balaguer, C. Robust Motion Control of a Soft Robotic System Using Fractional Order Control. In Advances in Service and Industrial Robotics; Ferraresi, C., Quaglia, G., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 147–155. [Google Scholar] [CrossRef]
- Chang, X.H.; Xiong, J.; Park, J.H. Fuzzy robust dynamic output feedback control of nonlinear systems with linear fractional parametric uncertainties. Appl. Math. Comput. 2016, 291, 213–225. [Google Scholar] [CrossRef]
- Barambones, O.; Gonzalez de Durana, J.; De la Sen, M. Robust speed control for a variable speed wind turbine. Int. J. Innov. Comput. Inf. Control IJICIC 2010, 8, 7627–7640. [Google Scholar]
- Iqbal, J.; Ullah, M.; Khan, S.G.; Khelifa, B.; Ćuković, S. Nonlinear control systems-A brief overview of historical and recent advances. Nonlinear Eng. 2017, 6, 301–312. [Google Scholar] [CrossRef]
- Bode, H.W. Network Analysis and Feedback Amplifier Design; Bell Telephone Laboratory Series; Van Nostrand: New York, NY, USA, 1945. [Google Scholar]
- Barbosa, R.S.; Machado, J.A.T.; Ferreira, I.M. Tuning of PID Controllers Based on Bode’s Ideal Transfer Function. Nonlinear Dyn. 2004, 38, 305–321. [Google Scholar] [CrossRef]
- Chen, Y.; Moore, K.L. Relay Feedback Tuning of Robust PID Controllers with Iso-damping Property. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2005, 35, 23–31. [Google Scholar] [CrossRef] [PubMed]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. (Eds.) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer Science & Business Media: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Oustaloup, A. La Dérivation non Entière Théorie, Synthèse et Applications; Hermès: Paris, France, 1995; p. 507. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Monje, C.A.; Vinagre, B.M.; Santamaría, G.E.; Tejado, I. Auto-tuning of fractional order PIλDμ controllers using a PLC. In Proceedings of the 2009 IEEE Conference on Emerging Technologies Factory Automation, Mallorca, Spain, 22–25 September 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Petras, I. Fractional order feedback control of a DC motor. J. Electr. Eng. 2009, 60, 117–128. [Google Scholar]
- Martín, F.; Monje, C.A.; Moreno, L.; Balaguer, C. DE-based tuning of PIλDμ controllers. ISA Trans. 2015, 59, 398–407. [Google Scholar] [CrossRef]
- Manti, M.; Pratesi, A.; Falotico, E.; Cianchetti, M.; Laschi, C. Soft assistive robot for personal care of elderly people. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; pp. 833–838. [Google Scholar] [CrossRef]
- Ljung, L. Experiments with Identification of Continuous Time Models. IFAC Proc. Vol. 2009, 42, 1175–1180. [Google Scholar] [CrossRef]
- Muñoz, J.; Copaci, D.; Monje, C.A.; Blanco, D.; Balaguer, C. Iso-m based adaptive fractional order control with application to a soft robotic neck. IEEE Access 2020, 1. [Google Scholar] [CrossRef]
- Muñoz, J.; Monje, C.A.; Nagua, L.F.; Balaguer, C. A graphical tuning method for fractional order controllers based on iso-slope phase curves. ISA Trans. 2020. [Google Scholar] [CrossRef]
- Martín Barrio, A.; Terrile, S.; Barrientos, A.; del Cerro, J. Robots Hiper-Redundantes: Clasificación, Estado del Arte y Problemática. Rev. Iberoam. Autom. Inform. Industrial 2018, 15, 351–362. [Google Scholar] [CrossRef]
- Martin, A.; Barrientos, A.; del Cerro, J. The Natural-CCD Algorithm, a Novel Method to Solve the Inverse Kinematics of Hyper-redundant and Soft Robots. Soft Robot. 2018, 5, 242–257. [Google Scholar] [CrossRef] [PubMed]
- Ansari, Y.; Manti, M.; Falotico, E.; Mollard, Y.; Cianchetti, M.; Laschi, C. Towards the development of a soft manipulator as an assistive robot for personal care of elderly people. Int. J. Adv. Robot. Syst. 2017, 14, 1729881416687132. [Google Scholar] [CrossRef]
- Nise, N.S. Frequency response techniques. In Control Systems Engineering; Wiley: Hoboken, NJ, USA, 2019; Chapter 10; pp. 525–612. [Google Scholar]
- Levy, E.C. Complex-Curve Fitting. IRE Trans. Autom. Control 1959, AC-4, 37–43. [Google Scholar] [CrossRef]
- Valerio, D.; da Costa, J.S. An Introduction to Fractional Control; Control, Robotics and Sensors; Institution of Engineering and Technology: London, UK, 2012. [Google Scholar] [CrossRef]









| l | |||
|---|---|---|---|
| Point 1 | 20 | 20 | 40 |
| Point 2 | −20 | 20 | 20 |
| Point 3 | −20 | −20 | 40 |
| Point 4 | 20 | −20 | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz, J.; Piqué, F.; A. Monje, C.; Falotico, E. Robust Fractional-Order Control Using a Decoupled Pitch and Roll Actuation Strategy for the I-Support Soft Robot. Mathematics 2021, 9, 702. https://doi.org/10.3390/math9070702
Muñoz J, Piqué F, A. Monje C, Falotico E. Robust Fractional-Order Control Using a Decoupled Pitch and Roll Actuation Strategy for the I-Support Soft Robot. Mathematics. 2021; 9(7):702. https://doi.org/10.3390/math9070702
Chicago/Turabian StyleMuñoz, Jorge, Francesco Piqué, Concepción A. Monje, and Egidio Falotico. 2021. "Robust Fractional-Order Control Using a Decoupled Pitch and Roll Actuation Strategy for the I-Support Soft Robot" Mathematics 9, no. 7: 702. https://doi.org/10.3390/math9070702
APA StyleMuñoz, J., Piqué, F., A. Monje, C., & Falotico, E. (2021). Robust Fractional-Order Control Using a Decoupled Pitch and Roll Actuation Strategy for the I-Support Soft Robot. Mathematics, 9(7), 702. https://doi.org/10.3390/math9070702






