Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect
Abstract
1. Introduction
2. Mathematical Framework
2.1. Basic Equation
2.2. Thermophysical Properties
2.3. Similarity Solution
3. Stability of the Solutions
3.1. Unsteady-State Problem
3.2. New Similarity Transformation
3.3. Introducing Linear Eigenvalue Equations
3.4. Relaxation of Boundary Condition
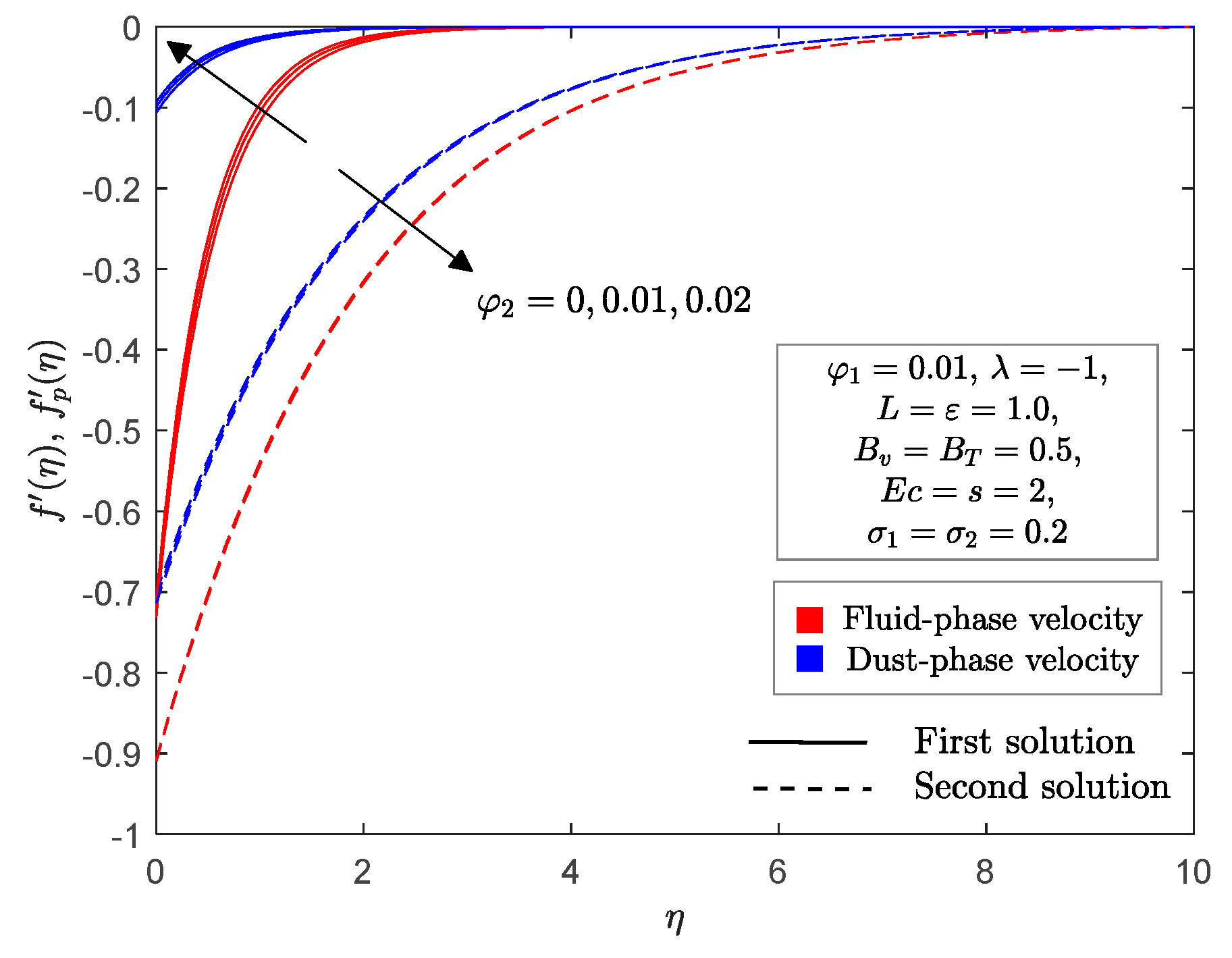
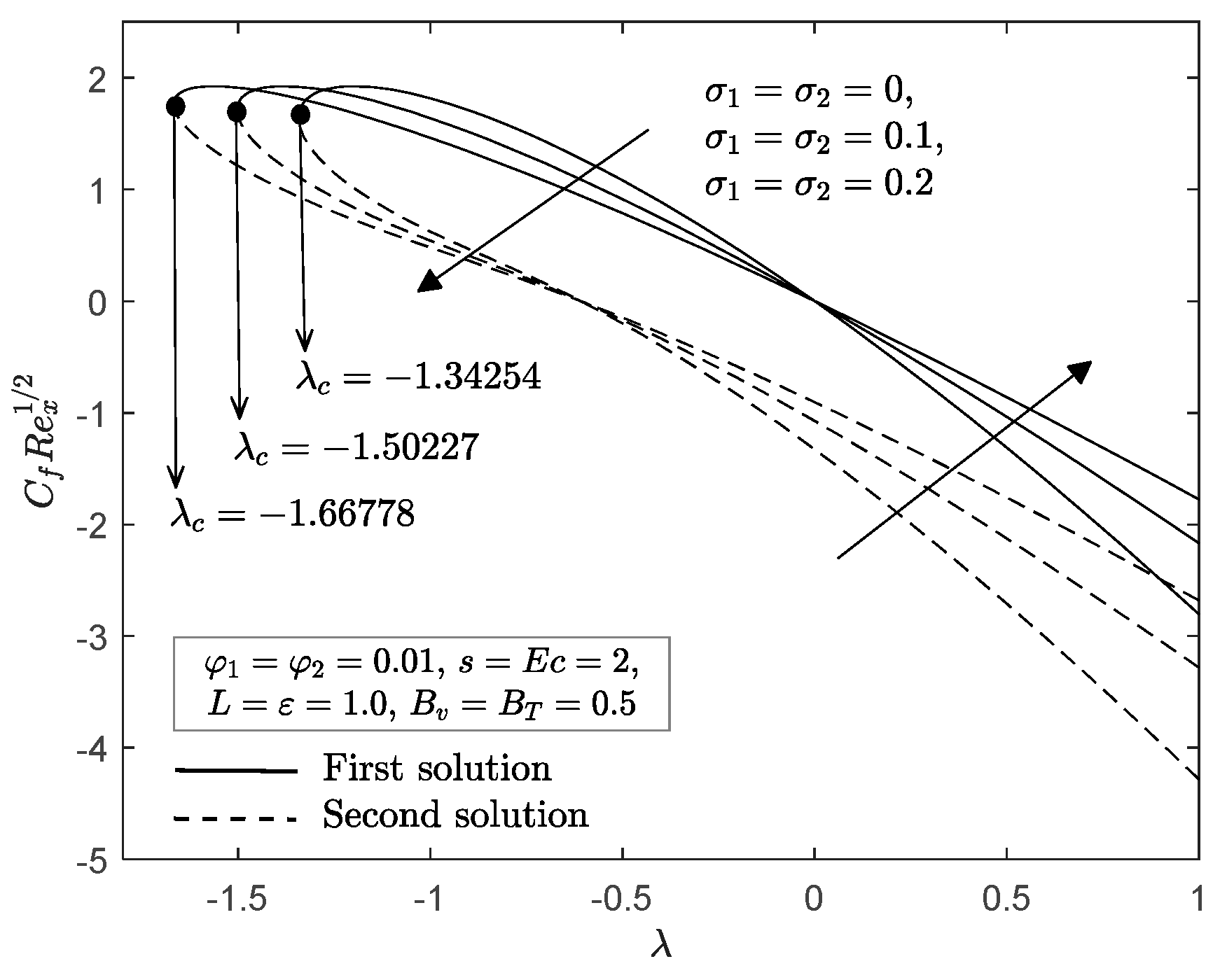
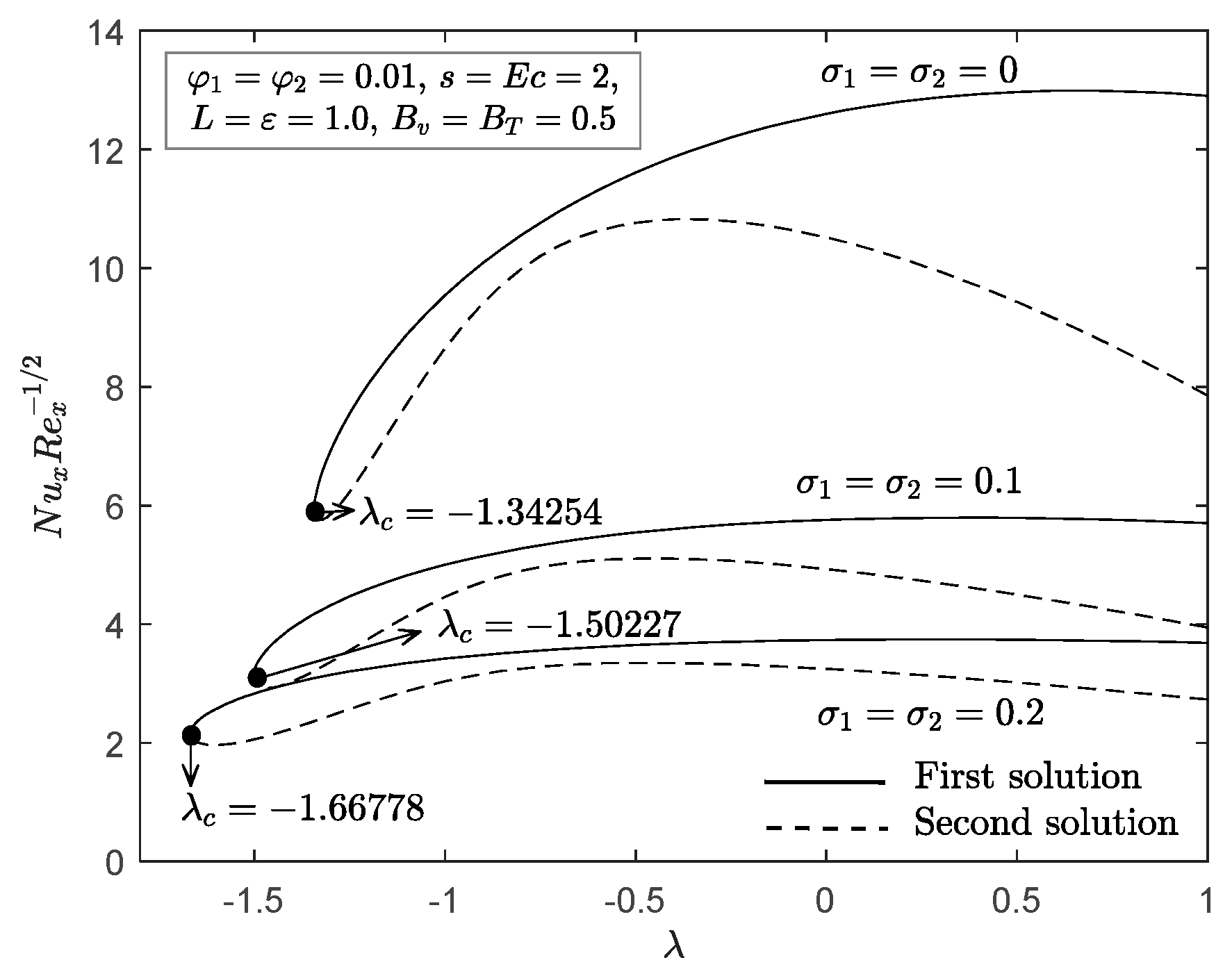
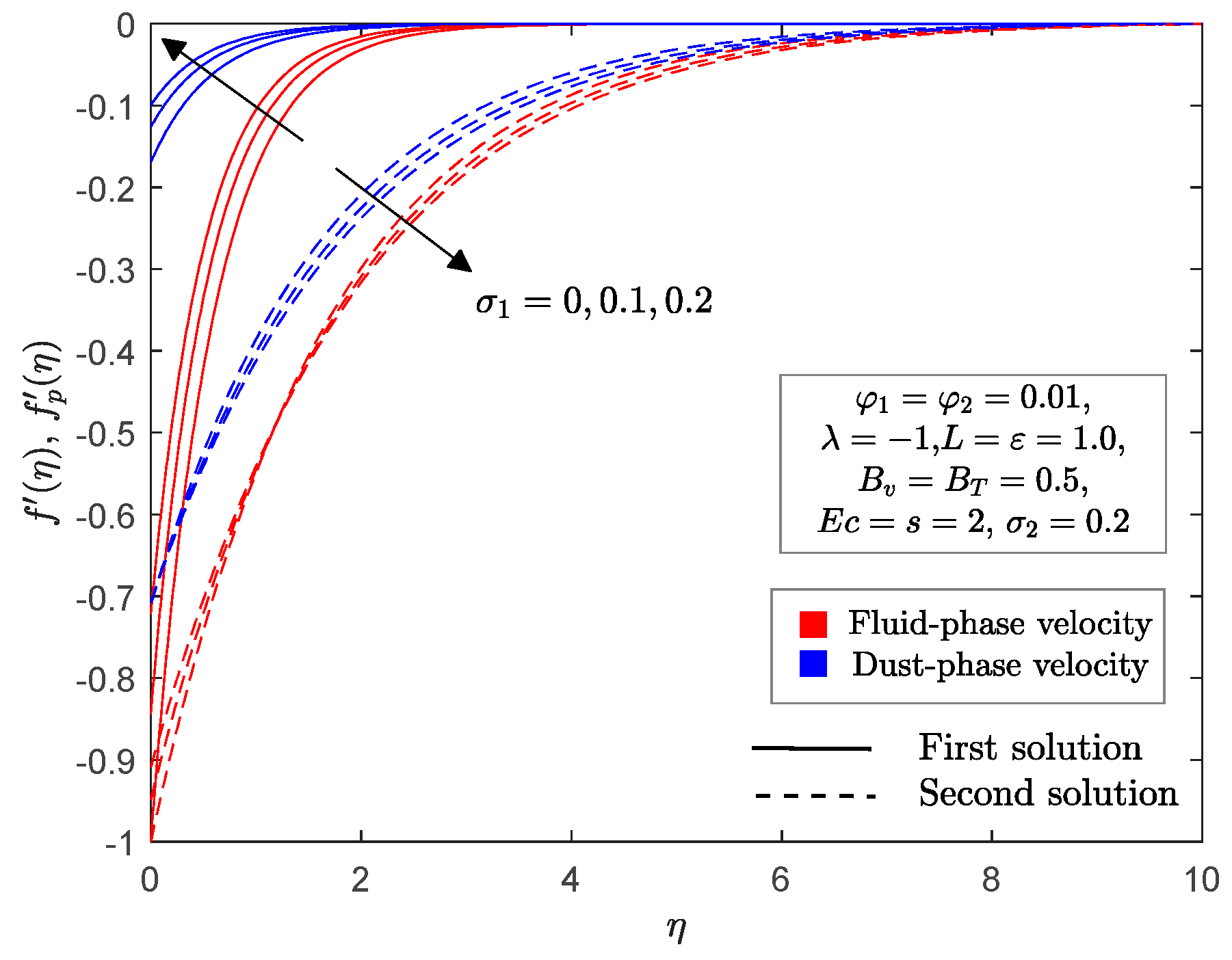
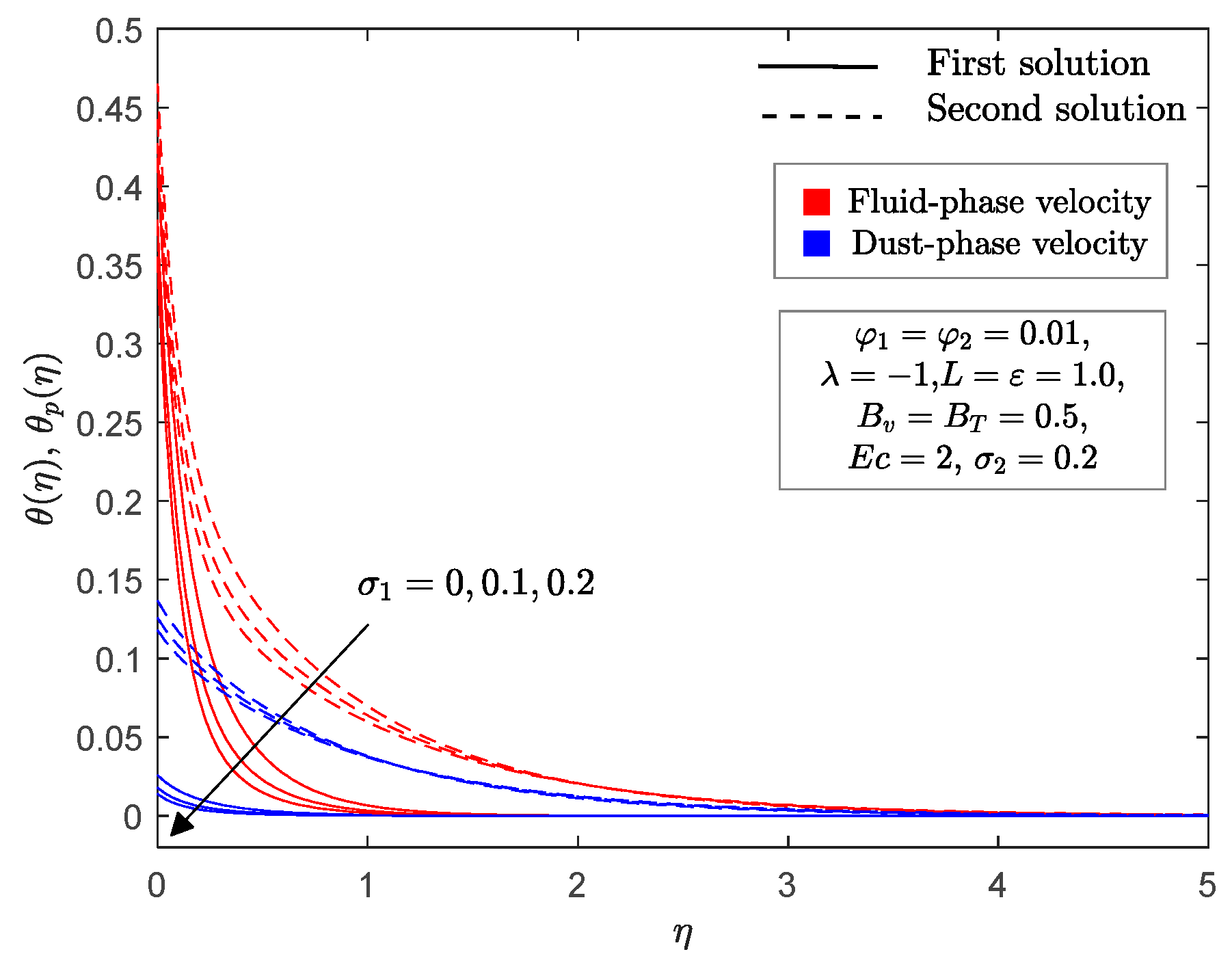
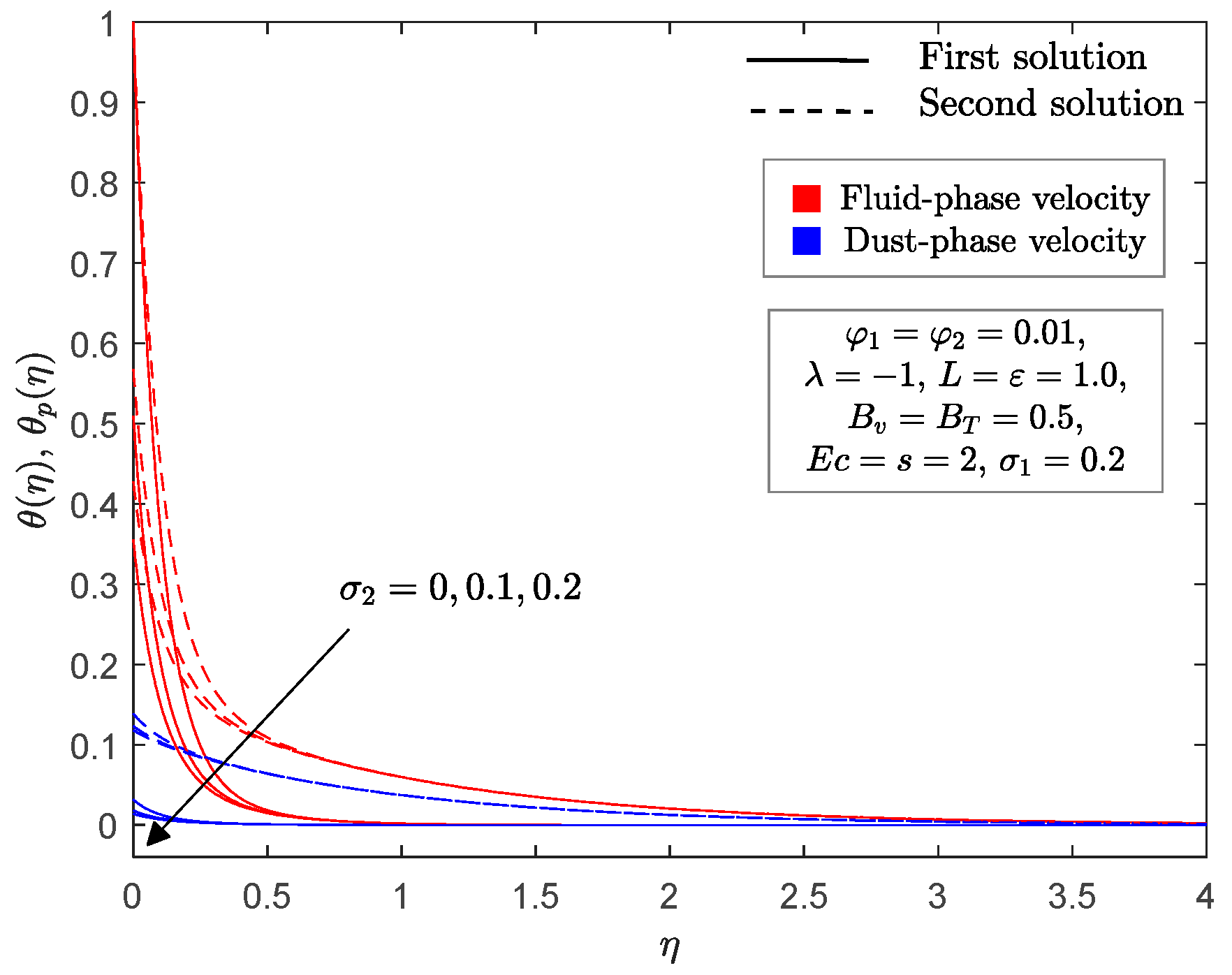
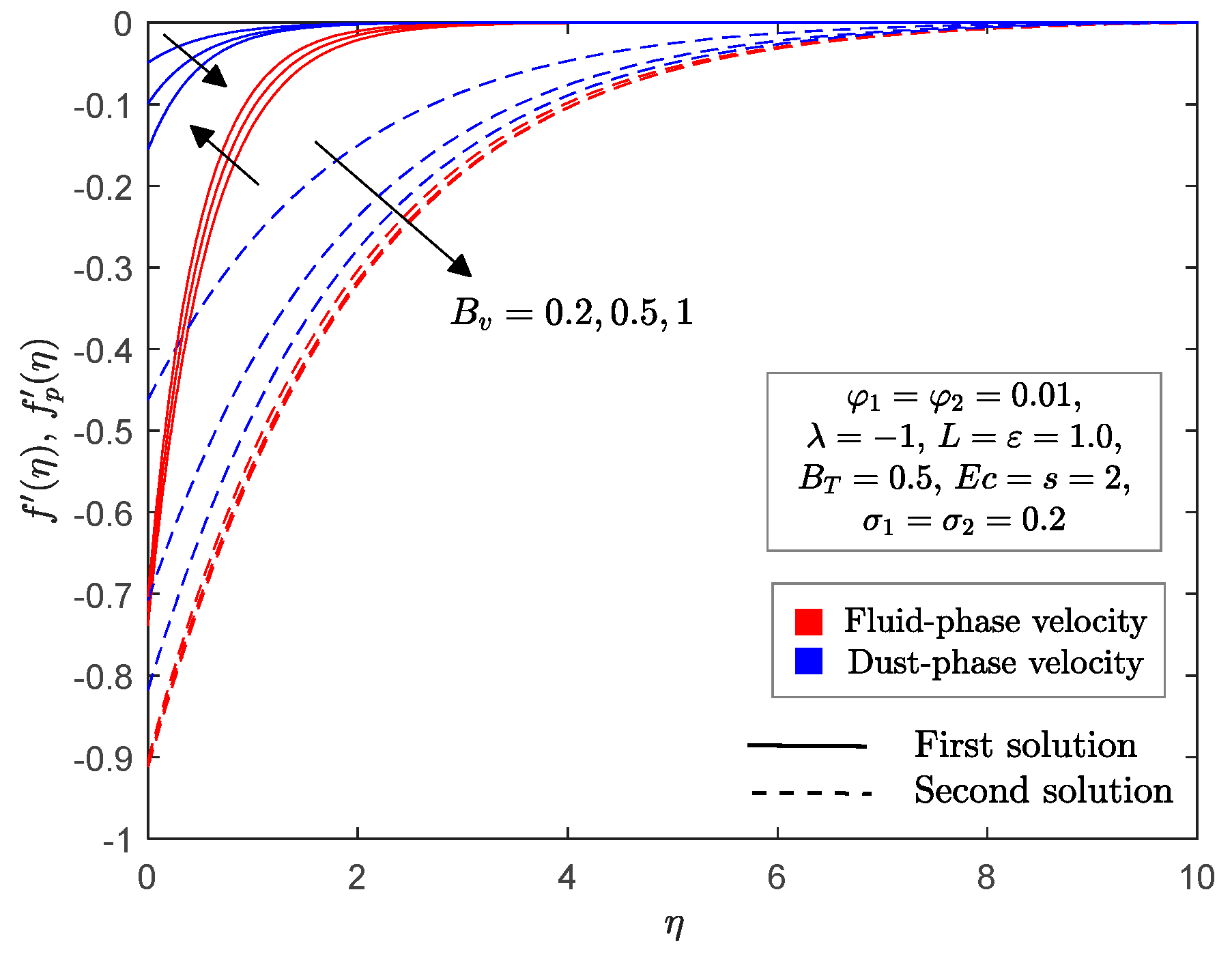
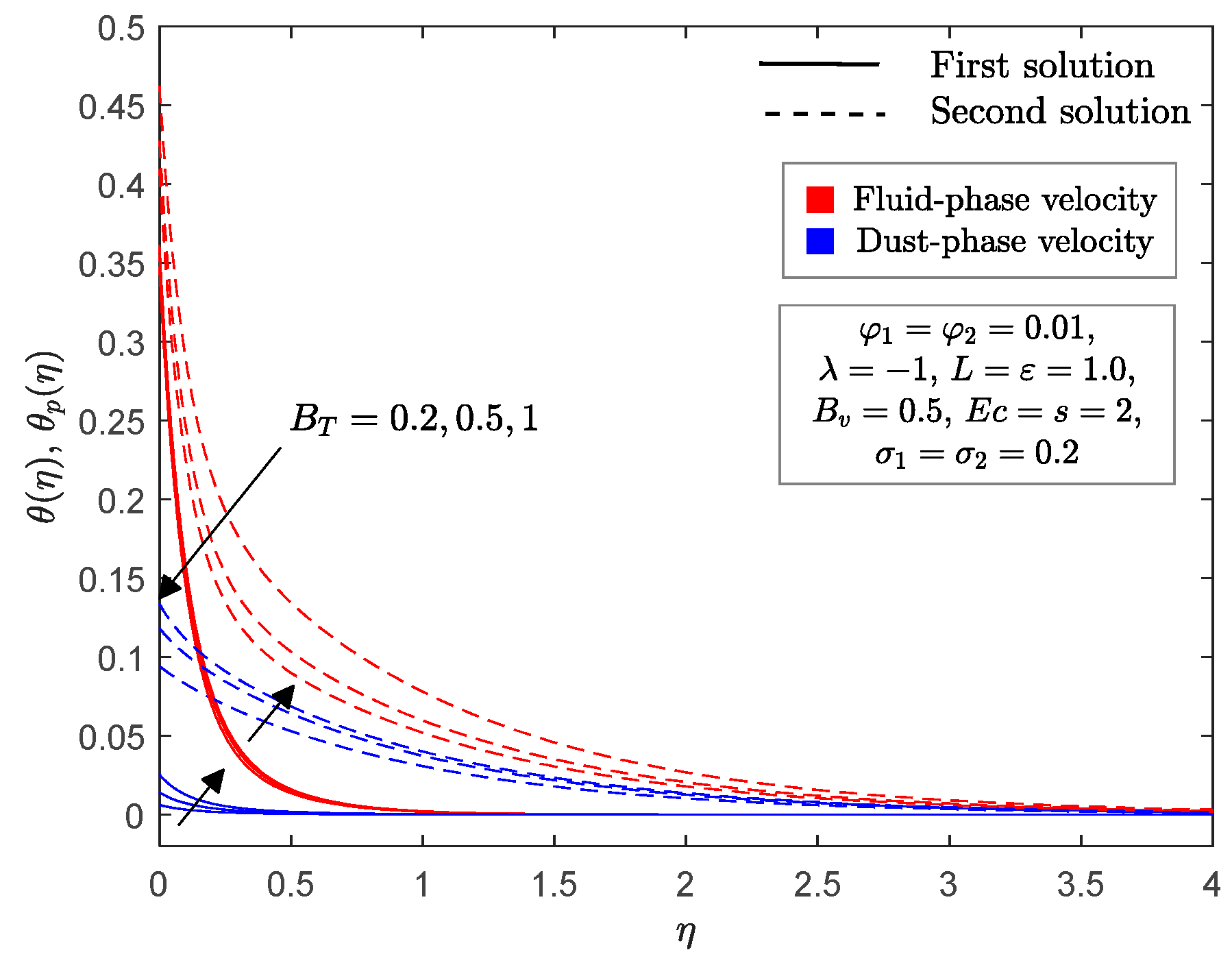
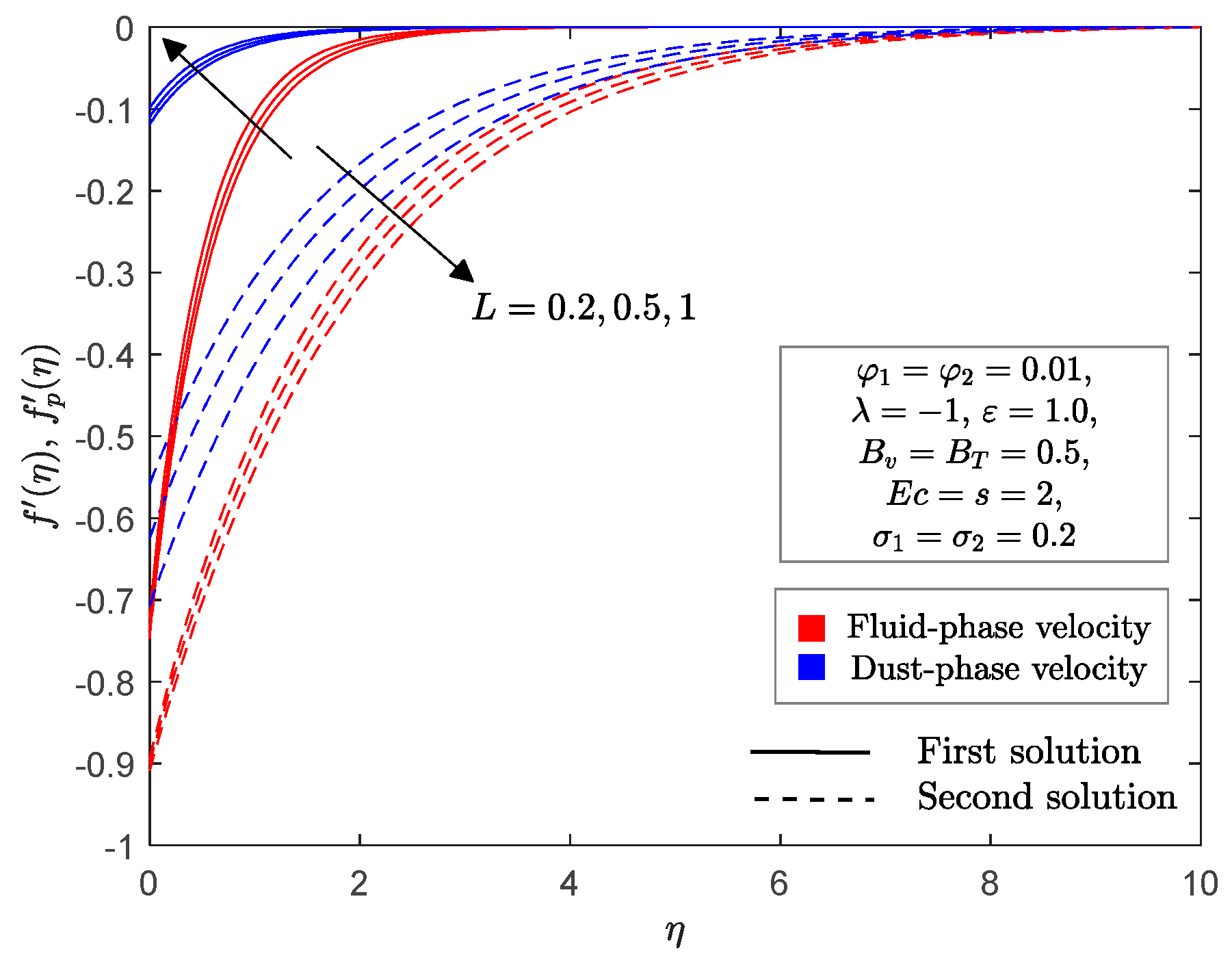
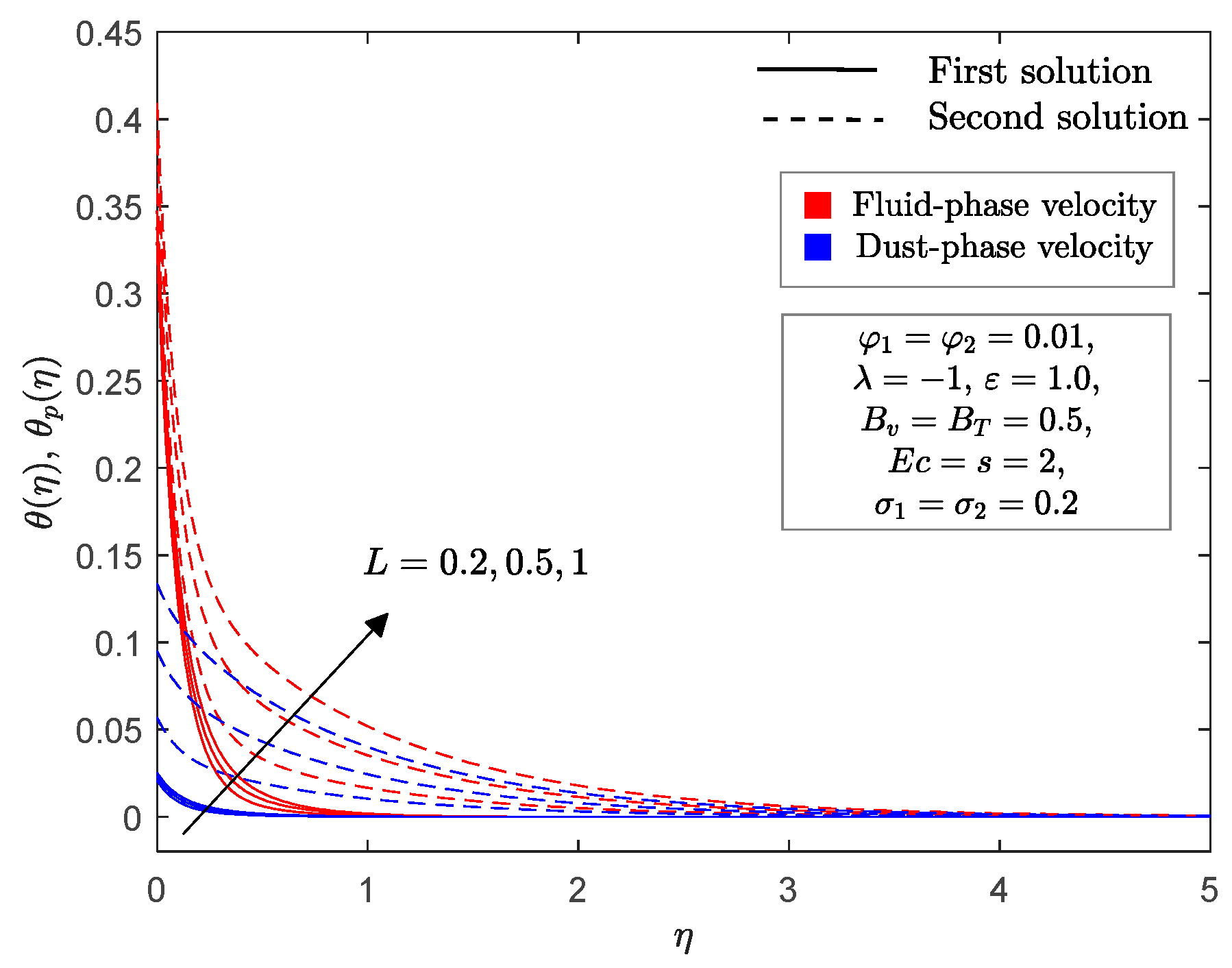
4. Numerical Solutions and Discussions
5. Conclusions
- The presence of double solutions is noticeable for a stretching and shrinking sheet when suction parameter is imposed.
- A stability analysis was carried out and the first solution proved to be stable, whereas the other solution was not.
- An increase in the Cu nanoparticle volume fraction in the dusty nanofluid has a tendency to improve the local Nusselt number for all range of , and to increase the local skin friction for shrinking sheet; however, the opposite is true for a stretching sheet.
- The simultaneous increase of velocity and thermal slip parameters decrease the local Nusselt number for fluid phase.
- The similarity solutions can be widened with an increase in Cu nanoparticle volume fraction and slip parameters (velocity and thermal ), thereby delaying boundary layer separation.
- The momentum thickness in fluid phase decreases and dust phase increases as velocity fluid interaction parameter increases.
- An upsurge of fluid interaction for temperature parameter decreases the thermal boundary layer thickness of the fluid phase, while it does the opposite in the dust phase.
- The mass concentration of dust particle decreases the momentum thickness but increases the thermal thickness in both phases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramesh, G.K.; Gireesha, B.; Bagewadi, C.S. Unsteady flow of a conducting dusty fluid between two circular cylinders. Acta Math. Univ. Comen. 2011, 80, 171–184. [Google Scholar]
- Gireesha, B.J.; Mahanthesh, B.; Manjunatha, P.T.; Gorla, R.S.R. Numerical solution for hydromagnetic boundary layer flow and heat transfer past a stretching surface embedded in non-Darcy porous medium with fluid-particle suspension. J. Niger. Math. Soc. 2015, 34, 267–285. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Magnetohydrodynamic two-phase dusty fluid flow and heat model over deforming isothermal surfaces. Phys. Fluids 2017, 29, 013302. [Google Scholar] [CrossRef]
- Saffman, P.G. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Chakrabarti, K.M. Note on boundary layer in a dusty gas. AIAA J. 1974, 12, 1136–1137. [Google Scholar] [CrossRef]
- Datta, N.; Mishra, S.K. Boundary layer flow of a dusty fluid over a semi-infinite flat plate. Acta Mech. 1982, 42, 71–83. [Google Scholar] [CrossRef]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic flow of a dusty fluid over a stretching sheet. Int. J. Non-Linear Mech. 1992, 27, 937–945. [Google Scholar] [CrossRef]
- Attia, H.A. Influence of temperature dependent viscosity on the MHD-channel flow of dusty fluid with heat transfer. Acta Mech. 2001, 151, 89–101. [Google Scholar] [CrossRef]
- Ajadi, S.O. A note on the unsteady flow of dusty viscous fluid between two parallel plates. J. Appl. Math. Comput. 2005, 18, 393–403. [Google Scholar] [CrossRef][Green Version]
- Damseh, R.A. On boundary layer flow of a dusty gas from a horizontal circular cylinder. Braz. J. Chem. Eng. 2010, 27, 653–662. [Google Scholar] [CrossRef][Green Version]
- Gireesha, B.J.; Chamkha, A.J.; Manjunatha, S.; Bagewadi, C.S. Mixed convective flow of a dusty fluid over a vertical stretching sheet with non-uniform heat source/sink and radiation. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 598–612. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comput. Math. Appl. 2010, 60, 660–669. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Gireesha, B.J.; Manjunatha, P.T. Melting phenomenon in MHD stagnation point flow of dusty fluid over a stretching sheet in the presence of thermal radiation and non-uniform heat source/sink. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 265–274. [Google Scholar] [CrossRef]
- Jalil, M.; Asghar, S.; Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng. 2017, 2017, 2307469. [Google Scholar] [CrossRef]
- Hamid, R.A.; Nazar, R.; Pop, I. Boundary layer flow of a dusty fluid over a permeable shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 758–772. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Mahanthesh, B.; Makinde, O.D.; Muhammad, T. Effects of Hall current on transient flow of dusty fluid with nonlinear radiation past a convectively heated stretching plate. Defect Diffus. Forum 2018, 387, 352–363. [Google Scholar] [CrossRef]
- Abbas, Z.; Hasnain, J.; Sajid, M. Effects of slip on MHD flow of a dusty fluid over a stretching sheet through porous space. J. Eng. Thermophys. 2019, 28, 84–102. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Shashikumar, N.S.; Ramesh, G.K. Magnetohydrodynamic flow of dusty fluid over Riga plate with deforming isothermal surfaces with convective boundary condition. Songklanakarin J. Sci. Technol. 2020, 42, 487–495. [Google Scholar]
- Choi, S.U.S.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Rafati, M.; Hamidi, A.A.; Niaser, M.S. Application of nanofluids in computer cooling systems (heat transfer performance of nanofluids). Appl. Therm. Eng. 2012, 45, 9–14. [Google Scholar] [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Najafi, G. Recent state of nanofluid in automobile cooling systems. J. Therm. Anal. Calorim. 2019, 135, 981–1008. [Google Scholar] [CrossRef]
- Sheikhpour, M.; Arabi, M.; Kasaeian, A.; Rabei, A.R.; Taherian, Z. Role of Nanofluids in Drug Delivery and Biomedical Technology: Methods and Applications. Nanotechnol. Sci. Appl. 2020, 13, 47. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, P.K.; Subramani, J.; Suyambazhahan, S.; Sathyamurthy, R. Nanofluids for solar collector applications: A review. Energy Procedia 2014, 61, 2416–2434. [Google Scholar] [CrossRef]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary layer stagnation-point flow toward a stretching/shrinking sheet in a nanofluid. J. Heat Transf. 2013, 135, 054501. [Google Scholar] [CrossRef]
- Pop, I.; Seddighi, S.; Bachok, N.; Ismail, F. Boundary layer flow beneath a uniform free stream permeable continuous moving surface in a nanofluid. J. Heat Mass Transf. Res. 2014, 1, 55–65. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. MHD flow past a nonlinear stretching/shrinking sheet in carbon nanotubes: Stability analysis. Chin. J. Phys. 2020, 65, 436–446. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Turkyilmazoglu, M.; Arifin, N.M.; Rosali, H. Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alex. Eng. J. 2020, 59, 497–507. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Gireesha, B.J.; Singh, B. MHD flow and heat transfer of dusty nanofluid embedded in porous medium over an exponentially stretching sheet. J. Nanofluids 2015, 4, 449–460. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow of dusty nanofluid over a stretching surface with volume fraction of dust particles. Ain Shams Eng. J. 2016, 7, 709–716. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Ganji, D.D.; Hatami, M. Fe3O4–(CH2OH)2 nanofluid analysis in a porous medium under MHD radiative boundary layer and dusty fluid. J. Mol. Liq. 2018, 258, 172–185. [Google Scholar] [CrossRef]
- Siddiqa, S.; Begum, N.; Hossain, M.A.; Gorla, R.S.R.; Al-Rashed, A.A. Two-phase natural convection dusty nanofluid flow. Int. J. Heat Mass Transf. 2018, 118, 66–74. [Google Scholar] [CrossRef]
- Kalpana, G.; Madhura, K.R.; Iyengar, S.S. Numerical computation on Marangoni convective flow of two-phase MHD dusty nanofluids under Brownian motion and thermophoresis effects. Heat Transf. Asian Res. 2020, 49, 626–650. [Google Scholar] [CrossRef]
- Mishra, S.R.; Khan, M.I.; Rout, B.C. Dynamics of dust particles in a conducting dusty nanomaterial: A computational approach. Int. Commun. Heat Mass Transf. 2020, 119, 104967. [Google Scholar] [CrossRef]
- Saha, L.K.; Bala, S.K.; Roy, N.C. Natural convection of dusty nanofluids within a concentric annulus. Eur. Phys. J. Plus 2020, 135, 1–20. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gamachu, D. Dusty Nanofluid Past a Centrifugally Stretching Surface. Math. Probl. Eng. 2020, 2020, 9163081. [Google Scholar] [CrossRef]
- Madhesh, D.; Kalaiselvam, S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar] [CrossRef]
- Tahat, M.S.; Benim, A.C. Experimental analysis on thermophysical properties of Al2O3/CuO hybrid nano fluid with its effects on flat plate solar collector. Defect Diffus. Forum 2017, 374, 148–156. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Anuar, N.S.; Bachok, N.; Pop, I. Radiative hybrid nanofluid flow past a rotating permeable stretching/shrinking sheet. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Jafarimoghaddam, A.; Pop, I. Cross flow and heat transfer past a permeable stretching/shrinking sheet in a hybrid nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.S.M. Dual solutions and stability analysis of a hybrid nanofluid over a stretching/shrinking sheet executing MHD flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Khan, M.R.; Pan, K.; Khan, A.U.; Nadeem, S. Dual solutions for mixed convection flow of SiO2− Al2O3/water hybrid nanofluid near the stagnation point over a curved surface. Phys. A Stat. Mech. Appl. 2020, 547, 123959. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed Convective Stagnation Point Flow towards a Vertical Riga Plate in Hybrid Cu-Al2O3/Water Nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Hatami, M.; Ganji, D.D. MHD boundary layer analysis for micropolar dusty fluid containing Hybrid nanoparticles (Cu-Al2O3) over a porous medium. J. Mol. Liq. 2018, 268, 813–823. [Google Scholar] [CrossRef]
- Raizah, Z.A. Natural Convection of Dusty Hybrid Nanofluids in an Enclosure Including Two Oriented Heated Fins. Appl. Sci. 2019, 9, 2673. [Google Scholar] [CrossRef]
- Reddy, M.G.; Rani, M.V.V.N.L.S.; Kumar, K.G.; Prasannakumar, B.C.; Lokesh, H.J. Hybrid dusty fluid flow through a Cattaneo–Christov heat flux model. Phys. A Stat. Mech. Appl. 2020, 551, 123975. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2011, 38, 917–922. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Wang, C.Y. Flow due to a stretching boundary with partial slip—an exact solution of the Navier–Stokes equations. Chem. Eng. Sci. 2002, 57, 3745–3747. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Slip effects on an unsteady boundary layer stagnation-point flow and heat transfer towards a stretching sheet. Chin. Phys. Lett. 2011, 28, 094702. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Khan, M.I.; Tamoor, M.; Hayat, T.; Alsaedi, A. MHD boundary layer thermal slip flow by nonlinearly stretching cylinder with suction/blowing and radiation. Results Phys. 2017, 7, 1207–1211. [Google Scholar] [CrossRef]
- Das, K. Slip flow and convective heat transfer of nanofluids over a permeable stretching surface. Comput. Fluids 2012, 64, 34–42. [Google Scholar] [CrossRef]
- Kho, Y.B.; Hussanan, A.; Mohamed, M.K.A.; Sarif, N.M.; Ismail, Z.; Salleh, M.Z. Thermal radiation effect on MHD Flow and heat transfer analysis of Williamson nanofluid past over a stretching sheet with constant wall temperature. J. Phys. Conf. Ser. 2017, 890, 012034. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Chamkha, A.J.; Rudraswamy, N.G.; Krishnamurthy, M.R. MHD flow and heat transfer of a nanofluid embedded with dust particles over a stretching sheet. J. Nanofluids 2015, 4, 66–72. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A Note on the correspondence between certain nanofluid flows and standard fluid flows. J. Heat Transf. 2015, 137, 024501. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2000, 2000, 1–27. [Google Scholar]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the Maltab PSE. ACM Trans. Math. Softw. (TOMS) 2001, 27, 299–316. [Google Scholar] [CrossRef]
- Hayat, T.; Qasim, M.; Mesloub, S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Methods Fluids 2011, 66, 963–975. [Google Scholar] [CrossRef]

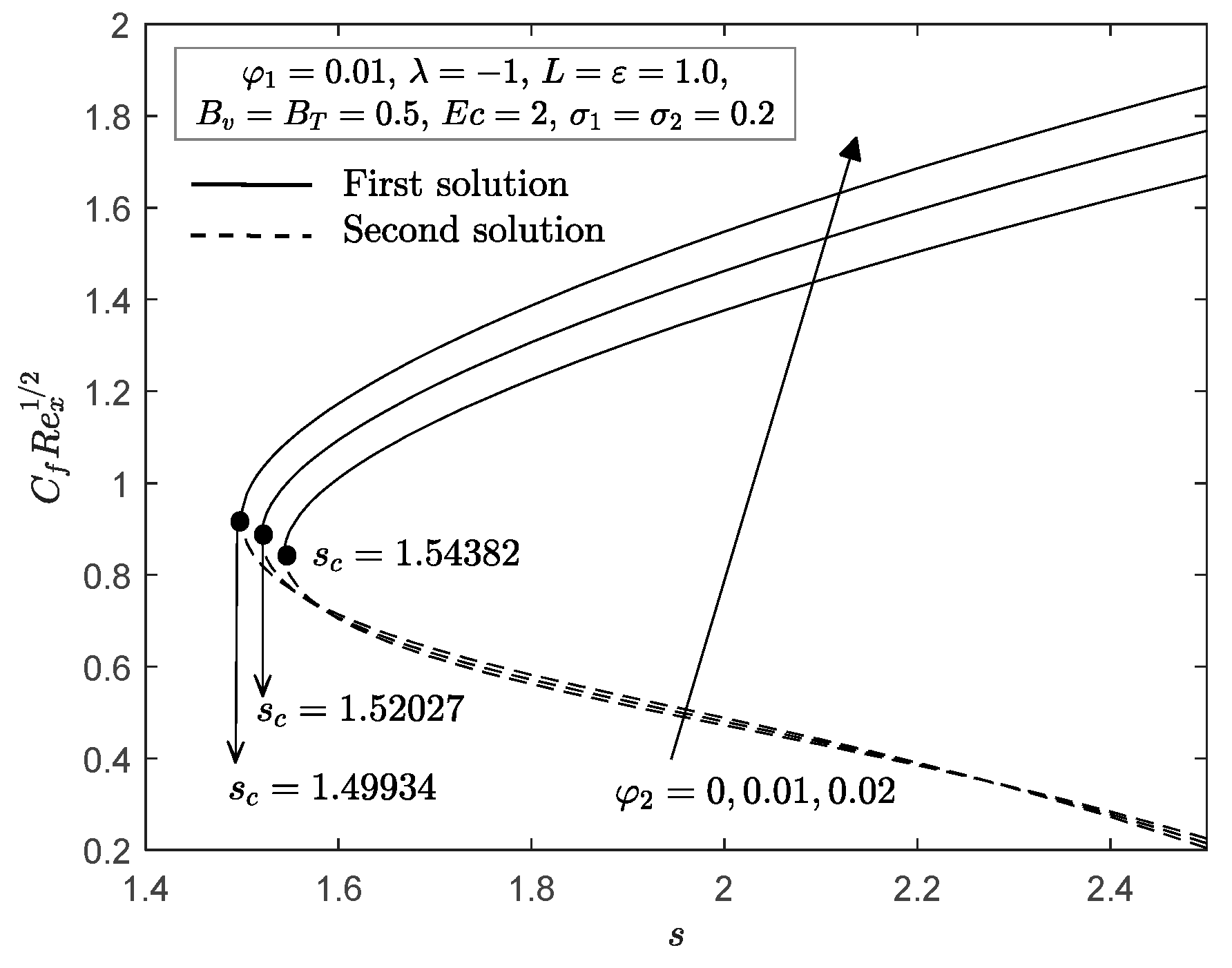
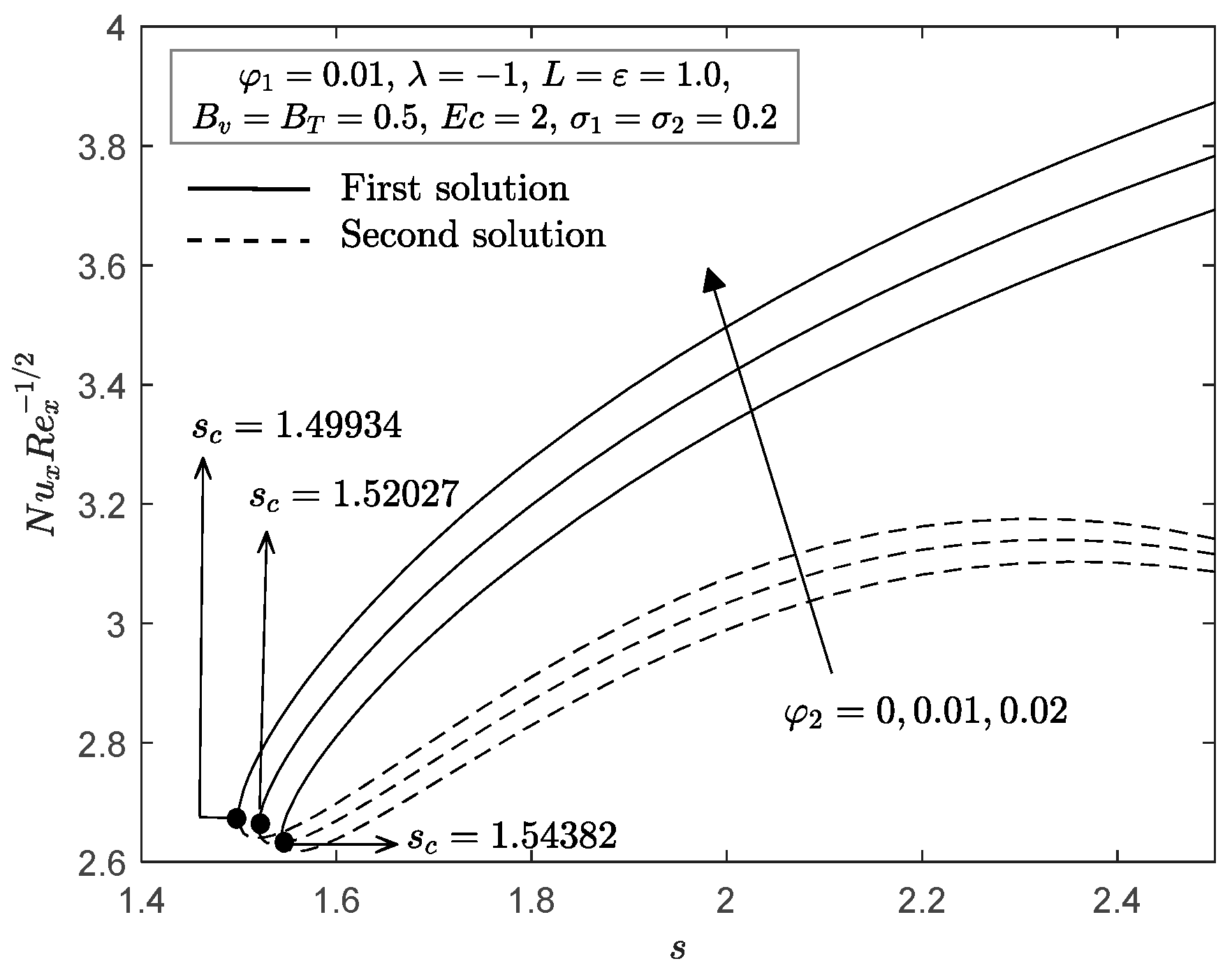
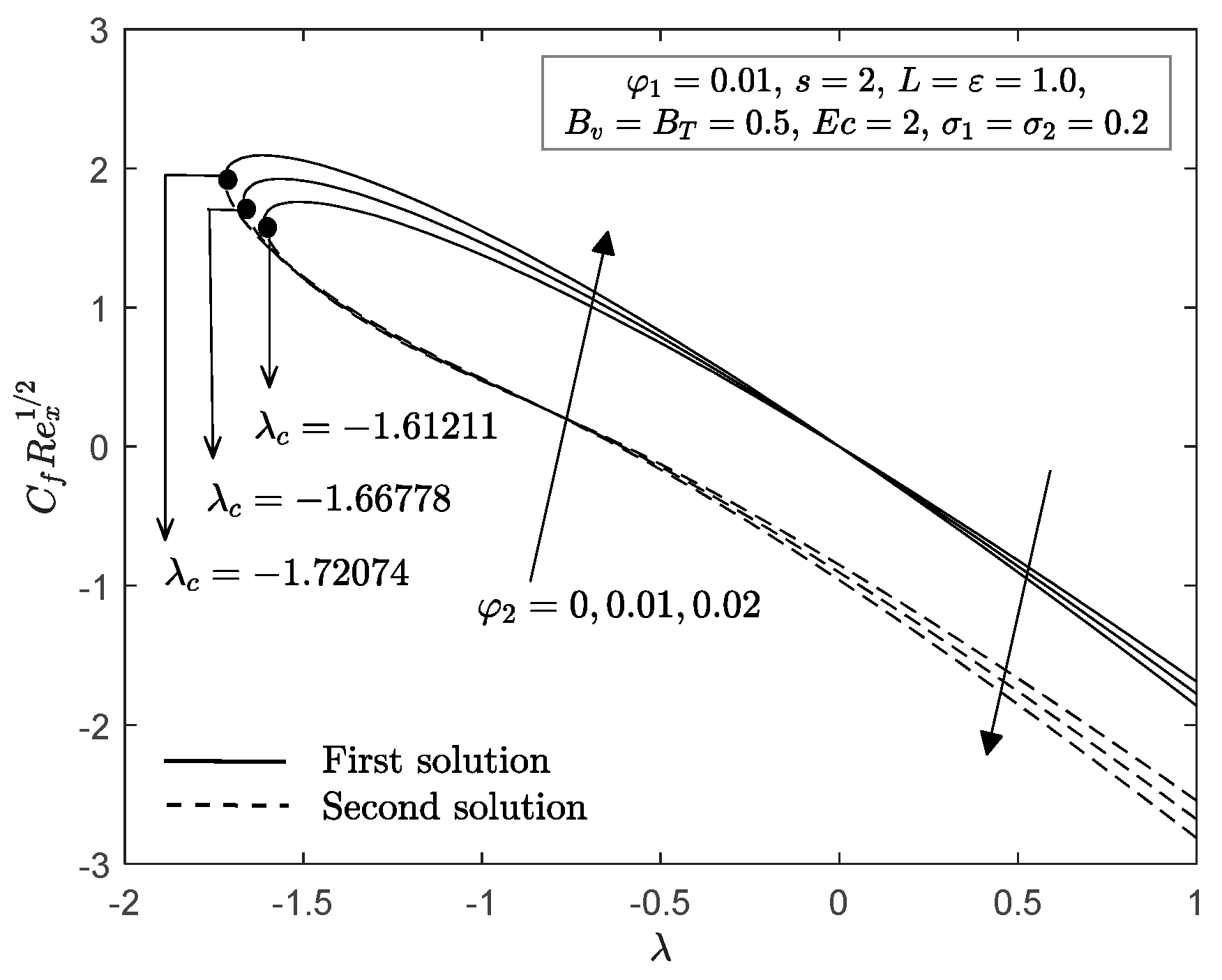
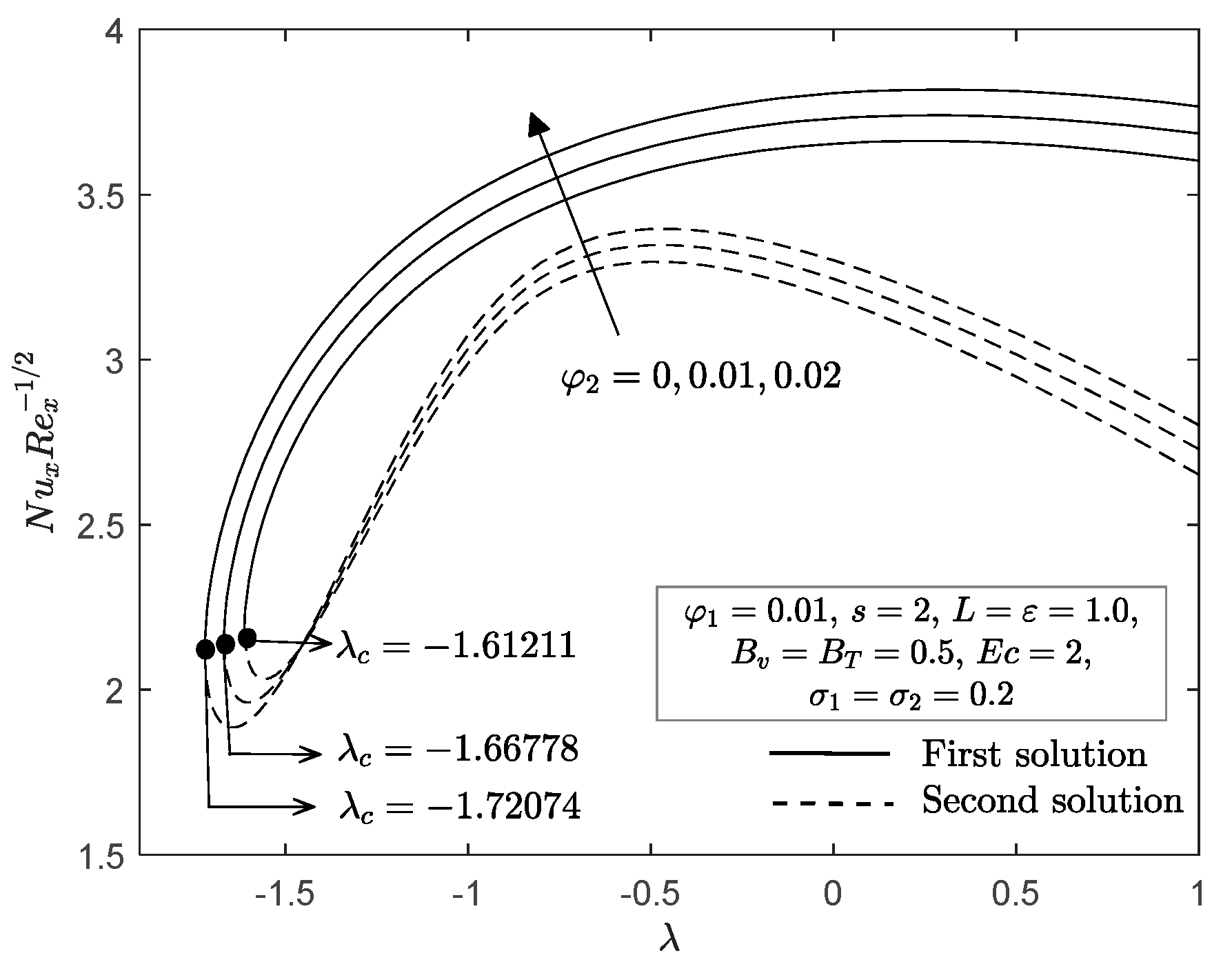


| Properties | Nanofluid | Hybrid Nanofluid |
|---|---|---|
| Density | ||
| Heat capacity | ||
| Dynamic viscosity | ||
| Thermal conductivity | where |
| Physical Properties | Cu | Water | Al2O3 |
|---|---|---|---|
| (Wm-1K-1) | 400 | 0.613 | 40 |
| (J kg-1K-1) | 385 | 4179 | 765 |
| (kg m-3) | 8933 | 997.1 | 3970 |
| Hayat et al. [65] (Homotopy Analysis Method) | Ibrahim and Shankar [53] (Shooting) | Present Result (Bvp4c) | |
|---|---|---|---|
| 0 | −1.000000 | −1.0000 | −1.000000 |
| 0.1 | −0.872082 | −0.8721 | −0.872083 |
| 0.2 | −0.776377 | −0.7764 | −0.776377 |
| 0.5 | −0.591195 | −0.5912 | −0.591196 |
| 2.0 | −0.283981 | −0.2840 | −0.283981 |
| 5.0 | −0.144841 | −0.1448 | −0.144842 |
| Gireesha et al. [57] | Naramgari and Sulochana [30] | Present Result | |
|---|---|---|---|
| 0.72 | 1.0885 | 1.088561 | 1.088527 |
| 1 | 1.3333 | 1.333333 | 1.333333 |
| 10 | 4.7968 | 4.796817 | 4.796873 |
| 1st Solution | 2nd Solution | ||
|---|---|---|---|
| 0 | −1.6121 | 0.0026 | −0.0027 |
| −1.612 | 0.0131 | −0.0130 | |
| −1.61 | 0.0590 | −0.0580 | |
| 0.01 | −1.6677 | 0.0115 | −0.0114 |
| −1.667 | 0.0363 | −0.0359 | |
| −1.66 | 0.1158 | −0.1120 | |
| 0.02 | −1.7207 | 0.0085 | −0.0085 |
| −1.72 | 0.0359 | −0.0355 | |
| −1.7 | 0.1924 | −0.1825 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anuar, N.S.; Bachok, N.; Pop, I. Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect. Mathematics 2021, 9, 643. https://doi.org/10.3390/math9060643
Anuar NS, Bachok N, Pop I. Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect. Mathematics. 2021; 9(6):643. https://doi.org/10.3390/math9060643
Chicago/Turabian StyleAnuar, Nur Syazana, Norfifah Bachok, and Ioan Pop. 2021. "Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect" Mathematics 9, no. 6: 643. https://doi.org/10.3390/math9060643
APA StyleAnuar, N. S., Bachok, N., & Pop, I. (2021). Numerical Computation of Dusty Hybrid Nanofluid Flow and Heat Transfer over a Deformable Sheet with Slip Effect. Mathematics, 9(6), 643. https://doi.org/10.3390/math9060643





