Abstract
The mathematical modeling of dusty Cu-Al2O3/water nanofluid flow driven by a permeable deformable sheet was explored numerically. Rather than no–slip conditions at the boundary, velocity slip and thermal slip were considered. To achieve the system of nonlinear ordinary differential equations (ODEs), we employed some appropriate transformations and solved them numerically using MATLAB software (built–in solver called bvp4c). The influences of relevant parameters on fluid flow and heat transfer characteristics are discussed and presented in graphs. The findings showed that double solutions appeared in the case of stretching and shrinking sheets which contributed to the analysis of stability. The stability analysis, therefore, confirmed that merely the first solution was a stable solution. The addition of nanometer-sized particles (Cu) was found to significantly strengthen the heat transfer rate of the dusty nanofluid. Meanwhile, an upsurge in the velocity and thermal slip was shown to decrease the local Nusselt number. The result also revealed that an increment of fluid particle interaction decreased the boundary layer thickness.
1. Introduction
For a number of years, studies of the heat transfer characteristics of dusty fluid flow (two-phase fluid)—in terms of understanding various real-world problems, especially in atmospheric, physiological and engineering fields—have captivated the attention of numerous researchers. For instance, the application of dust particles can be seen in the petroleum industry, soil erosion by natural winds, purification of crude oil, aerosol and paint spraying, fluidization, dust entrainment during a nuclear explosion in a cloud and waste water treatment [1,2,3]. Saffman [4] first formulated dusty fluid flow equations and evaluated the stability of the laminar flow of a dusty gas wherein particles were evenly scattered. After some years, Chakrabarti [5] conducted a study of dusty gas using boundary layer theory, and soon thereafter, Datta and Mishra [6] and Vajravelu and Nayfeh [7] examined dusty fluid flow over a semi-infinite flat plate and stretching sheet, respectively. Further, a number of mathematicians such as Attia [8], Ajadi [9], Damseh [10], Gireesha et al. [11], Makinde and Chinyoka [12] and Prasannakumara et al. [13] conducted investigations in this field. An exact analytical solution of magnetohydrodynamic (MHD) dusty fluid caused by a stretching sheet was studied by Jalil et al. [14]. Unlike in previous research, Hamid et al. [15] explored the permeable shrinking surface in a dusty fluid and observed the occurrence of dual solutions. Gireesha et al. [16] numerically studied the nonlinear thermal radiation and hall current impact on a dusty fluid in a heated stretching sheet, while Abbas et al. [17] examined dusty fluid flow in a porous medium and took the impact of slip and MHD into consideration. Recently, the dusty fluid flow in a Riga plate with MHD and convective boundary conditions was studied by Prasannakumara et al. [18].
All of the above-mention studies only involved viscous fluids. The inclusion of nanoparticles in a conventional fluid can change its flow and heat transfer capabilities, i.e., boosting its thermal conductivity. It seems that Choi and Eastman [19] first conceived the idea of a nanofluid, i.e., nanoparticles suspended in a base fluid. Since then, nanofluids have been widely used in industrial cooling applications [20,21], biomedical technology [22], solar thermal applications [23] and many others. Numerous researchers, such as Motsumi and Makinde [24], Bachok et al. [25], Pop et al. [26] and Anuar et al. [27,28] have explored the concept of nanofluid flow and heat transfer. However, there have been fewer studies on two-phase fluids. The investigation of MHD flows of a dusty nanofluid in a porous medium over an exponentially stretching sheet was explored by Gorla et al. [29]. Afterwards, Naramgari and Sulochana [30] performed a numerical study of dusty nanofluid flow when the sheet was stretched, and concluded that the rate of heat transfer was enhanced by an upsurge interaction between the nanofluid and the particle phase. An analysis of the MHD flow of dusty Fe3O4-ethylene glycol nanofluid was performed by Ghadikolaei et al. [31]. Siddiqa et al. [32] numerically analyzed the natural convective flow of a dusty nanofluid driven by a wavy vertical surface. Recently, Kalpana et al. [33], Mishra et al. [34], Saha et al. [35] and Ibrahim and Gamachu [36] explored the dusty nanofluid flow problem with different surfaces and aspects.
New kinds of nanofluids, known as hybrid nanofluids, which can efficiently improve heat transfer, are being introduced in industry. A hybrid nanofluid is a mixture of two types of nanoparticles suspended in a base fluid. This new kind of fluid, however, provides a great advance in heat conductivity, as proved by the work of Madhesh and Kalaiselvam [37], Tahat and Benim [38] and Devi and Devi [39]. A few researchers have undertaken mathematical investigations of the boundary layer flow of hybrid nanofluids on various surfaces such as in stretching/shrinking sheet [40,41,42], thin needle [43], curved surface [44] and Riga plate [45]. Ghadikolaei et al. [46] studied the behavior of a hybrid nanofluid (Cu-Al2O3) in a micropolar dusty fluid. In another study, Raizah [47] conducted a mathematical simulation on a dusty hybrid nanofluid in an enclosure with two inclined, heated fins. Recently, Reddy et al. [48] presented a remarkable study of a Darcy porous medium in a hybrid dusty nanofluid. However, research related to hybrid nanofluids suspended with dust particles is limited. Hence, the main purpose of this investigation is to address the behavior of a hybrid nanofluid flow suspended with uniform distribution of dust particles in a deformable sheet, i.e., stretching and shrinking. It should be pointed out that the deformable sheet is not a new topic among researchers in this field, since such applications are well recognized in processing industries, especially in polymer processing, glass fiber production, the cooling and drying of paper, and many others [49].
Other issues discussed in this work are the simultaneous effect of velocity and thermal slip. Most of the research literature ignores slip boundary conditions; however, the slip effect should be considered in some situations, for example, in a rarefied fluid problem, fluid flow on multiple interfaces, the polishing of artificial heart valves, etc. Andersson [50] and Wang [51] conducted earlier work that took the velocity slip boundary condition driven by a stretching sheet into account. Their concept was utilized by Bhattacharyya et al. [52], who investigated velocity and the thermal slip effect in an unsteady stagnation flow. Afterwards, Mukhopadhyay [53] examined both slip effects on an exponentially stretching sheet and observed that an increase in thermal slip decreased the temperature. By taking into consideration the impact of slips (velocity, thermal and solutal), Ibrahim and Shankar [54] examined the flow of a permeable stretching sheet in a nanofluid. Further, Khan et al. [55] numerically studied the viscous fluid flow induced by a nonlinear stretching cylinder with radiation, MHD, suction/blowing and velocity and thermal slip effects. In a recent study, Kho et al. [56] observed the reduction of boundary layer thickness for increasing velocity and thermal slip parameters in their investigation of Williamson nanofluid flow. Motivated by the aforementioned work, our aim is to examine the effect of both velocity and thermal slip on the heat transfer of a dusty hybrid nanofluid.
In brief, this research paper is an extension of the work of Gireesha et al. [57], who considered the flow of MHD nanofluid embedded with dust particles over a stretching sheet. They studied the dusty nanofluid model using copper as the nanoparticle, analyzed it numerically and obtained a unique solution. Therefore, the present study aims to theoretically study the dusty hybrid nanofluid in stretching/shrinking sheet and take into consideration the effect of slips. The utilization of alumina (Al2O3) and copper (Cu) as hybrid nanoparticles with water as a base fluid have not been previously applied in studies on the dusty fluid problem with velocity and thermal slip effects. In addition, this study also comprises a novel attempt to discover the shrinking features of a dusty hybrid nanofluid. The existence of nonunique solutions is acknowledged in the literature [25,27,28,40,42,49]; hence, this paper focuses on obtaining a nonunique solution as well as performing a stability analysis thereof. It is expected that these findings will help engineers and researchers to understand the heat transfer mechanism in dusty hybrid nanofluids. It is worth mentioning that this study is original, and the numerical results presented herein have never been published before.
2. Mathematical Framework
2.1. Basic Equation
The steady two-dimensional flow of a dusty fluid suspended in a hybrid nanofluid driven by a deformable sheet with surface temperature is investigated. The geometry of the problem is depicted in Figure 1. With velocity , where is a positive constant, the surface is stretched or shrunk linearly in the -direction, whilst the -axis is normal to it. Further, the temperature far from the surface is denoted by and the mass transfer velocity at the surface by .
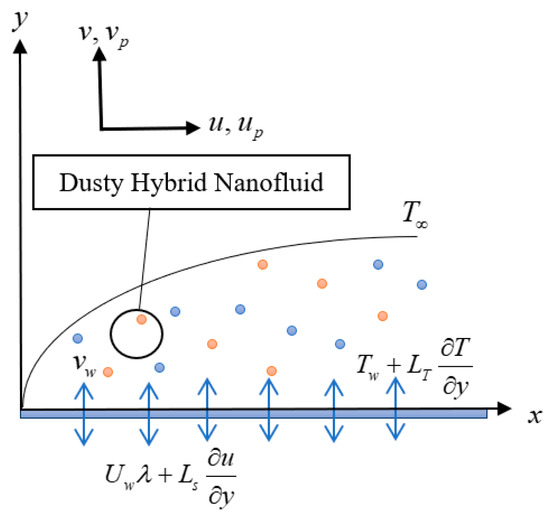
Figure 1.
Physical model (stretching, and shrinking, ).
Under this circumstance, the partial differential equations are as follows (see Devi and Devi [39] and Gireesha et al. [57]):
Fluid phase:
Dust phase:
Here, is the velocity components of the dust particle and fluid phases in the direction, while is the velocity component along the axis, and are the temperature of the dust particle and hybrid nanofluid, respectively, , and are the dust particle number, the mass of the dust particle and the Stokes drag coefficient, respectively, and are the specific heat of nanofluid and dust particles, respectively, and and are the relaxation time and thermal equilibrium time of the dust particle, respectively, i.e., the time needed by a dust cloud to adapt its velocity and temperature to the nanofluid. Further, is the density of the hybrid nanofluids, , and are the thermal conductivity, dynamic viscosity and heat capacity, respectively, of Cu–Al2O3/water.
The boundary conditions are as follows (Ibrahim and Shankar [53]):
Here, corresponds to the stretching and shrinking parameter where and signify the shrinking and stretching sheet, respectively, while signifies that of the static plate. In addition, and symbolize the velocity and thermal slip lengths, respectively. It is important to note that when , the no slip condition is indicated.
2.2. Thermophysical Properties
The thermophysical properties of nanofluids and hybrid nanofluids given by Devi and Devi [39] are presented in Table 1. In Table 1, subscript , , and denote the nanoparticle, nanofluid, hybrid nanofluid and fluid, respectively, whereas and indicate the first and second nanoparticles, respectively. Furthermore, represents the first nanoparticle volume fraction, while denotes the second. In this study, copper (Cu) and alumina (Al2O3) are taken into consideration as the second and first nanoparticle volume fractions, respectively, and water acts as a base fluid (Oztop and Abu-Nada [58]). Table 2 displays the thermophysical traits of base fluid and nanoparticles. It is important to note that Al2O3 is originally disseminated into the water to achieve the desired hybrid nanofluid (Cu-Al2O3/water). Afterwards, Cu is disseminated into the Al2O3/water nanofluid. In a remarkable study by Turkyilmazoglu [59], the nanofluids were shown to act as non-Newtonian fluids when the nanoparticle volume fraction exceeded 5–6%. Thus, in this study, the volume fraction of Al2O3 nanoparticles was set to 1%, and Cu was fluctuated from 0 to 2%, in correspondence with the work of [59]. Since the base fluid was water, the value of the Prandtl number was set to 6.2, i.e., room temperature, or nearly 295.15 K.

Table 1.
Physical properties of hybrid nanofluids.

Table 2.
Thermo physical properties of Cu, Al2O3 and water.
2.3. Similarity Solution
The following similarity variables are introduced (Naramgari and Sulochana [30]):
where is the similarity variable, is the kinematic viscosity, and are the dimensionless function for fluid phase, and and are the dimensionless function for dust phase. Further, primes denote the differentiation with respect to . In order for similarity solutions of Equations (1)–(6) together with Equation (7) to exist, we use
where is the transpiration rate constant, wherein and signify suction and injection, respectively, while refers to an impermeable plate. is a constant and is a characteristic length. Invoking Equation (8), Equations (1) and (4) are identically fulfilled, and Equations (2), (3), (5) and (6) transform into the following ordinary differential equation:
Fluid phase:
Dust phase:
where and are the fluid–particle interaction parameters for temperature and velocity, respectively, is the mass concentration of dust particles, is the ratio of specific heats, and and are the Eckert and Prandtl numbers, respectively, which are given as:
The boundary conditions are:
where and are the velocity and thermal slip parameters, respectively.
In this study, the physical quantities of interest are:
where denotes the skin friction coefficient and is the local Nusselt number. Using Equations (8) and (16), we get:
where is the local Reynolds number.
3. Stability of the Solutions
Due to the occurrence of nonuniqueness in the present research, the stability analysis was performed by referring to the work of Merkin [60], Weidman et al. [61] and Harris et al. [62]. These analyses have been implemented by other researchers too (see, for example, the work of Hamid et al. [15], Anuar et al. [27,28], Waini et al. [43] and Khashi’ie et al. [45]). Some important steps were implemented to identify the stability of solutions, i.e., (i) considering an unsteady governing equation; (ii) introducing new dimensionless time variables and similarity variables; (iii) implementing linear eigenvalue equations, and (iv) relaxing the boundary conditions.
3.1. Unsteady-State Problem
First, Equations (1)–(6) were converted into an unsteady case (dependent of time). So, continuity Equations (1) and (4) remain the same, while the other equations become:
Fluid phase:
Dust phase:
subjected to the following boundary conditions:
where denotes the time.
3.2. New Similarity Transformation
Next, a new time-dependent, dimensionless variable had to be introduced. Hence, we have (Hamid et al. [15]):
while Equation (8) is replaced by:
By substituting Equations (23) and (24) into Equations (18)–(22), we get:
Fluid phase:
Dust phase:
and the boundary conditions are:
3.3. Introducing Linear Eigenvalue Equations
The stability of the steady flow solutions can be explored by setting , , and , which satisfies the boundary value Equations (10)–(13) and Equation (15). Thus, the following equations are introduced (Weidman et al. [61]):
where , , , and their derivatives are relatively smaller than , , and . In addition, is the unknown eigenvalue which will be used to specify the stability of the solutions. Substituting Equation (30) into Equations (25)–(29) and letting , in which , , and , we have:
Fluid phase:
Dust phase:
The conditions now take the following form:
3.4. Relaxation of Boundary Condition
To solve the stability model, we needed to relax the boundary conditions as proposed by Harris et al. [62]. For that reason, the conditions as were replaced by new conditions . It should be pointed out that the linearized boundary value Equations (31)–(35), together with new conditions , yielded the unlimited set of unknown eigenvalues . If the smallest eigenvalues showed a positive sign, the solutions observed an initial decay of perturbation, and accordingly indicated a stable solution. On the other hand, as the smallest eigenvalues showed a negative sign, an early growth of disruption was noticed, which signified an unstable solution.
4. Numerical Solutions and Discussions
To solve the boundary value Equations (10)–(13) with the boundary conditions given by Equation (15), we adopted a built-in function called bvp4c from Matlab package. Bvp4c is a finite difference code that applies the three stage Lobato IIIa formula (Shampine et al. [63], Kierzenka and Shampine [64]). In this research, the appropriate finite values of was set to be 10. Further, to ensure the precision of the current algorithm, the current results of skin friction coefficient
were compared with previously reported solutions of Hayat et al. [65] and Ibrahim and Shankar [53]. These comparative solutions are revealed in Table 3 for selected values of velocity slip parameter . Additionally, a comparison of the values of heat transfer for the present method with those obtained by Gireesha et al. [57] and Naramgari and Sulochana [30] was made; see Table 4. It can be observed from these tables that good agreement with these methods was achieved, thereby confirming the consistency of the present approach.

Table 3.
Values of for extended sheet when and .

Table 4.
Comparative values of for stretching sheet when and .
In this section, the results of local skin friction , Nusselt number , velocity profiles for fluid phase and dust phase , as well as the temperature profiles for the fluid phase and dust phase are illustrated graphically to examine the impact of some governing parameters, namely, Cu nanoparticle volume fraction , suction parameter , velocity slip parameter , thermal slip parameter , fluid interaction parameter for velocity , fluid interaction parameter for temperature and mass concentration . Figure 2 and Figure 3 depict the influence of the Cu nanoparticle volume fraction parameter toward suction parameter on the local skin friction and Nusselt number for the shrinking sheet , as given in Equation (17). From these figures, it is interesting to see that two solutions are likely to occur for a particular range of suction parameters. For instance, when , the solutions are bound to exist when , while as increases to and , the range of suction increases, i.e., and . It should also be mentioned that the increment of the volume fraction of Cu nanoparticle from to enhances both and . Moreover, the values of and for the first solution increase as suction parameter increases, while the opposite was observed for the second solution.
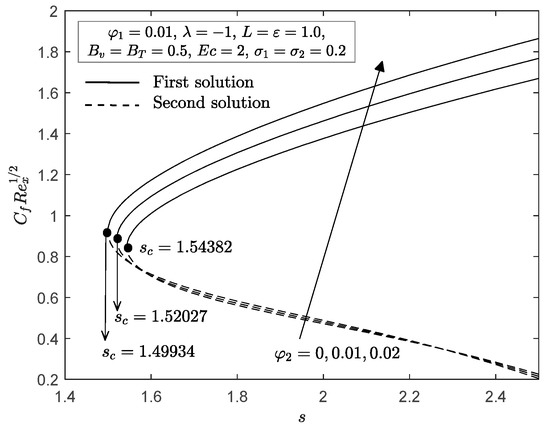
Figure 2.
with for various .
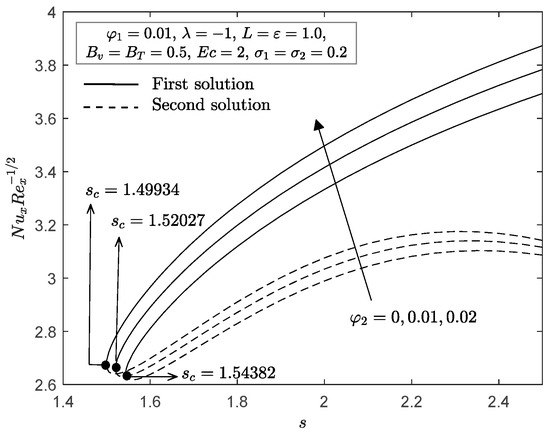
Figure 3.
with for various .
The effects of Cu nanoparticle volume fraction against stretching/shrinking parameter on the local skin friction and Nusselt number are shown in Figure 4 and Figure 5. It is apparent from these figures that for all values of stretching/shrinking parameter , dual solutions occurred. However, it should be noted that no solution exists when which indicates that the boundary layer separates from the surface and the principles of boundary layer theory are no longer valid. Moreover, is the critical point that connects the first and second solutions. From Figure 4, it may be seen that an increase in the Cu nanoparticle volume fraction enhances the local skin friction when the sheet is shrinking in both solutions, while it decreases when the sheet is stretched in both solutions. In addition, it is evident from Figure 5 that the enhancement in a Cu nanoparticle volume fraction improves the local Nusselt number in the first and second solutions. This finding proves that the increment of Cu nanoparticle volume fraction can improve the heat transfer efficiency. This also implies that the dusty hybrid nanofluid provides better heat performance than the dusty nanofluid. Furthermore, an enhancement of the Cu nanoparticle volume fraction on and can delay the boundary layer flow separation. Figure 6 and Figure 7 demonstrate the velocity and temperature profiles when the Cu nanoparticle volume fraction varies from to for both the fluid and dust phases. It reveals that increasing the Cu nanoparticle volume fraction decreases the momentum and thermal boundary layer thickness in the first solution of both phases. However, the opposite was observed with the second solution. Furthermore, we can see that the boundary layer thickness of the first solution and dust phase was slimmer than that of the fluid phase. In addition, all the published profiles are asymptotically satisfied with Equation (15) when is used in the bvp4c function (MATLAB); this supports the findings in Figure 4 and Figure 5.
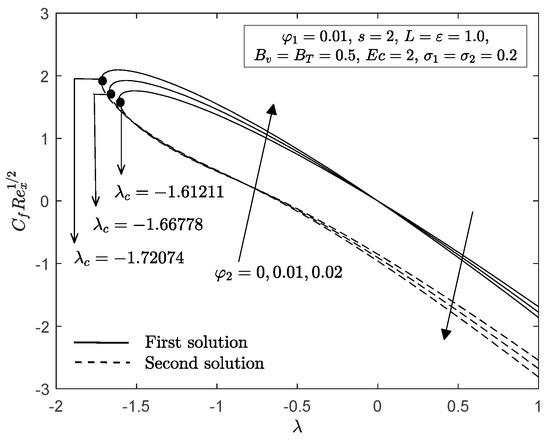
Figure 4.
with for various .
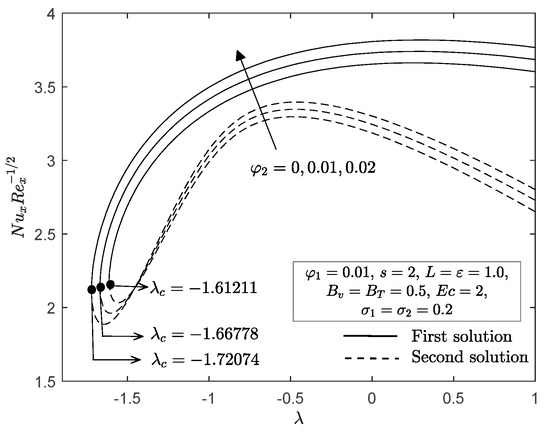
Figure 5.
with for various .
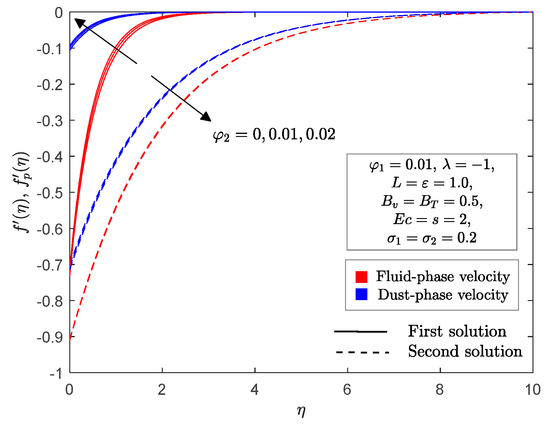
Figure 6.
for selected values of .
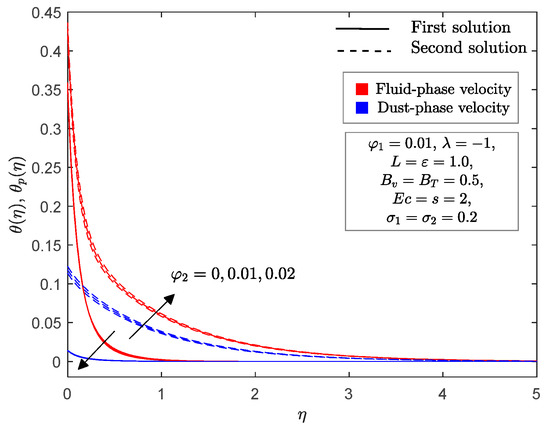
Figure 7.
for selected values of .
Figure 8 and Figure 9 show the impact of the no-slip parameter and slip parameters on the local skin friction and Nusselt number toward the permeable stretching/shrinking parameter . The occurrence of slip parameters (velocity, and thermal, ) consequently diminishes the local skin friction when the sheet is shrinking , but increases it for a stretching sheet in both solutions. In Figure 9, the local Nusselt number shows a declining trend in both solutions, along with a simultaneous increment of slip parameters . A simultaneous increase in both the velocity and thermal slip parameters postpones boundary layer separation, as shown in Figure 8 and Figure 9. A diminished momentum boundary layer thickness was observed in the first solution when the velocity slip parameter increased on the dusty hybrid nanofluid for both phases, as shown in Figure 10; however, the opposite occurred for the second solution. Note that when , it corresponds to thermal slip only, while when , it corresponds to velocity slip only. On the other hand, Figure 11 and Figure 12 illustrate the variation of the temperature profile of the fluid and dust phases when velocity and thermal slip parameters fluctuate from to , respectively. It is interesting to observe from these figures that for the first and second solutions, the thermal boundary layer thickness decreased with an increase in velocity and thermal slip parameters. However, we did not plot the velocity profiles for thermal slip parameter , as this parameter caused no changes in the velocity profiles.
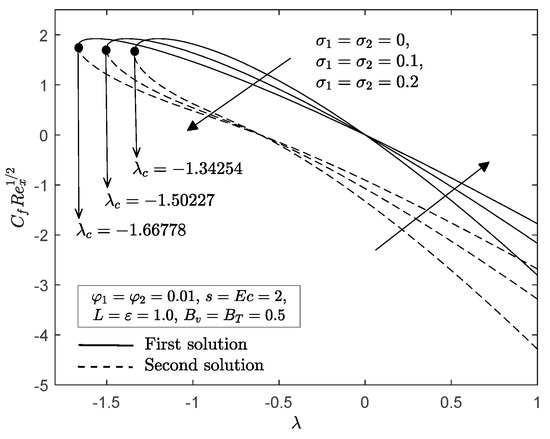
Figure 8.
with for various slip parameters.
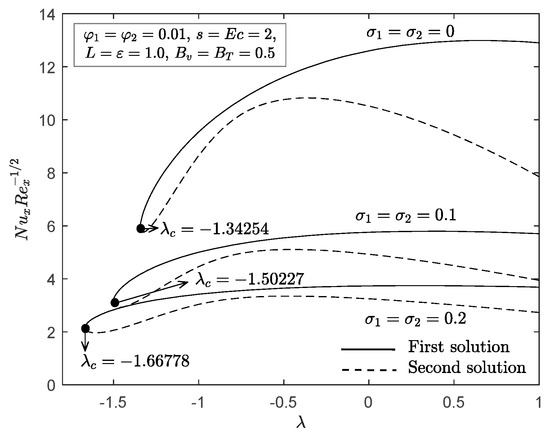
Figure 9.
with for various slip parameters.
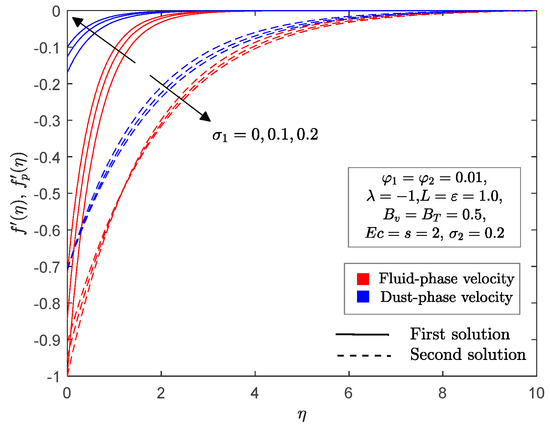
Figure 10.
for selected values of .
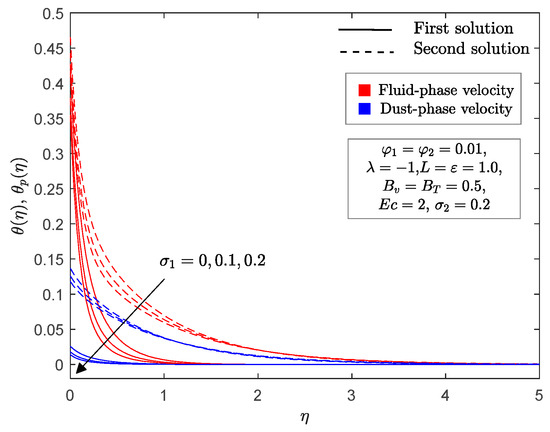
Figure 11.
for selected values of .
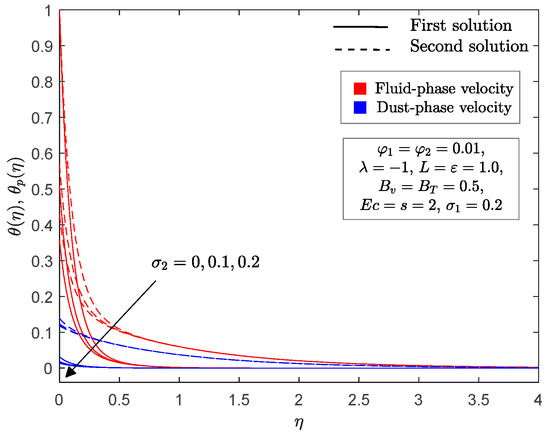
Figure 12.
for selected values of .
The distribution of velocity and temperature profiles for selected values of fluid particle interaction parameters for velocity and temperature are plotted in Figure 13 and Figure 14. For increasing velocity fluid particle interaction parameter , the momentum boundary layer thickness decreased for the fluid phase, while the opposite occurred for the dust phase in the first solution. Nevertheless, the thickness of the momentum boundary layer increased in the second solution for both phases. Additionally, the temperature profile in Figure 14 indicates that the thermal boundary layer thickness for the first and second solutions was diminished with increasing values of . Meanwhile, the temperature profile in the dust phase showed the opposite result from the fluid phase in both solutions. It is evident from Figure 13 and Figure 14 that a very high value of and will eventually cause the velocity and temperature for both phases to be the same.
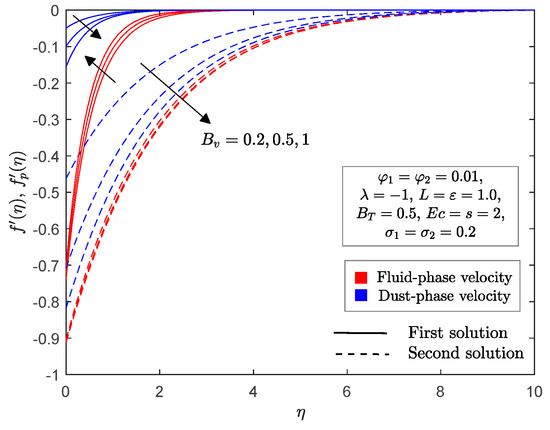
Figure 13.
for selected values of .
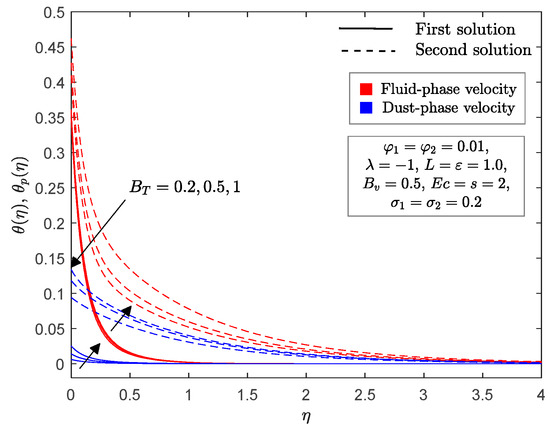
Figure 14.
for selected values of .
Figure 15 and Figure 16 are plotted to indicate the impact of mass concentration of dust particles on the velocity and temperature profiles for the fluid and dust phases in a permeable shrinking sheet . When the mass concentration increases, the thickness of the momentum boundary layer decreases for the fluid and dust phases in the first solution, while it increases in the second. This finding can be explained by the fact that the drag force between the hybrid nanofluid and dust particle will increase as the mass concentration increases; this will consequently slow down the fluid motion. On the other hand, thickening of the thermal boundary layer was noticed for the fluid and dust phases as the mass concentration increased in both solutions.
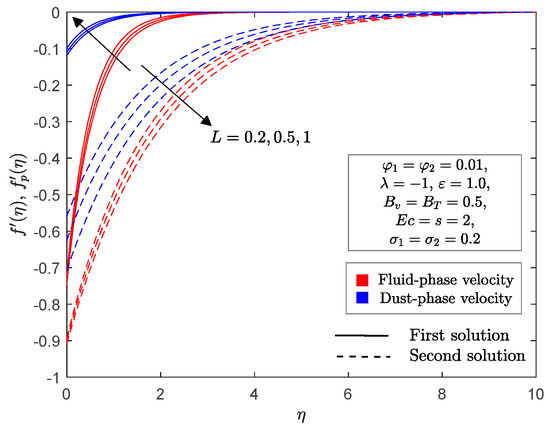
Figure 15.
for selected values of .
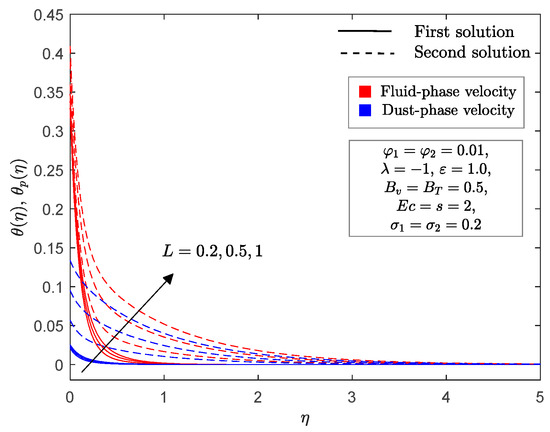
Figure 16.
for selected values of .
The boundary value Equations (10)–(13), together with Equation (15), provided nonunique solutions for some governing parameters. The phenomenon of nonunique solutions, namely, the first and second solutions, was proven; see Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. Accordingly, a stability analysis was performed to identify the most stable solutions. Linearized Equations (31)–(34), along with Equation (35), were numerically with the aid of the bvp4 function in MATLAB. The smallest eigenvalues on the selected parameter and from Figure 4 and Figure 5 are listed in Table 5. The values of , however, drew closer to zero in both (first and second) solutions as the stretching/shrinking parameter approached its critical value. Apart from this, it is shown that the second solution displayed negative values of , whereas the first demonstrated positive values. The smallest eigenvalues against when are plotted in Figure 17. This figure supports the findings presented in Table 5. In reference to the previous literature, we propose that the first solution is stable while the second is unstable. It is worth noting that this analysis is important in identifying the stable solution when nonunique solutions exist, so that the flow behavior can be accurately predicted.
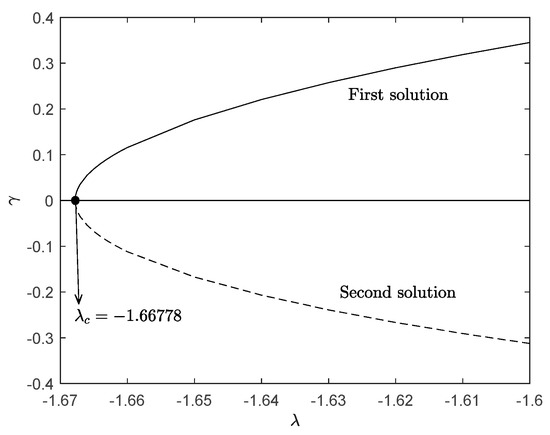
Figure 17.
Smallest eigenvalue versus .

Table 5.
Smallest eigenvalues for selected values of and .
5. Conclusions
The flow of a dusty hybrid nanofluid over a permeable deformable sheet with velocity and thermal slip was investigated numerically. The similarity solutions were produced by utilizing the bvp4c function in the MATLAB software (R2018a, MathWorks, Natick, MA, USA). The impact of emerging parameters was examined and illustrated graphically. The conclusions can be summarized as follows:
- The presence of double solutions is noticeable for a stretching and shrinking sheet when suction parameter is imposed.
- A stability analysis was carried out and the first solution proved to be stable, whereas the other solution was not.
- An increase in the Cu nanoparticle volume fraction in the dusty nanofluid has a tendency to improve the local Nusselt number for all range of , and to increase the local skin friction for shrinking sheet; however, the opposite is true for a stretching sheet.
- The simultaneous increase of velocity and thermal slip parameters decrease the local Nusselt number for fluid phase.
- The similarity solutions can be widened with an increase in Cu nanoparticle volume fraction and slip parameters (velocity and thermal ), thereby delaying boundary layer separation.
- The momentum thickness in fluid phase decreases and dust phase increases as velocity fluid interaction parameter increases.
- An upsurge of fluid interaction for temperature parameter decreases the thermal boundary layer thickness of the fluid phase, while it does the opposite in the dust phase.
- The mass concentration of dust particle decreases the momentum thickness but increases the thermal thickness in both phases.
Author Contributions
Conceptualization, N.B. and I.P.; methodology, formal analysis and writing—original draft preparation, N.S.A.; validation, N.S.A., N.B. and I.P.; writing—review and editing, supervision, N.B. and I.P.; funding acquisition, N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Grant Scheme (FRGS) under Ministry of Education with project number FRGS/1/2018/STG06/UPM/02/4.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to its large size.
Acknowledgments
The authors wish to express their sincere thanks to the very competent reviewers for the good comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramesh, G.K.; Gireesha, B.; Bagewadi, C.S. Unsteady flow of a conducting dusty fluid between two circular cylinders. Acta Math. Univ. Comen. 2011, 80, 171–184. [Google Scholar]
- Gireesha, B.J.; Mahanthesh, B.; Manjunatha, P.T.; Gorla, R.S.R. Numerical solution for hydromagnetic boundary layer flow and heat transfer past a stretching surface embedded in non-Darcy porous medium with fluid-particle suspension. J. Niger. Math. Soc. 2015, 34, 267–285. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Magnetohydrodynamic two-phase dusty fluid flow and heat model over deforming isothermal surfaces. Phys. Fluids 2017, 29, 013302. [Google Scholar] [CrossRef]
- Saffman, P.G. On the stability of laminar flow of a dusty gas. J. Fluid Mech. 1962, 13, 120–128. [Google Scholar] [CrossRef]
- Chakrabarti, K.M. Note on boundary layer in a dusty gas. AIAA J. 1974, 12, 1136–1137. [Google Scholar] [CrossRef]
- Datta, N.; Mishra, S.K. Boundary layer flow of a dusty fluid over a semi-infinite flat plate. Acta Mech. 1982, 42, 71–83. [Google Scholar] [CrossRef]
- Vajravelu, K.; Nayfeh, J. Hydromagnetic flow of a dusty fluid over a stretching sheet. Int. J. Non-Linear Mech. 1992, 27, 937–945. [Google Scholar] [CrossRef]
- Attia, H.A. Influence of temperature dependent viscosity on the MHD-channel flow of dusty fluid with heat transfer. Acta Mech. 2001, 151, 89–101. [Google Scholar] [CrossRef]
- Ajadi, S.O. A note on the unsteady flow of dusty viscous fluid between two parallel plates. J. Appl. Math. Comput. 2005, 18, 393–403. [Google Scholar] [CrossRef][Green Version]
- Damseh, R.A. On boundary layer flow of a dusty gas from a horizontal circular cylinder. Braz. J. Chem. Eng. 2010, 27, 653–662. [Google Scholar] [CrossRef][Green Version]
- Gireesha, B.J.; Chamkha, A.J.; Manjunatha, S.; Bagewadi, C.S. Mixed convective flow of a dusty fluid over a vertical stretching sheet with non-uniform heat source/sink and radiation. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 598–612. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T. MHD transient flows and heat transfer of dusty fluid in a channel with variable physical properties and Navier slip condition. Comput. Math. Appl. 2010, 60, 660–669. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Gireesha, B.J.; Manjunatha, P.T. Melting phenomenon in MHD stagnation point flow of dusty fluid over a stretching sheet in the presence of thermal radiation and non-uniform heat source/sink. Int. J. Comput. Methods Eng. Sci. Mech. 2015, 16, 265–274. [Google Scholar] [CrossRef]
- Jalil, M.; Asghar, S.; Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng. 2017, 2017, 2307469. [Google Scholar] [CrossRef]
- Hamid, R.A.; Nazar, R.; Pop, I. Boundary layer flow of a dusty fluid over a permeable shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 758–772. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Mahanthesh, B.; Makinde, O.D.; Muhammad, T. Effects of Hall current on transient flow of dusty fluid with nonlinear radiation past a convectively heated stretching plate. Defect Diffus. Forum 2018, 387, 352–363. [Google Scholar] [CrossRef]
- Abbas, Z.; Hasnain, J.; Sajid, M. Effects of slip on MHD flow of a dusty fluid over a stretching sheet through porous space. J. Eng. Thermophys. 2019, 28, 84–102. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Shashikumar, N.S.; Ramesh, G.K. Magnetohydrodynamic flow of dusty fluid over Riga plate with deforming isothermal surfaces with convective boundary condition. Songklanakarin J. Sci. Technol. 2020, 42, 487–495. [Google Scholar]
- Choi, S.U.S.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–103. [Google Scholar]
- Rafati, M.; Hamidi, A.A.; Niaser, M.S. Application of nanofluids in computer cooling systems (heat transfer performance of nanofluids). Appl. Therm. Eng. 2012, 45, 9–14. [Google Scholar] [CrossRef]
- Xian, H.W.; Sidik, N.A.C.; Najafi, G. Recent state of nanofluid in automobile cooling systems. J. Therm. Anal. Calorim. 2019, 135, 981–1008. [Google Scholar] [CrossRef]
- Sheikhpour, M.; Arabi, M.; Kasaeian, A.; Rabei, A.R.; Taherian, Z. Role of Nanofluids in Drug Delivery and Biomedical Technology: Methods and Applications. Nanotechnol. Sci. Appl. 2020, 13, 47. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, P.K.; Subramani, J.; Suyambazhahan, S.; Sathyamurthy, R. Nanofluids for solar collector applications: A review. Energy Procedia 2014, 61, 2416–2434. [Google Scholar] [CrossRef]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Boundary layer stagnation-point flow toward a stretching/shrinking sheet in a nanofluid. J. Heat Transf. 2013, 135, 054501. [Google Scholar] [CrossRef]
- Pop, I.; Seddighi, S.; Bachok, N.; Ismail, F. Boundary layer flow beneath a uniform free stream permeable continuous moving surface in a nanofluid. J. Heat Mass Transf. Res. 2014, 1, 55–65. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Arifin, N.M.; Rosali, H. MHD flow past a nonlinear stretching/shrinking sheet in carbon nanotubes: Stability analysis. Chin. J. Phys. 2020, 65, 436–446. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Turkyilmazoglu, M.; Arifin, N.M.; Rosali, H. Analytical and stability analysis of MHD flow past a nonlinearly deforming vertical surface in Carbon Nanotubes. Alex. Eng. J. 2020, 59, 497–507. [Google Scholar] [CrossRef]
- Gorla, R.S.R.; Gireesha, B.J.; Singh, B. MHD flow and heat transfer of dusty nanofluid embedded in porous medium over an exponentially stretching sheet. J. Nanofluids 2015, 4, 449–460. [Google Scholar] [CrossRef]
- Naramgari, S.; Sulochana, C. MHD flow of dusty nanofluid over a stretching surface with volume fraction of dust particles. Ain Shams Eng. J. 2016, 7, 709–716. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Ganji, D.D.; Hatami, M. Fe3O4–(CH2OH)2 nanofluid analysis in a porous medium under MHD radiative boundary layer and dusty fluid. J. Mol. Liq. 2018, 258, 172–185. [Google Scholar] [CrossRef]
- Siddiqa, S.; Begum, N.; Hossain, M.A.; Gorla, R.S.R.; Al-Rashed, A.A. Two-phase natural convection dusty nanofluid flow. Int. J. Heat Mass Transf. 2018, 118, 66–74. [Google Scholar] [CrossRef]
- Kalpana, G.; Madhura, K.R.; Iyengar, S.S. Numerical computation on Marangoni convective flow of two-phase MHD dusty nanofluids under Brownian motion and thermophoresis effects. Heat Transf. Asian Res. 2020, 49, 626–650. [Google Scholar] [CrossRef]
- Mishra, S.R.; Khan, M.I.; Rout, B.C. Dynamics of dust particles in a conducting dusty nanomaterial: A computational approach. Int. Commun. Heat Mass Transf. 2020, 119, 104967. [Google Scholar] [CrossRef]
- Saha, L.K.; Bala, S.K.; Roy, N.C. Natural convection of dusty nanofluids within a concentric annulus. Eur. Phys. J. Plus 2020, 135, 1–20. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gamachu, D. Dusty Nanofluid Past a Centrifugally Stretching Surface. Math. Probl. Eng. 2020, 2020, 9163081. [Google Scholar] [CrossRef]
- Madhesh, D.; Kalaiselvam, S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014, 97, 1667–1675. [Google Scholar] [CrossRef]
- Tahat, M.S.; Benim, A.C. Experimental analysis on thermophysical properties of Al2O3/CuO hybrid nano fluid with its effects on flat plate solar collector. Defect Diffus. Forum 2017, 374, 148–156. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Anuar, N.S.; Bachok, N.; Pop, I. Radiative hybrid nanofluid flow past a rotating permeable stretching/shrinking sheet. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Jafarimoghaddam, A.; Pop, I. Cross flow and heat transfer past a permeable stretching/shrinking sheet in a hybrid nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2020. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Sherif, E.S.M. Dual solutions and stability analysis of a hybrid nanofluid over a stretching/shrinking sheet executing MHD flow. Symmetry 2020, 12, 276. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Khan, M.R.; Pan, K.; Khan, A.U.; Nadeem, S. Dual solutions for mixed convection flow of SiO2− Al2O3/water hybrid nanofluid near the stagnation point over a curved surface. Phys. A Stat. Mech. Appl. 2020, 547, 123959. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed Convective Stagnation Point Flow towards a Vertical Riga Plate in Hybrid Cu-Al2O3/Water Nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Hosseinzadeh, K.; Hatami, M.; Ganji, D.D. MHD boundary layer analysis for micropolar dusty fluid containing Hybrid nanoparticles (Cu-Al2O3) over a porous medium. J. Mol. Liq. 2018, 268, 813–823. [Google Scholar] [CrossRef]
- Raizah, Z.A. Natural Convection of Dusty Hybrid Nanofluids in an Enclosure Including Two Oriented Heated Fins. Appl. Sci. 2019, 9, 2673. [Google Scholar] [CrossRef]
- Reddy, M.G.; Rani, M.V.V.N.L.S.; Kumar, K.G.; Prasannakumar, B.C.; Lokesh, H.J. Hybrid dusty fluid flow through a Cattaneo–Christov heat flux model. Phys. A Stat. Mech. Appl. 2020, 551, 123975. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Dual solutions in boundary layer stagnation-point flow and mass transfer with chemical reaction past a stretching/shrinking sheet. Int. Commun. Heat Mass Transf. 2011, 38, 917–922. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Wang, C.Y. Flow due to a stretching boundary with partial slip—an exact solution of the Navier–Stokes equations. Chem. Eng. Sci. 2002, 57, 3745–3747. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C. Slip effects on an unsteady boundary layer stagnation-point flow and heat transfer towards a stretching sheet. Chin. Phys. Lett. 2011, 28, 094702. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shankar, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Khan, M.I.; Tamoor, M.; Hayat, T.; Alsaedi, A. MHD boundary layer thermal slip flow by nonlinearly stretching cylinder with suction/blowing and radiation. Results Phys. 2017, 7, 1207–1211. [Google Scholar] [CrossRef]
- Das, K. Slip flow and convective heat transfer of nanofluids over a permeable stretching surface. Comput. Fluids 2012, 64, 34–42. [Google Scholar] [CrossRef]
- Kho, Y.B.; Hussanan, A.; Mohamed, M.K.A.; Sarif, N.M.; Ismail, Z.; Salleh, M.Z. Thermal radiation effect on MHD Flow and heat transfer analysis of Williamson nanofluid past over a stretching sheet with constant wall temperature. J. Phys. Conf. Ser. 2017, 890, 012034. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Chamkha, A.J.; Rudraswamy, N.G.; Krishnamurthy, M.R. MHD flow and heat transfer of a nanofluid embedded with dust particles over a stretching sheet. J. Nanofluids 2015, 4, 66–72. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A Note on the correspondence between certain nanofluid flows and standard fluid flows. J. Heat Transf. 2015, 137, 024501. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary layer flow near the stagnation point on a vertical surface in porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Kierzenka, J.; Reichelt, M.W. Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutor. Notes 2000, 2000, 1–27. [Google Scholar]
- Kierzenka, J.; Shampine, L.F. A BVP solver based on residual control and the Maltab PSE. ACM Trans. Math. Softw. (TOMS) 2001, 27, 299–316. [Google Scholar] [CrossRef]
- Hayat, T.; Qasim, M.; Mesloub, S. MHD flow and heat transfer over permeable stretching sheet with slip conditions. Int. J. Numer. Methods Fluids 2011, 66, 963–975. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).