Mathematical and Statistical Analysis of Doubling Times to Investigate the Early Spread of Epidemics: Application to the COVID-19 Pandemic
Abstract
1. Introduction
2. Data Sources
2.1. Representative Country-Level COVID-19 Data
2.2. Synthetic Epidemic Growth Data
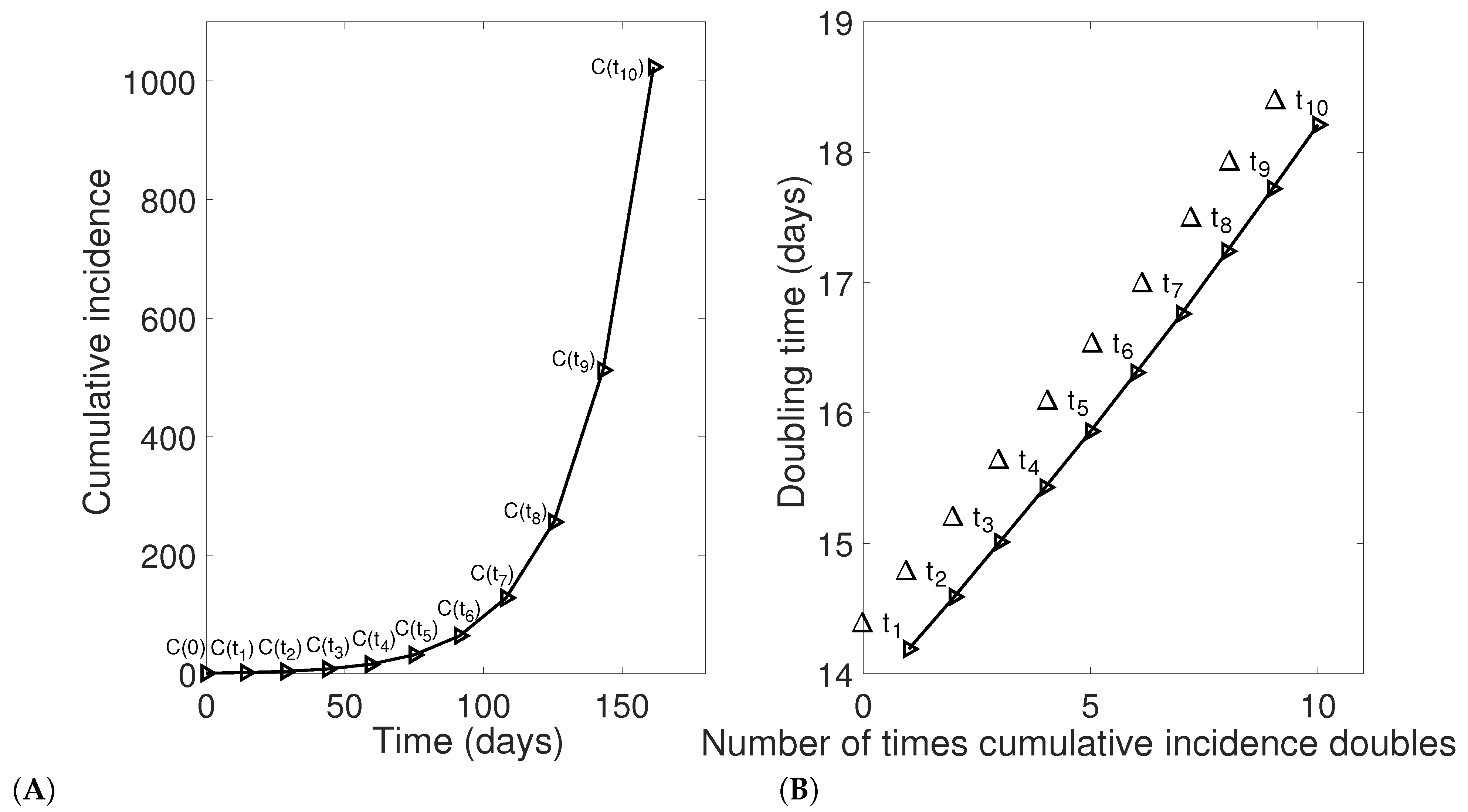
3. The Generalized-Growth Model for Early Ascending Phase
4. Evolution of Doubling Times for Sub-Exponential Growth. Mathematical Analysis
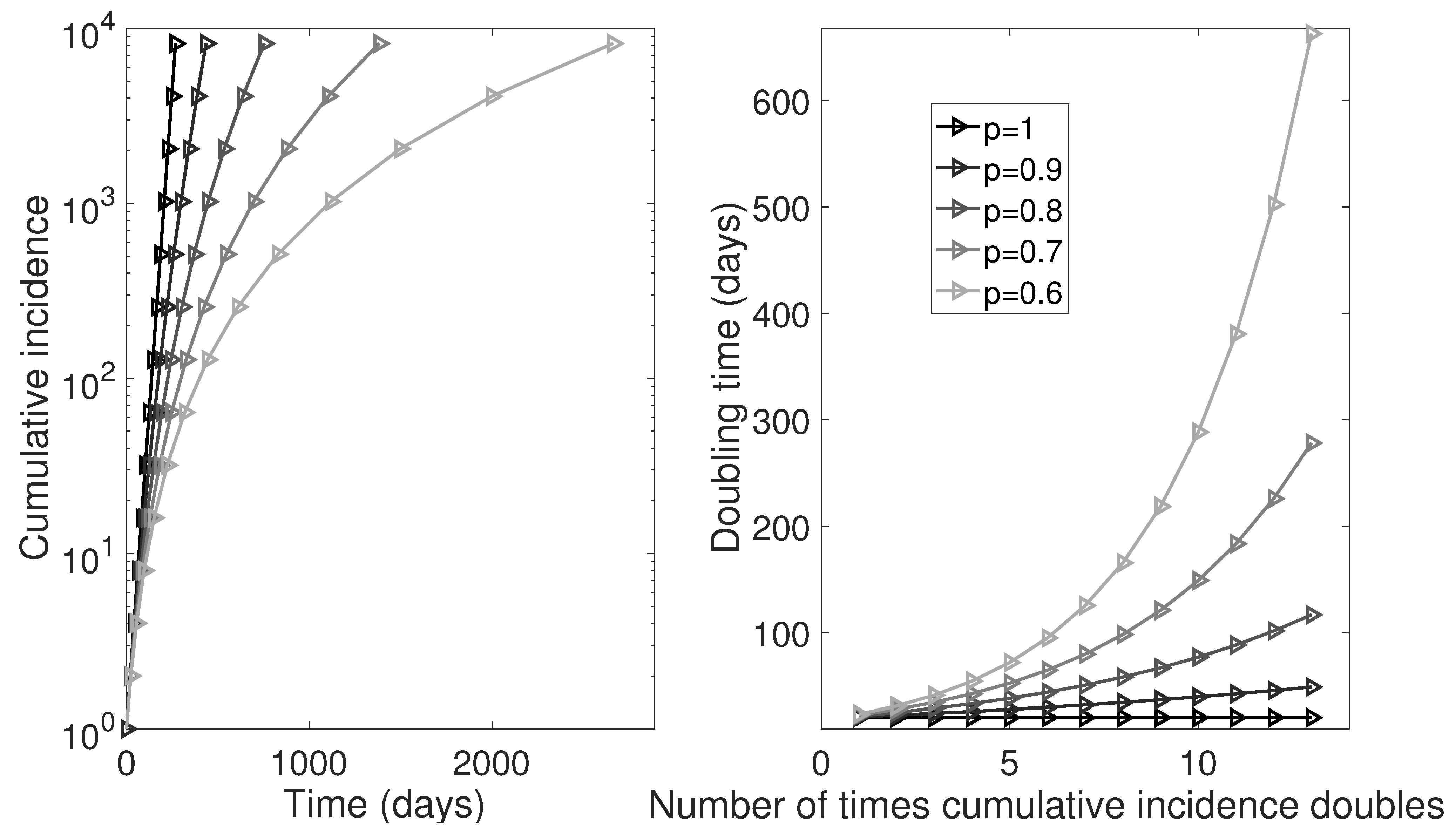
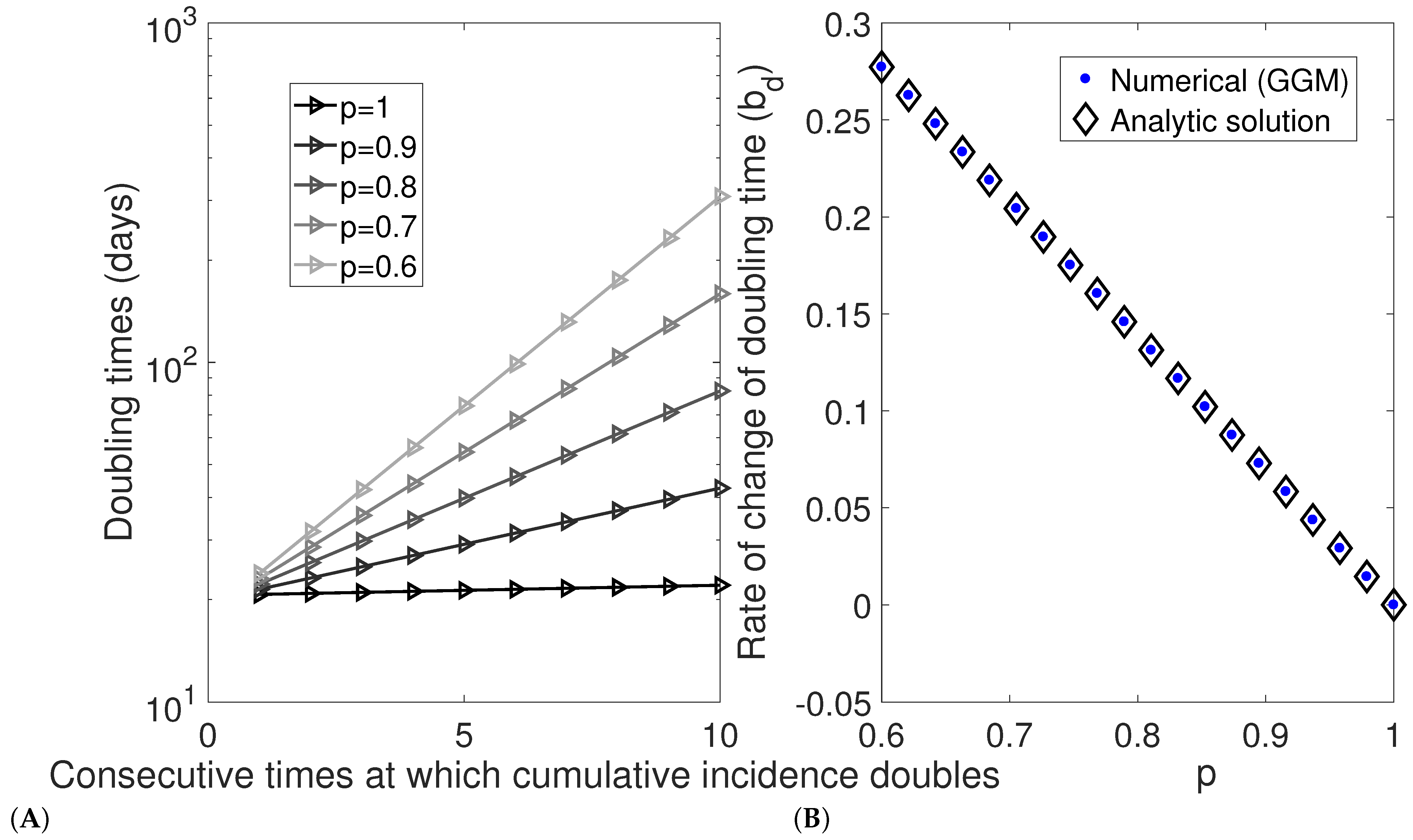
5. Simulation Studies to Verify Analytic Results
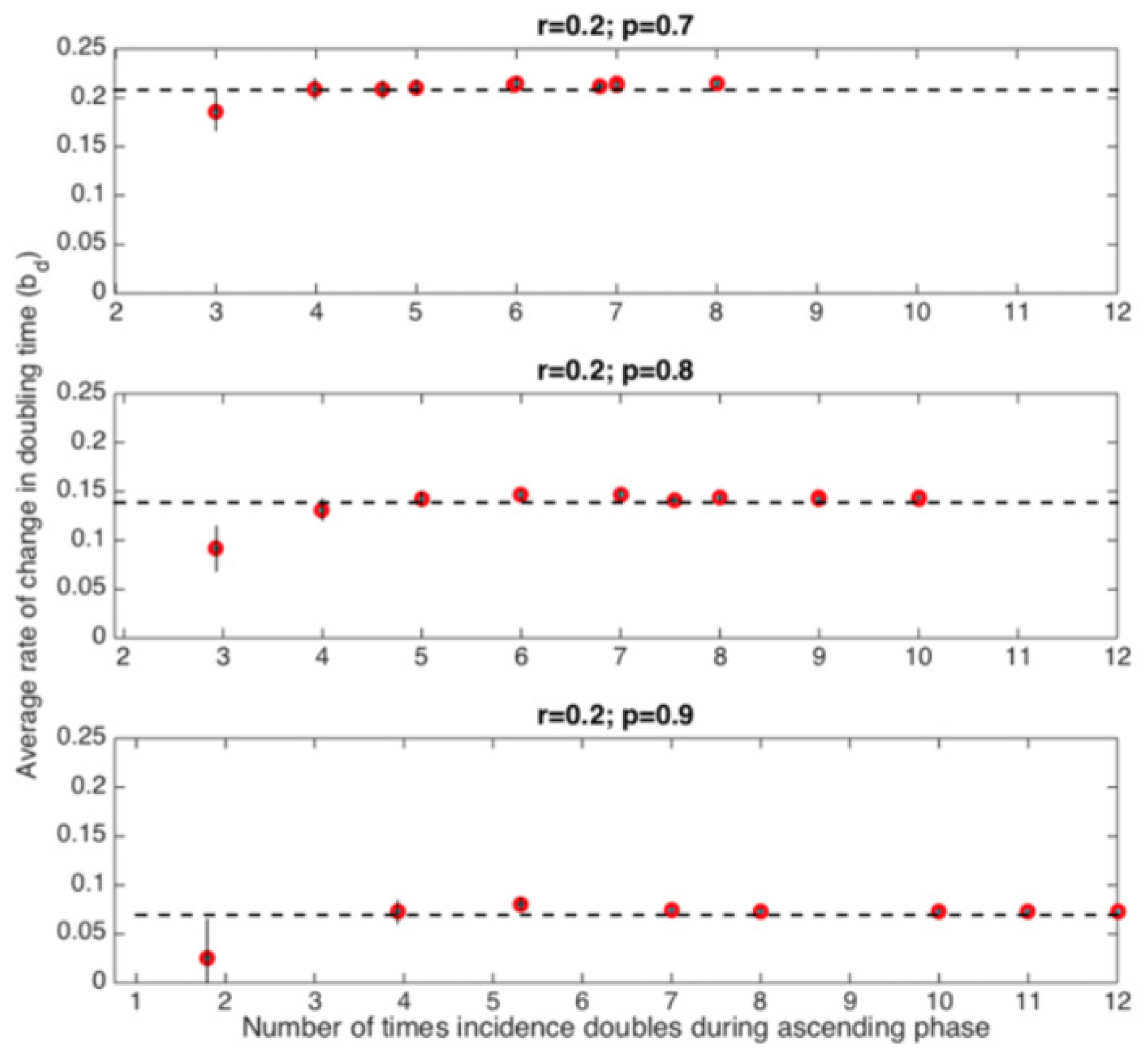
5.1. Estimating the Rate of Change of Doubling Times from Epidemic Data
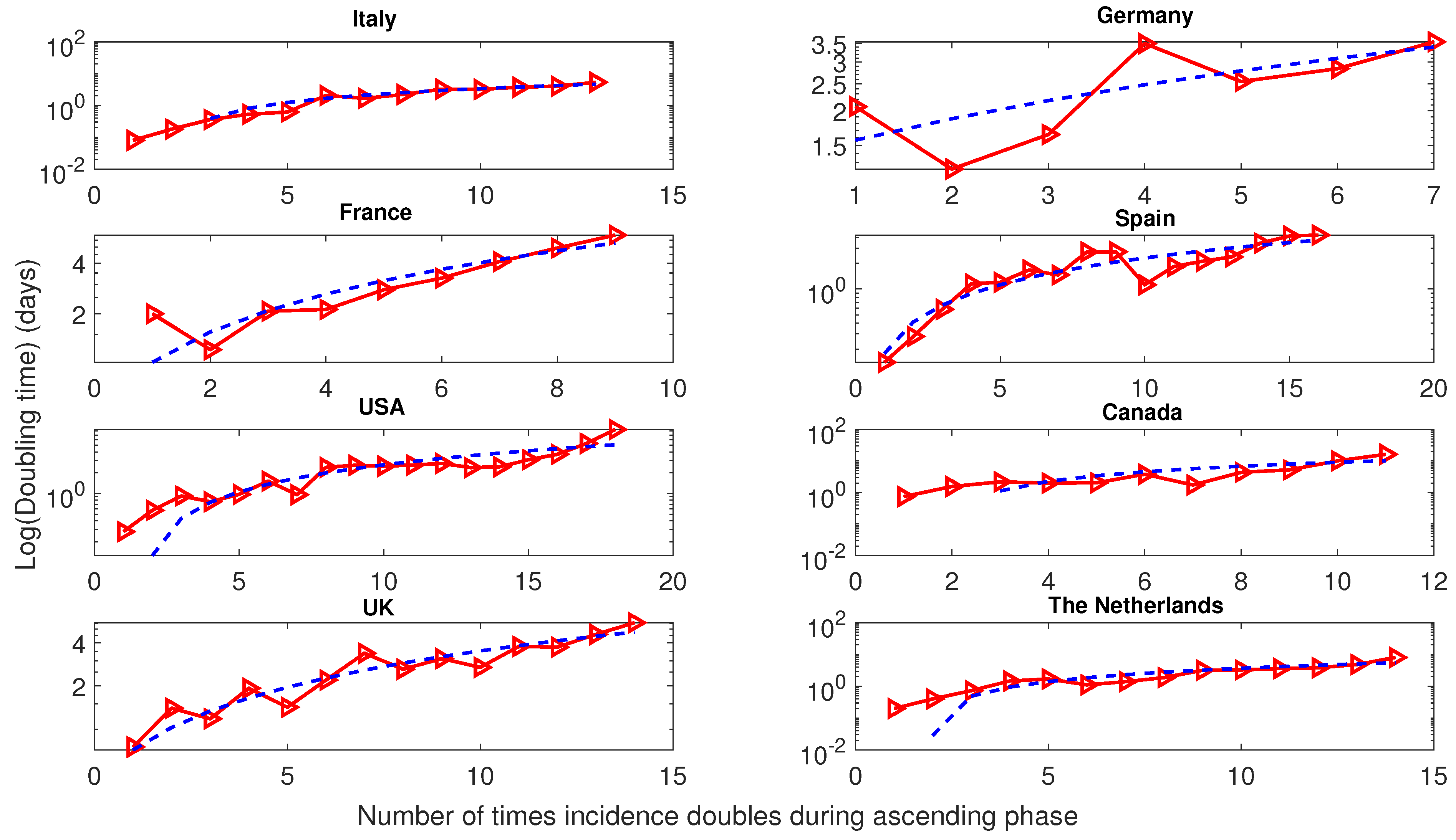
5.2. Doubling Time Analysis of COVID-19 Epidemics
6. Conclusions
- (1)
- Our approach provides a framework to numerically and mathematically characterize the rate at which the doubling time of an epidemic is changing over time.
- (2)
- We derive analytical formulas of the rate at which the doubling time is changing and test and illustrate our methodology using synthetic and COVID-19 epidemic data.
- (3)
- Our mathematical analysis (and proof) demonstrates that the series of epidemic doubling times increase approximately according to an exponential function with a rate that quantifies the rate of change of the doubling times. Our analytic results are in excellent agreement with numerical simulations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weiss, R.A.; McMichael, A.J. Social and environmental risk factors in the emergence of infectious diseases. Nat. Med. 2004, 10, S70–S76. [Google Scholar] [CrossRef]
- Lloyd-Smith, J.O.; Schreiber, S.J.; Kopp, P.E.; Getz, W.M. Superspreading and the effect of individual variation on disease emergence. Nat. Cell Biol. 2005, 438, 355–359. [Google Scholar] [CrossRef]
- Szendroi, B.; Csnyi, G. Polynomial epidemics and clustering in contact networks. Proc. R. Soc. Lond. Ser. Biol. Sci. 2004, 271 (Suppl. S5), S364–S366. [Google Scholar] [CrossRef] [PubMed]
- Chowell, G.; Viboud, C.; Hyman, J.M.; Simonsen, L. The Western Africa Ebola Virus Disease Epidemic Exhibits Both Global Exponential and Local Polynomial Growth Rates. PLoS Curr. 2014, 7, 7. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases of Humans; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Kenah, E.; Lipsitch, M.; Robins, J.M. Generation interval contraction and epidemic data analysis. Math. Biosci. 2008, 213, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Gostic, K.M.; McGough, L.; Baskerville, E.B.; Abbott, S.; Joshi, K.; Tedijanto, C.; Kahn, R.; Niehus, R.; Hay, J.A.; De Salazar, P.M.; et al. Practical considerations for measuring the effective reproductive number, Rt. PLoS Comput. Biol. 2020, 16, e1008409. [Google Scholar] [CrossRef]
- Chowell, G.; Viboud, C.; Simonsen, L.; Moghadas, S.M. Characterizing the reproduction number of epidemics with early sub-exponential growth dynamics. J. R. Soc. Interface 2016, 13. [Google Scholar] [CrossRef]
- Muniz-Rodriguez, K.; Fung, I.C.-H.; Ferdosi, S.R.; Ofori, S.K.; Lee, Y.; Tariq, A.; Chowell, G. Severe Acute Respiratory Syndrome Coronavirus 2 Transmission Potential, Iran, 2020. Emerg. Infect. Dis. 2020, 26, 1915–1917. [Google Scholar] [CrossRef] [PubMed]
- Shim, E.; Tariq, A.; Chowell, G. Spatial variability in reproduction number and doubling time across two waves of the COVID-19 pandemic in South Korea, February to July, 2020. Int. J. Infect. Dis. 2021, 102, 1–9. [Google Scholar] [CrossRef]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.; Yan, P.; Chowell, G. Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 2020, 5, 256–263. [Google Scholar] [CrossRef]
- Nishiura, H.; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Chowell, G., Hyman, J.M., Bettencourt, L.M.A., Castillo-Chavez, C., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 103–121. [Google Scholar]
- Muniz-Rodriguez, K.; Chowell, G.; Cheung, C.-H.; Jia, D.; Lai, P.-Y.; Lee, Y.; Liu, M.; Ofori, S.K.; Roosa, K.M.; Simonsen, L.; et al. Doubling Time of the COVID-19 Epidemic by Province, China. Emerg. Infect. Dis. 2020, 26, 1912–1914. [Google Scholar] [CrossRef] [PubMed]
- Yan, P.; Chowell, G. Quantitative Methods for Investigating Infectious Disease Outbreaks; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Anderson, R.M.; Medley, G.F. Epidemiology of HIV infection and AIDS: Incubation and infectious periods, survival and vertical transmission. AIDS 1988, 2 (Suppl. S1), 57–63. [Google Scholar] [CrossRef]
- Galvani, A.P.; Lei, X.; Jewell, N.P. Severe Acute Respiratory Syndrome: Temporal Stability and Geographic Variation in Case-Fatality Rates and Doubling Times. Emerg. Infect. Dis. 2003, 9, 991–994. [Google Scholar] [CrossRef]
- Betensky, R.A.; Feng, Y. Accounting for incomplete testing in the estimation of epidemic parameters. Int. J. Epidemiol. 2020, 49, 1419–1426. [Google Scholar] [CrossRef] [PubMed]
- Fung, I.C.-H.; Zhou, X.; Cheung, C.-N.; Ofori, S.K.; Muniz-Rodriguez, K.; Cheung, C.-H.; Lai, P.-Y.; Liu, M.; Chowell, G. Assessing Early Heterogeneity in Doubling Times of the COVID-19 Epidemic across Prefectures in Mainland China, January–February, 2020. Epidemiologia 2021, 2, 9. [Google Scholar] [CrossRef]
- World Health Organization: Coronavirus Disease (COVID-2019) Situation Reports; WHO: Geneva, Switzerland, 2020; Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 15 May 2020).
- Centro Nacional de Epidemiologa (isciii): COVID-19 Espana. Available online: https://cnecovid.isciii.es/ (accessed on 15 May 2020).
- Github: COVID-19. Available online: https://github.com/pcm-dpc/COVID-19 (accessed on 15 May 2020).
- Viboud, C.; Simonsen, L.; Chowell, G. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemics 2016, 15, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Shanafelt, D.W.; Jones, G.; Lima, M.; Perrings, C.; Chowell, G. Forecasting the 2001 Foot-and-Mouth Disease Epidemic in the UK. EcoHealth 2018, 15, 338–347. [Google Scholar] [CrossRef] [PubMed]
- Pell, B.; Kuang, Y.; Viboud, C.; Chowell, G. Using phenomenological models for forecasting the 2015 Ebola challenge. Epidemics 2018, 22, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Chowell, G.; Hincapie-Palacio, D.; Ospina, J.; Pell, B.; Tariq, A.; Dahal, S.; Moghadas, S.; Smirnova, A.; Simonsen, L.; Viboud, C. Using Phenomenological Models to Characterize Transmissibility and Forecast Patterns and Final Burden of Zika Epidemics. PLoS Curr. 2016, 8, 8. [Google Scholar] [CrossRef]
- Banks, H.T.; Hu, S.; Thompson, W.C. Modeling and Inverse Problems in the Presence of Uncertainty; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Chowell, G.; Ammon, C.; Hengartner, N.; Hyman, J. Transmission dynamics of the great influenza pandemic of 1918 in Geneva, Switzerland: Assessing the effects of hypothetical interventions. J. Theor. Biol. 2006, 241, 193–204. [Google Scholar] [CrossRef]
- Chowell, G.; Shim, E.; Brauer, F.; Diaz-Dueñas, P.; Hyman, J.M.; Castillo-Chavez, C. Modelling the transmission dynamics of acute haemorrhagic conjunctivitis: Application to the 2003 outbreak in Mexico. Stat. Med. 2005, 25, 1840–1857. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Smieszek, T.; Fiebig, L.; Scholz, R.W. Models of epidemics: When contact repetition and clustering should be included. Theor. Biol. Med. Model. 2009, 6, 11. [Google Scholar] [CrossRef]
- Read, J.M.; Keeling, M.J. Disease evolution on networks: The role of contact structure. Proc. R. Soc. B Boil. Sci. 2003, 270, 699–708. [Google Scholar] [CrossRef]
- Newman, M.E.J. Properties of highly clustered networks. Phys. Rev. E 2003, 68, 026121. [Google Scholar] [CrossRef] [PubMed]
- Fasina, F.O.; Shittu, A.; Lazarus, D.; Tomori, O.; Simonsen, L.; Viboud, C.; Chowell, G. Transmission dynamics and control of Ebola virus disease outbreak in Nigeria, July to September 2014. Eurosurveillance 2014, 19, 20920. [Google Scholar] [CrossRef] [PubMed]
- Maganga, G.D.; Kapetshi, J.; Berthet, N.; Ilunga, B.K.; Kabange, F.; Kingebeni, P.M.; Mondonge, V.; Muyembe, J.-J.T.; Bertherat, E.; Briand, S.; et al. Ebola Virus Disease in the Democratic Republic of Congo. N. Engl. J. Med. 2014, 371, 2083–2091. [Google Scholar] [CrossRef] [PubMed]
- Tariq, A.; Roosa, K.; Mizumoto, K.; Chowell, G. Assessing reporting delays and the effective reproduction number: The 2018–19 Ebola epidemic in DRC, May 2018–January 2019. Epidemics 2019, in press. [Google Scholar]
- Brookmeyer, R.; Gail, M.H. AIDS Epidemiology: A Quantitative Approach; Oxford University Press on Demand: Oxford, UK, 1994; Volume 22. [Google Scholar]
- Lawless, J. Adjustments for reporting delays and the prediction of occurred but not reported events. Can. J. Stat. 1994, 22, 15–31. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smirnova, A.; DeCamp, L.; Chowell, G. Mathematical and Statistical Analysis of Doubling Times to Investigate the Early Spread of Epidemics: Application to the COVID-19 Pandemic. Mathematics 2021, 9, 625. https://doi.org/10.3390/math9060625
Smirnova A, DeCamp L, Chowell G. Mathematical and Statistical Analysis of Doubling Times to Investigate the Early Spread of Epidemics: Application to the COVID-19 Pandemic. Mathematics. 2021; 9(6):625. https://doi.org/10.3390/math9060625
Chicago/Turabian StyleSmirnova, Alexandra, Linda DeCamp, and Gerardo Chowell. 2021. "Mathematical and Statistical Analysis of Doubling Times to Investigate the Early Spread of Epidemics: Application to the COVID-19 Pandemic" Mathematics 9, no. 6: 625. https://doi.org/10.3390/math9060625
APA StyleSmirnova, A., DeCamp, L., & Chowell, G. (2021). Mathematical and Statistical Analysis of Doubling Times to Investigate the Early Spread of Epidemics: Application to the COVID-19 Pandemic. Mathematics, 9(6), 625. https://doi.org/10.3390/math9060625






