Analytical Method for Geometric Nonlinear Problems Based on Offshore Derricks
Abstract
1. Introduction
2. Simplified Calculation Model of Derrick Members
3. The Analytical Method for the Bending Problem of the Compression Rod
3.1. Differential Equations and Solutions for Bending Compression
3.2. Decomposition of the Deflection Curve
3.3. Determination of the Undetermined Coefficient
4. Mechanics Principles of the Analytical Method
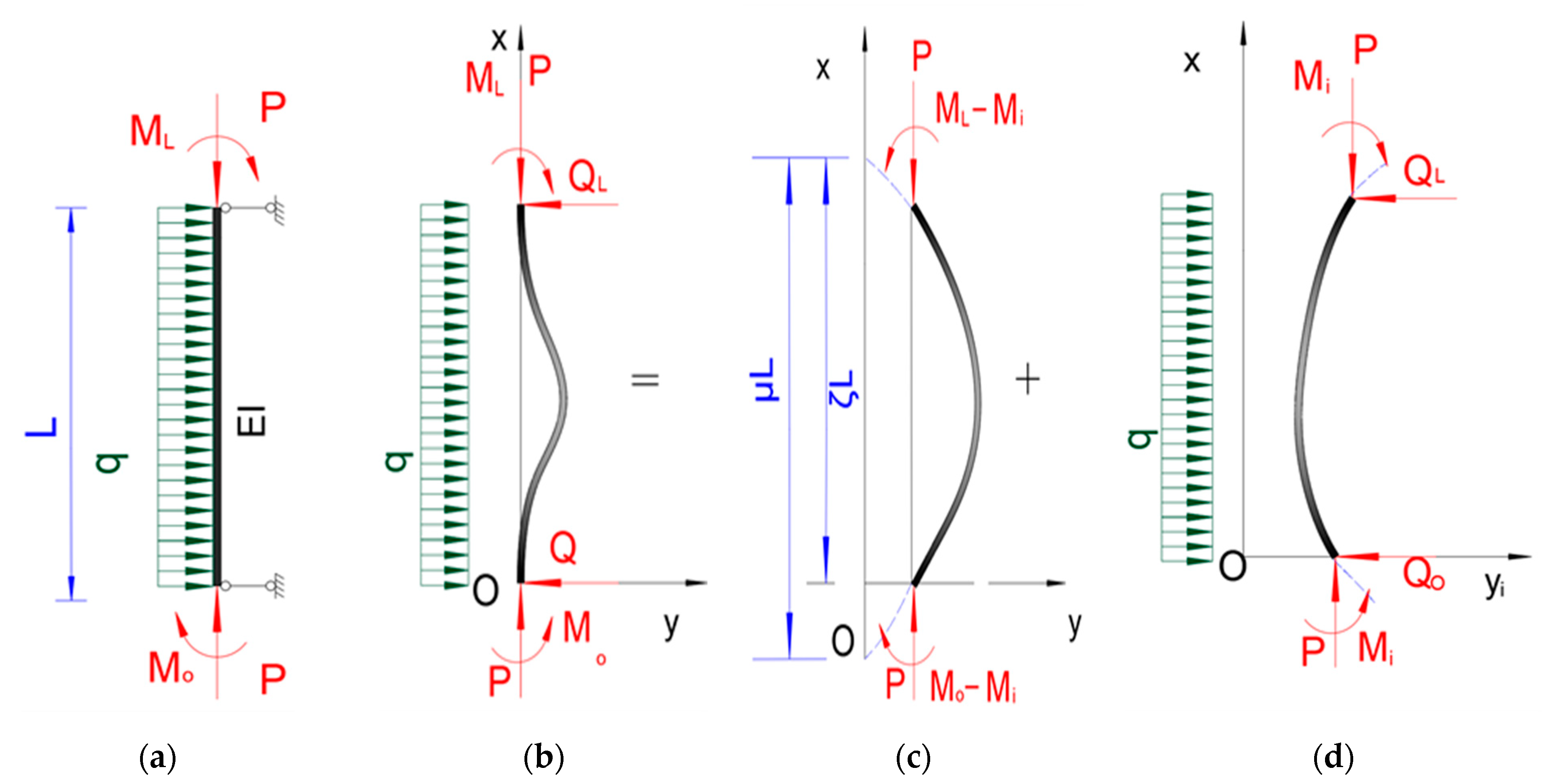
- Divide the load on the rod into two groups. The first group is composed of axial force , transverse uniform load , rod end shear forces and , and initial bending moment . The second group is composed of axial force and bending moment , at rod ends as shown in Figure 3;
- Under loads of the first group, the deformation of the rod is completed as follows. Firstly, a bending moment is imposed on the rod ends respectively, to obtain a bending equilibrium state with the initial deflection of . Next, add , , , and to the bending rod. As mentioned above, on the rod whose initial deformation is , , , , and only generate axial force instead of bending moment and shear force, and hence no new displacement will be generated. The deformation deflection curve of the rod is still the quadratic parabola ;
- The rod under loads of the second group is only affected by the axial force and the bending moments at rod ends, which is in a typical “Euler” bending equilibrium state [6,22]. The deformed deflection curve of the rod is sinusoidal. It is worth noting that the bending moments at rod ends are and because was deducted from the original bending moments at rod ends and , respectively. Instead, is added to the first group;
- Due to axial force is in both of the above two groups, the lateral displacement produced under loads of the two groups can be superposed. The superposition value is the final deformation value of the rod. This is the significance of mechanics of the solution for the bending equilibrium differential equations of the rod—Equation (23).
5. Application of Analytical Methods
5.1. In the Case That Bending Moments Exist at Rod Ends
5.2. In the Case That Bending Moments at Rod Ends Are Equal
6. Numerical Analysis of Compression Rod
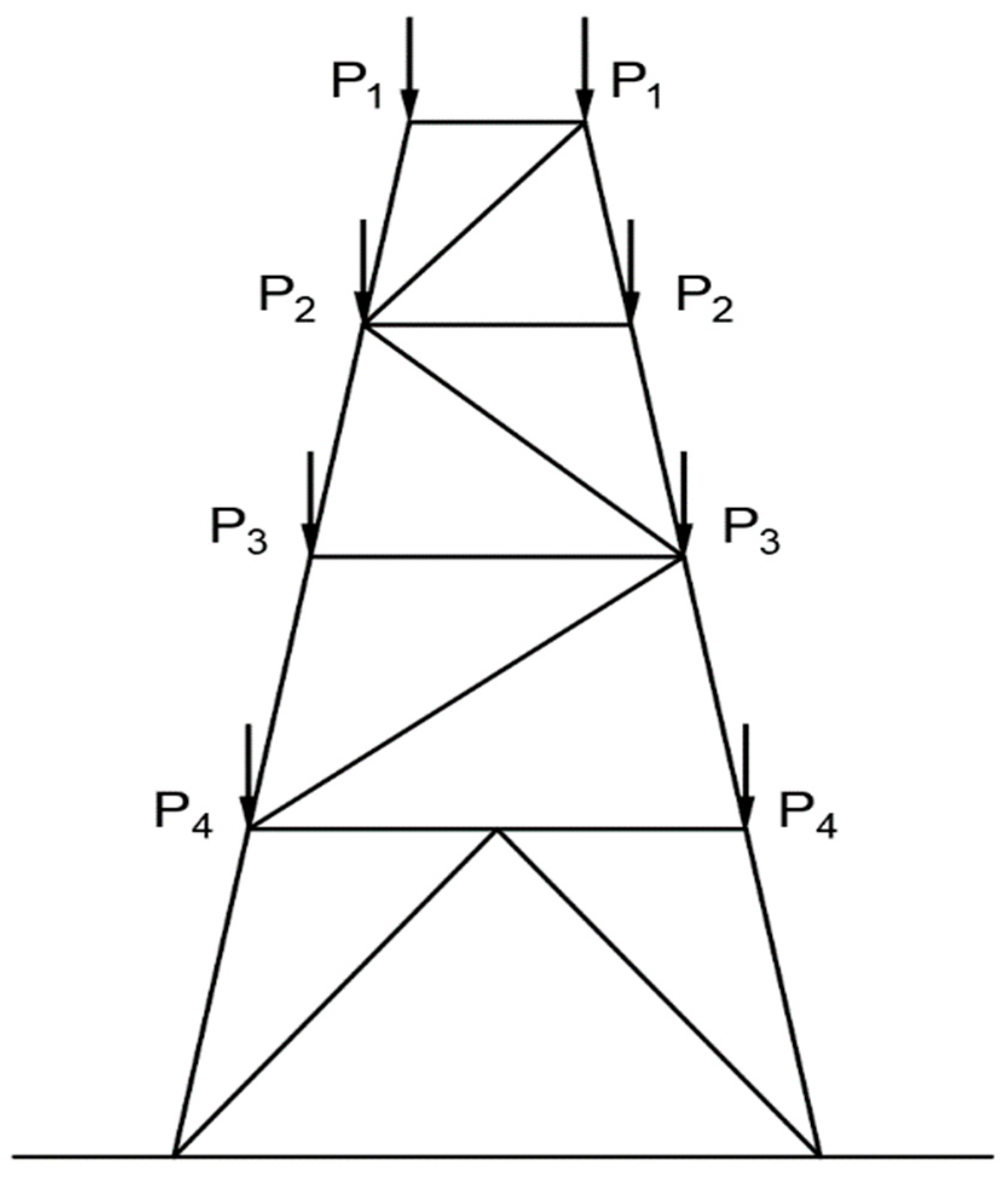
6.1. Simplified Model
6.2. Parameters
6.3. Ansys Modeling
7. Analysis of Calculation Results
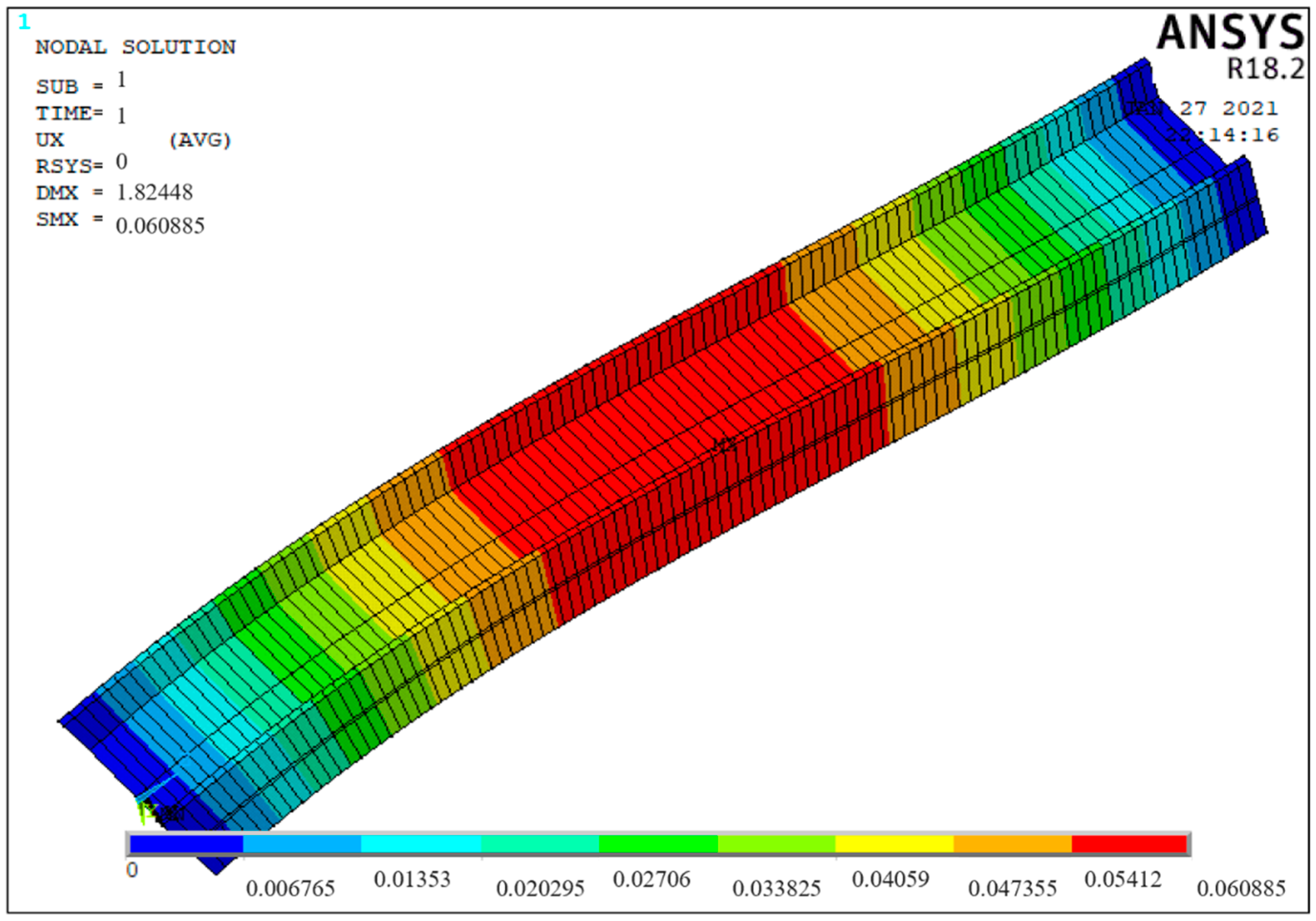
7.1. Displacement
7.2. Stress
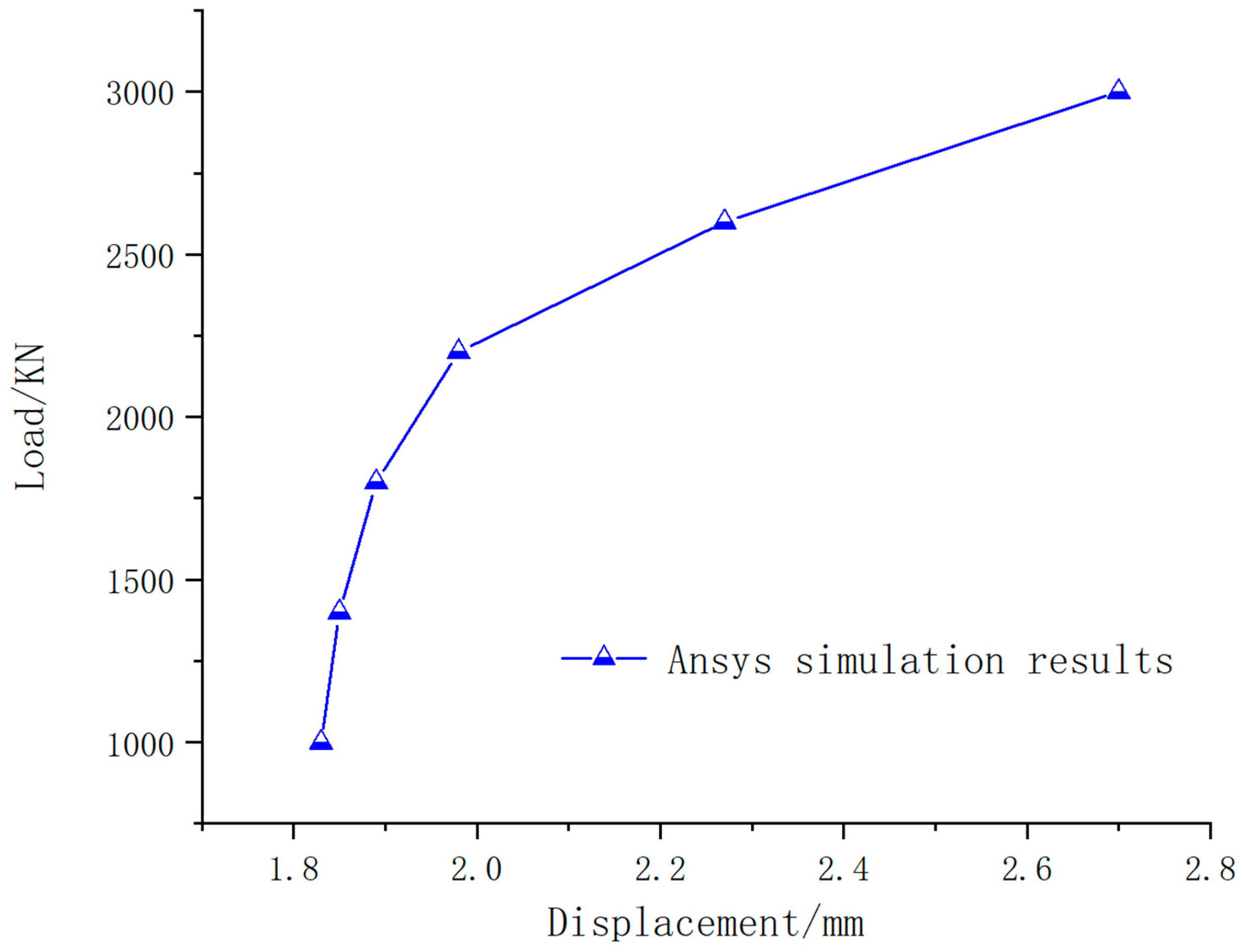
7.3. Comparative Results
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Y.Q.; Yuan, Y.Z.; Zhou, G.Q. Double Nonlinear Analysis of The Loading Capacity of Drilling Derrick Steel Structures Containing Defects and Defacements. Adv. Struct. Eng. 2009, 4, 43–49. [Google Scholar] [CrossRef]
- Song, X.F. The Safety Assessment of Offshore Platform’s Jacket Structure. Master’s Thesis, Harbin Engineering University, Harbin, China, 2014. [Google Scholar]
- Zhu, B.R.; Chen, G.M.; Zhang, K.; Lv, T.; Kang, J. Performance Assessment of In-service Offshore Drilling Derrick Structure. China Pet. Mach. 2014, 42, 38–42. [Google Scholar]
- Panayotounakos, D.E. Nonlinear and buckling analysis of continuous bars lying on rigid supports. AIAA J. 1986, 24, 479–484. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Panayotounakos, D.E. Exact solution of the non-linear differential equation concerning the elastic line of a straight rod due to terminal loading. Int. J. Non-Linear Mech. 1982, 17, 395–402. [Google Scholar] [CrossRef]
- Sotiropoulou, A.B.; Panayotounakos, D.E. Exact parametric analytic solutions of the elastica ODEs for bars including effects of the transverse deformation. Int. J. Non-Linear Mech. 2004, 39, 1555–1570. [Google Scholar] [CrossRef]
- Tang, Y.Q.; Zhou, Z.H.; Chan, S.L. Nonlinear Beam-Column Element under Consistent Deformation. Int. J. Struct. Stab. Dyn. 2015, 15, 1450068. [Google Scholar] [CrossRef]
- Chen, L. An integral approach for large deflection cantilever beams. Int. J. Non-Linear Mech. 2010, 45, 301–305. [Google Scholar] [CrossRef]
- Stampouloglou, I.H.; Theotokoglou, E.E.; Andriotaki, P.N. Asymptotic solutions to the non-linear cantilever elastica. Int. J. Non-Linear Mech. 2005, 40, 1252–1262. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A. Nonlinear elastic analysis and buckling of pinned–fixed arches. Int. J. Mech. Sci. 2013, 68, 212–223. [Google Scholar] [CrossRef]
- Sekulovic, M.; Salatic, R. Nonlinear analysis of frames with flexible connections. Comput. Struct. 2001, 79, 1097–1107. [Google Scholar] [CrossRef]
- Sitar, M.; Kosel, F.; Brojan, M. A simple method for determining large deflection states of arbitrarily curved planar elastica. Arch. Appl. Mech. 2014, 84, 263–275. [Google Scholar] [CrossRef]
- Zhu, Y.Y.; Hu, Y.J.; Cheng, C.J. Analysis of nonlinear stability and post-buckling for Euler-type beam-column structure. Appl. Math. Mech. 2011, 32, 719–728. [Google Scholar] [CrossRef]
- Hu, Z.P.; Pan, W.H.; Tong, J.Z. Exact Solutions for Buckling and Second-Order Effect of Shear Deformable Timoshenko Beam–Columns Based on Matrix Structural Analysis. Appl. Ences 2019, 9, 3814. [Google Scholar] [CrossRef]
- Scott, M.H.; Fenves, G.L.; Mckenna, F.; Filippou, F.C. Software Patterns for Nonlinear Beam-Column Models. J. Struct. Eng. 2015, 134, 562–571. [Google Scholar] [CrossRef]
- Zhang, Z. Study on Stability Capacity of Aluminum Beam-columns. Ph.D. Thesis, Tongji University, Shanghai, China, 2006. [Google Scholar]
- Polyanina, A.D.; Zhurova, A.I. Parametrically defined nonlinear differential equations, differential-algebraic equations, and implicit ODEs: Transformations, general solutions, and integration methods. Appl. Math. Lett. 2017, 64, 59–66. [Google Scholar] [CrossRef]
- Ozbasaran, H. Optimal design of I-section beam-columns with stress, non-linear deflection and stability constraints. Eng. Struct. 2018, 171, 385–394. [Google Scholar] [CrossRef]
- Vaz, M.A.; Silva, D.F.C. Post-buckling analysis of slender elastic rods subjected to terminal forces. Int. J. Non-Linear Mech. 2003, 38, 483–492. [Google Scholar] [CrossRef]
- Li, W.; Zhu, C.M.; Hu, X.Y. Analytical Solution for Geometric Nonlinearity of Compression Bars Considering P-Δ Effect. Tongji Daxue Xuebao/J. Tongji Univ. 2006, 34, 1299–1302+1308. [Google Scholar]
- Wang, X.; Yu, H.J.; Gu, Z.H.; Hu, W.N. A Geometric Nonlinear Method of Truss Booms Considering Second Order Effect. China Mech. Eng. 2019, 30, 1540–1544. [Google Scholar]
- Griner, G.M. A Parametric Solution to the Elastic Pole-Vaulting Pole Problem. J. Appl. Mech. 1984, 51, 409–414. [Google Scholar] [CrossRef]
- Andriotaki, P.N.; Stampouloglou, I.H.; Theotokoglou, E.E. Nonlinear asymptotic analysis in elastica of straight bars—Analytical parametric solutions. Arch. Appl. Mech. 2006, 76, 525–536. [Google Scholar] [CrossRef]
- Wang, S.B.; Wang, B. Analysis of the stability of marine K-type workover rig derrick based on ANSYS analysis. Sci. Technol. Commun. 2011, 16, 94–95. [Google Scholar]
- Filipich, C.P.; Rosales, M.B. A further study on the postbuckling of extensible elastic rods. Int. J. Non-Linear Mech. 2000, 35, 997–1022. [Google Scholar] [CrossRef]







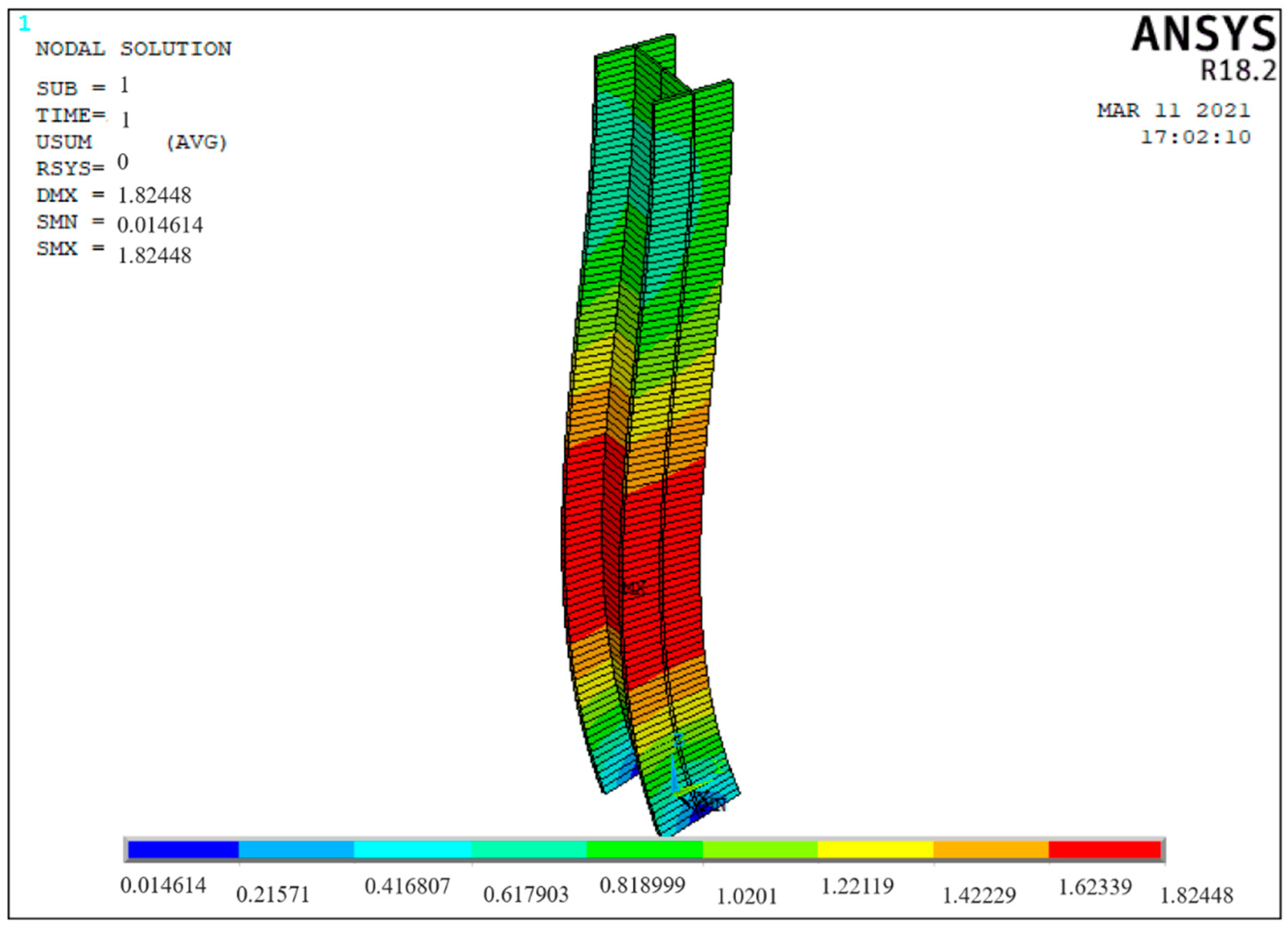

| Project | Load Value | Unit |
|---|---|---|
| Structural weight | 1200 | KN |
| Self-weight of the second floor | 36.13 | KN |
| Swimming system weight | 300 | KN |
| Crane weight | 107.212 | KN |
| Maximum hook load | 4500 | KN |
| Maximum drill string weight | 2200 | KN |
| Maximum pulling force of Working rope | 793.288 | KN |
| Standing root load | 62.125 | KN |
| Wind load | 4.4 | KN/m |
| Simulation Chart Name | Max | Position | Min | Position |
|---|---|---|---|---|
| Total displacement map | 1.82448 mm | Span | 0.014614 mm | Lower flange |
| X-direction displacement map | 1.82448 mm | Span | 0 mm | Both ends |
| Von Mises stress diagram | 226.637 MPa | Flanges at both ends | 0.121319 MPa | Mid-span and upper flange |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Cao, H.; Han, M.; Qin, P.; Liu, X. Analytical Method for Geometric Nonlinear Problems Based on Offshore Derricks. Mathematics 2021, 9, 610. https://doi.org/10.3390/math9060610
Li C, Cao H, Han M, Qin P, Liu X. Analytical Method for Geometric Nonlinear Problems Based on Offshore Derricks. Mathematics. 2021; 9(6):610. https://doi.org/10.3390/math9060610
Chicago/Turabian StyleLi, Chunbao, Hui Cao, Mengxin Han, Pengju Qin, and Xiaohui Liu. 2021. "Analytical Method for Geometric Nonlinear Problems Based on Offshore Derricks" Mathematics 9, no. 6: 610. https://doi.org/10.3390/math9060610
APA StyleLi, C., Cao, H., Han, M., Qin, P., & Liu, X. (2021). Analytical Method for Geometric Nonlinear Problems Based on Offshore Derricks. Mathematics, 9(6), 610. https://doi.org/10.3390/math9060610






