Abstract
A new high-order derivative-free method for the solution of a nonlinear equation is developed. The novelty is the use of Traub’s method as a first step. The order is proven and demonstrated. It is also shown that the method has much fewer divergent points and runs faster than an optimal eighth-order derivative-free method.
1. Introduction
In engineering and applied science, we encounter the problem of solving a nonlinear equation
For example, the Colebrook equation [1] to find the friction factor, or finding critical values of some nonlinear function. Another example is given by Ricceri [2] where the first eigenvalue of Helmholtz equation is found by minimizing a functional. See also [3]. Most numerical solution methods are based on Newton’s scheme, i.e., starting with an initial guess for the root , we create a sequence
The convergence is quadratic, that is,
To increase the order, one has to include higher derivatives, such as Halley’s scheme [4] using first and second derivatives and is of a cubic order. In order to avoid higher derivatives, one can use multipoint methods, see Petković et al. [5].
Derivative-free methods are either linear (such as Picard), super-linear (such as secant) or even quadratic, such as Steffensen’s method [6], given by
Because multistep methods are usually based on Newton’s steps, derivative-free methods are based on Steffensen’s method as the first step. There are several derivative-free methods based on Steffensen’s method for simple and multiple roots. See Kansal et al. [7] for such family of methods for multiple roots and Zhanlav and otgondorj [8] for simple roots. In a recent article, Neta [9] has shown that there is a better choice for a first step, even though it is NOT second order. Traub’s method [10], given by
is of order 1.839, and it runs faster and has better dynamics than several other derivative-free methods. Clearly, one cannot get optimal methods (see Kung and Traub [11]) this way. Kung and Traub [11] conjectured that multipoint methods without memory using d function evaluations could have an order no larger than . The efficiency index I is defined as . Thus, an optimal method of order 8 has an efficiency index of and an optimal method of order 4 has an efficiency index , which is better than Newton’s method for which . The efficiency index of optimal method cannot reach a value of 2. In fact, realistically, one uses methods of an order of at most 8. For high order derivative-free methods based on Steffensen’s method as a first step, see Zhanlav and Otgondorj [8] and references there. Such methods are especially useful when the derivative is very expensive to evaluate and, of course, when the function is non-differentiable.
Here, we develop a derivative-free method with memory based on Traub’s method (5) as the first step and the other two steps are based on replacing the derivative by the derivative of Newton interpolating polynomial of degree 3. In the next section, we will discuss the order of the scheme and the computational order of convergence, COC, defined by
where is the final approximation for the zero .
2. New Method
We suggest a 3-step method having (5) as the first step. The method is
The derivatives in the last two steps are approximated by the derivative of Newton interpolating polynomial of degree 3:
and
and is the divided difference.
Let us denote the errors , and . The error in the first step is given by Traub
The other two steps are of the same order as the Newton’s method, i.e., and Therefore, the order of the method is The efficiency index is higher than that of the 3-step optimal eighth order method. This is typical of methods with memory.
In Table 1, we list the computational order of convergence as defined by (6) for 16 different nonlinear functions. The values range from 6.622 to 7.394 with an average value of 6.872.

Table 1.
Computational order of convergence for several functions using our new method.
3. Dynamics Study of the Methods
The basin of attraction method was initially discussed by Stewart [12]. This is better than comparing methods on the basis of running several nonlinear functions using a certain initial value. In the last decade, many papers appeared using the idea of basin of attraction to compare the efficiency of many methods. See, for example, Chun and Neta [13,14] and references there.
In this section, we describe the experiments with our method as compared to TZKO [8].
We chose four polynomials and one non-polynomial function all having roots within a 6 by 6 square centered at the origin. The square is divided horizontally and vertically by equally spaced lines. We took the intersection of all these lines as initial points in the complex plane for the iterative schemes. The code collected the number of iteration or function evaluation to converge within a tolerance of and the root to which the sequence converged. If the sequence did not converge within 40 iterations, we denote it as a divergent point. We also collected the CPU run time to execute the code on all initial points using a Dell Optiplex 990 desktop computer.
We ran all methods on the following five examples, four of which are polynomials:
Remark 1.
The additional starting values are and .
It is clear from these tables that our method runs faster (see Table 2), uses fewer function-evaluations per point (see Table 3) and has much fewer divergent points (see Table 4). In fact, for 3 out of 5 examples, our method had NO divergent points. We now take an example known to be hard, i.e., the Wilkinson-type polynomial
which has roots at Our method runs fast and had no divergent points. TZKO requires more than double the CPU run time for our method and had 166,138 divergent points. The plots of the basins for this example are given in Figure 1.

Table 2.
CPU time (msec) for each example (1–5) and each of the methods.

Table 3.
Average number of function evaluations per point for each example (1–5) and each of the methods.

Table 4.
Number of black points for each example (1–5) and each of the methods.
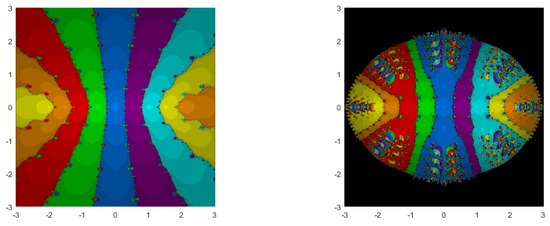
Figure 1.
Our method (left) and TZKO (right) for the roots of the polynomial (10).
4. Conclusions
We have developed a derivative-free method with memory based on Traub’s method as the first step. The method is of order 7.356 and has an efficiency index of 1.945, which is higher than any optimal eighth order method. We have shown that our method is faster, uses fewer function evaluations per point, and has much fewer divergent points.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Colebrook, C.F. Turbulent flows in pipes, with particular reference to the transition between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 130. [Google Scholar] [CrossRef]
- Ricceri, B. A class of equations with three solutions. Mathematics 2020, 8, 478. [Google Scholar] [CrossRef]
- Treantă, S. Gradient structures associated with a polynomial differential equation. Mathematics 2020, 8, 535. [Google Scholar] [CrossRef]
- Halley, E. A new, exact and easy method of finding the roots of equations generally and that without any previous reduction. Philos. Trans. R. Soc. Lond. 1694, 18, 136–148. [Google Scholar]
- Petković, M.S.; Neta, B.; Petković, L.D.; Džunić, J. Multipoint Methods for the Solution of Nonlinear Equations; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Steffensen, J.F. Remarks on iteration. Scand. Actuar. J. 1933, 1, 64–72. [Google Scholar] [CrossRef]
- Kansal, M.; Alshomrani, A.S.; Bhalla, S.; Behl, R.; Salimi, M. One parameter optimal derivative-free family to find the multiple roots of algebraic nonlinear equations. Mathematics 2020, 8, 2223. [Google Scholar] [CrossRef]
- Zhanlav, T.; Otgondorj, K. Comparison of some optimal derivative-free three-point iterations. J. Numer. Anal. Approx. Theory 2020, 49, 76–90. [Google Scholar]
- Neta, B. Basin attractors for derivative-free methods to find simple roots of nonlinear equations. J. Numer. Anal. Approx. Theory 2020, 49, 177–189. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice Hall: New York, NY, USA, 1964. [Google Scholar]
- Kung, H.T.; Traub, J.F. Optimal order of one-point and multipoint iteration. J. Assoc. Comput. Math. 1974, 21, 634–651. [Google Scholar] [CrossRef]
- Stewart, B.D. Attractor Basins of Various Root-Finding Methods. Master’s Thesis, Naval Postgraduate School, Department of Applied Mathematics, Monterey, CA, USA, June 2001. [Google Scholar]
- Chun, C.; Neta, B. Comparative study of methods of various orders for finding simple roots of nonlinear equations. J. Appl. Anal. Comput. 2019, 9, 400–427. [Google Scholar] [CrossRef]
- Chun, C.; Neta, B. Comparative study of methods of various orders for finding repeated roots of nonlinear equations. J. Comput. Appl. Math. 2018, 340, 11–42. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).