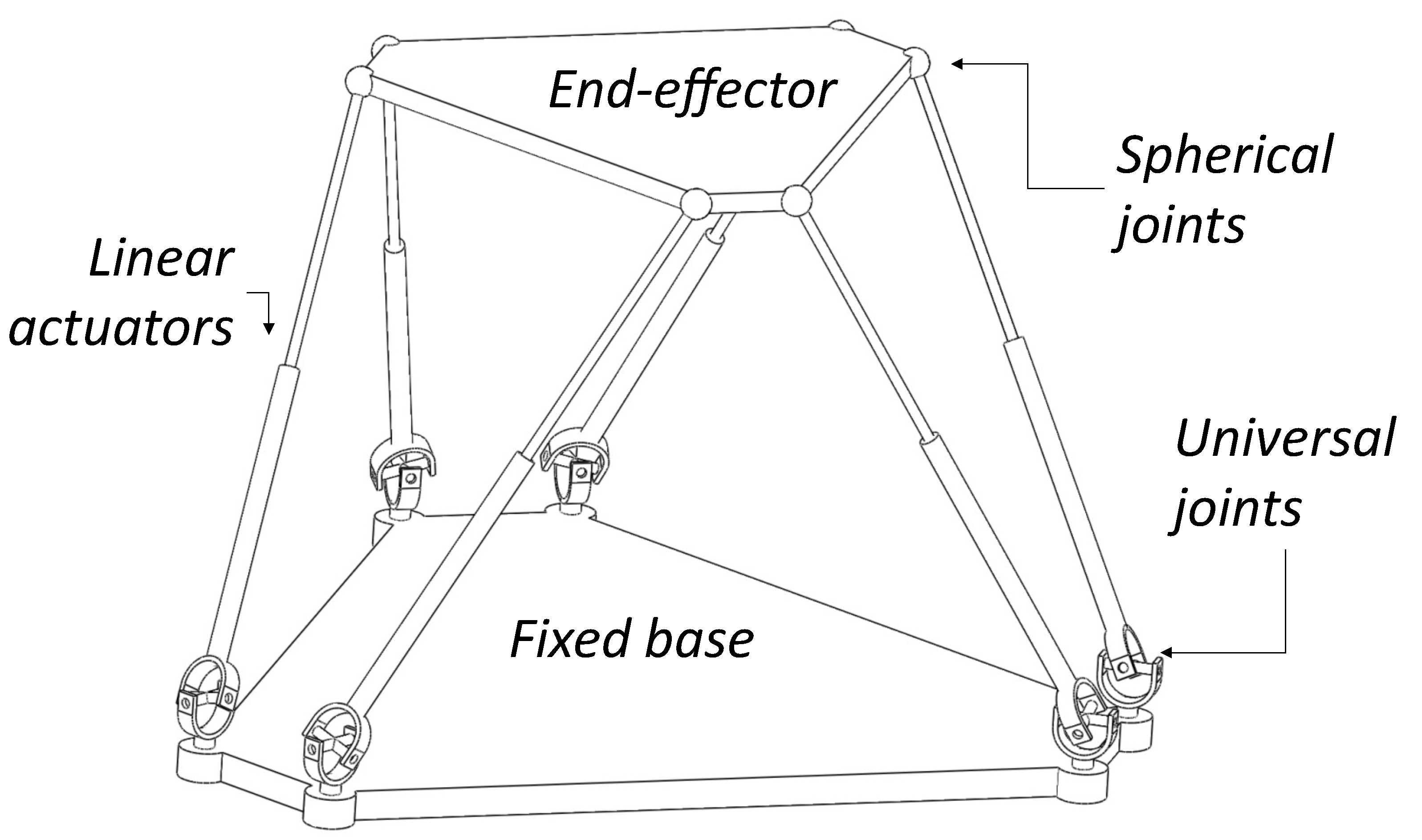
A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators
Abstract
1. Introduction
Contributions
2. Optimization Design Criteria
2.1. Kinematics Computation
2.2. Regular Workspace Computation Considering Sufficient Dexterity
Mono-Objective Optimization for Dimensional Synthesis
2.3. Computation of the Dynamics
Error and Energy Multi-Objective Optimization
3. Optimization Design Process: Implementation and Results
- Dimensional synthesis of the platform: Using a mono-objective optimization algorithm, we determine the lengths of a platform with minimum dimensions that, with a dexterity measure equal to or greater than 0.2, reaches the points inside a regular workspace.
- Error and energy optimization: Using the lengths of the previous stage and a multi-objective evolutionary algorithm, we approximate the Pareto set, that is, we obtain a set of arrays of gains of the PID controller with the best performance in both objectives.
3.1. Mono-Objective Optimization Algorithms
- For the BUMDA, the standard deviation of the objective function values of the population was less than .
- For the PSO, the relative change in the best objective function value over the last 20 iterations was less than , or the maximum number of iterations is met. The relative change was computed with the formula , where is the best function value in the k-th iteration.
- For the GA, the average relative change in the best objective function value over the last 50 generations was less than or equal to , or the maximum number of iterations is reached. The average relative change was computed as , where is the best function value in the k-th iteration.
3.2. Multi-Objective Optimization Algorithms
3.3. Mono-Objective Optimization Results
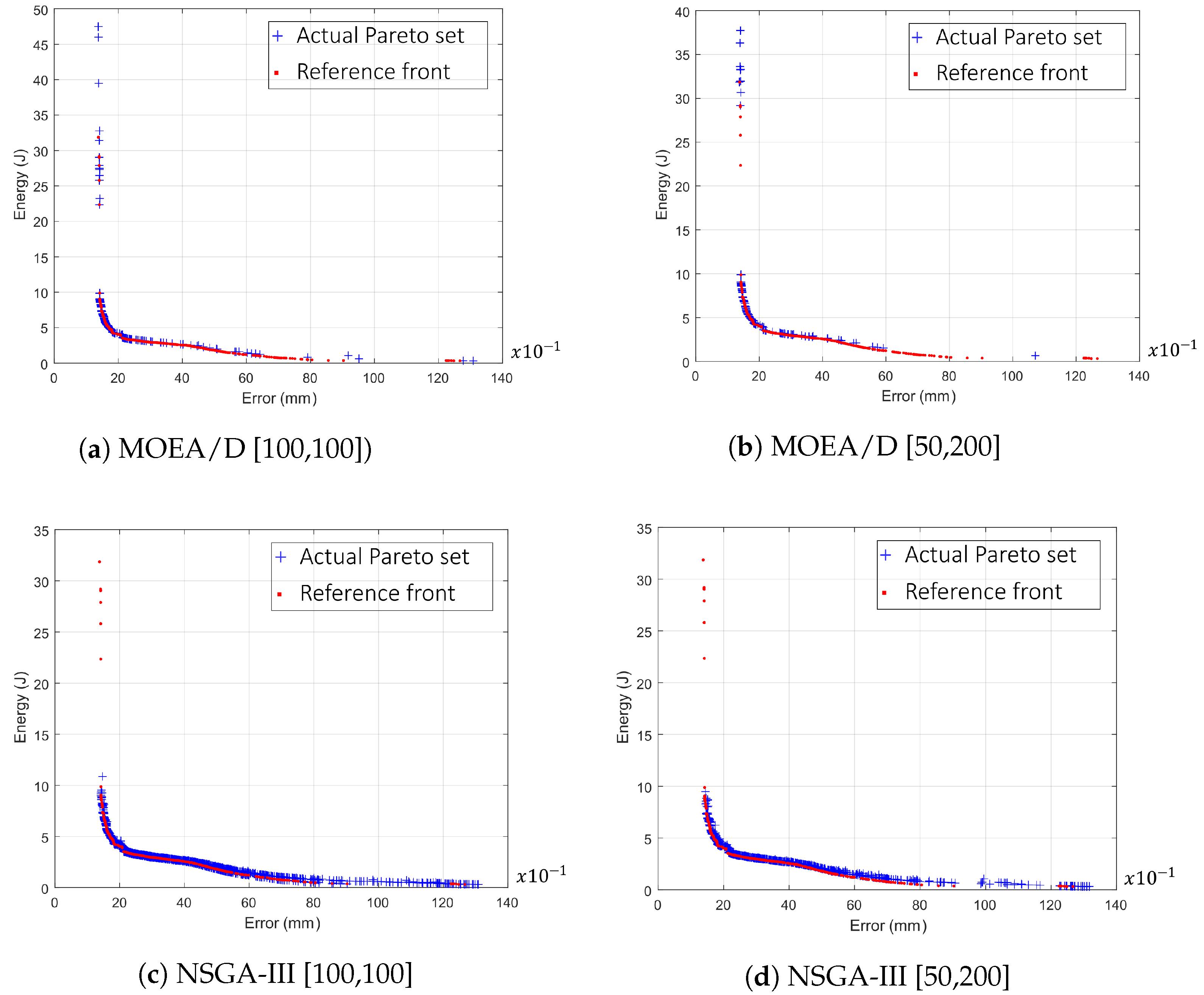
3.4. Multi-Objective Optimization Results
4. Discussion
4.1. Mono-Objective Optimization
4.2. Multi-Objective Optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, T.; Lian, B. Stiffness and mass optimization of parallel kinematic machine. Mech. Mach. Theory 2018, 120, 73–88. [Google Scholar] [CrossRef]
- Pedrammehr, S.; Mahboubkhah, M.; Khani, N. A study on vibration of Stewart platform-based machine tool table. Int. J. Adv. Manufac. Technol. 2013, 65, 991–1007. [Google Scholar] [CrossRef]
- Pugazhenthi, S.; Nagarajan, T.; Singaperumal, M. Optimal trajectory planning for a hexapod machine tool during contour machining. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 1247–1256. [Google Scholar] [CrossRef]
- Geng, Z.; Haynes, L.S. Six-degree-of-freedom active vibration isolation using a stewart platform mechanism. J. Robot. Syst. 1993, 10, 725–744. [Google Scholar] [CrossRef]
- Kazezkhan, G.; Xiang, B.; Wang, N.; Yusup, A. Dynamic modeling of the Stewart platform for the NanShan Radio Telescope. Adv. Mech. Eng. 2020, 12, 1–10. [Google Scholar] [CrossRef]
- Keshtkar, S.; Hernandez, E.; Oropeza, A.; Poznyak, A. Orientation of radio-telescope secondary mirror via adaptive sliding mode control. Neurocomputing 2017, 233, 43–51. [Google Scholar] [CrossRef]
- Velasco, J.; Calvo, I.; Barambones, O.; Venegas, P.; Napole, C. Experimental Validation of a Sliding Mode Control for a Stewart Platform Used in Aerospace Inspection Applications. Mathematics 2020, 8, 2051. [Google Scholar] [CrossRef]
- Botello-Aceves, S.; Valdez, S.I.; Becerra, H.M.; Hernandez, E. Evaluating concurrent design approaches for a Delta parallel manipulator. Robotica 2018, 36, 697–714. [Google Scholar] [CrossRef]
- Valdez, S.I.; Botello-Aceves, S.; Becerra, H.M.; Hernández, E.E. Comparison Between a Concurrent and a Sequential Optimization Methodology for Serial Manipulators Using Metaheuristics. IEEE Trans. Ind. Inform. 2018, 14, 3155–3165. [Google Scholar] [CrossRef]
- Panda, S.; Mishra, D.; Biswal, B. Revolute manipulator workspace optimization: A comparative study. Appl. Soft Comput. 2013, 13, 899–910. [Google Scholar] [CrossRef]
- Badescu, M.; Mavroidis, C. Workspace Optimization of 3-Legged UPU and UPS Parallel Platforms with Joint Constraints. J. Mech. Des. 2004, 126, 291–300. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, G.; Chen, N.; Li, Z. Optimal design of parallel manipulators for maximum effective regular workspace. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005; pp. 795–800. [Google Scholar] [CrossRef]
- Dereli, S.; Köker, R. A meta-heuristic proposal for inverse kinematics solution of 7-DOF serial robotic manipulator: Quantum behaved particle swarm algorithm. Artif. Intell. Rev. 2016, 53, 949–964. [Google Scholar] [CrossRef]
- Falconi, R.; Grandi, R.; Melchiorri, C. Inverse Kinematics of Serial Manipulators in Cluttered Environments using a new Paradigm of Particle Swarm Optimization. IFAC Proc. Vol. 2014, 47, 8475–8480. [Google Scholar] [CrossRef]
- Al-Dois, H.; Jha, A.K.; Mishra, R.B. Task-based design optimization of serial robot manipulators. Eng. Optim. 2013, 45, 647–658. [Google Scholar] [CrossRef]
- Kuçuk, S. Optimal trajectory generation algorithm for serial and parallel manipulators. Robot. Comput. Integrat. Manufac. 2017, 48, 219–232. [Google Scholar] [CrossRef]
- Ravichandran, R.; Heppler, G.; Wang, D. Task-based optimal manipulator/controller design using evolutionary algorithms. Proc. Dynam. Control Syst. Struc. Space 2004, 1–10. [Google Scholar]
- Boudreau, R.; Gosselin, C.M. The Synthesis of Planar Parallel Manipulators with a Genetic Algorithm. J. Mech. Des. 1999, 121, 533–537. [Google Scholar] [CrossRef]
- Patel, S.; Sobh, T. Task based synthesis of serial manipulators. J. Adv. Res. 2015, 6, 479–492. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Zhang, Y.; Huang, R.; Chen, X.; Li, Z. Optimization Algorithms for Kinematically Optimal Design of Parallel Manipulators. IEEE Trans. Autom. Sci. Eng. 2014, 11, 574–584. [Google Scholar] [CrossRef]
- Soltanpour, M.R.; Khooban, M.H. A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 2013, 74, 467–478. [Google Scholar] [CrossRef]
- Zhang, X.; Nelson, C.A. Multiple-Criteria Kinematic Optimization for the Design of Spherical Serial Mechanisms Using Genetic Algorithms. J. Mech. Des. 2011, 133, 011005. [Google Scholar] [CrossRef]
- Miller, K. Optimal Design and Modeling of Spatial Parallel Manipulators. Int. J. Robot. Res. 2004, 23, 127–140. [Google Scholar] [CrossRef]
- Yang, C.; Li, Q.; Chen, Q. Multi-objective optimization of parallel manipulators using a game algorithm. Appl. Math. Modell. 2019, 74, 217–243. [Google Scholar] [CrossRef]
- Hultmann Ayala, H.V.; dos Santos Coelho, L. Tuning of PID controller based on a multiobjective genetic algorithm applied to a robotic manipulator. Expert Syst. Appl. 2012, 39, 8968–8974. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, Z. Forward kinematics, performance analysis, and multi-objective optimization of a bio-inspired parallel manipulator. Robot. Comput. Integrat. Manufac. 2012, 28, 484–492. [Google Scholar] [CrossRef]
- Cirillo, A.; Cirillo, P.; De Maria, G.; Marino, A.; Natale, C.; Pirozzi, S. Optimal custom design of both symmetric and unsymmetrical hexapod robots for aeronautics applications. Robot. Comput. Integrat. Manufac. 2017, 44, 1–16. [Google Scholar] [CrossRef]
- Joumah, A.A.; Albitar, C. Design Optimization of 6-RUS Parallel Manipulator Using Hybrid Algorithm. Mod. Educ. Comput. Sci. Press 2018, 10, 83–95. [Google Scholar] [CrossRef][Green Version]
- Nabavi, S.N.; Shariatee, M.; Enferadi, J.; Akbarzadeh, A. Parametric design and multi-objective optimization of a general 6-PUS parallel manipulator. Mech. Mach. Theory 2020, 152, 103913. [Google Scholar] [CrossRef]
- Lara-Molina, F.A.; Rosário, J.M.; Dumur, D. Multi-Objective Design of Parallel Manipulator Using Global Indices. Benthnam Open 2010, 4, 37–47. [Google Scholar] [CrossRef][Green Version]
- SimWise 4D. 2020. Available online: https://www.design-simulation.com/SimWise4d/ (accessed on 1 March 2021).
- Valdez, S.I.; Hernández, A.; Botello, S. A Boltzmann based estimation of distribution algorithm. Inform. Sci. 2013, 236, 126–137. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Mezura-Montes, E.; Coello Coello, C.A. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evolution. Comput. 2011, 173–194. [Google Scholar] [CrossRef]
- Pedersen, M.E. Good Parameters for Particle Swarm Optimization; Hvass Laboratories: Luxembourg, 2010. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co. Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A Globally Convergent Augmented Lagrangian Algorithm for Optimization with General Constraints and Simple Bounds. SIAM J. Num. Anal. 1991, 28, 545–572. [Google Scholar] [CrossRef]
- Conn, A.R.; Gould, N.I.M.; Toint, P.L. A Globally Convergent Augmented Lagrangian Barrier Algorithm for Optimization with General Inequality Constraints and Simple Bounds. Math. Comput. 1997, 66, 261–288. [Google Scholar] [CrossRef]
- MATLAB, Help Particleswarm, Mathworks. 2020. Available online: https://www.mathworks.com/help/gads/particleswarm.html (accessed on 1 March 2021).
- MATLAB, Help ga, Mathworks. 2020. Available online: https://www.mathworks.com/help/gads/ga.html (accessed on 1 March 2021).
- Yarpiz. Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D). 2016. Available online: https://yarpiz.com/456/ypea126-nsga3 (accessed on 1 March 2021).
- Yarpiz. Implementation of Non-Dominated Sorting Genetic Algorithm III in MATLAB. 2015. Available online: https://yarpiz.com/95/ypea124-moead (accessed on 1 March 2021).
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evolution. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Li, H.; Deb, K.; Zhang, Q.; Suganthan, P.; Chen, L. Comparison between MOEA/D and NSGA-III on a set of novel many and multi-objective benchmark problems with challenging difficulties. Swarm Evolution. Comput. 2019, 46, 104–117. [Google Scholar] [CrossRef]
- Gong, Y. Design Analysis of a Stewart Platform for Vehicle Emulator Systems. Master’s Thesis, Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. [Google Scholar]

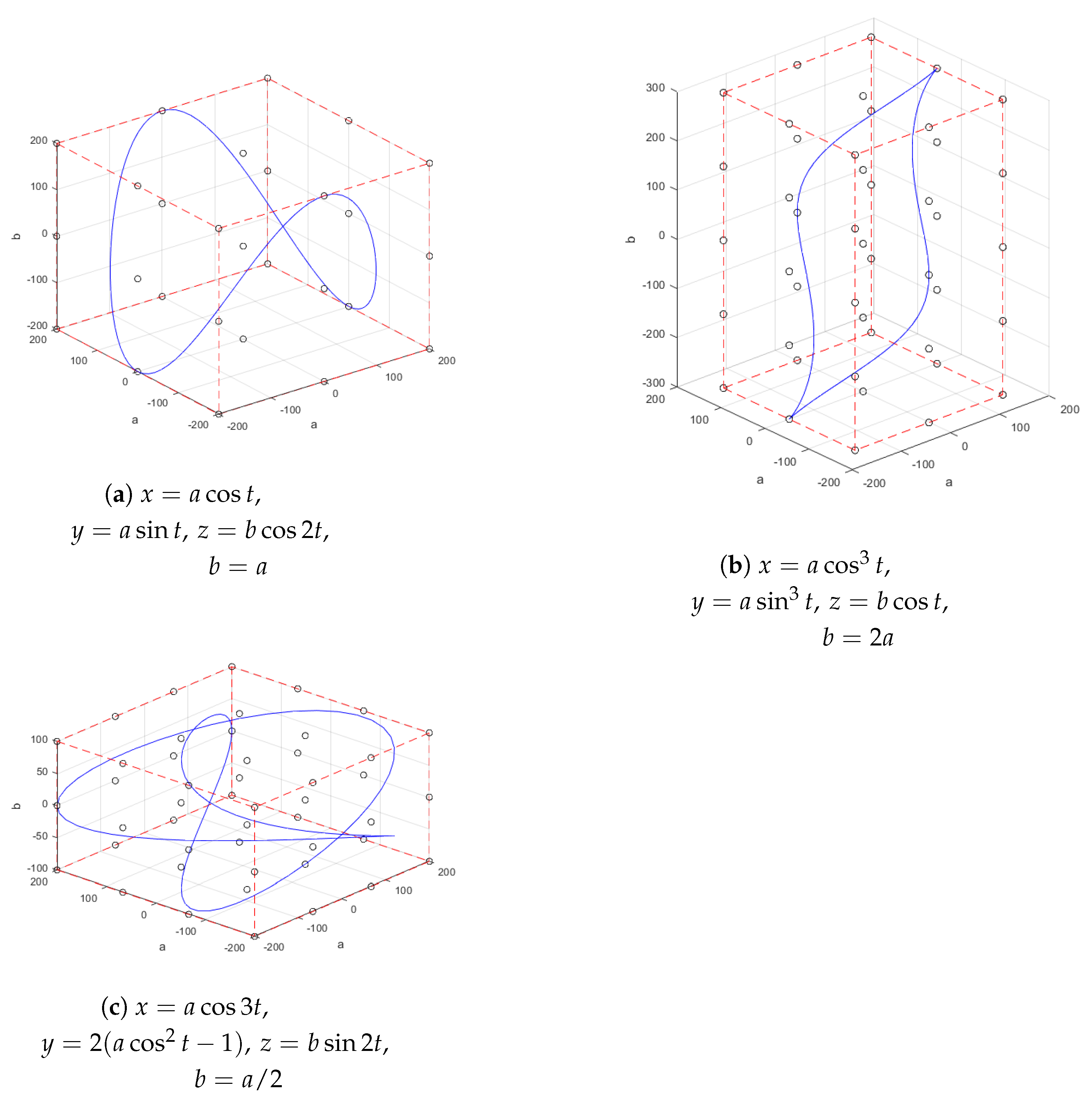


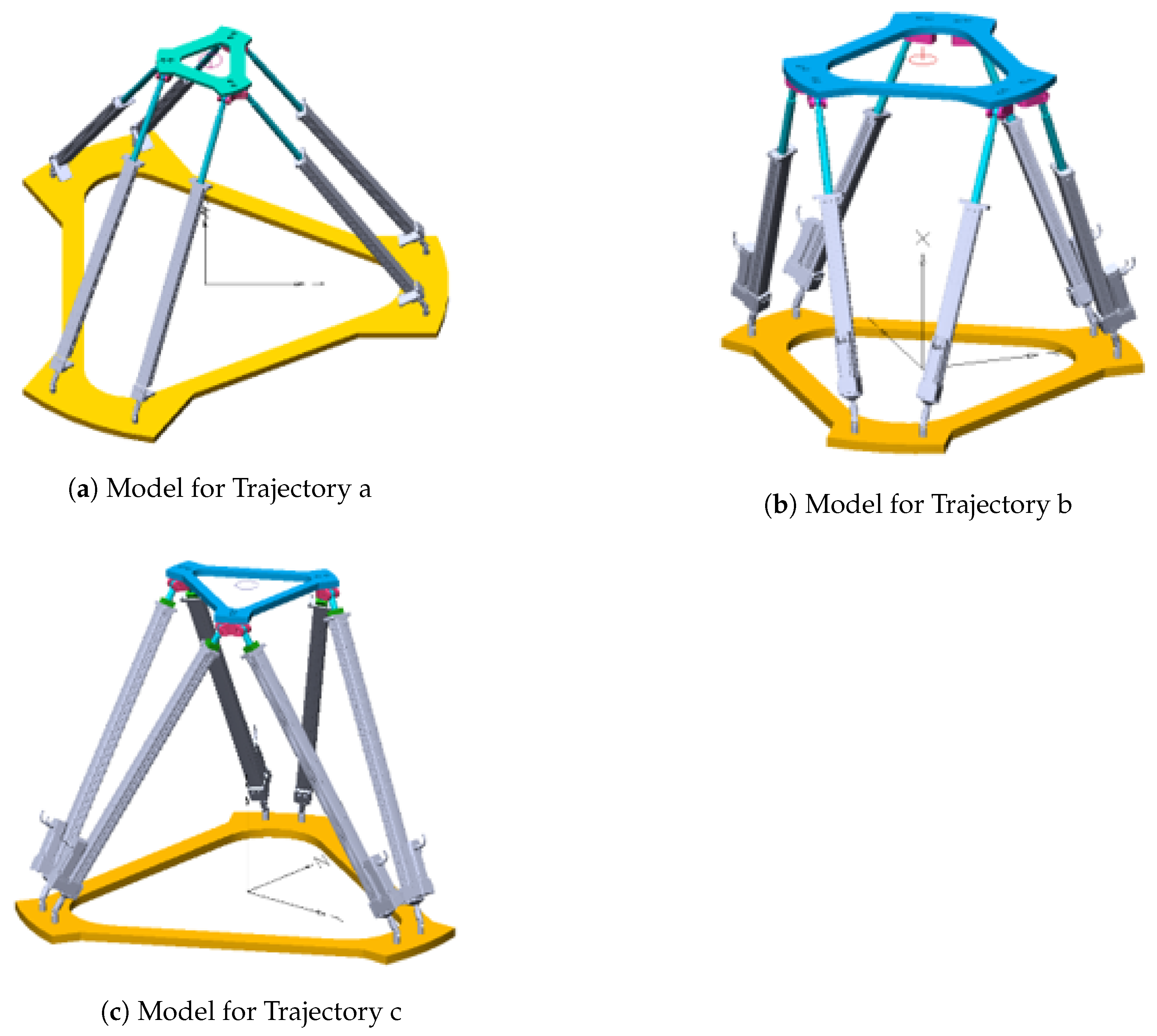


| Trajectory a | Trajectory b | Trajectory c |
|---|---|---|
| Traj. | Alg. | f | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a | BUMDA | 748.45 | 160.21 | 0.21 | 0.23 | 669.82 | 1099.29 | 26.56154 | 589 |
| PSO | 815.85 | 120.02 | 0.12 | 0.12 | 647.26 | 999.99 | 26.56024 | 17,100 | |
| GA | 876.03 | 120.03 | 0.26 | 0.13 | 664.66 | 999.99 | 26.53869 | 50,400 | |
| b | BUMDA | 927.03 | 151.24 | 0.19 | 0.23 | 837.33 | 1316.65 | 44.64526 | 442 |
| PSO | 592.71 | 240 | 0.09 | 0.12 | 710.25 | 1262.62 | 44.71426 | 10,080 | |
| GA | 691.70 | 260.54 | 0.21 | 0.12 | 736.93 | 1296.01 | 44.68719 | 20,600 | |
| c | BUMDA | 495.40 | 322.40 | 0.18 | 0.27 | 391.22 | 791.50 | 47.71379 | 2843 |
| PSO | 1113.84 | 160.00 | 0.11 | 0.12 | 578.97 | 500 | 47.53664 | 8100 | |
| GA | 988.34 | 160.04 | 0.12 | 0.13 | 521.48 | 499.88 | 45.58347 | 52,800 |
| Traj. | Algorithm | Wilcoxon | t-Test | ||
|---|---|---|---|---|---|
| a | BUMDA vs. PSO | × | × | ||
| BUMDA vs. GA | √ | √ | |||
| b | PSO vs. BUMDA | × | × | ||
| PSO vs. GA | × | × | |||
| c | BUMDA vs. PSO | √ | √ | ||
| BUMDA vs. GA | × | × | |||
| Algorithm [nPop,nGen] | Approx. Hypervolume (Higher Is Better) | Generational Distance (Lower Is Better) | Positive Inverse Generational Distance (Higher Is Better) |
|---|---|---|---|
| MOEA/D [100,100] | |||
| MOEA/D [50,200] | |||
| NSGA-III [100,100] | |||
| NSGA-III [50,200] |
| Algorithm Comparison [nPop,nGen] | Wilcoxon | t-Test | ||
|---|---|---|---|---|
| MOEA/D ([100,100] vs. [50,200]) | √ | √ | ||
| MOEA/D [100,100] vs. NSGA-III [100,100] | × | × | ||
| MOEA/D [100,100] vs. NSGA-III [50,200] | × | √ | ||
| MOEA/D [50,200] vs. NSGA-III [100,100] | × | × | ||
| MOEA/D [50,200] vs. NSGA-III [50,200] | × | √ | ||
| NSGA-III ([100,100] vs. [50,200]) | × | × | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ríos, A.; Hernández, E.E.; Valdez, S.I. A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators. Mathematics 2021, 9, 543. https://doi.org/10.3390/math9050543
Ríos A, Hernández EE, Valdez SI. A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators. Mathematics. 2021; 9(5):543. https://doi.org/10.3390/math9050543
Chicago/Turabian StyleRíos, Alejandra, Eusebio E. Hernández, and S. Ivvan Valdez. 2021. "A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators" Mathematics 9, no. 5: 543. https://doi.org/10.3390/math9050543
APA StyleRíos, A., Hernández, E. E., & Valdez, S. I. (2021). A Two-Stage Mono- and Multi-Objective Method for the Optimization of General UPS Parallel Manipulators. Mathematics, 9(5), 543. https://doi.org/10.3390/math9050543





