Abstract
In the last years, the distribution network operators (DNOs) assumed transition strategies of the electric distribution networks (EDNs) towards the active areas of the microgrids where, regardless of the operating regimes, flexibility, economic efficiency, low power losses, and high power quality are ensured. Artificial intelligence techniques, combined with the smart devices and real-time remote communication solutions of the enormous data amounts, can represent the starting point in establishing decision-making strategies to solve one of the most important challenges related to phase load balancing (PLB). In this context, the purpose of the paper is to prove that a decision-making strategy based on a limited number of PLB devices installed at the consumers (small implementation degree) leads to similar technical benefits as in the case of full implementation in the EDNs. Thus, an original bi-level PLB methodology, considering a clustering-based selection criterion of the consumers for placement of the switching devices, was proposed. A real EDN from a rural area belonging to a Romanian DNO has been considered in testing the proposed methodology. An implementation degree of the PLB devices in the EDN by 17.5% represented the optimal solution, leading to a faster computational time with 43% and reducing the number of switching operations by 92%, compared to a full implementation degree (100%). The performance indicators related to the unbalance factor and energy-saving highlighted the efficiency of the proposed methodology.
1. Introduction
Future electric distribution networks (EDNs) will cover the supply areas corresponding to the low voltage (LV) or medium voltage (MV) distribution feeders, which can be associated with the microgrids (μGs), each requiring efficient energy management [1]. With the rapid propagation of the “smart grid” concept, some μGs in neighbouring areas, which have a connection point (generally, an electric distribution substation or a tie line), can be interconnected to constitute a multi-microgrid (MμG) system [2]. Today, the transformation of the EDNs to satisfy the requirements of the μGs is technically possible due to the presence of automation devices and, more recently, smart meters that communicate using industry standards. On the other hand, there are challenges of the distribution networks operators (DNOs) to ensure the transition towards the active area of the μGs: the emergence of small-scale distributed generation sources (including the prosumers) and storage systems, the requirements for reducing the carbon footprint of electricity production that determines the change of the market model, and the presence of the bidirectional power flow [3].
In the current stage of this transition, the accelerated development in innovation and technology plays an important role leading to [4]:
- investments in the technical infrastructure of the actual EDNs to achieve flexibility able to adapt to new requirements;
- increasing the automation degree in the EDNs to ensure the resilience and integration of the distributed generation sources for an optimal operation;
- optimizing the topology to ensure continuity in the energy supply of the consumers.
In this context, the directions assumed by the DNOs aim to bring the EDNs from the passive in the active area, where Artificial Intelligence techniques, combined with advanced technologies and real-time remote communication solutions of the enormous data amounts, led to the development of the concepts, equipment, technologies, and solutions associated with the “smart grids” concept. The manufacturers must ensure adaptable and reliable solutions for the communication systems to allow interconnectivity with the smart metering system (SMS) of the DNOs. The possibilities of the advanced technologies and the dedicated platforms offer new opportunities to the equipment manufacturers to develop new architectures of the smart systems, including sensors, meters, data concentrators, and automation devices that can communicate with each other to ensure a high level of intelligence of the EDNs similar to μGs. These systems will provide support to operate optimal the technical infrastructure [4].
One of the main issues from operating the future EDNs (named μGs) that can be solved using these smart systems refers to the phase load balancing (PLB). Ideally, the EDNs should be all along in the symmetric and balanced regime. In real conditions, such an ideal operating associated with the current and voltage system is practically impossible due to the dynamic variation of the load absorbed by the single-phase (1-P) consumers. In these conditions, the operation regime of the EDNs becomes unbalanced, affecting the three-phase symmetry of voltage and current, with economic and technical losses for the DNO.
1.1. Literature Review
Currently, various solutions have been developed in the literature to solve the PLB problem. They consider the following objectives: the minimization of damages to the consumers, the minimization of unbalance degree, and the maximization of energy-saving. The optimal allocation of 1-P consumers represents an important research direction in the last years, mainly due to the SMS concept. Generally, many references from the literature refer to different variants of the PLB mechanisms. For example, [5,6,7] have investigated the PLB problem based on the automatic 1-P consumer allocation. The phase reconfiguration, or consumer reallocation, can be automatically operated to minimize the current unbalance [5] based on the specific devices with controllable switches connected on the low voltage (LV) side of the supply point (SP), identified through the electric substation connected to the medium voltage network of the DNO. The EDN with the simple topologies, such as a residential house [6] or experimental stand [7], were used in testing the solutions represented by a micro-controller and an active phase router.
Regarding the balancing devices with controllable switches, there are different approaches proposed in many research papers. The static transfer systems (STS)-based devices, with various costs and technical performances [8,9,10], were already implemented. These solutions follow reducing the purchase cost and the switching times. Other devices use a control system of the three-phase load unbalance [11] formed from two parallel components (magnetic holding relay and thyristor) that allow quickly switching the load between phases a, b, or c. The low cost, the high real-time performance, and a positive effect on reducing the unbalance degree represents the main advantages of this solution. An automatic phase load balancing device, based on a microcontroller and three relays, was proposed in the references [12,13,14]. The operating time of the relay is a significant technical parameter in the switching process. The results indicates that this solution is efficient, having a reduced cost in their implementation. Another variant of a three-phase balancing device having in its structure six relays and six contactors to ensure the balanced regime of three controllable loads, is presented in [15]. The conclusion is that increasing the loads can lead to a high cost due to the number of contactors. The solid-state relays and contactors connected to each phase represent the base of the solution adopted in [16]. The three triacs of relays operate such that no two triacs are in the “on state” at the same time because this state will create a short circuit among phases. A design of a phase-swapping device with magnetic latching relays proposed in [17] can represent an efficient solution having economic and technical benefits. Also, it uses a high-speed data transmission system that is the main advantage in the implementation of a remote-control scheme.
On the other hand, many researchers have considered the manual reallocation of the 1-P consumers on the LV three phases to minimize the power losses based on the off-line simulations [18,19,20]. The inability to reallocate all consumers simultaneously in the EDNs represents the main disadvantage of these methodologies, leading to additional power losses. The solution proposed in [19] is obtained based on the minimization of active power loss, considering a minimum number of selected 1-P consumers for swapping between the three phases of the grid. The optimal allocation of reactive power devices will not solve the PLB problem [19,21]. Also, the three-phase capacitor allocation led to high costs in the EDNs. In another perspective, the historical information about load balance can decrease the unbalance factor by more than 10%, only if the consumers could be allocated optimally on the phases [22].
Other analyses use the metaheuristics algorithms that tend to be considered less intricate for implementation: discrete Genetic Algorithm [18,23], Particle Swarm Optimization Algorithm [20], Gray Wolf Optimization Algorithm [24], Flower Pollination Algorithm [25], Ant Colony Optimization [26], or Nelder Mead combined with Bacterial Foraging Algorithm [27]. Most of these researches report that the performed studies aim to reach the global optimum. This observation is never correct for a heuristic method that runs on the real EDNs. At the same time, the computation time increases with the complexity of the problem.
The large-scale integration of the prosumers, storage systems, and electric vehicles represent other challenges of the DNOs. In this context, the PLB problem sparked, again, a particular interest of researchers. The authors have implemented in [28] a power market mechanism with financial benefits to encourage both consumers and local producers to participate in the PLB process. The balancing mode (using switching devices or manually) is missing due to commercial objectives subject to technical constraints.
The approaches from [29,30,31] solve the PLB problem through the smart integration of electric vehicles. Kikhavani M.R. et al. [29] addresses the optimal phase connection of Plug-in electric vehicles (PEVs) based on the power loss minimization and the improvement of the voltage profile. The algorithm commands phase switching devices connecting or disconnecting the optimal number of PEVs in two operational ways (vehicle-to-grid and grid-to vehicle). Reference [30] presents the adaptive coordination between the photovoltaic inverters and electric vehicle chargers based on a local controller device to solve the PLB problem. At the same time, the approach detailed in [31] proposes the LV modular bypass converters. The topology of an EDN without additional power losses represents the main characteristic of these active balancing methodologies.
The integration of energy storage systems in the EDNs with small-scale distributed generation represents another option to address optimal phase balancing [32]. The balancing speed represents the main limitation of the last four approaches [29,30,31,32], limited by a high number of switching operations associated with the electric vehicle and the storage systems. A comprehensive solution with smart transformers is presented in [33], while another study proposes a simple three-phase load balancing considering only the information provided by smart meters [34].
Table 1 presents a concise summary of the references with an emphasis on the main characteristics and the implementation method: type of EDN, balancing point (pole/supply point level), balancing mode (manual/automatic), optimization model (with objective function (OF) and constraints (C)), and switching operations. The objective function considers the minimization of unbalance current (UC), unbalance voltage (UV), unbalance factor (UF), cost optimization (CO), and active power losses (APL). Many other studies presented in the literature have proposed the same approaches to solve the PLB problem as the ones in the table.

Table 1.
Synthesis of the approaches proposed in the literature.
Concerning the MμG systems, the phase load balancing has not been treated as a stand-alone problem, being part of the energy management strategies from each EDN, seen as μG, [35,36]. The approach developed in [35] treats the economic operation in the MμG system, proposing an optimization model based on the multileader and multi-follower game. Thus, the tie-line power of the μGs is corrected to optimize the economic benefits quantified through a three-phase balanced regime. A control strategy for PLB applied in the neighbouring non-synchronous μGs was proposed in [36] and used at the level of each μG.
1.2. Contributions
Although many studies and papers addressed the PLB problem, some aspects still have not been considered. Thus, the analysis of all approaches highlights some weaknesses represented by a fully (100%) implementation degree with the PLB devices, with high investments and overheads for the DNOs, and the use of test grids, which does not consider all technical and economic operating conditions from the real grids, in the validation process. In these conditions, the purpose of the paper is to prove that a limited number of PLB devices (low implementation degree that means reduced investments) can lead to similar technical benefits as in the case of full implementation.
In the paper, the authors attempt to address the above weaknesses of the approaches from the literature, proposing a novel bi-level decision-making methodology characterized by the following original contributions:
- From the literature review, our decision-making strategy, included in the first step of the methodology, for the placement of the switching devices in the LV distribution networks is the first that contains a clustering-based consumers’ selection criterion. A qualification index was defined to select the optimal number of the consumers’ candidate groups in the decision-making process. This strategy significantly reduces the investments and overheads involved in network management for the DNO.
- Developing a new PLB algorithm that aims minimization of the unbalance factor at the SP level while ensuring that the unbalance constraints are satisfied at all poles where selected consumers in the first level are connected. The fast convergence and high accuracy represent strengths compared with other algorithms. Hence, the conflicting goals of accuracy and convergence speed are simultaneously achieved.
- Presenting a comparative study between full and low implementation degrees of the PLBE to demonstrate the effectiveness of the proposed decision-making methodology in a real EDN with complex topology and a high number of consumers.
1.3. Paper Organization
The organization of the next sections is the following: Section 2 particularizes the levels of the proposed methodology that integrates the clustering-based selection criterion of the consumers for the PLB process, Section 3 details the results obtained for a real EDN belonging to a Romanian DNO and a comparative study accomplished concerning the methodology where all consumers take part in the PLB process (full implementation degree) to highlight the accuracy and benefits of the proposed algorithm, and Section 4 includes the conclusions and the future works.
2. Materials and Methods
The proposed methodology, associated with the optimal placement of the PLBE in the consumption points, contains two hierarchical levels in the decision-making process:
- The first level integrates the K-means clustering-based algorithm to select the “candidate” groups containing 1-P consumers where the phase load balancing equipment (PLBE) could be installed, with a significant influence on the minimization of unbalance factor; the clustering simplifies the selection process leading at a relatively small number of 1-P consumers with the PLBE installed.
- The second level includes an improved iterative PLB algorithm to minimize the unbalance factor at the SP level, subject to the constraints where its value must be below an imposed limit by the decision-maker (DM) at poles with 1-P consumers from the “candidate” groups connected.
The number of consumers from the “candidate” groups who participated in the balancing process will influence the decision regarding the placement of the PLBE.
In the paper, the methodology is applied for a single EDN (associated with a μG), with the possibility to be extended for a multi-EDN system (MμG system), provided that the EDNs have the same supply point (an electric distribution substation) connected to the distribution network of the DNO to achieve the proposed objective, namely the minimization of the unbalance factor at the SP level.
Figure 1 presents the flow-chart of the methodology, highlighting the steps associated with each level. The next paragraphs detail its application process.
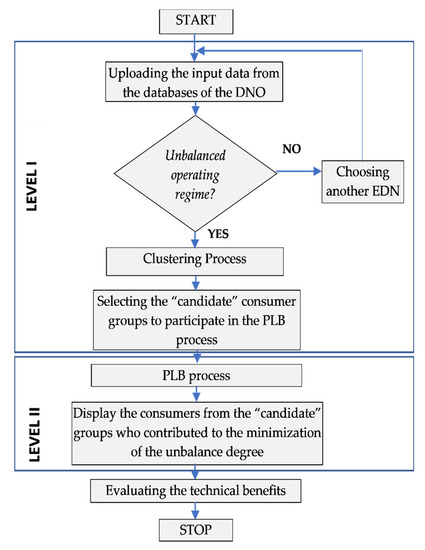
Figure 1.
The flow-chart of the proposed methodology.
2.1. The First Level—Selecting “Candidate” Consumer Groups
The first level refers to a decision-making process where the consumers’ “candidate” groups with PLBE installed are established based on the clustering process. The choice of the K-means algorithm was motivated by its advantages concerning other algorithms: easy implementation, working with the high-size database, guaranteed convergence, fast initialization of the centroids, and effortlessly accommodates to new samples [37,38,39]. The following sections described the main steps used in selecting the “candidate” consumer groups.
2.1.1. Input Data
The input data considered in the clustering process include for each consumer n, n = 1, …, NC, where NC represents the total number of the consumers, the requested current at the peak load hour, hPL, from the EDN, and the distance, Dn, n = 1, …, NC, from the SP (connected to the medium voltage electric distribution system of the DNO) to the poles where the consumer is connected. Thus, the consumers subjected to the clustering process have these features recorded in a matrix [ID], having the size NC×2:
where: NC represents the number of the consumers from the EDN integrated into the SMS; hPL is the hour of the peak load recorded in the EDN; In,hPL corresponds to the requested current by the consumer n, n = 1, …, NC at the hour hPL; Dn indicates the distance between the SP and the pole where the consumer n is connected.
The current profiles corresponding to the day of the peak load from the EDN are uploaded from the database of the SMS in a matrix [I], having the size NC×H:
where H is the analysed time period (in this case H = 24 h, with a sampling step Δh = 1 h).
The aggregation of the profiles at the LV level of the SP to identify the hour of the peak load represents the following step:
where: [I(SP)]1×H represents the vector of the currents aggregated at the LV level of the SP for each hour h, h = 1, …, H; hPL is the position from the vector [I(SP)] associated with the hour of the peak load recorded in the EDN; I(SP)max corresponds the maximum value of the total current (peak load) at the LV level of the SP.
The column hPL of the matrix [I], [IhPL], will be used in the clustering process as the first feature of the consumers, representing the requested currents at the hour of the peak load.
In addition to the current profiles, the branching type, tb, tb = {1-P, 3-P}, where 1-P is associated with the single-phase consumers and 3-P with the three-phase consumers, and connection phase, p = {a, b, c, abc}, for each consumer, are uploaded from the consumers’ database of the DNO based on the identification number of the analysed EDN and recorded in the vectors [Tb]1×Nc and [Ph]1×Nc. One of the phases from the set p = {a, b, c} will be used by 1-P consumers, and the 3-P consumers will have a three-phase branching {abc}.
Based on these data, the current profiles are aggregated on each phase at the SP level, and the unbalance factor (UF) is calculated for the peak load hour, hPL, using the formula [40]:
where p—the set of the phases (p = {a, b, c}); nph—the number of the phases (np = 3); Ip(hPL)—the total current on the phase p, at the LV level of the SP and hour hPL; Iav(hPL)—the average phase current at the SP level and the hour of the peak load, hPL;
If UF(hPL) has a value higher than 1.1 (limit value accepted by the DNO for the unbalance factor), the clustering algorithm starts to identify the consumers’ “candidate” groups.
The second column of the matrix [ID], corresponding to the other feature used in the clustering process, refers to the distances between the poles and the SP. The calculation of these distances is easy, knowing the topology of the EDN identified based on an algorithm proposed by the authors in [41]. Figure 2 explains the synthesis of the approach.
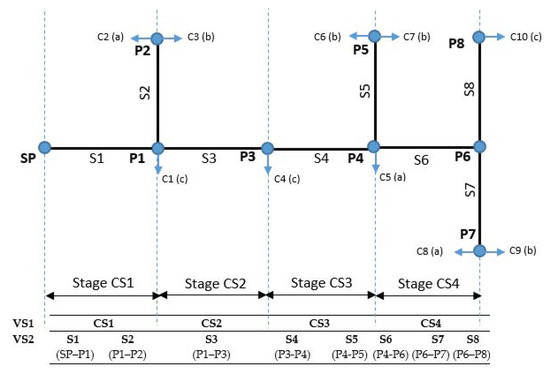
Figure 2.
The exemplification of the structure vectors-based approach.
The two structure-vectors, [VS1] and [VS2], identifies the topology of the EDN. The consecutive grouping of the distribution sections between two poles inside the connecting stage corresponds to the starting point to build the two vectors. The notations are the following: connecting stages CS1…CS4, sections S1…S8, poles P1…P8, and consumers C1…C10. The vectors [PT]1×NP and [S]1×NS, where NP and NS represent the total number of the poles and sections, record the data related to the topology of the EDN. The connected phases (a, b, or c) of the consumers are indicated between the round brackets. The values of the elements associated with the vectors [VS1] and [VS2] are highlighted under the single-line diagram of the EDN.
Using this topology and additional information obtained from the DNO regarding the distance between two successive poles, a distance-vector [D], having the size 1×NC, is built based on the allocation of the consumers to each pole. Table 2 presents the elements of this vector, associated with the topology from Figure 2.

Table 2.
The allocation of the consumers to the poles and the distances to the SP (see Figure 2).
The vector [D] represents the second feature of the consumers used in the clustering process (the second column from matrix [ID]).
The normalization of the two features corresponds to the last stage before starting the clustering process. The following relations represent the base of the normalization stage [42,43]:
where I*n,hPL—the normalized value of the requested current by the consumer n, n = 1, …, NC at the hour hPL; Dn*—the normalized value of the distance between the pole where the consumer n is connected and the SP; IhPl,min and IhPL,max—the lowest and highest value of requested currents at the hour hPL; Dmin and Dmax—the minimum and maximum values of the distances.
2.1.2. Clustering Process
The K-means algorithm receives as input data the normalized matrix [ID*]Nc×2, where each row [ID*n] = [I*n,hPL D*n] is associated with a consumer n = 1,…, NC, having as features the requested current at the peak load hour, hPL, and the distance, D*n, n = 1,…, NC, from the SP to the pole where the consumer is connected.
The K-means algorithm groups the consumers in clusters, denoted by C = {Ck | k = 1: K}. The grouping process considers the minimization of the following objective function:
where: mk—the centroid of the cluster k, k = 1, …, K; dist (. , .) represents the Euclidean distance in the two-dimensional space.
The algorithm starts with a random set of the centroids associated with the K clusters and then change the centroids into several iterations. Finally, it will find a partition that corresponds to a minimum of the function F [39,42,44].
The main steps of the algorithm are the following, see Figure 3:
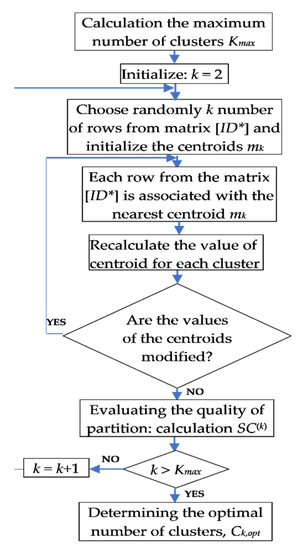
Figure 3.
The steps of the clustering process.
Initialization: It starts with the random selection of K centroids from the rows of the matrix [ID]:
M = {m1(0), …, mk(0), …, mK(0)}
Assigning: Each row from the input data matrix is associated with the nearest centroid:
Update: The new position of the centroids mk, k = 1, …, K, is recalculated as the average value of the features (current and distance) associated with the consumers from the clusters Ck.
The following formula sums up all the characteristics of the consumers belonging to the cluster Ck, k = 1, …, K, having the membership degree to it.
where nk—the number of consumers from the cluster Ck.
Stopping: Repeat Steps 2 and 3 (Assigning and Update) until a pass through the input data does not cause new assignments, and no change in the values of the centroids will not produce. Also, the maximum number of iterations of the algorithm can be limited.
However, there is a question regarding the final partition: Was the global optimum obtained?
The following steps have been completed to obtain the answer to this question:
- Calculation of the maximum number of clusters based on the formula [45]:
- Clustering: K-means clustering method is used for each partition in the Ck clusters, k = 2, …, Kmax, using the input data matrix.
- Evaluating the quality of partition: The evaluation is based on the silhouette coefficient calculated with the relation [46]:where: Nr and Ns—the number of the consumers assigned to the clusters r and s; dist(IDi, IDj)—the Euclidean distance in the two-dimensional space between the i-th and j-th rows from the matrix [ID*].
- Iterative process: Repeat Steps 2 and 3 (Clustering and Evaluating the quality of partition) to evaluate the quality of partitions between 2 and Kmax. The values of SC are recorded for each partition in the vector QP = [SC(2), SC(3), …, SC(Kmax)].
- Determining the optimal number of clusters through the calculation of the maximum value from the vector QP, SCmax. The partition with the value SCmax is associated with the optimal number of clusters, Ck,opt.
2.1.3. Selecting the “Candidate” Consumer Groups
The decision-making process uses a qualification index, QI, to select the candidate groups. It is defined for each interest area resulted from the zoning of the “distance-current” space. Each interest area has a degree of importance, Gi, (High, Medium, and Low) having a discrete value of the QI assigned. There are some differences between the urban and rural areas represented by the distances between consumers and the SP (shorter in the urban areas), the type of EDN (aerial in the rural areas), and the requested currents at the peak load (smaller values for the rural consumers).
Inside the interest areas, the clusters Ck,opt, obtained from the clustering process are represented by the centroids mk, with the average characteristics of the distances and requested currents of the consumers from each cluster.
The values of the index QI depend on the degrees of importance: Gi{7, 8, 9, 10}, for a High degree, Gi{4, 5, 6}, for a Medium degree, and Gi{1, 2, 3}, for a Low degree. The clusters with the centroids inside the areas with a High degree of importance represent “candidate” groups. They will participate in the PLB process in descending order of the QI, and depending on the stop criterion imposed by the DM on the unbalance factor, UF, all or only some of them will be chosen.
2.2. The Second Level—Phase Load Balancing Process
An iterative algorithm, which minimizes the unbalance factor on the LV side of the SP by switching the consumers assigned to the “candidate” groups from a phase to another, is proposed in the PLB process. It represents an improved variant of the algorithm proposed in [46], where all consumers integrated into the SMS take part in the PLB process following a single-iteration procedure, having as the objective the minimization of the unbalance factor to each pole. Even if the optimal solution has corresponded to a value of the unbalance factor very close to 1.0 (ideal target) at the SP level, the number of switching operations is very high.
In the proposed algorithm, the maximum number of iterations is equal to the number of the “candidate” consumer groups. In each iteration, all consumers from a “candidate” group, selected in descending order of the QI, are considered in the PLB process.
The algorithm starts with the end poles, aggregating the currents on each phase considering the allocation of consumers, and tracks the topology of the EDN, identified through the two structure-vectors [VS1] and [VS2] (see Section 2.1.1), until to the SP. The minimization of the unbalance factor at the SP level represents the objective of the PLB algorithm. To satisfy the constraints, the values of the unbalance factor calculated at the poles with the 1-P consumers from the “candidate” groups must be smaller than the imposed limit by the DM. Finally, the optimal solution corresponds to the coordination of the PLBE from the consumption points (CP) associated with the consumers from the “candidate” groups. Specifically, if the local PLB solutions obtained at each pole with the consumers from the “candidate” groups connected are optimal, then the global PLB solution at the SP level is also optimal.
Thus, the objective function of the PLB problem refers to the minimization of hourly unbalance factor inside the analysed period H at the level of the SP:
subject to:
where: h—the hour when the PLB process unfolds; GC—the “candidate” groups of the consumers with PLBE; UF(h)SP– the unbalance factor on the LV side of the SP; {PGC}—the set of the poles with least one consumer from the groups GC; {PT}—the set of all poles from the EDN; UF(h)P—the unbalance factor calculated at the pole P containing consumers from the groups GC; UFlim—the limit value agreed by the DM for the unbalance coefficient at the pole level; H—the analysed time period.
As pointed out above, the algorithm starts from the end poles to determine in the final step the minimum value of the unbalance factor at the SP level, UF(h)SP, at each hour h, based on the optimization models (18) and (19).
An aggregation process of the phase currents takes at each pole P place, starting with those from the end of the EDN. If consumers from the groups GC are connected at the pole P, then P{PGC} and the optimal local solution at the pole level is obtained considering all combinations between the allocations of each consumer from the groups GC on the phases, satisfying the constraint (19), where UF(h)P is calculated with the relation,
where: I(h){p},P—the phase currents aggregated at the pole P{PGC}, p = {a, b, c}; I(h)av,P—the average phase current calculated at the pole P{PGC}; nph—the number of the phases.
For the optimal combination of the consumers from the groups GC corresponding to the minimum value of UF(h)P, the phase currents, I(h){p},P, p = {a, b, c}, are calculated with the relation,
where: GI—the ignored groups of the consumers without PLBE; I(h){p},GI,P—the phase currents, p = {a, b, c}, belonging to the groups GI and aggregated at the pole P{PGC}; I(h){p},GC,P—the phase currents, p = {a, b, c}, belonging to the groups GC and aggregated at the pole P{PGC}; I(h){p},x—the phase currents, p = {a, b, c}, aggregated at the pole x{PT} (placed after the pole P in the EDN).
If the current pole is an end pole then I(h){p},x = 0. In the same context, if there are only the consumers belonging to groups GI connected at the pole P{PGC}, then the phase currents I(h){p},GC,P, p = {a, b, c}, are missing, also, from the relation (21).
The calculation of the phase currents associated with the consumers from groups GC connected at the pole P{PGC} is done with the relations,
where: I(h)a,GC,mi—the requested current by consumer mi belonging to the groups GC and allocated on the phase a at the pole P; I(h)b,GC,mj—the requested current by the consumer mj belonging to the groups GC and allocated on the phase b at the pole P; I(h)c,GC,ml—the requested current by the consumer ml belonging to the groups GC and allocated on the phase c at the pole P; N(h)a,GC,P, N(h)b,GC,P, N(h)c,GC,P—the number of the consumption points associated with the consumers allocated on each phase of the EDN, belonging to the groups GC, at the pole P.
For the consumers from group GI connected at the pole P{PGC}, the phase currents are calculated with the relations,
where: I(h)a,GI,ni—the requested current by consumer ni belonging to the groups GI and allocated on the phase a at the pole P; I(h)b,GC,nj—the requested current by the consumer nj belonging to the groups GI and allocated on the phase b at the pole P; I(h)c,GC,nl—the requested current by the consumer nl belonging to the groups GI and allocated on the phase c at the pole P; N(h)a,GI,P, N(h)b,GI,P, N(h)c,GI,P—the number of the consumption points associated with the consumers allocated on each phase of the EDN, belonging to the groups GI, at the pole P.
The number of consumers assigned to groups GC on each phase can be different at the hour h, compared to the previous hour, due to the switching process. Finally, it is verified if all consumers from both groups, allocated to the pole P{PGC}, were considered in the aggregation process using the relations,
where: N(h)P,{p},GI—the number of the consumption points associated with the consumers belonging to the groups GI, allocated on each phase p ={a, b, c} at the pole P; N(h)P,{p},GC—the number of the consumption points associated with the consumers belonging to the groups GC, allocated on each phase p ={a, b, c} at the pole P; N(h)P,{p}—the total number of the consumption points associated with the consumers allocated on each phase p ={a, b, c} at the pole P; NP—the total number of the consumption points associated with the consumers allocated at the pole P.
The aggregation process of the phase currents at the SP level is based on the relation,
where: I(h){p},SP—the phase currents, p ={a, b, c}, aggregated at the SP level (on the LV side); I(h){p},GI,SP—the phase currents of the consumers belonging to the groups GI and aggregated at the SP level; I(h){p},GC,SP—the phase currents of the consumers belonging to the groups GC and aggregated at the SP level.
The calculation of the phase currents associated with the groups GI is done with the relations,
where: I(h){p},GI,SP—the phase currents, p = {a,b,c}, of the consumers belonging to the group GI and aggregated at the SP level; I(h)a,GI,o—the requested current by the consumer o belonging to the groups GI and allocated on the phase a; I(h)b,GI,f—the requested current by the consumer f belonging to the groups GI and allocated on the phase b; I(h)c,GI,v—the requested current by the consumer v belonging to the groups GI and allocated on the phase c; N(h)a,GI, N(h)b,GI, N(h)c,GI—the number of the consumption points associated with the consumers belonging to the group GI, allocated on each phase p = {a, b, c} at the SP level.
The phase currents associated with the groups GC at the SP level, where the optimal phase for each consumer has been determined at the poles P{PGC}, are calculated with the relations,
where: I(h){p},GC,SP—the phase currents, p = {a,b,c}, of the consumers belonging to the groups GC and aggregated at the SP level; I(h)a,GC,q—the requested current by the consumer q belonging to the groups GC and allocated on the phase a; I(h)b,GC,e—the requested current by the consumer e belonging to the groups GC and allocated on the phase b; I(h)c,GC,w—the requested current by the consumer w belonging to the groups GC and allocated on the phase c; N(h)a,GC, N(h)b,GC, N(h)c,GC—the number of the consumption points associated with the consumers belonging to the groups GC, allocated on each phase p = {a, b, c} at the SP level.
The consumers considered in the aggregation process on each phase, n(h){p}, p = {a, b, c}, are verified to correspond with the total number of consumers from the EDN using the relations,
where: N(h){p},GC—the number of the consumption points associated with the consumers from the EDN allocated on each phase p = {a, b, c}, belonging to the groups GC; N{p},GI—the number of the consumption points associated with the consumers from the EDN allocated on each phase p = {a, b, c}, belonging to the groups GI; n(h){p}—the number of the consumers from the EDN allocated on each each phase p = {a, b, c}; NC—the number of the consumers from EDN.
Finally, the unbalance factor at the SP level at hour h, h = 1, …, H, see the relation (18), is calculated with the help of the aggregated phase currents on the LV side:
where:
The average value of the unbalance factor, UF(l)av,SP, on the LV side of the SP, in the analysed period, H, is calculated in each iteration l.
where: H—the analysed period and l—current iteration.
The stopping criterion of the iterative process verifies if the average value of the unbalance factor is below than a specified limit by the DM,
where: UFlim—the specified limit by the DM to stop the iterative process.
If the constraint (32) is not satisfied, the following “candidate” group is considered, and all steps are repeated.
For a better understanding, Figure 4 exemplifies the proposed PLB algorithm using the test EDN presented in Section 2.1.1, considering the hypothesis that consumer C9, connected to the pole P7, has a PLBE.
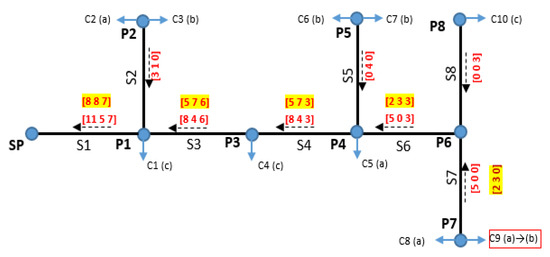
Figure 4.
The PLB procedure detailed for the EDN with 8 poles and 10 consumers.
The red values represent the initial phase currents on each section, and yellow highlights the modified values due to switching the consumer C9 from phase a to b. Thus, UF at the SP level reaches a very close value to the target (UF = 1.0) decreasing from 1.11 to 1.004. The effect of this switching operation, quantified through smaller UF, feels at the level of each pole.
The proposed methodology has the following advantages compared with the approaches from the literature:
- Applying in the real EDNs, with complex topologies and a high number of 1-P consumers.
- Use in the first level a clustering-based selection criterion, easy to implement in the decision-making strategies, to obtain the “candidate” groups of the 1-P consumers which participate in the PLB process, with significant influence on the minimization of the unbalance factor. This criterion is easy to implement in any decision-making strategy.
- Integration into the second level an iterative PLB algorithm that aims minimization of the unbalance factor at the SP level, subject to the constraints regarding its value below an imposed limit at the poles where the 1-P consumers from the “candidate” groups are connected. The fast computational time and convergence speed represent strengths compared with other algorithms.
Figure 5 presents the flow chart of the proposed iterative Algorithm (18)–(32).
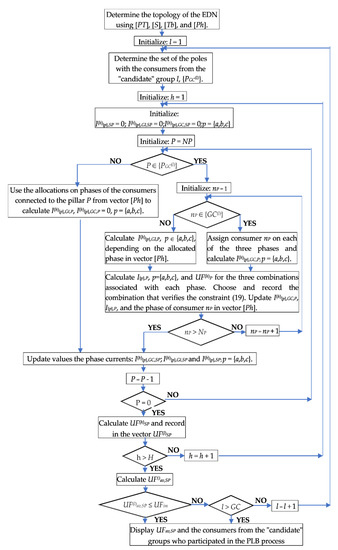
Figure 5.
The flow-chart of the proposed algorithm.
2.3. Integration of the Methodology in a Smart Balancing System
The architecture of a Smart Balancing System (SBS), which to integrate the proposed methodology, should have the following main components: the phase load balancing equipment (PLBE), composed of a smart meter (SM) and a switching device (SD), a high-speed data communication system, and the data concentrator from the supply point (SP). Figure 6 presents the implementation of the architecture for the EDN from Figure 5.
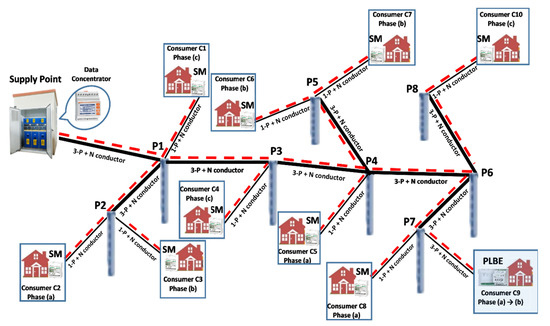
Figure 6.
The architecture of the SBS from an EDN used in the PLB process.
The red dashed lines correspond to the communication system, and the black lines signify the technical infrastructure with the four-wire conductors (three phases and neutral, 3-P + N) on the main trunk and two-wire conductors (one phase and neutral, 1-P + N) for the 1-P branching. The 1-P consumers must have the three-phase (3-P) branching and the PLBE to be involved in the PLB process, as is the case of the consumer C9. The other consumers will only have the SM.
The data concentrator installed at the SP level takes over, with a sampling step (1 h) set by the DM, the data regarding the current and the connection phase from each consumption point associated with the 1-P consumer.
The decision-making module, which includes the PLB algorithm, processes the data, and, finally, sends the command to SD from the PLBE structure to switch the consumer on the new phase according to the identified solution corresponding to a minimum unbalance degree.
The architecture of the SBS can have a significant impact on the operation of the EDNs only if the following requirements are satisfied:
- the communication infrastructure has a high-speed data transmission,
- the data concentrator located at the SP level, which integrates the decision-making module, has superior performances (high data acquisition and processing speed),
- the SD, integrated into the PLBE, performs fast switching between phases of the 1-P consumers.
However, a compromise must be between these requirements leading to a convenient cost for the DNO.
The methodology could also solve the PLB problem in a multi-EDN system with EDNs connected to the same SP. The decision-making will correspond to an optimal local balancing solution for each EDN, which leads to a global balancing solution at the level of the whole system. The objective is the same, namely minimization of the unbalance factor at the SP level. Thus, the data concentrator will contain the data from all EDNs and send simultaneous the command to SDs according to the solution corresponding to a minimum unbalance degree, see Figure 7.
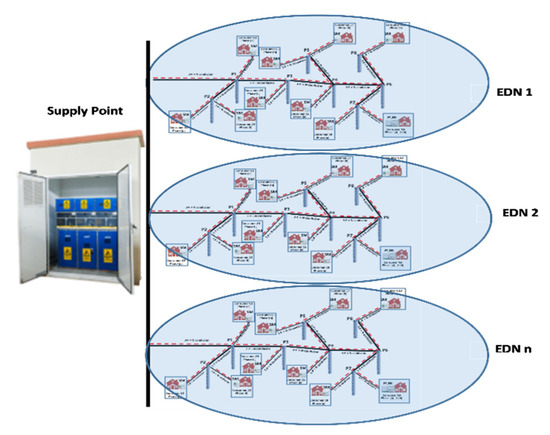
Figure 7.
The architecture of the SBS from a multiple-EDN system used in the PLB process.
3. Case Study
A real EDN, having the rated voltage of 0.4 kV, belonging to the DNO from the North-East Region of Romania, was considered in testing the proposed methodology. Figure 8 presents the topology of the analysed EDN, where for the type (1-P or 3-P) and allocation of the consumers on the phases were used the following colours: red (1-P consumer, phase a), blue (1-P consumer, phase b), yellow (1-P consumer, phase c), and magenta (3-P consumers).
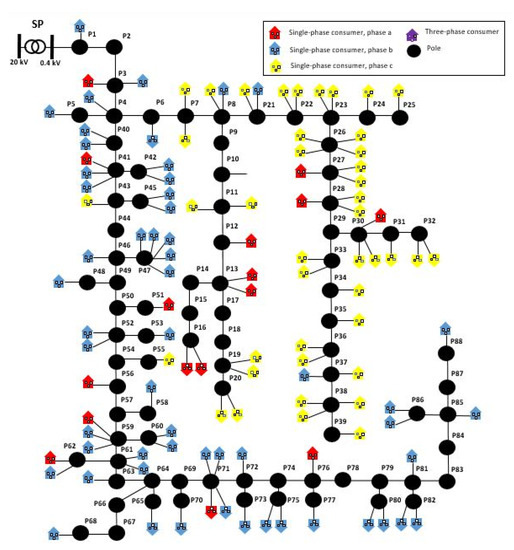
Figure 8.
The topology of the test EDN.
Table 3 presents details of the characteristics associated with the sections of the EDN. The data indicate that 62.5% (2.2 km) from the total length has the cross-section of phase and neutral conductors by 50 mm2, mainly on the main trunk. The lateral branches, having 1.32 km, contain both 1-P (18.2%) and 3-P (19.3%) conductors, with cross-sections less than 35 mm2.

Table 3.
The characteristics of the sections.
Figure 9 presents the type (1-P or 3-P) and the initial phase allocation for all consumers. The analysis of the information highlights that most of the 1-P consumers are allocated on the phase b (48.2%), followed by phase c (36.8%), and phase a (14%). Only one consumer (0.9%) connected at the pole P10 has 3-P branching. The vectors [Tb] and [Ph] will contain these data (see Table A1 from Appendix A).
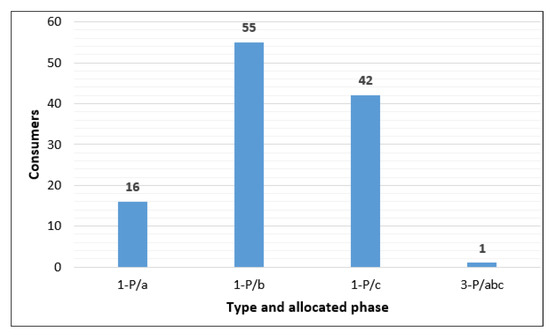
Figure 9.
The allocation of the consumers on the phases.
Another significant piece of information in testing the methodology refers to the consumers. In the analysed EDN, all consumers have the meters integrated into the SMS such that the current curves, with a sampling step by 1 h, can be available, see the Supplementary File Current Curves.
The information associated with the topology of the EDN and current profiles is uploaded from the databases, representing the input data of the proposed methodology.
In the first stage, the matrix [ID], having two columns associated with the vectors [IhPL] and [D], which contain the requested currents at the hour the peak load, hPL, and the distances, Dn, n = 1, …, NC, from the SP to the pole where each consumer is connected, is built. Then, based on the elements of the structure-vectors [VS1] and [VS2], all data related to the topology (poles and sections) are recorded in the vectors [PT] and [S]. Using these vectors and the additional information on the distance between two successive poles provided by the DNO according to the technical regulations in Romania, see Supplementary File Characteristics of the Sections, the calculation of the distances from the vector [D] is performed, knowing the allocation of the consumers to the poles. Finally, the current profiles from the day with peak load recorded in the EDN are uploaded in the matrix [I].
The aggregation of the current profiles is done at the SP level (on the LV side) to identify the hour of the peak load, hPL, as seen in Figure 10.
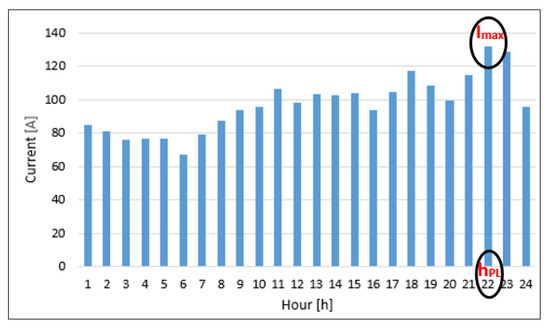
Figure 10.
The total current at the LV level of the SP.
In the following, the unbalance factor (UF) is calculated at the peak load hour (hPL = 22) to decide if the clustering process starts. Because the value of the UF was higher than 1.1 (UF = 1.18), the column [I22] from the matrix [I] together with the vector [D] have composed the matrix [ID] used in the clustering process based on the K-means algorithm. The maximum number of the partitions (Kmax = 10) was determined using the relation (14), knowing the number of consumers (NC = 114). The optimal number of clusters that resulted in the clustering process was five. The testing of the quality has done using the silhouette coefficient, SC. The value of SC, equal to 0.76, was maximum for a partition in five clusters, see Figure 11.
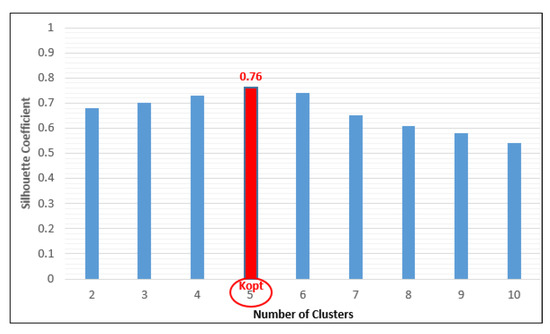
Figure 11.
The values of the silhouette coefficient for the maximum number of the partitions (Kmax = 10) with highlighting the optimal partition (Kopt = 5).
Table 4 presents the statistical indicators (mean, standard deviation, maximum, and minimum) of each cluster (consumers’ group) obtained in the clustering process based on the K-means algorithm.

Table 4.
The statistical indicators of the clusters.
Most consumers (80% of the total consumers used in the clustering process) belonging to the clusters (C1, C2, and C3) have small values of the requested currents at the hour. These values are usually because the electricity consumption of many consumers is under 1000 kW/year. On the other hand, the allocation of consumers at the poles indicates distances from SP between 0.2 and 1.2 km. Cluster C5 contains consumers having the requested current in the range [1.5 A, 4.5 A], and cluster C3 integrates those consumers with values over 6 A. The distances from consumers of cluster C5 and the SP have the medium lengths between 0.5 and 0.76 km.
In the next stage, the “candidate” groups have been chosen based on the qualification index, QI. Table 5 contains the information corresponding to the qualification index and the degrees of importance assigned to the proposed zones. A qualification index from 9 (the highest degree of importance) until 1 (the least degree of importance) will label each zone classified from Table 5. The zoning process was based on an analysis of the results obtained in the clustering process and presented above. Figure 12 shows the 3-D representation of clusters, considering the input variables: requested current, distance, and qualification index.

Table 5.
The value of the qualification index and the degrees of importance associated with zoning of the characteristics current-distance.
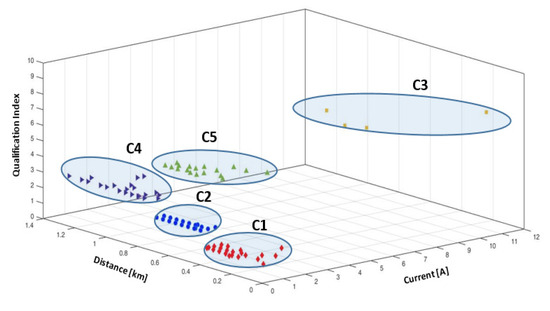
Figure 12.
The representation of the clusters depending on the qualification index.
The centroids, identified through the means from Table 4, will characterize each cluster in the identification process of the “candidate” groups. The interest zones for the PLB process will have the index QI between 9 and 4, in descending order, associated with the high and medium degrees of importance, see Figure 13. The clusters from these zones, highlighted in red, are Cluster C3 (high degree, QI = 7) and Cluster C5 (medium degree, QI = 5). These clusters represent the “candidate” groups for the PLB process in this case, where each consumer will have installed a PLBE.
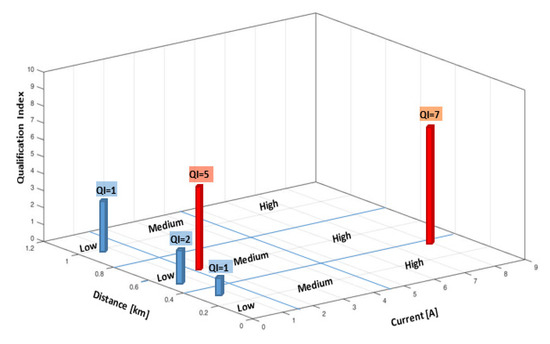
Figure 13.
The representation of the centroids with the value of the qualification index associated with each cluster.
The second level of the methodology refers to running the PLB algorithm considering the “candidate” groups in descending order of the QI (C3 and C5) until the convergence condition is satisfied. The agreed value to stop the iterative process was 1.01, meaning an acceptance of 1% for the unbalance factor at the SP level, and the imposed limit of the unbalance factor at the pole level, UFlim, see constraint (19), was 1.1 (maximum value accepted by the DNO in the EDNs).
The algorithm starts from the farthest points (P20, P39, and P88), aggregating the phase currents at each pole until the SP. The optimal solution, represented by the minimum average value of the UF at the SP level in the analysed period, is obtained through coordination of the PLBE installed to the consumers from the “candidate” groups. Thus, the best allocation of the consumers on the phases of the EDN is determined. Figure 14 shows the hourly values of the UF at the LV level of the SP obtained after applying the PLB algorithm.
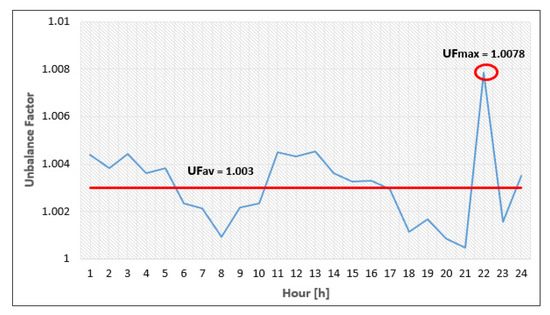
Figure 14.
The hourly values of the unbalance factor obtained with the proposed algorithm.
The analysis indicates a maximum of 1.0078 recorded at the peak load hour (hPL = 22) and a mean of 1.003. This last value is well below the target value of 1.01, set to stop the iterative process.
Figure 15 presents the phase switching operations corresponding to the consumers from the “candidate” groups in the analyzed period (24 h), and Table A2 from Appendix A contains details on the PLB process highlighted through the switching matrix.
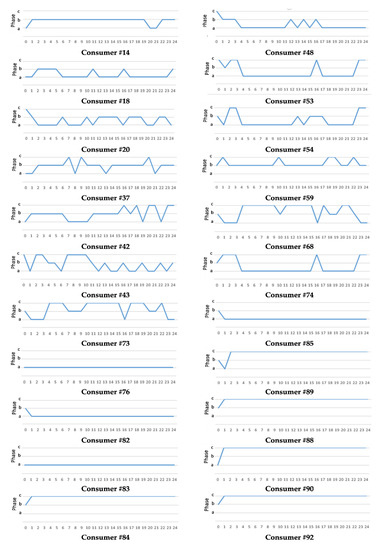
Figure 15.
The phase switching operations corresponding to the consumers from the “candidate” groups in the analyzed period (24 h).
The switching schemes correspond to the positions of the consumers in the EDN relative to the SP. The analysis of the switching operations concluded that the first eleven consumers (#14, #18, #20, #37, #42, #43, #48, #53, #54, #59, and #68) located closer to the SP, have a higher number of the switching operations (98, representing 81.7% of the total number) than the last eleven consumers, #73, #74, #76, #82, #83, #84, #85, #88, #89, #90, and #92 (22, representing 18.3% from the total number), located close to the end poles of the network. The switching of the consumers from one phase to another is different. The consumers with significant influence on the unbalance factor are #20, #37, #42, #43, and #68 (over ten switching operations), and the consumers #82, #84, #85, #89, #90, and #92 affect the PLB process less (only one switching operation). There are two consumers without any switching operation (#76 and #83).
The hours with a high number of switching operations are 1 (18 operations), 16 and 17 (9 operations), 2, 20, 22, and 23 (8 operations). However, there are two hours (3 and 5) where the PLBE did not work. Thus, 20 PLBE optimally located in the network lead at an unbalance factor of 1.003, very close to the ideal value (1.0). The implementation degree of the PLBE in this EDN is only 17.5%. The computational corresponding to the switching operations of the selected devices was by 0.72 s.
The results have been compared with those obtained in the case of the algorithms having a full implementation degree (FID): heuristic [47], particle swarm optimization (PSO) [48] and genetic algorithm (GA) [49]. The codes of the algorithms have been written in programming language Matlab2016, and it has run on a computer with the same characteristics as in [47]: processor Intel Core i7, 3.10 GHz, memory 4 GB RAM, and Windows 10 64-bit operating system.
The FID-based heuristic algorithm has proven faster (1.26 s) than PSO (348 s) and GA (291 s). Based on these results, the proposed algorithm was compared with the FID-based heuristic algorithm in terms of switching operations, see Figure 16.
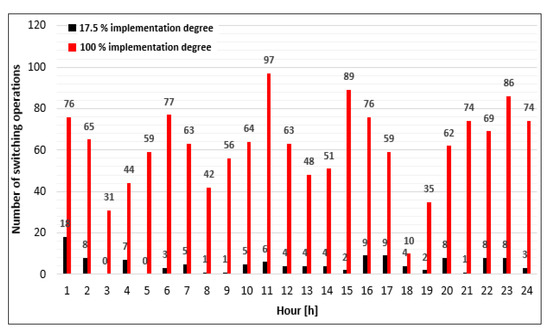
Figure 16.
Comparison between the two algorithms with 100% and 17.5% implementation degrees, considering the number of the switching operations.
The PLBE installed to all consumers in the FID-based heuristic algorithm performed a total number of the switching operations by 1470, compared to 120 associated with the PLBE installed to 20 consumers from the proposed algorithm. A reduction with approximately 92% of switching operations can be observed, correlated with a shorter time interval associated with the balancing process.
All switching operations lead at a balanced loading on the three phases at each hour from the analysed period on the LV side of the SP, compared with the initial situation (unbalance regime, 0% implementation degrees of the PLBE), see Figure 17 and Figure 18. Table A3 from Appendix A details the results on the phase currents and unbalance factors in all analysed cases (0%, 17.5%, and 100% implementation degrees).
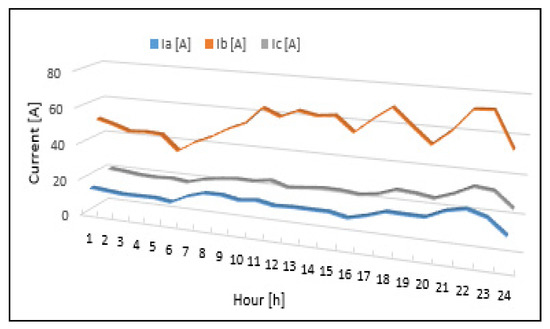
Figure 17.
The current curves on the three phases aggregated at the LV level of the SP, (0% implementation degree of the PLBE in the EDN).
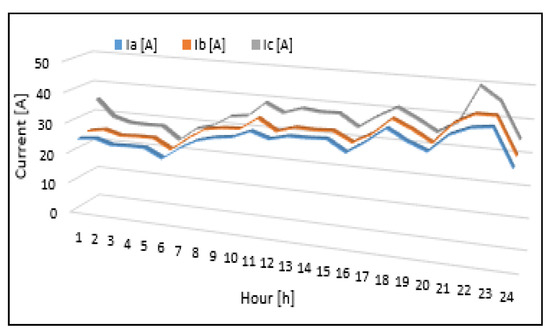
Figure 18.
The current curves on the three phases aggregated at the LV level of the SP (17.5% implementation degree of the PLBE in the EDN).
Table 6 presents a synthesis of the performance indicators (the computing time, the unbalance factor, and the energy-saving) for the three implemented degrees (0%, 100%, and 17.5%). Three algorithms (Heuristic, PSO, and AG) have been considered for the full implementation degree (100%).

Table 6.
The performance indicators obtained for both PLB algorithms.
The energy losses have been determined following the steady-state calculation at each hour using the forward/backward sweep-based algorithm developed in [41] for the balanced and unbalanced three-phase regimes of the EDNs.
The results highlight the advantages of the heuristic algorithm compared with the PSO and AG algorithms. The optimal solution, represented by the unbalance factor, is obtained quickly (1.26 s), and the energy-savings are very close. Consequently, the heuristic algorithm was considered the standard in comparing the results with the proposed algorithm. If the differences between the values of unbalance factor and energy-saving are small (0.3% and 1.5%, respectively), the computational time and the number of switching operations are on behalf of the proposed algorithm. It is 0.54 s faster, and the switching operations are reduced by 92%. All these indicators influence the investment politics of the DNOs, leading to a significant reduction of the PLBE and 3-P branching with similar energy-savings as in the case when the implementation degree of the PLBE is full (100%).
Table A4, Table A5 and Table A6 in Appendix A, show the detailed results of the steady-state calculation at each hour in the three cases (0%, 100% with the heuristic algorithm, and 17.5%). Figure 19 presents the energy losses on the phases (a, b, and c) and neutral (N) conductors. The analysis highlights a significant reduction of the energy losses on phase b and neutral for both implementation degrees. Also, the values of the energy losses in the conductors are very close, between 0.1 kWh (phase a), 0.5 kWh (phase b), 0.7 kWh (phase c), and 0.3 kWh (neutral).
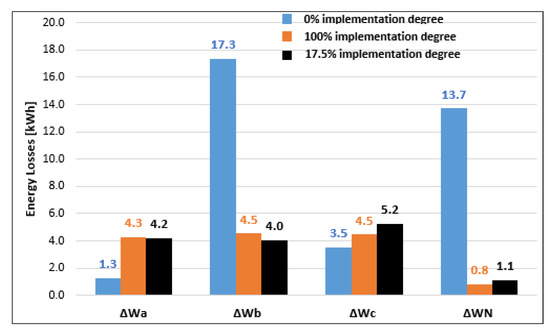
Figure 19.
The comparison between the energy losses in the phase and neutral conductors (0%, 100%, and 17.5% implemented degree of the PLBEs in the EDN).
The following relation was the basis in the evaluation of energy- saving (ΔWS):
where: ΔW0 represents the energy losses in the unbalance case (0% implementation degree of the PLBE in the EDN), and ΔWpg corresponds the energy losses in the balanced cases (pg = 100% and 17.5%).
4. Conclusions
In the paper, a novel bi-level methodology to optimal placement of the PLBE in the EDNs has been proposed. The first level refers to a decision-making process where the “candidate” groups of the consumers with the PLBE installed are identified based on the K-means clustering algorithm and a qualification index. The second level integrates the PLB process having as objective the minimization of the unbalance factor on the LV side of the SP by switching from a phase to other phases the switchable consumers from the “candidate” groups. The energy-saving has represented the base in the evaluation of the technical benefits. The aim has been achieved, the obtained results proving that a limited number of PLBE, associated with a reduced implementation degree, lead to similar technical benefits as in the full implementation and the reduced investments.
A real EDN from a rural area belonging to a Romanian DNO, with 114 consumers, was considered in testing the proposed methodology. All consumers have the meter integrated into the SMS. Following the clustering process, two “candidate” groups with 22 consumers have been selected based on the qualification index. Only 20 consumers participated in the PLB process because two consumers did not modify the connected phase in the analysed interval (24 h). The analysis of the obtained results highlighted the efficiency of the proposed algorithm. A comparison between three algorithms (heuristic, PSO, and AG) used to solve the PLB problem for a full implementation degree has been done. The heuristic algorithm leads the best results, and consequently, it represented the standard in comparing the results with the proposed algorithm. Thus, 20 PLBE installed to the consumers, representing an implementation degree by only 17.5%, led to similar technical benefits as in the case of a full implementation degree (100%), evaluated through the heuristic algorithm, highlighted through the unbalance factor (1.003 versus 1.0001) and an energy-saving (59.1% versus 60.6%), considering the number of switching operations decreases highly with the 92% (120 versus 1470). The computing time is 0.54 s faster, mainly due to the reduced number of the PLBE and the local optimal solutions identified only at the poles where the consumers from the “candidate” groups are connected.
On the other hand, the methodology leads to significant economic benefits due to the reduced number of PLBE and 3-P branching. This branching must replace the 1-P branching at the consumers with PLBE installed.
The aim was to demonstrate that a limited number of PLBE, associated with a low implementation degree that means reduced investments, can lead to similar technical benefits as in a full implementation.
Regarding the implementation, the methodology can have a significant impact on the operation of the EDNs only if the communication infrastructure has a high-speed data transmission and the data concentrator located at the level of the SP, integrating the decision-making algorithm for the optimal switching of the consumers on the phases, has superior performances (high data acquisition and processing speed).
The future work is concentrated on the active EDNs with prosumers to develop the solutions to integrate the small-scale distributed generation sources in the PLB process. The methodology will have an extension for multiple-EDNs, associated with a MμG system, with a common coupling point (an electric distribution substation), or multiple connection points identified by the tie lines.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-7390/9/5/542/s1. Table S1. Current Curves. Table S2. Characteristics of the Sections.
Author Contributions
Conceptualization, G.G.; methodology, G.G. and L.N.; software, G.G.; validation, B.-C.N., F.S., L.N., and E.C.; formal analysis, L.N. and E.C.; investigation, G.G., B.-C.N., F.S., L.N., and E.C.; writing—original draft preparation, G.G., B.-C.N., F.S., L.N., and E.C.; writing—review and editing, G.G. and B.-C.N.; supervision, G.G. All authors discussed the results and have agreed with the structure of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| 1-P | Single-phase consumer; |
| 3-P | Three-phase consumer; |
| APL | Active power losses; |
| C | Constraint; |
| CO | Cost optimization; |
| CP | Consumption point associated with the 1-P and 3-P consumer; |
| DN | Distribution Network; |
| DNO | Distribution Grid Operator; |
| DM | Decision-Maker; |
| FID | Full implementation degree |
| LV | Low voltage; |
| MμG | Multiple-microgids; |
| OF | Objective function; |
| PEVs | Plug-in electric vehicles; |
| PLB | Phase load balancing; |
| PLBE | Phase load balancing equipment; |
| SBS | Smart balancing system; |
| SD | Switching device; |
| SMS | Smart Metering System; |
| SM | Smart meter; |
| SP | Supply point; |
| STS | Static Transfer Systems; |
| UC | Unbalance current; |
| UV | Unbalance voltage; |
| UF | Unbalance factor; |
| μG | Microgrid |
| Ck,opt | Optimal number of clusters; |
| dist(IDi,IDj) | Euclidean distance in the two-dimensional space between the i-th and j-th consumers; |
| Dmin, Dmax | Minimum and maximum values determined of all distances calculated for the consumers, [km]; |
| Dn | The distance between the supply point and the pole where the consumer n is connected, [km]; |
| Dn* | The normalized value of the distances between the pole to which the consumer n is connected and SP; |
| [D] | Vector of the distances; |
| GC | The “candidate” consumer groups for the PLBE placement; |
| GI | The ignored consumer groups (without PLBE); |
| Gi | The degree of importance; |
| h | The hour when the PLB process unfolds; |
| H | The analyzed period, [hours]; |
| I(SP)max | The maximum value of the total current at the LV level of SP, [A]; |
| Iav(hPL) | The average value of the phase currents at the SP level and hour hPL, [A]; |
| I(h)av,SP | The hourly average phase current at SP level, [A]; |
| I(h)av,P | The hourly average value of the phase currents at the pole P, [A]; |
| In,hPL | The requested current by the consumer n, at the hour hPL, [A]; |
| I*n,hPL | The normalized value of the requested current by a consumer n, at hour hPL, [A]; |
| IhPL,min | Minimum value from all requested currents by the consumers at hour hPL, [A]; |
| IhPL,max | Maximum value from all requested currents by the consumers at hour hPL, [A]; |
| Ip(hPL) | The total current on the phase p, at the LV level of SP and hour hPL, [A]; |
| I(h)a,SP, I(h)b,SP, I(h)c,SP | The hourly phase currents aggregated at the level (on the LV side), [A]; |
| I(h)a,GC,mi | The hourly requested current by the consumer mi belonging to the groups GC and allocated on the phase a at the pole P, [A]; |
| I(h)a,GC,q | The hourly requested current by the consumer q belonging to the groups GC and allocated on the phase a, [A]; |
| I(h)a,GI,ni | The hourly requested current by the consumer ni belonging to the groups GI and allocated on the phase a at the pole P, [A]; |
| I(h)a,GI,o | The hourly requested current by the consumer o belonging to the groups GI and allocated on the phase a, [A]; |
| I(h)b,GC,e | The hourly requested current by the consumer e belonging to the groups GC and allocated on the phase b, [A]; |
| I(h)b,GC,mj | The hourly requested current by the consumer mj belonging to the candidate groups GC and allocated on the phase b at the pole P, [A]; |
| I(h)b,GI,f | The hourly requested current by the consumer f belonging to the groups GI and allocated on the phase b, [A]; |
| I(h)b,GI,nj | The hourly requested current by the consumer nj belonging to the groups GI and allocated on the phase b at the pole P, [A]; |
| I(h)c,GC,ml | The hourly requested current by the consumer ml belonging to the candidate groups GC and allocated on the phase c at the pole P, [A]; |
| I(h)c,GC,w | The hourly requested current by the consumer w belonging to the groups GC and allocated on the phase c, [A]; |
| I(h)c,GI,nl | The hourly requested current by the consumer nl belonging to the groups GI and allocated on the phase c at the pole P, [A]; |
| I(h)c,GI,v | The hourly requested current by the consumer v belonging to the groups GI and allocated on the phase c, [A]; |
| I(h){p},GI,P | The hourly phase currents belonging to the groups GI and aggregated at the pole P, p = {a,b,c}, [A]; |
| I(h){p},GC,P | The hourly phase currents belonging to the groups GC and aggregated at the pole P, p = {a,b,c}, [A]; |
| I(h){p},GI,SP | The hourly phase currents of the consumers belonging to the groups GI and aggregated at SP level, p = {a,b,c}, [A]; |
| I(h){p},GC,SP | The hourly phase currents of the consumers belonging to the groups GC and aggregated at SP level, p = {a,b,c}, [A]; |
| I(h){p},P | The hourly phase currents aggregated at the pole P, p = {a,b,c}, [A]; |
| I(h){p},x | The hourly phase currents aggregated at the pole x⊆{PT} (placed after the pole P in the EDN), [A]; |
| [I] | Matrix containing the current profiles of the consumers from the day when the peak load was recorded in the EDN; |
| [I(SP)] | Vector of the currents aggregated at the LV level of SP for each hour h, [A]; |
| [ID] | The matrix with the consumers’ characteristics subjected to the clustering process; |
| Kmax | Maximum number of clusters; |
| l | Index of the iteration from the PLB process; |
| mk | Centroid of the cluster k, k = 1, …, K; |
| {M} | Set of the centroids; |
| nk | The number of consumers from the cluster Ck; |
| nph | The number of phases (nph = 3); |
| n(h){p} | The number of the consumers from the EDN allocated on each from the three phases, p = {a,b,c}; |
| N{p},GI | The number of the consumers from the EDN allocated on each from the three phases, p = {a,b,c}, belonging to the groups GI; |
| N(h){p},GC | The number of the consumers from the EDN allocated on each from the three phases, p = {a,b,c}, belonging to the groups GC, at the hour h; |
| N(h)P | The number of the consumers allocated at the pole P; |
| N(h)P,{p},GC | The number of the consumers allocated on each from the three phases of the EDN, p = {a,b,c}, belonging to the groups GC, at the pole P and hour h; |
| NP,{p},GI | The number of the consumers allocated on each from the three phases of the EDN, p = {a,b,c} belonging to the groups GI, at the pole P; |
| Nr, Ns | The number of the consumers assigned to the clusters r and s; |
| NP | The total number of the poles; |
| NS | The total number of the sections; |
| p | Set of the connection phase, p = {a, b, c, abc}; |
| [Ph] | Vector of connection phase; |
| {PGC} | Set of poles with least one consumer from the “candidate” groups GC; |
| [PT] | Vector of the poles from the EDN; |
| {PT} | Set of all poles from the EDN; |
| QP | Vector of the silhouette coefficient; |
| QI | Qualification index; |
| [S] | Vector of the sections from the EDN; |
| SC | Silhouette coefficient; |
| tb | Set of the branching type tb = {1-P, 3-P}; |
| [Tb] | Vector of branching type; |
| UF(hPL) | The unbalance factor calculate for the peak load hour, hPL, [p.u.] |
| UF(h)P | The hourly unbalance factor calculated at the pole P, [p.u.]; |
| UF(h)SP | The hourly unbalance factor calculated on the LV side of SP, [p.u.]; |
| UFav,SP | The average value of the unbalance factor on the LV side of SP, [p.u.]; |
| UFlim | Limit value agreed by the DNO for the UF in the EDN, [p.u.]; |
| [VS1], [VT2] | The structure-vectors to identify the topology of the EDN; |
| Δh | The sampling step (Δh = 1 h, in our analysis); |
| ΔWS | The energy-saving, [%] |
| ΔW0 | Energy losses in the unbalance case (0% implementation degree of the PLBE installed in the EDN), [kWh] |
| ΔWpg | Energy losses in the balanced cases (pg = 100% and 17.5%), [kWh] |
Appendix A

Table A1.
The allocation of the consumers to the poles and phases (initial situation).
Table A1.
The allocation of the consumers to the poles and phases (initial situation).
| Consumer ID | Pole ID | Initial Phase/Branching | Consumer ID | Pole ID | Initial Phase/Branching | Consumer ID | Pole ID | Initial Phase/Branching |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | b/1-P/1-P | 39 | 28 | c/1-P | 77 | 52 | b/1-P |
| 2 | 3 | a/1-P | 40 | 28 | c/1-P | 78 | 52 | b/1-P |
| 3 | 3 | b/1-P | 41 | 30 | c/1-P | 79 | 53 | b/1-P |
| 4 | 4 | b/1-P | 42 | 30 | a/1-P | 80 | 55 | c/1-P |
| 5 | 5 | b/1-P | 43 | 30 | c/1-P | 81 | 56 | a/1-P |
| 6 | 6 | b/1-P | 44 | 31 | c/1-P | 82 | 58 | b/1-P |
| 7 | 7 | c/1-P | 45 | 32 | c/1-P | 83 | 59 | a/1-P |
| 8 | 7 | c/1-P | 46 | 32 | c/1-P | 84 | 59 | b/1-P |
| 9 | 8 | b/1-P | 47 | 33 | c/1-P | 85 | 59 | b/1-P |
| 10 | 8 | c/1-P | 48 | 33 | c/1-P | 86 | 60 | b/1-P |
| 11 | 10 | a b c/3-P | 49 | 34 | c/1-P | 87 | 60 | b/1-P |
| 12 | 11 | c/1-P | 50 | 35 | c/1-P | 88 | 61 | b/1-P |
| 13 | 11 | c/1-P | 51 | 36 | c/1-P | 89 | 61 | b/1-P |
| 14 | 12 | a/1-P | 52 | 36 | c/1-P | 90 | 62 | a/1-P |
| 15 | 13 | a/1-P | 53 | 37 | c/1-P | 91 | 62 | b/1-P |
| 16 | 13 | a/1-P | 54 | 37 | b/1-P | 92 | 63 | b/1-P |
| 17 | 16 | a/1-P | 55 | 38 | c/1-P | 93 | 65 | b/1-P |
| 18 | 16 | a/1-P | 56 | 38 | c/1-P | 94 | 68 | b/1-P |
| 19 | 19 | c/1-P | 57 | 38 | c/1-P | 95 | 70 | b/1-P |
| 20 | 19 | c/1-P | 58 | 39 | c/1-P | 96 | 71 | a/1-P |
| 21 | 20 | c/1-P | 59 | 40 | b/1-P | 97 | 71 | b/1-P |
| 22 | 20 | c/1-P | 60 | 40 | b/1-P | 98 | 71 | b/1-P |
| 23 | 21 | b/1-P | 61 | 41 | a/1-P | 99 | 71 | b/1-P |
| 24 | 21 | c/1-P | 62 | 41 | b/1-P | 100 | 72 | b/1-P |
| 25 | 22 | c/1-P | 63 | 41 | b/1-P | 101 | 73 | b/1-P |
| 26 | 22 | c/1-P | 64 | 42 | b/1-P | 102 | 75 | b/1-P |
| 27 | 23 | c/1-P | 65 | 42 | b/1-P | 103 | 75 | b/1-P |
| 28 | 23 | c/1-P | 66 | 43 | c/1-P | 104 | 76 | a/1-P |
| 29 | 24 | c/1-P | 67 | 45 | b/1-P | 105 | 77 | b/1-P |
| 30 | 25 | c/1-P | 68 | 45 | b/1-P | 106 | 80 | b/1-P |
| 31 | 26 | c/1-P | 69 | 46 | b/1-P | 107 | 80 | b/1-P |
| 32 | 26 | c/1-P | 70 | 47 | b/1-P | 108 | 81 | b/1-P |
| 33 | 26 | c/1-P | 71 | 47 | b/1-P | 109 | 82 | b/1-P |
| 34 | 26 | c/1-P | 72 | 47 | b/1-P | 110 | 82 | b/1-P |
| 35 | 27 | c/1-P | 73 | 47 | b/1-P | 111 | 85 | b/1-P |
| 36 | 27 | c/1-P | 74 | 47 | b/1-P | 112 | 86 | b/1-P |
| 37 | 27 | a/1-P | 75 | 48 | b/1-P | 113 | 86 | b/1-P |
| 38 | 28 | a/1-P | 76 | 51 | a/1-P | 114 | 88 | b/1-P |

Table A2.
The switching matrix and number of the switching operations.
Table A2.
The switching matrix and number of the switching operations.
| Consumer ID | Candidate Group | Hour | Switching Operations | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |||
| 14 | Cluster C5 | a | b | b | b | b | b | b | b | b | b | b | b | b | b | b | b | b | b | b | b | a | a | b | b | b | 3 |
| 18 | Cluster C5 | a | a | b | b | b | b | a | a | a | a | a | b | a | a | a | a | b | a | a | a | a | a | a | a | b | 7 |
| 20 | Cluster C5 | c | b | a | a | a | a | b | a | a | a | b | a | b | b | b | b | a | b | b | b | a | a | b | b | a | 12 |
| 37 | Cluster C5 | a | a | b | b | b | b | b | c | a | c | b | b | b | a | b | b | b | b | b | b | c | a | b | b | b | 10 |
| 42 | Cluster C5 | a | b | b | b | b | b | b | a | a | a | a | b | b | b | b | b | c | b | c | a | c | c | a | c | c | 10 |
| 43 | Cluster C5 | c | a | c | c | b | b | a | c | c | c | c | b | a | b | a | a | b | a | a | b | a | a | b | a | b | 16 |
| 48 | Cluster C5 | c | b | b | b | a | a | a | a | a | a | a | a | b | a | b | a | b | a | a | a | a | a | a | a | a | 8 |
| 53 | Cluster C5 | c | b | c | c | a | a | a | a | a | a | a | a | a | a | a | a | c | a | a | a | a | a | a | c | c | 6 |
| 54 | Cluster C5 | b | a | c | c | a | a | a | a | a | a | a | a | a | b | a | b | b | b | a | a | a | a | a | c | c | 8 |
| 59 | Cluster C3 | b | c | b | b | b | b | b | b | b | b | c | b | b | b | b | b | b | b | c | c | b | b | c | b | b | 8 |
| 68 | Cluster C3 | b | a | a | a | c | c | c | c | c | c | b | c | c | c | c | c | a | c | b | b | c | c | b | a | a | 10 |
| 73 | Cluster C3 | b | c | c | c | a | a | a | a | a | a | a | a | a | a | a | a | c | a | a | a | a | a | a | c | c | 5 |
| 74 | Cluster C5 | b | a | a | a | c | c | c | b | b | b | c | c | c | c | c | c | a | c | c | c | b | b | c | a | a | 9 |
| 76 | Cluster C5 | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | 0 |
| 82 | Cluster C5 | b | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | 1 |
| 83 | Cluster C5 | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | 0 |
| 84 | Cluster C3 | b | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | 1 |
| 85 | Cluster C5 | b | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | a | 1 |
| 88 | Cluster C5 | b | a | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | 2 |
| 89 | Cluster C5 | b | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | 1 |
| 90 | Cluster C5 | a | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | 1 |
| 92 | Cluster C5 | b | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | c | 1 |
| Switching Operations | 0 | 18 | 8 | 0 | 7 | 0 | 3 | 5 | 1 | 1 | 5 | 6 | 4 | 4 | 4 | 2 | 9 | 9 | 4 | 2 | 8 | 1 | 8 | 8 | 3 | 120 | |

Table A3.
The phase currents and unbalance factor at SP level for different implementation degrees of the PLBE in the EDN.
Table A3.
The phase currents and unbalance factor at SP level for different implementation degrees of the PLBE in the EDN.
| Hour | Implementation Degree | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 100% | 17.5% | ||||||||||
| Ia [A] | Ib [A] | Ic [A] | UF | Ia [A] | Ib [A] | Ic [A] | UF | Ia [A] | Ib [A] | Ic [A] | UF | |
| h1 | 14.9 | 51.3 | 20.0 | 1.29 | 28.3 | 28.2 | 28.2 | 1.00001 | 28.5 | 26.5 | 29.8 | 1.027 |
| h2 | 14.1 | 48.9 | 19.1 | 1.29 | 27.0 | 26.9 | 26.9 | 1.00001 | 25.1 | 26.4 | 29.3 | 1.004 |
| h3 | 13.3 | 45.8 | 18.2 | 1.29 | 25.4 | 25.4 | 25.4 | 1.00001 | 23.5 | 25.0 | 27.7 | 1.004 |
| h4 | 13.5 | 46.5 | 17.9 | 1.30 | 25.7 | 25.5 | 25.5 | 1.00001 | 23.8 | 25.3 | 27.6 | 1.004 |
| h5 | 13.7 | 46.0 | 18.4 | 1.28 | 25.6 | 25.7 | 25.7 | 1.00001 | 23.8 | 25.4 | 27.7 | 1.004 |
| h6 | 12.5 | 37.9 | 17.4 | 1.23 | 22.3 | 22.4 | 22.3 | 1.00001 | 21.0 | 22.2 | 23.7 | 1.002 |
| h7 | 16.9 | 43.5 | 20.0 | 1.18 | 26.5 | 26.4 | 26.4 | 1.00000 | 24.9 | 26.5 | 28.0 | 1.002 |
| h8 | 19.7 | 47.5 | 21.5 | 1.17 | 29.2 | 29.0 | 29.3 | 1.00001 | 28.0 | 30.0 | 29.5 | 1.001 |
| h9 | 19.9 | 52.7 | 22.5 | 1.20 | 31.1 | 31.3 | 31.2 | 1.00001 | 29.5 | 31.0 | 33.2 | 1.002 |
| h10 | 18.2 | 56.7 | 22.3 | 1.26 | 31.9 | 31.9 | 31.7 | 1.00000 | 30.3 | 31.3 | 33.9 | 1.002 |
| h11 | 19.4 | 65.7 | 23.9 | 1.30 | 35.6 | 35.4 | 35.7 | 1.00000 | 32.7 | 35.3 | 38.7 | 1.004 |
| h12 | 17.6 | 61.8 | 21.1 | 1.33 | 32.9 | 32.8 | 32.8 | 1.00000 | 30.8 | 31.7 | 35.9 | 1.004 |
| h13 | 18.1 | 65.8 | 22.0 | 1.35 | 34.4 | 34.7 | 34.6 | 1.00000 | 32.3 | 33.5 | 37.9 | 1.005 |
| h14 | 18.1 | 64.0 | 23.0 | 1.32 | 34.3 | 34.4 | 34.2 | 1.00000 | 32.4 | 33.3 | 37.3 | 1.004 |
| h15 | 18.1 | 65.1 | 22.9 | 1.33 | 34.5 | 34.6 | 34.7 | 1.00000 | 32.7 | 33.6 | 37.4 | 1.003 |
| h16 | 16.1 | 57.3 | 21.8 | 1.31 | 31.2 | 31.0 | 31.2 | 1.00000 | 29.2 | 30.6 | 33.7 | 1.003 |
| h17 | 18.6 | 65.1 | 23.2 | 1.32 | 34.7 | 35.1 | 34.8 | 1.00001 | 33.2 | 33.8 | 37.6 | 1.003 |
| h18 | 21.8 | 71.8 | 26.7 | 1.29 | 39.1 | 39.3 | 39.1 | 1.00000 | 37.7 | 39.0 | 40.9 | 1.001 |
| h19 | 21.6 | 63.2 | 26.0 | 1.23 | 36.2 | 36.2 | 36.3 | 1.00001 | 34.4 | 36.3 | 37.9 | 1.002 |
| h20 | 21.5 | 55.0 | 24.5 | 1.18 | 33.1 | 33.3 | 33.0 | 1.00000 | 32.0 | 32.9 | 34.5 | 1.001 |
| h21 | 26.0 | 62.9 | 28.1 | 1.17 | 38.1 | 38.4 | 38.3 | 1.00001 | 37.5 | 39.4 | 37.9 | 1.000 |
| h22 | 28.1 | 74.1 | 33.0 | 1.19 | 44.2 | 43.7 | 44.2 | 1.00001 | 40.1 | 42.6 | 49.4 | 1.008 |
| h23 | 25.2 | 74.7 | 32.0 | 1.22 | 42.9 | 42.9 | 43.0 | 1.00002 | 40.9 | 42.6 | 45.4 | 1.002 |
| h24 | 17.3 | 56.3 | 23.9 | 1.25 | 31.7 | 31.9 | 32.1 | 1.00002 | 29.7 | 31.5 | 34.5 | 1.004 |

Table A4.
The hourly power losses without the implementation of the PLBE in the EDN (0% implementation degree), [kW].
Table A4.
The hourly power losses without the implementation of the PLBE in the EDN (0% implementation degree), [kW].
| Hour | ΔPa | ΔPb | ΔPc | ΔPN | ΔPTotal |
|---|---|---|---|---|---|
| h1 | 0.033 | 0.555 | 0.109 | 0.441 | 1.138 |
| h2 | 0.029 | 0.505 | 0.099 | 0.402 | 1.035 |
| h3 | 0.026 | 0.446 | 0.089 | 0.355 | 0.916 |
| h4 | 0.027 | 0.457 | 0.087 | 0.363 | 0.933 |
| h5 | 0.027 | 0.449 | 0.092 | 0.357 | 0.925 |
| h6 | 0.023 | 0.314 | 0.081 | 0.252 | 0.670 |
| h7 | 0.042 | 0.421 | 0.108 | 0.332 | 0.902 |
| h8 | 0.056 | 0.505 | 0.125 | 0.395 | 1.081 |
| h9 | 0.057 | 0.605 | 0.137 | 0.474 | 1.273 |
| h10 | 0.049 | 0.680 | 0.135 | 0.535 | 1.399 |
| h11 | 0.055 | 0.895 | 0.154 | 0.706 | 1.810 |
| h12 | 0.046 | 0.791 | 0.121 | 0.622 | 1.579 |
| h13 | 0.048 | 0.892 | 0.131 | 0.703 | 1.775 |
| h14 | 0.048 | 0.848 | 0.143 | 0.671 | 1.711 |
| h15 | 0.048 | 0.875 | 0.142 | 0.691 | 1.757 |
| h16 | 0.039 | 0.686 | 0.129 | 0.546 | 1.400 |
| h17 | 0.051 | 0.877 | 0.146 | 0.691 | 1.765 |
| h18 | 0.070 | 1.069 | 0.193 | 0.842 | 2.174 |
| h19 | 0.068 | 0.854 | 0.183 | 0.672 | 1.777 |
| h20 | 0.068 | 0.670 | 0.164 | 0.527 | 1.429 |
| h21 | 0.099 | 0.882 | 0.214 | 0.693 | 1.888 |
| h22 | 0.115 | 1.195 | 0.292 | 0.949 | 2.551 |
| h23 | 0.093 | 1.189 | 0.276 | 0.949 | 2.507 |
| h24 | 0.044 | 0.675 | 0.155 | 0.542 | 1.415 |
| ΔW[kWh] | 1.260 | 17.335 | 3.504 | 13.712 | 35.811 |

Table A5.
The hourly power losses for a 100% implementation degree of the PLBE in the EDN, [kW].
Table A5.
The hourly power losses for a 100% implementation degree of the PLBE in the EDN, [kW].
| Hour | ΔPa | ΔPb | ΔPc | ΔPN | ΔPTotal |
|---|---|---|---|---|---|
| h1 | 0.120 | 0.143 | 0.146 | 0.021 | 0.431 |
| h2 | 0.110 | 0.134 | 0.130 | 0.020 | 0.393 |
| h3 | 0.097 | 0.119 | 0.116 | 0.018 | 0.350 |
| h4 | 0.116 | 0.118 | 0.103 | 0.019 | 0.356 |
| h5 | 0.115 | 0.119 | 0.104 | 0.018 | 0.356 |
| h6 | 0.086 | 0.080 | 0.089 | 0.012 | 0.268 |
| h7 | 0.121 | 0.130 | 0.110 | 0.025 | 0.387 |
| h8 | 0.147 | 0.148 | 0.146 | 0.034 | 0.475 |
| h9 | 0.182 | 0.166 | 0.155 | 0.040 | 0.543 |
| h10 | 0.182 | 0.176 | 0.162 | 0.032 | 0.551 |
| h11 | 0.223 | 0.199 | 0.227 | 0.041 | 0.691 |
| h12 | 0.194 | 0.170 | 0.195 | 0.038 | 0.596 |
| h13 | 0.176 | 0.226 | 0.217 | 0.044 | 0.663 |
| h14 | 0.209 | 0.212 | 0.185 | 0.038 | 0.644 |
| h15 | 0.179 | 0.224 | 0.215 | 0.038 | 0.656 |
| h16 | 0.172 | 0.154 | 0.175 | 0.028 | 0.528 |
| h17 | 0.181 | 0.226 | 0.218 | 0.037 | 0.663 |
| h18 | 0.228 | 0.283 | 0.274 | 0.046 | 0.832 |
| h19 | 0.199 | 0.241 | 0.233 | 0.041 | 0.715 |
| h20 | 0.189 | 0.208 | 0.171 | 0.037 | 0.603 |
| h21 | 0.253 | 0.252 | 0.253 | 0.056 | 0.815 |
| h22 | 0.332 | 0.297 | 0.364 | 0.063 | 1.056 |
| h23 | 0.322 | 0.327 | 0.289 | 0.050 | 0.989 |
| h24 | 0.153 | 0.186 | 0.183 | 0.026 | 0.547 |
| ΔW[kWh] | 4.287 | 4.539 | 4.461 | 0.820 | 14.107 |

Table A6.
The hourly power losses for a 17.5% implementation degree of the PLBE in the EDN, [kW].
Table A6.
The hourly power losses for a 17.5% implementation degree of the PLBE in the EDN, [kW].
| Hour | ΔPa | ΔPb | ΔPc | ΔPN | ΔPTotal |
|---|---|---|---|---|---|
| h1 | 0.122 | 0.120 | 0.188 | 0.043 | 0.472 |
| h2 | 0.115 | 0.109 | 0.160 | 0.036 | 0.420 |
| h3 | 0.100 | 0.097 | 0.144 | 0.032 | 0.373 |
| h4 | 0.106 | 0.099 | 0.134 | 0.023 | 0.362 |
| h5 | 0.106 | 0.100 | 0.135 | 0.022 | 0.363 |
| h6 | 0.082 | 0.077 | 0.099 | 0.016 | 0.275 |
| h7 | 0.113 | 0.113 | 0.144 | 0.036 | 0.405 |
| h8 | 0.140 | 0.143 | 0.163 | 0.043 | 0.490 |
| h9 | 0.157 | 0.153 | 0.200 | 0.050 | 0.560 |
| h10 | 0.170 | 0.175 | 0.185 | 0.046 | 0.576 |
| h11 | 0.202 | 0.187 | 0.265 | 0.047 | 0.701 |
| h12 | 0.181 | 0.151 | 0.230 | 0.044 | 0.607 |
| h13 | 0.199 | 0.170 | 0.255 | 0.049 | 0.672 |
| h14 | 0.198 | 0.169 | 0.244 | 0.044 | 0.655 |
| h15 | 0.203 | 0.172 | 0.248 | 0.045 | 0.667 |
| h16 | 0.156 | 0.145 | 0.210 | 0.044 | 0.554 |
| h17 | 0.206 | 0.174 | 0.250 | 0.044 | 0.676 |
| h18 | 0.264 | 0.270 | 0.269 | 0.071 | 0.874 |
| h19 | 0.219 | 0.227 | 0.231 | 0.045 | 0.721 |
| h20 | 0.184 | 0.180 | 0.220 | 0.062 | 0.645 |
| h21 | 0.251 | 0.254 | 0.271 | 0.081 | 0.857 |
| h22 | 0.297 | 0.312 | 0.387 | 0.067 | 1.063 |
| h23 | 0.296 | 0.287 | 0.389 | 0.097 | 1.069 |
| h24 | 0.158 | 0.157 | 0.223 | 0.052 | 0.591 |
| ΔW[kWh] | 4.222 | 4.040 | 5.245 | 1.140 | 14.648 |
References
- Nikmehr, N.; Najafi Ravadanegh, S. Optimal Power Dispatch of Multi-Microgrids at Future Smart Distribution Grids. IEEE Trans. Smart Grid 2015, 6, 1648–1657. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Tian, T.; Xu, Z.; Chen, R. Coordinated Control of Passive Transition from Grid-Connected to Islanded Operation for Three/Single-Phase Hybrid Multimicrogrids Considering Speed and Smoothness. IEEE Trans. Ind. Electron. 2020, 67, 1921–1931. [Google Scholar] [CrossRef]
- Khalid, M.; Akram, U.; Shafiq, S. Optimal Planning of Multiple Distributed Generating Units and Storage in Active Distribution Networks. IEEE Access 2018, 6, 55234–55244. [Google Scholar] [CrossRef]
- Grigoras, G.; Ivanov, O.; Neagu, B.C.; Pragma, K. Smart Metering Based Strategies for Improving Energy Efficiency in Microgrids. In Microgrid Architectures, Control and Protection Methods; Mahdavi Tabatabaei, N., Kabalci, E., Bizon, N., Eds.; Springer: Berlin, Germany, 2020; pp. 463–490. [Google Scholar]
- Liu, B.; Meng, K.; Dong, Z.; Wong, P.K.C.; Li, X. Load Balancing in Low-voltage Distribution Network via Phase Reconfiguration: An Efficient Sensitivity-based Approach. IEEE Trans. Pow. Deliv. 2020. [Google Scholar] [CrossRef]
- Haq, S.U.; Arif, B.; Khan, A.; Ahmed, J. Automatic Three Phase Load Balancing System by Using Fast Switching Relay in Three Phase Distribution System. In Proceedings of the International Conference on Power, Energy and Smart Grid (ICPESG), Mirpur, Pakistan, 9–10 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Narayanan, K.N.; Umanand, L. A Novel Active Phase Router for Dynamic Load Balancing in a Three Phase Microgrid. In Proceedings of the 2017 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Bangalore, India, 8–10 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- SinePuls, Single Phase STS Prepaid Meter. Available online: https://sinepulse.com/sites/default/files/smart-meter/SP_SINGLE_PHASE_STS_PREPAID_METER.pdf (accessed on 21 November 2020).
- Londian, Smart Prepaid Meter. Available online: http://www.londian.com.cn/en/index.php?s=/cms/209 (accessed on 21 November 2020).
- Novatek-Electro, Universal Automatic Electronic Phase Switch Pef-319. Available online: https://novatek-electro.com/en/products/phase-selector-switch/universal-automatic-electronic-phase-switch-pef-301.html (accessed on 21 November 2020).
- Yongxia, L.; Yulei, G. Design of Three Phase Load Unbalance Automatic Regulating System for Low Voltage Power Distribution Grids. In Proceedings of the MATEC Web of Conferences, Nanjing, China, 24–26 May 2018; Volume 173. [Google Scholar] [CrossRef]
- Siti, M.W.; Jimoh, A.A.; Nicolae, D.V. Distribution network phase load balancing as a combinatorial optimization problem using fuzzy logic and Newton–Raphson. Electr. Power Syst. Res. 2011, 81, 1079–1087. [Google Scholar] [CrossRef]
- Iyappan, M.; Karpagam, M.; Raviram, P. Automatic load sharing in Industrial Plant With Monitoring System Using Microcontroller. Int. J. App. Eng. Res. 2015, 114–120. [Google Scholar]
- Ofualagba, G.; Udoha, E.E. Design and Simulation of Automatic Phase Selector and Changeover Switch for 3-Phase Supply. Int. J. Nov. Res. Elec. Mech. Eng. 2017, 4, 28–35. [Google Scholar]
- Rashid, A.T.; Rashid, M.T. Design and Implementation of Load Balancing System for a Smart Home. In Proceedings of the 3rd International Scientific Conference for Renewable Energy (ISCRE’ 2018), Basrah, Iraq, 14–15 March 2018; pp. 1–6. [Google Scholar]
- Shakeel, M.O.B.; Jaffar, S.A.; Ali, M.F.; Zaidi, S.S. LV Three Phase Automatic Load Balancing System. In Proceedings of the International Conference on Energy, Environment and Sustainable Development 2016 (EESD 2016), Jamshoro, Pakistan, 1–3 November 2016. [Google Scholar]
- Bao, G.; Ke, S. Load Transfer Device for Solving a Three-Phase Unbalance Problem Under a Low-Voltage Distribution Network. Energies 2019, 12, 2842. [Google Scholar] [CrossRef]
- Homaee, O.; Najafi, A.; Dehghanian, M.; Attar, M.; Falaghi, H. A Practical Approach for Distribution Network Load Balancing by Optimal Re-Phasing of Single-Phase Customers Using Discrete Genetic Algorithm. Int. Trans. Electr. Energy Syst. 2019, 29, e2834. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Rau, S.-H.; Wu, C.-J.; Lee, W.-J. Improvement of Power Quality by Using Advanced Reactive Power Compensation. IEEE Trans. Ind. Appl. 2018, 54, 18–24. [Google Scholar] [CrossRef]
- Kalesar, B.M. Customers Swapping Between Phases for Loss Reduction Considering Daily Load Profile Modeling Smart Grid. In Proceedings of the CIRED Workshop 2016, Helsinki, Finland, 14–15 June 2016; pp. 1–4. [Google Scholar]
- Jianguo, Z.; Qiuye, S.; Huaguang, Z.; Yan, Z. Load Balancing and Reactive Power Compensation Based on Capacitor Banks Shunt Compensation in Low Voltage Distribution Networks. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 20–22 July 2012; pp. 6681–6686. [Google Scholar]
- Arias, J.; Calle, M.; Turizo, D.; Guerrero, J.; Candelo-Becerra, J.E. Historical Load Balance in Distribution Systems Using the Branch and Bound Algorithm. Energies 2019, 12, 1219. [Google Scholar] [CrossRef]
- Granada Echeverri, M.; Gallego Rendón, R.A.; López Lezama, J.M. Optimal Phase Balancing Planning for Loss Reduction in Distribution Systems Using a Specialized Genetic Algorithm. Ing. Y Cienc. 2012, 8, 121–140. [Google Scholar] [CrossRef]
- Al-Kharsan, I.H. A New Strategy for Phase Swapping Load Balancing Relying on a Meta-Heuristic MOGWO Algorithm. J. Mech. Contin. Math. Sci. 2020, 15, 84–102. [Google Scholar] [CrossRef]
- Mahendran, G.; Govindaraju, C. Flower Pollination Algorithm for Distribution System Phase Balancing Considering Variable Demand. Microprocess. Microsyst. 2020, 74, 103008. [Google Scholar] [CrossRef]
- Saffar, A.; Hooshmand, R.; Khodabakhshian, A. A New Fuzzy Optimal Reconfiguration of Distribution Systems for Loss Reduction and Load Balancing Using Ant Colony Search-Based Algorithm. App. Soft Comp. 2011, 11, 4021–4028. [Google Scholar] [CrossRef]
- Hooshmand, R.; Soltani, S.H. Simultaneous Optimization of Phase Balancing and Reconfiguration in Distribution Networks Using BF–NM Algorithm. Int. J. Electr. Power Energy Syst. 2012, 41, 76–86. [Google Scholar] [CrossRef]
- Olek, B.; Wierzbowski, M. Local Energy Balancing and Ancillary Services in Low-Voltage Networks with Distributed Generation, Energy Storage, and Active Loads. IEEE Trans. Ind. Electr. 2014, 62, 2499–2508. [Google Scholar] [CrossRef]
- Kikhavani, M.R.; Hajizadeh, A.; Shahirinia, A. Charging Coordination and Load Balancing of Plug-In Electric Vehicles in Unbalanced Low-Voltage Distribution Systems. IET Gen. Transm. Distrib. 2020, 14, 389–399. [Google Scholar] [CrossRef]
- Weckx, S.; Driesen, J. Load Balancing with EV Chargers and PV Inverters in Unbalanced Distribution Grids. IEEE Trans. Sustain. Energy 2015, 6, 635–643. [Google Scholar] [CrossRef]
- Evzelman, M.; Ur Rehman, M.M.; Hathaway, K.; Zane, R.; Costinett, D.; Maksimovic, D. Active Balancing System for Electric Vehicles with Incorporated Low-Voltage Bus. IEEE Trans. Power Electr. 2015, 31, 7887–7895. [Google Scholar] [CrossRef]
- Faessler, B.; Schuler, M.; Preißinger, M.; Kepplinger, P. Battery Storage Systems as Grid-Balancing Measure in Low-Voltage Distribution Grids with Distributed Generation. Energies 2017, 10, 2161. [Google Scholar] [CrossRef]
- De Carne, G.; Buticchi, G.; Liserre, M.; Yoon, C.; Blaabjerg, F. Voltage and Current Balancing in Low and Medium Voltage Grid by Means of Smart Transformer. In Proceedings of the IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Pasdar, A.; Mehne, H.H. Intelligent Three-Phase Current Balancing Technique for Single-Phase Load Based on Smart Metering. Int. J. Electr. Power Energy Syst. 2011, 33, 693–698. [Google Scholar] [CrossRef]
- Wang, C.; Tian, T.; Xu, Z.; Cheng, S.; Liu, S.; Chen, R. Optimal Management for Grid-Connected Three/Single-Phase Hybrid Multimicrogrids. IEEE Trans. Sustain. Energy 2020, 11, 1870–1882. [Google Scholar] [CrossRef]
- Hong, T.; de León, F. Controlling Non-Synchronous Microgrids for Load Balancing of Radial Distribution Systems. IEEE Trans. Smart Grid 2017, 8, 2608–2616. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. How Much Can K-Means Be Improved by Using Better Initialization and Repeats? Pattern Recognit. 2019, 93, 95–112. [Google Scholar] [CrossRef]
- Liang, J.; Bai, L.; Dang, C.; Cao, F. The K-Means-Type Algorithms Versus Imbalanced Data Distributions. IEEE Trans. Fuzzy Syst. 2012, 20, 728–745. [Google Scholar] [CrossRef]
- Li, M.J.; Ng, M.K.; Cheung, Y.; Huang, J.Z. Agglomerative Fuzzy K-Means Clustering Algorithm with Selection of Number of Clusters. IEEE Trans. Knowl. Data Eng. 2008, 20, 1519–1534. [Google Scholar] [CrossRef]
- Romanian Energy Regulatory Authority, Technical Norm Regarding the Determination of Own Technological Consumption in Electricity Networks-NTE-013/16/00 (in Romanian). 2016. Available online: https://legeaz.net/mo/anexa-ordin-anre-26-2016.pdf (accessed on 21 November 2020).
- Grigoras, G.; Neagu, B.-C. Smart Meter Data-Based Three-Stage Algorithm to Calculate Power and Energy Losses in Low Voltage Distribution Networks. Energies 2019, 12, 3008. [Google Scholar] [CrossRef]
- Li, T.; Ma, Y.; Endoh, T. Normalization-Based Validity Index of Adaptive K-Means Clustering for Multi-Solution Application. IEEE Access 2020, 8, 9403–9419. [Google Scholar] [CrossRef]
- Noroc, L.; Grigoras, G. Clustering-Based Consumers’ Selection to Optimal Placement of the Phase Load Balancing Devices. In Proceedings of the 11th International Conference and Exposition on Electrical and Power Engineering, Iasi, Romania, 22–23 October 2020; pp. 1–4. [Google Scholar]
- Sinaga, K.; Yang, M.S. Unsupervised K-Means Clustering Algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Xu, F.; Shu, X.; Zhang, X.; Fan, B. Automatic Diagnosis of Microgrid Networks’ Power Device Faults Based on Stacked Denoising Autoencoders and Adaptive Affinity Propagation Clustering. Complexity 2020, 8509142. [Google Scholar] [CrossRef]
- Rousseeuw, P. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Grigoras, G.; Neagu, B.C.; Gavrilas, M.; Tristiu, I.; Bulac, C. Optimal Phase Load Balancing in Low Voltage Distribution Networks Using a Smart Meter Data-Based Algorithm. Mathematics 2020, 8, 549. [Google Scholar] [CrossRef]
- Ivanov, O.; Grigoras, G.; Neagu, B.C. Smart Metering based Approaches to Solve the Load Phase Balancing Problem in Low Voltage Distribution Networks. In Proceedings of the International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 1–3 November 2018; pp. 1–6. [Google Scholar]
- Ivanov, O.; Neagu, B.C.; Gavrilas, M.; Grigoras, G.; Sfintes, C. Phase Load Balancing in Low Voltage Distribution Networks Using Metaheuristic Algorithms. In Proceedings of the International Conference on Electromechanical and Energy Systems (SIELMEN), Craiova, Romania, 9–11 October 2019; pp. 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).