Abstract
In this paper, we examine the influence of hybrid nanoparticles on flow and heat transfer over a permeable non-isothermal shrinking surface and we also consider the radiation and the magnetohydrodynamic (MHD) effects. A hybrid nanofluid consists of copper (Cu) and alumina (Al2O3) nanoparticles which are added into water to form Cu-Al2O3/water. The similarity equations are obtained using a similarity transformation and numerical results are obtained via bvp4c in MATLAB. The results show that dual solutions are dependent on the suction strength of the shrinking surface; in addition, the heat transfer rate is intensified with an increase in the magnetic parameter and the hybrid nanoparticles volume fractions for higher values of the radiation parameter. Furthermore, the heat transfer rate is higher for isothermal surfaces as compared with non-isothermal surfaces. Further analysis proves that the first solution is physically reliable and stable.
1. Introduction
In the history of fluid mechanics, flow development over stretching and shrinking surfaces was first described by Crane [1] and Wang [2], respectively. Meanwhile, Miklavčič and Wang [3] reported the existence of non-unique solutions for flow over a shrinking sheet. Since then, many studies have considered the effect of several physical parameters such as magnetohydrodynamic (MHD) and radiation on stretching and shrinking surfaces [4,5,6,7,8,9,10,11,12]. The effect of the MHD parameter is an important factor in many industrial and engineering applications, for example, MHD power generators, metallurgical process, crystal growth, metal casting, and cooling of nuclear reactors [13]. Thermal radiation is also important in designing innovative energy conversion systems operational at high temperatures [14].
In general, most previous studies have considered isothermal surface conditions; however, heating or cooling can occur under non-isothermal conditions for many practical applications such as in microelectromechanical (MEM) condensation applications, a thin-film solar energy collector device, the cooling of metallic plate in a cooling bath, metal spinning, paper production, and aerodynamic extrusion of plastic sheets [15,16]. In this respect, Soundalgekar and Ramana Murty [17], and Grubka and Bobba [18] considered flow over moving and stretching surfaces under non-isothermal conditions, respectively. This type of heating condition also has been reported by several researchers [19,20,21,22].
In 1995, Choi and Eastman [23] introduced nanofluids, which are a mixture of a base fluid and a single type of nanoparticle, to enhance thermal conductivity. Various studies on such fluids have been conducted [24,25,26,27,28,29]. Recently, some studies have found that advanced nanofluid consists of another type of nanoparticle that is mixed in with the regular nanofluid and improves its thermal properties, namely a ”hybrid nanofluid”. Prior experimental studies using hybrid nanoparticles have been conducted by several researchers [30,31,32] and numerical studies on the flow of hybrid nanofluids were studied by Takabi and Salehi [33]. Moreover, dual solutions of hybrid nanofluid flow were examined by Waini et al. [34,35,36,37,38,39]. Other physical aspects have been considered by several authors [40,41,42,43,44,45,46,47,48,49] and review papers are also available [50,51,52,53,54,55].
In this study, we aim at investigating the effects of Cu-Al2O3 hybrid nanoparticles on the radiative MHD flow over a permeable non-isothermal shrinking surface. The simultaneous effects of radiation and the hybrid nanoparticles are examined and the influence of magnetic field and variation of the temperature index is also considered. To the best of our knowledge, based on the above studies, the flow of hybrid nanofluids over non-isothermal shrinkage surfaces is not yet available in the literature, and therefore the results of this study are new. Most importantly, in this study, two solutions are discovered and the long-term stability of these solutions is investigated.
2. Mathematical Formulation
Let us consider the two-dimensional, laminar, and incompressible flow of a hybrid nanofluid over a permeable non-isothermal shrinking surface, as shown in Figure 1. The surface velocity is represented by where is constant and is the constant mass flux velocity. The flow is subjected to the combined effect of a transverse magnetic field of strength and the radiative heat flux , which is assumed to be applied normal to the surface in the positive -direction. Accordingly, the hybrid nanofluid equations (see Grubka and Bobba [18], Rashid et al. [20], Waini et al. [34]) are:
subject to:
where and represent the velocity components along the - and -axes and the temperature of the hybrid nanofluid is given by .
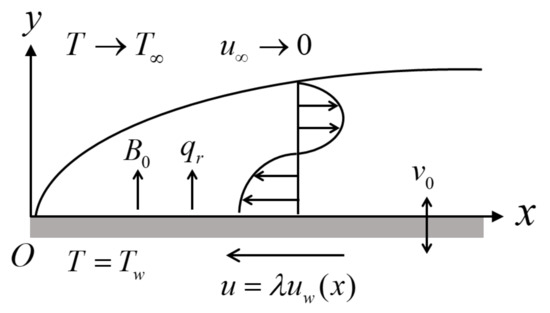
Figure 1.
The flow configuration.
The expression of the radiative heat flux is as follows [9]:
where and denote the Stefan–Boltzmann constant and the mean absorption coefficient, respectively. Following Rosseland [56], after employing a Taylor series, one gets . Then, Equation (3) becomes the following:
Furthermore, the thermophysical properties can be referred to in Table 1 and Table 2. Data from these tables are adapted from previous studies [26,33,34,57]. Note that (Al2O3) and (Cu) are nanoparticles volume fractions, and the subscripts and correspond to their solid components, while the subscripts and represent the hybrid nanofluid and the base fluid, respectively.

Table 1.
Thermophysical properties of nanoparticles and water.

Table 2.
Thermophysical properties of nanofluid and hybrid nanofluid.
For the similarity solution of Equations (1), (2), and (6), the surface temperature is taken as follows (see Grubka and Bobba [18], Rashid et al. [20]):
where is a characteristic length of the sheet and is a temperature characteristic. The ambient temperature is assumed to be constant and represents the temperature power-law index, with indicating an isothermal surface and indicating a non-isothermal surface.
Now, using the following similarity transformation:
with the stream function . Here, and , then:
From Equation (9), by setting , one obtains:
where is the constant mass flux parameter which determines the permeability of the surface. Here, and are for injection and suction cases, respectively, while represents an impermeable case.
On using Equations (8) and (9), Equation (1) is identically fulfilled. Now, Equations (2) and (6) are reduced to:
subject to the following:
where primes denote differentiation with respect to . Note that and represent the shrinking and stretching surfaces, while is a rigid surface. In addition, is the Prandtl number, while and are the radiation and the magnetic parameters, respectively, which are defined as follows:
The coefficient of the skin friction and the local Nusselt number are given as follows [9]:
Using Equations (8) and (15), one obtains:
where defines the local Reynolds number.
It should be noted that for , Equations (11) and (12) reduce to Equations (5) and (6) from Grubka and Bobba [18] when .
3. Stability Analysis
The temporal stability of the dual solutions as time evolves is studied. This analysis was first introduced by Merkin [58], and then followed by Weidman et al. [59]. Firstly, consider the new variables as follows:
Now, the unsteady form of Equations (2) and (3) are employed, while Equation (1) remains unchanged. On using (17), one obtains:
subject to the following:
Then, consider the following perturbation functions [59]:
Here, Equation (21) is used to apply a small disturbance on the steady solutions and of Equations (11)–(13). The functions and in Equation (19) are relatively small as compared with and . The sign (positive or negative) of the eigenvalue determines the stability of the solutions. By employing Equation (21), Equations (18) to (20) become:
subject to the following:
Without loss of generality, we set [60] to get the eigenvalues in Equations (22) and (23).
4. Results and Discussion
By utilising the package bvp4c in MATLAB software, Equations (11)–(13) were solved numerically. This solver employs the three-stage Lobatto IIIa formula [61]. The effect of several physical parameters on the flow behaviour is examined. The total composition of Al2O3 and Cu volume fractions are applied in a one-to-one ratio. For instance, of Al2O3 and of Cu are mixed to produce of Al2O3-Cu hybrid nanoparticles volume fractions, i.e., . Meanwhile, indicates a regular viscous fluid.
The values of for various values of and Pr when and (stretching sheet) are compared with Grubka and Bobba [18], and Ishak et al. [15] and the results for each m and Pr considered are comparable, as shown in Table 3. In addition, it should be noted that the values of increase for higher values of and Pr. Furthermore, Table 4 provides the values of and when , and (shrinking sheet) for different physical parameters. The consequence of increasing and values is to reduce the local Nusselt number for both branch solutions. However, the skin friction coefficient is not affected by these parameters. Moreover, the values of and for the first solution increase, but they decrease for the second solution as increases.

Table 3.
Values of under different values of and Pr when and (stretching sheet).

Table 4.
Values of and when , and (shrinking sheet) for different physical parameters.
The variations of against when for various values of are presented in Figure 2. Reductions in the values of on both solutions are observed with an increase in and . Moreover, the simultaneous effect of and on when can be observed in Figure 3. The values of on the first solution decrease with a high percentage of for smaller values of . This finding seems to contradict the fact that the added hybrid nanoparticles improve the heat transfer rate due to synergistic effects as discussed by Sarkar et al. [50]. However, it is interesting to note that this behaviour is opposite when higher values of are applied to the system where the enhancement in the values of are observed with a high percentage of . From these observations, we conclude that the rate of heat transfer could be controlled by manipulating the values of and .
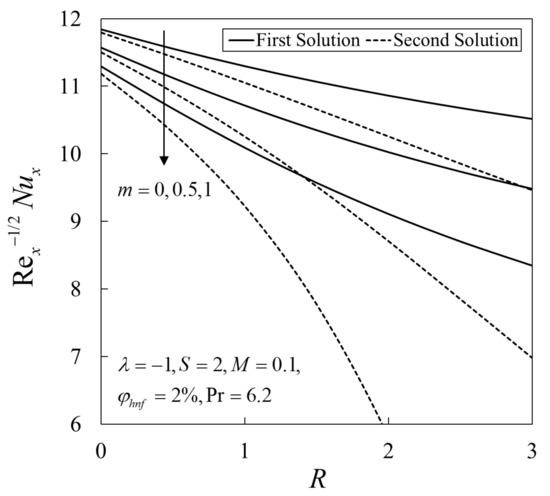
Figure 2.
Variations of the local Nusselt number against the radiation parameter for different values of .
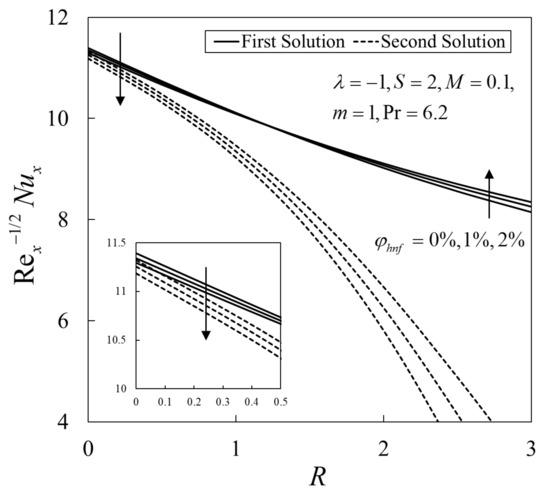
Figure 3.
Variations of the local Nusselt number against against the radiation parameter and for different values of .
Next, the variations of and against for various values of and are presented in Figure 4, Figure 5, Figure 6 and Figure 7, respectively. The enhancement in the values of and on the first solution are observed with an increase in S, and values. The dual solutions are also obtained when a suitable suction strength is imposed on the shrinking surface. The flow is unlikely to exist since the vorticity could not be confined in the boundary layer. These figures reveal that a sufficient suction strength is needed to preserve the flow over a shrinking sheet. The similarity solutions are terminated at (critical value) and this point is known as the bifurcation point of the solutions. The boundary layer separation is also delayed with an increase in and by expanding the domain of . Here, the critical values are for , respectively. Meanwhile, for , the critical values are , respectively. It can be seen that the presence of those parameters suppressed the vorticity generation due to the shrinking of the sheet and the steady boundary layer flow is maintained.
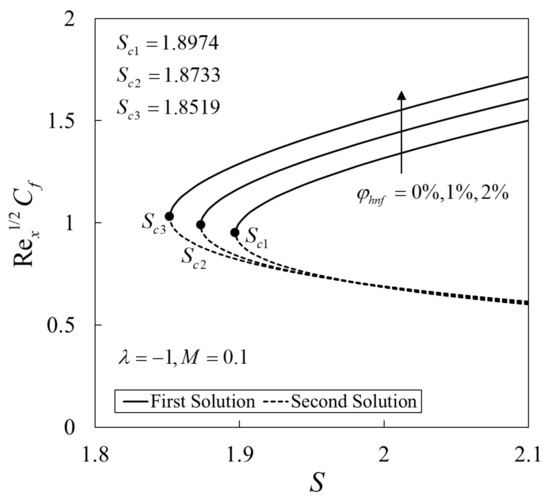
Figure 4.
Variations of the skin friction coefficient against suction parameter for different values of .
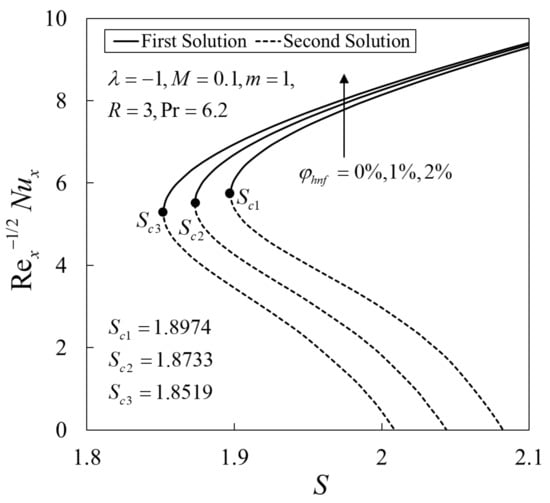
Figure 5.
Variations of the local Nusselt number against suction parameter for different values of .
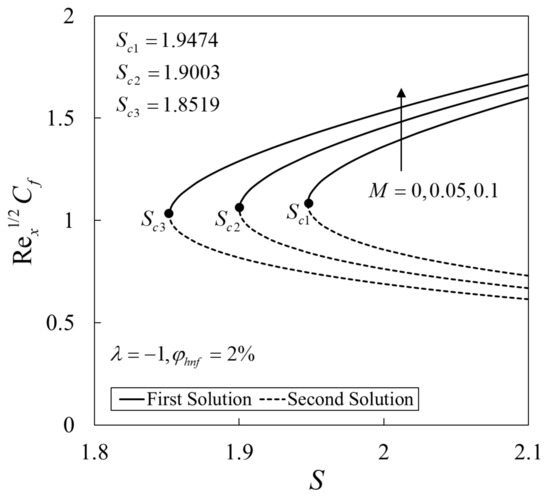
Figure 6.
Variations of the local Nusselt number against suction parameter for different values of .
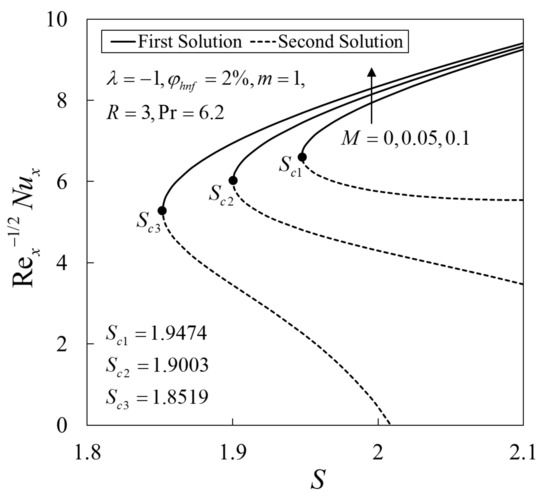
Figure 7.
Variations of the local Nusselt number against suction parameter for different values of .
The influence of and on the variations against are given in Figure 8 and Figure 9, respectively. The heat transfer rate is higher for the isothermal surface as compared with the non-isothermal surface . An increase in leads to a reduction in the values of . In addition, the boundary layer separation occurs at the same point where the critical value is for all values of and considered.
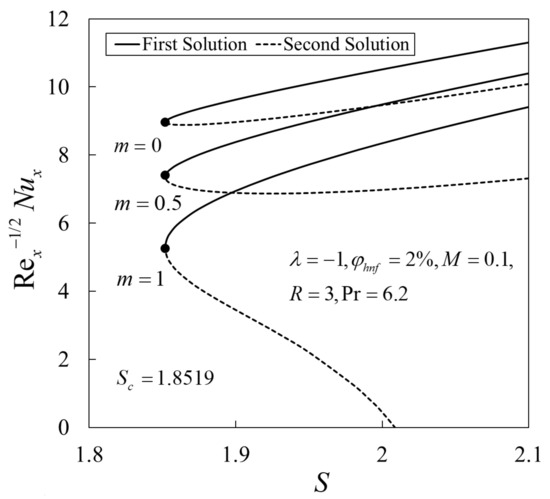
Figure 8.
Variations of the local Nusselt number against suction parameter for different values of .
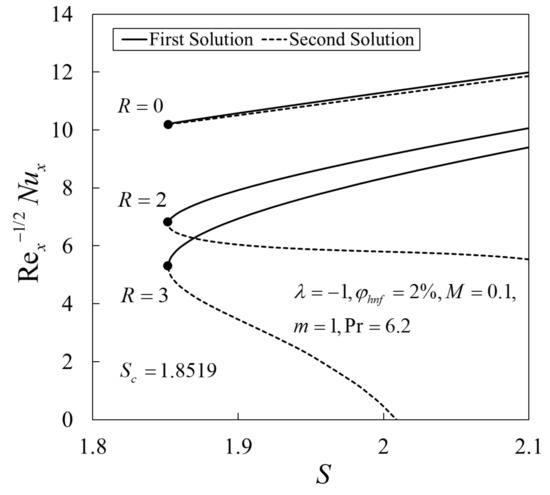
Figure 9.
Variations of the local Nusselt number against suction parameter for different values of .
The profiles of the velocity and the temperature for several pertinent parameters are presented in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17. There are dual solutions for and which satisfy the infinity boundary conditions (13) asymptotically. For more detail, the profiles of and for several values of when are given in Figure 10 and Figure 11. Note that the profiles of the first and the second solutions are merged towards some values of . This behaviour can also be seen in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 where the similarity solutions ended at .

Figure 10.
Velocity profiles or different values of suction strength .
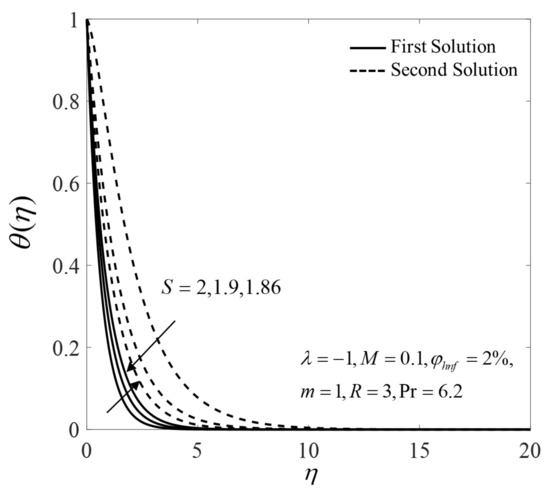
Figure 11.
Temperature profiles for different values of .
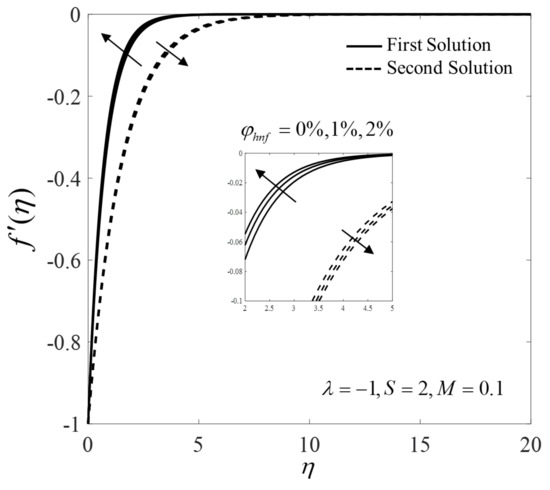
Figure 12.
Velocity profiles for different values of .

Figure 13.
Temperature profiles for different values of .
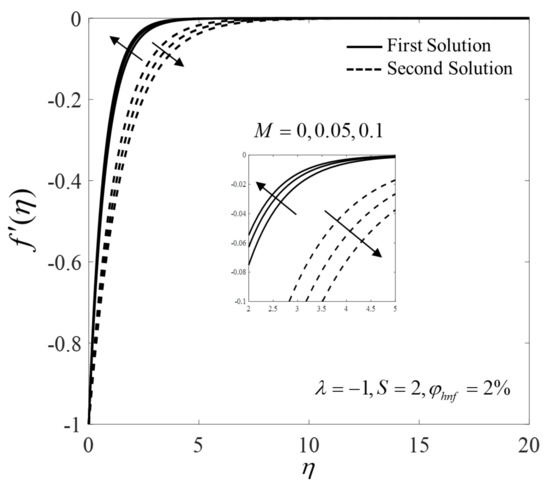
Figure 14.
Velocity profiles for different values of .
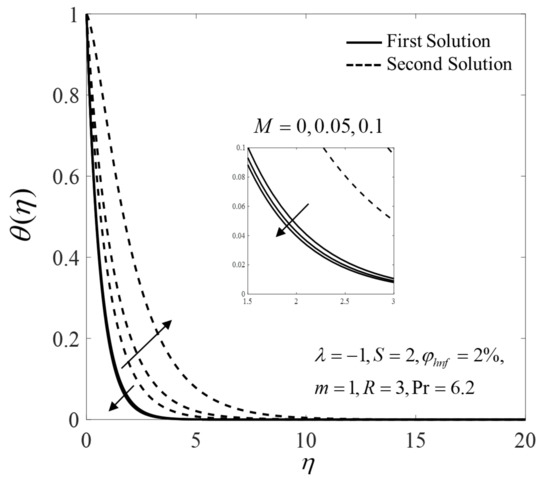
Figure 15.
Temperature profiles for different values of .
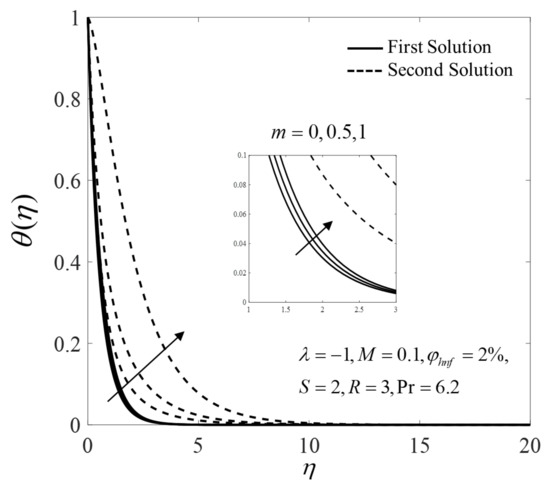
Figure 16.
Temperature profiles for different values of .
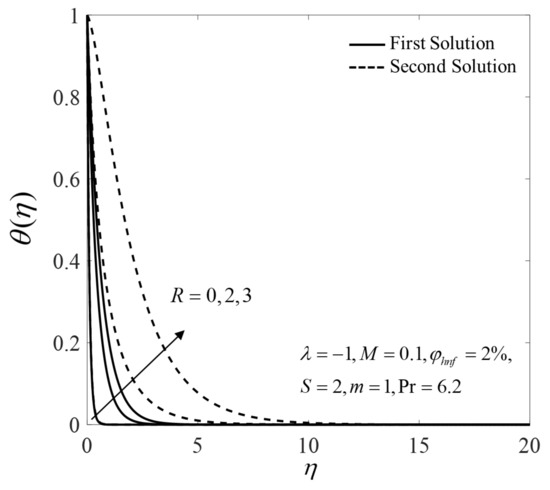
Figure 17.
Temperature profiles for different values of .
Next, an increase in and values lead to an upsurge in the velocity but reduces the temperature on the first solution, as shown in Figure 12, Figure 13, Figure 14 and Figure 15, respectively. Physically, the addition of the nanoparticles makes the fluid more viscous, and thus slows down the flow; the added nanoparticles also dissipate energy in the form of heat and consequently exert more energy which enhances the temperature. However, in this study, we discover that the velocity increases, but the temperature decreases, as increases. Furthermore, an increase in magnetic strength enhances the magnitude of Lorentz force and results in an increment in the velocity and a reduction in the temperature for the shrinking sheet case.
Moreover, Figure 16 and Figure 17 show the consequence effects of and on the temperature . It is seen that both branch solutions of show an increasing pattern for larger values of and ; in addition, the boundary layer thickness of the first and the second solutions expand as and increase. For , the temperature in the flow field increases due to direct variation of the wall temperature along the shrinking surface. Moreover, the radiation is dominant over conduction with an increase in . Therefore, the temperature increases due to the high radiation energy presence in the flow field.
The variations of against when are described in Figure 18. For the positive value of , it is noted that as time evolves . In the meantime, for the negative value of , . These behaviours show that the first solution is stable and physically reliable, while the second solution becomes unstable over time.
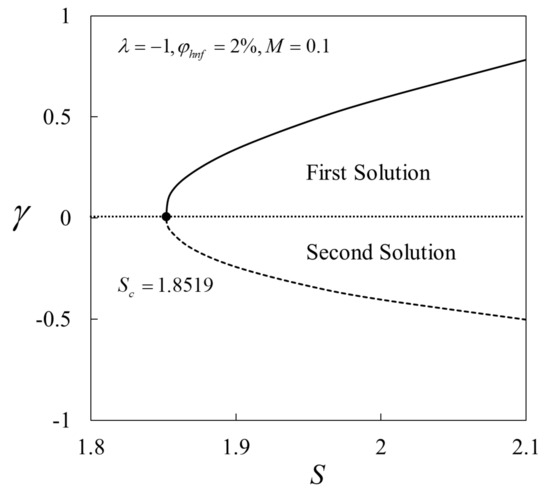
Figure 18.
Variations of the minimum eigenvalues against suction .
5. Conclusions
The flow and heat transfer over a permeable non-isothermal shrinking surface with radiation and magnetohydrodynamic (MHD) effects were examined in this paper. The findings revealed that dual solutions appeared when satisfactory suction strength was applied on the shrinking surface. Moreover, the heat transfer rate was enhanced with a high percentage of when higher values of the radiation parameter, , were applied to the system; additionally, the heat transfer rate was higher for the isothermal surface as compared with the non-isothermal surface . Increased and values also enhanced the skin friction coefficient and the local Nusselt number . The effect of , as well as , was to increase the temperature inside the boundary layer. Lastly, it was discovered that the first solution was stable, and thus physically reliable in the long run.
Author Contributions
Conceptualization, I.P.; funding acquisition, A.I.; methodology, I.W.; Project administration, A.I.; supervision, A.I. and I.P.; validation, I.P.; writing—original draft, I.W.; writing—review and editing, A.I., I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Universiti Kebangsaan Malaysia (project code DIP-2020-001).
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions. The financial supports received from the Universiti Kebangsaan Malaysia (project code: DIP-2020-001) and the Universiti Teknikal Malaysia Melaka are gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Andersson, H.I.; Aarseth, J.B.; Dandapat, B.S. Heat transfer in a liquid film on an unsteady stretching surface. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Miklavčič, M.; Wang, C.Y. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 64, 283–290. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. Closed-form exact solutions of MHD viscous flow over a shrinking sheet. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2853–2857. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Pop, I. MHD boundary layer flow due to an exponentially shrinking sheet. Magnetohydrodynamics 2011, 47, 337–344. [Google Scholar]
- Bhattacharyya, K. Effects of radiation and heat source/sink on unsteady MHD boundary layer flow and heat transfer over a shrinking sheet with suction/injection. Front. Chem. Eng. China 2011, 5, 376–384. [Google Scholar] [CrossRef]
- Ishak, A. MHD boundary layer flow due to an exponentially stretching sheet with radiation effect. Sains Malays. 2011, 40, 391–395. [Google Scholar]
- Ishak, A.; Yacob, N.A.; Bachok, N. Radiation effects on the thermal boundary layer flow over a moving plate with convective boundary condition. Meccanica 2011, 46, 795–801. [Google Scholar] [CrossRef]
- Cortell, R. Heat and fluid flow due to non-linearly stretching surfaces. Appl. Math. Comput. 2011, 217, 7564–7572. [Google Scholar] [CrossRef]
- Vyas, P.; Srivastava, N. Radiative boundary layer flow in porous medium due to exponentially shrinking permeable sheet. ISRN Thermodyn. 2012, 2012, 214362. [Google Scholar] [CrossRef]
- Yasin, M.H.M.; Ishak, A.; Pop, I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J. Magn. Magn. Mater. 2016, 407, 235–240. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J. King Saud Univ. Eng. Sci. 2017, 29, 68–74. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2020, in press. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Mujtaba, M.; Quadri, A.; Issa, C. Thermal radiation effects on MHD forced convection flow adjacent to a non-isothermal wedge in the presence of a heat source or sink. Heat Mass Transf. 2003, 39, 305–312. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Heat transfer over an unsteady stretching permeable surface with prescribed wall temperature. Nonlinear Anal. Real World Appl. 2009, 10, 2909–2913. [Google Scholar] [CrossRef]
- Muthtamilselvan, M.; Prakash, D. Unsteady hydromagnetic slip flow and heat transfer of nanofluid over a moving surface with prescribed heat and mass fluxes. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 703–715. [Google Scholar] [CrossRef]
- Soundalgekar, V.M.; Ramana Murty, T.V. Heat transfer in flow past a continuous moving plate with variable temperature. Wärme Stoffübertragung 1980, 14, 91–93. [Google Scholar] [CrossRef]
- Grubka, L.J.; Bobba, K.M. Heat Transfer Characteristics of a Continuous, Stretching Surface With Variable Temperature. J. Heat Transf. 1985, 107, 248–250. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Uddin, M.S.; Layek, G.C. Exact solution for thermal boundary layer in Casson fluid flow over permeable shrinking sheet with variable wall temperature and thermal radiation. Alex. Eng. J. 2016, 55, 1703–1712. [Google Scholar] [CrossRef]
- Rashid, I.; Haq, R.U.; Khan, Z.H.; Al-Mdallal, Q.M. Flow of water based alumina and copper nanoparticles along a moving surface with variable temperature. J. Mol. Liq. 2017, 246, 354–362. [Google Scholar] [CrossRef]
- Seth, G.S.; Singha, A.K.; Mandal, M.S.; Banerjee, A.; Bhattacharyya, K. MHD stagnation-point flow and heat transfer past a non-isothermal shrinking/stretching sheet in porous medium with heat sink or source effect. Int. J. Mech. Sci. 2017, 134, 98–111. [Google Scholar] [CrossRef]
- Uddin, M.S.; Bhattacharyya, K. Thermal boundary layer in stagnation-point flow past a permeable shrinking sheet with variable surface temperature. Propuls. Power Res. 2017, 6, 186–194. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995; Volume 66, pp. 99–105. [Google Scholar]
- Khanafer, K.; Vafai, K.; Lightstone, M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-Nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Pop, I. Stagnation-point flow over a stretching/shrinking sheet in a nanofluid. Nanoscale Res. Lett. 2011, 6, 623. [Google Scholar] [CrossRef] [PubMed]
- Yacob, N.A.; Ishak, A.; Pop, I.; Vajravelu, K. Boundary layer flow past a stretching/shrinking surface beneath an external uniform shear flow with a convective surface boundary condition in a nanofluid. Nanoscale Res. Lett. 2011, 6, 314. [Google Scholar] [CrossRef] [PubMed]
- Waini, I.; Ishak, A.; Pop, I. Dufour and Soret effects on Al2O3-water nanofluid flow over a moving thin needle: Tiwari and Das model. Int. J. Numer. Methods Heat Fluid Flow 2020, in press. [Google Scholar] [CrossRef]
- Turcu, R.; Darabont, A.; Nan, A.; Aldea, N.; Macovei, D.; Bica, D.; Vekas, L.; Pana, O.; Soran, M.L.; Koos, A.A.; et al. New polypyrrole-multiwall carbon nanotubes hybrid materials. J. Optoelectron. Adv. Mater. 2006, 8, 643–647. [Google Scholar]
- Jana, S.; Salehi-Khojin, A.; Zhong, W.H. Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives. Thermochim. Acta 2007, 462, 45–55. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3-Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloids Surf. A Physicochem. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Takabi, B.; Salehi, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Adv. Mech. Eng. 2014, 6, 147059. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow induced by an exponentially shrinking sheet. Chin. J. Phys. 2020, 68, 468–482. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics 2020, 8, 612. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Squeezed hybrid nanofluid flow over a permeable sensor surface. Mathematics 2020, 8, 898. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Mixed convection flow over an exponentially stretching/shrinking vertical surface in a hybrid nanofluid. Alex. Eng. J. 2020, 59, 1881–1891. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hiemenz flow over a shrinking sheet in a hybrid nanofluid. Results Phys. 2020, 19, 103351. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow towards a stagnation point on an exponentially stretching/shrinking vertical sheet with buoyancy effects. Int. J. Numer. Methods Heat Fluid Flow 2021, 31, 216–235. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Baleanu, D.; Nisar, K.S. Enhanced heat transfer in moderately ionized liquid due to hybrid MoS2/SiO2 nanofluids exposed by nonlinear radiation: Stability analysis. Crystals 2020, 10, 142. [Google Scholar] [CrossRef]
- Khan, U.; Zaib, A.; Khan, I.; Baleanu, D.; Sherif, E.S.M. Comparative investigation on MHD nonlinear radiative flow through a moving thin needle comprising two hybridized AA7075 and AA7072 alloys nanomaterials through binary chemical reaction with activation energy. J. Mater. Res. Technol. 2020, 9, 3817–3828. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Wahid, N.S. Flow and heat transfer of hybrid nanofluid over a permeable shrinking cylinder with Joule heating: A comparative analysis. Alex. Eng. J. 2020, 59, 1787–1798. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R.; Hafidzuddin, E.H.; Wahi, N. Non-axisymmetric Homann stagnation point flow and heat transfer past a stretching/shrinking sheet using hybrid nanofluid. Int. J. Numer. Methods Heat Fluid Flow 2020, in press. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Wahi, N.; Pop, I.; Nazar, R.; Hafidzuddin, E.H. Thermal marangoni flow past a permeable stretching/shrinking sheet in a hybrid Cu-Al2O3/water nanofluid. Sains Malays. 2020, 49, 211–222. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I. Mixed convective stagnation point flow towards a vertical Riga plate in hybrid Cu-Al2O3/water nanofluid. Mathematics 2020, 8, 912. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Unsteady three-dimensional MHD nonaxisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics 2020, 8, 784. [Google Scholar] [CrossRef]
- Zainal, N.A.; Nazar, R.; Naganthran, K.; Pop, I. Impact of anisotropic slip on the stagnation-point flow past a stretching/shrinking surface of the Al2O3-Cu/H2O hybrid nanofluid. Appl. Math. Mech. 2020, 41, 1401–1416. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Pop, I. Cu-Al2O3/water hybrid nanofluid stagnation point flow past MHD stretching/shrinking sheet in presence of homogeneous-heterogeneous and convective boundary conditions. Mathematics 2020, 8, 1237. [Google Scholar] [CrossRef]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.R.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Babu, J.A.R.; Kumar, K.K.; Rao, S.S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Yang, L.; Ji, W.; Mao, M.; Huang, J. An updated review on the properties, fabrication and application of hybrid-nanofluids along with their environmental effects. J. Clean. Prod. 2020, 257, 120408. [Google Scholar] [CrossRef]
- Rosseland, S. Astrophysik und Atom-Theoretische Grundlagen; Springer: Berlin/Heidelberg, Germany, 1931. [Google Scholar]
- Hussain, S.; Ahmed, S.E.; Akbar, T. Entropy generation analysis in MHD mixed convection of hybrid nanofluid in an open cavity with a horizontal channel containing an adiabatic obstacle. Int. J. Heat Mass Transf. 2017, 114, 1054–1066. [Google Scholar] [CrossRef]
- Merkin, J.H. On dual solutions occurring in mixed convection in a porous medium. J. Eng. Math. 1986, 20, 171–179. [Google Scholar] [CrossRef]
- Weidman, P.D.; Kubitschek, D.G.; Davis, A.M.J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. Int. J. Eng. Sci. 2006, 44, 730–737. [Google Scholar] [CrossRef]
- Harris, S.D.; Ingham, D.B.; Pop, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transp. Porous Media 2009, 77, 267–285. [Google Scholar] [CrossRef]
- Shampine, L.F.; Gladwell, I.; Thompson, S. Solving ODEs with MATLAB; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).