Developing Number Sense: An Approach to Initiate Algebraic Thinking in Primary Education
Abstract
1. Introduction
1.1. Theoretical Foundation
1.1.1. Visualization, Manipulation and Number-Space Linking
1.1.2. Development of Relational Thinking
1.1.3. Development of Flexible Quantitative Thinking
1.1.4. Understanding and Generalization of Patterns
1.1.5. Non-Algorithmic Calculation
2. Materials and Methods
2.1. Teaching Materials
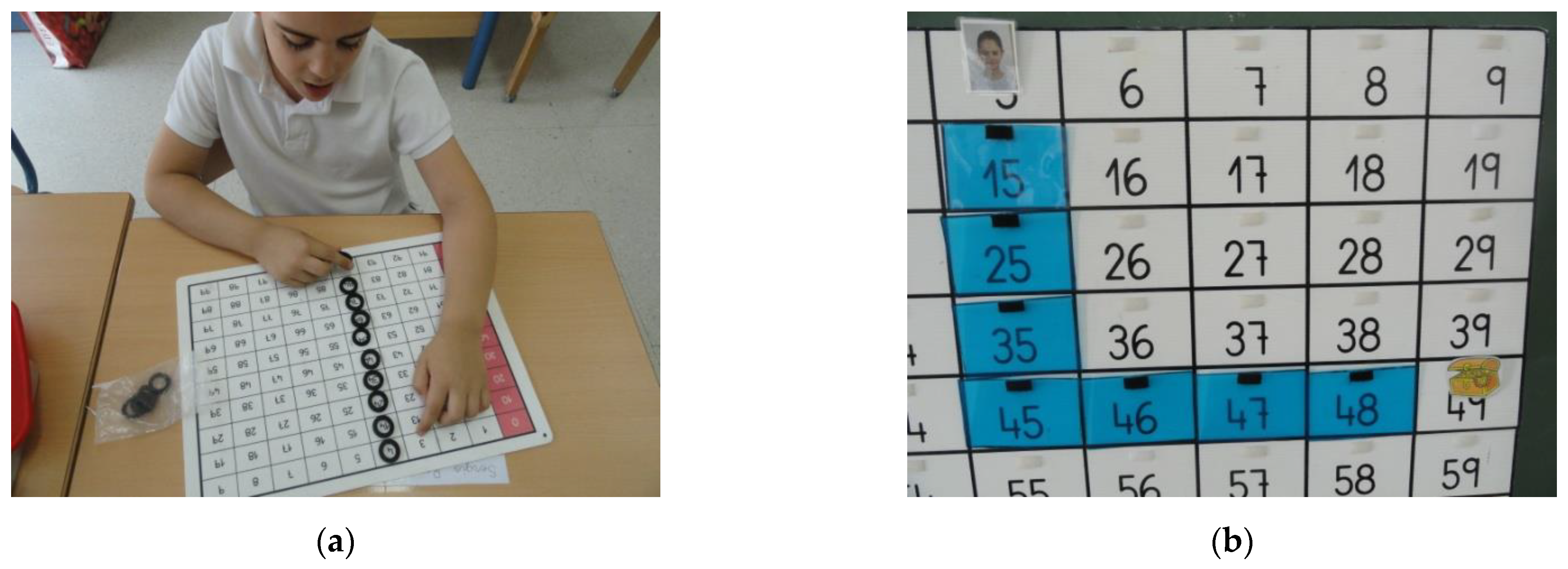
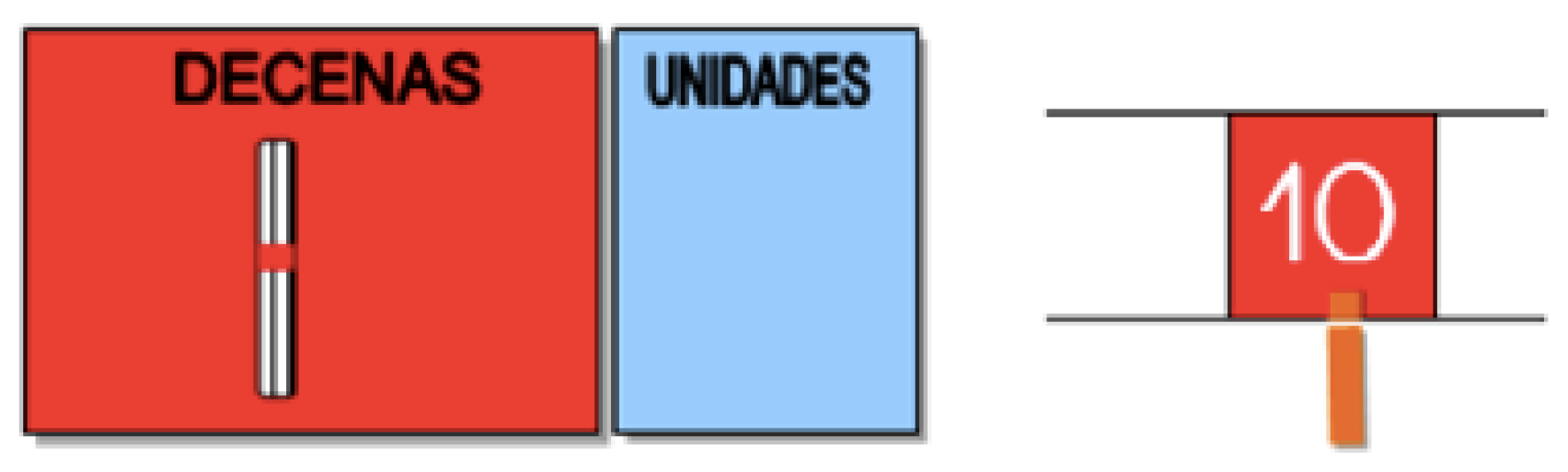
- Number line/tape (Figure 1): It is a tape which facilitates the appropriation of numbers as a linearly ordered, continuous and expandable sequence. It starts with 0, number used as starting point, absence of accounting elements or total loss, and end with 100, as a gateway to the numbers with hundreds that will be studied later on.
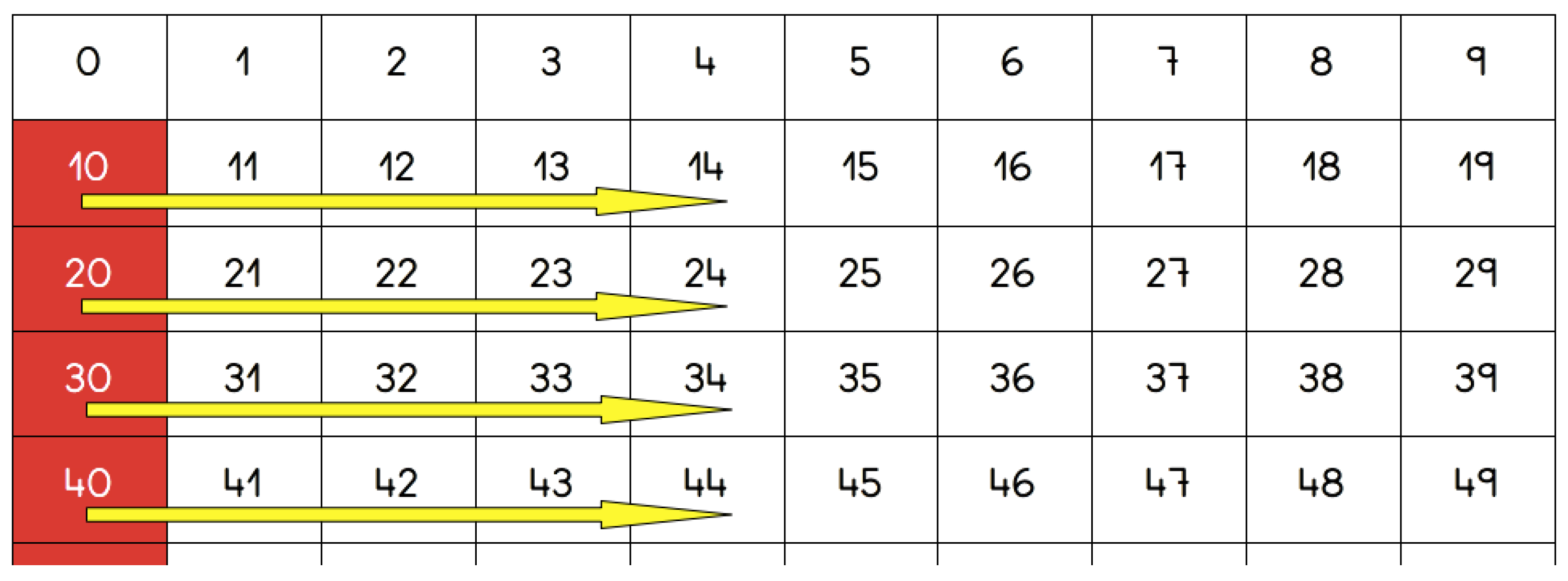
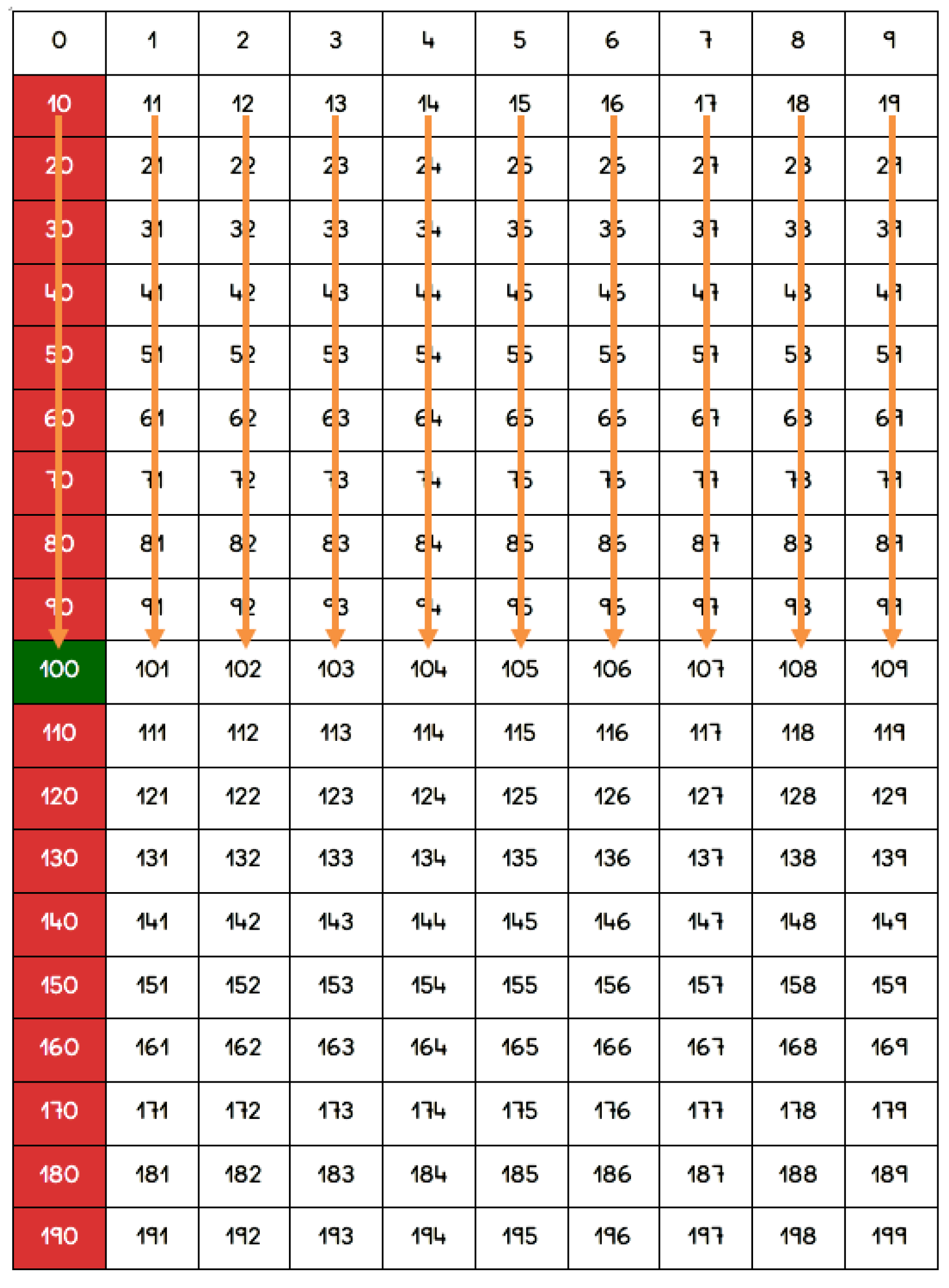
- Numerical panel: it presents the numbers from zero to ninety-nine by families, enabling new possibilities of analysis and relation.
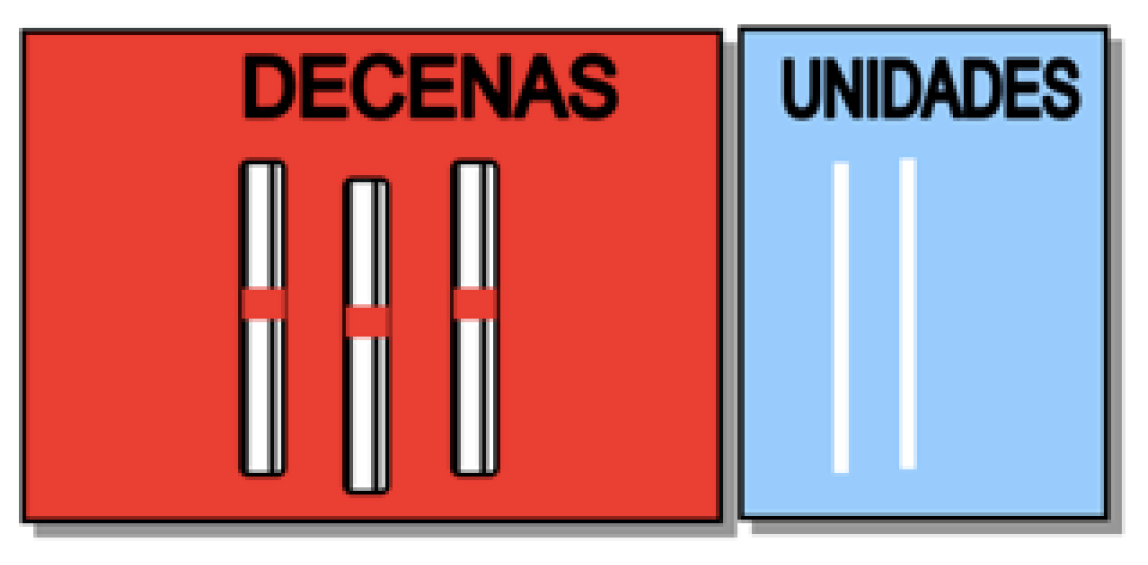
- Numbering box (Figure 4): it is a box with the separation of units, tens and hundreds. Additionally, numerous plastic sticks and red and green rubber bands are used. The whole resource is essential for understanding and working with our decimal number system. Through the use of the sticks and rubber bands, teachers will introduce students to the characteristics and rules of the system. They will be able to see equivalences and will manage to differentiate between different parts of the number without losing the idea of totality.

2.2. Transversal Issues
3. Results
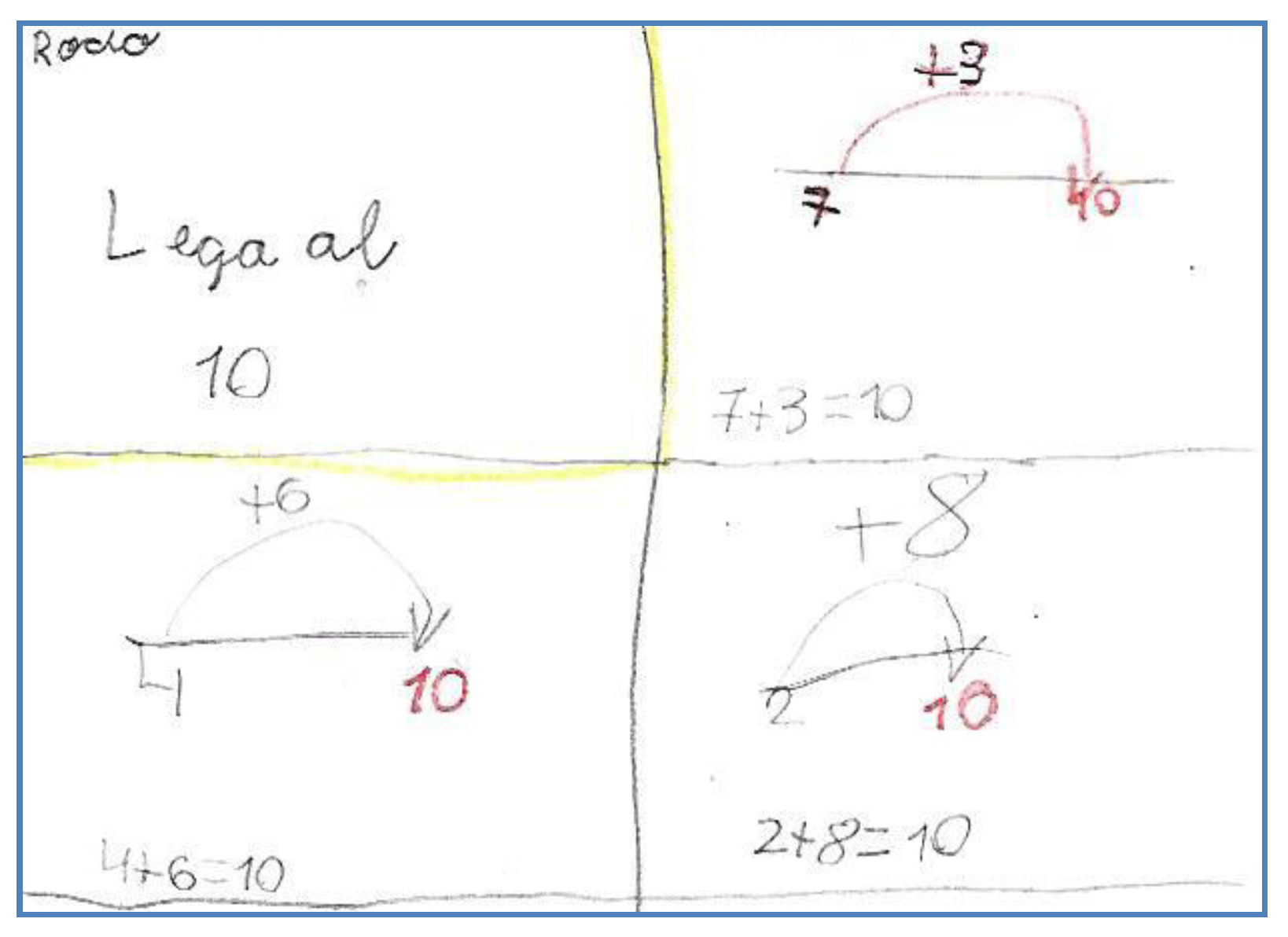
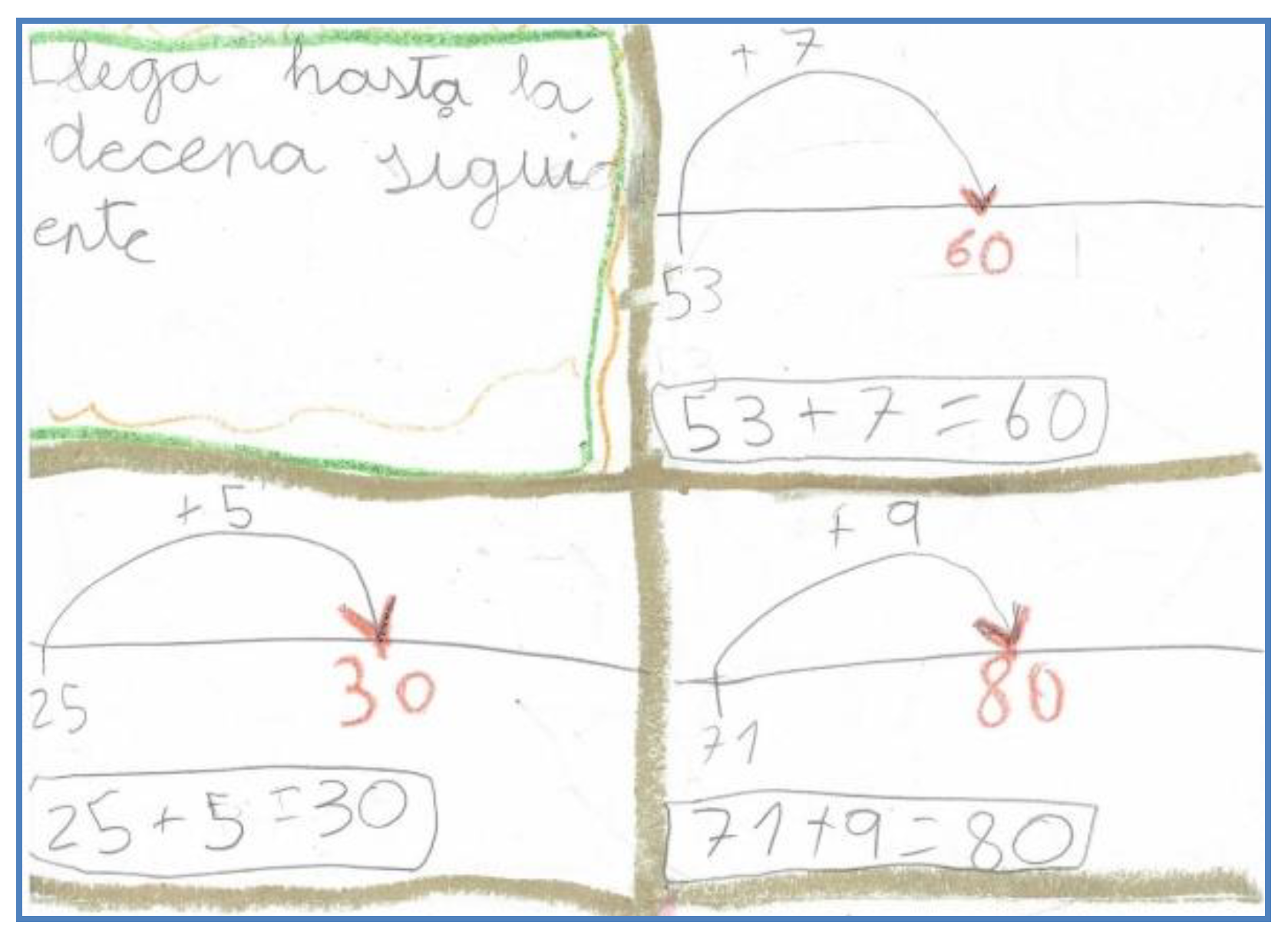
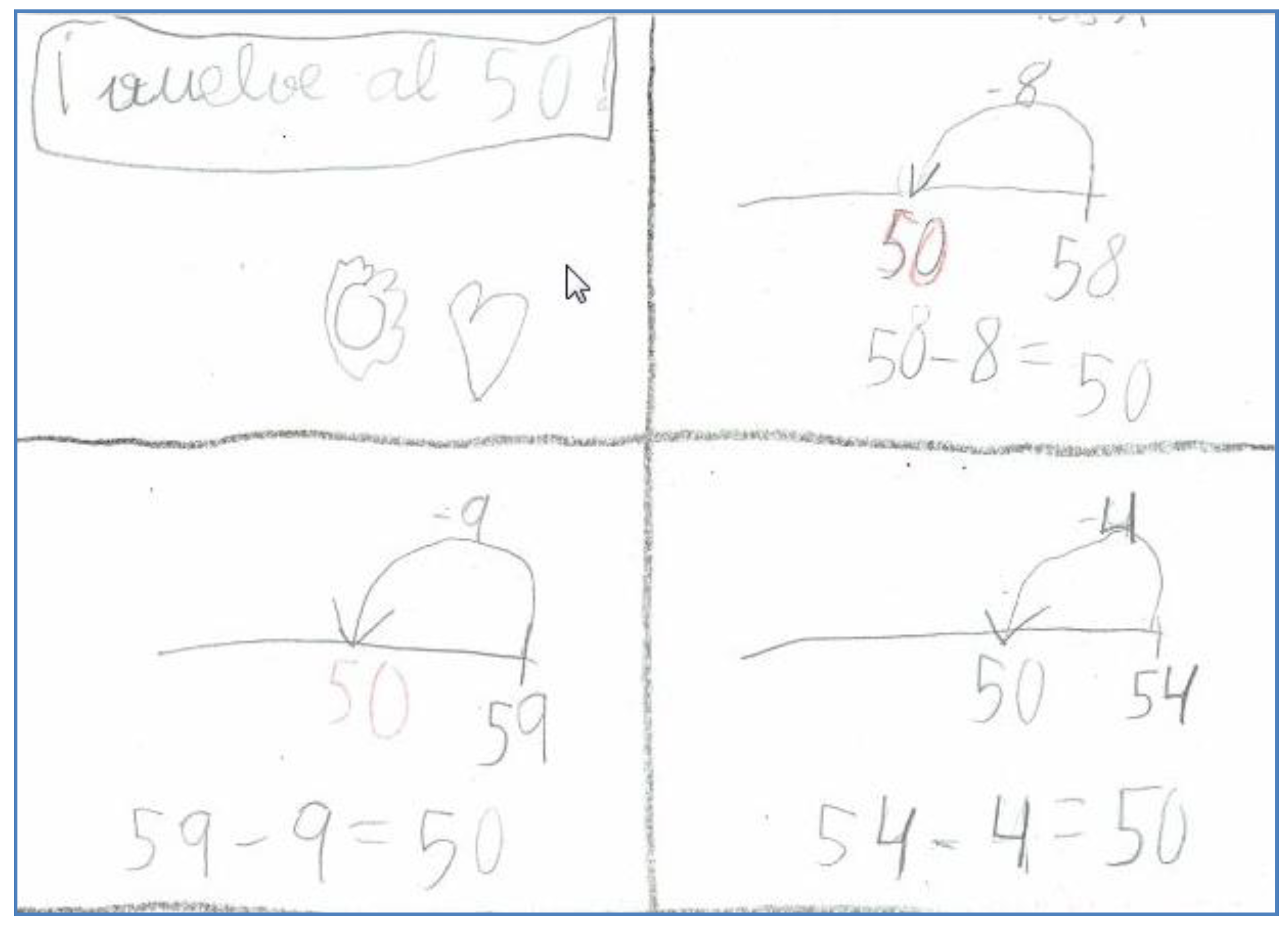
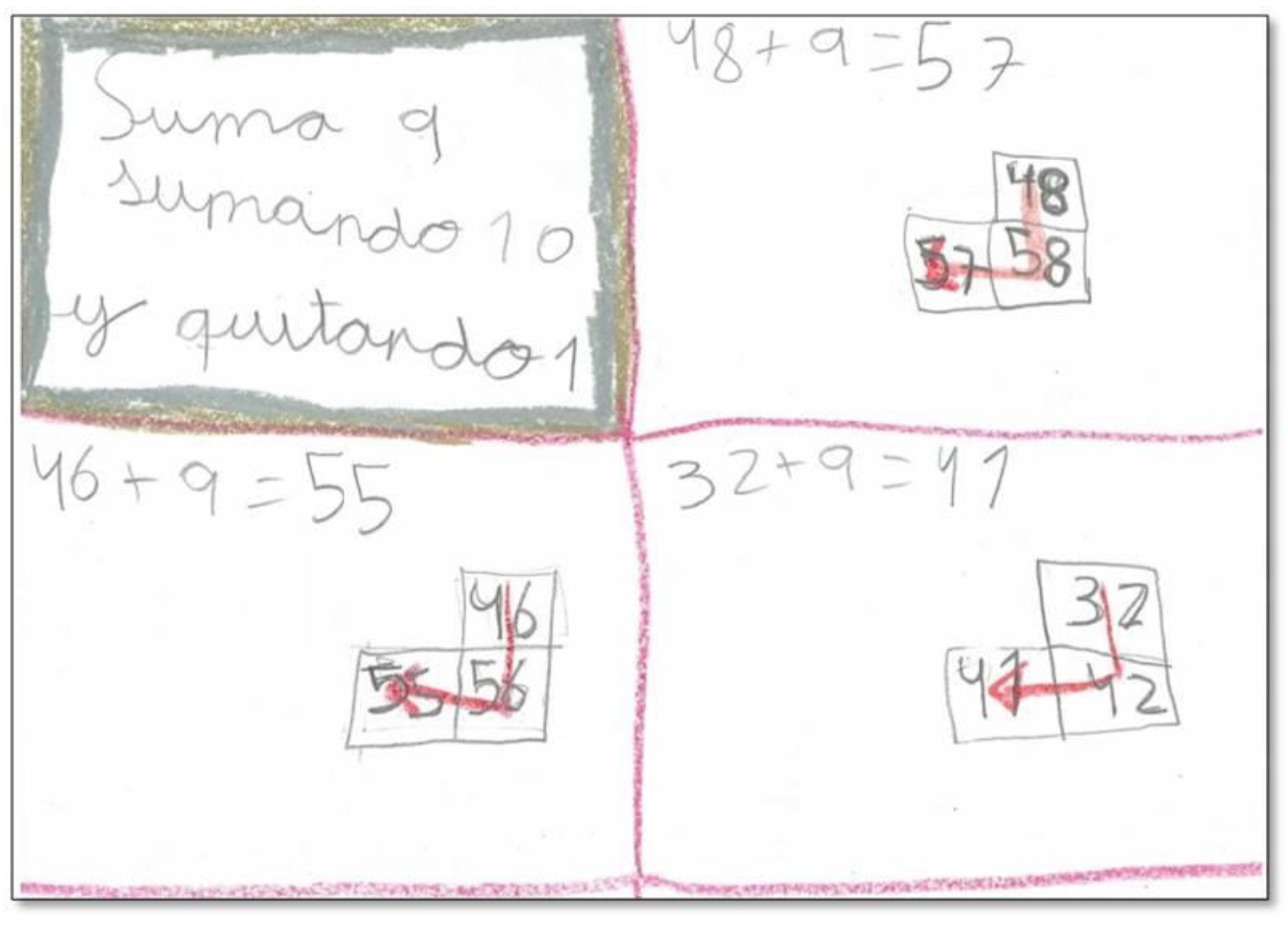
3.1. Relate a Number with the Previous Ten and the Next Ten
Teacher: How can we relate this number to fifty? How can we go from one to the other with operations?
Student: If we give one to fifty, we reach fifty-one.
Student: And if we take one from fifty-one, we go back to fifty.
Teacher: And with the next ten, how can we relate it to the number fifty-one?
Student: If we add nine, we get to sixty.
Student: And if we take away nine, we return to fifty-one.
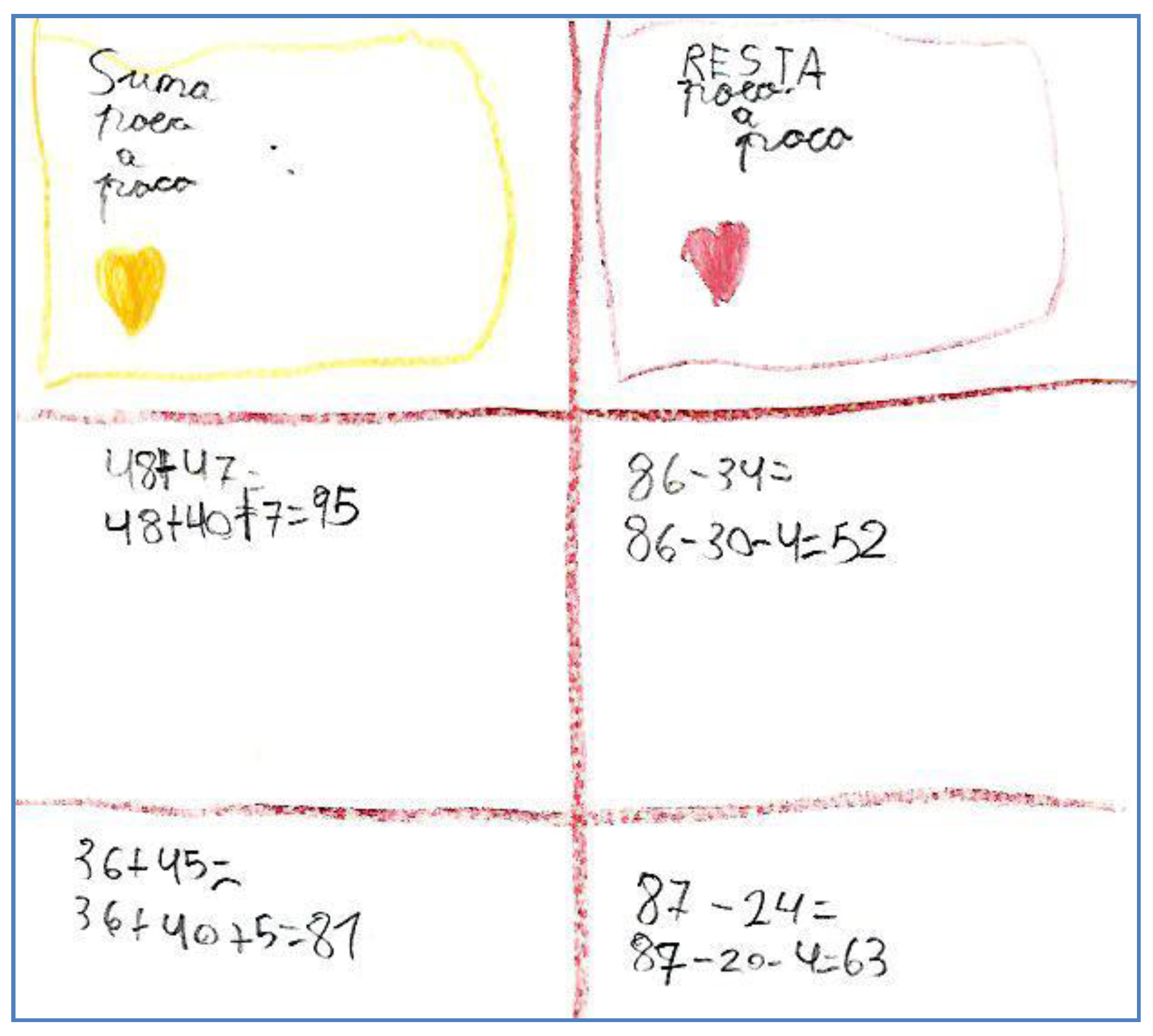
3.2. Verify and Generalize Numerical and Arithmetic Patterns
Teacher: If I add ten to ninety, I’ll reach one hundred, and a hundred minus ninety returns to ten... how do we express this relationship between ten and one hundred?
3.3. Know and Understand the Decimal Number System
Teacher: As we can see, fifty-two is five tens and two units, but we can also say that it is fifty units and two more units. How can we express this number with a sum?
Student: We can express it like this: 52 = 50 + 2.
Teacher: I suggest you do the operation 32 − 17 with the box.
3.4. Skip Kangaroo!
Student: If it takes a jump of five, it reaches thirty-three
Teacher: How will we express this by writing what you have just said? (The teacher writes on the board at the same time they tell what kangaroo has made)
Teacher: From what number has the kangaroo always jumped? What jumps has it made? With what jumps did it stay close to the start? With which did it get very far?...
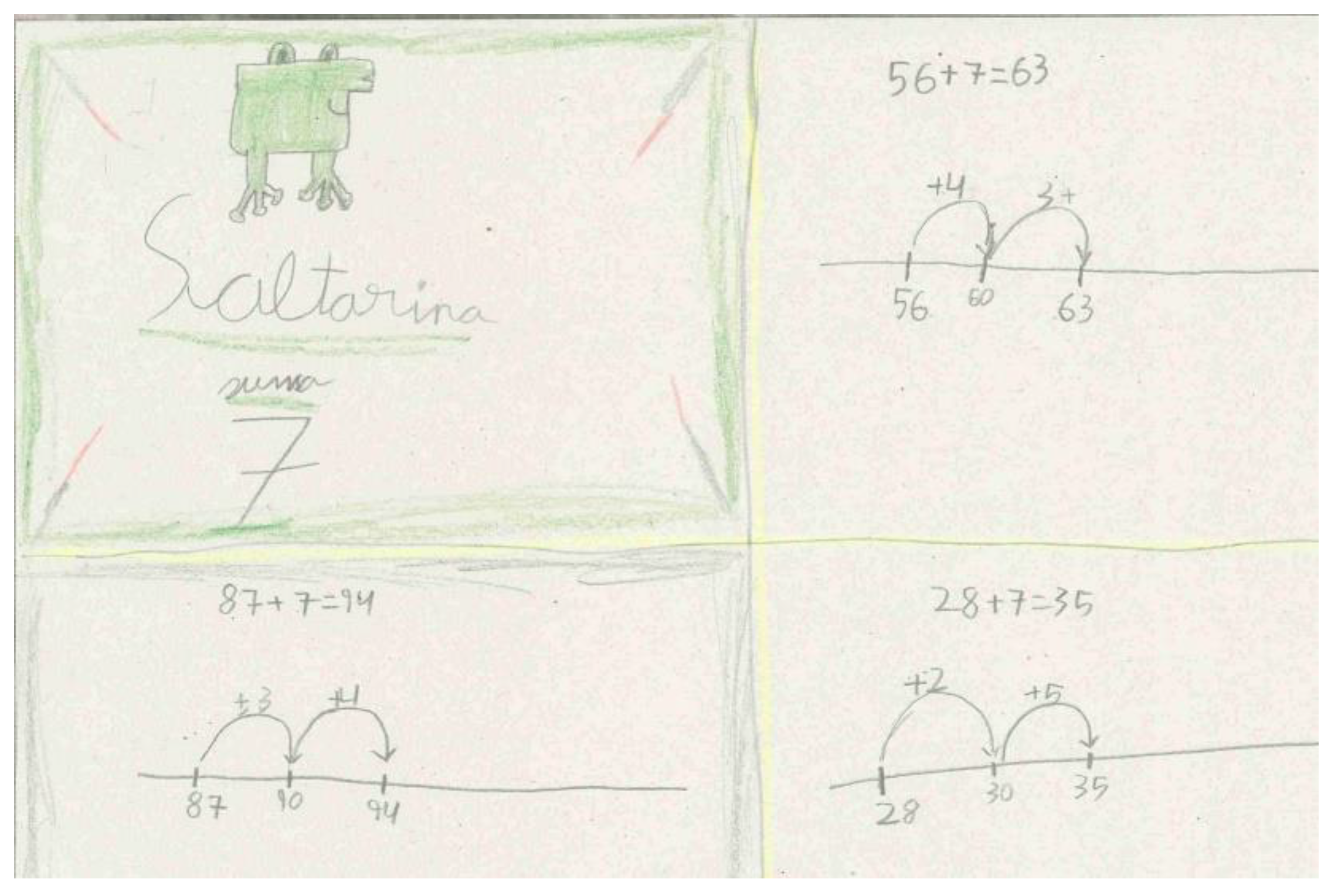
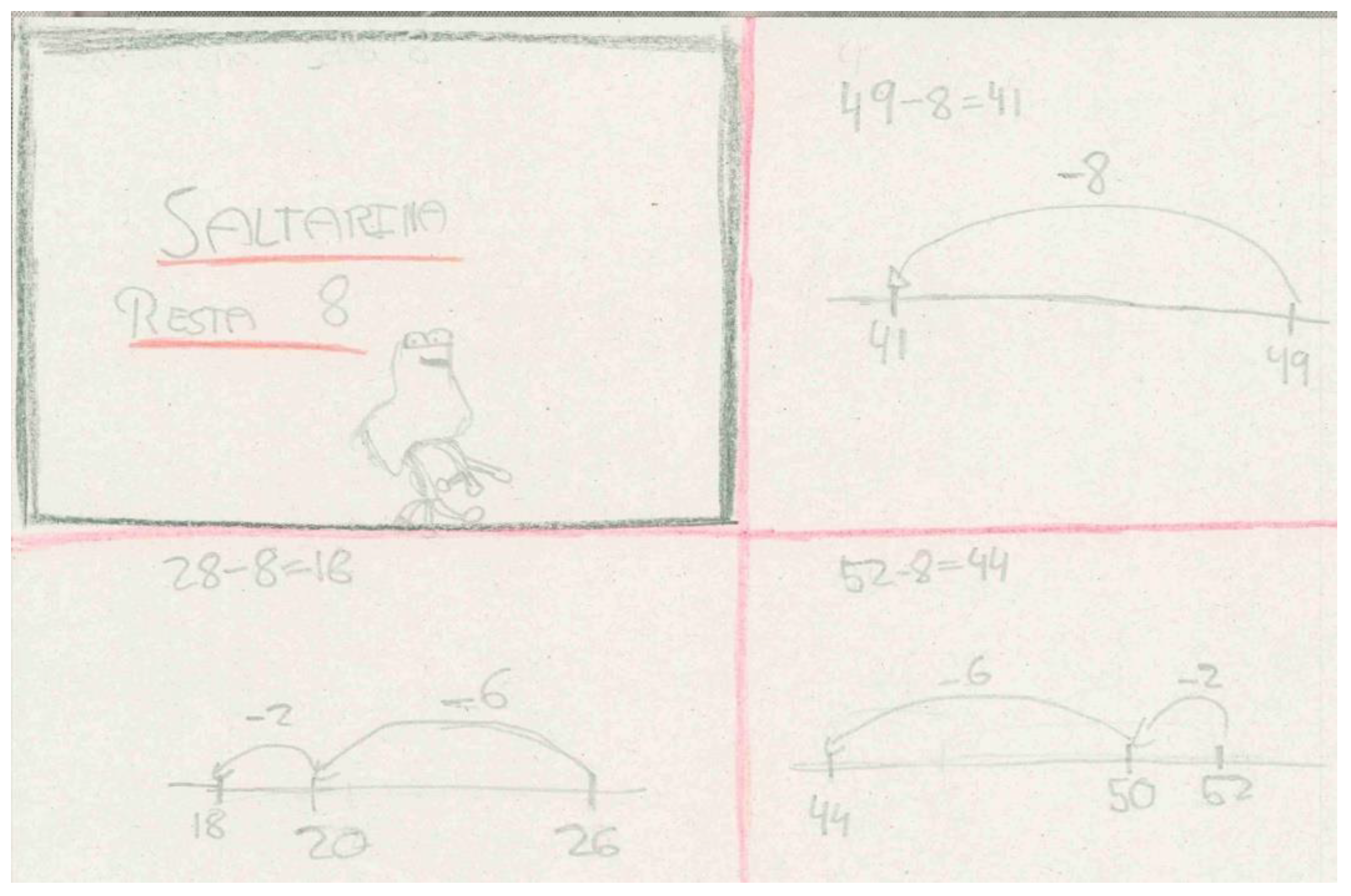
3.5. The Frog Saltarina
Teacher: Today, Saltarina adds seven, where will it stop, and which number will it reach?
Student: It will jump five to land on eighty and later it will jump two.
Teacher: Well done! Let’s check it!
The teacher performs the two movements with Saltarina, stopping at eighty and then reaching eighty-two.
Teacher: It has reached eighty-two! Let’s write what has happened.
Students: Saltarina was on seventy-five (the teacher writes 75), first it has made a leap forward of five to reach eighty (she writes +5) and then it has made another leap of two (+2). It has reached eighty-two (Figure 29).
Teacher: It has reached eighty-two!... What if it now adds nine?
Student: Now it has to jump eight to ninety and then one (Figure 30).
Teacher: And how do we narrate it with a calculation?
4. Discussion
- The importance of number sense development in the first years of mathematical learning, and the importance in this process of achieving significant learning of the decimal numbering system and a comprehensive and relational management of arithmetic operations and their properties, as suggested by [9,44]. All this is aligned with previous research that highlights that small changes in traditional arithmetic practice and learning environment can be key to conceptual understanding [7,45].
- The importance of algebra in secondary education, as a gateway to symbolic thinking in Mathematics, and the difficulties traditionally faced by both teachers and students of this educative level, in order to develop the competencies expected in this area.
- The steps that have been taken in recent years in research in mathematics education in relation to early algebra, in favor of an appropriate transition from concrete arithmetic to the symbolic language of algebra and its positive consequences in favor of abstract mathematical reasoning. Furthermore, in this sense, the relative abundance of specific examples, but the lack and the need to have reference methodological models that, with greater depth, make possible a real breakthrough in the context of practice in the classroom [13,14].
- Finally, the conviction that in the first years of school learning it is necessary to use manipulative resources for the construction of mathematical knowledge in general and the development of number sense in particular [10].
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NCTM. Principles and Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- Greeno, J. Number sense as situated knowing in a conceptual domain. J. Res. Math. Educ. 1991, 22, 170–218. [Google Scholar] [CrossRef]
- Cockcroft, W.H. Las Matemáticas sí Cuentan; MEC: Madrid, Spain, 1985. [Google Scholar]
- Van Amerom, B.A. Focusing on informal strategies when linking arithmetic to early algebra. Educ. Stud. Math. 2003, 54, 63–75. [Google Scholar] [CrossRef]
- Kieran, C. Algebraic Thinking in the Early Grades: What Is It? Math. Educ. 2004, 8, 139–151. [Google Scholar] [CrossRef]
- Vasco, C.E. Análisis semiótico del álgebra elemental. In Argumentación y Semiosis en la Didáctica del Lenguaje y las Matemáticas; Fondo de Publicaciones Universidad Distrital: Bogotá, Colombia, 2007. [Google Scholar]
- Chesney, D.L.; McNeil, N.M.; Petersen, L.A.; Dunwiddie, A.E. Arithmetic practice that includes relational words promotes understanding of symbolic equations. Learn. Individ. Differ. 2018, 64, 104–112. [Google Scholar] [CrossRef]
- Eu, L.; Akmar, S.; Somasundram, P. Year Five Pupils’ Understanding of Generalised Arithmetic. New Educ. Rev. 2017, 49, 176–188. [Google Scholar] [CrossRef]
- Hitt, F.; Saboya, M.; Zavala, C.C. Rupture or continuity: The arithmetico-algebraic thinking as an alternative in a modelling process in a paper and pencil and technology environment. Educ. Stud. Math. 2017, 94, 97–116. [Google Scholar] [CrossRef]
- García Pérez, M.T.; Adamuz-Povedano, N. Del Número al Sentido Numérico y de las Cuentas al Cálculo Táctico; Ediciones Octaedro S.L.: Barcelona, España, 2019; ISBN 9788417667467. [Google Scholar]
- Carpenter, T.P.; Franke, M.L.; Levi, L. Thinking Mathematically: Integrating Arithmetic and Algebra in Elementary School; Heinemann: Portsmouth, NH, USA, 2003; ISBN 978-0-325-07819-9. [Google Scholar]
- Carraher, D.W.; Schliemann, A. Early algebra is not the same as algebra early. In Algebra in the Early Grades; Erlbaum: Mahwah, NJ, USA, 2008; pp. 235–272. ISBN 9780874216561. [Google Scholar]
- Freiman, V.; Fellus, O.O. Closing the gap on the map: Davydov’s contribution to current early algebra discourse in light of the 1960s Soviet debates over word-problem solving. Educ. Stud. Math. 2021. [Google Scholar] [CrossRef]
- Kieran, C.; Pang, J.; Schifter, D.; Ng, S.F. Early Algebra: Research into Its Nature, Its Learning, Its Teaching; ICME-13 Topical Surveys; Springer: Cham, Germany, 2016; ISBN 978-3-319-32257-5. [Google Scholar]
- Bishop, A. Review of research in visualization in mathematics. Focus Learn. Probl. Math. 1989, 11, 7–16. [Google Scholar]
- Guzman, M. El Rincón de la Pizarra. Ensayo de Visualización en Análisis Matemático. Elementos Básicos del Análisis, 2nd ed.; Pirámide: Madrid, Spain, 2010; ISBN 978-84-368-2353-0. [Google Scholar]
- Hitt, F. Dificultades en el aprendizaje del cálculo. In Proceedings of the XI Encuentro de Profesores de Matemáticas del Nivel Medio Superior; Universidad Michoacana de San Nicolás de Hidalgo: Morelia, Mexico, 2003; pp. 81–108. [Google Scholar]
- Ordoñez, J.S.; Ramírez, G.; Bedoya, E. La visualización didáctica en la formación inicial de profesores de matemáticas: El caso de la derivada en el curso de Cálculo I. Rev. Colomb. Matemática Educ. 2015, 1, 160–165. [Google Scholar]
- Tall, D. Intuition and rigour: The role of visualization in the calculus. In Visualization in Teaching and Learning Mathematics; Mathematical Association of America: Washington, DC, USA, 1991; pp. 105–119. [Google Scholar]
- Laski, E.V.; Jor’dan, J.R.; Daoust, C.; Murray, A.K. What Makes Mathematics Manipulatives Effective? Lessons From Cognitive Science and Montessori Education. SAGE Open 2015, 5, 1–8. [Google Scholar] [CrossRef]
- McNeil, N.M.; Uttal, D.H. Rethinking the use of concrete materials in learning: Perspectives from development and education. Child Dev. Perspect. 2009, 3, 137–139. [Google Scholar] [CrossRef]
- ASOCOLME. Estándares Curriculares. Área de Matemáticas; Grupo Editorial Gaia: Bogotá, Colombia, 2002; ISBN 958964404X. [Google Scholar]
- Gallese, V.; Lakoff, G. The Brain’s concepts: The role of the Sensory-motor system in conceptual knowledge. Cogn. Neuropsychol. 2005, 22, 455–479. [Google Scholar] [CrossRef] [PubMed]
- Radford, L. Algebraic Thinking and the Generalization of Patterns: A Semiotic Perspective. In Proceedings of the 28th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Yucatán, México, 9–12 November 2006; pp. 1–21. [Google Scholar]
- Radford, L. The Progressive Development of Early Embodied Algebraic Thinking. Math. Educ. Res. J. 2014, 26, 257–277. [Google Scholar] [CrossRef]
- Dehaene, S. The Number Sense; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Dehaene, S.; Piazza, M.; Pinel, P.; Cohen, L. Three Parietal Circuit for Number Processing. In Handbook of Mathematical Cognition; Campbell, J.I.D., Ed.; Psychology Press: New York, NY, USA, 2005; pp. 443–454. [Google Scholar]
- OCDE. La Comprensión del Cerebro. El Nacimiento de una Ciencia del Aprendizaje; Ediciones UCSH: Santiago, Chile, 2009. [Google Scholar]
- Castro, E.; Rico, L.; Castro, E. Estructuras Aritméticas Elementales y su Modelización; Grupo Editorial IBeroamérica: Bogotá, Colombia, 1995. [Google Scholar]
- Carpenter, T.P.; Levi, L.; Loef, M.; Koehler, J. Algebra in elementary school: Developing relational thinking. Zentralblatt Didakt. Math. 2005, 37, 53–59. [Google Scholar] [CrossRef]
- Stephens, A.C. Equivalence and relational thinking: Preservice elementary teachers’ awareness of opportunities and misconceptions. J. Math. Teach. Educ. 2006, 9, 249–278. [Google Scholar] [CrossRef]
- Weaver, J. Developing Flexibility of Thinking and Performance. Arith. Teach. 1957, 4, 184–188. [Google Scholar] [CrossRef]
- Molina, M. Desarrollo de Pensamiento Relacional y Comprensión del Signo Igual por Alumnos de Tercero de Educación Primaria. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2006. [Google Scholar]
- Schifter, D.; Bastable, V.; Russell, S. Developing Mathematical Ideas; Number and Operations. Part 1: Building a System of Tens Video; Dale Seymour Publications: Parsippany, NJ, USA, 1999. [Google Scholar]
- Smith, J.P.; Thompson, P.W. Quantitative Reasoning and the Development of Algebraic Reasoning. In Algebra in the Early Grades; Erlbaum: New York, NY, USA, 2007; pp. 95–132. ISBN 9781410616463. [Google Scholar]
- Mason, J. Making use of children’s power to produce algebraic thinking. In Algebra in the Early Grades; Kaput, J.J., Carraher, D.W., Blanton, M., Eds.; Erlbaum: New York, NY, USA, 2008; pp. 57–94. ISBN 978-0-8058-5473-2. [Google Scholar]
- Mason, J.; Graham, A.; Johnston-Wilder, S. Developing Thinking in Algebra; Sage: London, UK, 2005. [Google Scholar]
- Davydov, V. Problems of Developmental Instruction: A Theoretical and Experimental Psychological Study; Nova Science Publishers: New York, NY, USA, 2008. [Google Scholar]
- Rivera, F. Teaching and Learning Patterns in School Mathematics; Springer: Dordrecht, The Netherlands, 2013; Volume 9789400727, ISBN 978-94-007-2711-3. [Google Scholar]
- Kaput, J.J. Maria Blanton Algebrafying the elementary mathematics experience. Part 1: Transforming task structures. In Proceedings of the 12th ICMI Study Conference: The Future of the Teaching and Learning of Algebra, Melbourne, Australia, 9–14 December 2001; The University of Melbourne: Melbourne, Australia, 2001; pp. 344–351. [Google Scholar]
- Adamuz-Povedano, N.; Bracho-López, R. La Aritmética del Siglo XXI; Los libro de la Catarata: Madrid, Spain, 2017. [Google Scholar]
- Guerrero, E.; Blanco, L.J. Diseño de un programa psicopedagógico para la intervención en los trastornos emocionales en la enseñanza y aprendizaje de las matemáticas. Rev. Iberoam. Educ. 2004, 33, 1–14. [Google Scholar]
- Pimm, D. El Lenguaje Matemático en el Aula; Morata: Madrid, Spain, 2003; ISBN 9788471123473. [Google Scholar]
- Adamuz-Povedano, N.; Bracho-López, R. Desarrollo del sentido numérico. In Del Número al Sentido Numérico y de las Cuentas al Cálculo Táctico; García Pérez, M.T., Adamuz-Povedano, N., Eds.; Ediciones Octaedro S.L.: Barcelona, Spain, 2019; pp. 13–30. ISBN 9788417667467. [Google Scholar]
- McNeil, N.M.; Fyfe, E.R.; Petersen, L.A.; Dunwiddie, A.E.; Brletic-Shipley, H. Benefits of Practicing 4 = 2 + 2: Nontraditional Problem Formats Facilitate Children’s Understanding of Mathematical Equivalence. Child Dev. 2011, 82, 1620–1633. [Google Scholar] [CrossRef] [PubMed]
- Russell, S.J.; Schifter, D.; Bastable, V. Developing Algebraic Thinking in the Context of Arithmetic. In Early Algebraization. Advances in Mathematics Education; Cai, J., Knuth, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 43–69. [Google Scholar]
- Ferrara, F.; Sinclair, N. An early algebra approach to pattern generalisation: Actualising the virtual through words, gestures and toilet paper. Educ. Stud. Math. 2016, 92, 1–19. [Google Scholar] [CrossRef]




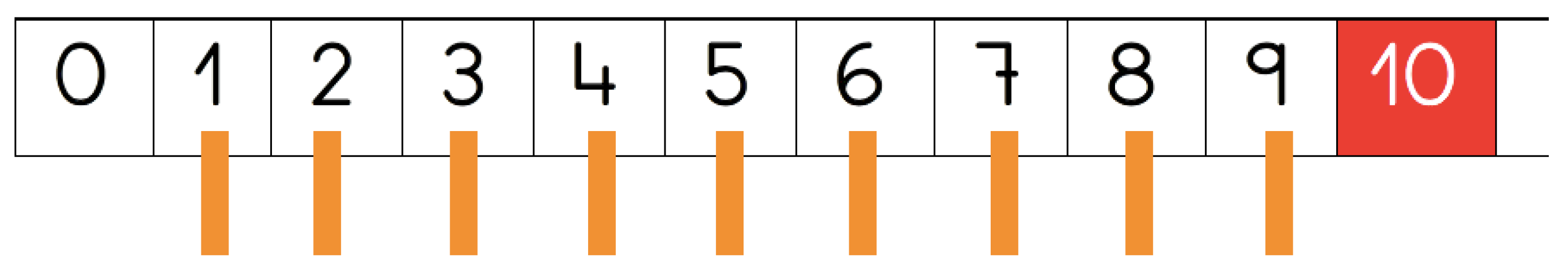



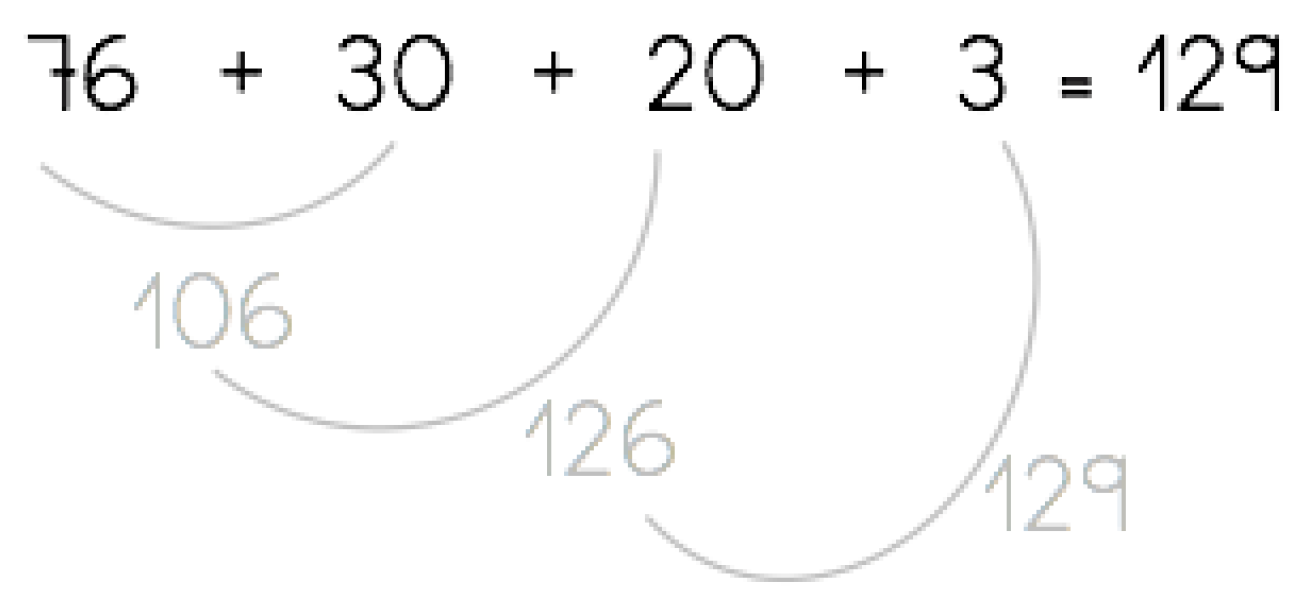















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamuz-Povedano, N.; Fernández-Ahumada, E.; García-Pérez, M.T.; Montejo-Gámez, J. Developing Number Sense: An Approach to Initiate Algebraic Thinking in Primary Education. Mathematics 2021, 9, 518. https://doi.org/10.3390/math9050518
Adamuz-Povedano N, Fernández-Ahumada E, García-Pérez MT, Montejo-Gámez J. Developing Number Sense: An Approach to Initiate Algebraic Thinking in Primary Education. Mathematics. 2021; 9(5):518. https://doi.org/10.3390/math9050518
Chicago/Turabian StyleAdamuz-Povedano, Natividad, Elvira Fernández-Ahumada, M. Teresa García-Pérez, and Jesús Montejo-Gámez. 2021. "Developing Number Sense: An Approach to Initiate Algebraic Thinking in Primary Education" Mathematics 9, no. 5: 518. https://doi.org/10.3390/math9050518
APA StyleAdamuz-Povedano, N., Fernández-Ahumada, E., García-Pérez, M. T., & Montejo-Gámez, J. (2021). Developing Number Sense: An Approach to Initiate Algebraic Thinking in Primary Education. Mathematics, 9(5), 518. https://doi.org/10.3390/math9050518





